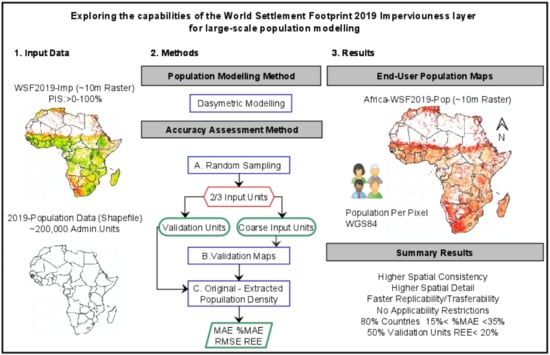
High-Resolution Gridded Population Datasets: Exploring the Capabilities of the World Settlement Footprint 2019 Imperviousness Layer for the African Continent
Abstract
:1. Introduction
2. Materials and Methods
2.1. WSF2019-Imperviousness Layer
2.2. Subnational 2019 Population Data
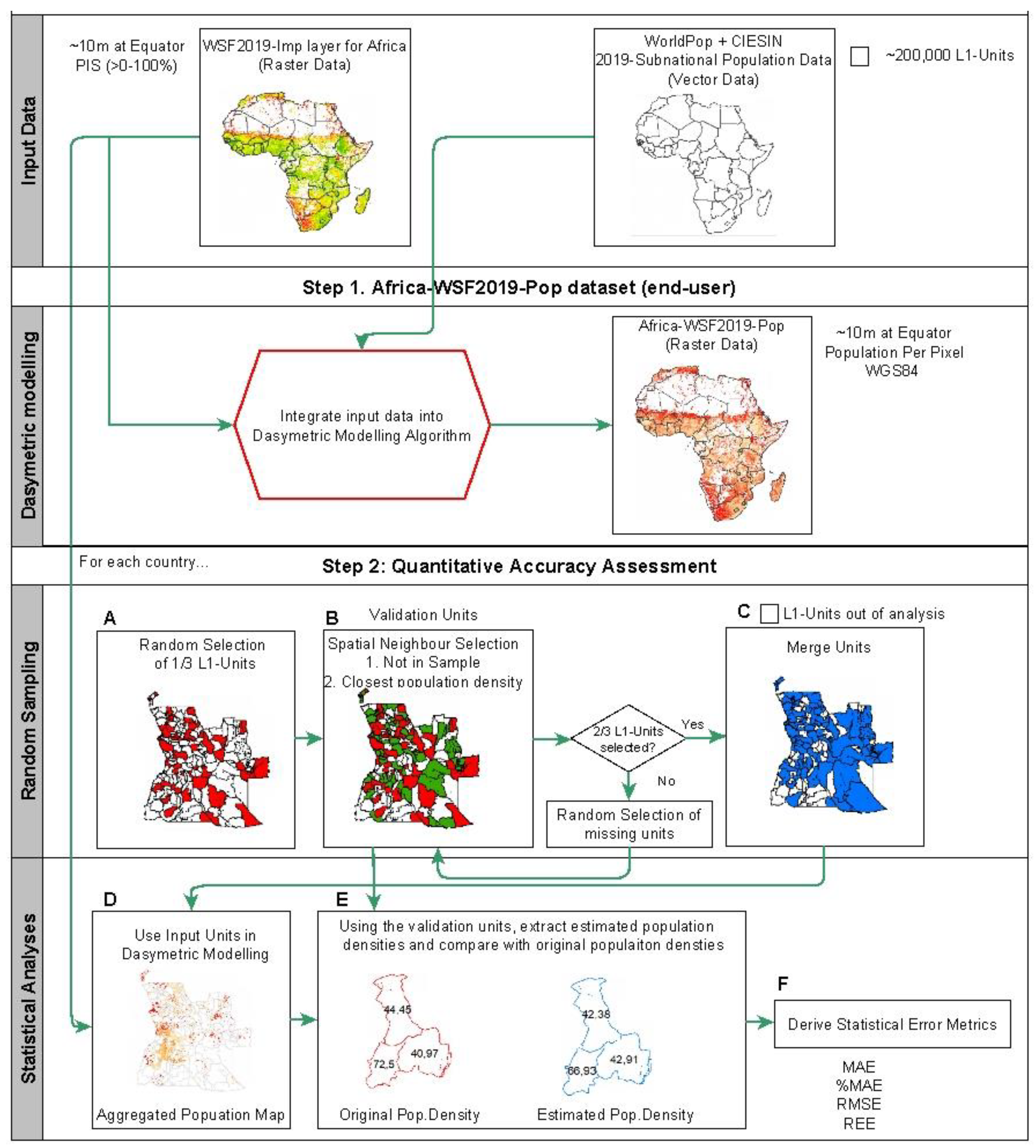
2.3. Dasymetric Modelling Approach
2.4. Quantitative Accuracy Assessment
2.4.1. Random Sampling
2.4.2. Statistical Analyses
3. Results
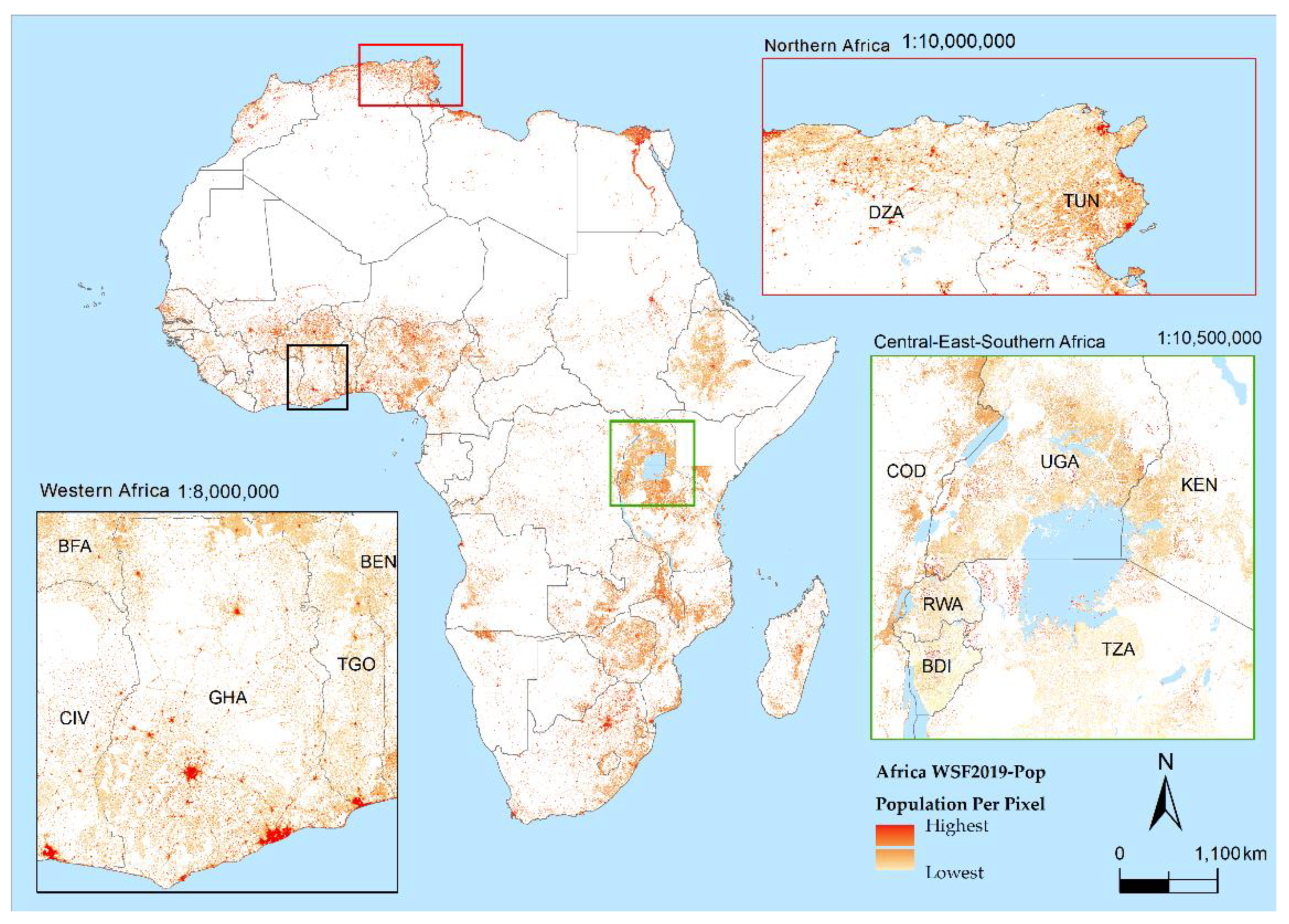
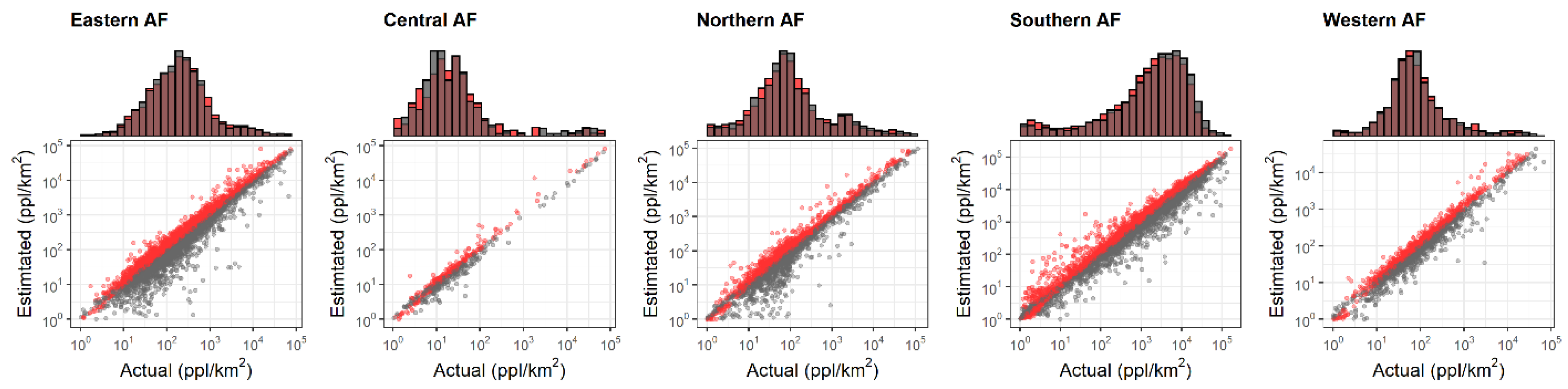
3.1. Africa —WSF2019-Pop Dataset
3.2. Quantitative Accuracy Assessment
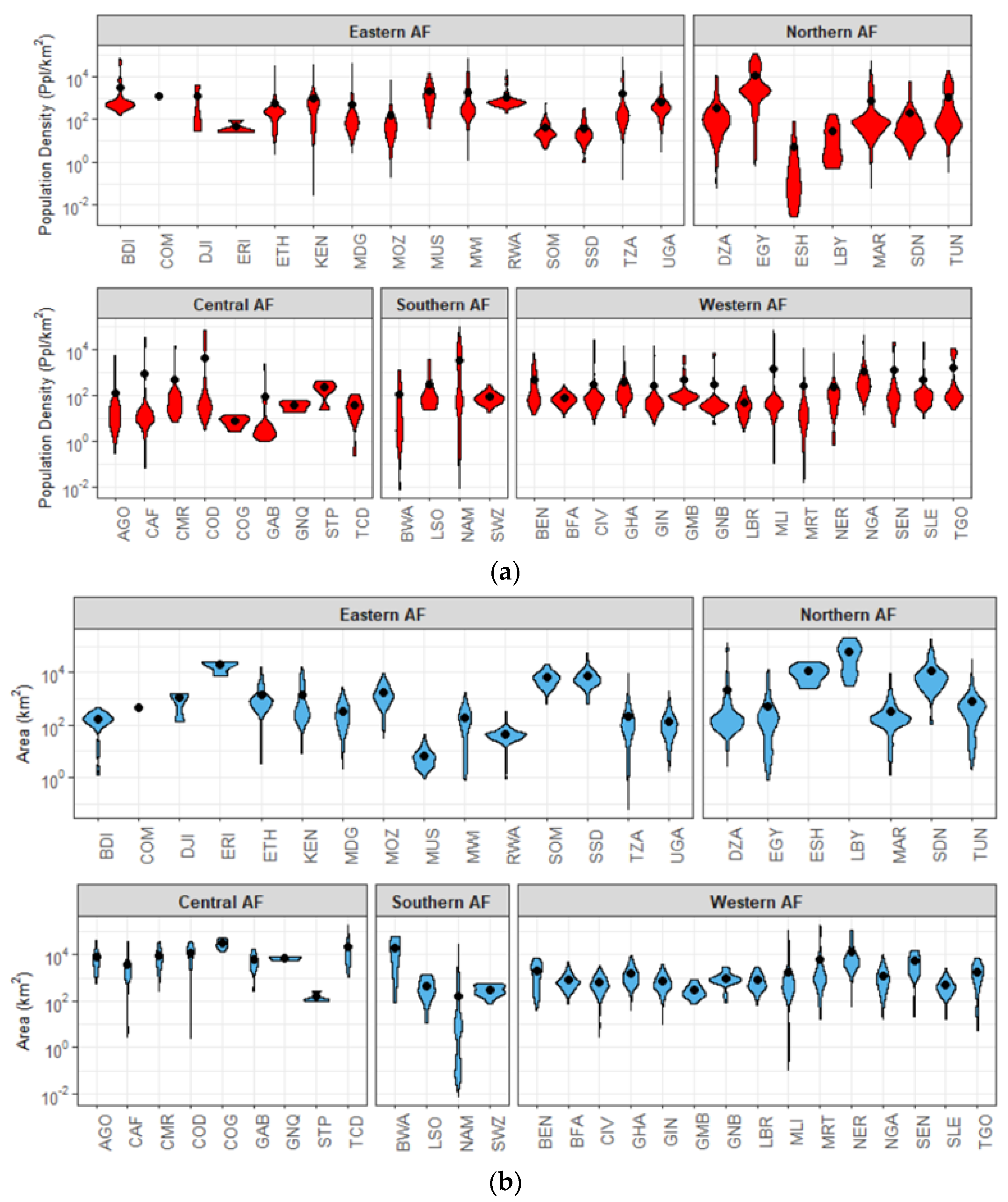
3.2.1. Random Sampling—Validation Unit Description
3.2.2. Statistical Analyses
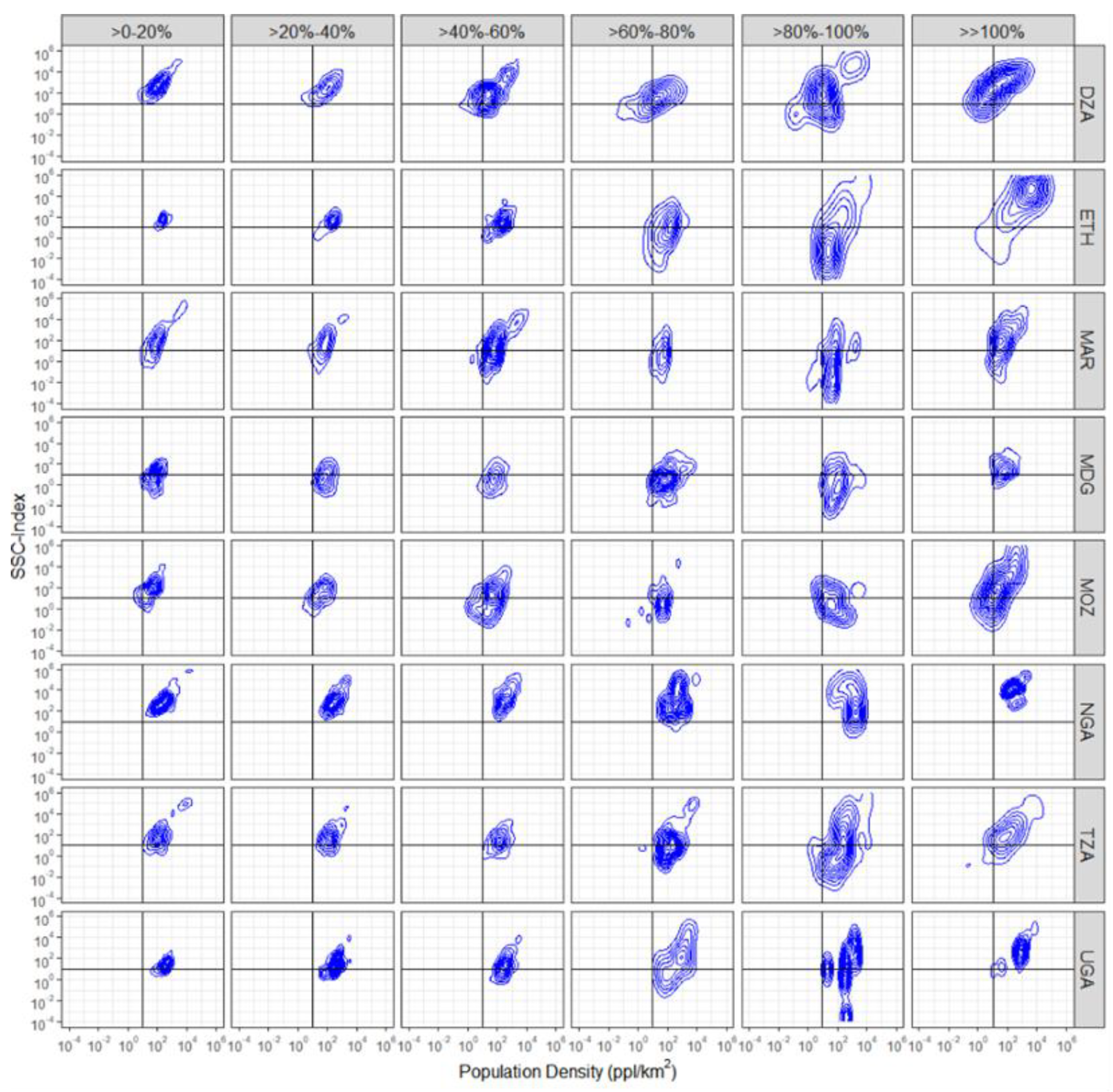
- For all countries, the majority of the validation units with REE between >0% and 40% are located in units with moderately high population densities and moderately high SSC-Index values (top-right quadrant);
- Errors tend to increase as the population density increases and the SSC-Index decreases (shift towards the bottom-right quadrant);
- Large errors (>100%) tend to be located in validation units with extremely high population density and extremely high SSC-Index values;
- Most of the validation units with low population densities and low SSC-Index generally fall within error ranges of REE > 60%.
4. Discussion
4.1. WSF2019-Pop Dataset: Qualitative Assessment
4.2. WSF2019-Pop Dataset: Quantitative Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. The future we want. In Proceedings of the Rio+20 United Nations Conference on Sustainable Development, Rio de Janeiro, Brazil, 20–22 June 2012. [Google Scholar]
- United Nations. Strengthening the Demographic Evidence Base for the Post-2015 Development Agenda. A Concise Report; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2016. [Google Scholar]
- Anderson, K.; Ryan, B.; Sonntag, W.; Kavvada, A.; Friedl, L. Earth observation in service of the 2030 Agenda for Sustainable Development. Geo-Spat. Inf. Sci. 2017, 20, 77–96. [Google Scholar] [CrossRef]
- Kavvada, A.; Metternicht, G.; Kerblat, F.; Mudau, N.; Haldorson, M.; Laldaparsad, S.; Friedl, L.; Held, A.; Chuvieco, E. Towards delivering on the sustainable development goals using earth observations. Remote Sens. Environ. 2020, 247, 111930. [Google Scholar] [CrossRef]
- Andries, A.; Morse, S.; Murphy, R.; Lynch, J.; Woolliams, E.; Fonweban, J. Translation of Earth observation data into sustainable development indicators: An analytical framework. Sustain. Dev. 2019, 27, 366–376. [Google Scholar] [CrossRef] [Green Version]
- Craglia, M.; Pogorzelska, K. The Economic Value of Digital Earth. In Manual of Digital Earth; Guo, H., Goodchild, M.F., Annoni, A., Eds.; Springer: Singapore, 2019; pp. 623–643. [Google Scholar]
- Kuffer, M.; Thomson, D.R.; Boo, G.; Mahabir, R.; Grippa, T.; Van Huysse, S.; Engstrom, R.; Ndugwa, R.; Makau, J.; Darin, E.; et al. The Role of Earth Observation in an Integrated Deprived Area Mapping “System” for Low-to-Middle Income Countries. Remote Sens. 2020, 12, 982. [Google Scholar] [CrossRef] [Green Version]
- Ansari, R.A.; Buddhiraju, K.M. Textural segmentation of remotely sensed images using multiresolution analysis for slum area identification. Eur. J. Remote Sens. 2019, 52, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Aguirre, M.S. Sustainable development: Why the focus on population? Int. J. Soc. Econ. 2002, 29, 923–945. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhao, X.; Fan, D.; Li, S. Geospatial Disaggregation of Population Data in Supporting SDG Assessments: A Case Study from Deqing County, China. ISPRS Int. J. Geo-Inf. 2019, 8, 356. [Google Scholar] [CrossRef] [Green Version]
- Galway, L.; Bell, N.; Sae, A.S.; Hagopian, A.; Burnham, G.; Flaxman, A.; Weiss, W.M.; Rajaratnam, J.; Takaro, T.K. A two-stage cluster sampling method using gridded population data, a GIS, and Google EarthTM imagery in a population-based mortality survey in Iraq. Int. J. Health Geogr. 2012, 11, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fries, B.; Smith, D.L.; Wu, S.; Dolgert, A.J.; Guerra, C.A.; Hay, S.I.; García, G.A.; Smith, J.M.; Oyono, J.N.M.; Donfack, O.T. Measuring the accuracy of gridded human population density surfaces: A case study in Bioko Island, Equatorial Guinea. bioRxiv 2020. [Google Scholar] [CrossRef]
- Hay, S.I.; Noor, A.M.; Nelson, A.; Tatem, A.J. The accuracy of human population maps for public health application. Trop. Med. Int. Health 2005, 10, 1073–1086. [Google Scholar] [CrossRef] [PubMed]
- Tatem, A.J.; Campiz, N.; Gething, P.W.; Snow, R.W.; Linard, C. The effects of spatial population dataset choice on estimates of population at risk of disease. Popul. Health Metr. 2011, 9, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linard, C.; Gilbert, M.; Snow, R.W.; Noor, A.M.; Tatem, A.J. Population Distribution, Settlement Patterns and Accessibility across Africa in 2010. PLoS ONE 2012, 7, e31743. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, A.; Bates, P.D.; Wing, O.; Sampson, C.; Quinn, N.; Neal, J. New estimates of flood exposure in developing countries using high-resolution population data. Nat. Commun. 2019, 10, 1814. [Google Scholar] [CrossRef] [Green Version]
- Calka, B.; Da Costa, J.N.; Bielecka, E. Fine scale population density data and its application in risk assessment. Geomat. Nat. Hazards Risk 2017, 8, 1440–1455. [Google Scholar] [CrossRef]
- Zischg, A.P.; Bermúdez, M. Mapping the Sensitivity of Population Exposure to Changes in Flood Magnitude: Prospective Application from Local to Global Scale. Front. Earth Sci. 2020, 8, 390. [Google Scholar] [CrossRef]
- Tuholske, C.; Caylor, K.; Evans, T.; Avery, R. Variability in urban population distributions across Africa. Environ. Res. Lett. 2019, 14, 085009. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, F.; Wang, J.; Cai, W.; Wang, C.; Wang, K. Provincial and gridded population projection for China under shared socioeconomic pathways from 2010 to 2100. Sci. Data 2020, 7, 83. [Google Scholar] [CrossRef] [Green Version]
- Bustos, M.F.A.; Hall, O.; Niedomysl, T.; Ernstson, U. A pixel level evaluation of five multitemporal global gridded population datasets: A case study in Sweden, 1990–2015. Popul. Environ. 2020, 42, 255–277. [Google Scholar] [CrossRef]
- Freire, S.; Schiavina, M.; Florczyk, A.J.; MacManus, K.; Pesaresi, M.; Corbane, C.; Borkovska, O.; Mills, J.; Pistolesi, L.; Squires, J.; et al. Enhanced data and methods for improving open and free global population grids: Putting ‘leaving no one behind’ into practice. Int. J. Digit. Earth 2020, 13, 61–77. [Google Scholar] [CrossRef] [Green Version]
- Tiecke, T.G.; Liu, X.; Zhang, A.; Gros, A.; Li, N.; Yetman, G.; Kilic, T.; Murray, S.; Blankespoor, B.; Prydz, E.B. Mapping the World Population One Building at a Time. arXiv 2017, arXiv:1712.05839. [Google Scholar]
- Stevens, F.F.; Gaughan, A.A.; Linard, C.; Tatem, A.A. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-Sensed and Ancillary Data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef] [Green Version]
- Doxsey-Whitfield, E.; MacManus, K.; Adamo, S.B.; Pistolesi, L.; Squires, J.; Borkovska, O.; Baptista, S.R. Taking Advantage of the Improved Availability of Census Data: A First Look at the Gridded Population of the World, Version 4. Pap. Appl. Geogr. 2015, 1, 226–234. [Google Scholar] [CrossRef]
- Freire, S.; Doxsey-Whitfield, E.; MacManus, K.; Mills, J.; Pesaresi, M. Development of new open and free multi-temporal global population grids at 250 m resolution. In Proceedings of the 19th AGILE Conference on Geographic Information Science, Helsinki, Finland, 14–17 June 2016. [Google Scholar]
- Balk, D.; Deichmann, U.; Yetman, G.; Pozzi, F.; Hay, S.; Nelson, A. Determining Global Population Distribution: Methods, Applications and Data. Adv. Parasitol. 2006, 62, 119–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhaduri, B.; Bright, E.; Coleman, P.; Urban, M.L. LandScan USA: A high-resolution geospatial and temporal modeling approach for population distribution and dynamics. GeoJournal 2007, 69, 103–117. [Google Scholar] [CrossRef]
- Dobson, J.E.; Bright, E.A.; Coleman, P.R.; Durfee, R.C.; Worley, B.A. LandScan: A global population database for estimating populations at risk. Photogramm. Eng. Remote Sens. 2000, 66, 849–857. [Google Scholar] [CrossRef]
- Mennis, J. Generating surface models of population using dasymetric mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Leyk, S.; Gaughan, A.E.; Adamo, S.B.; De Sherbinin, A.; Balk, D.; Freire, S.; Rose, A.; Stevens, F.R.; Blankespoor, B.; Frye, C.; et al. The spatial allocation of population: A review of large-scale gridded population data products and their fitness for use. Earth Syst. Sci. Data 2019, 11, 1385–1409. [Google Scholar] [CrossRef] [Green Version]
- Palacios-Lopez, D.; Bachofer, F.; Esch, T.; Heldens, W.; Hirner, A.; Marconcini, M.; Sorichetta, A.; Zeidler, J.; Kuenzer, C.; Dech, S.; et al. New Perspectives for Mapping Global Population Distribution Using World Settlement Footprint Products. Sustain. J. Rec. 2019, 11, 6056. [Google Scholar] [CrossRef] [Green Version]
- Maxar Technologies. Building Footprints. Available online: https://www.maxar.com/products/building-footprints (accessed on 6 January 2021).
- WorldPop. Gridded Maps of building patterns through sub-Saharan Africa (Version 1). 2020. Available online: https://doi.org//10.5258/SOTON/WP00677 (accessed on 15 December 2020).
- Population Counts/Contrain Individual Countries 2020 (100 m). Available online: https://www.worldpop.org/geodata/listing?id=78 (accessed on 1 January 2020).
- Nieves, J.J.; Sorichetta, A.; Linard, C.; Bondarenko, M.; Steele, J.E.; Stevens, F.R.; Gaughan, A.E.; Carioli, A.; Clarke, D.J.; Esch, T.; et al. Annually modelling built-settlements between remotely-sensed observations using relative changes in subnational populations and lights at night. Comput. Environ. Urban Syst. 2020, 80, 101444. [Google Scholar] [CrossRef] [PubMed]
- Reed, F.J.; Gaughan, A.E.; Stevens, F.R.; Yetman, G.; Sorichetta, A.; Tatem, A.J. Gridded Population Maps Informed by Different Built Settlement Products. Data 2018, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Esch, T.; Heldens, W.; Hirner, A.; Keil, M.; Marconcini, M.; Roth, A.; Zeidler, J.; Dech, S.; Strano, E. Breaking new ground in mapping human settlements from space—The Global Urban Footprint. ISPRS J. Photogramm. Remote Sens. 2017, 134, 30–42. [Google Scholar] [CrossRef] [Green Version]
- Esch, T.; Bachofer, F.; Heldens, W.; Hirner, A.; Marconcini, M.; Palacios-Lopez, D.; Roth, A.; Üreyen, S.; Zeidler, J.; Dech, S.; et al. Where We Live—A Summary of the Achievements and Planned Evolution of the Global Urban Footprint. Remote Sens. 2018, 10, 895. [Google Scholar] [CrossRef] [Green Version]
- Connecting the World with Better Maps. Available online: https://engineering.fb.com/2016/02/21/core-data/connecting-the-world-with-better-maps/ (accessed on 15 October 2020).
- Pesaresi, M.; Ehrlich, D.; Ferri, S.; Florczyk, A.; Freire, S.; Halkia, M.; Julea, A.; Kemper, T.; Soille, P.; Syrris, V. Operating procedure for the production of the Global Human Settlement Layer from Landsat data of the epochs 1975, 1990, 2000, and 2014. Publ. Off. Eur. Union 2016. [Google Scholar] [CrossRef]
- Pesaresi, M.; Huadong, G.; Blaes, X.; Ehrlich, D.; Ferri, S.; Gueguen, L.; Halkia, M.; Kauffmann, M.; Kemper, T.; Luigi, Z.; et al. A Global Human Settlement Layer from Optical HR/VHR RS Data: Concept and First Results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2102–2131. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Nieves, J.J.; King, A.; Sorichetta, A.; Linard, C.; Tatem, A.J. Comparisons of two global built area land cover datasets in methods to disaggregate human population in eleven countries from the global South. Int. J. Digit. Earth 2019, 13, 78–100. [Google Scholar] [CrossRef]
- Marconcini, M.; Metz-Marconcini, A.; Üreyen, S.; Palacios-Lopez, D.; Hanke, W.; Bachofer, F.; Zeidler, J.; Esch, T.; Gorelick, N.; Kakarla, A. Outlining where humans live—The World Settlement Footprint 2015. Sci. Data 2019. [Google Scholar] [CrossRef]
- Marconcini, M.; Metz-Marconcini, A.; Zeidler, J.; Esch, T. Urban Monitoring in Support of Sustainable Cities; 2015 Joint Urban Remote Sensisn Event (JURSE): Piscataway, NJ, USA, 2015. [Google Scholar]
- Azar, D.; Graesser, J.; Engstrom, R.; Comenetz, J.; Leddy, R.M., Jr.; Schechtman, N.G.; Andrews, T. Spatial refinement of census population distribution using remotely sensed estimates of impervious surfaces in Haiti. Int. J. Remote Sens. 2010, 31, 5635–5655. [Google Scholar] [CrossRef]
- Nieves, J.J.; Stevens, F.R.; Gaughan, A.E.; Linard, C.; Sorichetta, A.; Hornby, G.; Patel, N.N.; Tatem, A.J. Examining the correlates and drivers of human population distributions across low- and middle-income countries. J. R. Soc. Interface 2017, 14, 20170401. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Weng, Q.; Li, G. Residential population estimation using a remote sensing derived impervious surface approach. Int. J. Remote Sens. 2006, 27, 3553–3570. [Google Scholar] [CrossRef]
- Lloyd, C.T.; Chamberlain, H.; Kerr, D.; Yetman, G.; Pistolesi, L.; Stevens, F.R.; Gaughan, A.E.; Nieves, J.J.; Hornby, G.; MacManus, K.; et al. Global spatio-temporally harmonised datasets for producing high-resolution gridded population distribution datasets. Big Earth Data 2019, 3, 108–139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Center of International Earth Science Information Network (CIESIN). Documentation for the Gridded Population of the World (GPWv4.0) (Version 4); CIESIN: Palisades, NY, USA, 2015. [Google Scholar] [CrossRef]
- Kenya National Bureau of Statistics. Sub-County Boundaries; Office of General Director: Nairobi, Kenya, 2020. [Google Scholar]
- Kenya National Bureau of Statistics. Population and Housing Census 2019: Table: Census Volume 1 Question 1 Population by County and Subcounty. 2019. Available online: https://www.knbs.or.ke/?wpdmpro=2019-kenya-population-and-housing-census-volume-i-population-by-county-and-sub-county (accessed on 15 November 2020).
- Humanitarian Data Exchange. Malawi Traditional Authority. 2018. Available online: https://data.humdata.org/dataset/2018_malawi_ta_dataset-updated-admin3 (accessed on 15 November 2020).
- Malawi National Statistical Office. Population and Housing Census 2018, Series A Population Table (Series A). 2018. Available online: http://www.nsomalawi.mw/images/stories/data_on_line/demography/census_2018/2018%20MPHC%20Published%20Tables/Series%20A.%20Population%20Tables.xlsx (accessed on 15 November 2020).
- United Nations Statistics Division.Standard Country or Area Codes for Statistical Use (M49). 2020. Available online: https://unstats.un.org/unsd/methodology/m49/ (accessed on 23 September 2020).
- Calka, B.; Bielecka, E. GHS-POP Accuracy Assessment: Poland and Portugal Case Study. Remote Sens. 2020, 12, 1105. [Google Scholar] [CrossRef] [Green Version]
- Calka, B.; Bielecka, E. Reliability Analysis of LandScan Gridded Population Data. The Case Study of Poland. ISPRS Int. J. Geo-Inf. 2019, 8, 222. [Google Scholar] [CrossRef] [Green Version]
- Sinha, P.; Gaughan, A.E.; Stevens, F.R.; Nieves, J.J.; Sorichetta, A.; Tatem, A.J. Assessing the spatial sensitivity of a random forest model: Application in gridded population modeling. Comput. Environ. Urban Syst. 2019, 75, 132–145. [Google Scholar] [CrossRef]
- Ottensmann, J.R.M. On Population-Weighted Density. SSRN Electron. J. 2018. [Google Scholar] [CrossRef] [Green Version]
- Vandeput, N. Forecasting KPIs: RMSE, MAE, MAPE & Bias. Available online: https://towardsdatascience.com/forecast-kpi-rmse-mae-mape-bias-cdc5703d242d (accessed on 19 October 2020).
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Da Costa, J.N.; Bielecka, E.; Calka, B. Uncertainty Quantification of the Global Rural-Urban Mapping Project over Polish Census Data. In Proceedings of the “Environmental Engineering” 10th International Conference, Vilnius, Lithuania, 27–28 April 2017. [Google Scholar]
- Minitab LLC.Interpret the Key Results for Contour Plot. 2021. Available online: https://support.minitab.com/en-us/minitab/20/help-and-how-to/graphs/contour-plot/key-results/ (accessed on 8 February 2021).
- Lu, Z.; Im, J.; Rhee, J.; Hodgson, M. Building type classification using spatial and landscape attributes derived from LiDAR remote sensing data. Landsc. Urban Plan. 2014, 130, 134–148. [Google Scholar] [CrossRef]
- Xie, J.; Zhou, J. Classification of Urban Building Type from High Spatial Resolution Remote Sensing Imagery Using Extended MRS and Soft BP Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3515–3528. [Google Scholar] [CrossRef]
- Sturrock, H.J.W.; Woolheater, K.; Bennett, A.F.; Andrade-Pacheco, R.; Midekisa, A. Predicting residential structures from open source remotely enumerated data using machine learning. PLoS ONE 2018, 13, e0204399. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, C.T.; Sturrock, H.J.W.; Leasure, D.R.; Jochem, W.C.; Lázár, A.N.; Tatem, A.J. Using GIS and Machine Learning to Classify Residential Status of Urban Buildings in Low and Middle Income Settings. Remote Sens. 2020, 12, 3847. [Google Scholar] [CrossRef]
- Bai, Z.; Wang, J.; Wang, M.; Gao, M.; Sun, J. Accuracy assessment of multi-source gridded population distribution datasets in China. Sustainability 2018, 10, 1363. [Google Scholar] [CrossRef] [Green Version]
- Duque, J.C.; Laniado, H.; Polo, A. S-maup: Statistical test to measure the sensitivity to the modifiable areal unit problem. PLoS ONE 2018, 13, e0207377. [Google Scholar] [CrossRef] [PubMed]
- Sorichetta, A.; Hornby, G.M.; Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. High-resolution gridded population datasets for Latin America and the Caribbean in 2010, 2015, and 2020. Sci. Data 2015, 2, 150045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esch, T.; Zeidler, J.; Palacios-Lopez, D.; Marconcini, M.; Roth, A.; Mönks, M.; Leutner, B.; Brzoska, E.; Metz-Marconcini, A.; Bachofer, F.; et al. Towards a Large-Scale 3D Modeling of the Built Environment—Joint Analysis of TanDEM-X, Sentinel-2 and Open Street Map Data. Remote Sens. 2020, 12, 2391. [Google Scholar] [CrossRef]
- GFDRR. ThinkHazard! (Version 1). 2007. Available online: https://thinkhazard.org/en/ (accessed on 10 February 2021).




| Eastern Africa | |||||||||
| ISO | Year | 2019-UNPop | L1-U | ASR | ISO | Year | 2019-UNPop | L1-U | ASR |
| BDI | 2008 | 11,530,577 | 66 | 13 | MWI | 2019 | 18,628,749 | 73 | 14 |
| COM | 2013 | 850,891 | 93 | 21 | RWA | 2012 | 12,626,938 | 67 | 7 |
| DJI | 2009 | 973,557 | 77 | 52 | SOM | 2005 | 15,442,906 | 68 | 78 |
| ERI | 2012 | 3,497,117 | 82 | 127 | SSD | 2008 | 11,062,114 | 69 | 83 |
| ETH | 2007 | 112,078,727 | 67 | 35 | TZA | 2012 | 58,005,461 | 67 | 14 |
| KEN | 2019 | 52,573,967 | 68 | 36 | UGA | 2014 | 44,269,587 | 70 | 11 |
| MDG | 2010 | 26,969,306 | 69 | 19 | ZMB | 2010 | 17,861,034 | 69 | 67 |
| MOZ | 2007 | 30,366,043 | 65 | 40 | ZWE | 2012 | 14,645,473 | 80 | 63 |
| MUS | 2011 | 1,269,670 | 55 | 3 | |||||
| Central Africa | |||||||||
| ISO | Year | 2019-UNPop | L1-U | ASR | ISO | Year | 2019-UNPop | L1-U | ASR |
| AGO | 2014 | 31,825,299 | 161 | 87 | GAB | 2003 | 2,172,578 | 48 | 73 |
| CAF | 2012 | 4,745,179 | 174 | 58 | GNQ | 2014 | 1,920,917 | 39 | 29 |
| CMR | 2005 | 25,876,387 | 58 | 89 | STP | 2012 | 215,048 | 7 | 12 |
| COD | 2008 | 86,790,568 | 188 | 106 | TCD | 2009 | 15,946,882 | 62 | 142 |
| COG | 2007 | 5,380,504 | 12 | 166 | |||||
| Northern Africa | Southern Africa | ||||||||
| ISO | Year | 2019-UNPop | L1-U | ASR | ISO | Year | 2019-UNPop | L1-U | ASR |
| DZA | 2008 | 43,053,054 | 1540 | 41 | BWA | 2011 | 2,303,703 | 29 | 141 |
| EGY | 2006 | 100,388,076 | 385 | 49 | LSO | 2006 | 2,125,267 | 80 | 20 |
| ESH | 2014 | 582,455 | 27 | 103 | NAM | 2011 | 2,494,524 | 5473 | 12 |
| LBY | 2006 | 6,777,453 | 22 | 280 | SWZ | 2007 | 1,148,133 | 55 | 17 |
| MAR | 2014 | 36,471,766 | 1657 | 17 | ZAF | 2011 | 58,558,267 | 4 | |
| SDN | 2008 | 42,813,237 | 130 | 114 | |||||
| TUN | 2014 | 11,694,721 | 270 | 26 | |||||
| Western Africa | |||||||||
| ISO | Year | 2019-UNPop | L1-U | ASR | ISO | Year | 2019-UNPop | L1-U | ASR |
| BEN | 2013 | 11,801,151 | 77 | 39 | MLI | 2009 | 19,658,023 | 765 | 38 |
| BFA | 2006 | 20,321,383 | 351 | 28 | MRT | 2013 | 4,525,698 | 218 | 71 |
| CIV | 2014 | 25,716,554 | 519 | 25 | NER | 2012 | 23,310,719 | 66 | 127 |
| GHA | 2010 | 30,417,858 | 170 | 37 | NGA | 2006 | 200,963,603 | 774 | 34 |
| GIN | 2014 | 12,771,246 | 340 | 27 | SEN | 2013 | 16,296,362 | 45 | 66 |
| GMB | 2010 | 2,347,696 | 40 | 16 | SLE | 2004 | 7,813,207 | 160 | 21 |
| GNB | 2009 | 1,920,917 | 39 | 29 | TGO | 2010 | 8,082,359 | 40 | 38 |
| LBR | 2008 | 4,937,374 | 136 | 27 | |||||
| Eastern Africa | |||||||
| ISO | n | %Pop | %Area | ISO | n | %Pop | %Area |
| BDI | 86 | 67.43 | 64.84 | MWI | 283 | 67.46 | 67.66 |
| COM | 2 | 92.51 | 74.32 | RWA | 277 | 66.39 | 61.97 |
| DJI | 3 | 70.30 | 20.14 | SOM | 50 | 57.57 | 72.94 |
| ERI | 4 | 82.12 | 81.48 | SSD | 51 | 66.51 | 71.01 |
| ETH | 490 | 68.42 | 76.15 | TZA | 2428 | 64.29 | 70.85 |
| KEN | 229 | 63.50 | 71.34 | UGA | 918 | 68.88 | 74.57 |
| MDG | 828 | 68.70 | 67.05 | ZMB | 99 | 62.65 | 66.01 |
| MOZ | 275 | 62.54 | 71.95 | ZWE | 59 | 72.38 | 82.04 |
| MUS | 105 | 68.07 | 64.78 | ||||
| Central Africa | |||||||
| ISO | n | %Pop | %Area | ISO | n | %Pop | %Area |
| AGO | 108 | 55.79 | 72.15 | GAB | 31 | 76.64 | 72.99 |
| CAF | 115 | 71.90 | 72.34 | GNQ | 3 | 57.15 | 79.77 |
| CMR | 37 | 56.16 | 71.30 | STP | 4 | 48.01 | 60.36 |
| COD | 120 | 60.24 | 67.35 | TCD | 41 | 64.89 | 69.39 |
| COG | 7 | 25.62 | 66.64 | ||||
| Northern Africa | Southern Africa | ||||||
| ISO | n | %Pop | %Area | ISO | n | %Pop | %Area |
| DZA | 1026 | 60.40 | 81.71 | BWA | 17 | 77.81 | 61.66 |
| EGY | 225 | 70.70 | 13.14 | LSO | 53 | 65.61 | 76.83 |
| ESH | 16 | 73.94 | 62.85 | NAM | 3645 | 67.27 | 72.71 |
| LBY | 13 | 65.01 | 58.99 | SWZ | 35 | 63.95 | 67.39 |
| MAR | 1072 | 64.82 | 74.57 | ZAF | 68.16 | 76.45 | |
| SDN | 85 | 68.41 | 62.40 | ||||
| TUN | 176 | 67.13 | 76.69 | ||||
| Western Africa | |||||||
| ISO | n | %Pop | %Area | ISO | n | %Pop | %Area |
| BEN | 51 | 70.29 | 86.78 | MLI | 507 | 60.98 | 77.50 |
| BFA | 233 | 55.40 | 68.76 | MRT | 143 | 62.12 | 86.23 |
| CIV | 344 | 65.74 | 70.21 | NER | 44 | 70.28 | 55.12 |
| GHA | 113 | 60.45 | 75.22 | NGA | 515 | 65.33 | 68.31 |
| GIN | 226 | 67.46 | 68.79 | SEN | 29 | 58.33 | 78.74 |
| GMB | 25 | 80.82 | 70.63 | SLE | 106 | 66.34 | 72.30 |
| GNB | 26 | 75.88 | 76.50 | TGO | 25 | 70.76 | 76.84 |
| LBR | 89 | 46.35 | 74.22 | ||||
| Eastern Africa | |||||||||||
| ISO | n | %MAE | MAE | RMSE | ISO | n | %MAE | MAE | RMSE | ||
| BDI | 86 | 549.84 | 24.95 | 137.18 | 480.58 | MWI | 283 | 230.43 | 15.86 | 36.54 | 358.53 |
| COM | 2 | 837.55 | 72.23 | 604.96 | 788.36 | RWA | 277 | 672.72 | 18.47 | 124.23 | 237.25 |
| DJI | 3 | 208.99 | 17.36 | 36.28 | 77.82 | SOM | 50 | 27.31 | 35.14 | 9.60 | 27.68 |
| ERI | 4 | 36.18 | 25.50 | 9.23 | 10.26 | SSD | 51 | 19.05 | 62.82 | 11.97 | 24.79 |
| ETH | 490 | 114.34 | 26.12 | 29.87 | 155.43 | TZA | 2428 | 71.92 | 20.55 | 14.78 | 95.83 |
| KEN | 229 | 101.59 | 20.98 | 21.32 | 153.76 | UGA | 918 | 234.38 | 17.07 | 40.01 | 120.36 |
| MDG | 828 | 64.28 | 43.49 | 27.96 | 226.80 | ZMB | 99 | 25.13 | 17.98 | 4.52 | 28.23 |
| MOZ | 275 | 39.80 | 32.10 | 12.78 | 80.92 | ZWE | 59 | 36.30 | 18.88 | 6.85 | 33.05 |
| MUS | 105 | 1236.81 | 15.51 | 191.79 | 450.61 | ||||||
| Central Africa | |||||||||||
| ISO | n | %MAE | MAE | RMSE | ISO | n | %MAE | MAE | RMSE | ||
| AGO | 108 | 20.12 | 16.28 | 3.28 | 32.75 | GAB | 31 | 8.85 | 46.57 | 4.12 | 24.57 |
| CAF | 115 | 8.03 | 21.76 | 1.75 | 16.42 | GNQ | 3 | 36.39 | 22.97 | 8.36 | 8.96 |
| CMR | 37 | 44.54 | 31.03 | 13.82 | 154.31 | STP | 4 | 167.94 | 12.17 | 20.43 | 30.39 |
| COD | 120 | 36.72 | 24.14 | 8.86 | 68.36 | TCD | 41 | 11.89 | 26.19 | 3.11 | 6.96 |
| COG | 7 | 6.29 | 30.34 | 1.91 | 2.49 | ||||||
| Northern Africa | Southern Africa | ||||||||||
| ISO | n | %MAE | MAE | RMSE | ISO | n | %MAE | MAE | RMSE | ||
| DZA | 1026 | 12.13 | 15.75 | 1.91 | 24.44 | BWA | 17 | 5.07 | 38.24 | 1.94 | 16.25 |
| EGY | 225 | 593.57 | 13.96 | 82.86 | 602.45 | LSO | 53 | 58.78 | 21.21 | 12.47 | 25.41 |
| ESH | 16 | 2.38 | 6.64 | 0.16 | 0.49 | NAM | 3645 | 2.72 | 22.49 | 0.61 | 22.51 |
| LBY | 13 | 2.00 | 16.49 | 0.33 | 1.35 | SWZ | 35 | 66.11 | 18.89 | 12.49 | 18.45 |
| MAR | 1072 | 65.41 | 31.07 | 20.32 | 166.31 | ZAF | 41.41 | 16.72 | 6.92 | 119.90 | |
| SDN | 85 | 27.96 | 27.40 | 7.66 | 19.13 | ||||||
| TUN | 176 | 55.43 | 16.00 | 8.87 | 63.06 | ||||||
| Western Africa | |||||||||||
| ISO | n | Pop.D | %MAE | MAE | RMSE | ISO | n | Pop.D | %MAE | MAE | RMSE |
| BEN | 51 | 81.40 | 14.74 | 12.00 | 73.62 | MLI | 507 | 13.95 | 18.45 | 2.57 | 59.47 |
| BFA | 233 | 58.05 | 19.19 | 11.14 | 17.85 | MRT | 143 | 2.97 | 31.66 | 0.94 | 26.61 |
| CIV | 344 | 74.58 | 11.67 | 8.70 | 72.79 | NER | 44 | 27.93 | 24.08 | 6.73 | 16.25 |
| GHA | 113 | 103.44 | 21.61 | 22.36 | 103.16 | NGA | 515 | 210.99 | 26.74 | 56.42 | 182.42 |
| GIN | 226 | 51.09 | 28.53 | 14.57 | 150.39 | SEN | 29 | 61.85 | 7.82 | 4.84 | 26.93 |
| GMB | 25 | 255.63 | 8.16 | 20.86 | 66.46 | SLE | 106 | 99.47 | 15.23 | 15.15 | 40.94 |
| GNB | 26 | 57.22 | 15.37 | 8.80 | 33.80 | TGO | 25 | 128.71 | 13.88 | 17.86 | 117.41 |
| LBR | 89 | 32.24 | 24.90 | 8.03 | 14.05 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palacios-Lopez, D.; Bachofer, F.; Esch, T.; Marconcini, M.; MacManus, K.; Sorichetta, A.; Zeidler, J.; Dech, S.; Tatem, A.J.; Reinartz, P. High-Resolution Gridded Population Datasets: Exploring the Capabilities of the World Settlement Footprint 2019 Imperviousness Layer for the African Continent. Remote Sens. 2021, 13, 1142. https://doi.org/10.3390/rs13061142
Palacios-Lopez D, Bachofer F, Esch T, Marconcini M, MacManus K, Sorichetta A, Zeidler J, Dech S, Tatem AJ, Reinartz P. High-Resolution Gridded Population Datasets: Exploring the Capabilities of the World Settlement Footprint 2019 Imperviousness Layer for the African Continent. Remote Sensing. 2021; 13(6):1142. https://doi.org/10.3390/rs13061142
Chicago/Turabian StylePalacios-Lopez, Daniela, Felix Bachofer, Thomas Esch, Mattia Marconcini, Kytt MacManus, Alessandro Sorichetta, Julian Zeidler, Stefan Dech, Andrew J. Tatem, and Peter Reinartz. 2021. "High-Resolution Gridded Population Datasets: Exploring the Capabilities of the World Settlement Footprint 2019 Imperviousness Layer for the African Continent" Remote Sensing 13, no. 6: 1142. https://doi.org/10.3390/rs13061142
APA StylePalacios-Lopez, D., Bachofer, F., Esch, T., Marconcini, M., MacManus, K., Sorichetta, A., Zeidler, J., Dech, S., Tatem, A. J., & Reinartz, P. (2021). High-Resolution Gridded Population Datasets: Exploring the Capabilities of the World Settlement Footprint 2019 Imperviousness Layer for the African Continent. Remote Sensing, 13(6), 1142. https://doi.org/10.3390/rs13061142