Large-Scale Analysis of the Spatiotemporal Changes of Net Ecosystem Production in Hindu Kush Himalayan Region
Abstract
:1. Introduction
2. Materials and Methods
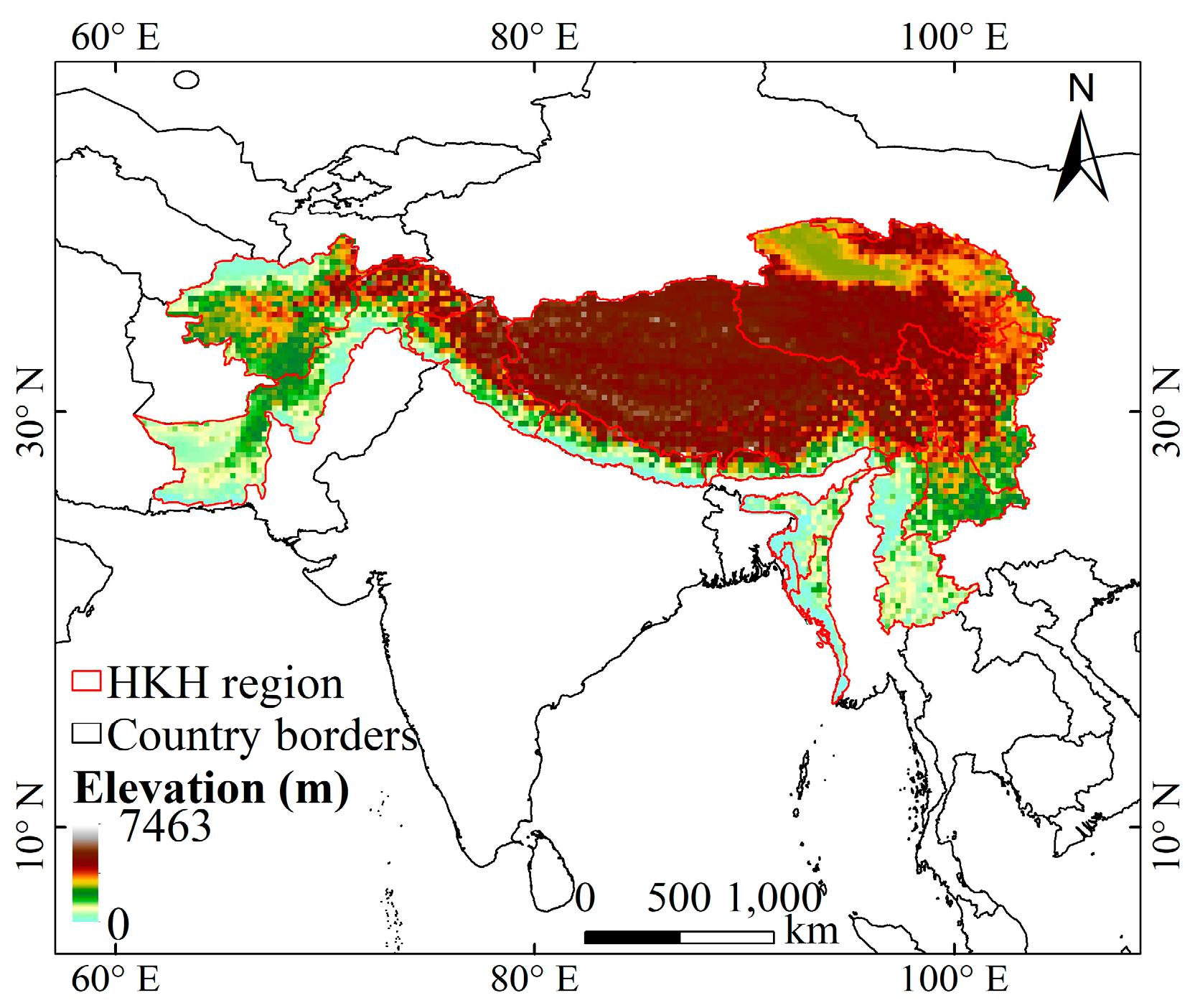
2.1. Study Area
2.2. Normalized Difference Vegetation Index (NDVI)
2.3. Meteorological Elements
2.4. Soil Attribute Data
2.5. Land Cover Type Data
2.6. Net Primary Production (NPP) Estimation Model
2.7. Geostatistical Model of Heterotrophic Respiration
2.8. Trend Analysis of Grassland Net Ecosystem Production (NEP)
2.9. Partial Correlation Analysis
3. Results
3.1. Validation of the NPP and NEP Calculations
3.1.1. Validation of the NPP Values
3.1.2. Reliability Analysis of the NEP Values
3.2. Spatial Characteristics of NPP and NEP
3.2.1. Spatial Characteristics of NPP
3.2.2. Spatial Characteristics of NEP
3.3. Temporal Trend of NPP and NEP
3.3.1. Interannual Variations
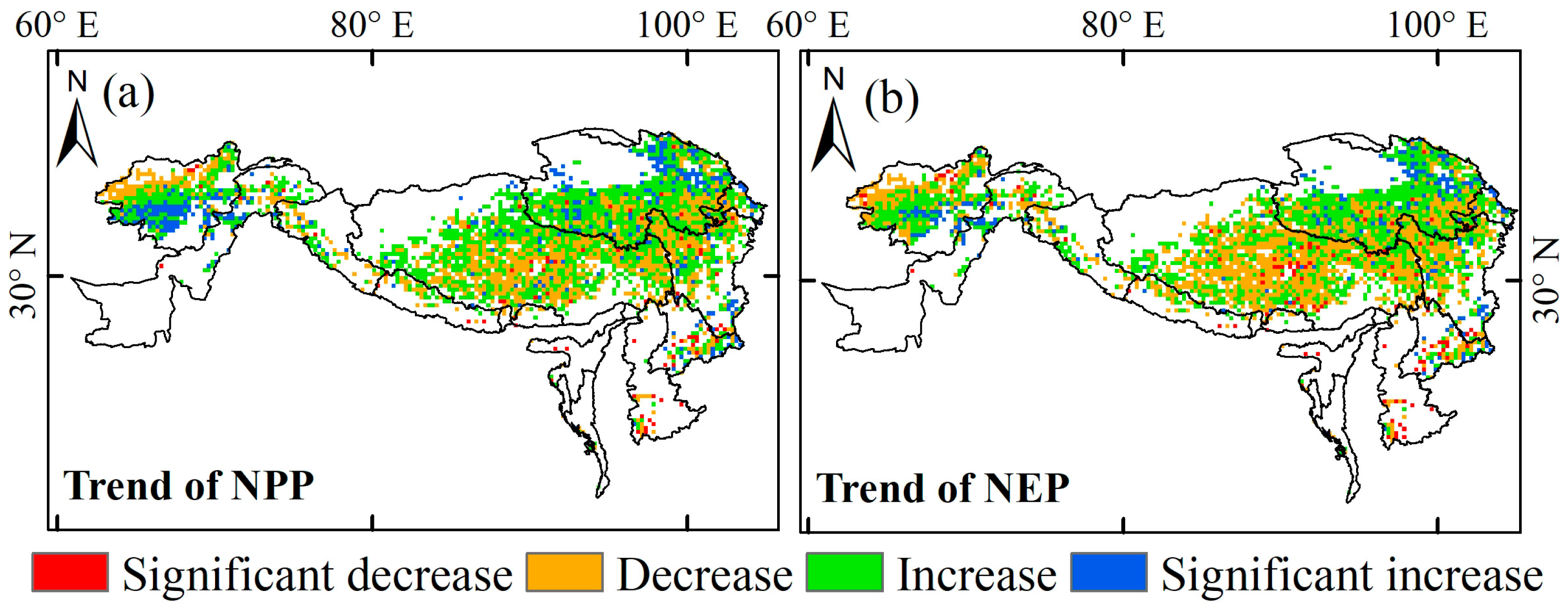
3.3.2. Time Series Change Trend Distribution
3.4. The Impact of Climate on NPP and NEP
3.4.1. The Impact of Climate on NPP
3.4.2. The Impact of Climate on NEP
4. Discussion
4.1. Sources of Uncertainty
4.2. The Potential Effect of the NEP Spatial Distribution
4.3. The Potential Effect of NEP Temporal Change
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peichl, M.; Leahy, P.; Kiely, G. Six-year Stable Annual Uptake of Carbon Dioxide in Intensively Managed Humid Temperate Grassland. Ecosystems 2010, 14, 112–126. [Google Scholar] [CrossRef]
- Jongen, M.; Pereira, J.S.; Aires, L.M.I.; Pio, C.A. The effects of drought and timing of precipitation on the inter-annual variation in ecosystem-atmosphere exchange in a Mediterranean grassland. Agric. For. Meteorol. 2011, 151, 595–606. [Google Scholar] [CrossRef]
- Lei, T.; Feng, J.; Lv, J.; Wang, J.; Song, H.; Song, W.; Gao, X. Net Primary Productivity Loss under different drought levels in different grassland ecosystems. J. Environ. Manag. 2020, 274, 111144. [Google Scholar] [CrossRef] [PubMed]
- Kato, T.; Tang, Y.; Gu, S.; Hirota, M.; Du, M.; Li, Y.; Zhao, X. Temperature and biomass influences on interannual changes in CO2 exchange in an alpine meadow on the Qinghai-Tibetan Plateau. Glob. Chang. Biol. 2006, 12, 1285–1298. [Google Scholar] [CrossRef]
- Smith, P.; Lanigan, G.; Kutsch, W.L.; Buchmann, N.; Eugster, W.; Aubinet, M.; Ceschia, E.; Béziat, P.; Yeluripati, J.B.; Osborne, B.; et al. Measurements necessary for assessing the net ecosystem carbon budget of croplands. Agric. Ecosyst. Environ. 2010, 139, 302–315. [Google Scholar] [CrossRef]
- Scurlock, J.M.O.; Hall, D.O. The global carbon sink: A grassland perspective. Glob. Chang. Biol. 1998, 4, 229–233. [Google Scholar] [CrossRef] [Green Version]
- Suyker, A.E.; Verma, S.B.; Burba, G.G. Interannual variability in net CO2 exchange of a native tallgrass prairie. Glob. Chang. Biol. 2003, 9, 255–265. [Google Scholar] [CrossRef]
- Svejcar, T.; Angell, R.; Bradford, J.A.; Dugas, W.; Emmerich, W.; Frank, A.B.; Gilmanov, T.; Haferkamp, M.; Johnson, D.A.; Mayeux, H.; et al. Carbon Fluxes on North American Rangelands. Rangel. Ecol. Manag. 2008, 61, 465–474. [Google Scholar] [CrossRef]
- Zhang, L.; Wylie, B.K.; Ji, L.; Gilmanov, T.G.; Tieszen, L.L. Climate-Driven Interannual Variability in Net Ecosystem Exchange in the Northern Great Plains Grasslands. Rangel. Ecol. Manag. 2010, 63, 40–50. [Google Scholar] [CrossRef]
- Sun, S.; Che, T.; Li, H.; Wang, T.; Ma, C.; Liu, B.; Wu, Y.; Song, Z. Water and carbon dioxide exchange of an alpine meadow ecosystem in the northeastern Tibetan Plateau is energy-limited. Agric. For. Meteorol. 2019, 275, 283–295. [Google Scholar] [CrossRef]
- Lv, W.; Luo, C.; Zhang, L.; Niu, H.; Zhang, Z.; Wang, S.; Wang, Y.; Jiang, L.; Wang, Y.; He, J.; et al. Net neutral carbon responses to warming and grazing in alpine grassland ecosystems. Agric. For. Meteorol. 2020, 280, 107792. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, Q.; Zhou, J.; Yue, P.; Wang, R.; Wang, S. East Asian summer monsoon substantially affects the inter-annual variation of carbon dioxide exchange in semi-arid grassland ecosystem in Loess Plateau. Agric. Ecosyst. Environ. 2019, 272, 218–229. [Google Scholar] [CrossRef]
- Meyers, T.P. A comparison of summertime water and CO2 fluxes over rangeland for well watered and drought conditions. Agric. For. Meteorol. 2001, 106, 205–214. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, H.; Jia, G.; Wylie, B.; Gilmanov, T.; Howard, D.; Ji, L.; Xiao, J.; Li, J.; Yuan, W.; et al. Net ecosystem productivity of temperate grasslands in northern China: An upscaling study. Agric. For. Meteorol. 2014, 184, 71–81. [Google Scholar] [CrossRef] [Green Version]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef] [Green Version]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Matsunaga, T.; Tan, Z.-H.; Saigusa, N.; Shirai, T.; Tang, Y.; Peng, S.; Fukuda, Y. Global terrestrial carbon fluxes of 1999–2019 estimated by upscaling eddy covariance data with a random forest. Sci. Data 2020, 7, 313. [Google Scholar] [CrossRef]
- Laurin, G.V.; Vittucci, C.; Tramontana, G.; Ferrazzoli, P.; Guerriero, L.; Papale, D. Monitoring tropical forests under a functional perspective with satellite-based vegetation optical depth. Glob. Chang. Biol. 2020, 26, 3402–3416. [Google Scholar] [CrossRef]
- Shang, Z.; Degen, A.A.; Rafiq, M.K.; Squires, V.R. Correction to: Carbon Management for Promoting Local Livelihood in the Hindu Kush Himalayan (HKH) Region; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; p. 1. [Google Scholar]
- Abbas, S.; Qamer, F.M.; Murthy, M.S.R.; Tripathi, N.K.; Ning, W.; Sharma, E.; Ali, G. Grassland Growth in Response to Climate Variability in the Upper Indus Basin, Pakistan. Climate 2015, 3, 697–714. [Google Scholar] [CrossRef]
- Panday, P.K.; Ghimire, B. Time-series analysis of NDVI from AVHRR data over the Hindu Kush–Himalayan region for the period 1982–2006. Int. J. Remote. Sens. 2012, 33, 6710–6721. [Google Scholar] [CrossRef]
- Qamer, F.M.; Xi, C.; Abbas, S.; Murthy, M.S.R.; Ning, W.; Anming, B. An Assessment of Productivity Patterns of Grass-Dominated Rangelands in the Hindu Kush Karakoram Region, Pakistan. Sustain. J. Rec. 2016, 8, 961. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wu, H.; Ding, Y.; Qin, J.; Li, H.; Liu, S.; Zeng, D. Interannual and seasonal variations in carbon exchanges over an alpine meadow in the northeastern edge of the Qinghai-Tibet Plateau, China. PLoS ONE 2020, 15, e0228470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Zhu, D.; Zhan, W.; Chen, H.; Zhu, Q.; Hao, Y.; Liu, W.; He, Y. Five-Year Measurements of Net Ecosystem CO2 Exchange at a Fen in the Zoige Peatlands on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 11803–11818. [Google Scholar] [CrossRef]
- Bin Hao, Y.; Cui, X.Y.; Wang, Y.F.; Mei, X.R.; Kang, X.M.; Wu, N.; Luo, P.; Zhu, D. Predominance of Precipitation and Temperature Controls on Ecosystem CO2 Exchange in Zoige Alpine Wetlands of Southwest China. Wetlands 2011, 31, 413–422. [Google Scholar] [CrossRef]
- Arun, A.; Ritu, V. Natural resource governance at multiple scales in the Hindu Kush Himalaya. ICIMOD Work. Pap. 2017, 4, 69. [Google Scholar]
- Ren, G.-Y.; Shrestha, A.B. Climate change in the Hindu Kush Himalaya. Adv. Clim. Chang. Res. 2017, 8, 137–140. [Google Scholar] [CrossRef]
- Wester, P.; Mishra, A.; Mukherji, A.; Shrestha, A.B. The Hindu Kush Himalaya Assessment: Mountains, Climate Change, Sustainability and People; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Gardelle, J.; Arnaud, Y.; Berthier, E. Contrasted evolution of glacial lakes along the Hindu Kush Himalaya mountain range between 1990 and 2009. Glob. Planet. Chang. 2011, 75, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Bookhagen, B.; Burbank, D.W. Topography, relief, and TRMM-derived rainfall variations along the Himalaya. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Zhao, C.; Wang, X. Elevational differences in the net primary productivity response to climate constraints in a dryland mountain ecosystem of northwestern China. Land Degrad. Dev. 2020, 31, 2087–2103. [Google Scholar] [CrossRef]
- Guo, D.; Song, X.; Hu, R.; Cai, S.; Zhu, X.; Hao, Y. Grassland type-dependent spatiotemporal characteristics of productivity in Inner Mongolia and its response to climate factors. Sci. Total. Environ. 2021, 775, 145644. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747. [Google Scholar] [CrossRef] [Green Version]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Yu, D.; Shi, P.; Shao, H.; Zhu, W.; Pan, Y. Modelling net primary productivity of terrestrial ecosystems in East Asia based on an improved CASA ecosystem model. Int. J. Remote. Sens. 2009, 30, 4851–4866. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Wang, C.; Gower, S.T. A global relationship between the heterotrophic and autotrophic components of soil respiration? Glob. Chang. Biol. 2004, 10, 1756–1766. [Google Scholar] [CrossRef]
- Raich, J.W.; Potter, C.S.; Bhagawati, D. Interannual variability in global soil respiration, 1980–1994. Glob. Chang. Biol. 2002, 8, 800–812. [Google Scholar] [CrossRef]
- Yu, G.; Zheng, Z.; Wang, Q.; Fu, Y.; Zhuang, J.; Sun, X.; Wang, Y. Spatiotemporal Pattern of Soil Respiration of Terrestrial Ecosystems in China: The Development of a Geostatistical Model and Its Simulation. Environ. Sci. Technol. 2010, 44, 6074–6080. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Yang, Z.; Xue, Y.; Shao, X.; Yu, T.; Hou, Q. Spatial analysis of land use change effect on soil organic carbon stocks in the eastern regions of China between 1980 and 2000. Geosci. Front. 2017, 8, 597–603. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Fu, Y.; Hou, Q.; Xia, X.; Yan, B.; Yang, Z. Soil organic carbon increase in semi-arid regions of China from 1980s to 2010s. Appl. Geochem. 2020, 116, 104575. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Myneni, R.B.; Chen, A.; Chevallier, F.; Dolman, A.J.; Janssens, I.A.; Peñuelas, J.; Zhang, G.; et al. Asymmetric effects of daytime and night-time warming on Northern Hemisphere vegetation. Nat. Cell Biol. 2013, 501, 88–92. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, D.H.; Zhao, X.; Liang, S.L.; Zhou, T.; Huang, K.C.; Tang, B.J.; Zhao, W.Q. Time-lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Liu, X.; Pei, F.; Li, X.; Du, G. Non-uniform time-lag effects of terrestrial vegetation responses to asymmetric warming. Agric. For. Meteorol. 2018, 252, 130–143. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, H.; Chen, B.; Zhang, H.; Innes, J.L.; Wang, G.; Yan, J.; Zheng, Y.; Zhu, Z.; Myneni, R.B. Changes in Vegetation Growth Dynamics and Relations with Climate over China’s Landmass from 1982 to 2011. Remote Sens. 2014, 6, 3263–3283. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yu, G.; Yang, J.; Wimberly, M.C.; Zhang, X.; Tao, J.; Jiang, Y.; Zhu, J. Climate-driven global changes in carbon use efficiency. Glob. Ecol. Biogeogr. 2013, 23, 144–155. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, F.; Cao, G.; Yang, W.; Zhou, Y. Spatiotemporal features of carbon source-sink and its relationship with climate factors in Qinghai-Tibet Plateau grassland ecosystem during 2001–2015. Res. Soil Water Conserv. 2019, 26, 76–81. [Google Scholar]
- Chai, X.; Shi, P.; Song, M.; Zong, N.; He, Y.; Zhao, G.; Zhang, X. Carbon flux phenology and net ecosystem productivity simulated by a bioclimatic index in an alpine steppe-meadow on the Tibetan Plateau. Ecol. Model. 2019, 394, 66–75. [Google Scholar] [CrossRef]
- Elsgaard, L.; Görres, C.-M.; Hoffmann, C.C.; Blicher-Mathiesen, G.; Schelde, K.; Petersen, S.O. Net ecosystem exchange of CO2 and carbon balance for eight temperate organic soils under agricultural management. Agric. Ecosyst. Environ. 2012, 162, 52–67. [Google Scholar] [CrossRef]
- Li, H.; Zhang, F.; Li, Y.; Wang, J.; Zhang, L.; Zhao, L.; Cao, G.; Zhao, X.; Du, M. Seasonal and inter-annual variations in CO2 fluxes over 10 years in an alpine shrubland on the Qinghai-Tibetan Plateau, China. Agric. For. Meteorol. 2016, 228–229, 95–103. [Google Scholar] [CrossRef]
- Wang, H.; Ma, M.; Wang, X.; Tan, J.; Gen, L.; Yu, W. Carbon flux variation characteristics and its influencing factors in an alpine meadow ecosystem on eastern Qinghai-Tibetan plateau. J. Arid Land Resour. Environ. Earth Sci. 2014, 28, 50–56. [Google Scholar]
- Pei, Z.; Zhou, C.; Ouyang, H.; Yang, W. A carbon budget of alpine steppe area in the Tibetan Plateau. Geogr. Res. 2010, 29, 102–110. [Google Scholar]
- Zhao, L.; Li, Y.; Xu, S.; Zhou, H.; Gu, S.; Yu, G.; Zhao, X. Diurnal, seasonal and annual variation in net ecosystem CO2 exchange of an alpine shrubland on Qinghai-Tibetan plateau. Glob. Chang. Biol. 2006, 12, 1940–1953. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y.; Li, H.; Yuan, L. Carbon and water fluxes and their coupling in an alpine meadow ecosystem on the northeastern Tibetan Plateau. Theor. Appl. Clim. 2020, 142, 1–18. [Google Scholar] [CrossRef]
- Niu, B.; He, Y.; Zhang, X.; Du, M.; Shi, P.; Sun, W. CO2 Exchange in an Alpine Swamp Meadow on the Central Tibetan Plateau. Wetlands 2017, 37, 525–543. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Lu, S.; Su, P.; Shang, L.; Li, Z. Biophysical regulation of carbon fluxes over an alpine meadow ecosystem in the eastern Tibetan Plateau. Int. J. Biometeorol. 2015, 60, 801–812. [Google Scholar] [CrossRef]
- Wang, B.; Jin, H.; Li, Q.; Chen, D.; Zhao, L.; Tang, Y.; Kato, T.; Gu, S. Diurnal and Seasonal Variations in the Net Ecosystem CO2 Exchange of a Pasture in the Three-River Source Region of the Qinghai−Tibetan Plateau. PLoS ONE 2017, 12, e0170963. [Google Scholar] [CrossRef] [PubMed]
- Luyssaert, S.; Schulze, E.-D.; Börner, A.; Knohl, A.; Hessenmöller, D.; Law, B.E.; Ciais, P.; Grace, J.D. Old-growth forests as global carbon sinks. Nat. Cell Biol. 2008, 455, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Dai, E.; Huang, Y.; Wu, Z.; Zhao, D. Analysis of spatio-temporal features of a carbon source/sink and its relationship to climatic factors in the Inner Mongolia grassland ecosystem. J. Geogr. Sci. 2016, 26, 297–312. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Kustas, W.P.; Anderson, M.C.; Prueger, J.H.; Scott, R.L. Effect of remote sensing spatial resolution on interpreting tower-based flux observations. Remote. Sens. Environ. 2008, 112, 337–349. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Xu, M.; Zhu, J.; Chen, N.; Jiang, Y.; Huang, K.; Zu, J.; Liu, Y.; Yu, G. Water availability is more important than temperature in driving the carbon fluxes of an alpine meadow on the Tibetan Plateau. Agric. For. Meteorol. 2018, 256-257, 22–31. [Google Scholar] [CrossRef]
- Heinsch, F.; Zhao, M.; Running, S.; Kimball, J.; Nemani, R.; Davis, K.; Bolstad, P.; Cook, B.; Desai, A.; Ricciuto, D.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1925. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Q.; He, J.; Lu, Y.; Ji, L.; Xiao, J.; Luo, T. Carbon dynamics of terrestrial ecosystems on the Tibetan Plateau during the 20th century: An analysis with a process-based biogeochemical model. Glob. Ecol. Biogeogr. 2010, 19, 649–662. [Google Scholar] [CrossRef]
- Piao, S.; Tan, K.; Nan, H.; Ciais, P.; Fang, J.; Wang, T.; Vuichard, N.; Zhu, B. Impacts of climate and CO2 changes on the vegetation growth and carbon balance of Qinghai–Tibetan grasslands over the past five decades. Glob. Planet. Chang. 2012, 98-99, 73–80. [Google Scholar] [CrossRef]







| Dataset | Spatial Resolution | Temporal Resolution | Source |
|---|---|---|---|
| NDVI | 1 km | monthly | MOD13A3 |
| Air temperature | 0.25 degree | monthly | ERA5 2m temperature |
| Precipitation | 0.25 degree | monthly | ERA5 total precipitation |
| Solar radiation | 0.25 degree | monthly | ERA5 surface solar radiation downwards |
| Land cover | 5.6 km | yearly | MCD12C1 |
| Soil attribute | 30 arc-second | - | HWSD v1.2 |
| ID | Site Name | Period | Latitude | Longitude | Vegetation Types |
|---|---|---|---|---|---|
| CN-HaM | Haibei Alpine Tibet site | 2002–2004 | 37.37 | 101.18 | Grassland |
| CN-Ha2 | Haibei Shrubland | 2003–2005 | 37.6086 | 101.3269 | Wetland |
| CN-Dan | Dangxiong | 2004–2005 | 30.4978 | 91.0664 | Grassland |
| Period | NEP (gC·m−2·yr−1) | References |
|---|---|---|
| 2001–2018 | 49.35–82.8 | Our study |
| 2009 | 156 | [52] |
| 2001 | 55.26 | [53] |
| 2003–2004 | 58.5–75.5 | [54] |
| 2008–2009 | 47.1–79.7 | [25] |
| 2013–2015 | 152.89–197.69 | [55] |
| 2015–2016 | 105.3–258.9 | [10] |
| 2009–2013 | 126.06–190.75 | [56] |
| 2002–2004 | 78.5–192.5 | [4] |
| 2010 | 156.4 | [57] |
| 2008 | 140.01 | [58] |
| 2013–2017 | 53–284 | [24] |
| 2009–2012 | 118.49–195.83 | [23] |
| 2001–2015 | 90–170 | [48] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Song, X.; Hu, R.; Zhu, X.; Jiang, Y.; Cai, S.; Zhang, Y.; Cui, X. Large-Scale Analysis of the Spatiotemporal Changes of Net Ecosystem Production in Hindu Kush Himalayan Region. Remote Sens. 2021, 13, 1180. https://doi.org/10.3390/rs13061180
Guo D, Song X, Hu R, Zhu X, Jiang Y, Cai S, Zhang Y, Cui X. Large-Scale Analysis of the Spatiotemporal Changes of Net Ecosystem Production in Hindu Kush Himalayan Region. Remote Sensing. 2021; 13(6):1180. https://doi.org/10.3390/rs13061180
Chicago/Turabian StyleGuo, Da, Xiaoning Song, Ronghai Hu, Xinming Zhu, Yazhen Jiang, Shuohao Cai, Yanan Zhang, and Xiaoyong Cui. 2021. "Large-Scale Analysis of the Spatiotemporal Changes of Net Ecosystem Production in Hindu Kush Himalayan Region" Remote Sensing 13, no. 6: 1180. https://doi.org/10.3390/rs13061180
APA StyleGuo, D., Song, X., Hu, R., Zhu, X., Jiang, Y., Cai, S., Zhang, Y., & Cui, X. (2021). Large-Scale Analysis of the Spatiotemporal Changes of Net Ecosystem Production in Hindu Kush Himalayan Region. Remote Sensing, 13(6), 1180. https://doi.org/10.3390/rs13061180






