Increasing Spatio-Temporal Resolution for Monitoring Alpine Solifluction Using Terrestrial Laser Scanners and 3D Vector Fields
Abstract
:1. Introduction
- We establish a new workflow for the monitoring of slowly moving landforms with higher spatial and temporal resolution based on the TLS point clouds and 3D vector field representation, with a particular focus on solifluction lobes;
- We compare this approach with the established point-wise and point-cloud-based approaches, and analyse the advantages and disadvantages, as well as the information they can retrieve about solifluction;
- We evaluate the spatial distribution and deformation pattern of movement for a particular solifluction lobe.
2. State of the Art
2.1. Strategies for Monitoring Solifluction
2.2. Using Point Clouds for Geomonitoring
2.3. Determining Deformations Using Point Clouds
3. Methods and Materials
3.1. Study Area
3.2. Georeferencing
3.2.1. Data Acquisition
- Changes in the air temperature of a 1 C increase or decrease, respectively, the distance by 1 mm/km (+1 C causes −1 mm/km);
- Changes in the air pressure of a 3 hPa increase or decrease, respectively, the distance by 1 mm/km (+3 hPa causes +1 mm/km).
3.2.2. Data Processing
- Analysing the observations from each station, eliminating outliers, reducing random and systematic errors following geodetic basics;
- Applying corrections to all measured distances accounting for changes in air temperature and air pressure based on the recorded values;
- Estimating the coordinates of the network points in a network adjustment based on the least-squares;
- Assessing the quality of the network: Analysing the estimated covariance matrices of the network points as well as the partial redundancies of each observation. While the first aspect concerns the accuracy of the network, the second one describes its reliability, i.e., its ability to detect outliers.
3.3. Point-Based Measurements with Total Station
3.4. Area-Based Measurements with Terrestrial Laser Scanner
3.4.1. Data Processing: Point Cloud Comparison
3.4.2. Data Processing: Local ICP
3.4.3. Data Processing: Feature Detection and Tracking
4. Results
4.1. Georeferencing
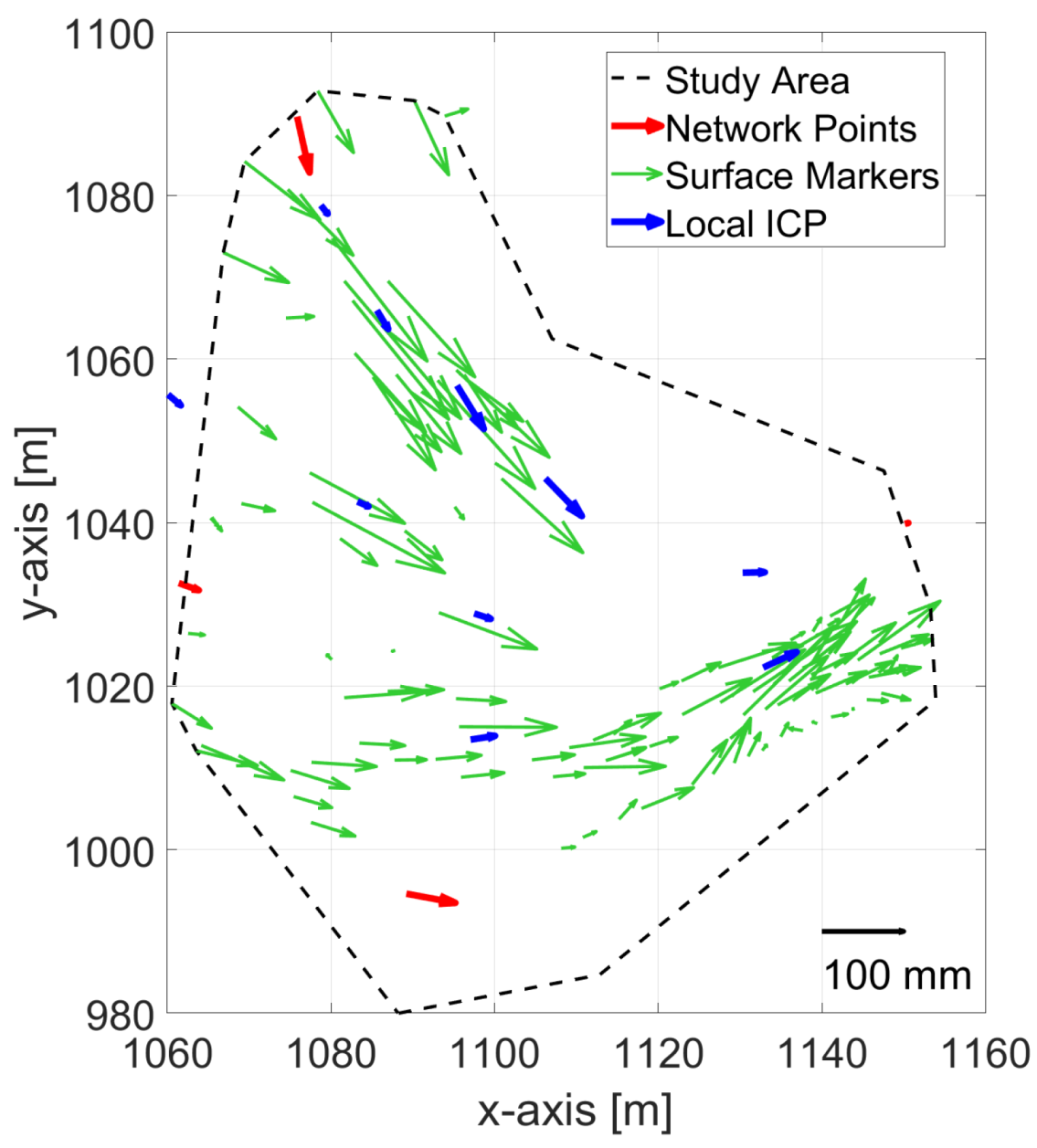
4.2. Point-Based Measurements: Comparison of Surface Markers Coordinates
4.3. Area-Based Measurements: Point Cloud Comparison
- This method does not rely on the pre-determined positions of the previously fixed markers. Hence, it can detect discrete movements over the whole study area, avoiding the pitfall of having large gaps between the measurements. This means it can reveal movement, even in regions where it was not a priori expected;
- However, the detected movements are still discrete, appearing only in locations where the movement was approximately perpendicular to the land surface. Therefore, although this approach has obvious advantages in comparison to the point-wise measurement method with a total station, it still lacks a high spatial resolution to faithfully represent the lobes’ movement;
- Finally, this method provides the magnitudes of the movement only in one direction (1D), perpendicular to the surface. Hence, it is not suitable for deriving 3D vector fields. Hence, it cannot reveal the full magnitude and the exact direction of the surface movement.
4.4. Area-Based Measurements: Local ICP
- First, we can observe the maximal vector lengths of about 65 mm, which are considerably smaller in comparison to the ones from the point-wise measurements (approximately 220 mm). Furthermore, if we compare the blue and green vectors in Figure 6, it is noticeable that the ICP-based movement magnitudes are actually smaller in every instance than the ones of the surface markers. Hence, like the M3C2 algorithm, this method is also not always capable of revealing the full magnitude of the movement. This is due to the fact that the ICP algorithm, despite being able to generate 3D vectors instead of 1D distances, is still only sensitive to movements in the direction of the local surface normals (1D);
- Second, we can observe that this method successfully and accurately detected the directions of the movements, which completely correspond to the directions estimated by measuring the surface markers. Hence, the advantage of this method in comparison to the M3C2 is the possibility of correctly parametrizing the direction of the surface motion;
- However, third, this is only possible if the distribution of surface normals in some smaller regions is relatively high, such is in the case of the lobes’ heads. For example, if the region contains some larger structural elements, such as rocks, the 3D motion of the surface can be reconstructed. Nevertheless, if the region is fairly planar, the complete motion can be overlooked. Thus, the true motion of the land surface can be estimated only in discrete locations and not over the whole surface. This, again, results in the limitation of the spatial resolution.
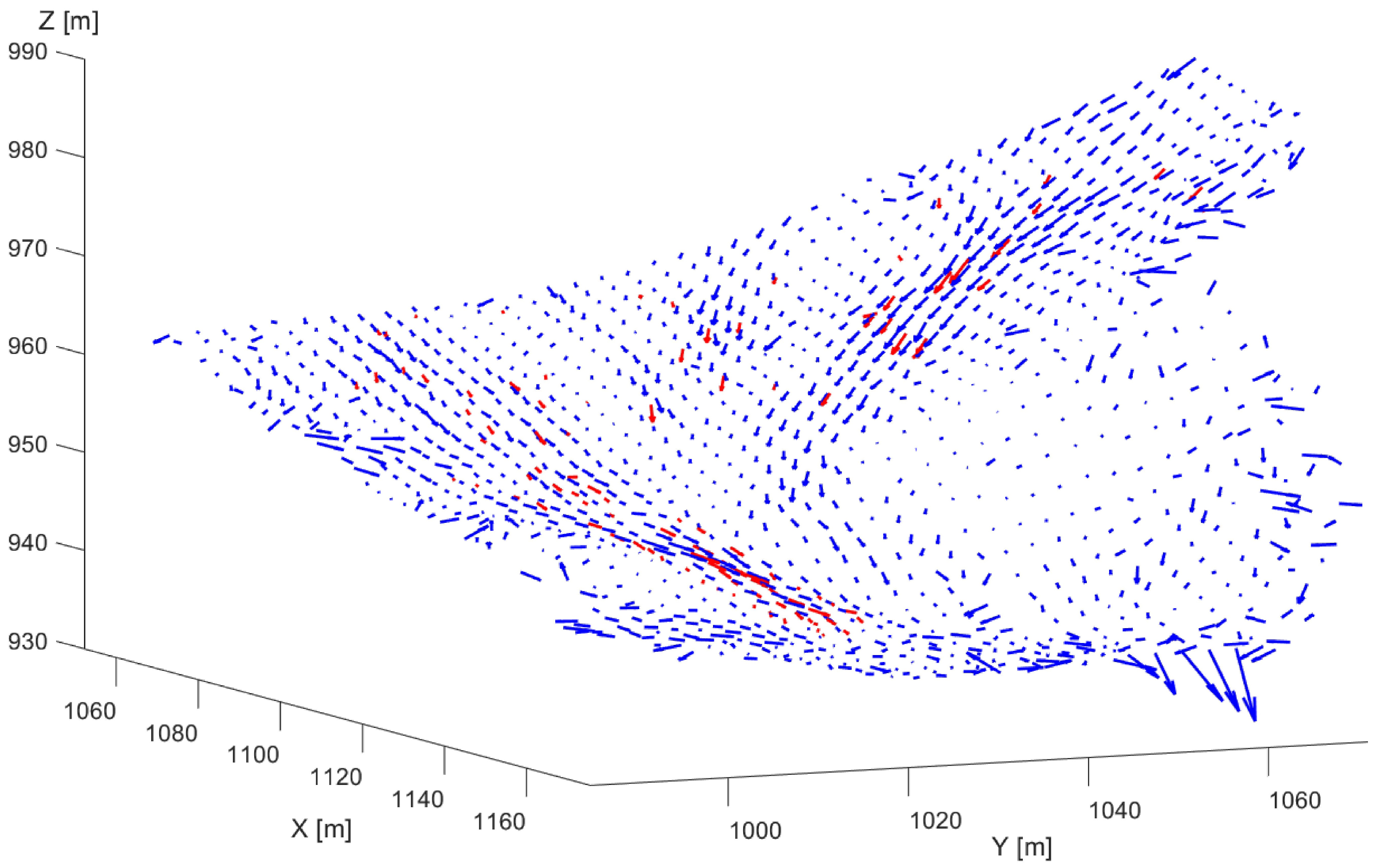
4.5. Area-Based Measurements: Feature Detection and Tracking
5. Discussion
- The point-wise measurements with total station and surface markers allow for the determination of movements at discrete points on the lobes’ surface. The disadvantage of this standard geomorphological method is that the spatial resolution of the measurements is very limited. However, measurement accuracy is relatively high, allowing for the detection of even small-scale land-surface movements;
- The comparison of TLS point clouds based on an M3C2 algorithm allows for the detection of changes in the geometry and volume at lobes’ heads. Unlike the previous method, it has increased spatial resolution in a sense that it is not restricted to a pre-determined set of marker locations. However, it is still limited to a few discrete locations, as detection is only possible where the surface structure allows for change detection. In such locations, it is possible to identify where the volume increases and decreases. However, it is not possible to estimate the exact magnitude and direction of the lobes’ movements [57];
- The transformation parameters determined locally with the ICP algorithm increase the amount of extracted information from point clouds by allowing for the estimation of correct directions and biased magnitudes. The magnitudes are systematically underestimated, as the ICP is sensitive to change detection only in the direction perpendicular to the observed surface. This also means that this method is limited to monitoring discrete locations where the land surface normals are parallel with the solifluction direction (at lobes’ heads);
- Finally, the developed feature detection and tracking workflow can be used to derive surface movements with similar measurement accuracy and fidelity to the established point-wise method, without being restricted to pre-determined marker locations, and produces a 3D vector field with high spatial resolution covering the whole study area.
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALS | Airborne Laser Scanner |
| DEM | Digital Elevation Model |
| DoF | Digital Ortophoto |
| DTM | Digital Terrain Model |
| GNSS | Global Navigation Satellite System |
| ICP | Iterative Closest Point |
| LiDAR | Light Detection and Ranging |
| MAD | Median Absolute Deviation |
| NHN | Normalhöhennull (heights above sea level) |
| TIN | Triangular Irregular Network |
| TLS | Terrestrial Laser Scanner |
| UAV | Unmanned Aerial Vehicle |
| WGS84 | World Geodetic System 1984 |
References
- Matsuoka, N. Solifluction rates, processes and landforms: A global review. Earth-Sci. Rev. 2001, 55, 107–134. [Google Scholar] [CrossRef]
- Ballantyne, C.K. Periglacial Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Eitel, J.U.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.S.; Glennie, C.L.; Joerg, P.C.; LeWinter, A.L.; Magney, T.S.; et al. Beyond 3-D: The new spectrum of lidar applications for earth and ecological sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef] [Green Version]
- Klingbeil, L.; Heinz, E.; Wieland, M.; Eichel, J.; Laebe, T.; Kuhlmann, H. On the UAV based Analysis of Slow Geomorphological Processes: A Case Study at a Solifluction Lobe in the Turtmann Valley. In Proceedings of the 4th Joint International Symposium on Deformation Monitoring (JISDM 2019), Athens, Greece, 15–17 May 2019; pp. 15–17. [Google Scholar]
- Eichel, J.; Draebing, D.; Kattenborn, T.; Senn, J.A.; Klingbeil, L.; Wieland, M.; Heinz, E. Unmanned aerial vehicle-based mapping of turf-banked solifluction lobe movement and its relation to material, geomorphometric, thermal and vegetation properties. Permafr. Periglac. Process. 2020, 31, 97–109. [Google Scholar] [CrossRef]
- Jaesche, P.; Veit, H.; Huwe, B. Snow cover and soil moisture controls on solifluction in an area of seasonal frost, eastern Alps. Permafr. Periglac. Process. 2003, 14, 399–410. [Google Scholar] [CrossRef]
- Matsuoka, N. Solifluction and mudflow on a limestone periglacial slope in the Swiss Alps: 14 years of monitoring. Permafr. Periglac. Process. 2010, 21, 219–240. [Google Scholar] [CrossRef]
- Fey, C.; Rutzinger, M.; Wichmann, V.; Prager, C.; Bremer, M.; Zangerl, C. Deriving 3D displacement vectors from multi-temporal airborne laser scanning data for landslide activity analyses. GIscience Remote Sens. 2015, 52, 437–461. [Google Scholar] [CrossRef]
- Gojcic, Z.; Zhou, C.; Wieser, A. F2S3: Robustified determination of 3D displacement vector fields using deep learning. J. Appl. Geod. 2020, 14, 177–189. [Google Scholar] [CrossRef]
- Wellmann, F.; Caumon, G. 3-D Structural geological models: Concepts, methods, and uncertainties. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 2018; Volume 59, pp. 1–121. [Google Scholar]
- Dematteis, N.; Giordan, D.; Zucca, F.; Luzi, G.; Allasia, P. 4D surface kinematics monitoring through terrestrial radar interferometry and image cross-correlation coupling. ISPRS J. Photogramm. Remote Sens. 2018, 142, 38–50. [Google Scholar] [CrossRef]
- Schrott, L.; Otto, J.C.; Götz, J.; Geilhausen, M.; Otto, J.C. Fundamental classic and modern field techniques in Geomorphology—An overview. Treatise Geomorphol. 2013. [Google Scholar] [CrossRef]
- Eichel, J.; Corenblit, D.; Dikau, R. Conditions for feedbacks between geomorphic and vegetation dynamics on lateral moraine slopes: A biogeomorphic feedback window. Earth Surf. Process. Landforms 2016, 41, 406–419. [Google Scholar] [CrossRef]
- Schwalbe, E.; Maas, H.G. The determination of high-resolution spatio-temporal glacier motion fields from time-lapse sequences. Earth Surf. Dyn. 2017, 5, 861–879. [Google Scholar] [CrossRef] [Green Version]
- Kienholz, C.; Amundson, J.M.; Motyka, R.J.; Jackson, R.H.; Mickett, J.B.; Sutherland, D.A.; Nash, J.D.; Winters, D.S.; Dryer, W.P.; Truffer, M. Tracking icebergs with time-lapse photography and sparse optical flow, LeConte Bay, Alaska, 2016–2017. J. Glaciol. 2019, 65, 195–211. [Google Scholar] [CrossRef] [Green Version]
- Lewkowicz, A.G. A solifluction meter for permafrost sites. Permafr. Periglac. Process. 1992, 3, 11–18. [Google Scholar] [CrossRef]
- Matsuoka, N. Continuous recording of frost heave and creep on a Japanese alpine slope. Arct. Alp. Res. 1994, 26, 245–254. [Google Scholar] [CrossRef]
- Jaesche, P.; Veit, H.; Stingl, H.; Huwe, B. Influence of water and heat dynamics on solifluction movements in a periglacial environment in the Eastern Alps (Austria). In Proceedings of the International Symposium Physics, Chemistry and Ecology of Seasonally Frozen Soils, Fairbanks, AK, USA, 10–12 June 1997. [Google Scholar]
- Yamada, S.; Matsumoto, H.; Hirakawa, K. Seasonal variation in creep and temperature in a solifluction lobe: continuous monitoring in the Daisetsu Mountains, northern Japan. Permafr. Periglac. Process. 2000, 11, 125–135. [Google Scholar] [CrossRef]
- Veit, H.; Stingl, H.; Emmerich, K.H.; John, B. Zeitliche und räumliche Variabilität solifluidaler Prozesse und ihre Ursachen-Eine Zwischenbilanz nach acht Jahren Solifluktionsmessungen (1985–1993) an der Meßstation. Z. FÜR Geomorphol. Suppl. Vol. 1995, 107–122. [Google Scholar] [CrossRef]
- Sailer, R.; Bollmann, E.; Hoinkes, S.; Rieg, L.; Sproß, M.; Stötter, J. Quantification of geomorphodynamics in glaciated and recently deglaciated terrain based on airborne laser scanning data. Geogr. Ann. Ser. A Phys. Geogr. 2012, 94, 17–32. [Google Scholar] [CrossRef]
- Kociuba, W. Assessment of sediment sources throughout the proglacial area of a small Arctic catchment based on high-resolution digital elevation models. Geomorphology 2017, 287, 73–89. [Google Scholar] [CrossRef]
- Arenson, L.U.; Kääb, A.; O’Sullivan, A. Detection and analysis of ground deformation in permafrost environments. Permafr. Periglac. Process. 2016, 27, 339–351. [Google Scholar] [CrossRef]
- Crawford, A.J.; Mueller, D.; Joyal, G. Surveying drifting icebergs and ice islands: deterioration detection and mass estimation with aerial photogrammetry and laser scanning. Remote Sens. 2018, 10, 575. [Google Scholar] [CrossRef] [Green Version]
- Scaioni, M.; Roncella, R.; Alba, M.I. Change detection and deformation analysis in point clouds. Photogramm. Eng. Remote Sens. 2013, 79, 441–455. [Google Scholar] [CrossRef]
- Kromer, R.A.; Abellán, A.; Hutchinson, D.J.; Lato, M.; Chanut, M.A.; Dubois, L.; Jaboyedoff, M. Automated terrestrial laser scanning with near-real-time change detection—Monitoring of the Séchilienne landslide. Earth Surf. Dyn. 2017, 5, 293–310. [Google Scholar] [CrossRef] [Green Version]
- Kayen, R.; Pack, R.T.; Bay, J.; Sugimoto, S.; Tanaka, H. Terrestrial-LIDAR visualization of surface and structural deformations of the 2004 Niigata Ken Chuetsu, Japan, earthquake. Earthq. Spectra 2006, 22, 147–162. [Google Scholar] [CrossRef]
- Wilkinson, M.; McCaffrey, K.; Roberts, G.; Cowie, P.; Phillips, R.; Michetti, A.M.; Vittori, E.; Guerrieri, L.; Blumetti, A.; Bubeck, A.; et al. Partitioned postseismic deformation associated with the 2009 Mw 6.3 L’Aquila earthquake surface rupture measured using a terrestrial laser scanner. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Kayer, R.; Stewart, J.P.; Collins, B.D. Recent advances in terrestrial LIDAR applications in geotechnical earthquake engineering. In Proceedings of the 5th International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego, CA, USA, 24–29 May 2010. [Google Scholar]
- Pesci, A.; Teza, G.; Casula, G.; Loddo, F.; De Martino, P.; Dolce, M.; Obrizzo, F.; Pingue, F. Multitemporal laser scanner-based observation of the Mt. Vesuvius crater: Characterization of overall geometry and recognition of landslide events. ISPRS J. Photogramm. Remote Sens. 2011, 66, 327–336. [Google Scholar] [CrossRef]
- Gumilar, I.; Abidin, H.Z.; Putra, A.D.; Haerani, N. 3D modelling of Mt. Talaga Bodas Crater (Indonesia) by using terrestrial laser scanner for volcano hazard mitigation. AIP Conf. Proc. 2015, 1658, 050008. [Google Scholar]
- Slatcher, N.; James, M.R.; Calvari, S.; Ganci, G.; Browning, J. Quantifying effusion rates at active volcanoes through integrated time-lapse laser scanning and photography. Remote Sens. 2015, 7, 14967–14987. [Google Scholar] [CrossRef] [Green Version]
- Telling, J.; Lyda, A.; Hartzell, P.; Glennie, C. Review of Earth science research using terrestrial laser scanning. Earth-Sci. Rev. 2017, 169, 35–68. [Google Scholar] [CrossRef] [Green Version]
- Höfle, B.; Griesbaum, L.; Forbriger, M. GIS-Based detection of gullies in terrestrial LiDAR data of the Cerro Llamoca Peatland (Peru). Remote Sens. 2013, 5, 5851–5870. [Google Scholar] [CrossRef] [Green Version]
- Kociuba, W.; Kubisz, W.; Zagórski, P. Use of terrestrial laser scanning (TLS) for monitoring and modelling of geomorphic processes and phenomena at a small and medium spatial scale in Polar environment (Scott River—Spitsbergen). Geomorphology 2014, 212, 84–96. [Google Scholar] [CrossRef]
- Vericat, D.; Smith, M.; Brasington, J. Patterns of topographic change in sub-humid badlands determined by high resolution multi-temporal topographic surveys. Catena 2014, 120, 164–176. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: an approach for capturing rockfall magnitude–frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef] [Green Version]
- Anders, K.; Winiwarter, L.; Lindenbergh, R.; Williams, J.G.; Vos, S.E.; Höfle, B. 4D objects-by-change: Spatiotemporal segmentation of geomorphic surface change from LiDAR time series. ISPRS J. Photogramm. Remote Sens. 2020, 159, 352–363. [Google Scholar] [CrossRef]
- Ulrich, V.; Williams, J.G.; Zahs, V.; Anders, K.; Hecht, S.; Höfle, B. Measurement of rock glacier surface change over different timescales using terrestrial laser scanning point clouds. Earth Surf. Dyn. 2021, 9, 19–28. [Google Scholar] [CrossRef]
- Barbarella, M.; Fiani, M.; Lugli, A. Uncertainty in terrestrial laser scanner surveys of landslides. Remote Sens. 2017, 9, 113. [Google Scholar] [CrossRef] [Green Version]
- Pfeiffer, J.; Zieher, T.; Bremer, M.; Wichmann, V.; Rutzinger, M. Derivation of Three-Dimensional Displacement Vectors from Multi-Temporal Long-Range Terrestrial Laser Scanning at the Reissenschuh Landslide (Tyrol, Austria). Remote Sens. 2018, 10, 1688. [Google Scholar] [CrossRef] [Green Version]
- Fey, C.; Wichmann, V. Long-range terrestrial laser scanning for geomorphological change detection in alpine terrain—Handling uncertainties. Earth Surf. Process. Landforms 2017, 42, 789–802. [Google Scholar] [CrossRef]
- Holst, C.; Kuhlmann, H. Challenges and Present Fields of Action at Laser Scanner Based Deformation Analyses. J. Appl. Geodesy 2016, 10, 17–25. [Google Scholar] [CrossRef]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Wunderlich, T.; Niemeier, W.; Wujanz, D.; Holst, C.; Neitzel, F.; Kuhlmann, H. Areal Deformation from TLS Point Clouds—The Challenge. Allg.-Vermess.-Nachrichten 2016, 123. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Sensor fusion IV: control paradigms and data structures. Int. Soc. Opt. Photonics 1992, 1611, 586–606. [Google Scholar]
- Teza, G.; Galgaro, A.; Zaltron, N.; Genevois, R. Terrestrial laser scanner to detect landslide displacement fields: A new approach. Int. J. Remote Sens. 2007, 28, 3425–3446. [Google Scholar] [CrossRef]
- Wujanz, D.; Avian, M.; Krueger, D.; Neitzel, F. Identification of stable areas in unreferenced laser scans for automated geomorphometric monitoring. Earth Surf. Dyn. 2018, 6, 303–317. [Google Scholar] [CrossRef] [Green Version]
- Lane, S.N.; Westaway, R.M.; Murray Hicks, D. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing. EArth Surf. Process. Landforms J. Br. Geomorphol. Res. Group 2003, 28, 249–271. [Google Scholar] [CrossRef]
- Wagner, A.; Wiedemann, W.; Wunderlich, T. Fusion of laser-scan and image data for deformation monitoring—Concept and perspective. In Proceedings of the 7th International Conference on Engineering Surveying (INGEO 2017), Lisbon, Portugal, 18–20 October 2017; pp. 157–164. [Google Scholar]
- Chmelina, K.; Jansa, J.; Hesina, G.; Traxler, C. A 3-d laser scanning system and scan data processing method for the monitoring of tunnel deformations. J. Appl. Geod. 2012, 6, 177–185. [Google Scholar] [CrossRef]
- Pejić, M. Design and optimisation of laser scanning for tunnels geometry inspection. Tunn. Undergr. Space Technol. 2013, 37, 199–206. [Google Scholar] [CrossRef]
- Nuttens, T.; De Wulf, A.; Bral, L.; De Wit, B.; Carlier, L.; De Ryck, M.; Stal, C.; Constales, D.; De Backer, H. High resolution terrestrial laser scanning for tunnel deformation measurements. In Proceedings of the FIG Congress, Sydney, Australia, 1–16 April 2010; Volume 2010. [Google Scholar]
- Alba, M.; Fregonese, L.; Prandi, F.; Scaioni, M.; Valgoi, P. Structural monitoring of a large dam by terrestrial laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 6. [Google Scholar]
- Wang, J.; Kutterer, H.; Fang, X. External error modelling with combined model in terrestrial laser scanning. Surv. Rev. 2016, 48, 40–50. [Google Scholar] [CrossRef]
- Holst, C.; Schmitz, B.; Kuhlmann, H. Investigating the applicability of standard software packages for laser scanner based deformation analyses. In Proceedings of the FIG Working Week, Helsinki, Finland, 29 May–2 June 2017. [Google Scholar]
- Holst, C.; Schunck, D.; Nothnagel, A.; Haas, R.; Wennerbäck, L.; Olofsson, H.; Hammargren, R.; Kuhlmann, H. Terrestrial laser scanner two-face measurements for analyzing the elevation-dependent deformation of the onsala space observatory 20-m radio telescope’s main reflector in a bundle adjustment. Sensors 2017, 17, 1833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caspary, W.; Rüeger, J. Concepts of Network and Deformation Analysis; University of New South Wales: Kensington, Australia, 1987; Volume 11. [Google Scholar]
- Höck, V.; Pestal, G. Geologische Karte der Republik Österreich 1: 50,000, Blatt 153, Großglockner (Geological map of Austria 1: 50,000 Sheet 153, Großglockner); Geologische Bundesanstalt: Vienna, Austria, 1994. [Google Scholar]
- Stingl, H.; Garleff, K.; Höfner, T.; Huwe, B.; Jaesche, P.; John, B.; Veit, H.; Schrott, L. Grundfragen des alpinen Periglazials: Ergebnisse, Probleme und Perspektiven periglazialmophologischer Untersuchungen im Langzeitprojekt “ Glorer Hütte” in der Südlichen Glockner-/Nördichen Schobergruppe (Südliche Hohe Tauern, Osttirol). In Quantifizierung von rezenten und postglazialen Sedimentflüssen in den Ostalpen. Salzburger Geographische Arbeiten; Otto, J.-C., Schrott, L., Eds.; Universität Salzburg: Salzburg, Austria, 2010; Volume 46, pp. 15–42. [Google Scholar]
- Reshetyuk, Y. Self-Calibration and Direct Georeferencing in Terrestrial Laser Scanning. Ph.D. Thesis, KTH, Stockholm, Sweden, 2009. [Google Scholar]
- Ogundare, J. Precision Surveying: The Principles and Geomatics Practice; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zogg, H.M.; Lienhart, W.; Nindl, D. Leica TS30: The Art of Achieving Highest Accuracy and Performance; White Paper Leica Geosystems AG; Leica Geosystems AG: Heerbrugg, Switzerland, 2009. [Google Scholar]
- Heunecke, O.; Kuhlmann, H.; Welsch, W.; Eichhorn, A.; Neuner, H. Handbuch Ingenieurgeodäsie: Auswertung geodätischer Überwachungsmessungen, 2nd ed.; Herbert Wichmann Verlag: Heidelberg, Germany, 2013; ISBN 9783879074679, 3879074674. [Google Scholar]
- Wujanz, D.; Burger, M.; Mettenleiter, M.; Neitzel, F. An intensity-based stochastic model for terrestrial laser scanners. ISPRS J. Photogramm. Remote Sens. 2017, 125, 146–155. [Google Scholar] [CrossRef]
- Wujanz, D. Terrestrial Laser Scanning for Geodetic Deformation Monitoring; Technische Universitaet Berlin: Berlin, Germany, 2016. [Google Scholar]
- Förstner, W.; Wrobel, B.P. Photogrammetric Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Burrough, P.; McDonnell, R. Spatial information systems and geostatistics. Burrough Mcdonnell Princ. Geogr. Inf. Syst. 1998, 333. [Google Scholar]
- Jianbo, S.; Tomasi, C. Good features to track. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE features. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 214–227. [Google Scholar]
- Ridefelt, H.; Boelhouwers, J.; Etzelmüller, B. Local variations of solifluction activity and environment in the Abisko Mountains, Northern Sweden. Earth Surf. Process. Landforms 2011, 36, 2042–2053. [Google Scholar] [CrossRef]
- Kellerer-Pirklbauer, A. Solifluction rates and environmental controls at local and regional scales in central Austria. Nor. Geogr.-Tidsskr.-Nor. J. Geogr. 2018, 72, 37–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]

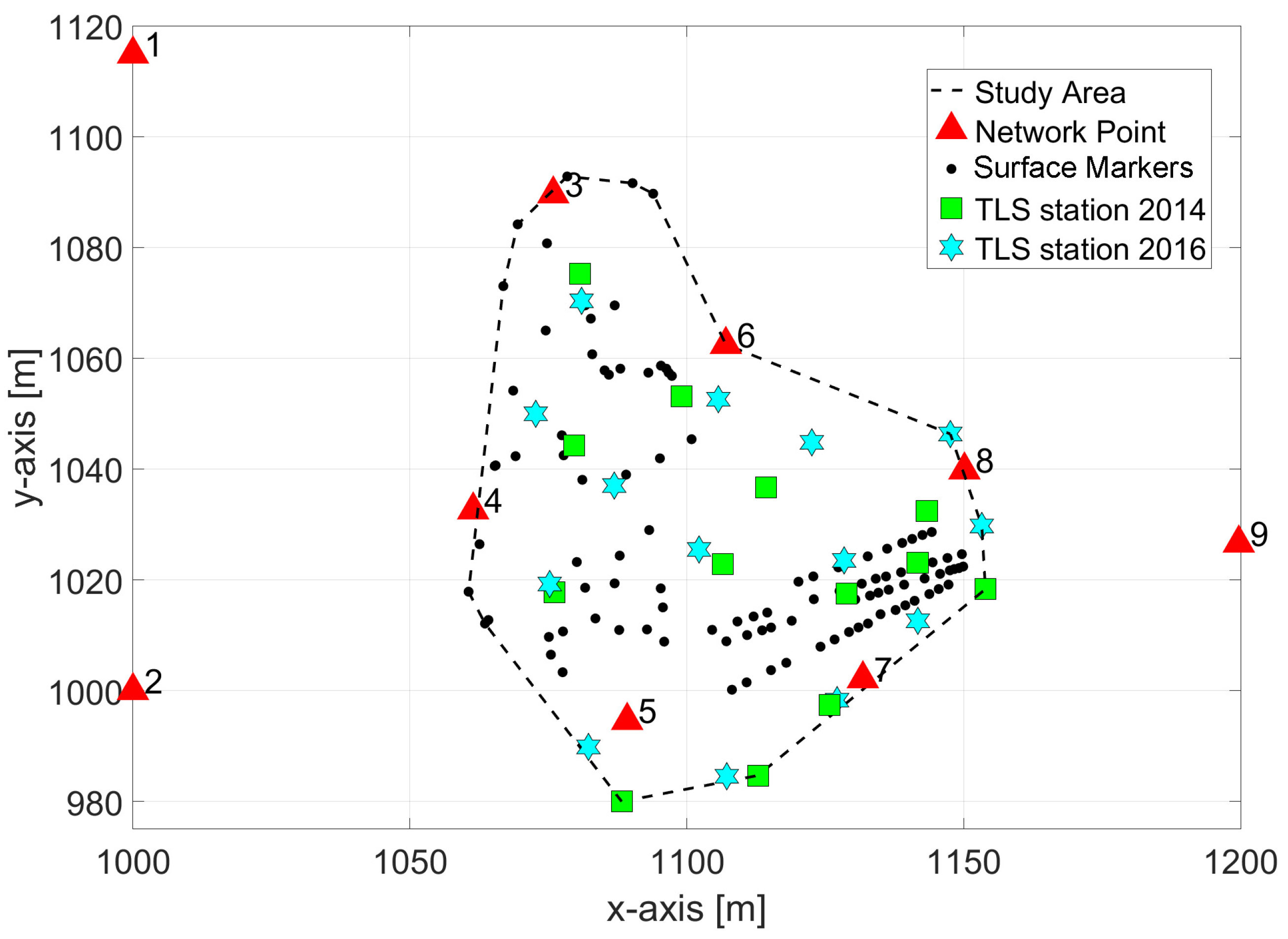
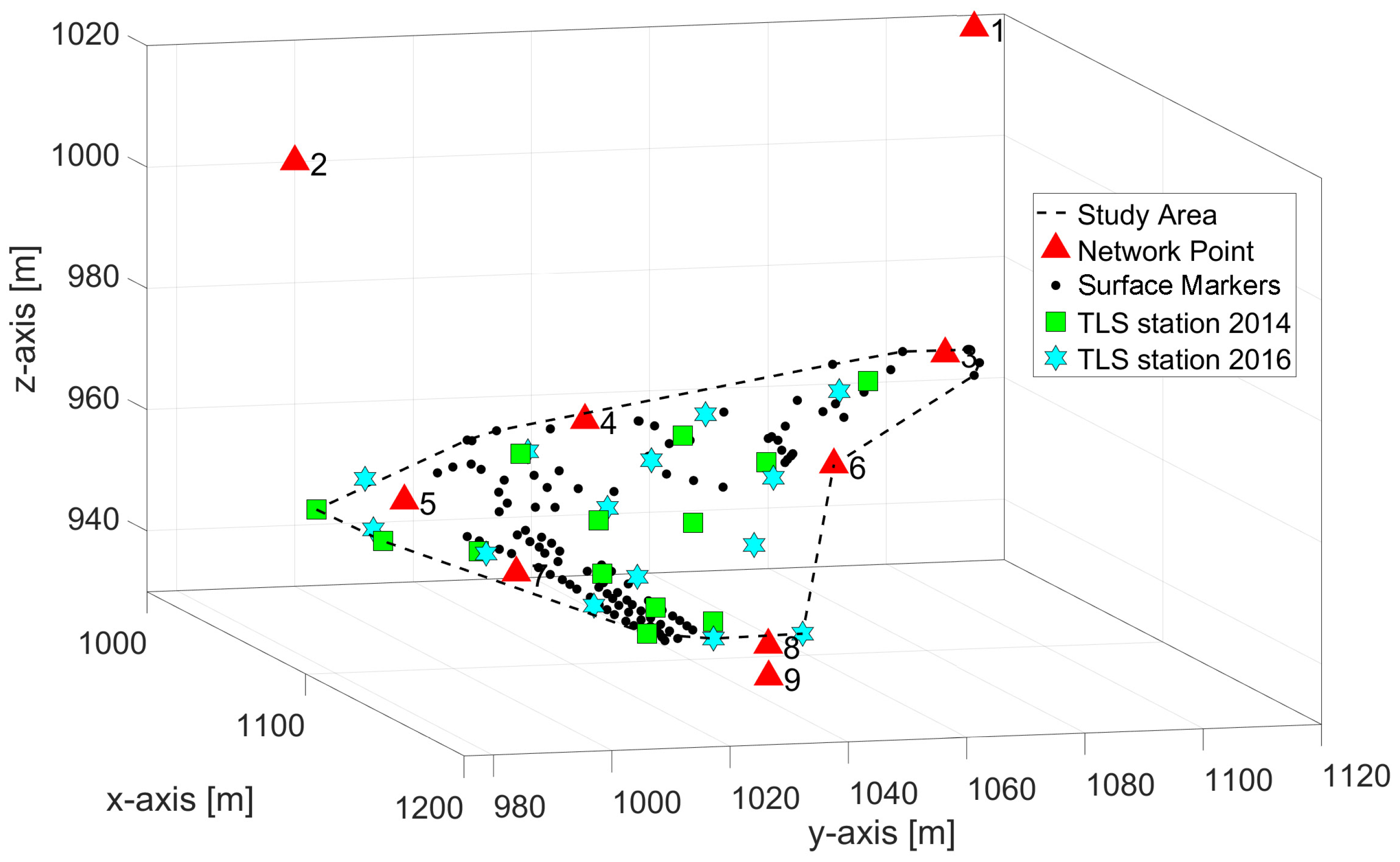
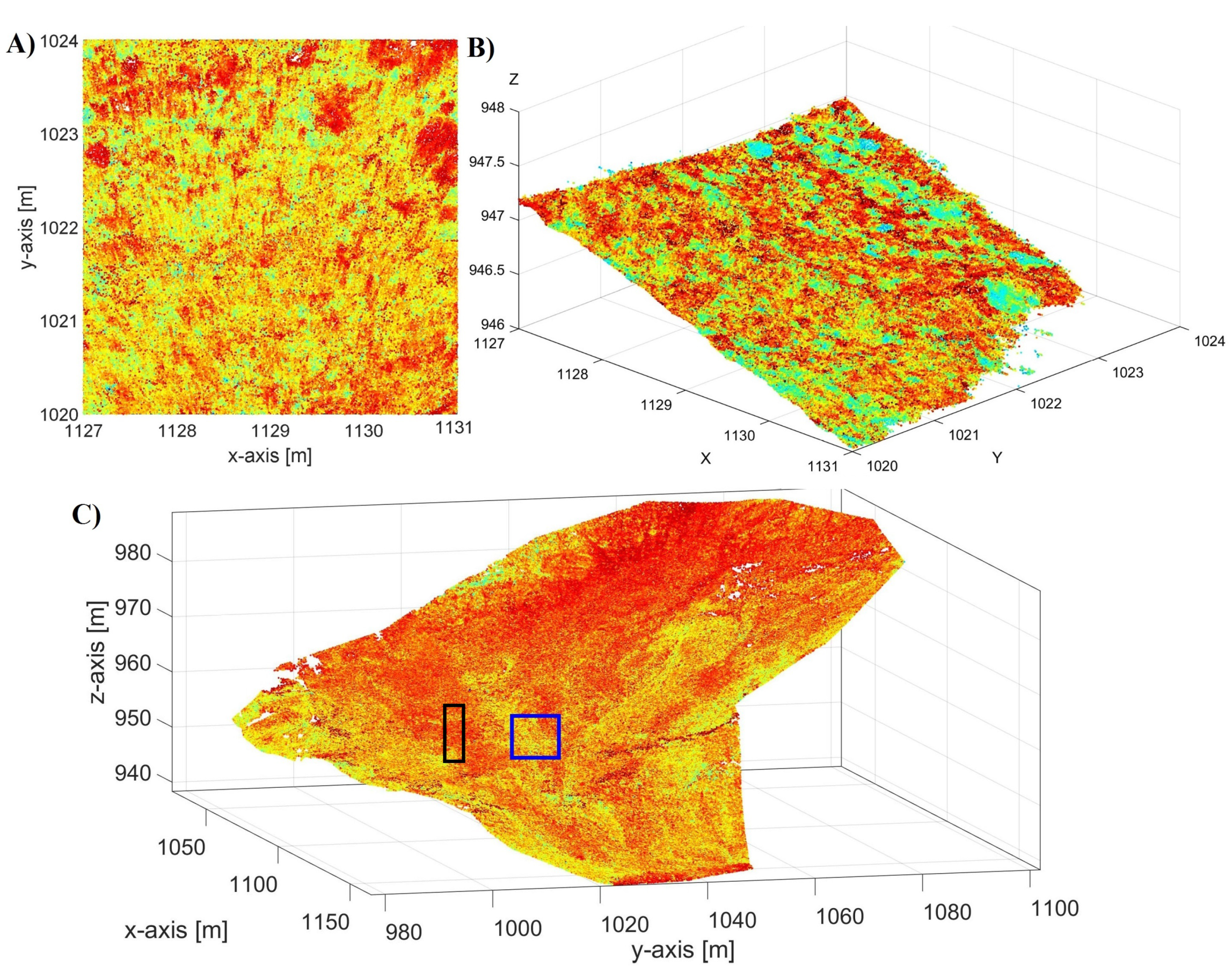
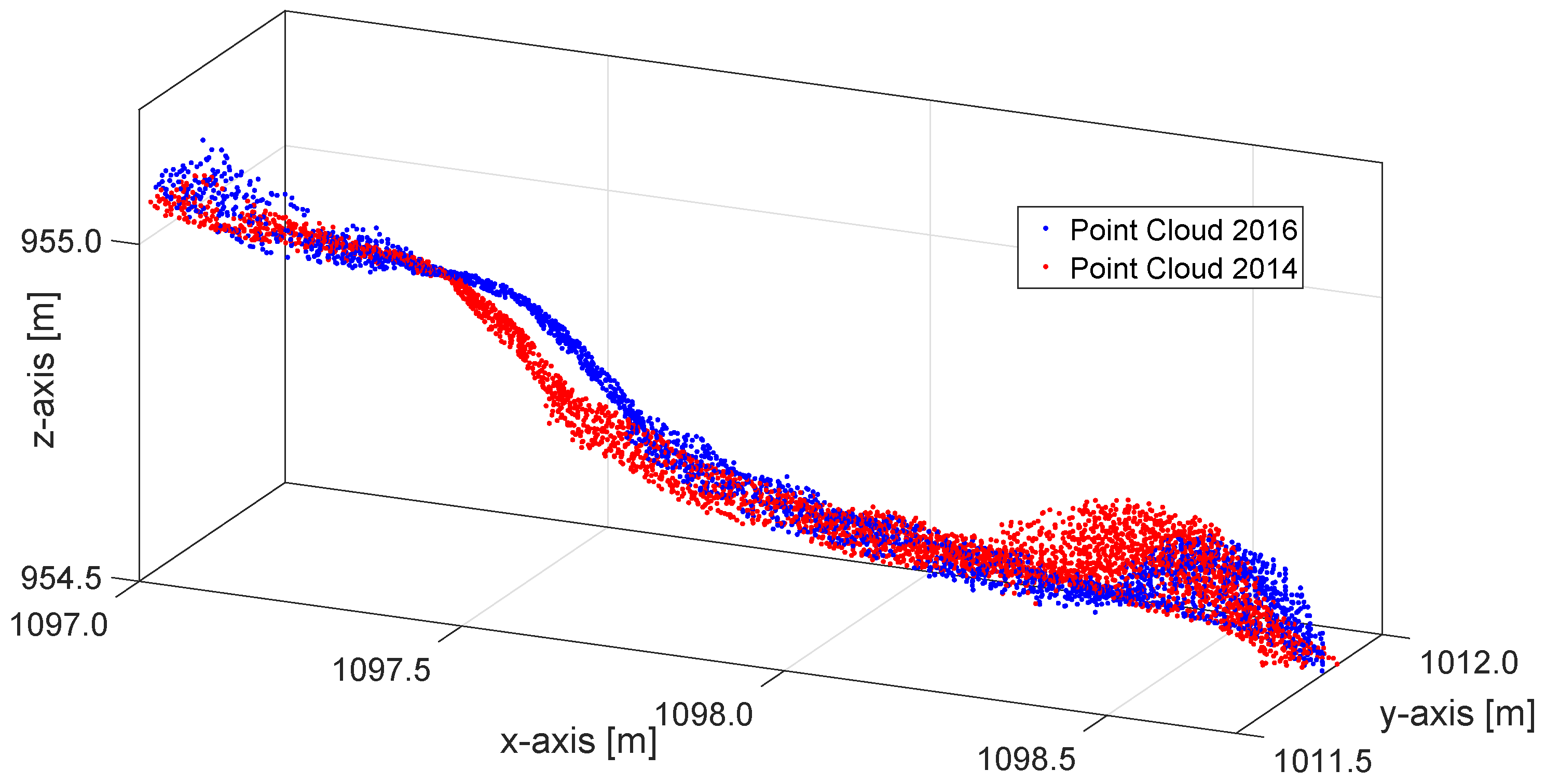


| No. | x [m] | y [m] | z [m] | [mm] | [mm] | [mm] | [mm] | Stable |
|---|---|---|---|---|---|---|---|---|
| 1 | 999.9919 | 1114.8805 | 1017.8782 | <0.2 | <0.8 | 1.7 | −0.9 | yes |
| 2 | 999.9942 | 999.9980 | 1000.0019 | <0.2 | <0.8 | 1.0 | −0.5 | yes |
| 3 | 1075.8894 | 1089.6349 | 975.3597 | <0.2 | <0.8 | 70.3 | −20.9 | no |
| 4 | 1061.4230 | 1032.5943 | 964.5047 | <0.2 | <0.8 | 26.1 | 0.0 | no |
| 5 | 1089.2357 | 994.6102 | 956.3786 | <0.2 | <0.8 | 61.0 | −8.2 | no |
| 6 | 1107.0519 | 1062.4591 | 962.2790 | <0.2 | <0.8 | 0.1 | −3.7 | yes () |
| 7 | 1131.7983 | 1002.1349 | 950.0082 | <0.2 | <0.8 | 0.2 | 1.3 | yes |
| 8 | 1150.1347 | 1039.8193 | 939.2219 | <0.2 | <0.8 | 4.6 | 2.4 | no |
| 9 | 1199.6758 | 1026.6174 | 941.1861 | <0.2 | <0.8 | 0.9 | 0.2 | yes |
| No. | x [m] | y [m] | z [m] | [mm] | [mm] | [mm] |
|---|---|---|---|---|---|---|
| 1 | 1097 | 1013 | 954 | 30.3 | 10.2 | ≈2 |
| 2 | 1095 | 1056 | 962 | 62.5 | 12.7 | ≈2 |
| 3 | 1106 | 1045 | 957 | 64.2 | 12.3 | ≈2 |
| 4 | 1085 | 1066 | 966 | 27.1 | 11.6 | ≈2 |
| 5 | 1078 | 1078 | 971 | 13.5 | 16.1 | ≈2 |
| 6 | 1060 | 1055 | 968 | 20.7 | 5.9 | ≈2 |
| 7 | 1097 | 1028 | 955 | 21.5 | 7.2 | ≈2 |
| 8 | 1132 | 1022 | 945 | 45.2 | 10.7 | ≈2 |
| 9 | 1130 | 1033 | 945 | 27.2 | 4.1 | ≈2 |
| 10 | 1083 | 1042 | 961 | 15.0 | 14.6 | ≈2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holst, C.; Janßen, J.; Schmitz, B.; Blome, M.; Dercks, M.; Schoch-Baumann, A.; Blöthe, J.; Schrott, L.; Kuhlmann, H.; Medic, T. Increasing Spatio-Temporal Resolution for Monitoring Alpine Solifluction Using Terrestrial Laser Scanners and 3D Vector Fields. Remote Sens. 2021, 13, 1192. https://doi.org/10.3390/rs13061192
Holst C, Janßen J, Schmitz B, Blome M, Dercks M, Schoch-Baumann A, Blöthe J, Schrott L, Kuhlmann H, Medic T. Increasing Spatio-Temporal Resolution for Monitoring Alpine Solifluction Using Terrestrial Laser Scanners and 3D Vector Fields. Remote Sensing. 2021; 13(6):1192. https://doi.org/10.3390/rs13061192
Chicago/Turabian StyleHolst, Christoph, Jannik Janßen, Berit Schmitz, Martin Blome, Malte Dercks, Anna Schoch-Baumann, Jan Blöthe, Lothar Schrott, Heiner Kuhlmann, and Tomislav Medic. 2021. "Increasing Spatio-Temporal Resolution for Monitoring Alpine Solifluction Using Terrestrial Laser Scanners and 3D Vector Fields" Remote Sensing 13, no. 6: 1192. https://doi.org/10.3390/rs13061192
APA StyleHolst, C., Janßen, J., Schmitz, B., Blome, M., Dercks, M., Schoch-Baumann, A., Blöthe, J., Schrott, L., Kuhlmann, H., & Medic, T. (2021). Increasing Spatio-Temporal Resolution for Monitoring Alpine Solifluction Using Terrestrial Laser Scanners and 3D Vector Fields. Remote Sensing, 13(6), 1192. https://doi.org/10.3390/rs13061192







