The Estimation of Magnetite Prospective Resources Based on Aeromagnetic Data: A Case Study of Qihe Area, Shandong Province, China
Abstract
:1. Introduction
2. Theory and Methods
2.1. Extraction Method for Magnetite-Caused Magnetic Anomaly
2.2. Regularization Inversion Method
2.3. Combined Model Weighting Function
2.4. Constraints on Model Parameters
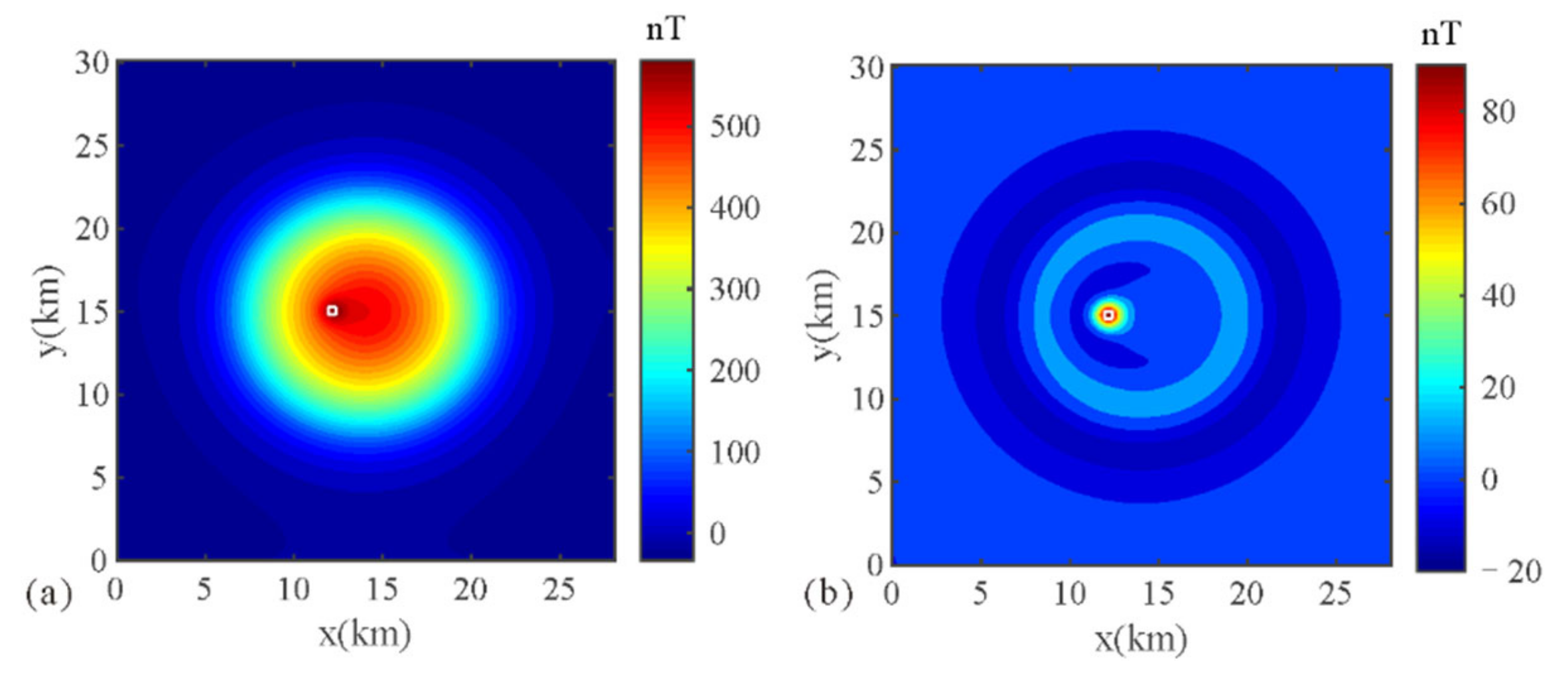
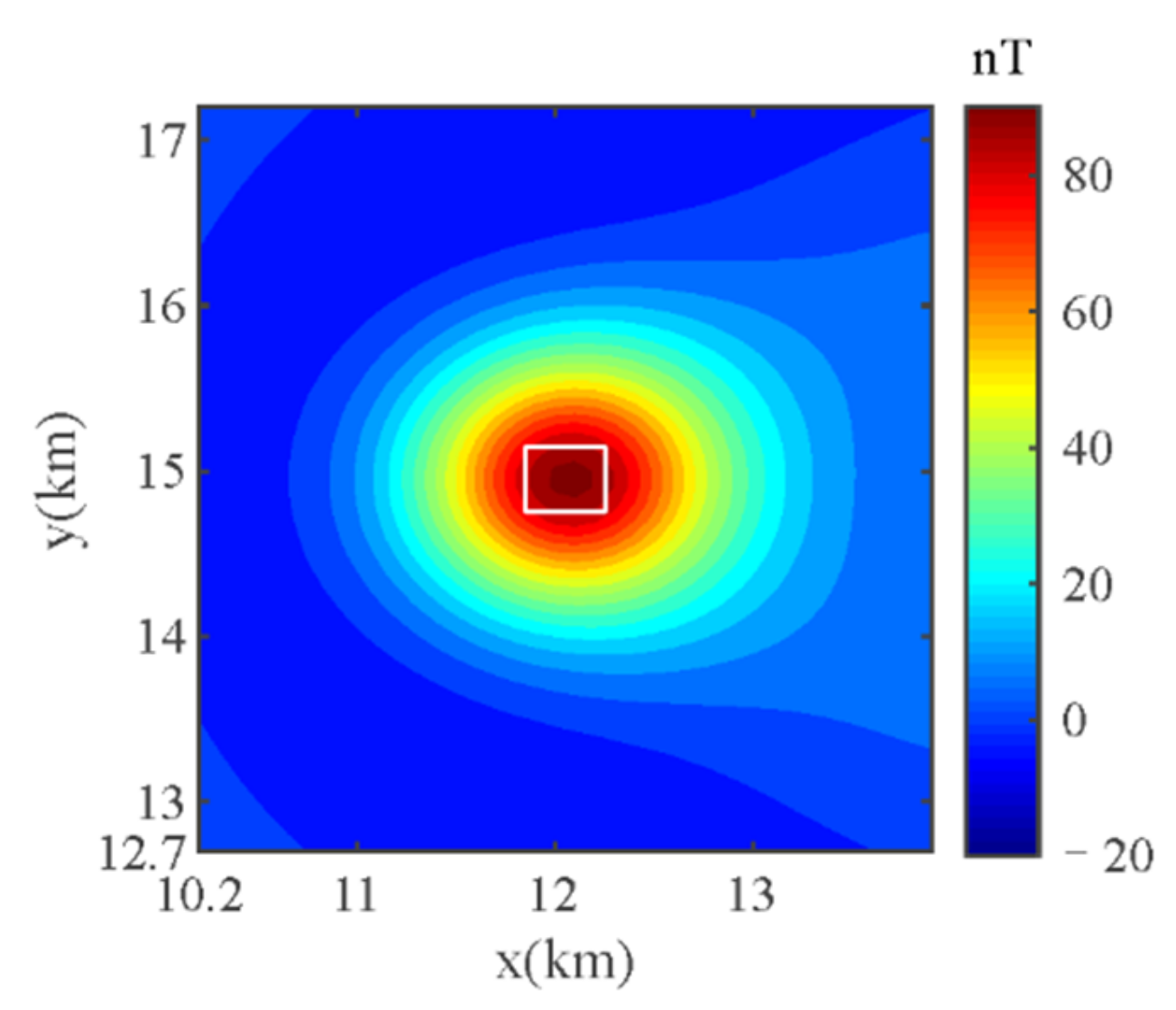
3. Synthetic Model Test
4. Real Data Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiong, S.Q. Innovation and application of airborne geophysical exploration technology. J. Geomech. 2020, 26, 791–818. [Google Scholar] [CrossRef]
- Schmid, S.M.; Kissling, E. The arc of the western Alps in the light of geophysical data on deep crustal structure. Tectonics 2000, 19, 62–85. [Google Scholar] [CrossRef]
- Etgen, J.; Gray, S.H.; Zhang, Y. An overview of depth imaging in exploration geophysics. Geophysics 2009, 74, WCA5–WCA17. [Google Scholar] [CrossRef]
- Malehmir, A.; Juhlin, C.; Wijns, C.; Urosevic, M.; Valasti, P.; Koivisto, E. 3D reflection seismic imaging for open-pit mine planning and deep exploration in the Kevitsa Ni-Cu-PGE deposit, northern Finland. Geophysics 2012, 77, WC95–WC108. [Google Scholar] [CrossRef] [Green Version]
- Dzikunoo, E.A.; Vignoli, G.; Jørgensen, F.; Yidana, S.M.; Banoeng-Yakubo, B. New regional stratigraphic insights from a 3D geological model of the Nasia sub-basin, Ghana, developed for hydrogeological purposes and based on reprocessed B-field data originally collected for mineral exploration. Solid Earth 2020, 11, 349–361. [Google Scholar] [CrossRef] [Green Version]
- Zaher, M.A.; Saibi, H.; Mansour, K.; Khalil, A.; Soliman, M. Geothermal exploration using airborne gravity and magnetic data at Siwa Oasis, Western Desert, Egypt. Renew. Sustain. Energy Rev. 2018, 82, 3824–3832. [Google Scholar] [CrossRef]
- Smith, R.S.; O’Connell, M.D.; Poulsen, L.H. Using airborne electromagnetics surveys to investigate the hydrogeology of an area near Nyborg, Denmark. Near Surf. Geophys. 2004, 2, 123–130. [Google Scholar] [CrossRef]
- Murphy, B.S. Airborne geophysics and the Indian scenario. J. Indian Geophyiscal Union 2007, 11, 1–28. [Google Scholar]
- Soengkono, S. Deep interpretation of gravity and airborne magnetic data of the central Taupo Volcanic Zone. In Proceedings of the 33rd New Zealand Geothermal Workshop, Auckland, New Zealand, 21–23 November 2011. [Google Scholar]
- Battalgazy, N.; Madani, N. Categorization of mineral resources based on different geoatatistical simulation algorithms: A case study from an iron ore deposit. Nat. Resour. Res. 2019, 28, 1329–1351. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Zhu, Z.X.; Yan, J.D. The application of SD method in mineral resources reserves calculation in the Jiguanzi Copper-gold deposit, Daye, Hubei province. Geol. Prospect. 2004, 40, 82. [Google Scholar]
- Ars, J.M.; Tarits, P.; Hautot, S.; Bellanger, M.; Coutant, O.; Maia, M. Joint inversion of gravity and surface wave data constrained by magnetotelluric: Application to deep geothermal exploration of crustal fault zone in felsic basement. Geothermics 2019, 80, 56–68. [Google Scholar] [CrossRef]
- Jiang, W.; Korsch, R.J.; Doublier, M.P.; Duan, J.; Costelloe, R. Mapping Deep Electrical Conductivity Structure in the Mount Isa region, Northern Australia: Implications for Mineral Prospectivity. J. Geophys. Res. Solid Earth 2019, 124, 10655–10671. [Google Scholar] [CrossRef] [Green Version]
- Heinonen, S.; Malinowski, M.; Hloušek, F.; Gislason, G.; Buske, S.; Koivisto, E.; Wojdyla, M. Cost-effective seismic exploration: 2D reflection imaging at the Kylylahti massive sulfide deposit, Finland. Minerals 2019, 9, 263. [Google Scholar] [CrossRef] [Green Version]
- McCafferty, A.E.; Phillips, J.D.; Driscoll, R.L. Magnetic and gravity gradiometry framework for mesoproterozoic iron oxide-apatite and iron oxide-copper-gold deposits, southeast Missouri. Econ. Geol. 2016, 111, 1859–1882. [Google Scholar] [CrossRef]
- Yang, D.; Oldenburg, D.W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit. Geophysics 2012, 77, B23–B34. [Google Scholar] [CrossRef]
- Koné, A.Y.; Nasr, I.H.; Traoré, B.; Amiri, A.; Inoubli, M.H.; Sangaré, S.; Qaysi, S. Geophysical Contributions to Gold Exploration in Western Mali According to Airborne Electromagnetic Data Interpretations. Minerals 2021, 11, 126. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Alfouzan, F.A.; Cox, L.; Alotaibi, A.; Alyousif, M.; Sunwall, D.; Endo, M. Large-scale 3D modeling and inversion of multiphysics airborne geophysical data: A case study from the Arabian Shield, Saudi Arabia. Minerals 2018, 8, 271. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Sun, S.; Lu, H. Application of Airborne Electromagnetics and Magnetics for Mineral Exploration in the Baishiquan–Hongliujing Area, Northwest China. Remote Sens. 2021, 13, 903. [Google Scholar] [CrossRef]
- Martinez, C.; Li, Y. Lithologic characterization using airborne gravity gradient and aeromagnetic data for mineral exploration: A case study in the Quadrilátero Ferrífero, Brazil. Interpretation 2015, 3, SL1–SL13. [Google Scholar] [CrossRef]
- Airo, M.L.; Loukola-Ruskeeniemi, K. Characterization of sulfide deposits by airborne magnetic and gamma-ray responses in eastern Finland. Ore Geol. Rev. 2004, 24, 7–84. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.V.; Ferraccioli, F.; Jordan, T.A.; Matsuoka, K.; Zakrajsek, A.; Ghidella, M.; Greenbaum, J.S. Exploring the Recovery Lakes region and interior Dronning Maud Land, East Antarctica, with airborne gravity, magnetic and radar measurements. Geol. Soc. Lond. Spec. Publ. 2018, 461, 23–34. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Carranza, E.J.M. Performance evaluation of RBF-and SVM-based machine learning algorithms for predictive mineral prospectivity modeling: Integration of SA multifractal model and mineralization controls. Earth Sci. Inform. 2019, 12, 277–293. [Google Scholar] [CrossRef]
- Granek, J. Application of Machine Learning Algorithms to Mineral Prospectivity Mapping. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2016. [Google Scholar]
- Melo, A.T.; Li, Y. September. Geology differentiation of geophysical inversions using machine learning. In Proceedings of the International Workshop on Gravity, Electrical & Magnetic Methods and Their Applications, Xi’an, China, 19–22 May 2019. [Google Scholar]
- Kim, D.; Choi, J.; Kim, D.; Byun, J. Predicting mineralogy using a deep neural network and fancy PCA. SEG Tech. Program Expand. Abstr. 2020. [Google Scholar] [CrossRef]
- Bai, P.; Vignoli, G.; Viezzoli, A.; Nevalainen, J.; Vacca, G. (Quasi-) Real-Time Inversion of Airborne Time-Domain Electromagnetic Data via Artificial Neural Network. Remote Sens. 2020, 12, 3440. [Google Scholar] [CrossRef]
- Zahra, H.S.; Oweis, H.T. Application of high-pass filtering techniques on gravity and magnetic data of the eastern Qattara Depression area, Western Desert, Egypt. NRIAG J. Astron. Geophys. 2016, 5, 106–123. [Google Scholar] [CrossRef] [Green Version]
- Utsugi, M. 3-D inversion of magnetic data based on the L1-L2 norm regularization. Earth Planets Space 2019, 71, 73. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.J.; Li, Y.G. Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model. Geophys. J. Int. 2014, 197, 882–899. [Google Scholar] [CrossRef] [Green Version]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef] [Green Version]
- Fournier, D.; Oldenburg, D.; David, K. Robust and flexible mixed-norm inversion. SEG Tech. Program Expand. Abstr. 2016, 1542–1547. [Google Scholar] [CrossRef]
- Li, Y.G.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Li, Y.G.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Commer, M. Three-dimensional gravity modelling and focusing inversion using rectangular meshes. Geophys. Prospect. 2011, 59, 966–979. [Google Scholar] [CrossRef]
- Zhdanov, M.S. Geophysical Inverse Theory and Regularization Problems; Elsevier: Amsterdam, The Netherlands, 2002; Volume 36. [Google Scholar]
- Silva, J.B.; Medeiros, W.E.; Barbosa, V.C. Gravity inversion using convexity constraint. Geophysics 2000, 65, 102–112. [Google Scholar] [CrossRef]
- Gao, X.H. The Study and Application of 3D Inversion Methods of Gravity & Magnetic and Their Gradient Tensor Data; Jilin University: Changchun, China, 2019. [Google Scholar]
- Gomez-Ortiz, D.; Agarwal, B.N.P. 3DINVER. M: A MATLAB program to invert the gravity anomaly over a 3D horizontal density interface by Parker-Oldenburg’s algorithm. Comput. Geosci. 2005, 31, 513–520. [Google Scholar] [CrossRef]
- Gao, X.H.; Sun, S.Y. Comment on “3DINVER.M: A MATLAB program to invert the gravity anomaly over a 3D horizontal density interface by Parker-Oldenburg’s algorithm”. Comput. Geosci. 2018, 127, 133–137. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.Y. Solution of Ill-Posed Problem; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef] [Green Version]
- Last, B.J.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Vignoli, G.; Deiana, R.; Cassiani, G. Focused inversion of vertical radar profile (VRP) traveltime data. Geophysics 2012, 77, H9–H18. [Google Scholar] [CrossRef]
- Vignoli, G.; Sapia, V.; Menghini, A.; Viezzoli, A. Examples of improved inversion of different airborne electromagnetic datasets via sharp regularization. J. Environ. Eng. Geophys. 2017, 22, 51–61. [Google Scholar] [CrossRef]
- Sun, J.J.; Li, Y.G. Geophysical inversion using petrophysical constraints with application to lithology differentiation. SEG Tech. Program Expand. Abstr. 2011. [Google Scholar] [CrossRef] [Green Version]
- Rezaie, M.; Moradzadeh, A.; Kalate, A.N. 3D gravity data-space inversion with sparseness and bound constraints. J. Min. Environ. 2017, 8, 227–235. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, J.G.; Li, F.; Chen, C.; Mei, B.; Jin, S.G.; Dohm, J.H. A new bound constraints method for 3-D potential field data inversion using Lagrangian multipliers. Geophys. J. Int. 2015, 201, 267–275. [Google Scholar] [CrossRef]
- Guillen, A.; Menichetti, V. Gravity and magnetic inversion with minimization of a specific functional. Geophysics 1984, 49, 1354–1360. [Google Scholar] [CrossRef]
- Zhdanov, M.; Tolstaya, E. Minimum support nonlinear parametrization in the solution of a 3D magnetotelluric inverse problem. Inverse Probl. 2004, 20, 937. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Barbosa, V.C.F.; Silva, J.B.C. Generalized compact gravity inversion. Geophysics 1994, 59, 57–68. [Google Scholar] [CrossRef]
- Hao, X.Z.; Yang, Y.H.; Li, Y.P.; Gao, L.H.; Chen, L. Ore-controlling Characteristics and Prospecting criteria of iron deposits in Qihe area of Western Shandong. J. Jilin Univ. Earth Sci. Ed. 2019, 49, 982–991. [Google Scholar]
- Wu, C.P.; Yu, C.C.; Wang, W.P.; Ma, X.B.; Fan, Z.G.; Zhu, H.W. Physical characteristics of rocks and ores and their application in Qihe area, Western Shandong. Adv. Earth Sci. 2019, 34, 1099–1107. [Google Scholar]
- Wu, C.P.; Yu, C.C.; Zhou, M.L.; Wang, W.P.; Ma, X.B.; Li, S.Q. Residual calculation of airborne and ground magnetic field and its prospecting application in heavily covered plain area. Prog. Geophys. 2020, 35, 0663–0668. [Google Scholar] [CrossRef]
- Zhu, Y.Z.; Zhou, M.L.; Gao, Z.J.; Zhang, X.B. The discovery of the Qihe-Yucheng skarn type rich iron deposit in Shandong and its exploration significance. Geol. Bull. China 2018, 37, 938–944. [Google Scholar]
- Wang, W.P.; Wu, C.P.; Ma, X.B. Aeromagnetic field feature and iron ore target prospecting in deep coverage area of Qihe in Shandong Province. Geol. Surv. China 2020, 7, 23–29. [Google Scholar] [CrossRef]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Xiong, S.; Yu, C.; Zhang, D.; Wu, C. The Estimation of Magnetite Prospective Resources Based on Aeromagnetic Data: A Case Study of Qihe Area, Shandong Province, China. Remote Sens. 2021, 13, 1216. https://doi.org/10.3390/rs13061216
Gao X, Xiong S, Yu C, Zhang D, Wu C. The Estimation of Magnetite Prospective Resources Based on Aeromagnetic Data: A Case Study of Qihe Area, Shandong Province, China. Remote Sensing. 2021; 13(6):1216. https://doi.org/10.3390/rs13061216
Chicago/Turabian StyleGao, Xiuhe, Shengqing Xiong, Changchun Yu, Dishuo Zhang, and Chengping Wu. 2021. "The Estimation of Magnetite Prospective Resources Based on Aeromagnetic Data: A Case Study of Qihe Area, Shandong Province, China" Remote Sensing 13, no. 6: 1216. https://doi.org/10.3390/rs13061216
APA StyleGao, X., Xiong, S., Yu, C., Zhang, D., & Wu, C. (2021). The Estimation of Magnetite Prospective Resources Based on Aeromagnetic Data: A Case Study of Qihe Area, Shandong Province, China. Remote Sensing, 13(6), 1216. https://doi.org/10.3390/rs13061216



