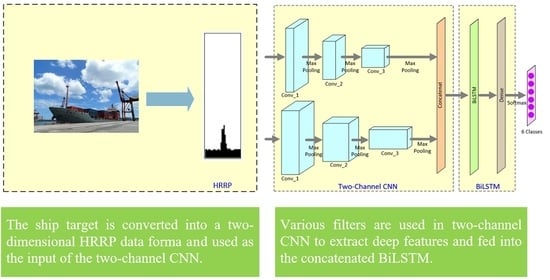
We conducted experiments on the HRRP dataset to evaluate the effectiveness of the proposed approach. The experiments are divided into two parts according to the computing platforms.
The first parts of the test were performed on the CPU of a notebook equipped with Intel®Core™ i5-7300HQ CPU @ 2.50 GHz × 2, 16 GB RAM and NVIDIA GeForce GTX 1050 GPU. The software was programmed using Python 3.6 and mainly based on the deep-learning framework TensorFlow 1.9.0 + Keras 2.2.4.
Experiments 1 to 3 were executed on the CPU platform. According to various condition settings, the parameter settings for which LSTM or BiLSTM exhibited a high recognition accuracy were determined. Based on the results of Experiments 1–3, Experiment 4 was performed to determine how to concatenate a two-channel CNN with LSTM or BiLSTM. Then, the designed deep neural network was executed on the CPU and GPU platforms to determine the highest recognition accuracy according to various condition settings and analyze the time cost.
5.2. Experiments
The split rate of the dataset was divided into the training set and the test set and affected the recognition accuracy of the training model. It is well known that the neural networks usually perform well with a lot of training data. According to our previous study [
15], we have used different split ratios of the training and test datasets in the experiments, which also confirm this result. Therefore, we will no longer discuss the split ratio of training and test datasets in this study. In these experiments, all HRRP data were randomly divided at a ratio of 7:3, which resulted in 145,282 samples of training dataset and 62,263 samples of test dataset. In the training process, 20% of the training dataset was used as the validation dataset, and the accuracy of the validation dataset was used to evaluate the quality of the model. The initial learning rate was set to 0.0001, and the batch size was 300.
Experiment 1: The number of layers in LSTM was fixed as one layer, and the number of neurons was increased in this layer for experiments.
Table 2 lists that the overall test accuracy was between 98% and 99%. When the number of hidden layer neurons gradually increased, the accuracy also increased. When the number of neurons was 300, the test accuracy was 98.77%. As the number of neurons increased to 500, the increase in test accuracy was marginal. Therefore, an increase in neurons improved accuracy. Although the optimal accuracy was achieved when the number of neurons was approximately 500, the increment was not high. For similar experiments with BiLSTM, when the number of neurons was 500, the highest test accuracy of 98.96% was achieved.
Experiment 2: The previous experiment demonstrated that as the number of neurons increased, the test accuracy increased. Therefore, the second experiment was performed to investigate whether the use of multilayer LSTM affects the accuracy of the network. Here, 300 neurons were evenly distributed in two, three and four layers of LSTM.
Table 3 indicates that the test accuracy did not increase significantly as the number of LSTM layers increased (the number of neurons in each layer decreased). Multiple LSTM layers required more test time, which is not conducive to practical applications. When the number of neurons was 100 and the three LSTM layers were used, the optimal accuracy of 98.85% was achieved. Furthermore, the training time of a single-layer LSTM of 300 was longer than that of a single-layer LSTM. Therefore, an overly complex architecture does not considerably improve the test accuracy but increases the time cost. Experiments were conducted in a similar manner with BiLSTM. When the number of neurons was 100 and LSTM was three layered, the optimal test accuracy of 99.06% was achieved.
Experiment 3: The previous two experiments revealed that fixing the total number of neurons and increasing the number of LSTM layers did not improve the accuracy considerably. Although Experiment 1 revealed that the optimal test accuracy was achieved for approximately 500 neurons, the benefit was not substantially higher than that for 300 neurons for various numbers of layers. In Experiment 3, the number of LSTM layers was increased under a fixed 300 neurons in each layer.
Table 4 displays that the highest test accuracy was obtained when the number of neurons in each layer was 300. The test accuracy did not increase with the number of LSTM layers. Overly complex architecture does not improve the test accuracy but increases time constraints. However, Experiments 3 and 4 revealed that with two LSTM layers, the network with more neurons in each layer had a higher test accuracy. Too many LSTM layers resulted in decreased test accuracy.
Experiment 4: The experiments were first simulated on the CPU to determine a satisfactory concatenated network structure. The aforementioned experiments indicated that optimal results were obtained when two layers of LSTM were used and the number of neurons in each layer was 300. Therefore, we used a two-channel CNN to concatenate with LSTM and BiLSTM, respectively. First, the number of neurons in each LSTM layer was set to 300, and the number of LSTM layers was fixed to two. Then, a test accuracy of 99.15% was obtained by concatenating the two-channel CNNs with the two-layer LSTM in 160.5 s, which is high. Because the proposed network structure is complex, we speculate that an overly complex network cannot considerably improve recognition accuracy. As displayed in
Table 5, we concatenated the two-channel CNN with one-layer LSTM and obtained a test accuracy of 99.11%. This accuracy is not considerably lower than that for concatenating two-layer LSTM. A similar experiment was conducted for the BiLSTM experiment. A test accuracy of 99.21% was obtained when a two-channel CNN was concatenated with a two-layer BiLSTM. When the number of BiLSTM layers was set to 1, the test accuracy was 99.24%. For the final experiment, we concatenated a two-channel CNN with one-layer LSTM and BiLSTM. As presented in
Table 6, when the number of neurons was 300, the two-channel CNN concatenated with one-layer BiLSTM achieved the optimal test accuracy of 99.24%.
Table 5 and
Table 6 indicate that the proposed model exhibited a superior recognition accuracy, regardless of whether it was concatenated with LSTM or BiLSTM. The execution results on the GPU differed slightly from those of the CPU. However, reproduction of the accuracy was difficult despite repeated tests. However, the difference in the test result when using the GPU was less than 0.1%. Studies have revealed that this phenomenon could be attributed to the complex set of GPU libraries, some of which may introduce their own randomness and prevent accurate reproduction of the results. Regarding time cost evaluation, we analyzed the results from various execution platforms. Because our model is complex, the data of 62,263 chips of HRRP ship data were tested in 178.65 s when executed on the CPU, which indicates that approximately 2.87 ms are required to recognize a chip of HRRP ship data. When executed on the GPU, testing was completed in 18.38 s, which indicates that approximately 0.30 ms are required to recognize a chip of HRRP ship data. For radar systems, a dwell time is typically 10–20 ms. Therefore, the time required for the proposed deep-learning model for radar systems is feasible. System-on-chips equipped with GPUs can be used in radar systems.
Figure 10 displays the confusion matrix of the recognition results using the proposed two-channel CNN concatenated with BiLSTM model.
Figure 10a presents the results for the model running on the CPU, and
Figure 10b displays the results for the model running on the GPU. The results of the confusion matrix indicate that ships with similar HRRPs do have higher chances of being confused.
For the CPU model, Delta ships were incorrectly predicted as Alpha ships 59 times; Alpha ships were incorrectly predicted as Delta ships 69 times; Epsilon ships were incorrectly predicted as Delta ships in 94 cases; Delta ships were incorrectly predicted as Epsilon ships in 41 cases.
For the GPU model, Delta ships were incorrectly predicted as Alpha ships 54 times; Alpha ships were incorrectly predicted as Delta ships 74 times; Epsilon ships were incorrectly predicted as Delta ships in 70 cases; Delta ships were incorrectly predicted as Epsilon ships in 60 cases.
From the analysis of the aforementioned results, although the confusion matrices of the data in different environments were not the same, the results of ships easily confused with each other were consistent and with no violation.
Figure 11 illustrates the recognition accuracy curves of the proposed two-channel CNN–BiLSTM model.
Figure 11a presents the results for the model running on the CPU, and
Figure 10b displays the confusion matrix for the model running on the GPU.
Figure 12 illustrates the loss curve of the proposed two-channel CNN–BiLSTM model.
Figure 11a displays the recognition accuracy curve of the model running on the CPU, and
Figure 11b displays the recognition accuracy of the model running on the GPU.
Figure 11 and
Figure 12 indicate that the accuracy of the validation set did not increase considerably after approximately 60 epochs, and the loss of the validation set did not decrease considerably after approximately 60 epochs. According to our experimental records, when running on the CPU, the highest accuracy of 99.27% was obtained in 63 epochs in the validation set, and the loss in the validation set was 2.44%. When running on the GPU, the accuracy of the validation set reached the highest accuracy of 99.29% in 73 epochs, and the loss of the validation set was 2.47%.
Finally, the results were compared with some well-known network architectures. As displayed in
Table 7, we summarized all the experiments performed on the same HRRP dataset and conducted with the same training and validation datasets. Comparisons of LeNet, AlexNet, ZFNet and VGG16 revealed that deeper networks may not achieve superior results. However, deeper layers exhibited superior results in the VGG architecture.
Table 7 indicates that the proposed approach outperformed the two-channel LeNet and AlexNet.