3.2. Feature Extraction and Matching Performances in Low-Light Conditions
All tests were conducted using fixed camera station systems (see
Section 2.2) whose stereo-pair orientation was performed in optimal daytime conditions and with the support of several ground control points (GCP). However, performing an image block orientation might still be required (e.g., if the stereo-pair relative orientation changes over time). In this context, it is worth assessing if a standard structure from motion procedure (e.g., the one implemented in Metashape) can extract enough tie points to estimate a reliable orientation solution for the stereo-pairs.
Figure 4a,b show the number of valid tie points extracted at each ISO speed setting for Sites A, B and C (acquisitions A1, A2, A3 and A4 for Site A, acquisition B1 for Site B and acquisitions C1 and C2 for Site C). The figure refers to the image block for which the images were not pre-processed with the Wallis filter.
If Wallis-filtered images are used, the number of extracted keypoints is much higher, as expected by the increase in the gray value variance in areas with uniform texture. The number of valid extracted tie points, on the other hand, was significantly lower using Wallis-filtered images (ca. 50% on average). While, at first sight, this could have been seen as contradictory, it should be noted that, especially with an increasing level of noise (i.e., with a higher ISO speed), the filter tends to amplify the noise itself, leading to a sort of random identification of keypoints. The identification of distinctive features is, therefore, driven by the high variability of the gray value where noise occurs, rather than by the gray value variability where the object texture shows relevant features. As a consequence, most of the keypoints extracted do not result in valid homologous points during feature matching. This hypothesis was confirmed by visual inspection of keypoints and matched tie points performed on a sample of both raw and pre-processed (Wallis-filtered) stereo-pairs.
It can be observed that the number of extracted tie points is strongly dependent on the site and acquisition features: in Site A, the number of tie points is much higher (more than 4600 for acquisition A1 using ISO 200) than Sites B and C (less than 1000 for Site B and around 1400 for Site C). It is worth noting that during the daytime, a total of 5800 tie points were extracted for Site A, whereas a total of 1800 and 2100 tie points were extracted for Site B and for Site C, respectively. Even with similar acquisition settings, a significant variability was experienced for different acquisitions. For instance, in Site A, with lower ISO speeds (e.g., ISO 200), the number of valid matches for acquisition A3 (cloudy weather conditions) was approximately half of the one obtained in A1 (clear sky). For the same site, some acquisitions produced a high number of matches even with a high ISO speed (e.g., more than 900 valid tie points with ISO 25,600 in A4), while others performed much worse with a lower ISO speed (see, for instance, the 190–200 matches in A2 and A3 at ISO 6400). For Site A, the reduced number of valid tie points with a higher ISO speed was evident from the beginning (e.g., the valid matches for ISO 3200 are one third of the ones for ISO 200), while, for Sites B and C, the number of extracted tie points tended to slightly decrease for ISO speeds lower than 6400.
The number of extracted valid tie points is not necessarily a good indicator of the actual achievable quality of the image orientation. Image point accuracy, spatial distribution in the image frame and the possibility of identifying a lower or greater number of GCP on the image strongly affect the final result. Moreover, to correctly assess the quality of the orientation solution, the most reliable approach would be to identify a good number of check points and compare their estimated coordinates (dependent on the actual accuracy of the stereo-pair orientation) with known coordinates surveyed during the daytime with independent (and hopefully more precise) instrumentation. Unfortunately, such approach was quite impractical at the tested sites given the intrinsic difficulty in correctly identifying natural object features on the night-time images (identifying the GCP for every single acquisition represented a great effort already) and the time required to perform the check point identification on all 672 stereo-pairs.
3.3. DSM Reconstruction Accuracy
In this section, the DSM reconstruction accuracy obtained with different camera setups and exposition values is presented and analyzed.
As introduced in
Section 2.3, the influence of pre-processing image equalization and enhancement provided by the use of a Wallis filter should be carefully verified. Many dense matching algorithms for point cloud reconstruction use a similar (or the same) local radiometric model correction for brightness and contrast invariance during template matching and, therefore, the use of Wallis-filtered images might not improve the results.
Table 5 reports the aggregated average RMS (Root Mean Square) differences with respect to (w.r.t.) the reference model for each test site considering the DSM generation by using both original (raw) or pre-processed (with the Wallis filter) images.
It is worth noting that regardless of the site, the Wallis pre-processed images always produced worse results, even if the differences from the two datasets were very small (at maximum, for Site B, Wallis-filtered images produced 3.4% worse results). This seems to indicate that the improved average value and variance of the gray value, even if they make the textures of the object surface for a human observer more evident, do not positively affect the matching algorithm performance. On the contrary, probably due to roundoff truncation during the radiometric transformation, the results are slightly worse.
It might be interesting to evaluate the response for all the ISO speed settings of the images.
Figure 5 shows the average RMS differences for every single site and ISO speed. The DSM obtained for the three sites clearly showed different behaviors. For Site A, the use of Wallis-filtered data produced slightly worse results (maximum 1.3% worse). As far as Sites A and B are considered, for low ISO speeds, up to ISO 1600, the higher the ISO speed, the worse the results. For higher speeds, the behavior was reversed: the differences were smaller for higher ISO speeds. Site A ISO speed 51,200 (the cameras used at Sites B and C have a maximum ISO speed of 25,600) is the only case for which the Wallis DSM are slightly better than the raw image-generated ones (0.1% better). On the contrary, for Site C, the lower the ISO speed considered, the worse the difference between Wallis-filtered and raw image DSM.
In the following, since in any case the discrepancies between raw and Wallis-filtered image DSM accuracies are very small (the worst case being for Site B with a low ISO speed where Wallis DSM were only 5% less accurate), only the raw image-generated DSM will be considered.
The box plots reported in
Figure 6a–c for Sites A, B and C, respectively, represent the level of accuracy achieved for the different test sites using different ISO speed settings. For Site B, having just one acquisition period and this at lower ISO (i.e., ISO 200 and ISO 280), only a single camera parameter combination can be obtained (shutter speed = 30 s, aperture = f/2.8 and EV
r = +1).
As expected, the RMS of the differences tends to increase with a higher ISO speed for all the different sites. The images with a higher ISO speed become noisier and, consequently, the image point matching becomes less accurate. At the same time, with higher ISO values, the repeatability of the results is lower with a wider range of variation. In Site A, for instance, the reconstructed DSM with ISO 200 report an RMS of the differences between 35 and 43 mm (mean RMS is 38.7 mm and the standard deviation is 3.9 mm), while for ISO 12,800, for which the maximum range of variation is reported, the differences vary between 34 and 67 mm (mean RMS is 47.7 mm with a standard deviation of 8.3 mm). For the highest ISO speed (ISO 51,200), the range is between 42 and 67 mm with an average RMS of 55 mm (ca. 40% higher than ISO 200) and a standard deviation of 7.2 mm.
For the other sites, the ranges of variation appear significantly more compact for the same ISO speed settings. However, the number of acquisitions (B1, C1 and C2) and stereo-pairs considered (117 for Site B and 239 for Site C) was lower than for Site A (four different acquisitions with a total of 316 stereo-pairs). For Site B, the average RMS is almost constant up to ISO 6400 (ranging between 43 and 47 mm) and starts growing for higher ISO speeds. The average RMS for ISO 25,600 is 57.3 mm (ca. 32% higher than the best average RMS obtained for ISO 2200). As in the previous case, higher ISO values increase the variability of the results in the same class: excluding ISO 200 and ISO 280, for which only one stereo-pair was considered, the standard deviations range between 3.9 (ISO 400) and 10.3 mm (ISO 25,600).
Similar results, although with smaller standard deviations, can be observed for Site C. The average RMS, for lower ISO speeds, is almost constant, varying from 42 (ISO 280) to 44 mm (ISO 3200). Then, the accuracy of the DSM becomes significantly lower with higher ISO values: for ISO 25,600, the evaluated RMS ranges between 44 and 70 mm with an average value of 55.1 mm (ca. 31% worse than ISO 280) and a standard deviation of 6.2 mm.
For Site A, if every single acquisition (A1, A2, A3 and A4) is considered independently, it can be shown that in two cases (A1 and A2), the RMS is higher, for most of the ISO speed settings, than the other two acquisitions (A3 and A4).
Figure 7a,b report the average RMS and standard deviation of RMS, respectively, for each acquisition and for each ISO speed. It can be seen that acquisition A3 has some issues, especially for high ISO speeds.
The previous results have shown that using a high ISO strongly influences the overall accuracy and repeatability of the DSM reconstruction. The study of the influence of the other two acquisition parameters (shutter speed and aperture) would also provide more insights into the best camera configuration for low-light conditions. Therefore, in the current experiments, several combinations of shutter and aperture were considered for image acquisition while keeping the ISO speed and the exposure level (EVr) fixed. As an example, considering an ISO speed of 12800 and a specific relative exposure value (e.g., EVr = 0), Equation (4) is satisfied using a shutter speed of 30 s and setting the aperture to f/11. Decreasing the shutter interval by one stop and simultaneously increasing the aperture by one stop (e.g., shutter is now 15 s and aperture is set to f/8), Equation (4) is still satisfied and, as far as the exposure value is concerned, the two acquisition parameter sets can be considered equivalent.
Figure 8 shows the average increment (or decrement if negative) of the RMS of the differences between the night-time DSM and the reference 3D model considering different shutter/aperture combinations for each site. Please note that, for simplicity, in
Figure 8, the combination with the highest possible shutter (30 s) is considered as a reference (i.e., all the RMSs are compared to the ISO and EV
r corresponding to the 30 s shutter DSM).
Figure 8 clearly shows that using longer exposure times (shutter), and consequently smaller apertures, usually leads to better results. This is also observed for a limited to low RMS increase (i.e., indicating a worse DSM accuracy) for Site A and, to a minor extent, for Site C. On the contrary, combinations of longer exposure time for Site B outperform the others, and a significant decrease in accuracy is experienced (almost 50% worse) with very short exposure times. This result seems a bit counterintuitive compared to best practices for daytime acquisition, for which it is well known that the use of a too small aperture (which in this context would consequently mean setting longer exposure times) reduces the sharpness of the image.
Finally, the influence of over- or under-exposition on DSM accuracy was considered. Following the same line of thoughts as in the previous analysis, the DSM accuracy obtained with different exposure values was analyzed. Considering a DSM obtained with a neutral relative exposure value (EV
r = 0) as a reference, its accuracy can be compared with the accuracy of all the under-exposed (EV
r = +1) or over-exposed (EV
r = −1) models with similar exposure settings. In particular, the results shown in
Figure 9 refer to the sum of models acquired with a one stop higher or lower ISO speed and the same shutter and aperture, models with a one stop higher or lower aperture and the same ISO speed and shutter and models with the same ISO speed and aperture but with one stop longer or shorter exposure times. The use of correctly exposed images involves the best gray value dynamic range and, most likely, well-contrasted features on the images. This should increase the accuracy of the image matching algorithm during the DSM reconstruction. However, as previously pointed out, higher exposure levels (e.g., obtained using a higher ISO speed) can also imply a greater level of noise. As shown in
Figure 2, under-exposed shots usually produce a more compact gray value histogram (less contrast).
Figure 9 shows the increment in RMS (a positive value indicates less accurate results) of DSM comparisons for the different sites. Results are also presented for all three sites together (All sites) using under- or over-exposed images. Note that for Site A, only full-step EV over-/under-exposed images were acquired (EV
r = −1 and EV
r = +1), while for Sites B and C, also half-step EVs were considered (EV
r = −0.5 and EV
r = +0.5). For Site A, the images correctly exposed generate the worst results. If under-exposed generated DSM are considered only, an RMS of 3.4% can be observed. For the other two sites, such behavior is also confirmed: for Site B, the over-exposed images are less accurate while the under-exposed ones are more accurate than EV
r = 0. For Site C, over-exposed and correctly exposed DSM produce similar results, but the under-exposed ones are, on average, more accurate (1.8%). In all cases, the average differences range from −3.4% (Site A—under-exposed (more accurate)) to +2.0% (Site B—over-exposed (less accurate)).
3.4. Failed DSM Reconstruction
According to
Table 4, the proposed processing workflow did not always produce a valid DSM reconstruction with the matching parameters indicated in
Section 2.5. The problem was particularly evident for Site A but different for each acquisition period: for acquisition A1, 18% of the DSM cannot be processed, whereas this is 50% for acquisition A2 and 30% for acquisition A3, while acquisition A4 produced the highest number of valid DSM with a failure ratio of only 11%. On the contrary, for the other two test sites, just few (i.e., 1% for Site B) or no (for Site C) models failed.
It should be noted that, by changing the dense matching parameters used for DSM processing and, in particular, down-sampling the images of the stereo-pair, many of (if not all) the DSM could be reconstructed.
Table 6 shows the number of invalid (failed) DSM as a function of the down-sampling ratio used: down-sampling = 1, corresponding to the Metashape “matching quality” = “Ultra High”, means that no down-sampling occurred, while, for instance, down-sampling = 4 (matching quality = “Medium”) means the image size was reduced four times along its width and height.
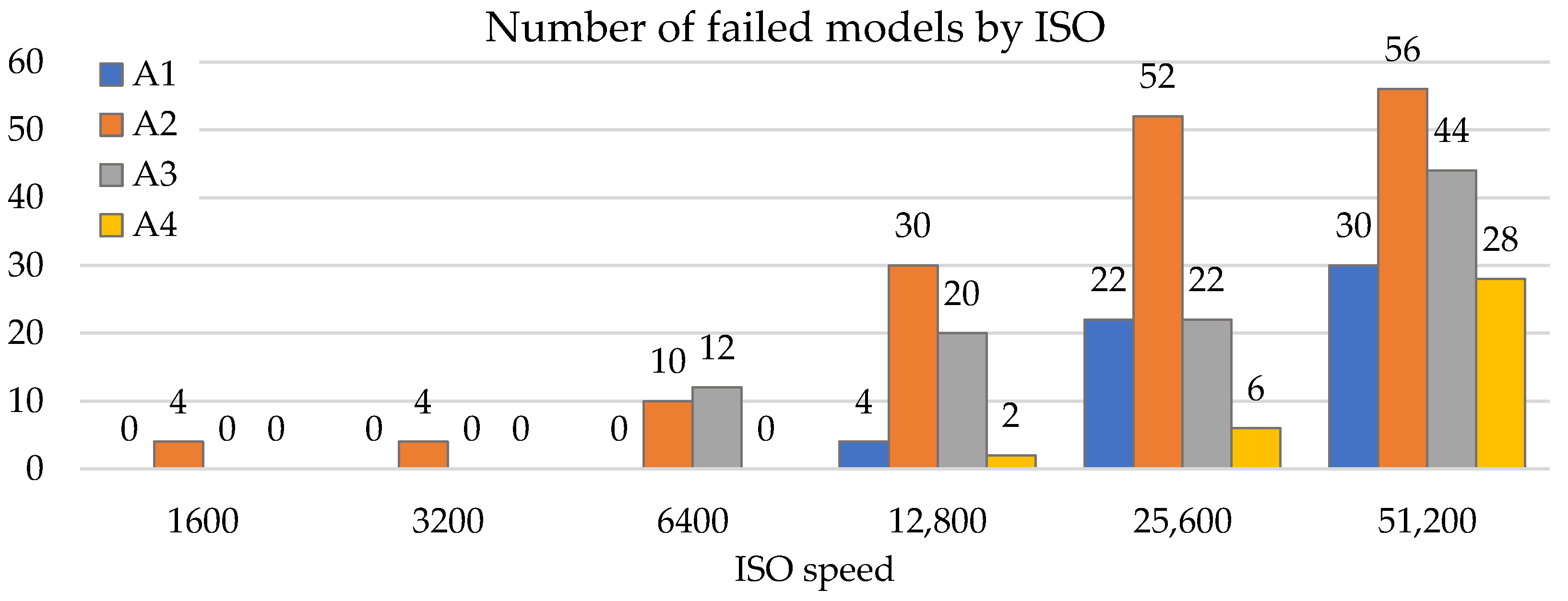
Figure 10 shows the number of failed models for the highest-quality dense matching settings (no down-sampling) grouped by ISO speed: in all cases, a dense matching failure occurred more frequently for higher ISO speeds (usually more than 6400).
At first, the hypothesis that failure in the reconstruction was caused by some movements of the camera during the image acquisition phase was considered. This would reasonably explain why the issue has become relevant for Site A only, where mining operations were active during the acquisition. To verify this assumption, the same models were processed estimating the relative orientation of the stereo-pair, acquiring a set of tie points, as illustrated in
Section 2.5 and
Section 3.2. It should be noted that, at least for acquisitions A1 and A4, even with a high ISO speed, the process uses a high number of tie points and should be considered reliable. Except for one single case, however, for all the failed models, dense matching failure occurred regardless of stereo-pair fixed or relative orientation. These results indicate that the failure of the dense matching process seems not to be related to some unwanted movement of the cameras.
The use of Wallis-filtered images to improve or worsen the successful rate of the dense matching procedure was also considered. In two cases, the DSM reconstruction failed using the raw image pairs but was successful using the Wallis-filtered data. On the contrary, the Wallis dataset failed on 12 stereo-pairs, whereas the raw image set was successfully reconstructed. This seems to confirm the results obtained in
Section 3.3: Wallis filtering, as far as Metashape’s dense matching algorithms are concerned, does not improve the final outcome of the process. On the contrary, to some extent, it generally produces worst results and, in some cases, leads to a failed reconstruction.
3.5. Correlation between Reconstruction Accuracy and Image Quality Scores
Section 2.4 presents several image quality assessment methods and their corresponding image quality scores. According to the results in
Section 3.3, the influence of a selected ISO speed on the accuracy of the final photogrammetric product is evident. However, it is worth noting that with a higher ISO, beside a decrease in average accuracy, the results in the same class (i.e., captured with the same ISO speed) tend to show also a much greater variability (see
Figure 6). In some cases, the best results (minimum RMS) obtained with a very high ISO (e.g., ISO 25,600 or ISO 51,200) are more accurate or at least comparable with the results obtained with much lower ISO speeds. Finding a correlation between the actual level of accuracy achievable during DSM reconstruction and one (or more) image quality score(s) would help in predicting the optimal image for the subsequent processing for a particular low-light camera setup.
All the IQA methods considered in this work are not designed for this specific purpose (with the exception of the Metashape image quality index, MIQI) and some are specifically devoted to express a quality score that simulates the human perception. It is likely (but it is out of the scope of the present work) that the design of a specific image quality assessment method for night-time images focused on the DSM reconstruction accuracy would produce much better results.
To evaluate the correlation between the DSM reconstruction accuracy and the different image quality scores, a simple linear regression between IQA scores (more precisely, the average IQA score of the two images of the stereo-pair) and the corresponding RMS of the difference in the DSM with the reference model was computed by least squares. Then, the coefficient of determination, R2, was used to evaluate the robustness of the prediction of the regression and, consequently, the reliability of a specific IQA score to describe the variability of the DSM accuracy.
The analysis has to be performed considering that different sites have different image block geometries and, consequently, different behaviors in terms of photogrammetric accuracy. It is therefore useless trying to fit a single model to all the data. Additionally, even for the same site, different conditions (e.g., weather, cloud cover) might influence the acquisition and, consequently, the quality of the images. In the following, all the results are considered by first aggregating the data by each single site and then by single acquisition.
Many of the IQA scores considered are strongly dependent on the image average intensity and contrast which makes the raw images, acquired with different relative exposures, prone to provide significantly different IQA scores but similar RMS. It is therefore suggested to use the Wallis-filtered dataset only, so that the images are equalized to a similar intensity and local level of contrast. This should make the IQA score sensitive to the actual noise level of the data only (which should be the main parameter affecting the final DSM accuracy) and not to the image exposure.
Table 5 shows that using Wallis-filtered, instead of raw, images slightly affects the RMS (less than 4%).
Finally, it is worth noting that some methods (i.e., PSNR and SSIM) are FR-IQA, which means that the score computation requires a comparison with a reference image (in this case, the night-time images that provided the lowest RMS are used), while others are objective blind NR-IQA and do not have this limitation.
Table 7 shows the coefficients of determination obtained using the different IQA scores, aggregating all the data by site. The best result for each site is presented in bold.
The SSIM score performs quite well (70–75%) for Sites B and C but provides unsatisfactory results for Site A, where IlNiqe seems to be the most resilient IQA method. However, IlNiqe performs quite poorly for the other two test sites. At Site A, all the other IQA scores give very low predictability of the DSM accuracy as a function of the image quality score, which seems to confirm the need to evaluate their performance considering the data grouped by single acquisition (
Table 8).
An in-depth analysis of the dispersion of IQA score vs. RMS highlights some issues affecting the dataset.
Figure 11 shows a selection of some of the most common problems found in the investigation.
Figure 11a shows a very low PSNR score for some image pairs collected at Site A (visible in the lower left region of the chart), even if the images, after an operator check, do not seem affected by a high level of noise or by other distortion effects. The dashed red line represents the estimated regression model (
R2 coefficient is 4.2%). The same problem seems to affect, in some acquisitions, the RMS of individual image pairs: e.g., in acquisition C2 (see
Figure 11b), a single image pair produced a DSM with a much higher RMS than all the others. It is worth noting that, in Site C, BRISQUE and IlNiqe showed a different behavior if compared with the other test sites, with lower scores (which should indicate a higher image quality) for the image pairs that produced the worst (higher) RMS.
Finally,
Figure 11c shows that the use of MIQI produced, in all sites and acquisitions (in particular, in Site C), two distinct clusters of data points. Following a thorough check of the data, it was concluded that the lower cluster (i.e., with lower image quality) was produced by all the image pairs with an aperture of f/2. It seems, therefore, that the loss of image sharpness, apparently quite drastic, passing from an aperture of f/2.8 to f/2, was well caught by the MIQI algorithm but did not affect the final DSM accuracy.
Considering these issues, all the linear regressions and their corresponding coefficients of determination were computed using a robust regression fitting algorithm, capable of filtering the most evident outliers. For MIQI, the dataset was split considering image pairs with f/2 apertures individually.
Table 9 and
Table 10 show the
R2 of the robust fitted IQA–RMS models: for MIQI, two values are reported, the first referring to the f/2 subset, and the second to the remaining dataset. For the other scores, the difference (in percent) in the coefficient w.r.t. in the not robust fitted test is provided in brackets.
It can be concluded that the actual capability of the IQA scores to explain the accuracy variability of the DSM is strongly site-dependent (and for Site A also acquisition-dependent). SSIM provided very good results for Sites B and C, for both site- and acquisition-grouped data, but its prediction capability results in being much lower for Site A. It should be highlighted once more that SSIM and PSNR are FR-IQA methods and require reference images to evaluate the score. For Site A, on the contrary, IlNiqe and BRISQUE provided the best results: for acquisition A1 (cloudy) and A4 (partly cloudy), where IlNiqe scores an
R2 of ca. 80%, the other IQA methods showed much lower performances (BRISQUE being the second best with ca. 56–57%). For acquisition A2 (partly cloudy), BRISQUE performed much better than the others, while for acquisition A3 (clear sky), the
R2 coefficient resulted in being almost the same for all the IQA scores, with BRISQUE still being the best. According to the results in
Table 7 and
Table 8, MIQI provided very low
R2 coefficients for all sites and acquisitions. However, if the analysis is performed considering two distinct datasets, one with all the images captured with the wider aperture (f/2) and one with all the other images, much better results can be observed.