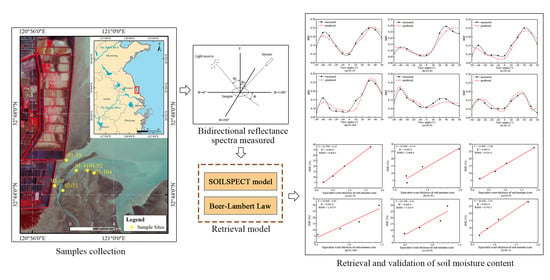
Retrieving Photometric Properties and Soil Moisture Content of Tidal Flats Using Bidirectional Spectral Reflectance
Abstract
:1. Introduction
2. Study Area and Data Sources
2.1. Study Area
2.2. Data Acquisition and Instruments
3. Methodology
3.1. Gradient setting of SMC
3.2. Bidirectional Reflectance Model and its Extension
3.3. Model Parameter Retrieval and Evaluation Methods
4. Results
4.1. Descriptive Statistics of SMC and Particle Size
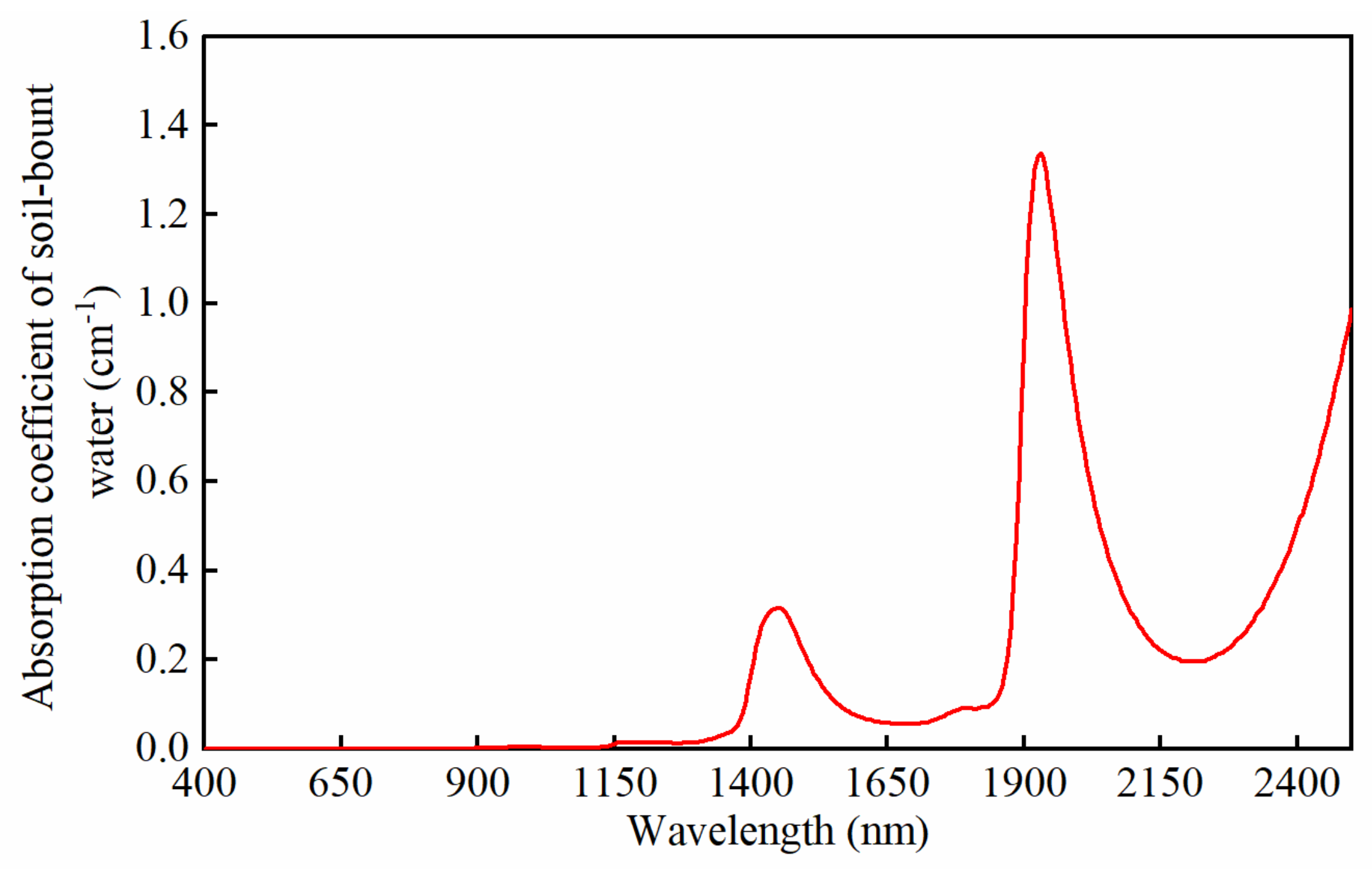
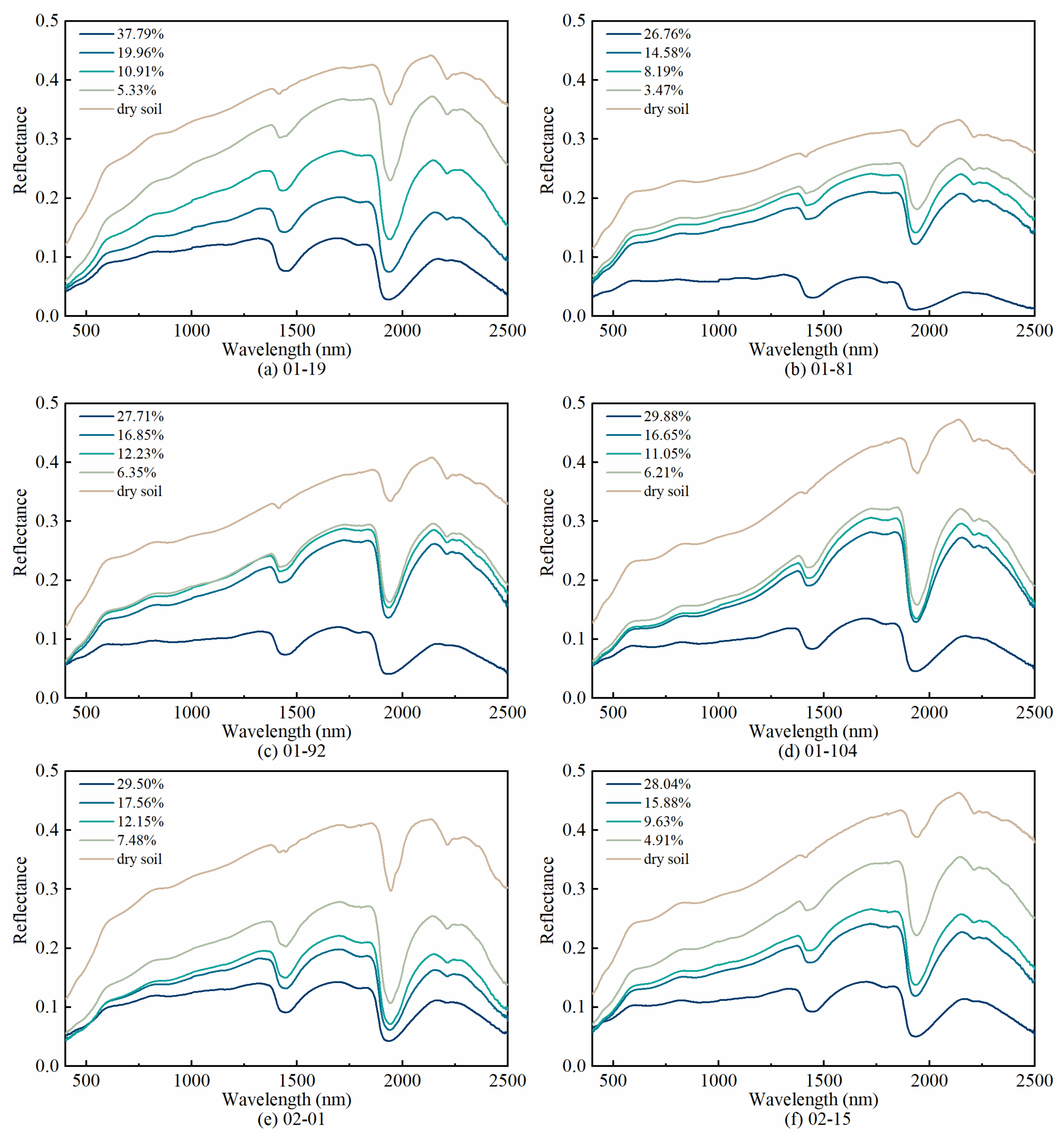
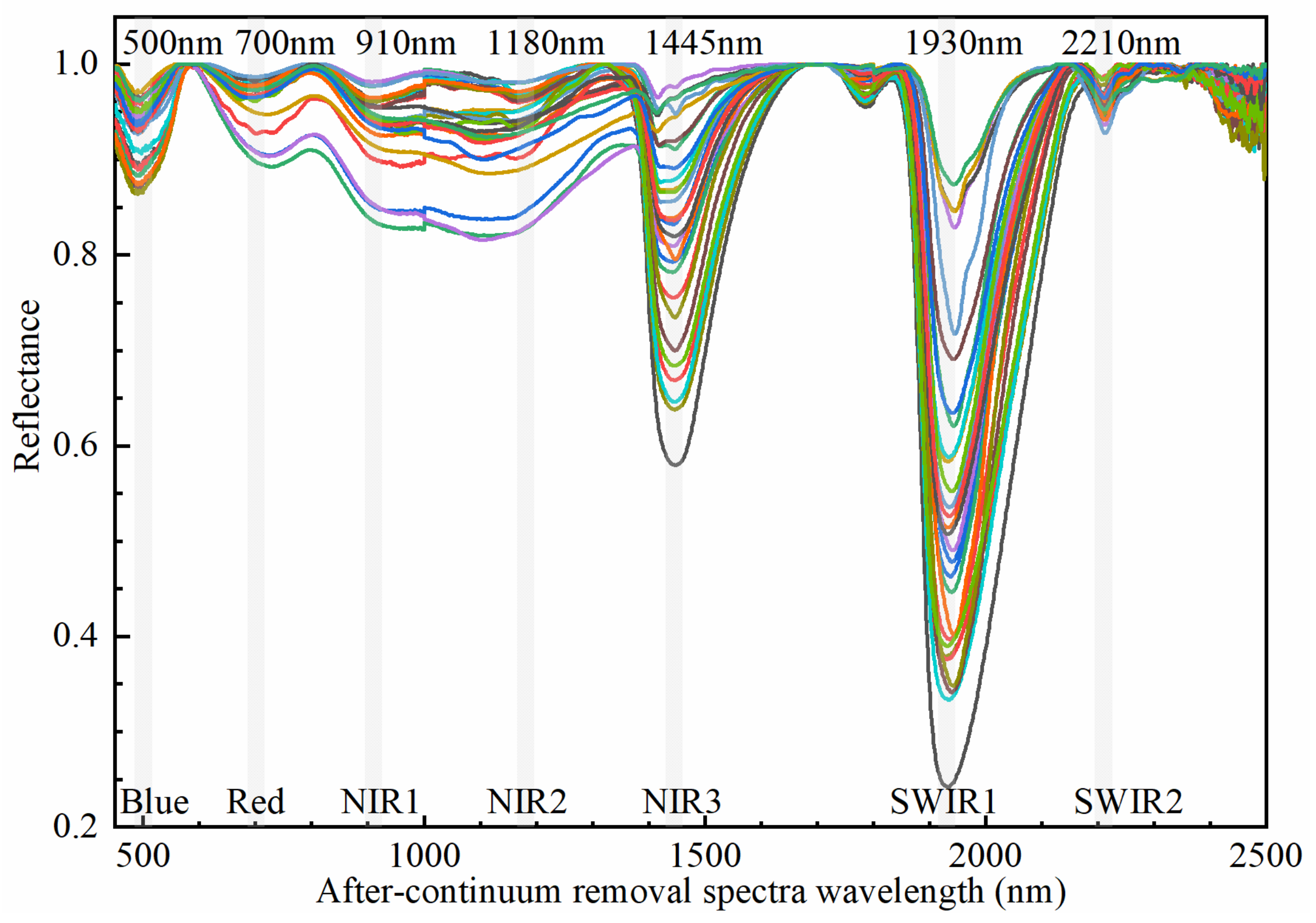
4.2. Reflectance Features of Soil Samples
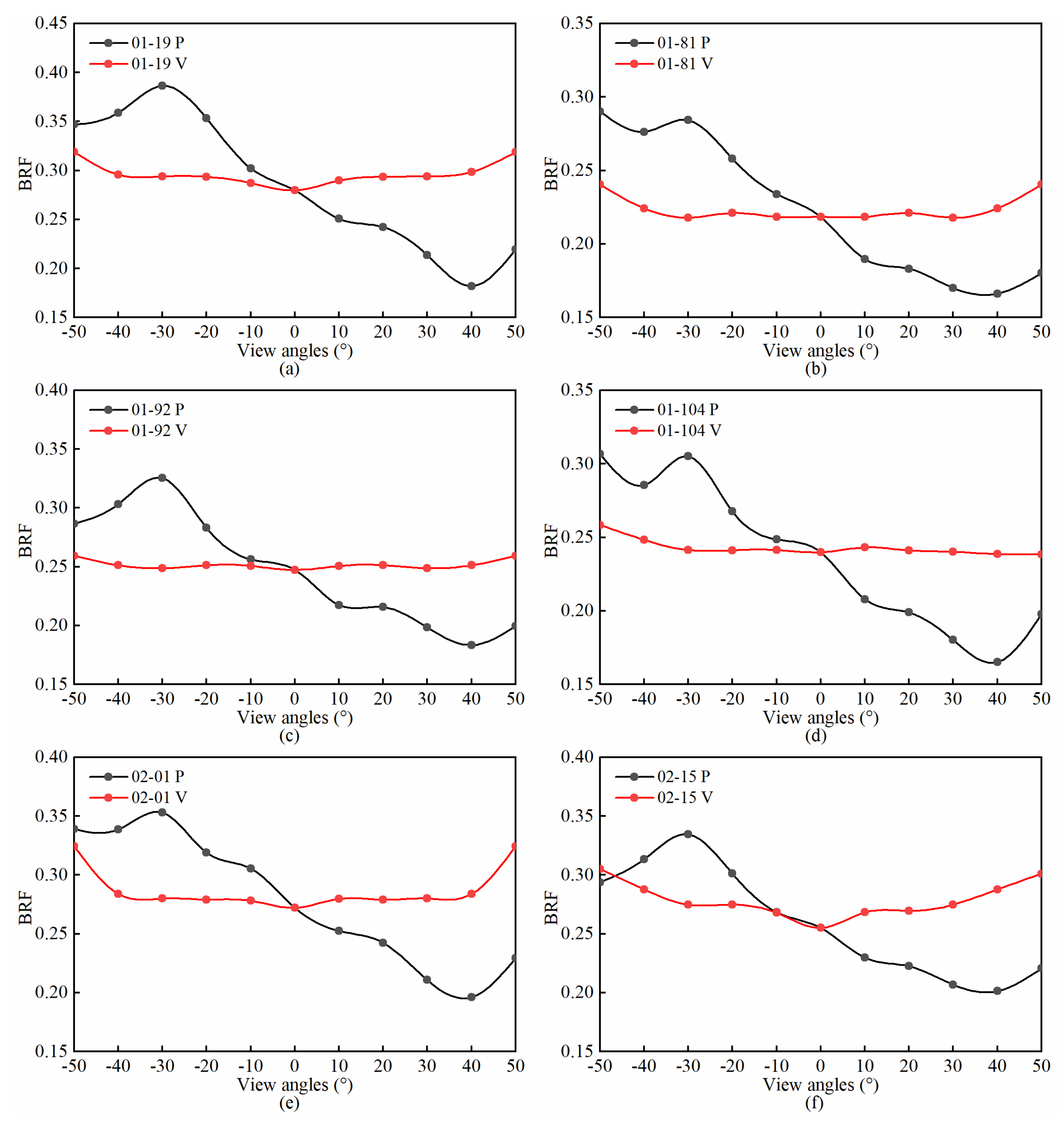
4.3. Retrieval Results of the Model Parameters
4.4. Retrieval Results and Validation of SMC
5. Discussion
6. Conclusions
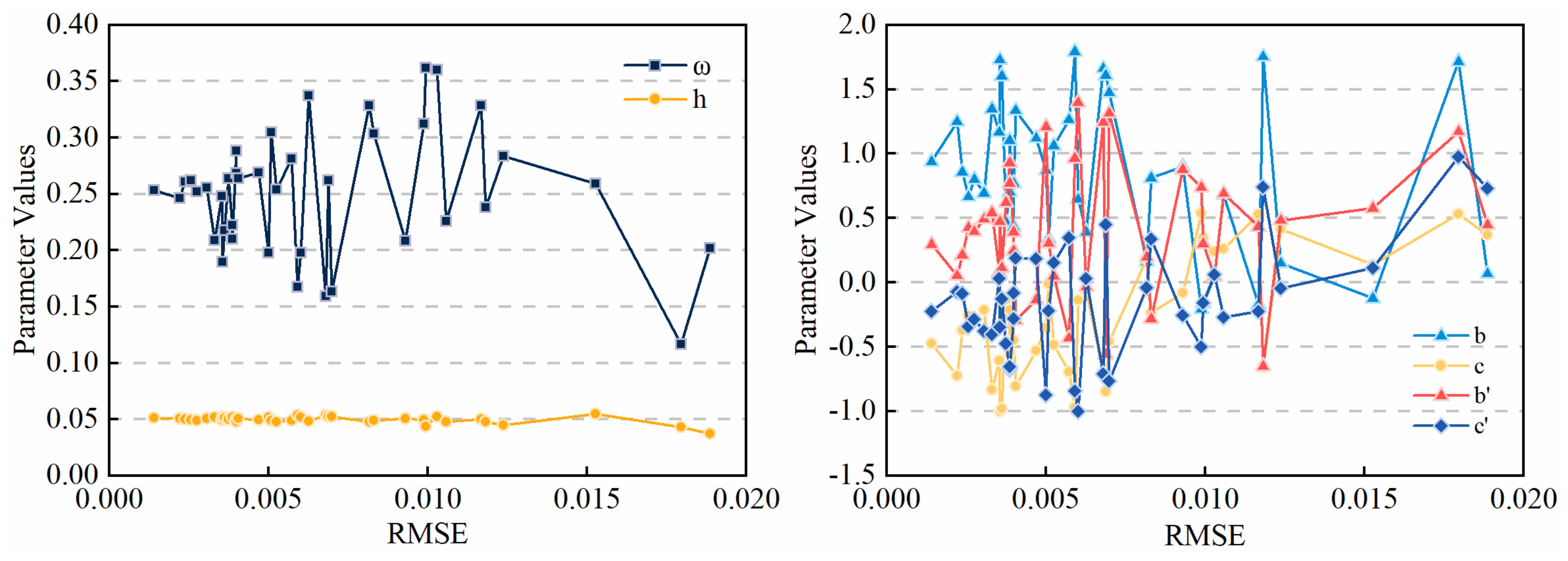
- The stability of each parameter was evaluated by selecting a set of model parameter results from existing studies. The stability results followed the order: h > ω > b > b′ > c > c′, and showed that the soil surface roughness, h, is the most stable among the six parameters.
- Model parameters retrieval was achieved by combining the particle swarm optimization algorithm for seven characteristic bands, which were identified by the continuum removal method. The parameters retrieval procedure was not sensitive to the initial values. Among all the parameters, the single scattering albedo ω had a strong correlation with soil moisture and showed an increasing trend as the soil moisture decreased for each soil sample. The larger the particle size in the dry soil samples was, the smaller the ω was. However, the change in ω with particle size did not demonstrate a general trend for soil samples with different water content. This phenomenon has important implications for using the soil particle size measured in the laboratory as one of the parameters for water content estimation. In this procedure, the soil surface state should be fully considered, especially in tidal flats. In the dry soil samples, the roughness parameter, h, showed an increasing trend as the particle size increased. The four parameters of the phase function, b, c, b′, and c′, had an impact on the scattering of the soil surface. Forward scattering was dominant in the soil surface with the highest moisture, while backscattering was dominant during the gradual drying process.
- A regression analysis of model-estimated soil equivalent water thickness ξ and the measured SMC, demonstrated a significant positive correlation, as the determination coefficient was about 0.95 and the RMSE was 1.58.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murray, N.J.; Phinn, S.R.; DeWitt, M.; Ferrari, R.; Johnston, R.; Lyons, M.B.; Clinton, N.; Thau, D.; Fuller, R.A. The global distribution and trajectory of tidal flats. Nat. Cell Biol. 2019, 565, 222–225. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Morphodynamics of Holocene salt marshes: A review sketch from the Atlantic and Southern North Sea coasts of Europe. Quat. Sci. Rev. 2000, 19, 1155–1231. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Liu, D.; Wang, E.; Liu, K.; Ding, Y.; Yao, P.; Zhao, M. Spatial and seasonal variations of organic carbon distributions in typical intertidal sediments of China. Org. Geochem. 2020, 142, 103993. [Google Scholar] [CrossRef]
- Phang, V.X.H.; Chou, L.M.; Friess, D.A. Ecosystem carbon stocks across a tropical intertidal habitat mosaic of mangrove forest, seagrass meadow, mudflat and sandbar. Earth Surf. Process. Landf. 2015, 40, 1387–1400. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Kettner, A.J.; Overeem, I.; Hutton, E.W.H.; Hannon, M.T.; Brakenridge, G.R.; Day, J.W.; Vorosmarty, C.J.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Oost, A.; Hoekstra, P.; Wiersma, A.; Flemming, B.; Lammerts, E.; Pejrup, M.; Hofstede, J.; van der Valk, B.; Kiden, P.; Bartholdy, J.; et al. Barrier island management: Lessons from the past and directions for the future. Ocean Coast. Manag. 2012, 68, 18–38. [Google Scholar] [CrossRef]
- Passeri, D.L.; Hagen, S.C.; Medeiros, S.C.; Bilskie, M.V.; Alizad, K.; Wang, D. The dynamic effects of sea level rise on low-gradient coastal landscapes: A review. Earth’s Futur. 2015, 3, 159–181. [Google Scholar] [CrossRef]
- Schmutz, P.P.; Namikas, S.L. Measurement and modeling of the spatiotemporal dynamics of beach surface moisture content. Aeolian Res. 2018, 34, 35–48. [Google Scholar] [CrossRef]
- Nield, J.M.; Wiggs, G.F.; Squirrell, R.S. Aeolian sand strip mobility and protodune development on a drying beach: Examining surface moisture and surface roughness patterns measured by terrestrial laser scanning. Earth Surf. Process. Landf. 2010, 36, 513–522. [Google Scholar] [CrossRef]
- Smit, Y.; Donker, J.J.A.; Ruessink, G. Spatiotemporal Surface Moisture Variations on a Barred Beach and their Relationship with Groundwater Fluctuations. Hydrology 2019, 6, 8. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Gong, Z.; Dai, W.; Lu, C.; Zhang, X.; Cybele, S.; Guo, H. Feasibility of Elevation Mapping in Muddy Tidal Flats by Remotely Sensed Moisture (RSM) Method. J. Coast. Res. 2018, 85, 291–295. [Google Scholar] [CrossRef]
- Tan, K.; Chen, J.; Zhang, W.; Liu, K.; Tao, P.; Cheng, X. Estimation of soil surface water contents for intertidal mudflats using a near-infrared long-range terrestrial laser scanner. ISPRS J. Photogramm. Remote. Sens. 2020, 159, 129–139. [Google Scholar] [CrossRef]
- Gaskin, G.; Miller, J. Measurement of Soil Water Content Using a Simplified Impedance Measuring Technique. J. Agric. Eng. Res. 1996, 63, 153–159. [Google Scholar] [CrossRef]
- Edwards, B.L.; Namikas, S.L.; D’Sa, E.J. Simple infrared techniques for measuring beach surface moisture. Earth Surf. Process. Landf. 2012, 38, 192–197. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Bittelli, M.; Pallepati, R.R.; Mahajan, P. Comparison of soil water content estimation equations using ground penetrating radar. J. Hydrol. 2020, 588, 125039. [Google Scholar] [CrossRef]
- De Queiroz, M.G.; da Silva, T.G.F.; Zolnier, S.; Jardim, A.M.D.R.F.; de Souza, C.A.A.; Júnior, G.D.N.A.; de Morais, J.E.F.; de Souza, L.S.B. Spatial and temporal dynamics of soil moisture for surfaces with a change in land use in the semi-arid region of Brazil. Catena 2020, 188, 104457. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Jin, S.; Sun, C.; Wei, X. Evolution of the topography of tidal flats and sandbanks along the Jiangsu coast from 1973 to 2016 observed from satellites. ISPRS J. Photogramm. Remote. Sens. 2019, 150, 27–43. [Google Scholar] [CrossRef]
- Su, S.L.; Singh, D.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Kim, C.-H.; Lee, Y.-K.; Won, J.-S.; Chun, S.-S.; Lee, S. Detecting the intertidal morphologic change using satellite data. Estuar. Coast. Shelf Sci. 2008, 78, 623–632. [Google Scholar] [CrossRef]
- Schmutz, P.P.; Namikas, S.L. Utility of the Delta-T Theta Probe for Obtaining Surface Moisture Measurements from Beaches. J. Coast. Res. 2011, 27, 478. [Google Scholar] [CrossRef]
- Ambrosone, M.; Matese, A.; Di Gennaro, S.F.; Gioli, B.; Tudoroiu, M.; Genesio, L.; Miglietta, F.; Baronti, S.; Maienza, A.; Ungaro, F.; et al. Retrieving soil moisture in rainfed and irrigated fields using Sentinel-2 observations and a modified OPTRAM approach. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102113. [Google Scholar] [CrossRef]
- Price, J.C. On the analysis of thermal infrared imagery: The limited utility of apparent thermal inertia. Remote. Sens. Environ. 1985, 18, 59–73. [Google Scholar] [CrossRef]
- Verhoef, A. Remote estimation of thermal inertia and soil heat flux for bare soil. Agric. For. Meteorol. 2004, 123, 221–236. [Google Scholar] [CrossRef]
- Telling, J.; Lyda, A.; Hartzell, P.; Glennie, C. Review of Earth science research using terrestrial laser scanning. Earth Sci. Rev. 2017, 169, 35–68. [Google Scholar] [CrossRef] [Green Version]
- Baghdadi, N.; Boyer, N.; Todoroff, P.; El Hajj, M.; Bégué, A. Potential of SAR sensors TerraSAR-X, ASAR/ENVISAT and PALSAR/ALOS for monitoring sugarcane crops on Reunion Island. Remote. Sens. Environ. 2009, 113, 1724–1738. [Google Scholar] [CrossRef]
- Lakhankar, T.; Krakauer, N.; Khanbilvardi, R. Applications of microwave remote sensing of soil moisture for agricultural applications. Int. J. Terraspace Sci. Eng. 2009, 2, 81–91. [Google Scholar]
- Weidong, L.; Baret, F.; Xingfa, G.; Qingxi, T.; Lanfen, Z.; Bing, Z. Relating soil surface moisture to reflectance. Remote. Sens. Environ. 2002, 81, 238–246. [Google Scholar] [CrossRef]
- Dalal, R.C.; Henry, R.J. Simultaneous Determination of Moisture, Organic Carbon, and Total Nitrogen by Near Infrared Reflectance Spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Vthi, D.N.; Ha, N.T.T.; Dang, Q.T.; Koike, K.; Trong, N.M. Effective Band Ratio of Landsat 8 Images Based on VNIR-SWIR Reflectance Spectra of Topsoils for Soil Moisture Mapping in a Tropical Region. Remote. Sens. 2019, 11, 716. [Google Scholar] [CrossRef] [Green Version]
- Stoner, E.R.; Baumgardner, M.F.; Weismiller, R.A.; Biehl, L.L.; Robinson, B.F. Extension of Laboratory-measured Soil Spectra to Field Conditions. Soil Sci. Soc. Am. J. 1980, 44, 572–574. [Google Scholar] [CrossRef] [Green Version]
- Khanna, S.; Palacios-Orueta, A.; Whiting, M.L.; Ustin, S.L.; Riaño, D.; Litago, J. Development of angle indexes for soil moisture estimation, dry matter detection and land-cover discrimination. Remote. Sens. Environ. 2007, 109, 154–165. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, X.; Wang, J.; Yang, H.; Huang, W.; Feng, H. A method of estimating soil moisture based on the linear decomposition of mixture pixels. Math. Comput. Model. 2013, 58, 606–613. [Google Scholar] [CrossRef]
- Peng, J.; Shen, H.; He, S.W.; Wu, J.S. Soil moisture retrieving using hyperspectral data with the application of wavelet analysis. Environ. Earth Sci. 2013, 69, 279–288. [Google Scholar] [CrossRef]
- Bablet, A.; Vu, P.; Jacquemoud, S.; Viallefont-Robinet, F.; Fabre, S.; Briottet, X.; Sadeghi, M.; Whiting, M.; Baret, F.; Tian, J. MARMIT: A multilayer radiative transfer model of soil reflectance to estimate surface soil moisture content in the solar domain (400–2500 nm). Remote. Sens. Environ. 2018, 217, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.; Jones, S.B.; Philpot, W.D. A linear physically-based model for remote sensing of soil moisture using short wave infrared bands. Remote. Sens. Environ. 2015, 164, 66–76. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Hanocq, J. Modeling spectral and bidirectional soil reflectance. Remote. Sens. Environ. 1992, 41, 123–132. [Google Scholar] [CrossRef]
- Muller, E.; Décamps, H. Modeling soil moisture–reflectance. Remote. Sens. Environ. 2001, 76, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Stoner, E.R.; Baumgardner, M.F. Characteristic Variations in Reflectance of Surface Soils. Soil Sci. Soc. Am. J. 1981, 45, 1161–1165. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Space Phys. 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 3. Correction for macroscopic roughness. Icarus 1984, 59, 41–59. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Bidirectional Reflectance Spectroscopy: 5. The coherent backscatter opposition effect and aniso-tropic scattering. Icarus 2002, 157, 523–534. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B.; Wells, E. Bidirectional reflectance spectroscopy: 2. Experiments and observations. J. Geophys. Res. Space Phys. 1981, 86, 3055–3060. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 6. Effects of porosity. Icarus 2008, 195, 918–926. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.-J.; Zhao, C.-J.; Huang, W.-J.; Wang, J.-H. Extension of the Hapke bidirectional reflectance model to retrieve soil water content. Hydrol. Earth Syst. Sci. 2011, 15, 2317–2326. [Google Scholar] [CrossRef] [Green Version]
- Chappell, A.; Zobeck, T.M.; Brunner, G. Using bi-directional soil spectral reflectance to model soil surface changes induced by rainfall and wind-tunnel abrasion. Remote. Sens. Environ. 2006, 102, 328–343. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, P.; Liu, Q.; Chappell, A. Retrieving photometric properties of desert surfaces in China using the Hapke model and MISR data. Remote. Sens. Environ. 2009, 113, 213–223. [Google Scholar] [CrossRef]
- Wang, Y. The Mudflat System of China. Can. J. Fish. Aquat. Sci. 1983, 40, s160–s171. [Google Scholar] [CrossRef]
- Hapke, B. Theoretical Photometric Function for the Lunar Surface. Astron. J. 1963, 68, 279. [Google Scholar] [CrossRef]
- Pinty, B.; Verstraete, M.M.; Dickinson, R.E. A physical model for predicting bidirectional reflectances over bare soil. Remote. Sens. Environ. 1989, 27, 273–288. [Google Scholar] [CrossRef]
- Bach, H.; Mauser, W. Modelling and model verification of the spectral reflectance of soils under varying moisture conditions. In Proceedings of the IGARSS ’94—1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–2 August 1994; Volume 4, pp. 2354–2356. [Google Scholar]
- Segelstein, D. The Complex Refractive Index of Water; University of Missouri-Kansas City: Kansas City, MO, USA, 1981. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Ångström, A. The Albedo of Various Surfaces of Ground. Geogr. Ann. 1925, 7, 323–342. [Google Scholar] [CrossRef]
- Planet, W.G. Some comments on reflectance measurements of wet soils. Remote. Sens. Environ. 1970, 1, 127–129. [Google Scholar] [CrossRef]
- Cheng, J.L.; Shi, Z.; Li, H.Y. Measurement and simulation of bi-directional reflectance on three zonal soils in the south-east of China. N. Z. J. Agric. Res. 2007, 50, 1177–1185. [Google Scholar] [CrossRef]
- Yao, Y.M.; Liu, Y.; Gao, M.F.; Chen, Z.X. Hyperspectral inversion of soil moisture content based on SOIL-SPECT model. In Proceedings of the 7th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Hangzhou, China, 6–9 August 2018; pp. 450–455. [Google Scholar]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Goldshleger, N.; Ben-Dor, E.; Benyamini, Y.; Agassi, M.; Blumberg, D.G. Characterization of soil’s structural crust by spectral reflectance in the SWIR region (1.2–2.5 mum). Terra Nova 2001, 13, 12–17. [Google Scholar] [CrossRef]
- Cipra, J.E.; Baumgardner, M.F.; Stoner, E.R.; Macdonald, R.B. Measuring Radiance Characteristics of Soil with a Field Spectroradiometer. Soil Sci. Soc. Am. J. 1971, 35, 1014–1017. [Google Scholar] [CrossRef]
- Eshel, G.; Levy, G.J.; Singer, M.J. Spectral Reflectance Properties of Crusted Soils under Solar Illumination. Soil Sci. Soc. Am. J. 2004, 68, 1982–1991. [Google Scholar] [CrossRef]
- Chen, J.; Menges, C.; Leblanc, S. Global mapping of foliage clumping index using multi-angular satellite data. Remote. Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Nolin, A.W.; Payne, M.C. Classification of glacier zones in western Greenland using albedo and surface roughness from the Multi-angle Imaging SpectroRadiometer (MISR). Remote. Sens. Environ. 2007, 107, 264–275. [Google Scholar] [CrossRef]
- Twomey, S.A.; Bohren, C.F.; Mergenthaler, J.L. Reflectance and albedo differences between wet and dry surfaces. Appl. Opt. 1986, 25, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Philpot, W.D. Soil directional (biconical) reflectance in the principal plane with varied illumination angle under dry and saturated conditions. Opt. Express 2018, 26, 23883–23897. [Google Scholar] [CrossRef] [PubMed]
- Lekner, J.; Dorf, M.C. Why some things are darker when wet. Appl. Opt. 1988, 27, 1278–1280. [Google Scholar] [CrossRef] [PubMed]

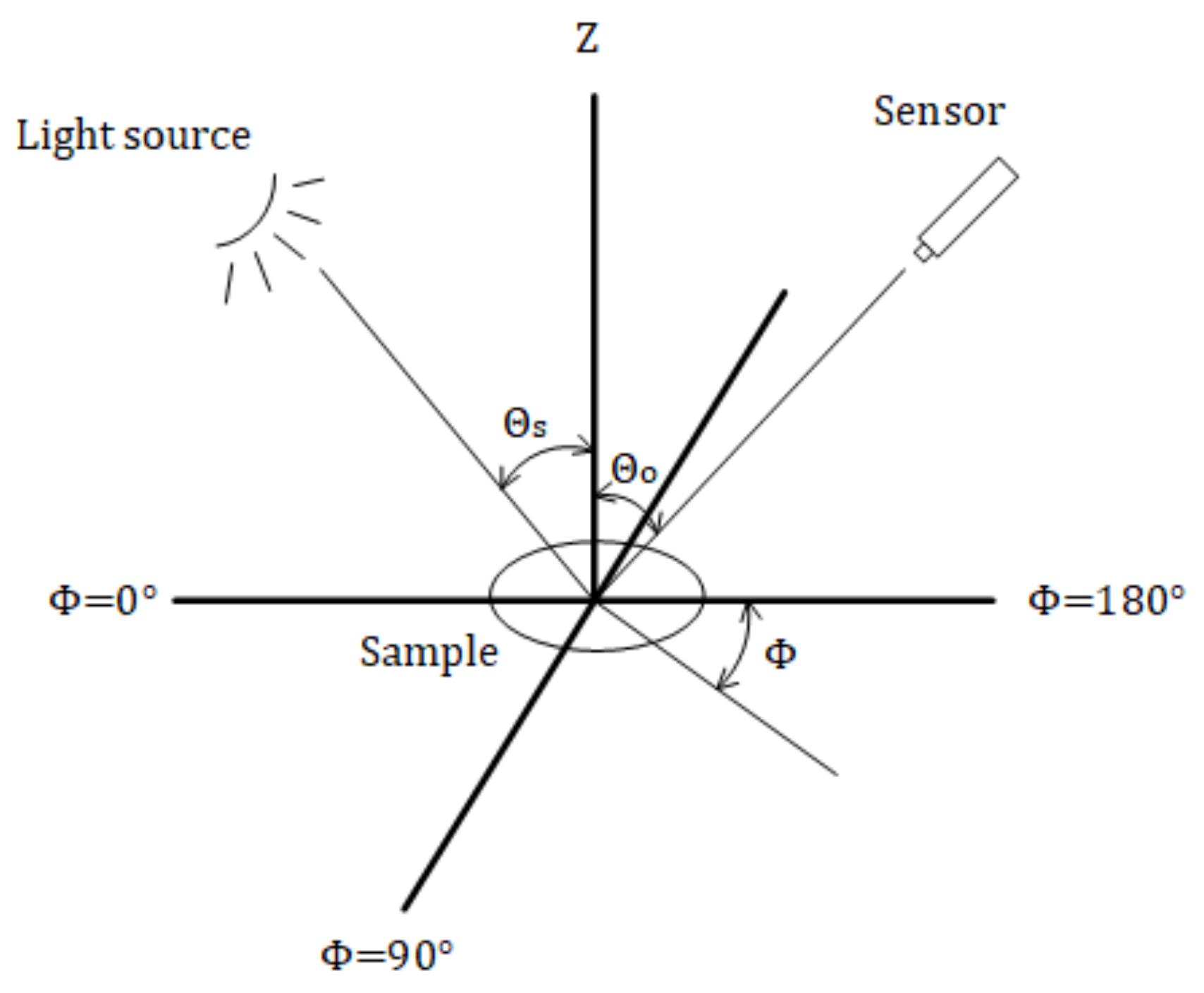




| Light Source | Sensor | ||||||
|---|---|---|---|---|---|---|---|
| Zenith Angle (°) | Azimuth Angle (°) | Zenith Angle (°) | |||||
| 30 | 0 | 0 | 10 | 20 | 30 | 40 | 50 |
| 90 | 0 | 10 | 20 | 30 | 40 | 50 | |
| 180 | 0 | 10 | 20 | 30 | 40 | 50 | |
| 270 | 0 | 10 | 20 | 30 | 40 | 50 | |
| 60 | 0 | 0 | 10 | 20 | 30 | 40 | 50 |
| 90 | 0 | 10 | 20 | 30 | 40 | 50 | |
| 180 | 0 | 10 | 20 | 30 | 40 | 50 | |
| 270 | 0 | 10 | 20 | 30 | 40 | 50 | |
| Parameters | Value Range | |
|---|---|---|
| SOILSPECT model | Single scattering albedo (ω) | 0–1 |
| Soil surface roughness (h) | 0–1.5 | |
| The coefficient of the scattering phase function (b) | −2–2 | |
| The coefficient of the scattering phase function (c) | −1–1 | |
| The coefficient of the scattering phase function (b′) | −2–2 | |
| The coefficient of the scattering phase function (c′) | −1–1 | |
| PSO algorithm | Size of the population (N) | 50–1000 |
| Number of Iterations (g) | 100–4000 | |
| Inertia weight (Ω) | 0.5–1 | |
| Individual learning factor (c1) | 0–4 | |
| Group learning factor (c2) | 0–4 |
| Samples | Soil Moisture Content (%) | Particle Size (%) | |||||
|---|---|---|---|---|---|---|---|
| SMC1 | SMC2 | SMC3 | SMC4 | SAND | SILT | CLAY | |
| 01-19 | 37.79 | 19.96 | 10.91 | 5.33 | 16.44 | 78.27 | 5.29 |
| 01-81 | 26.76 | 14.58 | 8.19 | 3.47 | 85.53 | 12.97 | 1.50 |
| 01-92 | 27.71 | 16.85 | 11.18 | 6.35 | 54.23 | 43.64 | 2.13 |
| 01-104 | 29.88 | 16.65 | 11.05 | 6.21 | 36.78 | 59.87 | 3.35 |
| 02-01 | 29.50 | 17.56 | 12.15 | 7.48 | 28.90 | 66.85 | 4.25 |
| 01-19 | 37.79 | 19.96 | 10.91 | 5.33 | 70.71 | 27.90 | 1.39 |
| Parameter | ω | h | b | c | b′ | c′ |
|---|---|---|---|---|---|---|
| Initial | 0.25 | 0.05 | 1 | −0.5 | 0.25 | −0.2 |
| Mean | 0.250 8 | 0.049 6 | 0.843 5 | −0.266 0 | 0.403 5 | −0.149 4 |
| S.D. | 0.054 5 | 0.003 1 | 0.588 0 | 0.445 4 | 0.497 7 | 0.437 8 |
| Samples | SMC | Characteristic Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| 500 nm | 700 nm | 910 nm | 1180 nm | 1445 nm | 1930 nm | 2210 nm | ||
| 01-19 | SMC1 | 0.336 7 | 0.452 7 | 0.575 0 | 0.603 8 | 0.348 1 | 0.218 2 | 0.524 1 |
| SMC2 | 0.385 0 | 0.552 8 | 0.696 6 | 0.707 8 | 0.705 8 | 0.494 6 | 0.616 9 | |
| SMC3 | 0.511 4 | 0.628 5 | 0.739 2 | 0.737 4 | 0.767 2 | 0.596 1 | 0.703 1 | |
| SMC4 | 0.559 3 | 0.684 8 | 0.805 2 | 0.890 5 | 0.881 8 | 0.832 0 | 0.890 9 | |
| Dry soil | 0.624 1 | 0.725 2 | 0.895 0 | 0.930 7 | 0.934 5 | 0.919 7 | 0.943 7 | |
| 01-81 | SMC1 | 0.242 8 | 0.308 6 | 0.337 2 | 0.383 8 | 0.235 1 | 0.164 5 | 0.428 0 |
| SMC2 | 0.251 8 | 0.318 9 | 0.411 9 | 0.476 8 | 0.427 2 | 0.236 2 | 0.616 9 | |
| SMC3 | 0.276 2 | 0.350 5 | 0.434 2 | 0.496 8 | 0.482 3 | 0.265 2 | 0.687 4 | |
| SMC4 | 0.290 4 | 0.359 9 | 0.480 9 | 0.503 7 | 0.503 6 | 0.305 3 | 0.670 5 | |
| Dry soil | 0.381 8 | 0.489 9 | 0.711 7 | 0.749 2 | 0.778 2 | 0.701 8 | 0.758 5 | |
| 01-92 | SMC1 | 0.258 0 | 0.272 2 | 0.350 1 | 0.422 9 | 0.408 9 | 0.225 8 | 0.528 0 |
| SMC2 | 0.291 6 | 0.384 2 | 0.471 9 | 0.573 5 | 0.559 2 | 0.440 1 | 0.625 2 | |
| SMC3 | 0.302 4 | 0.420 2 | 0.538 8 | 0.595 4 | 0.629 0 | 0.515 3 | 0.627 2 | |
| SMC4 | 0.280 9 | 0.444 9 | 0.582 6 | 0.686 7 | 0.674 4 | 0.585 7 | 0.678 5 | |
| Dry soil | 0.485 8 | 0.610 9 | 0.782 9 | 0.836 4 | 0.837 2 | 0.801 4 | 0.825 2 | |
| 01-104 | SMC1 | 0.234 6 | 0.252 5 | 0.290 9 | 0.387 3 | 0.347 3 | 0.243 4 | 0.428 0 |
| SMC2 | 0.213 2 | 0.330 8 | 0.422 8 | 0.450 0 | 0.505 7 | 0.411 1 | 0.625 2 | |
| SMC3 | 0.288 1 | 0.362 6 | 0.450 7 | 0.541 1 | 0.560 4 | 0.496 9 | 0.616 9 | |
| SMC4 | 0.247 1 | 0.340 8 | 0.487 2 | 0.609 4 | 0.589 0 | 0.560 2 | 0.627 2 | |
| Dry soil | 0.474 8 | 0.650 6 | 0.799 0 | 0.804 6 | 0.832 0 | 0.819 7 | 0.835 7 | |
| 02-01 | SMC1 | 0.339 6 | 0.369 3 | 0.465 1 | 0.477 6 | 0.390 1 | 0.244 7 | 0.624 1 |
| SMC2 | 0.221 7 | 0.353 8 | 0.506 8 | 0.554 2 | 0.445 9 | 0.332 1 | 0.720 5 | |
| SMC3 | 0.265 4 | 0.415 7 | 0.545 1 | 0.593 8 | 0.509 1 | 0.385 1 | 0.782 4 | |
| SMC4 | 0.297 6 | 0.460 2 | 0.640 9 | 0.735 8 | 0.668 3 | 0.467 6 | 0.675 9 | |
| Dry soil | 0.531 4 | 0.685 2 | 0.848 2 | 0.890 7 | 0.905 7 | 0.889 2 | 0.896 6 | |
| 02-15 | SMC1 | 0.175 4 | 0.292 9 | 0.381 2 | 0.404 8 | 0.357 5 | 0.200 3 | 0.424 1 |
| SMC2 | 0.265 2 | 0.328 8 | 0.450 7 | 0.561 1 | 0.521 1 | 0.349 0 | 0.677 2 | |
| SMC3 | 0.231 8 | 0.377 6 | 0.519 4 | 0.615 8 | 0.547 1 | 0.405 3 | 0.693 5 | |
| SMC4 | 0.334 4 | 0.448 3 | 0.567 0 | 0.706 6 | 0.624 7 | 0.496 8 | 0.796 5 | |
| Dry soil | 0.506 0 | 0.562 8 | 0.699 0 | 0.822 8 | 0.817 3 | 0.772 0 | 0.839 3 | |
| Samples | SMC | h | b | c | b′ | c′ | Θ | RMSE |
|---|---|---|---|---|---|---|---|---|
| 01-19 | SMC1 | 0.007 1 | −0.525 7 | 0.053 1 | 0.448 1 | −0.134 0 | 0.175 2 | 0.027 3 |
| SMC2 | 0.032 4 | −0.980 8 | 0.333 9 | 0.672 5 | −0.009 9 | 0.326 9 | 0.017 5 | |
| SMC3 | 0.009 2 | −0.330 3 | 0.060 0 | 0.728 9 | 0.009 0 | 0.110 1 | 0.018 8 | |
| SMC4 | 0.014 9 | −0.817 5 | 0.133 5 | 0.119 4 | 0.189 8 | 0.272 5 | 0.039 0 | |
| Dry soil | 0.042 4 | −0.974 6 | 0.182 4 | 0.666 9 | 0.064 1 | 0.324 9 | 0.028 4 | |
| 01-81 | SMC1 | 0.008 4 | −0.703 7 | 0.591 7 | −0.099 6 | −0.076 9 | 0.234 6 | 0.025 2 |
| SMC2 | 0.019 9 | −0.611 3 | 0.230 9 | 0.642 5 | −0.006 3 | 0.203 8 | 0.018 1 | |
| SMC3 | 0.030 2 | 0.166 9 | −0.006 5 | 0.130 6 | −0.216 5 | −0.055 6 | 0.010 1 | |
| SMC4 | 0.070 8 | 0.576 5 | 0.240 9 | 0.090 4 | −0.209 5 | −0.192 2 | 0.025 5 | |
| Dry soil | 0.157 3 | 0.719 7 | 0.015 4 | −0.009 1 | 0.191 9 | −0.239 9 | 0.035 4 | |
| 01-92 | SMC1 | 0.016 7 | −0.749 4 | 0.585 0 | 0.817 9 | −0.360 3 | 0.249 8 | 0.024 7 |
| SMC2 | 0.016 0 | −0.868 4 | 0.655 3 | 0.822 4 | −0.204 9 | 0.289 5 | 0.010 2 | |
| SMC3 | 0.027 5 | 0.566 9 | −0.072 5 | 0.850 9 | 0.034 2 | −0.189 0 | 0.021 1 | |
| SMC4 | 0.033 3 | 0.760 7 | 0.298 8 | 0.599 7 | −0.240 8 | −0.253 6 | 0.018 2 | |
| Dry soil | 0.091 2 | 0.634 1 | 0.121 2 | 0.217 9 | 0.310 3 | −0.211 4 | 0.020 4 | |
| 01-104 | SMC1 | 0.017 2 | −0.590 9 | 0.395 4 | 0.354 1 | 0.097 3 | 0.197 0 | 0.026 2 |
| SMC2 | 0.029 3 | −0.870 1 | 0.723 5 | 1.013 7 | −0.418 2 | 0.290 0 | 0.020 4 | |
| SMC3 | 0.012 0 | 0.044 3 | 0.285 8 | 0.347 0 | −0.337 6 | −0.014 8 | 0.009 9 | |
| SMC4 | 0.005 3 | 0.577 9 | −0.073 3 | 0.548 3 | −0.614 6 | −0.192 6 | 0.009 1 | |
| Dry soil | 0.053 2 | 0.562 7 | 0.051 0 | 0.495 7 | −0.324 9 | −0.187 6 | 0.022 4 | |
| 02-01 | SMC1 | 0.023 7 | 0.005 7 | 0.144 7 | 1.006 2 | −0.258 0 | −0.001 9 | 0.019 0 |
| SMC2 | 0.009 6 | −0.567 1 | 0.338 6 | 1.091 4 | −0.106 0 | 0.189 0 | 0.008 0 | |
| SMC3 | 0.010 3 | −0.216 0 | −0.108 5 | 0.706 6 | −0.268 3 | 0.072 0 | 0.007 0 | |
| SMC4 | 0.009 4 | −0.029 6 | 0.021 8 | 0.537 1 | −0.414 1 | 0.009 9 | 0.016 9 | |
| Dry soil | 0.062 5 | −0.262 8 | 0.072 1 | 0.421 0 | 0.259 1 | 0.087 6 | 0.028 3 | |
| 02-15 | SMC1 | 0.017 4 | −0.314 6 | 0.321 5 | 1.159 6 | −0.372 2 | 0.104 9 | 0.016 0 |
| SMC2 | 0.024 1 | −0.289 0 | 0.599 2 | 0.620 4 | −0.047 9 | 0.096 3 | 0.016 1 | |
| SMC3 | 0.024 1 | 0.378 4 | −0.047 4 | 0.261 9 | −0.346 8 | −0.126 1 | 0.012 3 | |
| SMC4 | 0.036 9 | 0.448 0 | 0.186 5 | 0.880 4 | −0.512 9 | −0.149 3 | 0.013 4 | |
| Dry soil | 0.112 8 | 0.406 6 | −0.289 5 | 0.324 7 | 0.055 5 | −0.135 5 | 0.023 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Xu, M.; Xu, H.; Zhou, W. Retrieving Photometric Properties and Soil Moisture Content of Tidal Flats Using Bidirectional Spectral Reflectance. Remote Sens. 2021, 13, 1402. https://doi.org/10.3390/rs13071402
Gao C, Xu M, Xu H, Zhou W. Retrieving Photometric Properties and Soil Moisture Content of Tidal Flats Using Bidirectional Spectral Reflectance. Remote Sensing. 2021; 13(7):1402. https://doi.org/10.3390/rs13071402
Chicago/Turabian StyleGao, Chen, Min Xu, Hanzeyu Xu, and Wei Zhou. 2021. "Retrieving Photometric Properties and Soil Moisture Content of Tidal Flats Using Bidirectional Spectral Reflectance" Remote Sensing 13, no. 7: 1402. https://doi.org/10.3390/rs13071402
APA StyleGao, C., Xu, M., Xu, H., & Zhou, W. (2021). Retrieving Photometric Properties and Soil Moisture Content of Tidal Flats Using Bidirectional Spectral Reflectance. Remote Sensing, 13(7), 1402. https://doi.org/10.3390/rs13071402