Quantifying the Impact of Solar Spectra on the Inter-Calibration of Satellite Instruments
Abstract
:1. Introduction
2. Methodology
2.1. Solar Spectra
2.1.1. MCST Solar Spectrum
2.1.2. Kurucz (MODTRAN 4.0)
2.1.3. Thuillier 2003
2.1.4. SOLAR-ISS, Version 2
2.1.5. SCIAMACHY, Version 9
2.1.6. LASP WHI
2.1.7. TSIS-1 SIM
2.1.8. TSIS-1 HSRS
2.2. NOAA-20 VIIRS RSB Calibration
2.3. Resampling of Multiple Solar Spectra
2.4. Computation of ESUN
3. Results and Discussion
3.1. Solar Spectra and ESUN Differences
3.2. Inter-Band Calibration Consistency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haigh, J.D. The Sun and the Earth’s Climate. Living Rev. Sol. Phys. 2007, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48, RG4001. [Google Scholar] [CrossRef]
- Neckel, H.; Labs, D. The solar radiation between 3300 and 12500 Å. Sol. Phys. 1984, 90, 205–258. [Google Scholar] [CrossRef]
- Arvesen, J.C.; Griffin, R.N.; Pearson, B.D. Determination of Extraterrestrial Solar Spectral Irradiance from a Research Aircraft. Appl. Opt. 1969, 8, 2215. [Google Scholar] [CrossRef]
- Thekaekara, M.P.; Kruger, R.; Duncan, C.H. Solar Irradiance Measurements from a Research Aircraft. Appl. Opt. 1969, 8, 1713. [Google Scholar] [CrossRef]
- Neckel, H.; Labs, D. Improved data of solar spectral irradiance from 0.33 to 1.25μ. Sol. Phys. 1981, 74, 231–249. [Google Scholar] [CrossRef]
- Markham, B.L.; Barker, J.L. Radiometric properties of U.S. processed landsat MSS data. Remote Sens. Environ. 1987, 22, 39–71. [Google Scholar] [CrossRef]
- Robel, J.; Graumann, A. NOAA KLM User’s Guide; National Oceanic and Atmospheric Administration: Maryland, MD, USA, 2014.
- McCluney, W.R. The extraterrestrial solar spectrum. Sol. Energy 1974, 15, 319. [Google Scholar] [CrossRef]
- Thuillier, G.; Hersé, M.; Simon, P.C.; Labs, D.; Mandel, H.; Gillotay, D.; Foujols, T. The visible solar spectral irradiance from 350 to 850 nm as measured by the solspec spectrometer during the ATLAS I mission. Sol. Phys. 1998, 177, 41–61. [Google Scholar] [CrossRef]
- Smith, E.V.P.; Gottlieb, D.M. Solar flux and its variations. Space Sci. Rev. 1974, 16, 771–802. [Google Scholar] [CrossRef] [Green Version]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Desnos, Y.L. Working group on calibration and validation. Eur. Space Agency 2002, 22, 2–3. [Google Scholar]
- Kneubuhler, M.; Schaepman, M.; Thome, K.; Baret, F.; Muller, A. Calibration and Validation of Envisat MERIS Part 1: Vicarious Calibration at Rail Road Valley Playa (NV). In Proceedings of the Envisat Validation Workshop, Frascati, Italy, 9–13 December 2002. [Google Scholar]
- Gorroño, J.; Fomferra, N.; Peters, M.; Gascon, F.; Underwood, C.I.; Fox, N.P.; Kirches, G.; Brockmann, C. A radiometric uncertainty tool for the sentinel 2 mission. Remote Sens. 2017, 9, 178. [Google Scholar] [CrossRef] [Green Version]
- Uprety, S.; Cao, C.; Blonski, S.; Shao, X. Assessing the NOAA-20 and S-NPP VIIRS Radiometric Consistency. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization V, Honolulu, HI, USA, 25–26 September 2018; p. 32. [Google Scholar]
- Kurucz, R.L. High Resolution Irradiance Spectrum from 300 to 1000 nm. In Proceedings of the AFRL Transmission Meeting, Monterey, CA, USA, 18–20 January 2006. [Google Scholar]
- Kurucz, R.L. The solar irradiance by computation. In Proceedings of the 17th Annual Conference on Atmospheric Transmission Models, Bedford, MA, USA, 6–8 June 1995; Volume 95, pp. 333–334. [Google Scholar]
- Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Richtsmeier, S.C.; Pukall, B.; et al. MODTRAN4 radiative transfer modeling for atmospheric correction. In Proceedings of the SPIE 3756, Optical Spectroscopic Techniques and Instrumentation for Atmospheric and Space Research III, Denver, CO, USA, 18–23 July 1999. [Google Scholar]
- Zhang, L.; Hu, S.; Yang, H.; Wu, T.; Tong, Q.; Zhang, F. The effects of solar irradiance spectra on calculation of narrow band top-of-atmosphere reflectance. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 49–58. [Google Scholar] [CrossRef]
- Shanmugam, P.; Ahn, Y.H. Reference solar irradiance spectra and consequences of their disparities in remote sensing of the ocean colour. Ann. Geophys. 2007, 25, 1235–1252. [Google Scholar] [CrossRef]
- Bhatt, R.; Doelling, D.R.; Haney, C.; Spangenberg, D.A.; Scarino, B.; Gopalan, A. Clouds and the Earth’s Radiant Energy System strategy for intercalibrating the new-generation geostationary visible imagers. J. Appl. Remote Sens. 2020, 14, 1. [Google Scholar] [CrossRef]
- Thome, K.; Markham, B.; Barker, J.; Slater, P.; Biggar, S. Radiometric calibration of Landsat. Photogramm. Eng. Remote Sens. 1997, 63, 853–858. [Google Scholar]
- Chance, K.; Kurucz, R.L. An improved high-resolution solar reference spectrum for earth’s atmosphere measurements in the ultraviolet, visible, and near infrared. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1289–1295. [Google Scholar] [CrossRef]
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Aaron, D.; Leigh, L.; Mishra, N. The ground-based absolute radiometric calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Shao, X.; Wu, X.; Kondratovich, V.; Li, Z. Validation of early GOES-16 ABI on-orbit geometrical calibration accuracy using SNO method. In Proceedings of the SPIE Optical Engineering + Applications, Earth Observing Systems XXII, San Diego, CA, USA, 6–10 August 2017; p. 30. [Google Scholar]
- Bhatt, R.; Doelling, D.; Scarino, B.; Haney, C.; Gopalan, A. Cross-Calibration of Aqua-MODIS and NPP-VIIRS Reflective Solar Bands for a Seamless Record of CERES Cloud and Flux Properties. In Proceedings of the IGARSS 2018—IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4332–4335. [Google Scholar]
- Uprety, S.; Cao, C.; Shao, X. Radiometric consistency between GOES-16 ABI and VIIRS on Suomi NPP and NOAA-20. J. Appl. Remote Sens. 2020, 14, 032407. [Google Scholar] [CrossRef]
- Li, S.; Ganguly, S.; Dungan, J.L.; Wang, W.; Nemani, R.R. Sentinel-2 MSI Radiometric Characterization and Cross-Calibration with Landsat-8 OLI. Adv. Remote Sens. 2017, 6, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI radiometric cross comparison over desert sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 operational land imager radiometric calibration and stability. Remote Sens. 2014, 6, 12275–12308. [Google Scholar] [CrossRef] [Green Version]
- Doelling, D.R.; Bhatt, R.; Scarino, B.R.; Gopalan, A.; Haney, C.O.; Minnis, P.; Bedka, K.M. A consistent AVHRR visible calibration record based on multiple methods applicable for the NOAA degrading orbits. Part II: Validation. J. Atmos. Ocean. Technol. 2016, 33, 2517–2534. [Google Scholar] [CrossRef]
- Labs, D.; Neckel, H. Transformation of the absolute solar radiation data into the “International Practical Temperature Scale of 1968”. Sol. Phys. 1970, 15, 79–87. [Google Scholar] [CrossRef]
- Pierce, A.K.; Slaughter, C.D.; Weinberger, D. Solar limb darkening in the interval 7404-24 018 Å, II. Sol. Phys. 1977, 52, 179–189. [Google Scholar] [CrossRef]
- Kurucz, R.L.; Furenlid, I.; Brault, J.; Testerman, L. Solar Flux Atlas from 296 to 1300 nm; National Solar Observatory Atlas: New Mexico, NM, USA, 1984. [Google Scholar]
- Pierce, A.K. Relative Solar Energy Distribution in the Spectral Region 10,000–25,000 a. Astrophys. J. 1954, 119, 312. [Google Scholar] [CrossRef]
- Acharya, P.; Berk, A.; Bernstein, L.; Robertson, D.; Chetwynd, J. Recent Upgrades to MODTRAN—New Solar Irradiance and Instrument Scanning Functions; National Solar Observatory: Boulder, CO, USA, 1998. [Google Scholar]
- Cebula, R.P.; Hilsenrath, E.; Guenther, B. Calibration of the Shuttle Borne Solar Backscatter Ultraviolet Spectrometer. In Proceedings of the SPIE 1109, Optical Radiation Measurements II, Orlando, FL, USA, 27–31 March 1989; Volume 1109, p. 205. [Google Scholar]
- Cebula, R.P.; Thuillier, G.O.; VanHoosier, M.E.; Hilsenrath, E.; Herse, M.; Brueckner, G.E.; Simon, P.C. Observations of the solar irradiance in the 200–350 nm interval during the ATLAS-1 Mission: A comparison among three sets of measurements-SSBUV, SOLSPEC, and SUSIM. Geophys. Res. Lett. 1996, 23, 2289–2292. [Google Scholar] [CrossRef]
- Fontenla, J.M.; Avrett, E.H.; Loeser, R. Energy balance in the solar transition region. III—Helium emission in hydrostatic, constant-abundance models with diffusion. Astrophys. J. 1993, 406, 319. [Google Scholar] [CrossRef]
- Kurucz, R. Atomic and Molecular Data for Opacity Calculations. Rev. Mex. Astron. Astrofis. 1992, 23, 45–48. [Google Scholar]
- Kurucz, R. Remaining line opacity problems for the solar spectrum. Rev. Mex. Astron. Astrofís. 1992, 23, 187–194. [Google Scholar]
- Meftah, M.; Damé, L.; Bolsée, D.; Pereira, N.; Snow, M.; Weber, M.; Bramstedt, K.; Hilbig, T.; Cessateur, G.; Boudjella, M.Y.; et al. A New Version of the SOLAR-ISS Spectrum Covering the 165–3000 nm Spectral Region. Sol. Phys. 2020, 295, 14. [Google Scholar] [CrossRef]
- Meftah, M.; Bolsée, D.; Damé, L.; Hauchecorne, A.; Pereira, N.; Irbah, A.; Bekki, S.; Cessateur, G.; Foujols, T.; Thiéblemont, R. Solar Irradiance from 165 to 400 nm in 2008 and UV Variations in Three Spectral Bands During Solar Cycle 24. Sol. Phys. 2016, 291, 3527–3547. [Google Scholar] [CrossRef] [Green Version]
- Meftah, M.; Damé, L.; Bolsée, D.; Pereira, N.; Sluse, D.; Cessateur, G.; Irbah, A.; Sarkissian, A.; Djafer, D.; Hauchecorne, A.; et al. A New Solar Spectrum from 656 to 3088 nm. Sol. Phys. 2017, 292, 101. [Google Scholar] [CrossRef]
- Meftah, M.; Damé, L.; Bolsée, D.; Hauchecorne, A.; Pereira, N.; Sluse, D.; Cessateur, G.; Irbah, A.; Bureau, J.; Weber, M.; et al. SOLAR-ISS: A new reference spectrum based on SOLAR/SOLSPEC observations. Astron. Astrophys. 2018, 611, A1. [Google Scholar] [CrossRef]
- Thuillier, G.; Foujols, T.; Bolsée, D.; Gillotay, D.; Hersé, M.; Peetermans, W.; Decuyper, W.; Mandel, H.; Sperfeld, P.; Pape, S.; et al. SOLAR/SOLSPEC: Scientific Objectives, Instrument Performance and Its Absolute Calibration Using a Blackbody as Primary Standard Source. Sol. Phys. 2009, 257, 185–213. [Google Scholar] [CrossRef]
- Mcclintock, W.; Rottman, G.; Woods, T. Solar–Stellar Irradiance Comparison Experiment II (Solstice II): Instrument Concept and Design. In Solar Physics—SOL PHYS; Springer: Berlin, Germany, 2007; Volume 230, pp. 225–258. [Google Scholar]
- Rottman, G. The SORCE mission. In Solar Physics; Springer: Berlin, Germany, 2007; Volume 230, pp. 7–25. [Google Scholar]
- Thuillier, G.; Floyd, L.; Woods, T.N.; Cebula, R.; Hilsenrath, E.; Hersé, M.; Labs, D. Solar irradiance reference spectra for two solar active levels. Adv. Space Res. 2004, 34, 256–261. [Google Scholar] [CrossRef]
- Kurucz, R.L.; Bell, B. Atomic Line List; Smithsonian Astrophysical Observatory: Cambridge, MA, USA, 1995. [Google Scholar]
- Fontenla, J.M.; Stancil, P.C.; Landi, E. Solar spectral irradiance, solar activity, and the near-ultra-violet. Astrophys. J. 2015, 809, 157. [Google Scholar] [CrossRef] [Green Version]
- Hilbig, T.; Weber, M.; Bramstedt, K.; Noël, S.; Burrows, J.P.; Krijger, J.M.; Snel, R.; Meftah, M.; Damé, L.; Bekki, S.; et al. The New SCIAMACHY Reference Solar Spectral Irradiance and Its Validation. Sol. Phys. 2018, 293, 121. [Google Scholar] [CrossRef]
- Burrows, J.P.; Hölzle, E.; Goede, A.P.H.; Visser, H.; Fricke, W. SCIAMACHY-scanning imaging absorption spectrometer for atmospheric chartography. Acta Astronaut. 1995, 35, 445–451. [Google Scholar] [CrossRef]
- Skupin, J.; Noël, S.; Wuttke, M.W.; Gottwald, M.; Bovensmann, H.; Weber, M.; Burrows, J.P. SCIAMACHY solar irradiance observation in the spectral range from 240 to 2380 nm. Adv. Space Res. 2005, 35, 370–375. [Google Scholar] [CrossRef]
- Pagaran, J.; Harder, J.W.; Weber, M.; Floyd, L.E.; Burrows, J.P. Intercomparison of SCIAMACHY and SIM vis-IR irradiance over several solar rotational timescales. Astron. Astrophys. 2011, 528, A67. [Google Scholar] [CrossRef] [Green Version]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noël, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY: Mission objectives and measurement modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Gloudemans, A.M.S.; Schrijver, H.; Kleipool, Q.; van den Broek, M.M.P.; Straume, A.G.; Lichtenberg, G.; van Hees, R.M.; Aben, I.; Meirink, J.F. The impact of SCIAMACHY near-infrared instrument calibration on CH 4 and CO total columns. Atmos. Chem. Phys. Discuss. 2005, 5, 2369–2383. [Google Scholar] [CrossRef] [Green Version]
- Woods, T.N.; Chamberlin, P.C.; Harder, J.W.; Hock, R.A.; Snow, M.; Eparvier, F.G.; Fontenla, J.; McClintock, W.E.; Richard, E.C. Solar Irradiance Reference Spectra (SIRS) for the 2008 Whole Heliosphere Interval (WHI). Geophys. Res. Lett. 2009, 36, L01101. [Google Scholar] [CrossRef] [Green Version]
- Mcclintock, W.E.; Rottman, G.J.; Woods, T.N. Solar–Stellar Irradiance Comparison Experiment II (Solstice II): Instrument Concept and Design. Sol. Phys. 2005, 230, 225–258. [Google Scholar] [CrossRef]
- Harder, J.W.; Fontenla, J.; Lawrence, G.; Woods, T.; Rottman, G. The spectral irradiance monitor: Measurement equations and calibration. Sol. Phys. 2005, 230, 169–204. [Google Scholar] [CrossRef]
- Woods, T.; Eparvier, F.; Bailey, S.; Chamberlin, P.; Lean, J.; Rottman, G.; Solomon, S.; Tobiska, W.K.; Woodraska, D. Solar EUV Experiment (SEE): Mission overview and first results. J. Geophys. Res. Space Phys. 2005, 110, 1312. [Google Scholar] [CrossRef] [Green Version]
- Woods, T.; Eparvier, F.; Jones, A.; Judge, D.; Lean, J.; Mariska, J.; Mcmullin, D.; Warren, H.; Berthiaume, G.; Bailey, S. The EUV Variability Experiment (EVE) on the Solar Dynamics Observatory (SDO): Science plan and instrument overview. ESA SP 2006, 617, 19–24. [Google Scholar]
- Chamberlin, P.C.; Hock, R.A.; Crotser, D.A.; Eparvier, F.G.; Furst, M.; Triplett, M.A.; Woodraska, D.L.; Woods, T.N. EUV variability experiment (EVE); multiple EUV grating spectrographs (MEGS), radiometric calibrations and results. In Proceedings of the Solar Physics and Space Weather Instrumentation II, San Diego, CA, USA, 26–30 August 2007. [Google Scholar]
- Chamberlin, P.C.; Woods, T.N.; Crotser, D.A.; Eparvier, F.G.; Hock, R.A.; Woodraska, D.L. Solar cycle minimum measurements of the solar extreme ultraviolet spectral irradiance on 14 April 2008. Geophys. Res. Lett. 2009, 36, L05102. [Google Scholar] [CrossRef]
- Harder, J.W.; Thuillier, G.; Richard, E.C.; Brown, S.W.; Lykke, K.R.; Snow, M.; McClintock, W.E.; Fontenla, J.M.; Woods, T.N.; Pilewskie, P. The SORCE SIM solar spectrum: Comparison with recent observations. Sol. Phys. 2010, 263, 3–24. [Google Scholar] [CrossRef] [Green Version]
- Kopp, G.; Lawrence, G.; Rottman, G. The Total Irradiance Monitor (TIM): Science results. In The Solar Radiation and Climate Experiment (SORCE); Springer: Berlin, Germany, 2005. [Google Scholar]
- Richard, E.; Harber, D.; Harder, J.; Pilewskie, P.; Brown, S.; Smith, A.; Lykke, K. Future Long-term Measurements of Solar Spectral Irradiance by JPSS TSIS. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2011; p. GC23A-0917. [Google Scholar]
- Richard, E.C.; Pilewskie, P.; Kopp, G.; Coddington, O.; Woods, T.N.; Wu, D.L. Continuing the Solar Irradiance Data Record with TSIS. In AGU Fall Meeting Abstracts; American Geophysical Union: San Fracisco, DC, USA, 2016; p. A11I-0133. [Google Scholar]
- Richard, E.; Harber, D.; Coddington, O.; Drake, G.; Rutkowski, J.; Triplett, M.; Pilewskie, P.; Woods, T. SI-traceable spectral irradiance radiometric characterization and absolute calibration of the TSIS-1 spectral irradiance monitor (SIM). Remote Sens. 2020, 12, 1818. [Google Scholar] [CrossRef]
- Coddington, O.M.; Richard, E.C.; Harber, D.; Pilewskie, P.; Woods, T.N.; Chance, K.; Liu, X.; Sun, K. The TSIS-1 Hybrid Solar Reference Spectrum. Geophys. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Hall, L.A.; Anderson, G.P. High-resolution solar spectrum between 2000 and 3100 Å. J. Geophys. Res. 1991, 96, 12927. [Google Scholar] [CrossRef]
- Gröbner, J.; Kröger, I.; Egli, L.; Hülsen, G.; Riechelmann, S.; Sperfeld, P. The high-resolution extraterrestrial solar spectrum (QASUMEFTS) determined from ground-based solar irradiance measurements. Atmos. Meas. Tech. 2017, 10, 3375–3383. [Google Scholar] [CrossRef] [Green Version]
- Toon, G.C. The Solar Spectrum: An Atmospheric Remote Sensing Perspective; University of Toronto Seminar: Toronto, ON, Canada, 2013. [Google Scholar]
- Toon, G.C. Solar Line List for GGG2014. Available online: https://mark4sun.jpl.nasa.gov/toon/solar/solar_spectrum.html (accessed on 11 December 2020).
- Lean, J. Evolution of the Sun’s Spectral Irradiance Since the Maunder Minimum. Geophys. Res. Lett. 2000, 27, 2425–2428. [Google Scholar] [CrossRef] [Green Version]
- Prša, A.; Harmanec, P.; Torres, G.; Mamajek, E.; Asplund, M.; Capitaine, N.; Christensen-Dalsgaard, J.; Depagne, É.; Haberreiter, M.; Hekker, S.; et al. Nominal Values for Selected Solar and Planetary Quantities: Iau 2015 Resolution B3. Astron. J. 2016, 152, 41. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. NOAA-20 VIIRS reflective solar bands on-orbit calibration using solar diffuser and solar diffuser stability monitor. In Proceedings of the SPIE 10764, Earth Observing Systems XXIII, San Diego, CA, USA, 19–23 August 2018; p. 47. [Google Scholar]
- Xiong, X.; Cao, C.; Lei, N.; Chiang, K.; Angal, A.; Li, Y.; Blonski, S.; Wang, W.; Choi, T. Early results from NOAA-20 (JPSS-1) VIIRS on-orbit calibration and characterization. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1112–1115. [Google Scholar]
- Choi, T.J.; Shao, X.; Blonski, S.; Wang, W.; Uprety, S.; Cao, C. NOAA-20 VIIRS initial on-orbit radiometric calibration using scheduled lunar observations. In Proceedings of the SPIE 11127, Earth Observing Systems XXIV, San Diego, CA, USA, 11–15 August 2019; p. 72. [Google Scholar]
- TSIS-1 SIM Line Shape Function. Available online: https://lasp.colorado.edu/home/tsis/data/ssi-data/#tsis_sim_lsf (accessed on 11 December 2020).
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Estimating fractional snow cover from MODIS using the normalized difference snow index. Remote Sens. Environ. 2004, 89, 351–360. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Salomonson, V.V. Algorithm Theoretical Basis Document (ATBD), MODIS Snow and Sea Ice Global Mapping Project. 2013. Available online: https://modis-snow-ice.gsfc.nasa.gov/?c=atbd (accessed on 4 April 2021).
- Platnick, S.; Li, J.Y.; King, M.D.; Gerber, H.; Hobbs, P.V. A solar reflectance method for retrieving the optical thickness and droplet size of liquid water clouds over snow and ice surfaces. J. Geophys. Res. Atmos. 2001, 106, 15185–15199. [Google Scholar] [CrossRef] [Green Version]
- Platnick, S.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Baum, B.A.; Riédi, J.C.; Frey, R.A. The MODIS cloud products: Algorithms and examples from terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–472. [Google Scholar] [CrossRef] [Green Version]
- Minnis, P.; Sun-Mack, S.; Chen, Y.; Chang, F.-L.; Yost, C.R.; Smith, W.L.; Heck, P. CERES MODIS cloud product retrievals for Edition 4, Part I: Algorithm Changes. IEEE Trans. Geosci. Remote Sens. 2021, 54, 2744–2780. [Google Scholar] [CrossRef]
- Bhatt, R.; Doelling, D.R.; Angal, A.; Xiong, X.; Haney, C.; Scarino, B.R.; Wu, A.; Gopalan, A. Response Versus Scan-Angle Assessment of MODIS Reflective Solar Bands in Collection 6.1 Calibration. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2276–2289. [Google Scholar] [CrossRef]
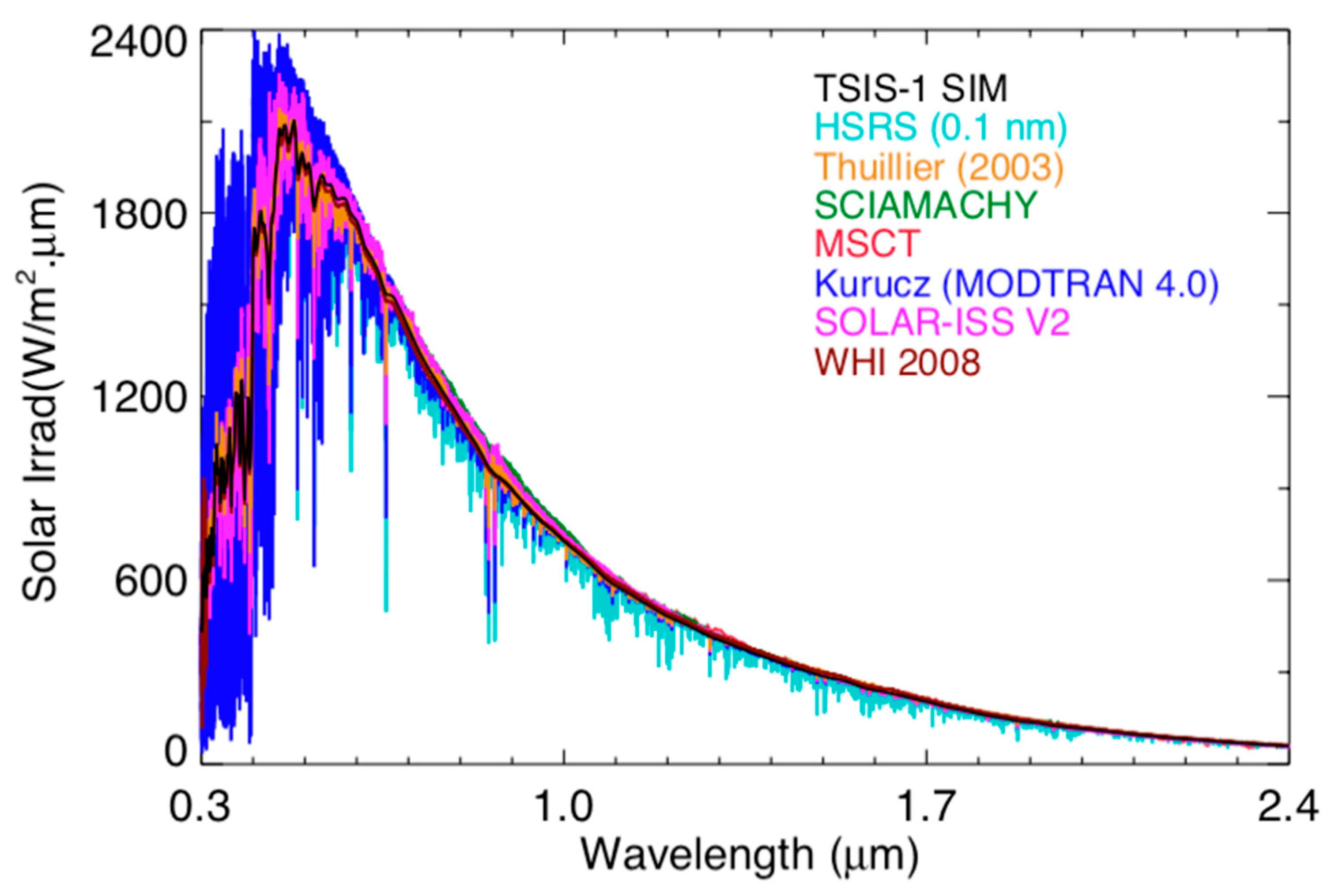
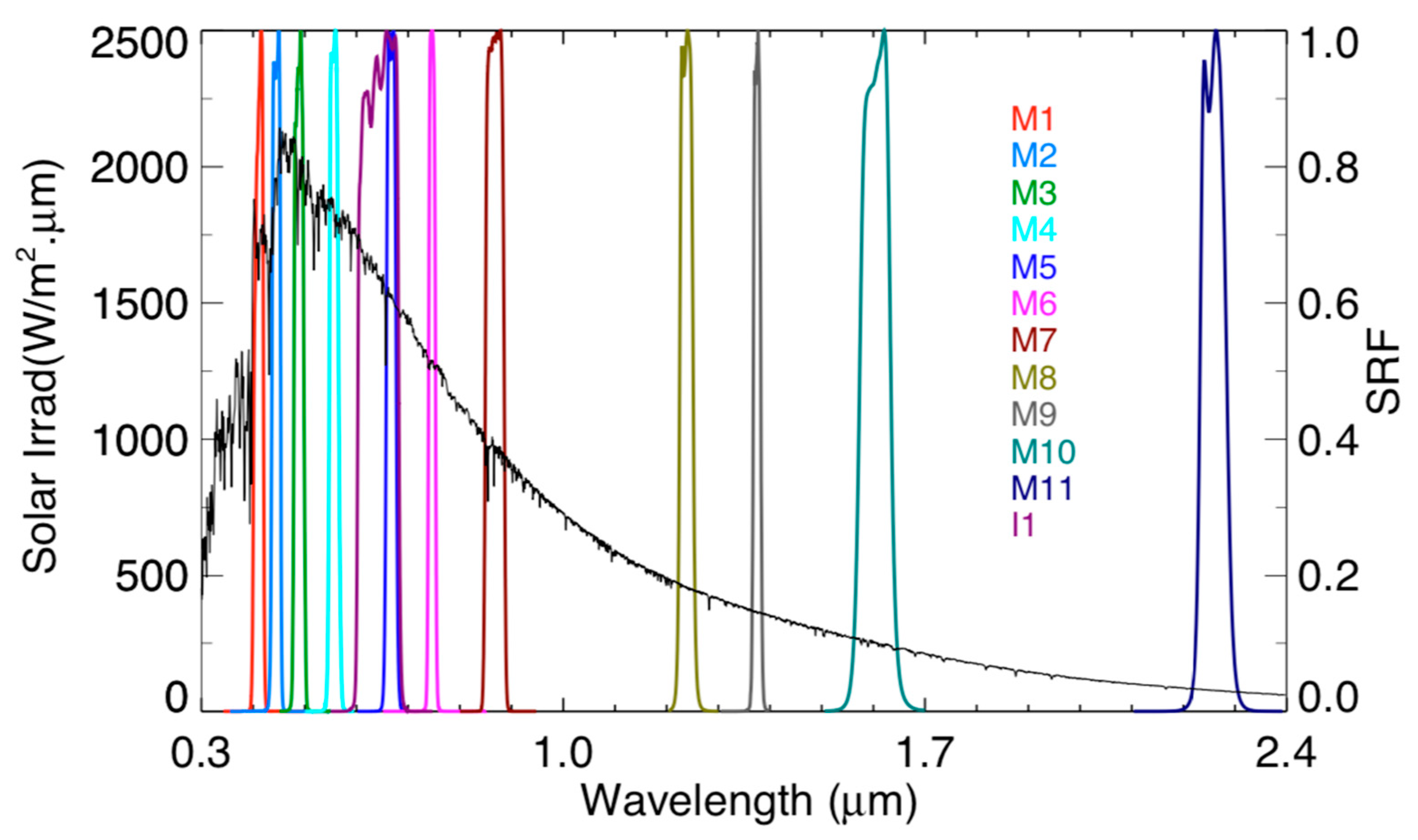




| Name | Description | Uncertainty (%) |
|---|---|---|
| TSIS-1 SIM | Measured by TSIS-1 SIM instrument on ISS | 0.24–0.41% |
| HSRS | High-resolution solar line data normalized to the absolute irradiance scale of the TSIS-1 SIM and CSIM instruments | 0.3–1.3% |
| Thuillier 2003 | Measured by SOLSPEC and SOSP spectrometers from ATLAS and EURECA missions | 1–3% |
| SCIAMACHY V9 | Measured by SCIAMACHY instrument on board the Environment Satellite | 3–6% |
| Kurucz (MODTRAN) | A theoretical spectrum of the solar continuum supplemented with observed and predicted solar lines | NA |
| MCST | Combination of Thuillier, Neckel and Labs, and Smith and Gottlieb used by MODIS L1B datasets | 2–3% |
| SOLAR-ISS V2 | Based on SOLAR/SOLSPEC spectroradiometer on ISS supplemented with observed and predicted solar lines | ~1.26% |
| WHI 2008 | Derived for the 2008 Whole Heliosphere Interval (WHI) using a combination of temporally coincident satellite and sounding rocket observations | 3% |
| Spectrum | 205–2390 nm (W/m2) | +52.0 W/m2 (115–205 nm and 2390–100,000 nm) | Difference from IAU TSI (1361 W/m2) (W/m2) | % Difference |
|---|---|---|---|---|
| MCST | 1335.1 | 1387.1 | +15.1 | +1.1 |
| Thuillier 2003 | 1315.2 † | 1367.2 † | +6.2 † | +0.5 |
| SOLAR-ISS V2 | 1320.8 | 1372.8 | +11.8 | +0.9 |
| WHI 2008 | 1309.1 ‡ | 1361.1 ‡ | +0.1 ‡ | 0 |
| Kurucz (MODTRAN 4.0) | 1315.2 | 1367.2 | +6.2 | +0.5 |
| TSIS-1 HSRS (0.1 nm) | 1310.7 | 1362.7 | +1.7 | +0.1 |
| TSIS-1 SIM | 1309.0 | 1361.0 | 0 | 0 |
| VIIRS Band | Percentage Difference in ESUN Relative to Thuillier (ESUN, Thuillier − ESUN, X) | ||||||
|---|---|---|---|---|---|---|---|
| MCST | TSIS-1 SIM | HSRS (0.1 nm) | SCIAMACHY | Kurucz (MODTRAN) | SOLAR ISS | WHI 2009 | |
| M1 | −1.40 | −0.54 | −0.51 | 1.32 | −0.08 | −2.28 | 0.81 |
| M2 | −1.41 | −0.61 | −0.56 | 0.23 | 2.09 | −1.71 | 0.78 |
| M3 | −1.40 | −0.78 | −0.78 | −0.34 | −0.48 | −1.54 | 0.15 |
| M4 | −1.40 | −2.26 | −2.06 | −2.41 | −2.06 | −1.33 | −1.02 |
| M5 | −1.44 | −0.98 | −1.40 | −2.56 | −1.64 | −1.15 | 0.54 |
| I1 | −1.43 | −0.95 | −1.30 | −2.06 | −1.42 | −2.0 | 0.42 |
| M6 | −1.40 | 0.41 | 0.25 | −2.39 | −0.24 | −1.95 | 2.12 |
| M7 | −2.71 | 0.12 | 0.18 | −4.65 | 0.21 | −3.23 | 0.65 |
| M8 | −4.33 | 0.88 | 0.77 | −3.57 | −0.19 | −1.39 | −1.45 |
| M9 | −0.56 | 2.48 | 2.35 | 0.69 | 1.62 | 0.12 | −0.75 |
| M10 | 1.11 | 3.96 | 3.60 | 3.61 | 2.18 | 2.99 | −0.45 |
| M11 | 10.23 | 4.14 | 4.11 | NA | 2.89 | 6.00 | −1.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatt, R.; Doelling, D.R.; Coddington, O.; Scarino, B.; Gopalan, A.; Haney, C. Quantifying the Impact of Solar Spectra on the Inter-Calibration of Satellite Instruments. Remote Sens. 2021, 13, 1438. https://doi.org/10.3390/rs13081438
Bhatt R, Doelling DR, Coddington O, Scarino B, Gopalan A, Haney C. Quantifying the Impact of Solar Spectra on the Inter-Calibration of Satellite Instruments. Remote Sensing. 2021; 13(8):1438. https://doi.org/10.3390/rs13081438
Chicago/Turabian StyleBhatt, Rajendra, David R. Doelling, Odele Coddington, Benjamin Scarino, Arun Gopalan, and Conor Haney. 2021. "Quantifying the Impact of Solar Spectra on the Inter-Calibration of Satellite Instruments" Remote Sensing 13, no. 8: 1438. https://doi.org/10.3390/rs13081438
APA StyleBhatt, R., Doelling, D. R., Coddington, O., Scarino, B., Gopalan, A., & Haney, C. (2021). Quantifying the Impact of Solar Spectra on the Inter-Calibration of Satellite Instruments. Remote Sensing, 13(8), 1438. https://doi.org/10.3390/rs13081438






