Spatio-Temporal Changes of Mass Balance in the Ablation Area of the Muz Taw Glacier, Sawir Mountains, from Multi-Temporal Terrestrial Geodetic Surveys
Abstract
:1. Introduction
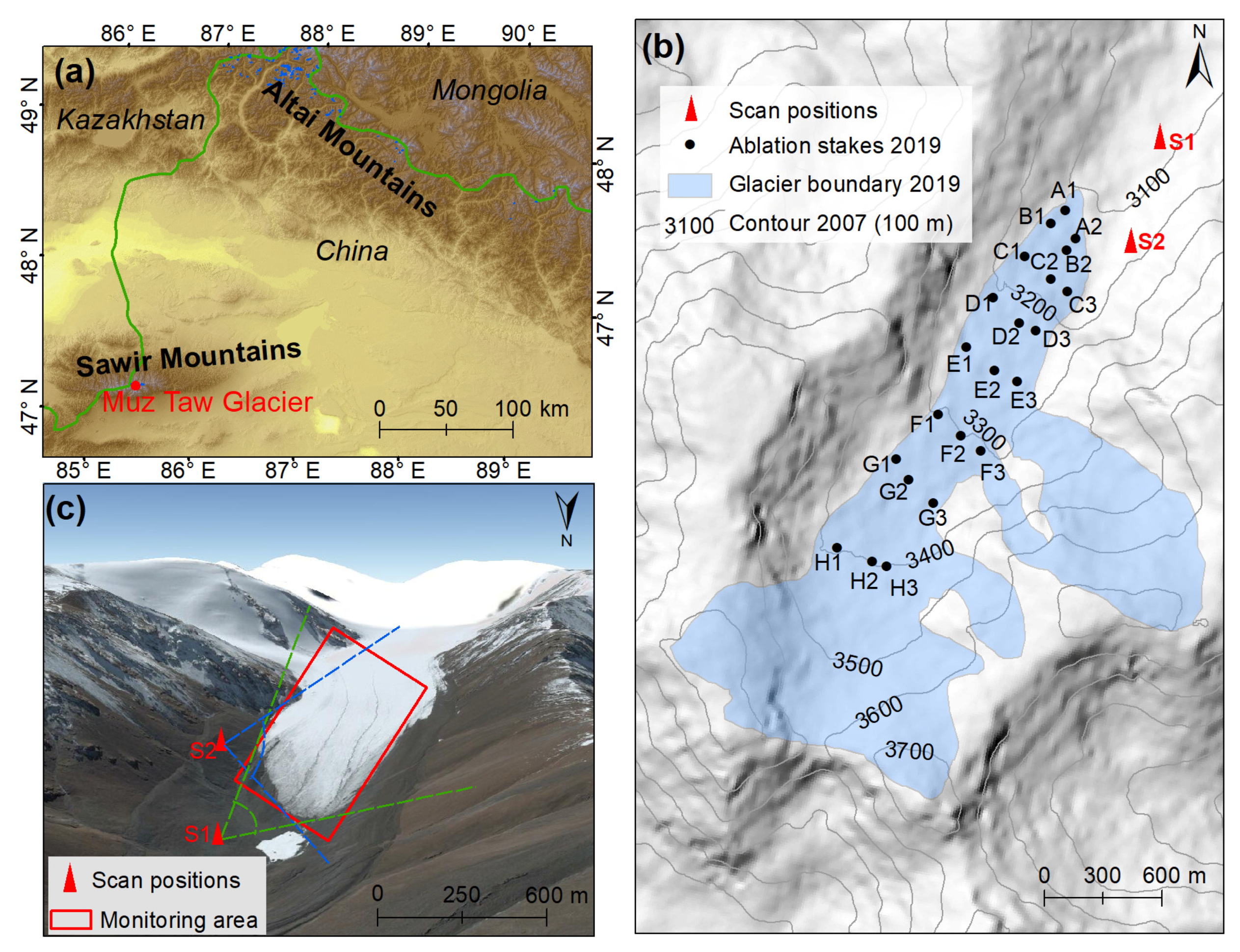
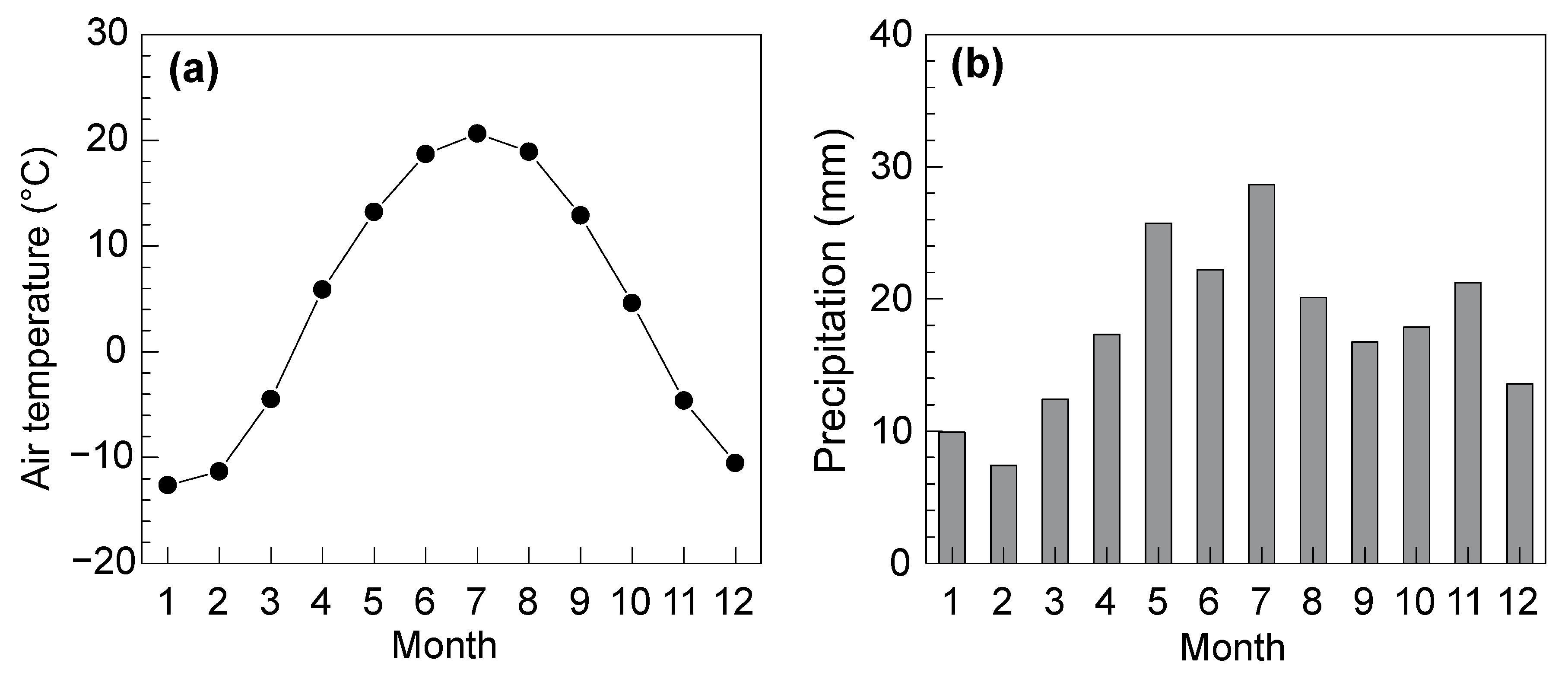
2. Study Area
3. Data and Methods
3.1. TLS Surveys and Data Processing
3.2. Geodetic Mass Balance
3.3. Glaciological Mass Balance
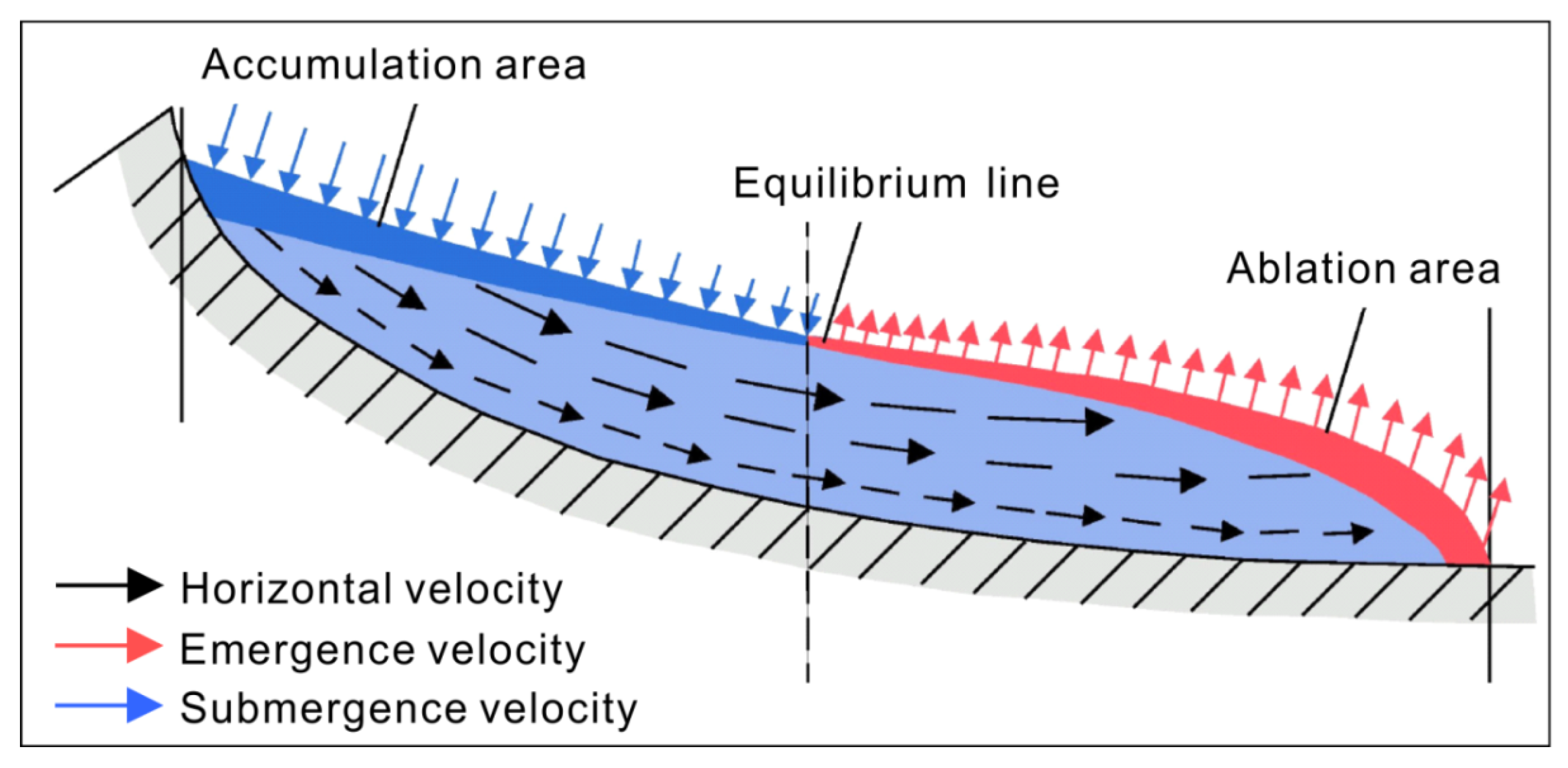
3.4. Emergence Velocity
3.5. Uncertainty Estimates
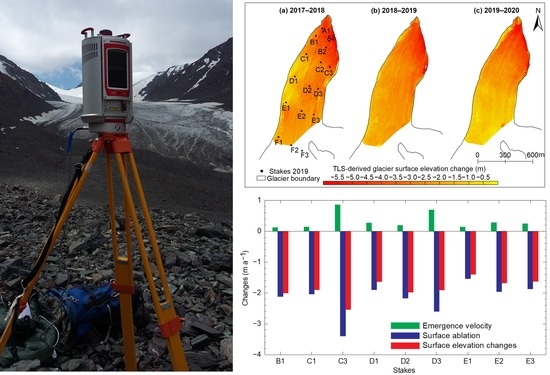
4. Results
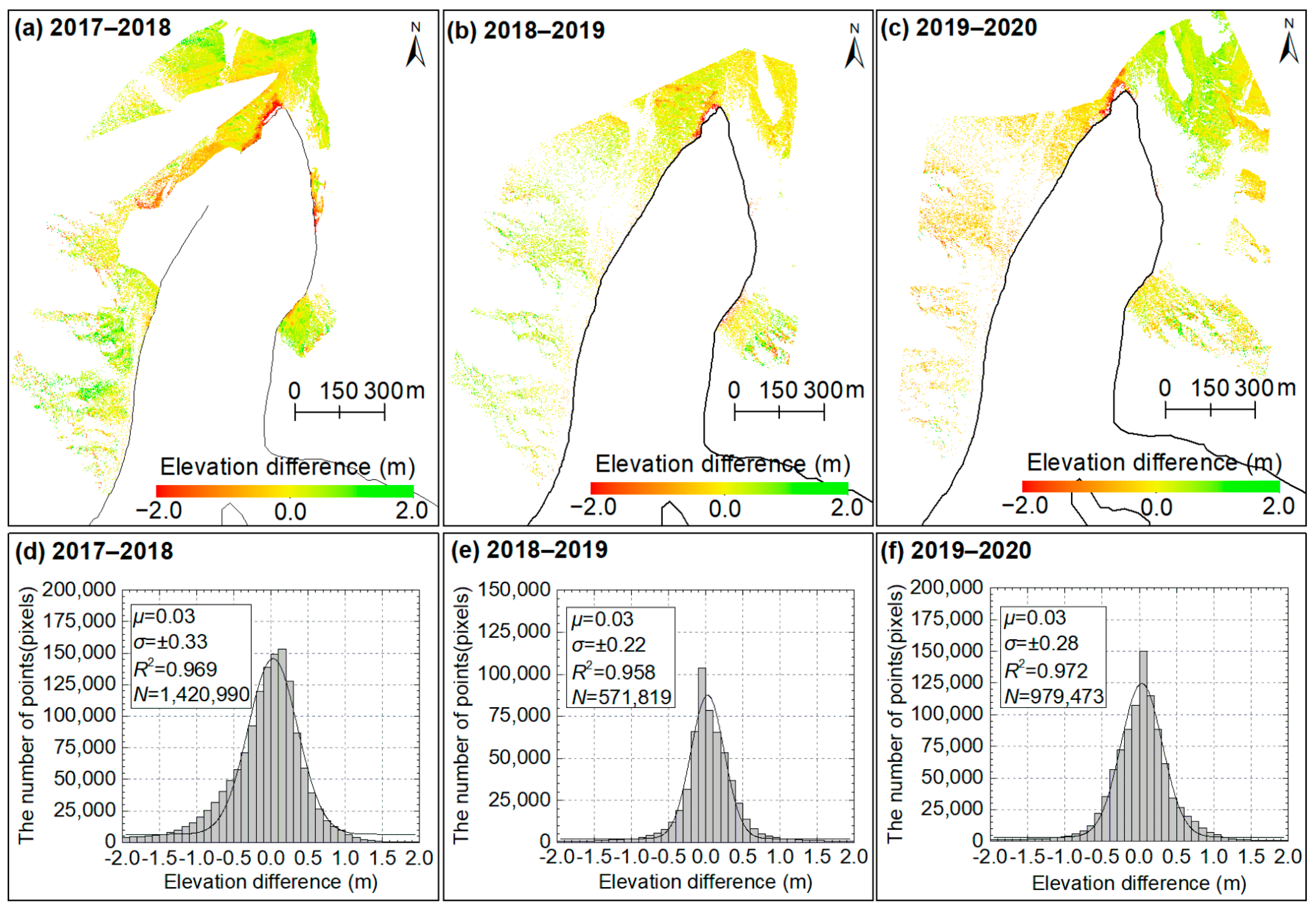
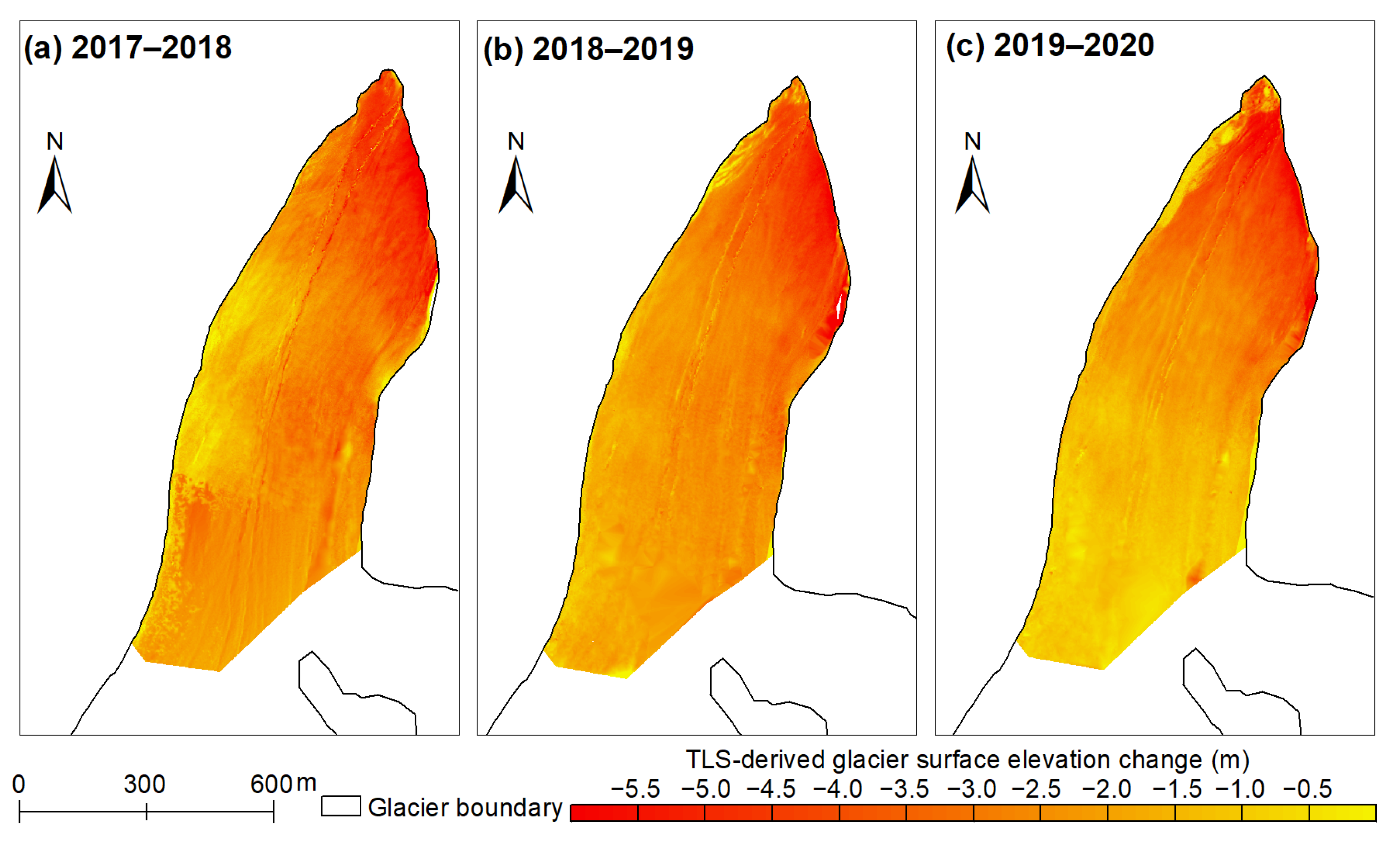
4.1. Glacier Surface Elevation and Geodetic Mass Changes
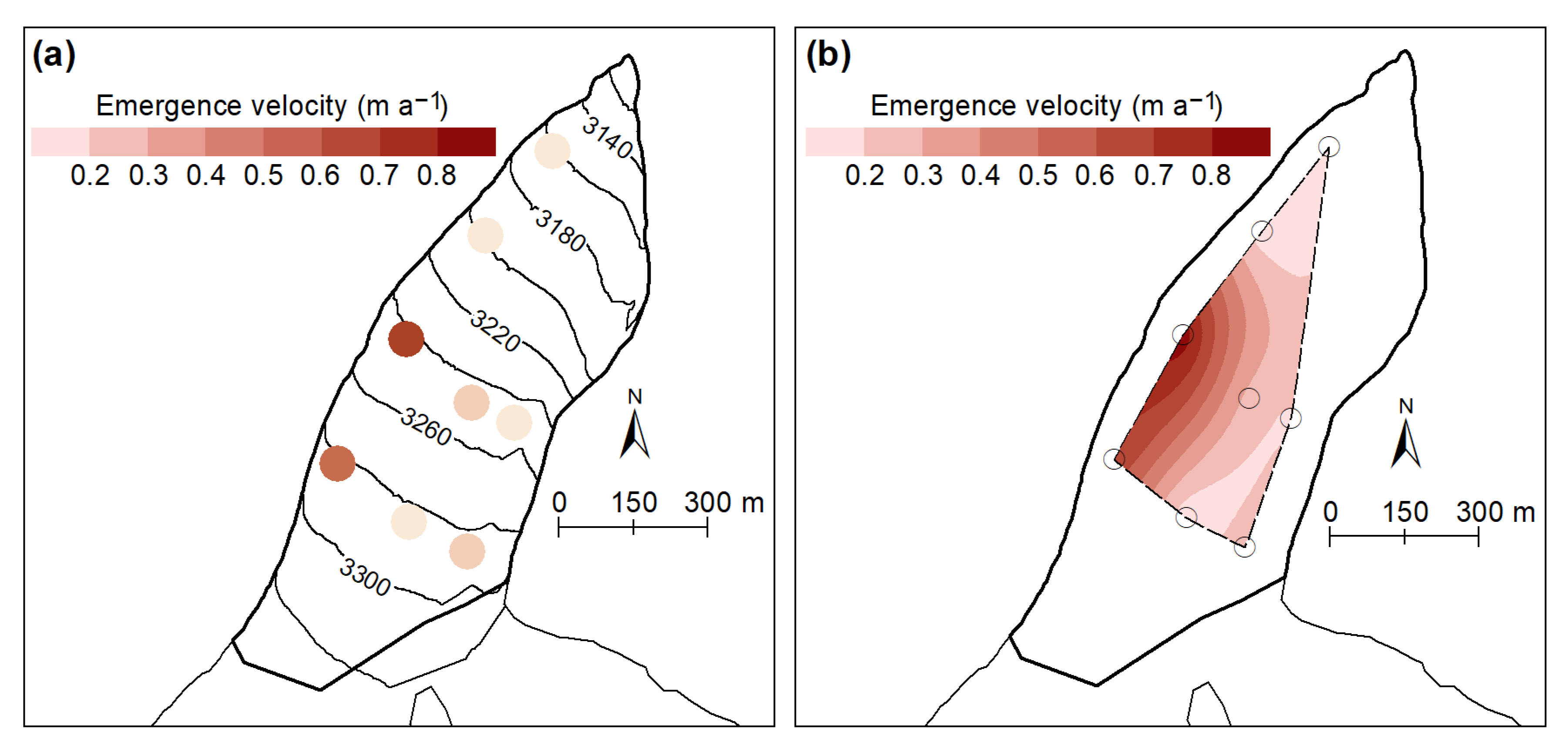
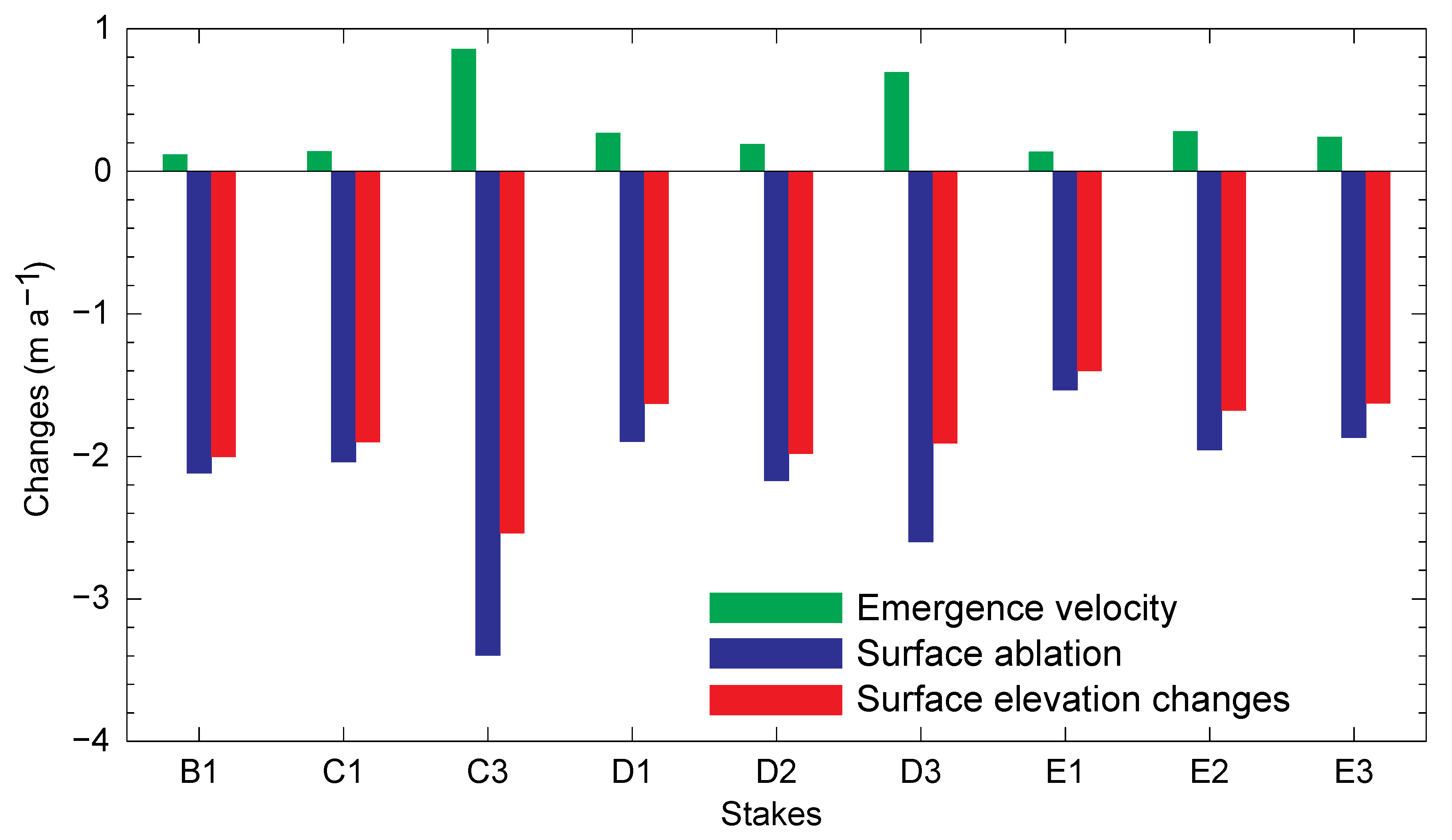
4.2. Surface Ablation and Emergence Velocity
5. Discussion
5.1. Accuracy of DEM Differencing and Geodetic Mass Balance
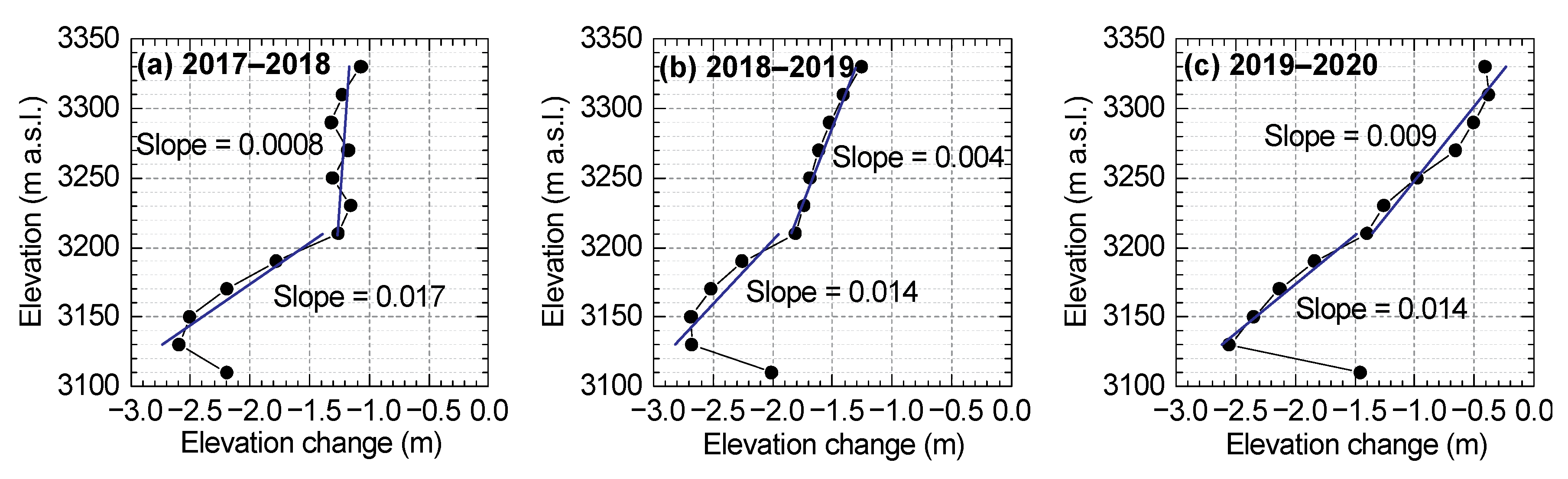
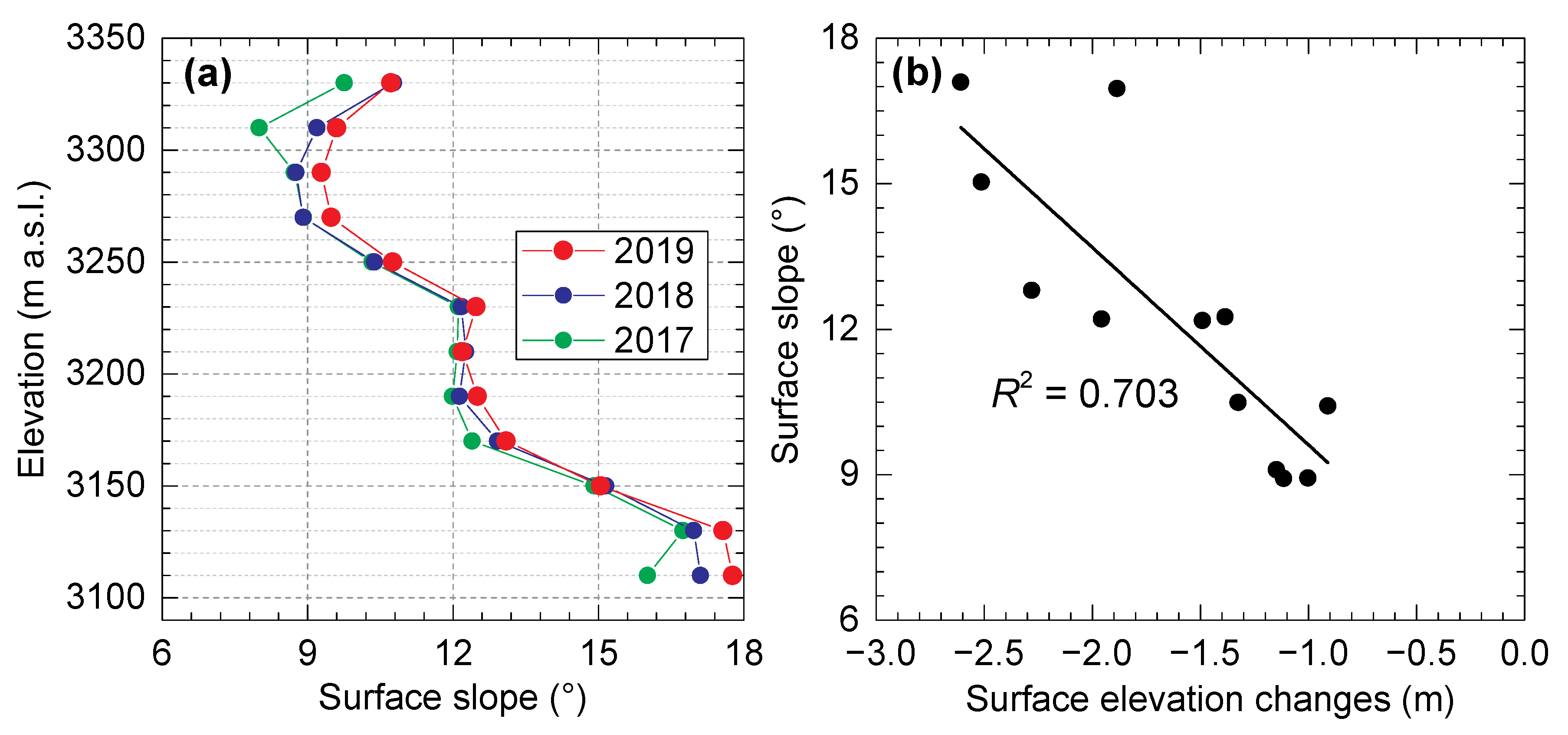
5.2. Spatiotemporal Variability of Glacier Surface Elevation and Mass Changes
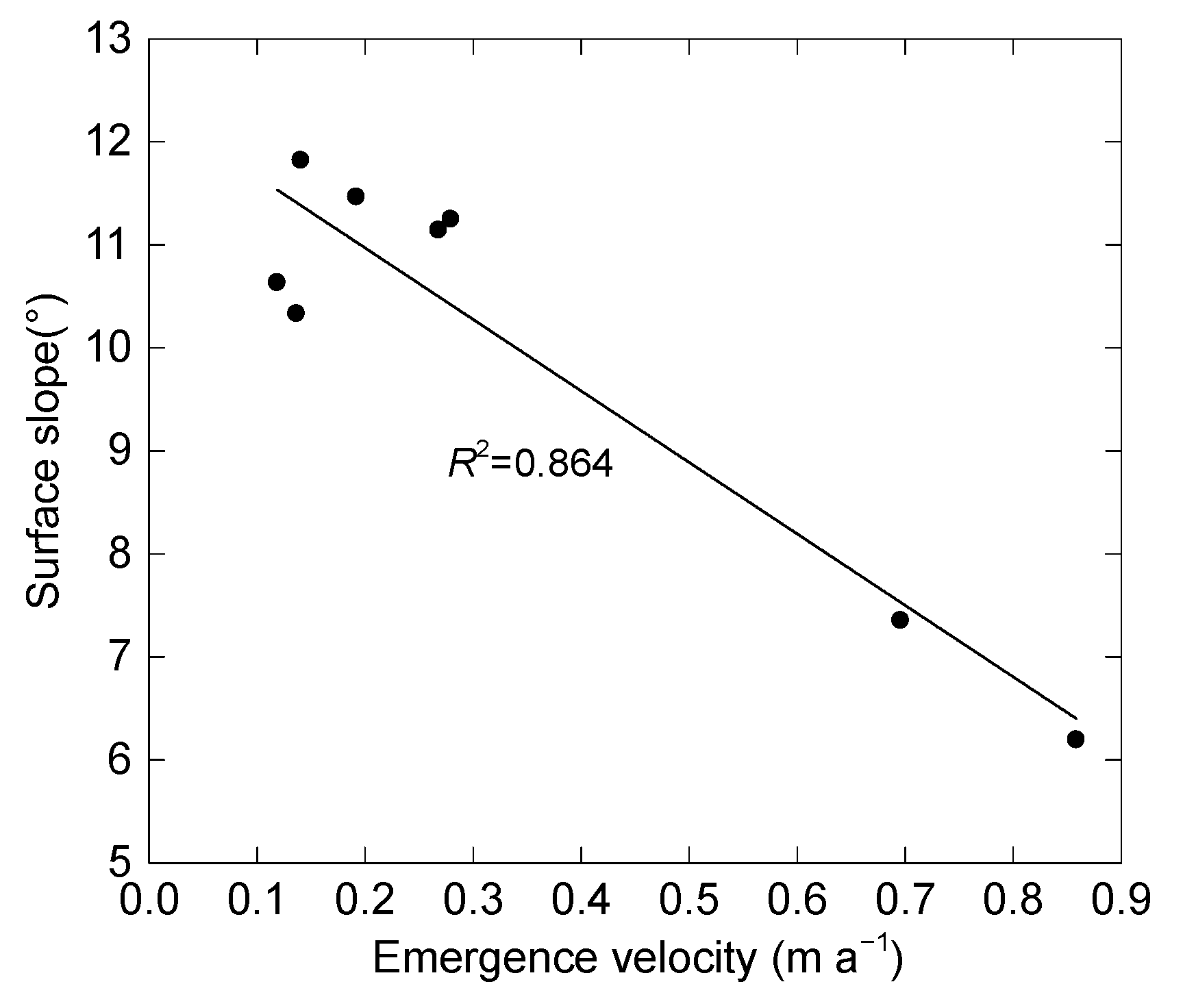
5.3. Influence of Emergence Velocity and Mass Balance on Surface Lowering
5.4. Limitations and Further Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hagg, W.J.; Braun, L.N.; Uvarov, V.N.; Makarevich, K.G. A comparison of three methods of mass-balance determination in the Tuyuksu glacier region, Tien Shan, Central Asia. J. Glaciol. 2004, 50, 505–510. [Google Scholar] [CrossRef] [Green Version]
- Kaser, G.; Cogley, J.G.; Dyurgerov, M.B.; Meier, M.F.; Ohmura, A. Mass balance of glaciers and ice caps: Consensus estimates for 1961–2004. Geophys. Res. Lett. 2006, 33, L19501. [Google Scholar] [CrossRef] [Green Version]
- Huss, M.; Hock, R. Global-scale hydrological response to future glacier mass loss. Nat. Clim. Chang. 2018, 8, 135–140. [Google Scholar] [CrossRef] [Green Version]
- Kääb, A.; Leinss, S.; Gilbert, A.; Bühler, Y.; Gascoin, S.; Evans, S.G.; Bartelt, P.; Berthier, E.; Brun, F.; Chao, W.; et al. Massive collapse of two glaciers in western Tibet in 2016 after surge-like instability. Nat. Geosci. 2018, 11, 114–120. [Google Scholar] [CrossRef] [Green Version]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Hoelzle, M.; Azisov, E.; Barandun, M.; Huss, M.; Farinotti, D.; Gafurov, A.; Hagg, W.; Kenzhebaev, R.; Kronenberg, M.; Machguth, H.; et al. Reestablishing glacier monitoring in Kyrgyzstan and Uzbekistan, Central Asia. Geosci. Instrum. Method. Data Syst. 2017, 6, 397–418. [Google Scholar] [CrossRef] [Green Version]
- WGMS (World Glacier Monitoring Service). Global Glacier Change Bulletin No. 3 (2016–2017); ISC(WDS)/IUGG(IACS)/UNEP/UNESCO/WMO; Zemp, M., Gärtner-Roer, I., Nussbaumer, S.U., Bannwart, J., Rastner, P., Paul, F., Hoelzle, M., Eds.; World Glacier Monitoring Service: Zurich, Switzerland, 2020; pp. 1–274. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D.A. spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir–Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef] [Green Version]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Dustman, D.; Mölg, T.; Bolch, T. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Wei, J.; Liu, S.; Guo, W.; Xu, J.; Bao, W.; Shangguan, D. Changes in glacier volume in the north bank of the Bangong Co Basin from 1968 to 2007 based on historical topographic maps, SRTM, and ASTER stereo images. Arct. Antarct. Alp. Res. 2015, 47, 301–311. [Google Scholar] [CrossRef] [Green Version]
- Bolch, T.; Pieczonka, T.; Mukherjee, K.; Shea, J. Brief communication: Glaciers in the Hunza catchment (Karakoram) have been nearly in balance since the 1970s. Cryosphere 2017, 11, 531–539. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.; Yu, W.; Wu, G.; Xu, B.; Yang, W.; Zhao, H.; Wang, W.; Li, S.; Wang, N.; Li, Z.; et al. Glacier anomalies and relevant disaster risks on the Tibetan Plateau and surroundings. Chin. Sci. Bull. 2019, 64, 2770–2782. [Google Scholar] [CrossRef] [Green Version]
- Panagiotopoulos, F.; Shahgedanova, M.; Hannachi, A.; Stephenson, D.B. Observed Trends and Teleconnections of the Siberian High: A Recently Declining Center of Action. J. Clim. 2005, 18, 1411–1422. [Google Scholar] [CrossRef] [Green Version]
- Huai, B.; Li, Z.; Wang, F.; Wang, W.; Wang, P.; Li, K. Glacier volume estimation from ice-thickness data, applied to the Muz Taw glacier, Sawir Mountains, China. Environ. Earth. Sci. 2015, 74, 1861–1870. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Li, Z.; Zhang, M. Glacier changes in the Sawuer Mountain during 1977–2017 and their response to climate change. J. Nat. Resour. 2019, 34, 802–814. [Google Scholar]
- Fischer, A. Comparison of direct and geodetic mass balances on a multi-annual time scale. Cryosphere 2011, 5, 107–124. [Google Scholar] [CrossRef] [Green Version]
- Schumann, G.J.; Bates, P.D. The need for a high-accuracy, open-access global DEM. Front. Earth Sci. 2018, 6, 225. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.P.; Jong, S.M.D. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Fischer, M.; Huss, M.; Kummert, M.; Hoelzle, M. Application and validation of long-range terrestrial laser scanning to monitor the mass balance of very small glaciers in the Swiss Alps. Cryosphere 2016, 10, 1279–1295. [Google Scholar] [CrossRef] [Green Version]
- Fugazza, D.; Scaioni, M.; Corti, M.; D’Agata, C.; Azzoni, R.S.; Cernuschi, M.; Claudio, S.; Diolaiuti, G.A. Combination of UAV and terrestrial photogrammetry to assess rapid glacier evolution and map glacier hazards. Nat. Hazards Earth Syst. Sci. 2018, 18, 1055–1071. [Google Scholar] [CrossRef] [Green Version]
- Réveillet, M.; Vincent, C.; Six, D.; Rabatel, A.; Sanchez, O.; Piard, L.; Laarman, O. Spatio-temporal variability of surface mass balance in the accumulation zone of the Mer de Glace, French Alps, from multitemporal terrestrial LiDAR measurements. J. Glaciol. 2021, 67, 137–146. [Google Scholar] [CrossRef]
- Hooke, R.L. Principles of Glacier Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019; pp. 1–539. [Google Scholar]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Academic Press: New York, NY, USA, 2010; pp. 1–704. [Google Scholar]
- Berthier, E.; Vincent, C. Relative contribution of surface mass balance and ice-flux changes to the accelerated thinning of Mer de Glace, French Alps, over 1979–2008. J. Glaciol. 2012, 58, 501–512. [Google Scholar] [CrossRef] [Green Version]
- Stocker-Waldhuber, M.; Fischer, A.; Helfricht, K.; Kuhn, M. Long-term records of glacier surface velocities in the Ötztal Alps (Austria). Earth Syst. Sci. Data 2019, 11, 705–715. [Google Scholar] [CrossRef] [Green Version]
- Deschamps-Berger, C.; Nuth, C.; Van Pelt, W.; Berthier, E.; Kohler, J.; Altena, B. Closing the mass budget of a tidewater glacier: The example of Kronebreen, Svalbard. J. Glaciol. 2019, 65, 136–148. [Google Scholar] [CrossRef] [Green Version]
- Nuimura, T.; Fujita, K.; Sakai, A. Downwasting of the debris-covered area of Lirung Glacier in Langtang Valley, Nepal Himalaya, from 1974 to 2010. Quat. Int. 2017, 455, 93–101. [Google Scholar] [CrossRef]
- Brun, F.; Wagnon, P.; Berthier, E.; Shea, J.M.; Immerzeel, W.W.; Kraaijenbrink, P.D.; Christian, V.; Camille, R.; Dibas, S.; Arnaud, Y. Ice cliff contribution to the tongue-wide ablation of Changri Nup Glacier, Nepal, central Himalaya. Cryosphere 2018, 12, 3439–3457. [Google Scholar] [CrossRef] [Green Version]
- RIEGL Laser Measurement Systems. 3D Terrestrial Laser Scanner Riegl VZ®-4000/Riegl VZ®-6000 General Description and Data Interfaces; RIEGL Laser Measurement Systems: Horn, Austria, 2014; pp. 1–466. [Google Scholar]
- Shi, Y. Concise China Glacier Inventory; Shanghai Science Popularization Press: Shanghai, China, 2005; pp. 1–490. [Google Scholar]
- Wang, F.; Yue, X.; Wang, L.; Li, H.; Du, Z.; Ming, J.; Li, Z. Applying artificial snowfall to reduce the melting of the Muz Taw Glacier, Sawir Mountains. Cryosphere 2020, 14, 2597–2606. [Google Scholar] [CrossRef]
- CH/Z 3017-2015. Technical Specifications for Three-Dimensional Laser Scanning; National Administration of Surveying, Mapping and Geo-Information of the People’s Republic of China: Beijing, China, 2015; pp. 1–17.
- Lichti, D.D.; Gordon, S.J.; Tipdecho, T. Error models and propagation in directly georeferenced terrestrial laser scanner networks. J. Surv. Eng. 2005, 131, 135–142. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N. A method for registration of 3-D shapes. IEEE T. Pattern Anal. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Perroy, R.L.; Bookhagen, B.; Asner, G.P.; Chadwick, O.A. Comparison of gully erosion estimates using airborne and ground-based LiDAR on Santa Cruz Island, California. Geomorphology 2010, 118, 288–300. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Revuelto, J.; Rico, I.; Chueca-Cía, J.; Julián, A.; Serreta, A.; Serrano, E.; Vicente-Serrano, S.M.; Azorin Molina, C.; Alonso-González, E.; et al. Thinning of the Monte Perdido Glacier in the Spanish Pyrenees since 1981. Cryosphere 2016, 10, 681–694. [Google Scholar] [CrossRef] [Green Version]
- Fey, C.; Wichmann, V. Long-range terrestrial laser scanning for geomorphological change detection in alpine terrain–handling uncertainties. Earth Surf. Proc. Land. 2017, 42, 789–802. [Google Scholar] [CrossRef]
- Østrem, G.; Brugman, M. Glacier Mass-Balance Measurements: A Manual for Field and Office Work; NHRI Science Report; Arctic Institute of North America: Saskatoon, SK, Canada, 1991; pp. 1–224. [Google Scholar]
- Kaser, G.; Fountain, A.; Jansson, P. A Manual for Monitoring the Mass Balance of Mountain Glaciers, International Hydrological Programme (IHP-VI. Technical Documents in Hydrology 59); UNESCO: Paris, France, 2003; pp. 9–26. [Google Scholar]
- Zemp, M.; Thibert, E.; Huss, M.; Stumm, D.; Rolstad Denby, C.; Nuth, C.; Nussbaumer, S.U.; Moholdt, G.; Mercer, A.; Mayer, C.; et al. Reanalysing glacier mass balance measurement series. Cryosphere 2013, 7, 1227–1245. [Google Scholar] [CrossRef] [Green Version]
- Beedle, M.J.; Menounos, B.; Wheate, R. An evaluation of mass-balance methods applied to Castle Creek Glacier, British Columbia, Canada. J. Glaciol. 2014, 60, 262–276. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A. Brief communication: Thinning of debris-covered and debris-free glaciers in a warming climate. Cryosphere 2017, 11, 133–138. [Google Scholar] [CrossRef] [Green Version]
- Pettersson, R.; Jansson, P.; Huwald, H.; Blatter, H. Spatial pattern and stability of the cold surface layer of Storglaciären, Sweden. J. Glaciol. 2007, 53, 99–109. [Google Scholar] [CrossRef] [Green Version]
- Gabbud, C.; Micheletti, N.; Lane, S.N. Lidar measurement of surface melt for a temperate Alpine glacier at the seasonal and hourly scales. J. Glaciol. 2015, 61, 963–974. [Google Scholar] [CrossRef] [Green Version]
- Klug, C.; Bollmann, E.; Galos, S.P.; Nicholson, L.; Prinz, R.; Rieg, L.; Sailer, R.; Stötter, J.; Kaser, G. Geodetic reanalysis of annual glaciological mass balances (2001–2011) of Hintereisferner, Austria. Cryosphere 2018, 12, 833–849. [Google Scholar] [CrossRef] [Green Version]
- Rolstad, C.; Haug, T.; Denby, B. Spatially integrated geodetic glacier mass balance and its uncertainty based on geostatistical analysis: Application to the western Svartisen ice cap, Norway. J. Glaciol. 2009, 55, 666–680. [Google Scholar] [CrossRef] [Green Version]
- Joerg, P.C.; Morsdorf, F.; Zemp, M. Uncertainty assessment of multi-temporal airborne laser scanning data: A case study on an Alpine glacier. Remote Sens. Environ. 2012, 127, 118–129. [Google Scholar] [CrossRef] [Green Version]
- Huss, M.; Bauder, A.; Funk, M. Homogenization of long term mass balance time series. Ann. Glaciol. 2009, 50, 198–206. [Google Scholar] [CrossRef] [Green Version]
- Thibert, E.; Vincent, C.; Blanc, R.; Eckert, N. Glaciological and volumetric mass balance measurements: Error analysis over 51 years, Sarennes Glacier, French Alps. J. Glaciol. 2008, 54, 522–532. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Li, Z.; Zhou, P.; Li, H.; Yu, G.; Xu, C.; Wang, L. Long-term change in ice velocity of Urumqi Glacier No.1, Tian Shan, China. Cold Reg. Sci. Technol. 2018, 145, 177–184. [Google Scholar] [CrossRef]
- Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef] [Green Version]
- Hartzell, P.J.; Gadomski, P.J.; Glennie, C.L.; Finnegan, D.C.; Deems, J.S. Rigorous error propagation for terrestrial laser scanning with application to snow volume uncertainty. J. Glaciol. 2015, 61, 1147–1158. [Google Scholar] [CrossRef] [Green Version]
- Farías-Barahona, D.; Vivero, S.; Casassa, G.; Schaefer, M.; Burger, F.; Seehaus, T.; Iribarren-Anacona, P.; Braun, F.E.H.; Braun, H. Geodetic mass balances and area changes of Echaurren Norte Glacier (Central Andes, Chile) between 1955 and 2015. Remote Sens. 2019, 11, 260. [Google Scholar] [CrossRef] [Green Version]
- Barandun, M.; Huss, M.; Sold, L.; Farinotti, D.; Azisov, E.; Salzmann, N.; Usubaliev, R.; Merkushkin, A.; Hoelzle, M. Reanalysis of seasonal mass balance at Abramov glacier 1968–2014. J. Glaciol. 2015, 61, 1103–1117. [Google Scholar] [CrossRef] [Green Version]
- Thomson, L.I.; Zemp, M.; Copland, L.; Cogley, J.G.; Ecclestone, M.A. Comparison of geodetic and glaciological mass budgets for White Glacier, Axel Heiberg Island, Canada. J. Glaciol. 2017, 63, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Wagnon, P.; Brun, F.; Khadka, A.; Berthier, E.; Shrestha, D.; Vincent, C.; Yves, A.; Delphine, S.; Vincent, C.; Arnaud, Y.; et al. Reanalysing the 2007–19 glaciological mass-balance series of Mera Glacier, Nepal, Central Himalaya, using geodetic mass balance. J. Glaciol. 2021, 67, 117–125. [Google Scholar] [CrossRef]
- Basantes-Serrano, R.; Rabatel, A.; Francou, B.; Vincent, C.; Maisincho, L.; Cáceres, B.; Galarraga, R.; Alvarez, D. Slight mass loss revealed by reanalyzing glacier mass balance observations on Glaciar Antisana 15 during the 1995–2012 period. J. Glaciol. 2016, 62, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Mölg, T.; Maussion, F.; Yang, W.; Scherer, D. The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier. Cryosphere 2012, 6, 1445–1461. [Google Scholar] [CrossRef] [Green Version]
- Dehecq, A.; Gourmelen, N.; Gardner, A.S.; Brun, F.; Goldberg, D.; Nienow, P.W.; Etienne, B.; Christian, V.; Patrick, W.; Trouvé, E. Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 2019, 12, 22–27. [Google Scholar] [CrossRef]
- Sakai, A.; Fujita, K.; Duan, K.; Pu, J.; Nakawo, M.; Yao, T. Five decades of shrinkage of July 1st glacier, Qilian Shan, China. J. Glaciol. 2006, 52, 11–16. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Li, Z.; Li, H.; Wang, F.; Zhou, P. Long-range terrestrial laser scanning measurements of annual and intra-annual mass balances for Urumqi Glacier No. 1, eastern Tien Shan, China. Cryosphere 2019, 13, 2361–2383. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Zhao, C.; Westoby, M.; Yao, T.; Wang, Y.; Pellicciotti, F.; Zhou, J.; He, Z.; Miles, E. Seasonal Dynamics of a Temperate Tibetan Glacier Revealed by High-Resolution UAV Photogrammetry and In Situ Measurements. Remote Sens. 2020, 12, 2389. [Google Scholar] [CrossRef]
- Span, N.; Kuhn, M.H.; Schneider, H. 100 years of ice dynamics of Hintereisferner, Central Alps, Austria, 1894–1994. Ann. Glaciol. 1997, 24, 297–302. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.; Liu, C. Introduction to Glaciology; Shanghai Popular Science Press: Shanghai, China, 2010; pp. 1–490. [Google Scholar]
- Müller, D.; Walter, T.R.; Schöpa, A.; Witt, T.; Steinke, B.; Gudmundsson, M.T.; Dürig, T. High-resolution digital elevation modeling from TLS and UAV campaign reveals structural complexity at the 2014/2015 Holuhraun eruption site, Iceland. Front. Earth Sci. 2017, 5, 59. [Google Scholar] [CrossRef] [Green Version]
- Son, S.W.; Kim, D.W.; Sung, W.G.; Yu, J.J. Integrating UAV and TLS approaches for environmental management: A case study of a waste stockpile area. Remote Sens. 2020, 12, 1615. [Google Scholar] [CrossRef]


| Date (dd/mm/yyyy) | Number of Points | Scanning Range (with Overlap) (km2) | Average Point Density (Points m−2) | Angle Resolution of Fine Scanning (°) | Total Scan Time (min) |
|---|---|---|---|---|---|
| 13 September 2017 | 15,547,327 | 5.36 | 1.90 | 0.020 | 71 |
| 4 September 2018 | 12,596,421 | 5.70 | 5.21 | 0.020 | 75 |
| 13 September 2019 | 11,606,873 | 4.18 | 2.76 | 0.020 | 71 |
| 15 September 2020 | 14,041,073 | 5.88 | 2.37 | 0.020 | 72 |
| Mass Balance Year | σMSA (m) | Number of Points (n) | (m a−1) | (m w.e a−1) | (m w.e a−1) | (m a−1) |
|---|---|---|---|---|---|---|
| 2017–2018 | 0.08 | 48,531 | 0.15 | 0.13 | — | — |
| 2018–2019 | 0.07 | 44,379 | 0.09 | 0.09 | 0.03 | 0.11 |
| 2019–2020 | 0.10 | 49,390 | 0.13 | 0.11 | — | — |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Li, Z.; Wang, F.; Mu, J. Spatio-Temporal Changes of Mass Balance in the Ablation Area of the Muz Taw Glacier, Sawir Mountains, from Multi-Temporal Terrestrial Geodetic Surveys. Remote Sens. 2021, 13, 1465. https://doi.org/10.3390/rs13081465
Xu C, Li Z, Wang F, Mu J. Spatio-Temporal Changes of Mass Balance in the Ablation Area of the Muz Taw Glacier, Sawir Mountains, from Multi-Temporal Terrestrial Geodetic Surveys. Remote Sensing. 2021; 13(8):1465. https://doi.org/10.3390/rs13081465
Chicago/Turabian StyleXu, Chunhai, Zhongqin Li, Feiteng Wang, and Jianxin Mu. 2021. "Spatio-Temporal Changes of Mass Balance in the Ablation Area of the Muz Taw Glacier, Sawir Mountains, from Multi-Temporal Terrestrial Geodetic Surveys" Remote Sensing 13, no. 8: 1465. https://doi.org/10.3390/rs13081465
APA StyleXu, C., Li, Z., Wang, F., & Mu, J. (2021). Spatio-Temporal Changes of Mass Balance in the Ablation Area of the Muz Taw Glacier, Sawir Mountains, from Multi-Temporal Terrestrial Geodetic Surveys. Remote Sensing, 13(8), 1465. https://doi.org/10.3390/rs13081465