Extended Pseudo Invariant Calibration Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors
Abstract
:1. Introduction
1.1. Cross-Calibration and Its Requirements
1.2. PICS-Based Cross-Calibration of Sensors
1.3. Limitations of PICS-Based Approach
1.4. The New Approach of Cluster-Based Cross-Calibration
2. Sensor Descriptions
2.1. Landsat 8 OLI
2.2. Landsat 7 ETM+
2.3. Sentinel 2A/2B MSI
3. Methodology
3.1. EPICS Selection
3.2. Process
3.2.1. Cloud Filtering and Outlier Removal
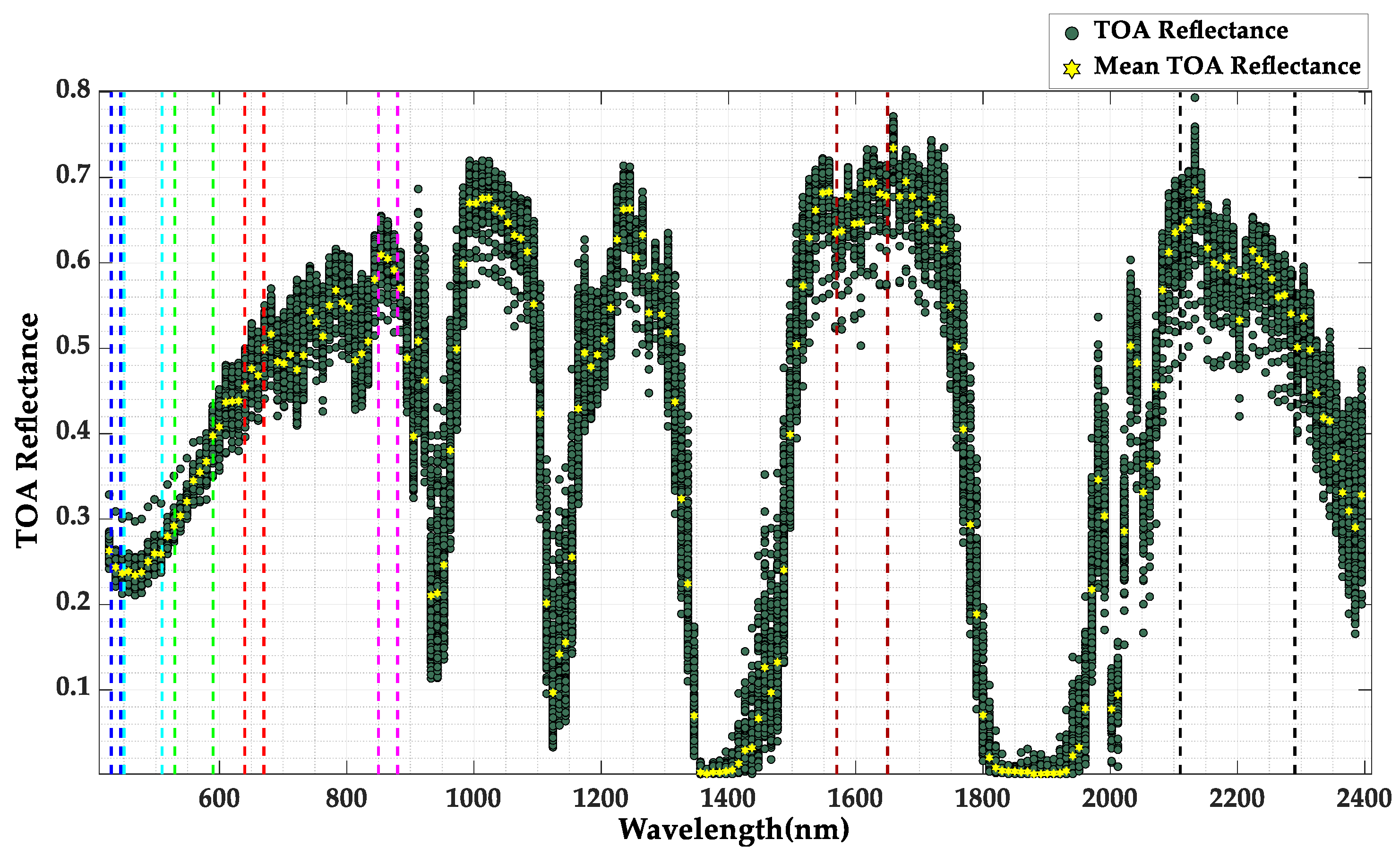
3.2.2. Conversion of Image Data to TOA Reflectance
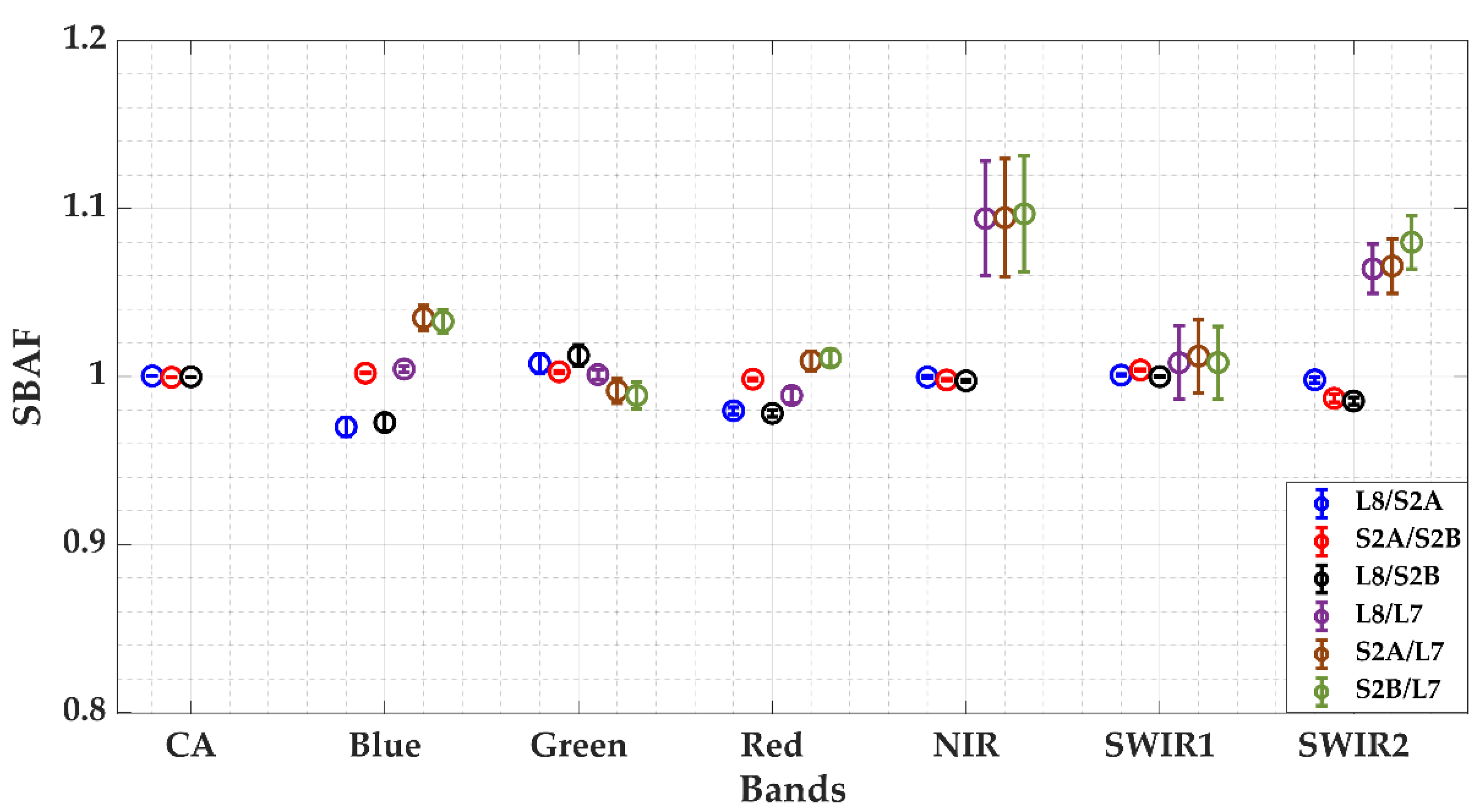
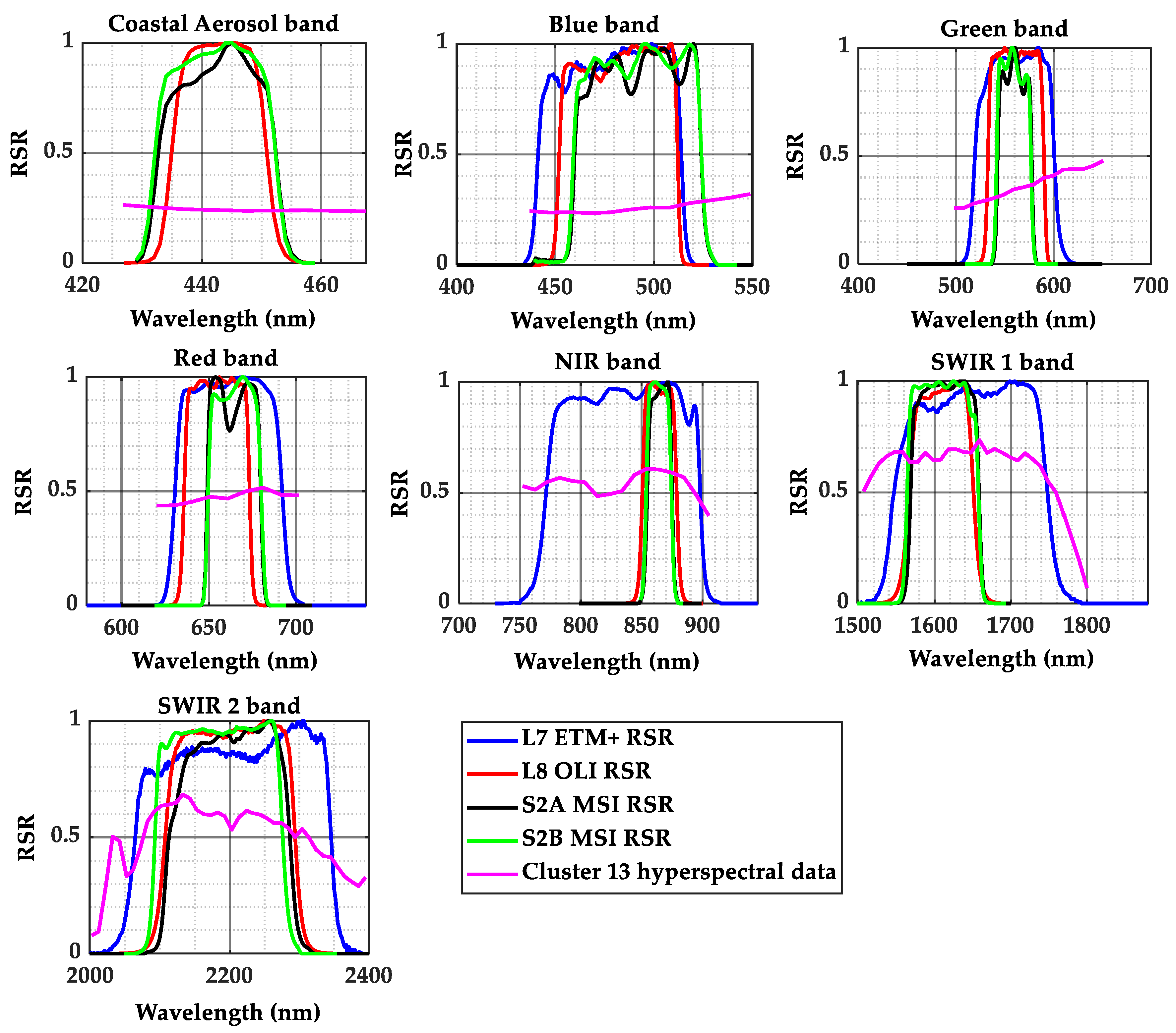
3.2.3. Estimation of Spectral Band Adjustment Factor
3.2.4. Bidirectional Reflectance Distribution Function Normalization
3.2.5. Data Smoothening and Trend Identification Using Modified Savitzky–Golay Filter
3.2.6. Trend-to-Trend Cross-Calibration Gain
3.2.7. Uncertainty Analysis
4. Results
4.1. Spectral Band Adjustment Factor for Cluster 13
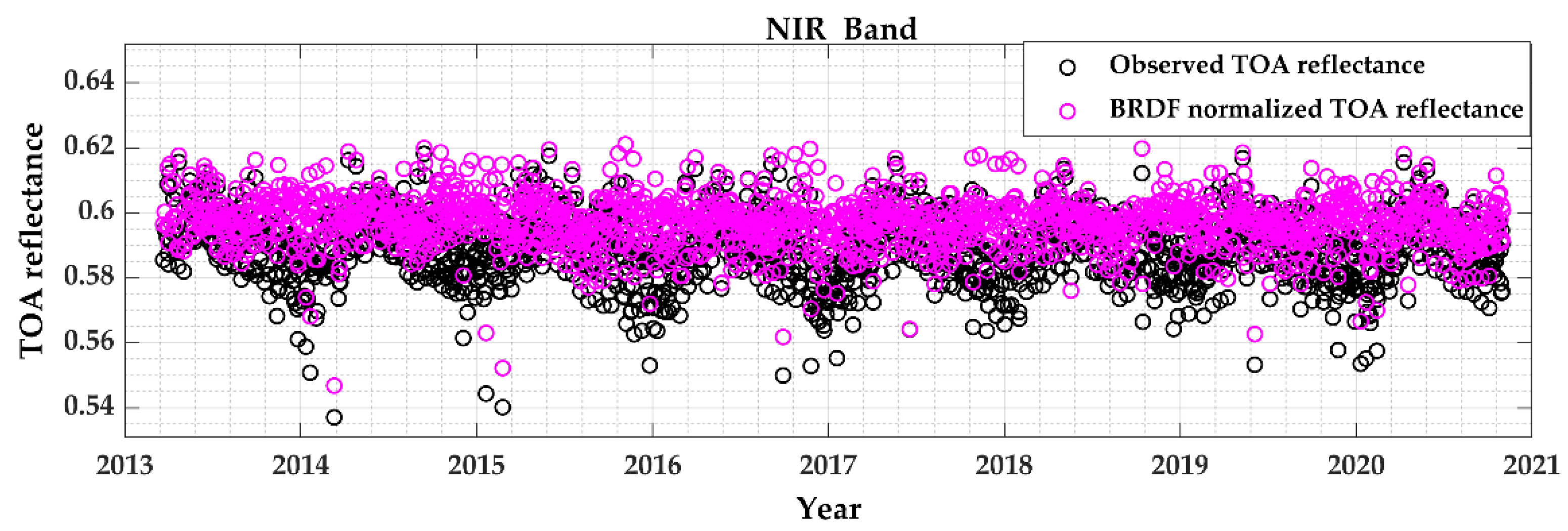
4.2. BRDF Normalization of the TOA Reflectance of the Sensor
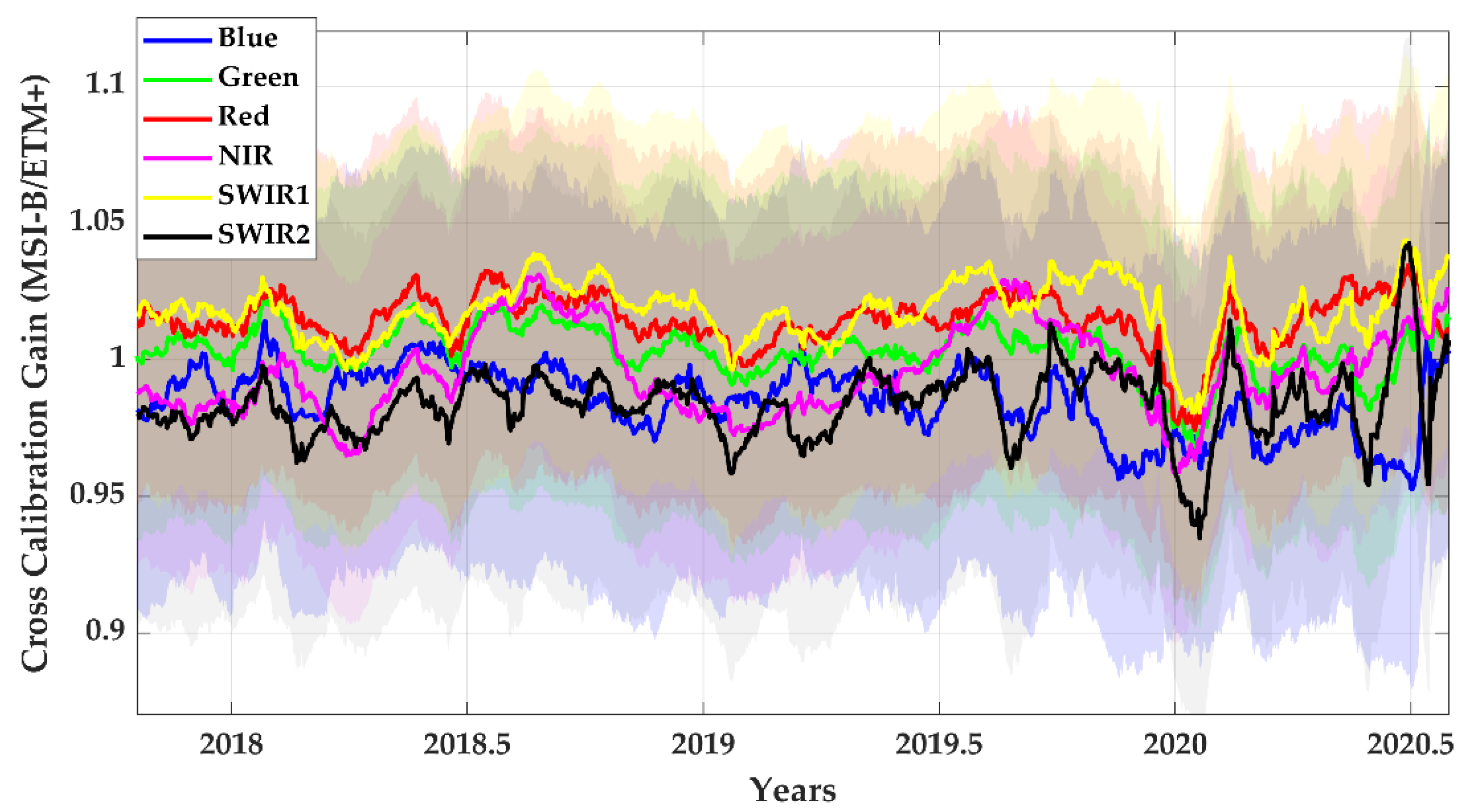
4.3. Data Trend Identification with Daily Coincident Acquisitions
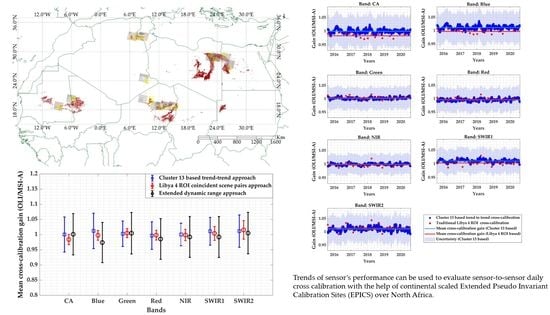
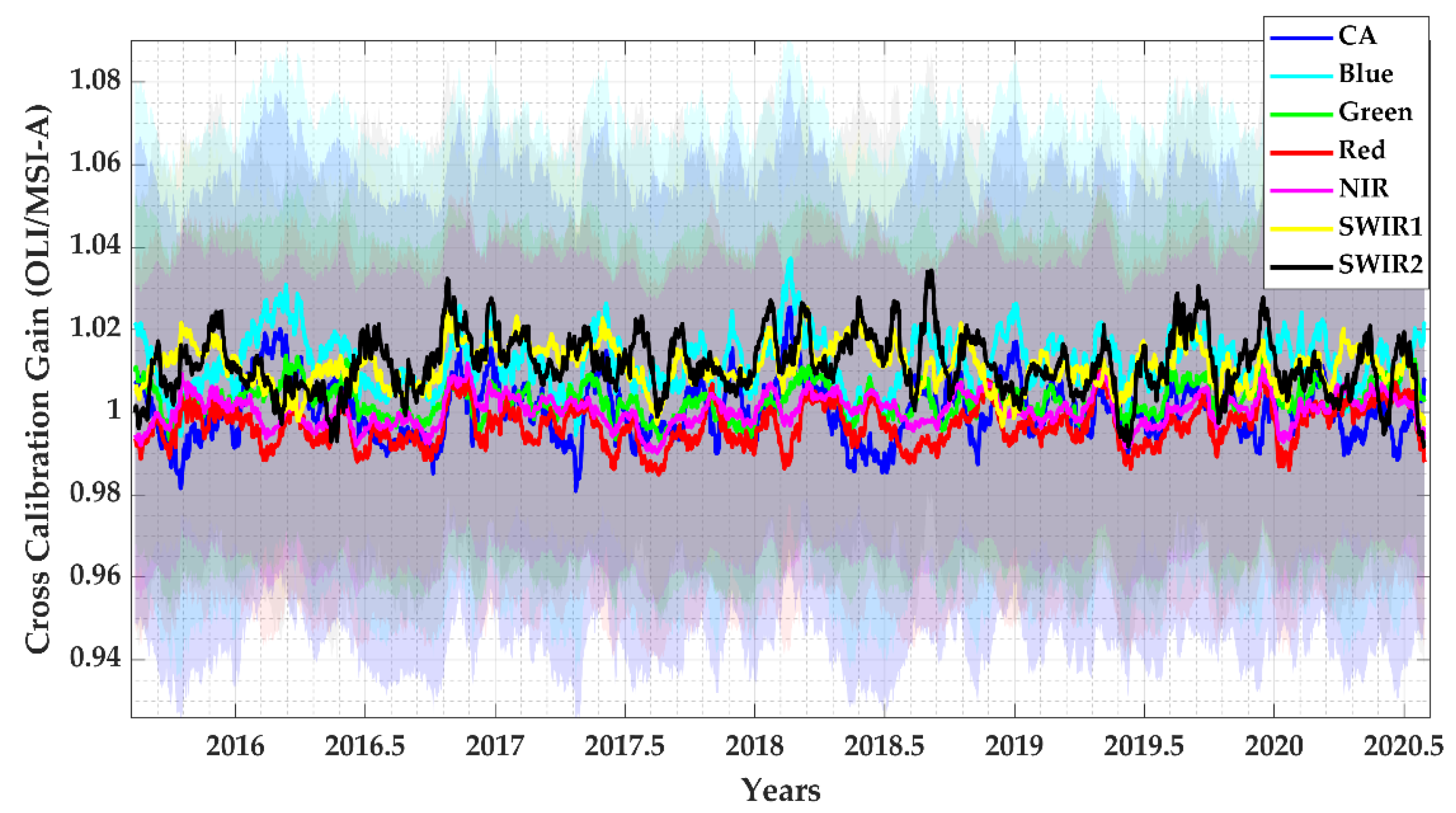
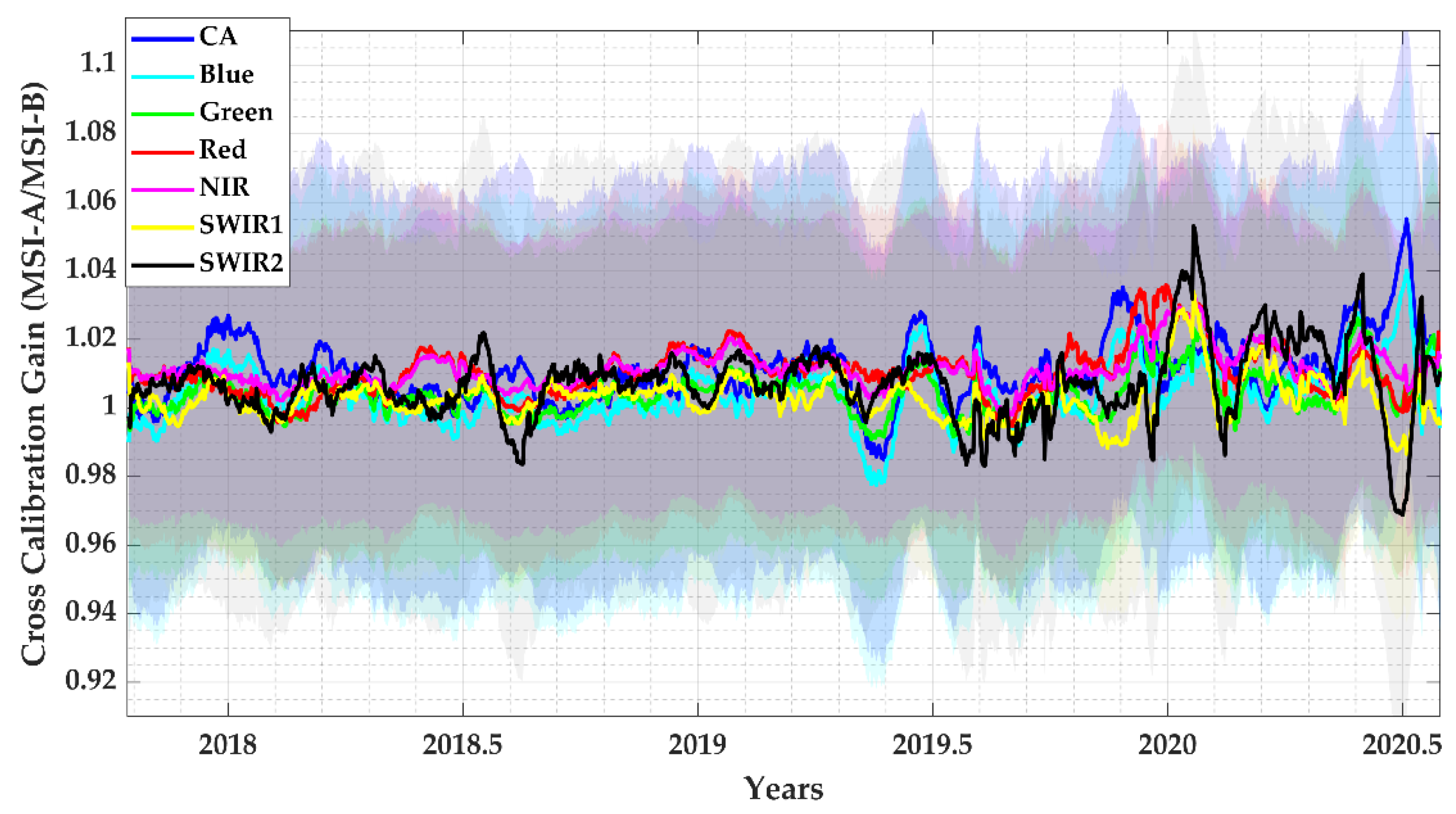
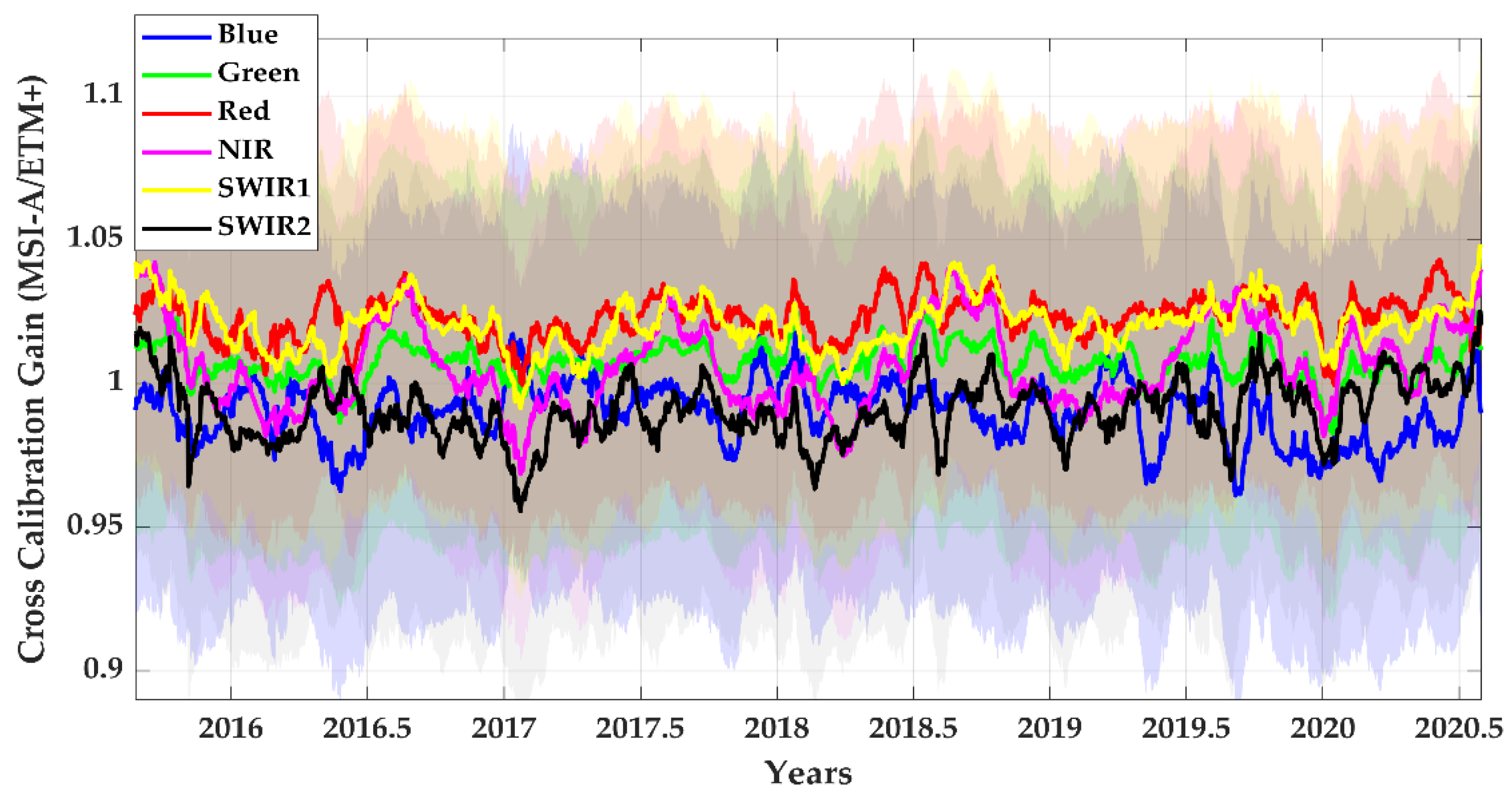
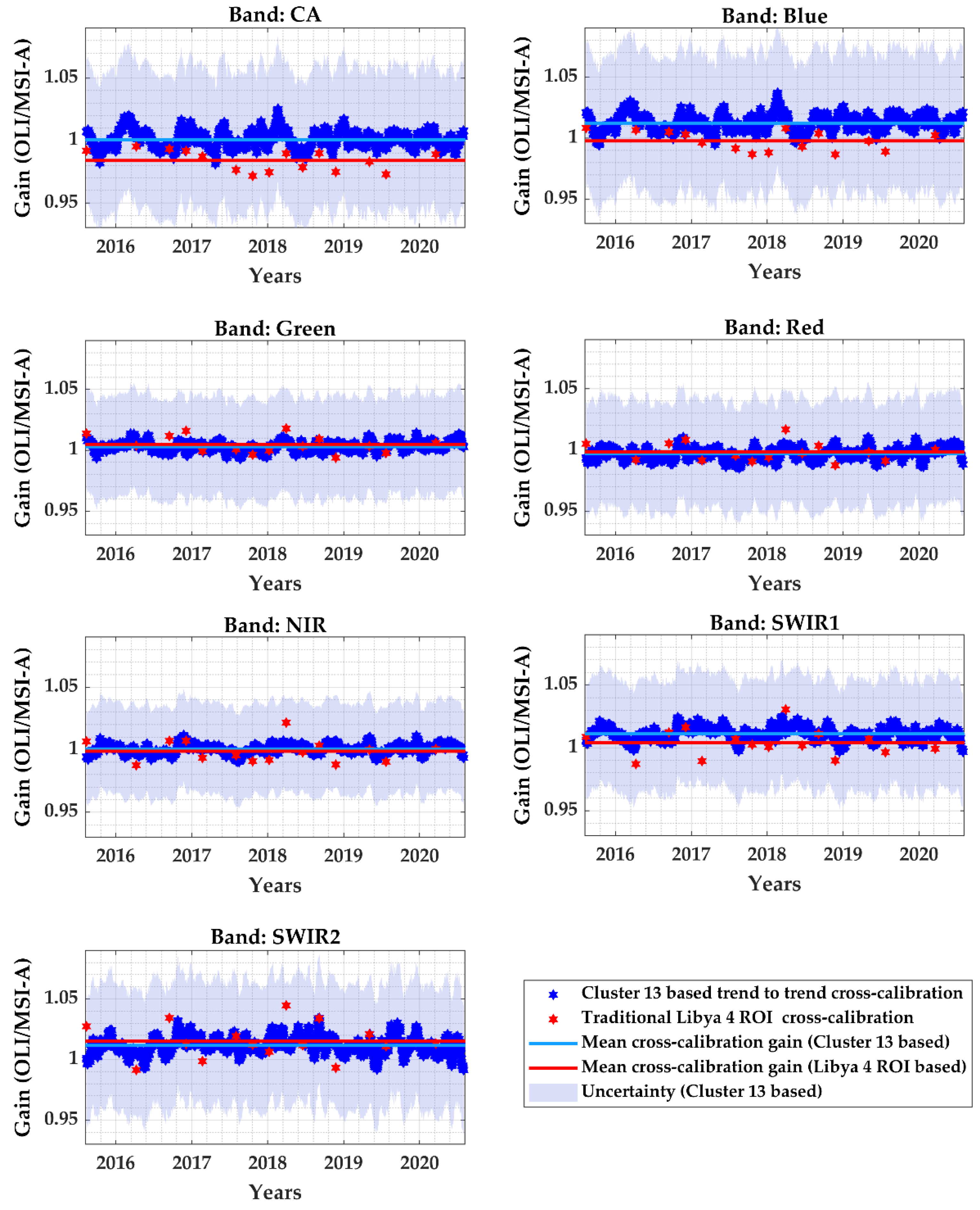
4.4. Cross-Calibration Gain with Their Uncertainties
5. Validation of the New Cluster-Based Approach
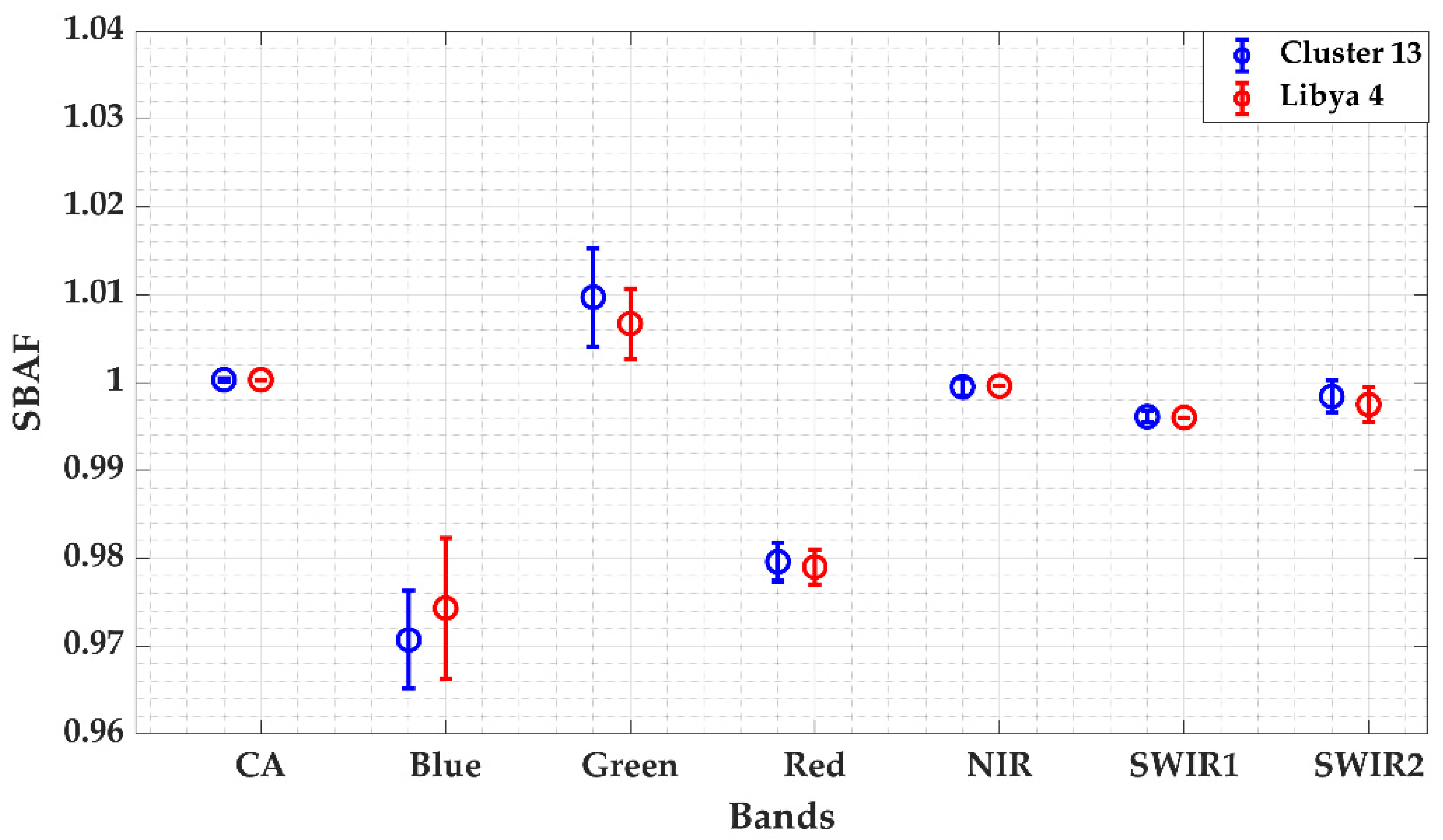
5.1. Spectral Band Adjustment Factor for Libya 4 ROI and Cluster 13
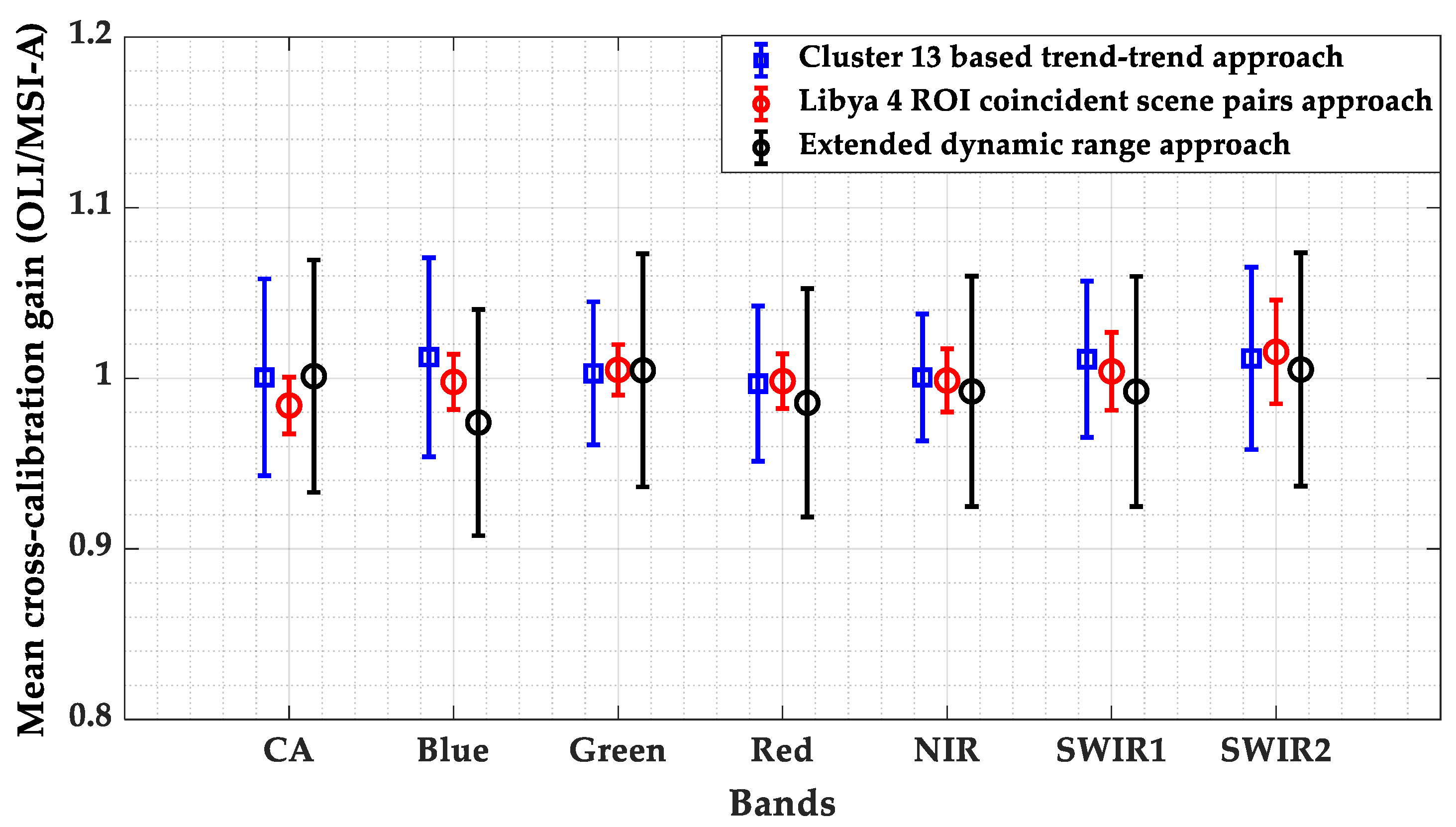
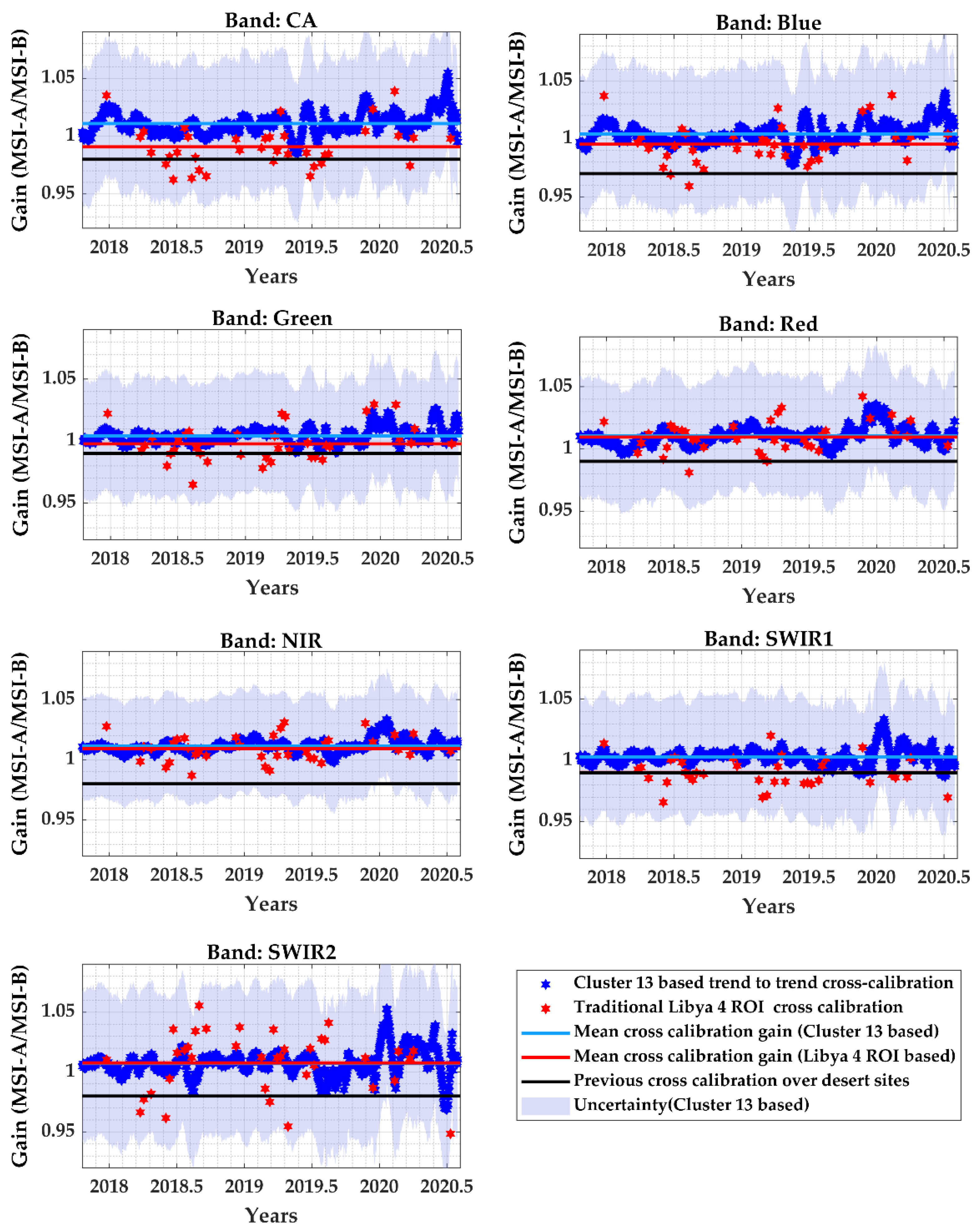
5.2. Cluster-Based Trend Totrend Cross-Calibration vs. Traditional PICS-Based Cross-Calibration Gain along with the Associated Uncertainty
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barrientos, C.; Mattar, C.; Nakos, T.; Perez, W. Radiometric Cross-Calibration of the Chilean Satellite FASat-C Using RapidEye and EO-1 Hyperion Data and a Simultaneous Nadir Overpass Approach. Remote Sens. 2016, 8, 612. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Morton, D.; Masek, J.; Wu, A.; Nagol, J.; Xiong, X.; Levy, R.; Vermote, E.; Wolfe, R. Impact of sensor degradation on the MODIS NDVI time series. Remote Sens. Environ. 2012, 119, 55–61. [Google Scholar] [CrossRef] [Green Version]
- Dinguirard, M.; Slater, P.N. Calibration of space-multispectral imaging sensors: A review. Remote Sens. Environ. 1999, 68, 194–205. [Google Scholar] [CrossRef]
- Sterckx, S.; Livens, S.; Adriaensen, S. Rayleigh, deep convective clouds, and cross-sensor desert vicarious calibration validation for the PROBA-V mission. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1437–1452. [Google Scholar] [CrossRef]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and characterization of Saharan and Arabian desert sites for the calibration of optical satellite sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D.R. Applications of spectral band adjustment factors (SBAF) for cross-calibration. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1267–1281. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.; Choi, T.; Angal, A.; Xiong, X. Use of EO-1 Hyperion data to calculate spectral band adjustment factors (SBAF) between the L7 ETM+ and Terra MODIS sensors. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Piscataway, NJ, USA, 25–30 July; pp. 1667–1670.
- Bacour, C.; Briottet, X.; Bréon, F.-M.; Viallefont-Robinet, F.; Bouvet, M. Revisiting Pseudo Invariant Calibration Sites (PICS) over sand deserts for vicarious calibration of optical imagers at 20 km and 100 km scales. Remote Sens. 2019, 11, 1166. [Google Scholar] [CrossRef] [Green Version]
- Helder, D.L.; Basnet, B.; Morstad, D.L. Optimized identification of worldwide radiometric pseudo-invariant calibration sites. Can. J. Remote Sens. 2010, 36, 527–539. [Google Scholar] [CrossRef]
- Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI radiometric cross comparison over desert sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
- Farhad, M. Cross Calibration and Validation of Landsat 8 OLI and Sentinel 2A MSI. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2018. Available online: https://openprairie.sdstate.edu/etd/2687/ (accessed on 15 April 2021).
- Pinto, C.; Ponzoni, F.; Castro, R.; Leigh, L.; Mishra, N.; Aaron, D.; Helder, D. First in-flight radiometric calibration of MUX and WFI on-board CBERS-4. Remote Sens. 2016, 8, 405. [Google Scholar] [CrossRef] [Green Version]
- Doelling, D.; Helder, D.; Schott, J.; Stone, T.; Pinto, C. Vicarious calibration and validation. In Reference Module in Earth Systems and Environmental Sciences. Comprehensive Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2018; Volume 1, pp. 475–518. [Google Scholar]
- Vuppula, H. Normalization of Pseudo-Invariant Calibration Sites for Increasing the Temporal Resolution and Long-Term Trending. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2017. Available online: https://openprairie.sdstate.edu/etd/2180/ (accessed on 15 April 2021).
- Shrestha, M.; Leigh, L.; Helder, D. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Sites (EPICS) for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 875. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, M.; Hasan, M.; Leigh, L.; Helder, D. Extended Pseudo Invariant Calibration Sites (EPICS) for the Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2019, 11, 1676. [Google Scholar] [CrossRef] [Green Version]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 operational land imager radiometric calibration and stability. Remote Sens. 2014, 6, 12275–12308. [Google Scholar] [CrossRef] [Green Version]
- Goward, S.N.; Masek, J.G.; Williams, D.L.; Irons, J.R.; Thompson, R. The Landsat 7 mission: Terrestrial research and applications for the 21st century. Remote Sens. Environ. 2001, 78, 3–12. [Google Scholar] [CrossRef]
- Andrefouet, S.; Bindschadler, R.; Brown.d.Colstoun, E.; Choate, M.; Chomentowski, W.; Christopherson, J.; Doorn, B.; Hall, D.; Holifield, C.; Howard, S. Preliminary Assessment of the Value of Landsat-7 ETM+ Data Following Scan Line Corrector Malfunction. United States Geological Survey (USGS), 2003. Available online: https://www.usgs.gov/media/files/preliminary-assessment-value-landsat-7-etm-slc-data (accessed on 15 April 2021).
- Drusch, M.; del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Li, J.; Roy, D.P. A global analysis of Sentinel-2A, Sentinel-2B and Landsat-8 data revisit intervals and implications for terrestrial monitoring. Remote Sens. 2017, 9, 902. [Google Scholar]
- Kaewmanee, M. PICS Trending Analysis: S2A, S2B. Presented at the Landsat 8th Technical Interchange Meeting [Online]. January 2020. [Google Scholar]
- Hasan, M.N.; Shrestha, M.; Leigh, L.; Helder, D. Evaluation of an Extended PICS (EPICS) for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 1755. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, M.; Hasan, N.; Leigh, L.; Helder, D. Derivation of Hyperspectral Profile of Extended Pseudo Invariant Calibration Sites (EPICS) for Use in Sensor Calibration. Remote Sens. 2019, 11, 2279. [Google Scholar] [CrossRef] [Green Version]
- Jing, X.; Leigh, L.; Helder, D.; Pinto, C.T.; Aaron, D. Lifetime Absolute Calibration of the EO-1 Hyperion Sensor and Its Validation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9466–9475. [Google Scholar] [CrossRef]
- Helder, D.; Thome, K.J.; Mishra, N.; Chander, G.; Xiong, X.; Angal, A.; Choi, T. Absolute radiometric calibration of Landsat using a pseudo invariant calibration site. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1360–1369. [Google Scholar] [CrossRef]
- Farhad, M.; Kaewmanee, M.; Leigh, L.; Helder, D. Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sens. 2020, 12, 806. [Google Scholar] [CrossRef]
- Kaewmanee, M. Pseudo Invariant Calibration Sites: PICS Evolution. In Proceedings of the CALCON 2018, Utah State University, Logan, UT, USA, 18–20 June 2018. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Barsi, J.A.; Markham, B.L.; Czapla-Myers, J.S.; Helder, D.L.; Hook, S.J.; Schott, J.R.; Haque, M.O. Landsat-7 ETM+ radiometric Calibration Status. In Proceedings of the Earth Observing Systems XXI, Event: SPIE Optical Engineering + Applications, San Diego, CA, USA, 19 September 2016; p. 99720C. [Google Scholar]
- Revel, C.; Lonjou, V.; Marcq, S.; Desjardins, C.; Fougnie, B.; Coppolani-Delle Luche, C.; Guilleminot, N.; Lacamp, A.-S.; Lourme, E.; Miquel, C. Sentinel-2A and 2B absolute calibration monitoring. Eur. J. Remote Sens. 2019, 52, 122–137. [Google Scholar] [CrossRef] [Green Version]








| Charactersctic\Sensor | Landsat ETM+ | Landsat OLI | MSI |
|---|---|---|---|
| Number of Bands | 8 | 10 | 13 |
| (1 pan, 6 multispectral, 1 thermal) | (1 pan, 6 multispectral, 1 thermal) | (All multispectral) | |
| Spatial Resolution (m) | 15, 30, 60 | 15, 30, 100 | 10, 20, 60 |
| (pan, multispectral, thermal) | (pan, multispectral, thermal) | (All multispectral) | |
| Swath width (km) | 183 | 183 | 290 |
| Orbit altitude (km) | 705 | 705 | 786 |
| Equatorial crossing time | 10:00–10:15 | 10:00–10:15 | 10:30 |
| Revisit frequency (days) | 16 | 16 | 10 |
| Sources of Uncertainty | Type | Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | ||
| Temporal uncertainty (%) | A | 2.04 | 1.96 | 1.39 | 1.46 | 1.01 | 1.16 | 2.58 |
| Spatial uncertainty (%) | 2.70 | 2.74 | 1.26 | 1.76 | 0.87 | 1.88 | 1.43 | |
| SBAF uncertainty (%) | 0.01 | 0.29 | 0.28 | 0.11 | 0.05 | 0.03 | 0.09 | |
| BRDF uncertainty (%) | 3.40 | 3.39 | 1.87 | 2.28 | 1.33 | 2.29 | 2.98 | |
| MSI calibration uncertainty (%) | B | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 |
| OLI calibration uncertainty (%) | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| Total (%) | 5.77 | 5.76 | 4.18 | 4.56 | 3.72 | 4.52 | 5.28 | |
| Cross Calibration | Bands | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|---|
| L8 vs. S2A | Gain | 1.0005 | 1.0123 | 1.0029 | 0.9968 | 1.0005 | 1.0111 | 1.0116 |
| Uncertainty (%) | 5.77 | 5.76 | 4.18 | 4.56 | 3.72 | 4.52 | 5.28 | |
| L8 vs. S2B | Gain | 0.9970 | 0.9805 | 0.9933 | 0.9993 | 1.0055 | 1.0074 | 1.0096 |
| Uncertainty (%) | 5.77 | 5.76 | 4.18 | 4.56 | 3.72 | 4.52 | 5.28 | |
| S2A vs. S2B | Gain | 1.0109 | 1.0042 | 1.0042 | 1.0105 | 1.0115 | 1.0029 | 1.0072 |
| Uncertainty (%) | 5.95 | 5.99 | 4.83 | 4.75 | 4.21 | 4.86 | 6.33 | |
| L8 vs. L7 | Gain | - | 1.0007 | 1.0092 | 1.0206 | 1.0070 | 1.0322 | 1.0009 |
| Uncertainty (%) | - | 7.20 | 6.01 | 6.29 | 5.92 | 6.35 | 6.87 | |
| S2A vs. L7 | Gain | - | 0.9902 | 1.0072 | 1.0231 | 1.0064 | 1.0209 | 0.9906 |
| Uncertainty (%) | - | 7.41 | 6.50 | 6.44 | 6.25 | 6.60 | 7.70 | |
| S2B vs. L7 | Gain | - | 0.9847 | 1.0032 | 1.0146 | 0.9956 | 1.0176 | 0.9838 |
| Uncertainty (%) | - | 7.36 | 6.50 | 6.44 | 6.26 | 6.66 | 7.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khakurel, P.; Leigh, L.; Kaewmanee, M.; Pinto, C.T. Extended Pseudo Invariant Calibration Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2021, 13, 1545. https://doi.org/10.3390/rs13081545
Khakurel P, Leigh L, Kaewmanee M, Pinto CT. Extended Pseudo Invariant Calibration Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors. Remote Sensing. 2021; 13(8):1545. https://doi.org/10.3390/rs13081545
Chicago/Turabian StyleKhakurel, Prathana, Larry Leigh, Morakot Kaewmanee, and Cibele Teixeira Pinto. 2021. "Extended Pseudo Invariant Calibration Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors" Remote Sensing 13, no. 8: 1545. https://doi.org/10.3390/rs13081545
APA StyleKhakurel, P., Leigh, L., Kaewmanee, M., & Pinto, C. T. (2021). Extended Pseudo Invariant Calibration Site-Based Trend-to-Trend Cross-Calibration of Optical Satellite Sensors. Remote Sensing, 13(8), 1545. https://doi.org/10.3390/rs13081545