A Neural-Network Based Spatial Resolution Downscaling Method for Soil Moisture: Case Study of Qinghai Province
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Microwave Data
2.1.2. Data from Land Surface Model
2.1.3. MODIS Data and Terrain Data
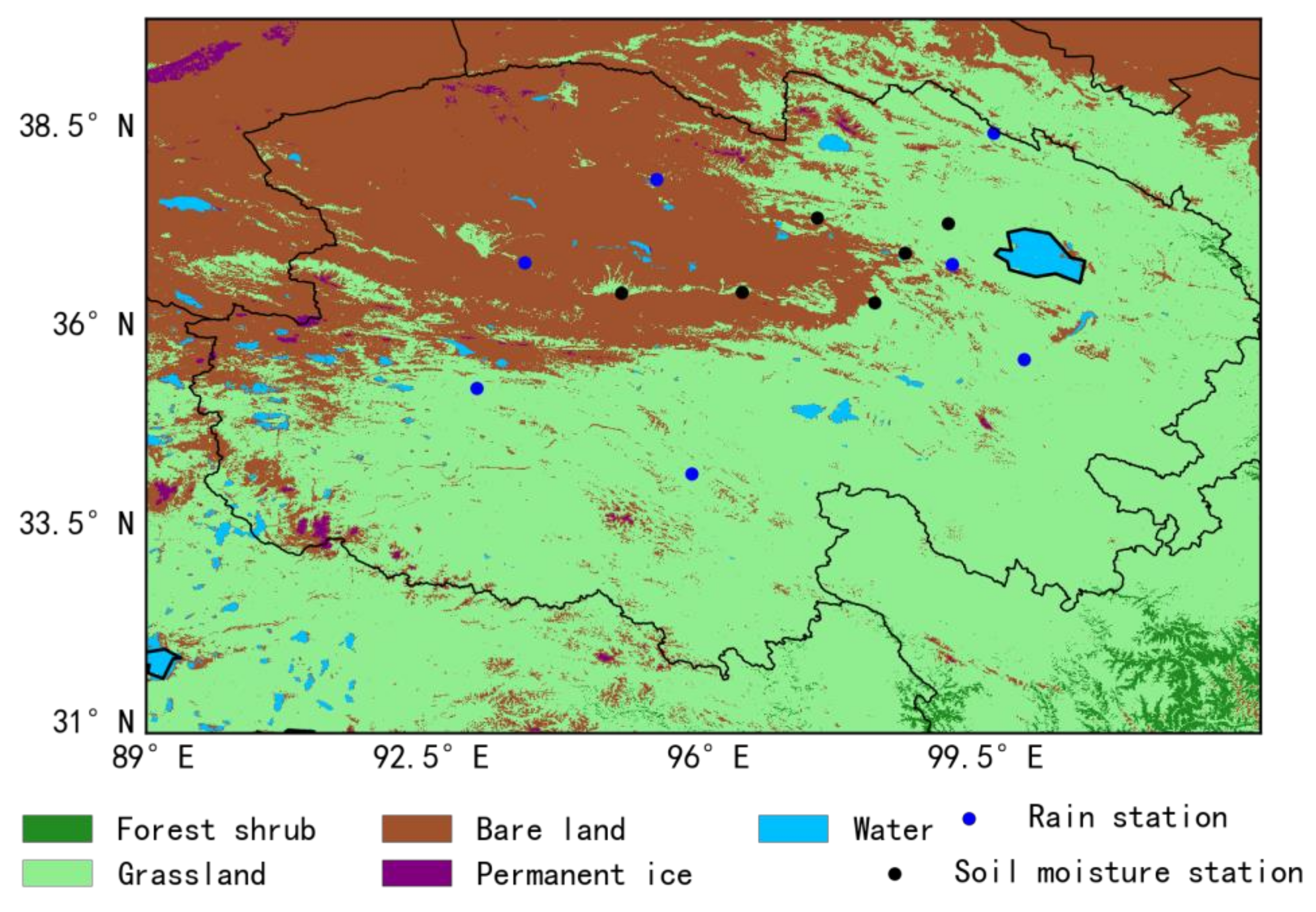
2.1.4. In Situ Observations
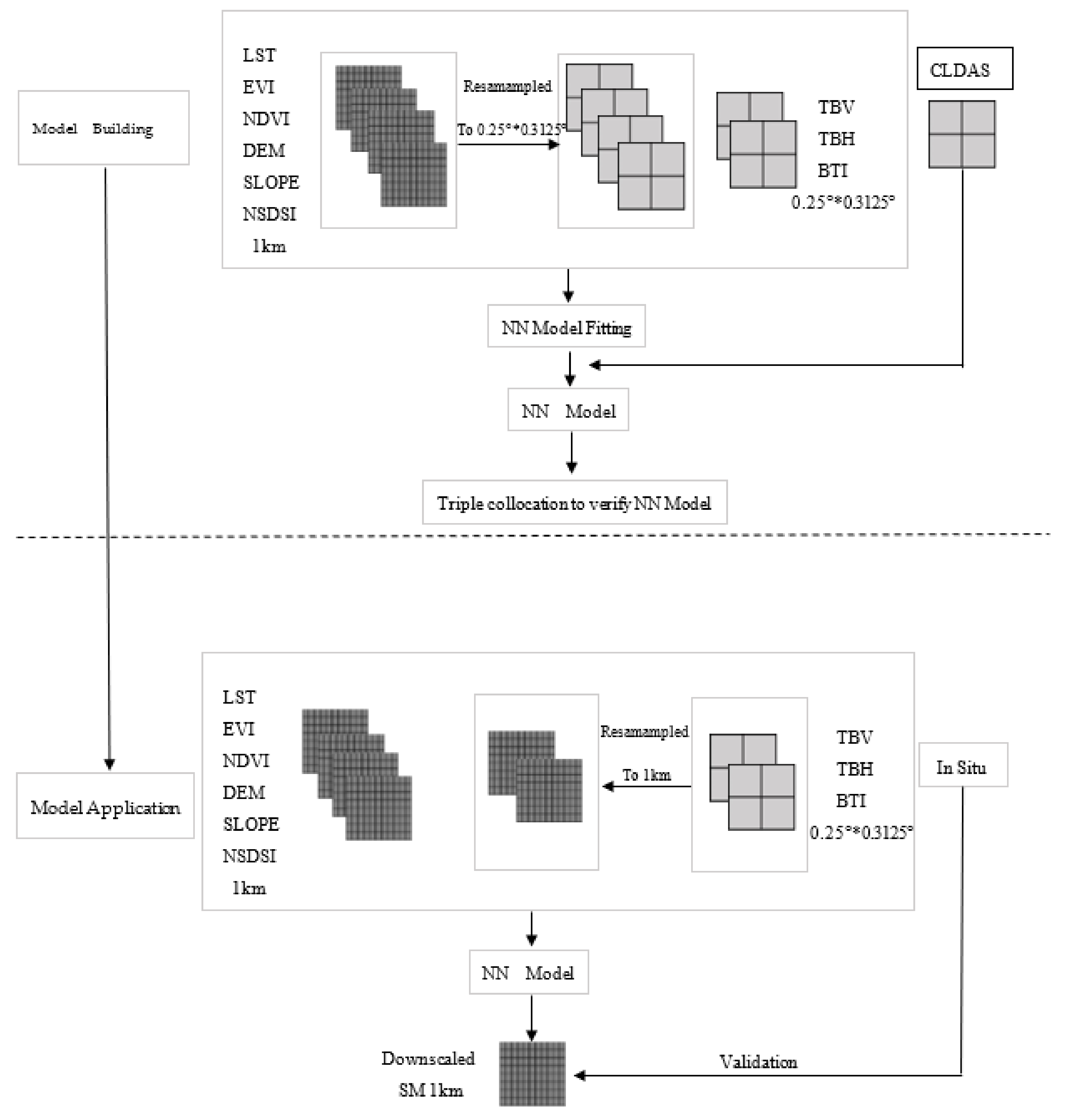
2.1.5. Data Preprocessing
2.2. Method
2.2.1. Triple Collocation Method
2.2.2. Evaluation Index
- (1)
- Spatial correlation: ρspatial
- (2)
- Temporal correlation: ρtemporal
- (3)
- Root mean square error: RMSE
- (4)
- Mean absolute error: MAE
- Aggregate auxiliary data (NDVI, EVI, LST, NSDSI, DEM, and SLOPE) into a grid with a resolution of 0.25° × 0.3125°, which is consistent with the spatial resolution of the resampling microwave data (Tbh, Tbv, σ40, and BTI). Specific bands of microwave data are available in Section 2.1.1. The relationship between these different input variables and the ground model CLDAS SM was established through the NN, and the quality of the NN SM was evaluated by comparing it with the CLDAS SM.
- Evaluate the SM dataset obtained from the NN model by using the TC method.
- Input the 1 km medium-resolution data from 2017 to 2018 into the verified NN model to obtain 1-km-resolution SM data.
- Use the data collected from the ground station to verify the downscaled NN SM data.
3. Results and Discussion
3.1. Selection Microwave Band
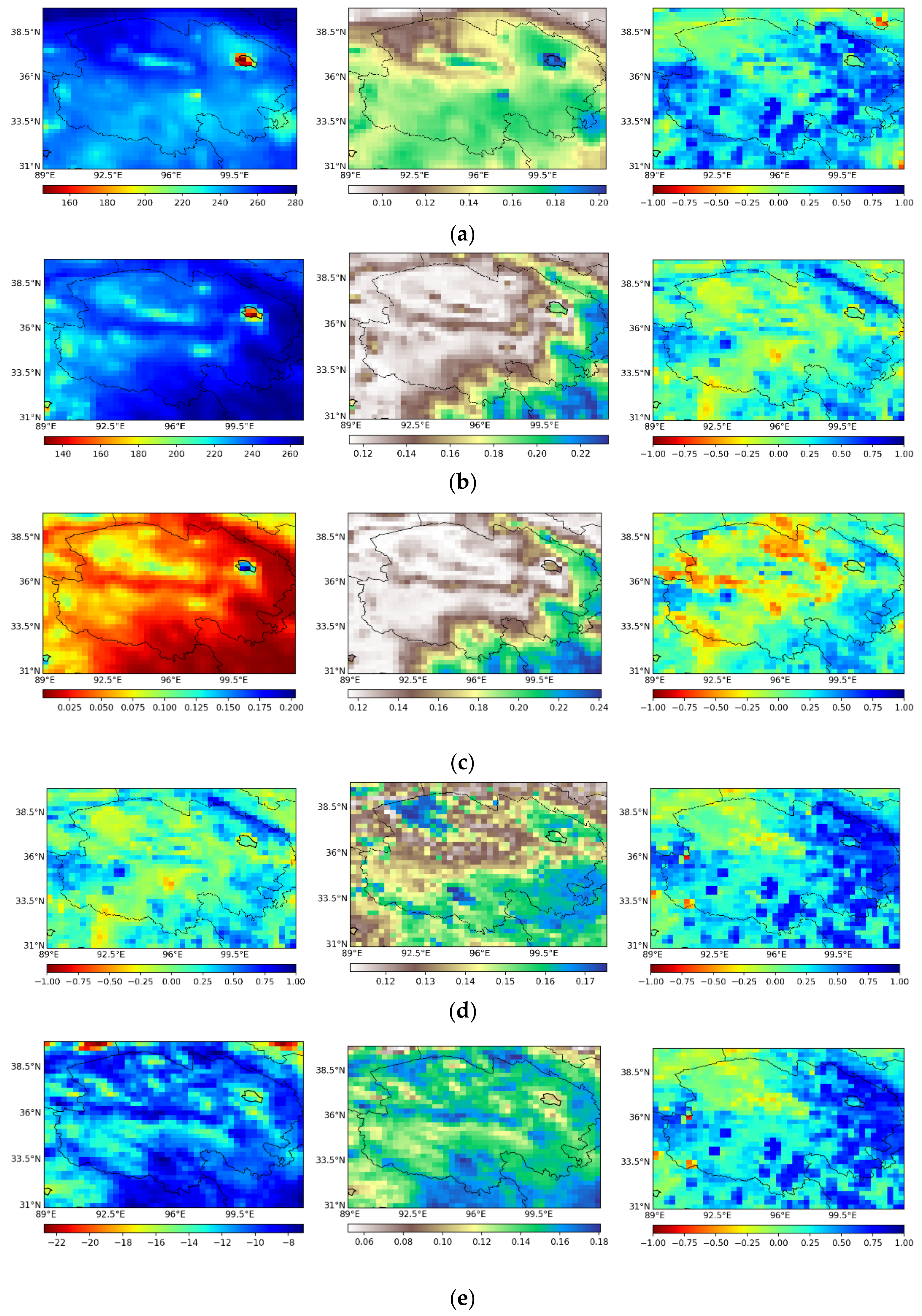
3.2. Selection of Auxiliary Data
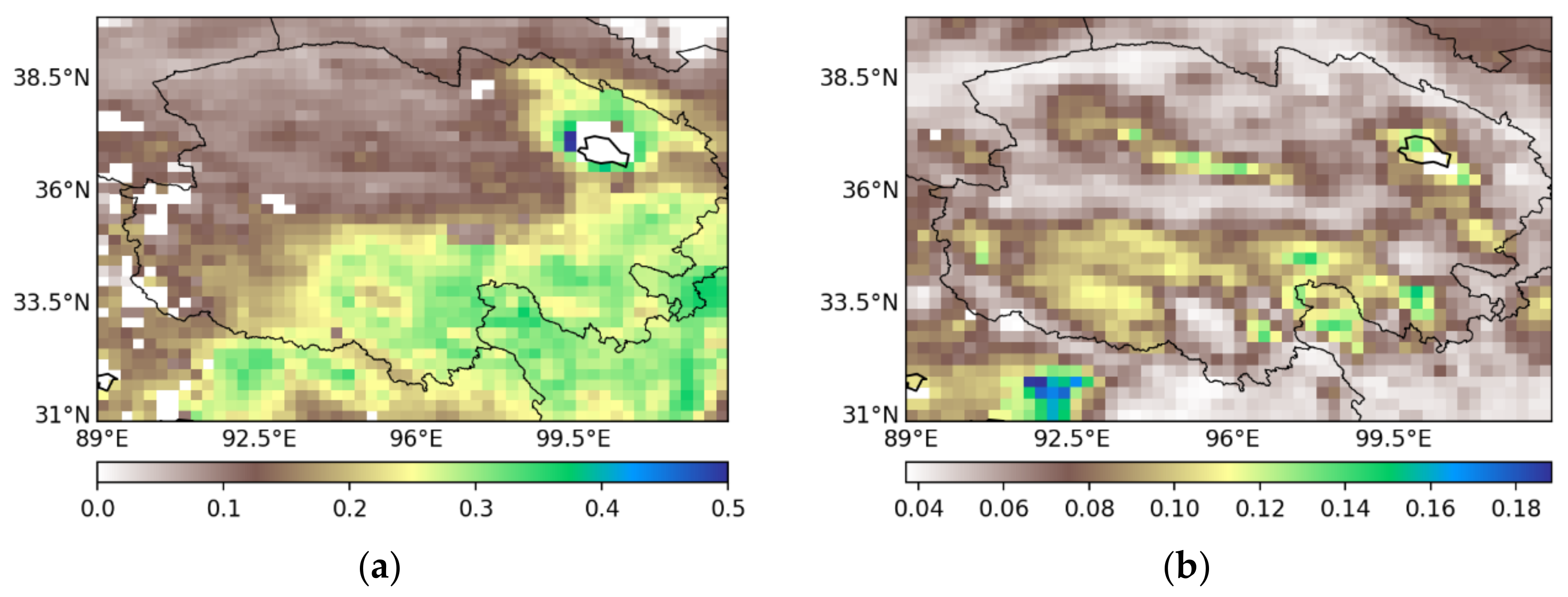
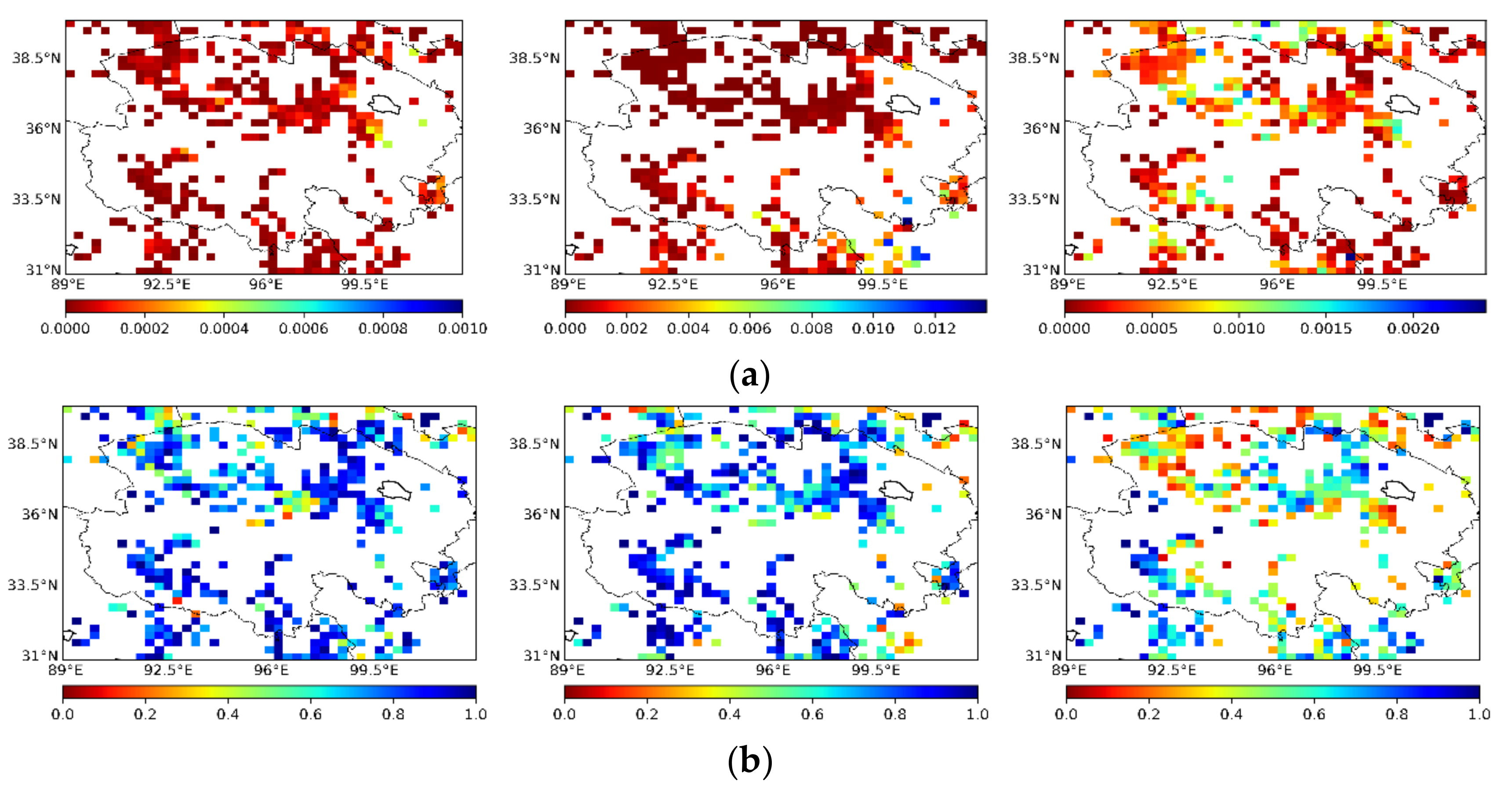
3.3. Triple Collocation Method to Verify Soil Moisture as Determined by Neural Network
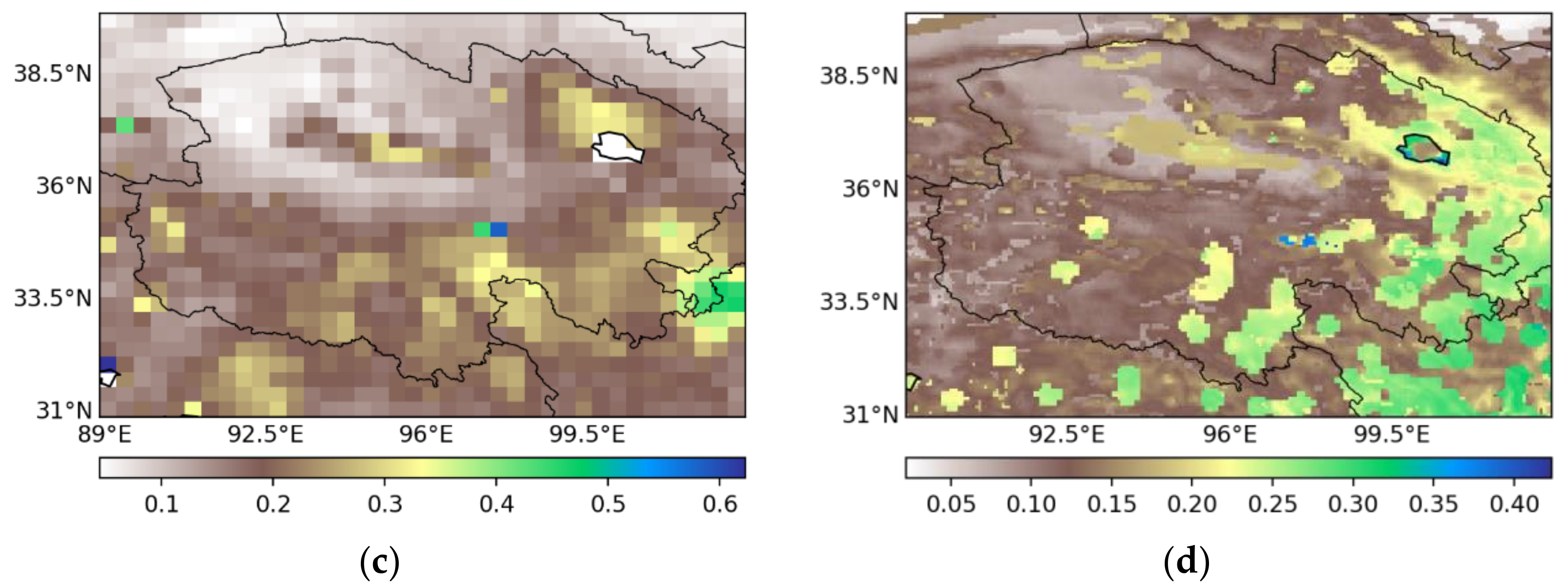
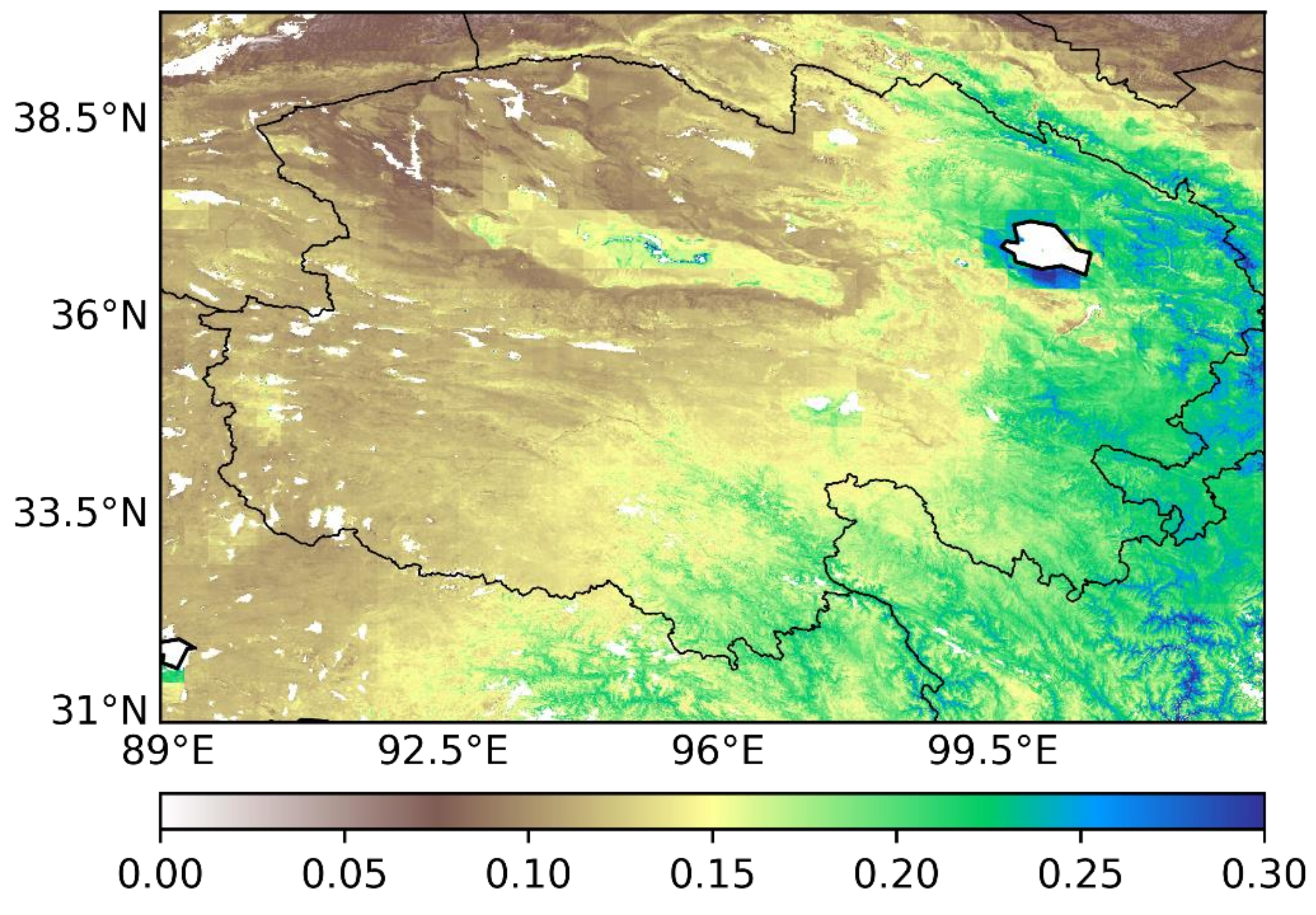
3.4. Verification of Downscaled Soil Moisture from Neural Network
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar]
- Keshavarz, M.R.; Vazifedoust, M.; Alizadeh, A. Drought monitoring using a Soil Wetness Deficit Index (SWDI) derived from MODIS satellite data. Agric. Water Manag. 2014, 132, 37–45. [Google Scholar]
- Rosenzweig, C.; Tubiello, F.N.; Goldberg, R.; Mills, E.; Bloomfield, J. Increased crop damage in the US from excess precipitation under climate change. Glob. Environ. Chang. 2002, 12, 197–202. [Google Scholar]
- Miller, G.R.; Baldocchi, D.D.; Law, B.E. Meyers An analysis of soil moisture dynamics using multi-year data from a network of micrometeorological observation sites. Adv. Water Resour. 2007, 30, 1065–1081. [Google Scholar]
- Mladenova, I.; Lakshmi, V.; Jackson, T.J.; Walker, J.P.; Merlin, O.; Jeu, R.A.M. De Validation of AMSR-E soil moisture using L-band airborne radiometer data from National Airborne Field Experiment 2006. Remote Sens. Environ. 2011, 115, 2096–2103. [Google Scholar]
- Zhang, P.; Yang, J.; Dong, C.; Lu, N.; Yang, Z.; Shi, J. General introduction on payloads, ground segment and data application of Fengyun 3A. Front. Earth Sci. China 2009, 3, 367–373. [Google Scholar]
- Zabolotskikh, E.V.; Mitnik, L.M.; Chapron, B. New approach for severe marine weather study using satellite passive microwave sensing. Geophys. Res. Lett. 2013, 40, 3347–3350. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS L: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar]
- Medeiros, J. Design and Development of the SMAP Microwave Radiometer Electronics. In Proceedings of the Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment, Pasadena, CA, USA, 24–27 March 2014. [Google Scholar]
- Figa-Saldaña, J.; Wilson, J.J.W.; Attema, E.; Gelsthorpe, R.; Drinkwater, M.R.; Stoffelen, A. The advanced scatterometer (ascat) on the meteorological operational (MetOp) platform: A follow on for european wind scatterometers. Can. J. Remote Sens. 2002, 28, 404–412. [Google Scholar]
- Njoku, E.G.; Wilson, W.J.; Yueh, S.H.; Dinardo, S.J.; Bolten, J. Observations of soil moisture using a passive and active low-frequency microwave airborne sensor during SGP99. Geosci. Remote Sens. IEEE Trans. 2002, 40, 2659–2673. [Google Scholar]
- Das, N.N.; Entekhabi, D.; Njoku, E.G. An algorithm for merging SMAP radiometer and radar data for high-resolution soil-moisture retrieval. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1504–1512. [Google Scholar]
- Zhan, X.; Houser, P.R.; Walker, J.P.; Crow, W.T. A method for retrieving high-resolution surface soil moisture from hydros L-band radiometer and radar observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1534–1544. [Google Scholar]
- Wilson, D.J.; Western, A.W.; Grayson, R.B. A terrain and data-based method for generating the spatial distribution of soil moisture. Adv. Water Resour. 2005, 28, 43–54. [Google Scholar]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine Learning Techniques for Downscaling SMOS Satellite Soil Moisture Using MODIS Land Surface Temperature for Hydrological Application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar]
- Yang, K.; Zhu, L.; Chen, Y.; Zhao, L.; Qin, J.; Lu, H.; Tang, W.; Han, M.; Ding, B.; Fang, N. Land surface model calibration through microwave data assimilation for improving soil moisture simulations. J. Hydrol. 2016, 533, 266–276. [Google Scholar]
- Chen, W.; Shen, H.; Huang, C.; Li, X. Improving soil moisture estimation with a dual ensemble Kalman smoother by jointly assimilating AMSR-E brightness temperature and MODIS LST. Remote Sens. 2017, 9, 273. [Google Scholar]
- Chauhan, N.S.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar]
- Liu, Z.; Zhou, P.; Zhang, F. Spatiotemporal characteristics of dryness/wetness conditions across Qinghaiprovince, Northwest China. Agric. For. Meteorol. 2013, 182–183, 101–108. [Google Scholar]
- Qi, Y.; Li, S.; Ran, Y.; Wang, H.; Wu, J.; Lian, X.; Luo, D. Mapping Frozen Ground in the Qilian Mountains in 2004–2019 Using Google Earth Engine Cloud Computing. Remote Sens. 2021, 13, 149. [Google Scholar]
- Liu, S.; Zhang, Y.; Cheng, F.; Hou, X.; Zhao, S. Response of Grassland Degradation to Drought at Different Time-Scales in Qinghai Province: Spatio-Temporal Characteristics, Correlation, and Implications. Remote Sens. 2017, 9, 1329. [Google Scholar]
- Cui, Y.; Long, D.; Hong, Y.; Zeng, C.; Zhou, J.; Han, Z.; Liu, R.; Wan, W. Validation and reconstruction of FY-3B/MWRI soil moisture using an artificial neural network based on reconstructed MODIS optical products over the Tibetan Plateau. J. Hydrol. 2016, 543, 242–254. [Google Scholar]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar]
- Lucchesi, R. File Specification for GEOS-5 FP; NASA Global Modeling and Assimilation Office (GMAO) Office Note No. 4 (Version 1.0); NASA: Washington, DC, USA, 2013. [Google Scholar]
- Hu, F.; Wei, Z.; Zhang, W.; Dorjee, D.; Meng, L. A spatial downscaling method for SMAP soil moisture through visible and shortwave-infrared remote sensing data. J. Hydrol. 2020, 590, 125360. [Google Scholar]
- Van der Vliet, M.; Van der Schalie, R.; Rodriguez-Fernandez, N.; Colliander, A.; de Jeu, R.; Preimesberger, W.; Scanlon, T.; Dorigo, W. Reconciling Flagging Strategies for Multi-Sensor Satellite Soil Moisture Climate Data Records. Remote Sens. 2020, 12, 3439. [Google Scholar]
- Ghulam, A.; Qin, Q.; Teyip, T.; Li, Z.-L. Modified perpendicular drought index (MPDI): A real-time drought monitoring method. ISPRS J. Photogramm. Remote Sens. 2007, 62, 150–164. [Google Scholar]
- Kolassa, J.; Gentine, P.; Prigent, C.; Aires, F. Soil moisture retrieval from AMSR-E and ASCAT microwave observation synergy. Part 1: Satellite data analysis. Remote Sens. Environ. 2016, 173, 1–14. [Google Scholar]
- Scipal, K.; Holmes, T.; De Jeu, R.; Naeimi, V.; Wagner, W. A possible solution for the problem of estimating the error structure of global soil moisture data sets. Geophys. Res. Lett. 2008, 35, 2–5. [Google Scholar]
- Gruber, A.; Su, C.-H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar]
- Chen, F.; Crow, W.T.; Bindlish, R.; Colliander, A.; Burgin, M.S.; Asanuma, J.; Aida, K. Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation. Remote Sens. Environ. 2018, 214, 1–13. [Google Scholar]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar]
- Ge, L.; Hang, R.; Liu, Y.; Liu, Q. Comparing the performance of neural network and deep convolutional neural network in estimating soil moisture from satellite observations. Remote Sens. 2018, 10, 1327. [Google Scholar]
- Kolassa, J.; Reichle, R.H.; Liu, Q.; Alemohammad, S.H.; Gentine, P.; Aida, K.; Asanuma, J.; Bircher, S.; Caldwell, T.; Colliander, A.; et al. Estimating surface soil moisture from SMAP observations using a Neural Network technique. Remote Sens. Environ. 2018, 204, 43–59. [Google Scholar] [PubMed]
- Rodríguez-Fernández, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Cabot, F.; Jiménez, C.; Mahmoodi, A.; Drusch, M. Soil moisture retrieval using neural networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Nonlinear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar]
- Rumelhart, D.E.; Chauvin, Y. Backpropagation: Theory, Architectures, and Applications; Psychology Press: Hove, UK, 1995. [Google Scholar]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards improved spatio-temporal resolution soil moisture retrievals from the synergy of SMOS and MSG SEVIRI spaceborne observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar]
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Walker, J.P. Downscaling SMOS-Derived Soil Moisture Using MODIS Visible/Infrared Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar]





| Satellite | Unit | Ascending/Descending | Spatial Resolution | Time Series |
|---|---|---|---|---|
| SMAP | m3/m3 | 18:00/6:00 | 36 km | 2015–present |
| AMSR2 | m3/m3 | 13:30/1:30 | 0.25° | 2012–present |
| FY3C | m3/m3 | 13:40/1:40 | 25 km | 2014–present |
| ASCAT | m3/m3 | —— | 25 km | 2007–present |
| GEOS-5 | m3/m3 | —— | 0.25° × 0.3125° | 2014–present |
| CLDAS | m3/m3 | —— | 0.0625° × 0.0625° | 2017–present |
| Input Variables | Dataset | Spatial Resolution | Temporal Resolutions | Time Series |
|---|---|---|---|---|
| NDVI | MOD13A2 | 1 km | 16 days | 2000–present |
| EVI | MOD13A2 | 1 km | 16 days | 2000–present |
| LST | MOD11A1 | 1 km | daily | 2000–present |
| DEM | SRTM | 90 m | - | 2000 |
| SLOPE | SRTM | 90 m | - | 2000 |
| NSDSI | MOD09A1 | 500 m | 8 days | 2000–present |
| Ascending | ρspatial | ρtemporal | RMSE | MAE | Descending | ρspatial | ρtemporal | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| SMAP | SMAP | ||||||||
| 1.41 Tbv | 0.388 | 0.322 | 0.065 | 0.053 | 1.41 Tbv | 0.374 | 0.235 | 0.066 | 0.055 |
| 1.41 Tbh | 0.254 | 0.333 | 0.067 | 0.055 | 1.41 Tbh | 0.306 | 0.260 | 0.068 | 0.056 |
| 1.41 MPDI | 0.186 | 0.291 | 0.069 | 0.057 | 1.41 MPDI | 0.121 | 0.259 | 0.070 | 0.058 |
| AMSR2 | AMSR2 | ||||||||
| 6.9 Tbv | 0.159 | 0.158 | 0.070 | 0.058 | 6.9 Tbv | 0.250 | 0.182 | 0.068 | 0.056 |
| 6.9 Tbh | 0.396 | 0.187 | 0.064 | 0.052 | 6.9 Tbh | 0.474 | 0.182 | 0.062 | 0.050 |
| 6.9 MPDI | 0.486 | 0.186 | 0.063 | 0.051 | 6.9 MPDI | 0.509 | 0.214 | 0.061 | 0.050 |
| 7.3 Tbv | 0.171 | 0.176 | 0.069 | 0.057 | 7.3 Tbv | 0.275 | 0.166 | 0.067 | 0.056 |
| 7.3 Tbh | 0.406 | 0.191 | 0.063 | 0.052 | 7.3 Tbh | 0.488 | 0.194 | 0.061 | 0.050 |
| 7.3 MPDI | 0.491 | 0.186 | 0.062 | 0.051 | 7.3 MPDI | 0.511 | 0.217 | 0.061 | 0.050 |
| 10.7 Tbv | 0.186 | 0.201 | 0.069 | 0.057 | 10.7 Tbv | 0.312 | 0.216 | 0.066 | 0.054 |
| 10.7 Tbh | 0.459 | 0.202 | 0.062 | 0.050 | 10.7 Tbh | 0.525 | 0.205 | 0.059 | 0.048 |
| 10.7 MPDI | 0.513 | 0.182 | 0.061 | 0.050 | 10.7 MPDI | 0.529 | 0.214 | 0.060 | 0.049 |
| FY3C | FY3C | ||||||||
| 10.7 Tbv | 0.249 | 0.183 | 0.067 | 0.055 | 10.7 Tbv | 0.182 | 0.232 | 0.067 | 0.055 |
| 10.7 Tbh | 0.471 | 0.188 | 0.061 | 0.049 | 10.7 Tbh | 0.428 | 0.233 | 0.060 | 0.049 |
| 10.7 MPDI | 0.511 | 0.177 | 0.060 | 0.049 | 10.7 MPDI | 0.470 | 0.185 | 0.060 | 0.049 |
| ASCAT | ASCAT | ||||||||
| σ40 | 0.259 | 0.334 | 0.066 | 0.054 | BTI | 0.269 | 0.336 | 0.064 | 0.053 |
| Input Variable | ρspatial | ρtemporal | RMSE | MAE |
|---|---|---|---|---|
| SMAP_TBV_A_AMSR2_TBH_D | 0.621 | 0.393 | 0.053 | 0.043 |
| SMAP_TBV_A_AMSR2_TBH_D_σ40 | 0.604 | 0.393 | 0.051 | 0.041 |
| SMAP_TBV_A_AMSR2_TBH_D_BTI | 0.597 | 0.401 | 0.051 | 0.041 |
| SMAP_TBV_A_AMSR2_MPDI_D | 0.600 | 0.362 | 0.055 | 0.044 |
| SMAP_TBV_A_AMSR2_MPDI_D_σ40 | 0.583 | 0.354 | 0.053 | 0.043 |
| SMAP_TBV_A_AMSR2_MPDI_D_BTI | 0.573 | 0.381 | 0.053 | 0.042 |
| Auxiliary Input Variable | ρspatial | ρtemporal | RMSE | MAE |
|---|---|---|---|---|
| TBV_TBH_BTI | 0.597 | 0.401 | 0.051 | 0.041 |
| Use of vegetation data | ||||
| TBV_TBH_BTI_NDVI | 0.623 | 0.409 | 0.050 | 0.040 |
| TBV_TBH_BTI_EVI | 0.614 | 0.409 | 0.051 | 0.040 |
| Use of terrain data | ||||
| TBV_TBH_BTI_SLOPE | 0.616 | 0.407 | 0.051 | 0.040 |
| TBV_TBH_BTI_DEM | 0.634 | 0.412 | 0.049 | 0.039 |
| TBV_TBH_BTI_SLOPE _NDVI | 0.636 | 0.415 | 0.050 | 0.040 |
| TBV_TBH_BTI_DEM _NDVI | 0.658 | 0.443 | 0.048 | 0.038 |
| TBV_TBH_BTI _DEM_SLOPE_NDVI | 0.676 | 0.450 | 0.047 | 0.037 |
| Use of land surface temperature data | ||||
| TBV_TBH_BTI _LST | 0.604 | 0.441 | 0.049 | 0.039 |
| TBV_TBH_BTI_LST _NDVI | 0.617 | 0.448 | 0.049 | 0.039 |
| TBV_TBH_BTI_LST _NDVI_DEM_SLOPE | 0.663 | 0.477 | 0.046 | 0.036 |
| Use of surface reflectance data | ||||
| TBV_TBH_BTI_NSDSI | 0.608 | 0.410 | 0.051 | 0.040 |
| TBV_TBH_BTI_NSDSI _NDVI | 0.631 | 0.417 | 0.050 | 0.040 |
| TBV_TBH_BTI_NSDSI _NDVI_DEM_SLOPE | 0.684 | 0.453 | 0.047 | 0.037 |
| TBV_TBH_BTI_ NSDSI _NDVI_DEM_SLOPE _LST | 0.669 | 0.475 | 0.046 | 0.036 |
| Station | Delingha | Dulan | Golmud | Nuomuhong | Tianjun | Wulan |
|---|---|---|---|---|---|---|
| CLDAS | 0.427 | 0.759 | −0.025 | −0.270 | 0.391 | 0.670 |
| SMAP | 0.185 | 0.762 | −0.587 | 0.193 | 0.548 | 0.776 |
| AMSR2 | 0.117 | 0.328 | −0.655 | 0.051 | 0.398 | 0.584 |
| DOWNSCALED | 0.212 | 0.768 | −0.524 | 0.251 | 0.620 | 0.616 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, A.; Zhang, Z.; Zhu, H. A Neural-Network Based Spatial Resolution Downscaling Method for Soil Moisture: Case Study of Qinghai Province. Remote Sens. 2021, 13, 1583. https://doi.org/10.3390/rs13081583
Lv A, Zhang Z, Zhu H. A Neural-Network Based Spatial Resolution Downscaling Method for Soil Moisture: Case Study of Qinghai Province. Remote Sensing. 2021; 13(8):1583. https://doi.org/10.3390/rs13081583
Chicago/Turabian StyleLv, Aifeng, Zhilin Zhang, and Hongchun Zhu. 2021. "A Neural-Network Based Spatial Resolution Downscaling Method for Soil Moisture: Case Study of Qinghai Province" Remote Sensing 13, no. 8: 1583. https://doi.org/10.3390/rs13081583
APA StyleLv, A., Zhang, Z., & Zhu, H. (2021). A Neural-Network Based Spatial Resolution Downscaling Method for Soil Moisture: Case Study of Qinghai Province. Remote Sensing, 13(8), 1583. https://doi.org/10.3390/rs13081583






