1.1.1. Spatial Resolution
Spatial resolution is one of the most misunderstood and misleading features of remotely sensed data. Within the remote sensing community, its common definition is the minimum size of the targets on the ground that can be resolved (i.e., distinguished) by the sensor. However, in many cases, this interpretation of the concept is not suitable to the wide spectrum of current applications of satellite imagery (see the cases of hot spot detection, sub-pixel mapping, etc.). Thus, the choice of the most suitable metric for representing and measuring this feature is not straightforward as it appears on a first instance [
6,
7]. Within the scientific community, this topic has been an open question for decades (e.g., [
8]), and nowadays, it is still an active field of research (e.g., [
9]).
When discussing the concept of spatial resolution of remotely sensed data, it is important to clarify the existing differences between the concepts of spatial resolution and pixel size (PS). The first is an intrinsic native feature of the data (depending on the physical and geometric characteristics of the observing system); the latter depends on the characteristics of the processing applied to the original data (e.g., resampling) that allow displaying the images with a PS equal to or different than the native spatial resolution of the product [
10].
Concerning the terminology used for quantifying the spatial resolution concept, it is important to point out that the most widely used metrics are those based on the geometric properties of the imaging system. For all types of EO spaceborne platforms, the full across-track angular coverage is called the field of view (FOV), and the corresponding ground coverage is called the ground-projected field of view (GFOV) (also known as swath width). The angle subtended by a single detector element on the axis of the optical system is called instantaneous field of view (IFOV), whereas its projection onto the Earth’s surface is called ground-projected instantaneous field of view (GIFOV; also known as instantaneous geometric field of view-IGFOV) [
1]. The mathematical description of these parameters can be found in [
1,
5,
11], as well as additional details about the topic. End-users of EO-derived products generally prefer to use the term GIFOV. On the other hand, system/sensor engineers prefer the angular parameters IFOV because it has the same values in image and object space [
1].
The images derived by EO optical systems are composed of data acquired in a bidirectional sampling process, whose components are defined across-track and along-track. In this process, the along-track platform velocity also plays a role [
1]. The distance on the ground in the two scanning directions, known as ground sampling distance (GSD), is another common metric used for defining spatial resolution. The GSD of an instrument can be defined in order to match the GIFOV at nadir. However, the GSD can be made smaller than the GIFOV in the across-track direction to achieve better image quality [
1,
7]. This can generate further confusion, as highlighted by [
7] that raised the following issues representative of the complexity of the topic: “does across-track performance improve just because the data are resampled at smaller intervals compared to IGFOV? Can 5-m IGFOV sensor data, sampled at 1 m, have the same performance as a 1-m IGFOV sensor? What is the maximum allowable ratio of IGFOV over GSD?”
Although from a geometrical and theoretical point of view the spatial resolution can be described by the abovementioned parameters, their values do not necessarily provide the minimum size of objects that can be detectable in an image. In fact, blurring effects due to optic phenomena (e.g., aberration, diffraction) may be present and lead to image degradation. In addition, the nominal IFOV dimension can be degraded because of different (technical/physical) reasons that may reduce the detector size [
6]. Conversely, objects smaller than a declared spatial resolution may be sufficiently brighter or darker than their surroundings to change the overall radiance of the pixel and be recognized [
6]. In Landsat thematic mapper (TM) imagery, for instance, there can be observed features (such as roads) with widths much smaller than the specified 30 m spatial resolution, providing that there is adequate contrast compared to the surroundings [
7].
Other metrics have been developed for quantifying the spatial resolution concept (e.g., Rayleigh diffraction limit-RDL, ground spot size-GSS, Rayleigh resolution criterion-RRC, sparrow metric), but they are less used than the one previously reported. Examples of these metrics can be found in [
9], to which the reader is invited to refer for a more detailed explanation.
Finally, a special mention deserves to be reserved to another metric widely used as a standard for quantifying the spatial resolution of an image: i.e., the full width at half maximum (FWHM) of the normalized line spread function (LSF). Because of the strong link of this parameter with another important aspect of the image quality, i.e., the image sharpness-this metric will be extensively described in the following sections of this paper.
1.1.2. Radiometric Resolution
As previously anticipated, other aspects exist that, in addition to spatial resolution, concur to the definition of the overall quality of optical images. Such aspects are not only related to the geometrical properties of the imaging systems but also to the process of data acquisition and image formation, as well as intrinsic sensor characteristics.
When an EO optical sensor acquires data, it integrates the continuous incoming energy (i.e., the electromagnetic radiation), converts it to an electrical signal, and quantizes it to an integer value (the digital number—
DN) to store the measurement at each pixel. In this process, a finite number of bits is used to code the continuous data measurements as binary numbers. If Q is the number of bits used to store the measurements, the number of discrete
DNs available to store the measurements is 2
Q, so that the resulting
DN can be any integer ranging from 0 to
DNmax = 2
Q − 1. This range represents the radiometric resolution of the sensor, and the number of bits available to quantize the energy (i.e., Q) is also known as pixel depth. The higher the radiometric resolution, the closer the approximation of the quantized data is to the original continuous signal. However, for scientific measurements, not all bits are always significant, especially in bands with high noise or low signal levels [
1].
This last consideration allows us to introduce in the discussion another concept: the signal-to-noise ratio (
SNR). Although, to a first-order, an image pixel is characterized by the geometrical properties of the EO acquisition system (e.g., GSD, GIFOV) and by the radiometric resolution, the capability of identifying targets in a digital image also depends on its contrast with the surrounding features (refer to the example of the roads in Landsat TM imagery previously described), in relation to the sensor’s ability to detect small differences in radiance. This is measured by the
SNR, which is defined as the ratio of the recorded signal to the total noise present [
1,
6,
12]. A common, simple way to estimate the
SNR is given by the ratio between the mean of the signal and its standard deviation [
13], computed over homogeneous areas [
14]. However, several and more complex alternative strategies have been developed to measure this parameter: e.g., as a function of land cover type and/or wavelength; or by using specific targets such as highly contrasting features such as edges, via the edge method (EM) [
14,
15]. Therefore, some authors also pointed out the need to have a standardized methodology for
SNR assessment that can enable a fair comparison when comparing results provided by different sources [
12].
1.1.3. Image Sharpness
Image sharpness is a terminology used as an opposite of image blur, which limits the visibility of details. Most of the image blur is introduced during the acquisition time by both the optical system and the potential motion of the sensor [
15].
Image sharpness can be measured by the point spread function (PSF), which describes the response that an electro-optical system has to a point source [
16]. Indeed, a digital image can be defined as a collection of object point sources modulated by the intensity at each object location. Each of these object points becomes blurred when viewed by an electro-optical sensor, owing to optical aberrations, sensor motion, finite detector size, diffraction, and atmospheric effects. The PSF is approximately independent of position across a region of the acquisition system’s field of view, and the sharper it is, the sharper the object will appear in the system output image [
16]. However, in practice, the direct estimation of the image PSF can be a complex task [
6]. Therefore, point targets are not widely used to estimate image quality [
16].
Within this context, another important image parameter commonly measured is the LSF, which results from the integration of the PSF. Physically, the LSF is the image of a line or a line of points. The LSF can also be expressed as the derivative of the Edge Spread Function (ESF), which is the response of an electro-optical system to an edge or a step function. In practical terms, this corresponds to regions of the image where a sudden shift in
DN is registered. To summarize, in optical terminology, the PSF is the image of a point source, the LSF is the image of a line source, and the ESF is the image of an edge source. From a theoretical point of view, the imperfect imaging behavior of any optical system that results in image blur can be detected and represented using any of these functions. [
1]. On the other hand, depending on the specific application and its associated operational issues/challenges, one function may be more suitable than the others.
As previously described, the measurement of the two-dimensional PSF is complicated and requires laboratory measures or a special array of concave mirrors, making its use for quality monitoring analyses complicated. Instead, for such purposes, the estimation of the one-dimensional function LSF (and ESF) is simpler and can be obtained with on-orbit methods (i.e., directly applied to satellite-derived images), such as the EM. The latter, also known as “knife EM” or “slanted EM”, is one of the most widely used approaches for sharpness assessment that, as previously described, could also be used for
SNR estimation via edge targets [
12,
15,
17,
18]).
An important metric that can be used to quantify the sharpness level of an image acquired by optical sensors via the EM is the FWHM of the normalized LSF (hereinafter, the term FWHM will be referred to this parameter) [
9,
12,
14,
16,
18]. The latter is calculated by measuring the width of the normalized LSF at a value of 0.5, as shown in
Figure 1 [
9,
14,
16,
18]. Therefore, smaller values of FWHM correspond to steeper slopes of LSFs, which in turn are associated to sharper images [
16]. The FWHM value is expressed in pixels, and it can then be translated to metric units by taking into account the image PS. Consequently, it can also be used to quantify the effective spatial resolution of the images [
9,
14,
16,
19]. Indeed, and as previously anticipated, the FWHM is also considered de facto a standard metric for the spatial resolution of digital images [
9].
Other widely used image sharpness metrics are obtained through the evaluation of the modulation transfer function (MTF), which measures “the change in contrast, or modulation, of an optical system’s response at each spatial frequency” [
20]. The MTF is mathematically defined as the Fourier transform of the LSF of an imaging system. Consequently, it is the direct transposition of the LSF in the frequency domain. As such, it carries the same fundamental information. The MTF is usually normalized with respect to its maximum value, and the frequency axis is normalized with respect to the sampling frequency at which the LSF is oversampled [
20]. The MTF is most often evaluated at the Nyquist frequency, which is generally defined as half the sampling frequency of a discrete signal processing system and, in the case of imaging systems, it is defined as “the highest spatial frequency that can be imaged without causing aliasing” [
20]. Less often, the MTF is evaluated at half the Nyquist frequency and, in some contexts, the normalized frequency value at which the MTF reaches half its maximum value (MTF50) is of interest [
20]. In any case, the higher the MTF value, the sharper the image, the greater the aliasing effects [
16]. Additional theoretical details about the MTF can be found in [
10,
12,
14,
16,
18]. Most of the time, the MTF characteristics are measured before the launch. However, since vibrations during the launch and sensor degradation through time may alter its original values, on-orbit MTF determination techniques have been developed. Some of them are based on a comparative approach between test images against others whose MTF is already known. Other approaches, such as those based on the EM, exploit manmade/artificial or natural edge targets imaged by the sensors, from which the ESF and the related LSF are estimated and, subsequently, the MTF is retrieved via LSF Fourier Transformation (see
Figure 1) [
12,
14,
16,
18].
Image sharpness can also be estimated with an additional metric that can be retrieved by applying the EM: i.e., the relative edge response (RER), that estimates the effective slope of the normalized ESF within ±0.5 pixels of the center of the edge [
16,
20].
In this complex framework, there exist other metrics conceived for characterizing the image quality by linking the spatial resolution and the sharpness concepts: the effective instantaneous field of view (EIFOV) and the radiometrically accurate IFOV (RAIFOV). The first one is defined as the ground resolution corresponding to a spatial frequency for which the system MTF is 50%. The second one is defined as the ground resolution for which the MTF is higher than 0.95 [
7,
10].
It is noteworthy to highlight that, within the scientific community, the most used sharpness metrics are the FWHM, the MTF (e.g., at Nyquist frequency), and the RER [
9,
12,
16,
20]. All of them can be estimated by using a specific on-orbit workflow: the EM (
Figure 1).
A study ([
20]) showed that these three metrics have fixed relationships and that can be used to classify the sharpness level of an image in different categories: aliased, balanced, and blurry. In their work, the authors also provided different examples of these categories of images, as well as different examples of sharpness-related functions and metrics. The reader is thus referred to [
20] for having a more detailed description of the topic.
Despite the fact that the EM has some well-known drawbacks (e.g., it can be influenced by the atmospheric effects on the signal recorded by the sensor, its different methodological implementation may lead to significantly different results [
12,
15], etc.), it is particularly important for monitoring the sensor performances through time. Moreover, if implemented in a standardized manner, it can enable a fair comparison between the sharpness levels of different sensors independently estimated by different entities.
As previously explained, the EM aims at quantifying the sharpness level of an image (i.e., of each single band of the product, in the case of multiband data such as those acquired by optical multispectral sensors) by directly using the edges present in the scene. Although there exist different implementations of the EM, most of the time, it is composed by the following steps, also reported in
Figure 1 [
12,
14,
16,
20]:
- (a)
Edge detection
- (b)
Edge sub-pixel estimation
- (c)
Computation of the ESF
- (d)
Computation of the LSF
- (e)
Computation of the MTF
- (e′)
MTF estimation at a specific frequency (e.g., Nyquist)
Because the EM results strongly rely on the characteristics of edges selected for performing the sharpness assessment (i.e., the choice of different edges present in the same scene may lead to different results), when implementing this method, one important issue to handle with caution is the definition of the edges to be used for the analysis [
14]. Importantly, such edges should also be oriented in multiple directions in order to account for any asymmetries in the PSF when computing the corresponding ESF and LSF [
1]. Often, if the sharpness assessment is performed along with specific/preferential directions (i.e., edges oriented along and across the satellite orbit), the overall sharpness level is computed as their geometric mean [
9,
16]. Ideal edges are those artificially and specifically built for EM applications (e.g., black and white tarps [
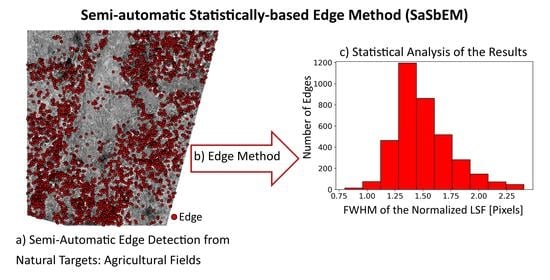
16]); nevertheless, images acquired on these specific target areas are not always available. If these targets cannot be clearly resolved by the spatial resolution of the sensor (i.e., the GSD) or images of such areas are not available, different solutions should be explored. One of the most accredited alternatives is based on the definition of the edges by exploiting manmade/artificial (e.g., buildings, runways, roads) and/or natural targets (e.g., agricultural fields, shorelines, canals) [
16,
17,
19,
21]. In these cases, most of the time, the edge selection is still performed by a human operator [
14,
17]. Consequently, the definition of automatic or semi-automatic approaches of edge selection for performing EM-based sharpness assessments from digital images is still an active field of research, not only in the EO domain [
22,
23,
24,
25,
26].
Although there exist diverse EMs that share the same conceptual framework, their different methodological implementation may lead to different FWHM, MTF, or RER results. Most of the time, this fact prevents a fair comparison among different studies. Consequently, the development of a standard methodology to robustly estimate the EM-derived sharpness metrics should be encouraged [
12].
Within this context, another important aspect must be taken into account when comparing the same sharpness metric computed from different images: i.e., their processing level. Indeed, it must be highlighted that the sharpness assessment should be (theoretically) carried out on raw images/data in order to avoid effects and artifacts due to image pre-processing (e.g., orthorectification, resampling) that prevent the evaluation of the ”pure” performance of the instrument used for acquiring the data [
9,
20]. If raw data are not available, the sharpness assessment should be referred to a specific processing level of the product derived from the sensor under investigation. Importantly, results should be then interpreted accordingly, especially when comparing the outcome of the sharpness assessment against other results obtained by different analyses. The importance of providing quality information at “product level”, in addition to the one provided at “instrument level”, was highlighted by [
5].