1. Introduction
Ground moving target indication (GMTI) and track formation have received growing attention in both civilian and military applications [
1,
2,
3], with the development of synthetic aperture radar (SAR) technique. However, moving targets are defocused and dislocated in SAR image due to unknown motion parameters [
4], especially in the case of long dwell time. Therefore, velocity estimation is very important for moving target imaging, as well as track generation.
Target motion introduces variations in both Doppler spectrum and range cell migration (RCM) [
5,
6,
7], which will result in target position shift and resolution distortion in SAR image. Moreover, the effect on SAR image is different in side-looking and azimuth squint-looking. In side-looking, target motion in the range direction leads to shift of Doppler centroid frequency, which in turn results in azimuth dislocation and extra RCM. Target motion in the azimuth direction will mainly introduce Doppler frequency modulated rate variation, leading to image defocusing [
8]. However, in azimuth squint-looking, both range and azimuth motions have influence on azimuth dislocation and defocusing, providing a new challenge for velocity map reconstruction.
Based on the effects mentioned above, several methods were proposed [
9,
10,
11,
12,
13,
14]. A GMTI approach using the reflectivity displacement method (RDM) was proposed [
9] by analyzing the frequency shift and evaluating of Doppler Rate Map with high target radar cross section, where the Doppler Rate variation and range cell migration (RCM) were used for azimuth velocity and range velocity determination, respectively. Additionally, more efficient RCM evaluation was carried out with geometry-information-aided Radon transform for range velocity estimation in [
10]; more accurate two-dimension search methods based on velocity correlation function (VCF) [
11,
12] and different geometrical figures due to target velocity vectors [
13] were analyzed with high computational complexity. In order to obtain better moving target imaging quality in high-resolution SAR system, the higher-order motion parameters could be estimated based on the polynomial phase signal (PPS) model [
14,
15,
16] and the Hough-high-order ambiguity function transform [
17]. However, the estimation performance of these methods would deteriorate in the case of low signal-to-clutter ratio (SCR) and PPS model is sensitive to RCM effects.
To improve the estimation accuracy, based on the multiple-channel receiving technique, three classic methods were developed, including displacement phase center antenna (DPCA) [
18], along-track interferometry (ATI) [
19], and space time adaptive processing (STAP) [
20], with more degrees of freedom to detect moving targets. For the DPCA method, the stationary background clutter is removed by subtracting signals from different receiving channels. By interference processing using signals from different receiving channels, the residual phase is used for target range velocity estimation, whereas the detection performance eventually depends on the signal-to-clutter-plus-noise ratio (SCNR). To address this issue, detectors were constructed by combining amplitude and phase of ATI information [
21,
22]. As for the STAP method, it has the best performance in theory. However, it is very time-consuming and difficult to implement in practice. Furthermore, a new Doppler-DPCA and Doppler-ATI method was developed in [
23], measuring temporal Doppler shift with ultra-narrowband continuous waveforms instead of range in the conventional wideband SAR system. However, all the aforementioned methods suffer from the problem of velocity ambiguity and are incapable of azimuth velocity estimation in side-looking mode. The dual-beam ATI employed with a pair of antennas each producing a forward and an aft beam in a single pass could resolve surface velocity vector estimate of slow ocean current [
24] with low spatial resolution, which is not effective for relatively small-size moving ships and vehicles detection especially with strong stationary clutter.
Recently, two innovative methods were studied based on sequential SAR images [
25,
26,
27,
28,
29,
30], including the bi-directional (BiDi) mode [
25,
26,
27,
28,
29] and the multiple azimuth squint angle (MASA) mode [
30]. The BiDi mode works with two main lobes pointing to different directions simultaneously in azimuth, and the same area is observed twice with a short time lag between two acquisitions. However, the pulse repetition frequency (PRF) have to be doubled for distinguishing the signal from two different directions in the azimuth frequency domain, with the range-swath reduced in half, which is undesirable for earth observing. To overcome this shortcoming, a novel MASA mode was proposed, observing the same area from different azimuth squint angles, without PRF increasing. Nevertheless, the MASA mode is only suitable for target azimuth velocity estimation. According to the analysis in [
30], the effect of range motion on azimuth velocity estimation is negligible when azimuth squint angles’ absolute value of two acquisitions is equal to each other, whereas most SAR systems cannot strictly meet this requirement. Therefore, the azimuth velocity estimation accuracy deteriorates with an unknown range velocity, especially when target moves fast along the range direction. In addition, moving targets could even be buried in stationary background clutters and cannot be distinguished, and this issue has not been considered yet. Therefore, there is a need to deal with the effects on azimuth velocity estimation caused by unknown range velocity and strong stationary clutter.
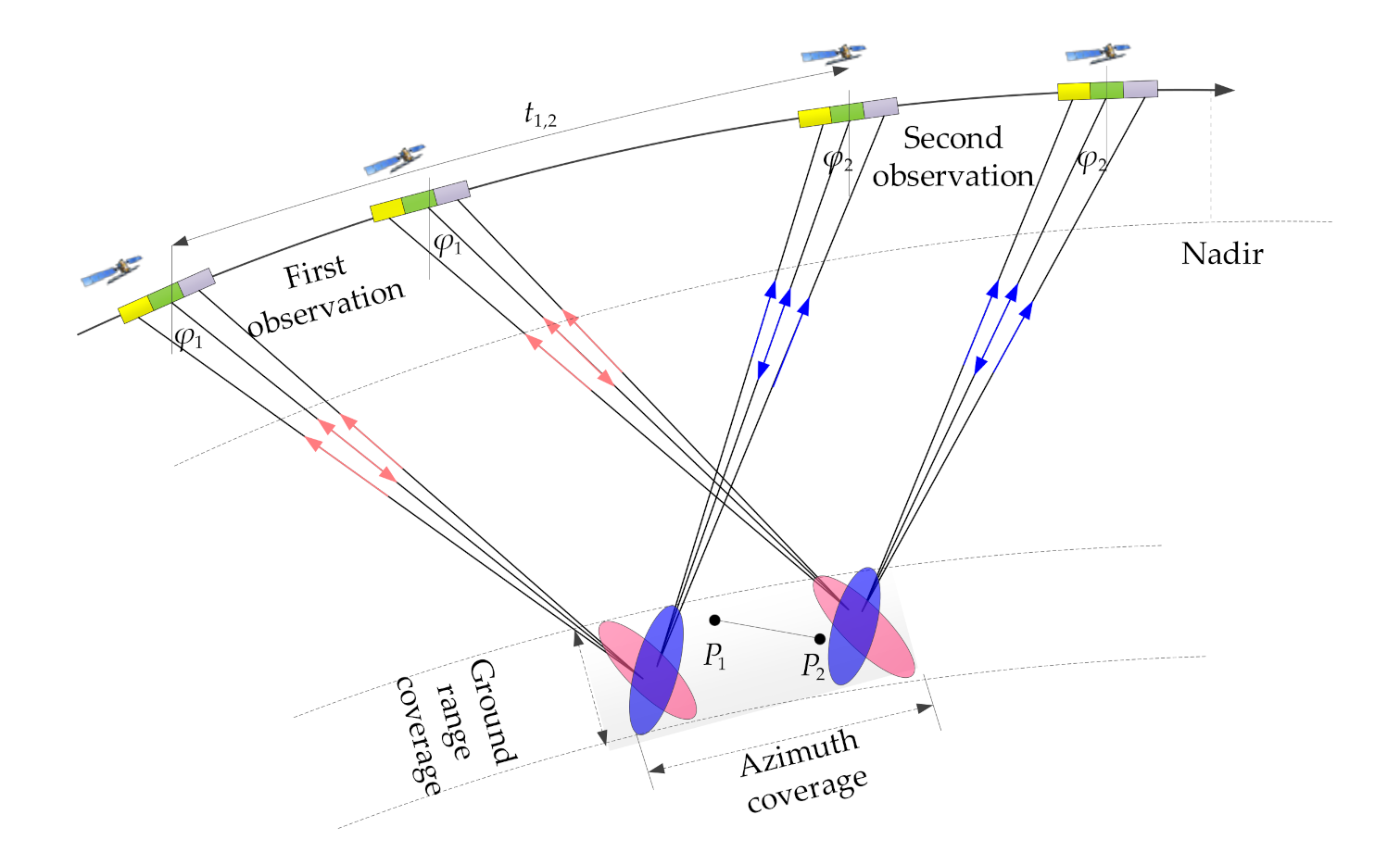
In this paper, a novel velocity estimation method is proposed based on multi-channels MASA (MC-MASA) mode, which introduces multiple-channel receiving technique on MASA mode. On this basis, the DPCA technique in azimuth squint-looking is introduced for background clutter remove, which has better performance on azimuth velocity estimation with sequential SAR images. However, the range velocity estimation accuracy is low based on MASA mode with imaging position offset no matter along azimuth or range direction. For target azimuth-and-range velocity preliminarily reconstruction, the interferometric phase of ATI related to the target line-of-sight velocity is adopted with at least two acquisitions. Additionally, the detectable velocity range is double after DPCA process compared with that before clutter suppression, which could improve velocity ambiguity. However, the ATI method becomes ineffective when moving target energy is suppressed together with stationary clutter at some certain velocity and squint angle combinations. Therefore, in order to achieve a high target azimuth-and-range velocity map reconstruction accuracy even in some relatively complex situations, the circumstances are divided into three cases with different iterative strategies according to SAR acquisitions, i.e., iterative combinations of the method with moving target position shift among sequential SAR images and ATI interferometric method. The iterative strategies could also make up the blind spots of velocity estimation based on the traditional ATI method and MASA mode. Finally, the performance of the proposed method is demonstrated by experimental results.
This paper is organized as follows: In
Section 2, the MC-MASA mode is presented, as well as an analysis of target motion effects on SAR image. In
Section 3, based on the MC-MASA mode, the background clutter suppression method is introduced. In
Section 4 and
Section 5, azimuth velocity and range velocity estimation methods are derived and analyzed in detail. Experimental results are provided in
Section 6 and conclusions are drawn in
Section 7.
3. Background Clutter Suppression
In this section, a background clutter suppression method is presented based on the MC-MASA mode with squint observation.
After range pulse compression, the azimuth signal for receiving channel
can be represented as,
where
is the target complex reflectivity,
denotes the azimuth window function and
. In moderate-resolution SAR system, the higher order terms (
) of slant range influence little which could be neglected. Even if in the high-resolution SAR system, some higher order terms could be compensated during clutter suppression as the effect of target motion on them is small. Therefore, the approximation in Equation (11) is meaningful in the following analysis.
Target energy will be focused after pulse compression with increased signal-to-noise ratio (SNR) which is beneficial for velocity estimation. Based on the principle of stationary phase (POSP), the signal in the azimuth-frequency domain is
where
denotes azimuth frequency variable with respect to the azimuth time variable.
In some classic SAR image formation algorithms, such as the range Doppler algorithm (RDA) [
31], the chirp scaling algorithm (CSA) [
32], and the deramp chirp scaling algorithm (DCS) [
33], the azimuth position of target on a SAR image is usually at the time corresponding to Doppler centroid frequency. Consequently, the azimuth matched filtering function for azimuth signal compression is constructed as,
After multiplying
by
in Equation (12), one has
where
denotes the equivalent azimuth frequency after frequency shift.
In order to compensate for the variation of receiving signal due to the CEPC interval, the following azimuth compensation filtering function is employed
Discrete processing in the frequency domain incurs a small error when
is not an integer and the maximum phase error of channel
can be deduced as
where
is PRF of the system and
is the number of azimuth pulses. However, in the azimuth time domain,
(
is an integer) is required for compensating for the variation between different channels commented as DPCA condition, which is not necessary in the frequency domain. When
, the time-consuming interpolation operation is needed. Therefore, it is computationally efficient to perform the processing in the frequency domain without interpolation.
With phase compensation, the signal is transformed to
After performing azimuth IFFT,
where
denotes compression gain of azimuth and
is product of the envelope of
after pulse compression and the influence of defocusing, whose amplitude can be assumed as a
function, and then the moving target will be well focused at
as Equation (9a). The defocusing effect is considered in
Section 6.
Afterwards, stationary clutters can be removed by subtracting acquisitions from different channels. Taking channels
and
as an example, one has
where
Thus
where
.
It can be seen from Equation (21) that the stationary clutters would be removed as
and the residual intensity of moving target varies with target ERV after DPCA processing. Unless the residual phase
of moving target is proportional to
, moving target could be retained and identified. Different from the side-looking mode where the residual target intensity is related to target range velocity, the intensity is dependent on target ERV in squint-looking. In other words, the moving target would be subtracted together with clutter when
even if the target has velocity both along azimuth and range direction. This characteristic makes the subsequent velocity estimation complicated and diversified with different SAR acquisition combinations which would be discussed in
Section 5. Generally, moving target would be more obvious after DPCA process and this is beneficial for the estimation method based on target imaging information in
Section 4.
5. Azimuth-and-Range Velocity Estimation Based on MC-MASA Mode
As discussed in
Section 4, target range velocity cannot be obtained based on image position offset, and the unknown range velocity affects estimation accuracy of azimuth velocity seriously. Therefore, based on the MC-MASA mode, a novel ATI technique is introduced and discussed in detail to reconstruct the azimuth-and-range velocity map after clutter removal in this section. Its performance is analyzed by considering interferometric phase and system parameters. Finally, according to the obtained SAR acquisitions and residual target energy, the circumstances are divided into three cases with different iterative estimation strategies.
5.1. Target Azimuth-and-Range Velocity Estimation
By multiplying a complex conjugate of one image with the other image, the interferogram from channels
and
is obtained as
where “*” denotes the complex conjugate.
Then, interferometric phase
and ERV estimation result
are given by
The obtained ERV contains both target azimuth and range velocities because of their interaction on the linear term of range history in azimuth squint-looking, which is different from side-looking. However, clutters would severely affect the interferometric phase of moving targets, degrading the estimation accuracy. In the worst situation, when moving target is totally submerged in background clutters, velocity estimation methods based on ATI only will fail. Fortunately, the signal after DPCA retains the phase information of moving targets, i.e., Equation (19) has all the phase information of a moving target in Equation (18). Therefore, interferometric processing of two acquisitions after clutter suppression is also effective for target velocity estimation. These two acquisitions are based on signals from three receiving channels of which every two are processed with DPCA. However, only amplitude with DPCA or interferometric phase with ATI can be obtained with dual-channel signals from which the velocity of moving targets is difficult to be estimated in low SCR.
Taking channels
for example, two images
and
after clutter suppression are obtained from channel
and channel
, respectively. Then, the interferogram is expressed as
According to Equation (35), phase
and the estimated ERV
based on DPCA-ATI can be deduced as
From Equation (37), the estimated ERV of a certain squint angle is related to the interferometric phase of channels and after DCPA processing. The signal of channel plays an important role in clutter suppression and is cancelled during the interference process.
According to the projection relationship between the moving target equivalent velocity in the slant range plane and actual velocity in the horizontal ground plane shown in
Figure 2, target azimuth and range velocities can be derived based on the combination of two ERV results with
and
, as
With the increase of the azimuth steering span, more than two acquisitions can be obtained in the MC-MASA mode. Therefore, the least-square solution of an overdetermined equation is the more suitable result
where
is the number of effective SAR acquisitions and
is the estimated azimuth and range velocities, respectively.
It can be noticed that the interferometric phase after DPCA is half as before which can reduce the possibility of ambiguity velocity, i.e., the detectable ERV range is doubled. Moreover, ATI processing after DPCA can further suppress the clutter.
Phase wrapping results in target ERV ambiguity when the interferometric phase exceeds
. The maximum estimate target ERV in Equation (37) is given by
With the parameters listed in
Table 1,
is
when
and
. The corresponding ground velocity is basically doubled as
. If
is chosen, this velocity will be doubled again. Therefore, the estimated maximum ambiguity-free velocity based on the spaceborne radar system can cover the velocity of most ground and maritime moving targets. For airborne SAR system, there are three baseline combinations if the distance between CEPCs is different (noted as
) in MC-MASA mode in this paper which could further expand the range of estimated velocity. Meanwhile, due to the finite ambiguity number of target velocity, several comparisons of Radon transform results of RCM [
10] could resolve the problem of target ERV ambiguity with low complexity.
Target azimuth-and-range velocity reconstruction needs two observations based on the MC-MASA mode and the others can be used to further improve estimation accuracy.
5.2. Velocity Estimation Sensitivity Analysis
Interferometric phase directly determines the estimated target velocity as Equation (37), so the phase extraction method is important. Apart from phase, the sensitivity of
is also related to system parameters, such as platform velocity, CEPC interval and squint angle. These factors will be analyzed specifically. Unless otherwise stated, parameters listed in
Table 1 and
Table 2 are chosen for the subsequent analysis, corresponding to
.
Sensitivity to interferometric phase
With the above parameters, each phase error of 0.1 rad will result in an ERV error of 1.27 m/s. After clutter suppression, the moving target can be distinguished by amplitude threshold judgment. When the extended target size is larger than one pixel on a SAR image, it will occupy multiple pixels and each point corresponds to one phase which is affected by the residual clutter at the same position. It is generally assumed that clutters are subject to Gaussian distributions, i.e., its amplitude follows the Rayleigh distribution and its phase follows the uniform distribution. Therefore, the minimum mean square error (MMSE) criterion can be used to reduce interferometric phase error by statistical analysis for this situation.
Sensitivity to platform velocity
With the above parameters, each platform velocity error of 100 m/s only leads to a target ERV error of 0.27 m/s, indicating that ERV is not very sensitive to platform velocity. In spaceborne SAR, the actual path of satellite is approximated to a straight line [
34], so equivalent platform velocity is adopted in SAR imaging.
Sensitivity to squint angle
With the above parameters, each squint angle error of 0.1 rad leads to a target ERV error of −0.35 m/s and a small squint angle can decrease this error. The same for platform velocity, it is the equivalent squint angle in spaceborne SAR.
Assuming that
and
are the ERV estimation error of squint angle
and
, respectively. Then, the estimation error of
and
can be derived as
In the small squint angle mode, the azimuth velocity estimation error is larger than that of range direction in most cases, about times, which is negatively correlated with the absolute value of squint angle. Therefore, combination of large squint angles should be chosen for azimuth velocity estimation under the premise of an accurate squint angle.
Sensitivity to CEPC interval
With the above parameters, every interval error of 0.1 m leads to a target ERV error of −0.36 m/s and a large interval is needed for accurate ERV estimation. However, a large CEPC interval would deteriorate situation of velocity ambiguity. Therefore, the choice of is trade-off by considering both SAR system parameters and the moving target velocity range. For higher accuracy, with the actual path of satellite is straightened, this interval also has a small approximation change. Additionally, the smaller the wavelength is, the better the accuracy is.
5.3. Estimation Process
The method based on the MASA mode in
Section 4 is only capable of target azimuth velocity estimation with the same absolute values of the squint angles. Both target azimuth and range velocities can be extracted from the phase difference as aforementioned discussion, whereas estimation accuracy of azimuth velocity is poor. Therefore, these two methods could be combined to improve estimation accuracy and application scope. The estimation process should be chosen according to the situations considered. Note that in the subsequent analysis, method 1 and method 2 denote the method in
Section 4 and
Section 5, respectively.
In order to extract more information of moving targets, the stationary clutter is removed firstly for all acquisitions. As both method 1 and method 2 are based on two acquisitions, only two images with squint angle and are analyzed in the following cases. In addition, the relationship of squint angles is an important factor for velocity estimation. Therefore, different cases are discussed, with different corresponding processes.
The estimated azimuth velocity from method 1 has a small error and range velocity can be extracted by method 2 from either of the two images. The worst situation is that the moving target on image is removed together with clutter after DPCA processing due to a nearly zero ERV. Now azimuth velocity can be estimated firstly if the targets on both images can be distinguished clearly before clutter removal. Then, range velocity is obtained from the image of .
The ERV extraction criterion is that the interference phase of a moving target is clustered around a certain value, which will be further illustrated in subsequent simulations. The range velocity can be firstly extracted with method 2 which can compensate the estimation error in azimuth velocity of method 1. Finally, with an iterative process, more accurate and are obtained successively with method 2 and method 1, respectively.
For this case, moving target can be distinguished on images of and with method 1 after clutter suppression. However, method 2 is only effective for ERV extraction with image . The erroneous azimuth velocity from method 1 and interferometric phase of image can be combined for estimation of range velocity with method 2. Finally, with iterations, more accurate is obtained from method 1 with compensation of range motion and then is estimated again with method 2. If the azimuth position offset caused by is less than half a pixel, its effect on azimuth velocity estimation of method 1 can be ignored. and are the final results.
In either case, when target EAV exceeds a certain threshold
, the moving target should be refocused, as defocusing will lead to reduction of SCR, which in turn reduces velocity estimation accuracy. Here,
corresponds to the target gain attenuated by 3dB. The criterion for setting the velocity threshold
in [
30] is the main lobe separation, not considering the effect of SCR. According to the parameters in
Table 1,
as shown in
Figure 6;
is 24 m/s with resolution
, larger than
.
The filter function of quadratic phase error correction in the azimuth-frequency domain is given by
For a small squint angle, estimation accuracy of azimuth velocity depends strongly on the squint angle, while that of range direction is hardly affected by it. Therefore, it is better to choose combinations of large squint angles for better estimation performance. Moreover, if there are more than two acquisitions, it is better to choose combinations corresponding to Case 1 with the simplest process and best accuracy.
The flowchart of the proposed method is shown in
Figure 7.