Regionalization of an Existing Global Forest Canopy Height Model for Forests of the Southern United States
Abstract
:1. Introduction
Objectives
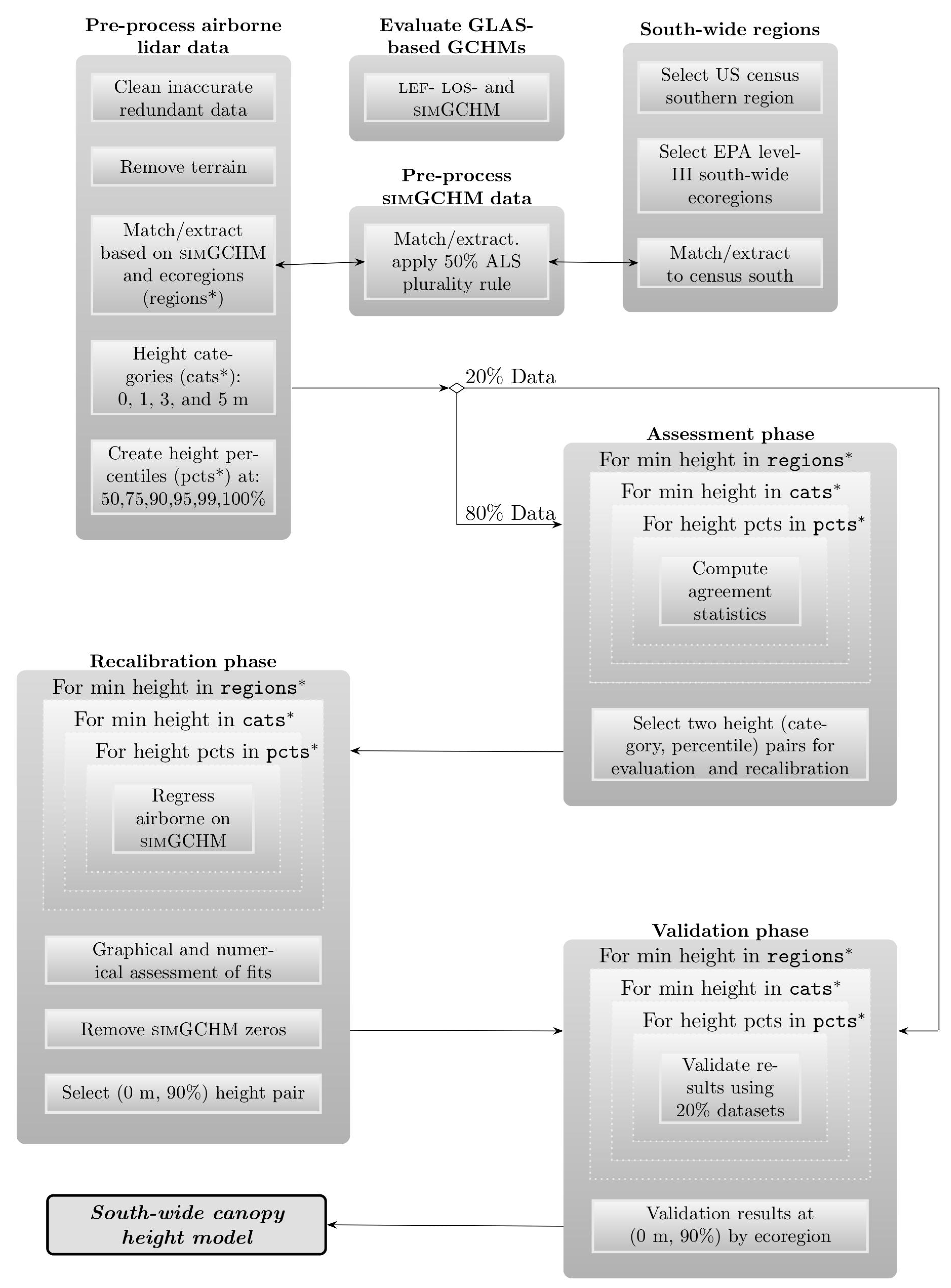
2. Materials and Methods
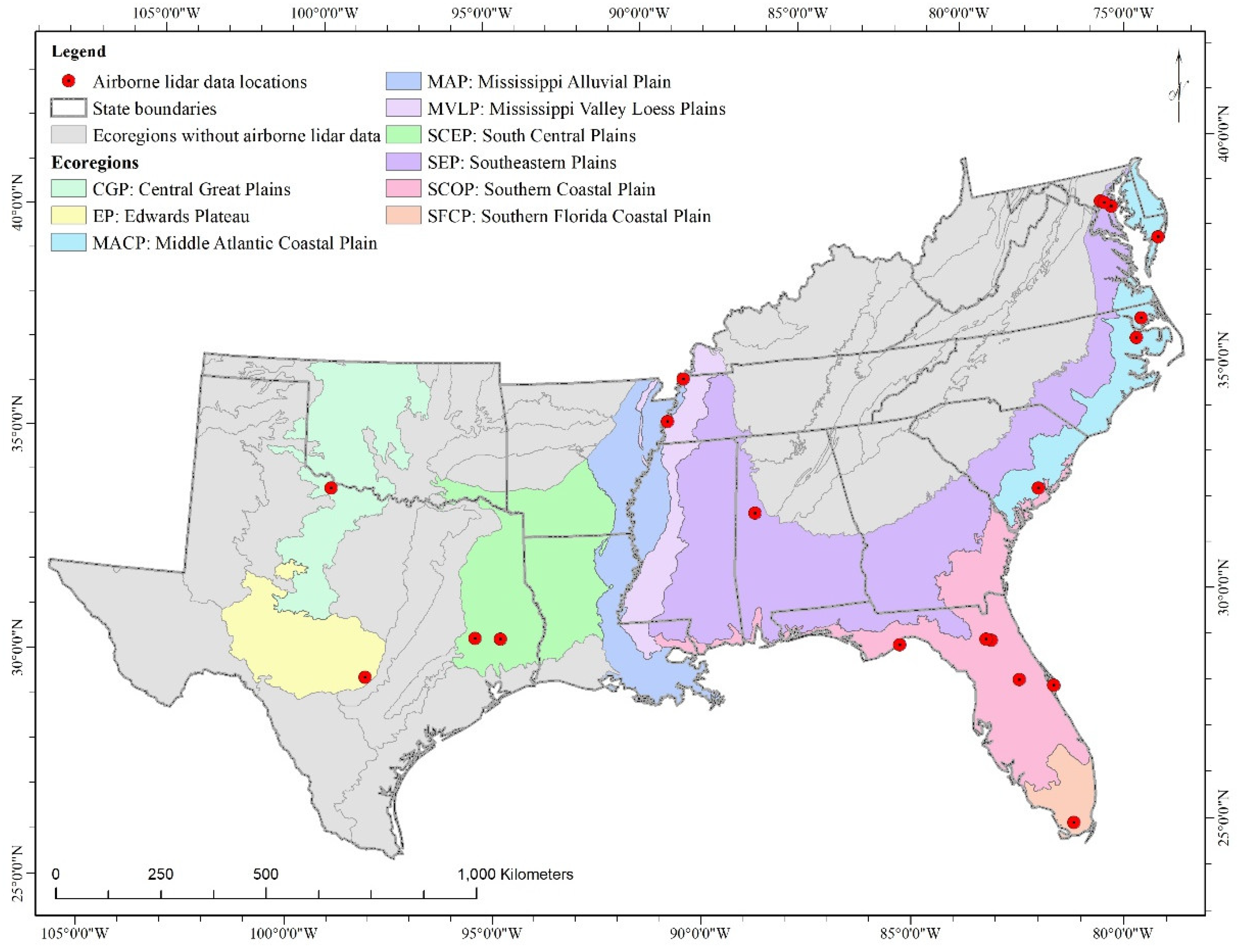
2.1. Study Area
2.2. Selection of the Reference GCHM
- lefGCHM (acronym ours). Lefsky [11] combined data from both the GLAS and the Moderate Resolution Imaging Spectroradiometer (MODIS) sensor systems. Ground data from four forested sites in the United States and three in the Brazilian Amazon were used for GLAS data calibration. MODIS data were used for stratification and attribution of forest patches. This attribution, together with the globally available GLAS and MODIS data, then allowed for global prediction of forest canopy heights. The focus of Lefsky [11] was on methodological development; it stands out as the first GCHM to reveal the distribution of forest canopy height globally. It was later employed, by Saatchi et al. [21], to investigate tropical forest carbon stock across three continents.
- simGCHM. Simard et al. [12] integrated GLAS RH100-derived estimates of canopy height from the GLA14 land product for 2005 with various forest, tree, topographical, and climatic variables in order to generate a wall-to-wall global canopy height map. RH100 values are defined as the distance between the beginning of the laser pulse-echo and the corresponding location of the ground peak [22,23,24], thus representing vegetation canopy height. As with lefGCHM, the generation of simGCHM was primarily method-oriented.
- losGCHM. Like Lefsky [11], Los et al. [13] combined GLAS and MODIS data; furthermore, like Simard et al. [9], they also included SRTM-derived data. With these data, they created coarse-resolution (0.5° × 0.5°) vegetation height and vegetation cover fraction products for latitudes between 60° S and 60° N. The authors stated that the maps were created for use in climate and ecological models but did not, themselves, develop a particular application. losGCHM has been used, by Bevan et al. [35], to investigate the response of vegetation after the 2003 European drought.
2.3. The Airborne Lidar Data
2.3.1. Height Categories
- 0 m ≔ All airborne lidar points (include all ground points);
- 1 m ≔ Points greater than 1 m (without ground, short grass, and rock points);
- 3 m ≔ Points greater than 3 m (without ground, short/tall grass, rock, and short shrub points), and
- 5 m ≔ Points greater than 5 m (without ground, short/tall grass, rock, and short/tall shrub points).
2.3.2. Plurality Rule and Height Percentiles
2.4. Analysis
2.4.1. Assessment Phase
2.4.2. Recalibration Phase
2.4.3. Validation Phase
3. Results
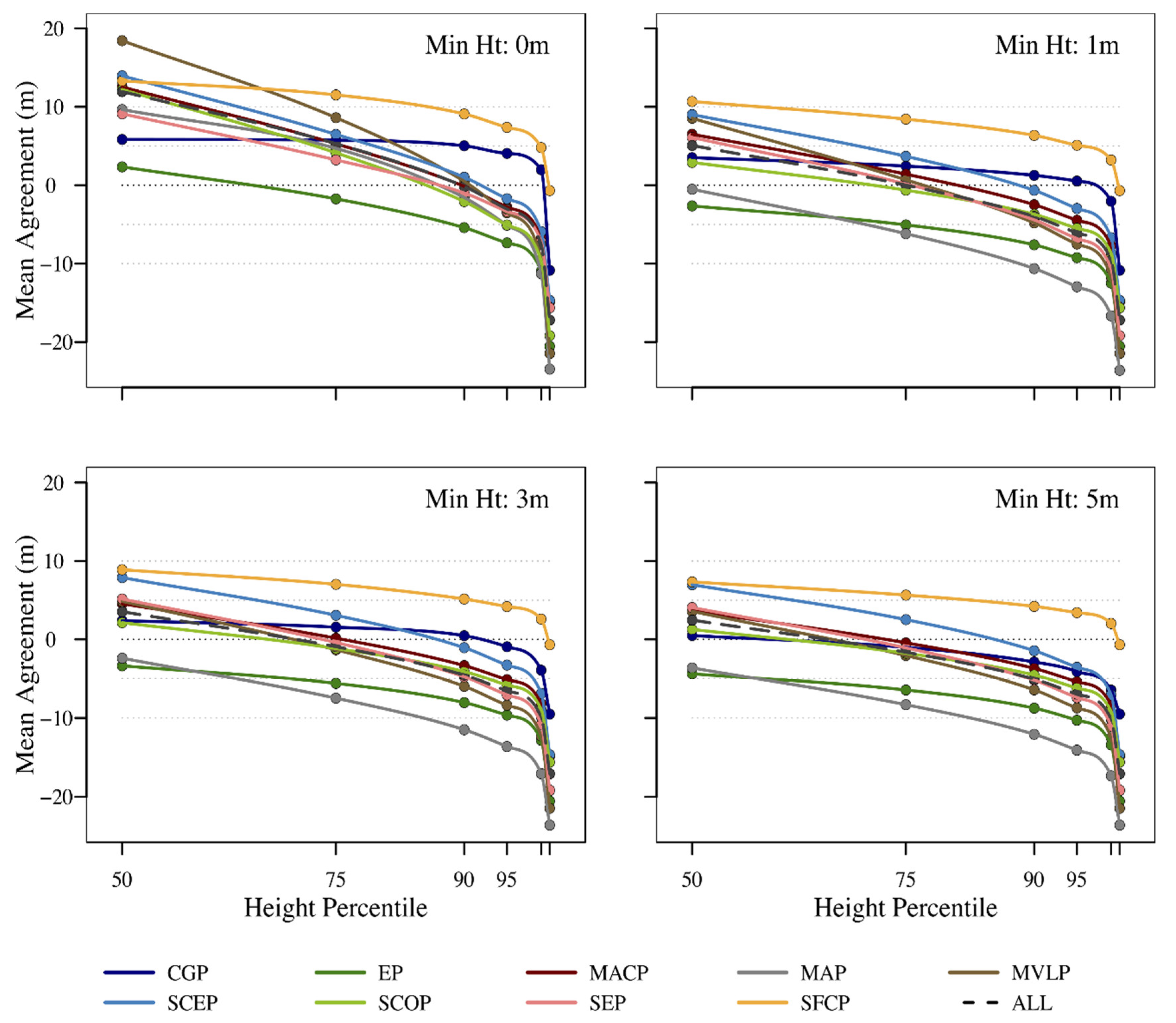
3.1. Assessment Phase
3.2. Recalibration Phase
3.3. Validation Phase
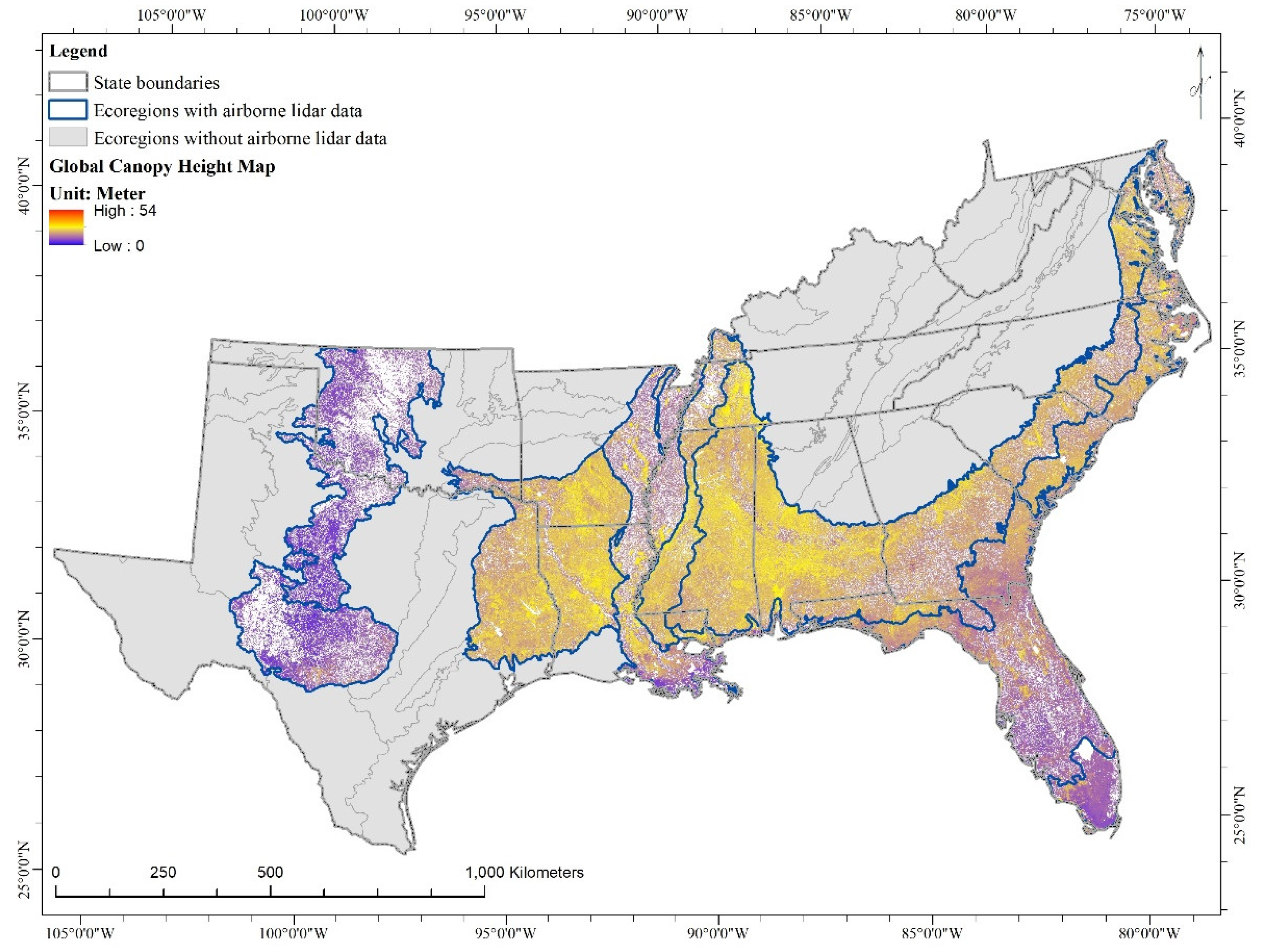
3.4. The South-Wide GCHM
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Means, J.; Acker, S.; Fitt, B.; Renslow, M.; Emerson, L.; Hendrix, C. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
- Popescu, S.; Wynne, R.; Nelson, R. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Lefsky, M.; Harding, D.; Keller, M.; Cohen, W.; Carabajal, C.; del Bom Espirito-Santo, F.; de Oliveira, R., Jr. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32, L22S02, Erratum in Lefsky, M.; Harding, D.; Keller, M.; Cohen, W.; Carabajal, C.; del Bom Espirito-Santo, F.; de Camargo, P. Correction to “Estimates of forest canopy height and aboveground biomass using ICESat’’. Geophys. Res. Lett. 2006, 32, L05501. [Google Scholar] [CrossRef] [Green Version]
- Mustonen, J.; Packalén, P.; Kangas, A. Automatic segmentation of forest stands using a canopy height model and aerial photography. Scand. J. For. Res. 2008, 23, 534–545. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bailly, J.S.; Barbier, N.; Gond, V.; Hérault, B.; El Hajj, M.; Fabre, F.; Perrin, J. Regional scale rain-forest height mapping using regression-kriging of spaceborne and airborne LiDAR data: Application on French Guiana. Remote Sens. 2016, 8, 240. [Google Scholar] [CrossRef] [Green Version]
- Ni, X.; Zhou, Y.; Cao, C.; Wang, X.; Shi, Y.; Park, T.; Choi, S.; Myneni, R.B. Mapping forest canopy height over continental China using multi-source remote sensing data. Remote Sens. 2015, 7, 8436–8452. [Google Scholar] [CrossRef] [Green Version]
- Ni, X.; Park, T.; Choi, S.; Shi, Y.; Cao, C.; Wang, X.; Lefsky, M.A.; Simard, M.; Myneni, R.B. Allometric scaling and resource limitations model of tree heights: Part 3. Model optimization and testing over continental China. Remote Sens. 2014, 6, 3533–3553. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Choi, S.; Ni, X.; Ganguly, S.; Zhang, G.; Duong, H.V.; Lefsky, M.A.; Simard, M.; Saatchi, S.S.; Lee, S.; et al. Allometric scaling and resource limitations model of tree heights: Part 1. Model optimization and testing over continental USA. Remote Sens. 2013, 5, 284–306. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K. Photon counting LiDAR: An adaptive ground and canopy height retrieval algorithm for ICESat-2 data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Narine, L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Lefsky, M. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Simard, M.; Pinto, N.; Fisher, J.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Los, S.; Rosette, J.; Kljun, N.; North, P.; Chasmer, L.; Suárez, J.; Berni, J. Vegetation height and cover fraction between 60° S and 60° N from ICESat GLAS data. Geosci. Model Dev. 2012, 5, 413–432. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A combined GLAS and MODIS estimation of the global distribution of mean forest canopy height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Bolton, D.; Coops, N.; Wulder, M. Investigating the agreement between global canopy height maps and airborne Lidar derived height estimates over Canada. Can. J. Remote Sens. 2013, 39, 139–151. [Google Scholar] [CrossRef]
- Census Regions and Divisions of the United States. Available online: https://www2.census.gov/geo/pdfs/maps-data/maps/reference/us_regdiv.pdf (accessed on 20 December 2019).
- Köppen, W.; Volken, E.; Brönnimann, S. The thermal zones of the earth according to the duration of hot, moderate and cold periods and to the impact of heat on the organic world . Meteorol. Z. 2011, 20, 351–360, (Translated from: Die Wärmezonen der Erde, nach der Dauer der heissen, gemässigten und kalten Zeit und nach der Wirkung der Wärme auf die organische Welt betrachtet. Meteorol. Z. 1884, 1, 215–226). [Google Scholar]
- Wiken, E.; Nava, F.; Griffith, G. North American Terrestrial Ecoregions-Level III. Technical; Commission for Environmental Cooperation: Montreal, QC, Canada, 2011. [Google Scholar]
- Omernik, J.; Griffith, G. Ecoregions of the Conterminous United States: Evolution of a Hierarchical Spatial Framework. Environ. Manag. 2014, 54, 1249–1266. [Google Scholar] [CrossRef] [PubMed]
- Ecoregions|Ecosystem Research|US EPA. Available online: https://www.epa.gov/eco-research/ecoregions (accessed on 20 December 2019).
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [Green Version]
- Harding, D.; Carabajal, C. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Boudreau, J.; Nelson, R.; Margolis, H.; Beaudoin, A.; Guindon, L.; Kimes, D. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.; Kimes, D.; Blair, J.; Kovacs, K. Forest vertical structure from GLAS: An evaluation using LVIS and SRTM data. Remote Sens. Environ. 2008, 112, 107–117. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Hijmans, R.; Cameron, S.; Parra, J.; Jones, P.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Farr, T.; Rosen, P.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Alsdorf, D. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef] [Green Version]
- USGS. Shuttle Radar Topography Mission, 30 Arc Second Product, Version 2.0. Technical; Global Land Cover Facility; University of Maryland: College Park, MD, USA, 2006.
- Hansen, M.; DeFries, R.; Townshend, J.; Carroll, M.; Dimiceli, C.; Sohlberg, R. Global percent tree cover at a spatial resolution of 500 meters: First results of the MODIS vegetation continuous fields algorithm. Earth Interact. 2003, 7, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Hagolle, O.; Lobo, A.; Maisongrande, P.; Cabot, F.; Duchemin, B.; De Pereyra, A. Quality assessment and improvement of temporally composited products of remotely sensed imagery by combination of VEGETATION 1 and 2 images. Remote Sens. Environ. 2005, 94, 172–186. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Wofsy, S. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Baldocchi, D. ‘Breathing’ of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Bevan, S.; Los, S.; North, P. Response of vegetation to the 2003 European drought was mitigated by height. Biogeosciences 2014, 11, 2897–2908. [Google Scholar] [CrossRef] [Green Version]
- Rosette, J.; North, P.; Suárez, J. Vegetation height estimates for a mixed temperate forest using satellite laser altimetry. Int. J. Remote Sens. 2008, 29, 1475–1493. [Google Scholar] [CrossRef]
- Global 1 km Forest Canopy Height (Simard et al., 2011). Available online: https://webmap.ornl.gov/wcsdown/dataset.jsp?ds_id=10023 (accessed on 20 December 2019).
- G-LiHT. Available online: https://gliht.gsfc.nasa.gov/ (accessed on 20 December 2019).
- Airborne Remote Sensing|NSF NEON|Open Data to Understand our Ecosystems. Available online: https://www.neonscience.org/data-collection/airborne-remote-sensing (accessed on 20 December 2019).
- Home|OpenTopography. Available online: https://opentopography.org/ (accessed on 20 December 2019).
- Hodgson, M.; Jensen, J.; Schmidt, L.; Schill, S.; Davis, B. An evaluation of LIDAR- and IFSAR-derived digital elevation models in leaf-on conditions with USGS Level 1 and Level 2 DEMs. Remote Sens. Environ. 2003, 84, 295–308. [Google Scholar] [CrossRef]
- Wulder, M.; White, J.; Bater, C.; Coops, N.; Hopkins, C.; Chen, G. Lidar plots-a new large-area data collection option: Context, concepts, and case study. Can. J. Remote Sens. 2012, 38, 600–618. [Google Scholar] [CrossRef]
- Drake, J.; Dubayah, R.; Knox, R.; Clark, D.; Blair, J. Sensitivity of large-footprint lidar to canopy structure and biomass in a neotropical rainforest. Remote Sens. Environ. 2002, 81, 378–392. [Google Scholar] [CrossRef]
- St-Onge, B.; Vega, C.; Fournier, R.; Hu, Y. Mapping canopy height using a combination of digital stereo-photogrammetry and lidar. Int. J. Remote Sens. 2008, 29, 3343–3364. [Google Scholar] [CrossRef]
- Kane, V.; McGaughey, R.; Bakker, J.; Gersonde, R.; Lutz, J.; Franklin, J. Comparisons between field- and LiDAR-based measures of stand structural complexity. Can. J. For. Res. 2010, 40, 761–773. [Google Scholar] [CrossRef]
- Alexander, C.; Bøcher, P.; Arge, L.; Svenning, J.-C. Regional-scale mapping of tree cover, height and main phenological tree types using airborne laser scanning data. Remote Sens. Environ. 2014, 147, 156–172. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley Publishing Company: Boston, MA, USA, 1977. [Google Scholar]




| Code | Name | n | n′ |
|---|---|---|---|
| CGP | Central Great Plains | 26 | 20 |
| EP | Edwards Plateau | 7 | 2 |
| MACP | Middle Atlantic Coastal Plain | 148 | 133 |
| MAP | Mississippi Alluvial Plain | 151 | 79 |
| MVLP | Mississippi Valley Loess Plain | 192 | 171 |
| SCEP | South Central Plains | 191 | 190 |
| SCOP | Southeastern Plains | 363 | 289 |
| SEP | Southern Coastal Plains | 128 | 115 |
| SFCP | Southern Florida Coastal Plains | 49 | 48 |
| All | Ecoregions Combined | 1258 | 1039 |
| Abbr | Description |
|---|---|
| CGP | Mostly mixed-grass prairie, with some scattered low trees and shrubs in the south. Much of this ecological region is now cropland. At the south are grasslands, along with some shrubs, brushes, and yucca. The land uses are dominated by dryland and irrigated cropland, as well as some pastureland and rangeland. |
| EP | Juniper–oak savanna and mesquite–oak savanna. Most of the region is used for grazing. |
| MACP | Low-elevation flat plains with many swamps, marshes, and estuaries. Forest cover is mostly loblolly and some shortleaf pine, with patches of oak, sweetgum, and cypress near major streams. Pine plantations for pulpwood and lumber are typical, with some areas of cropland, especially in the central and northern parts of the region. Less cropland occurs in the southern portion than in the central and northern parts of the region. |
| MAP | Bottomland deciduous forest covered the region before much of it was cleared for cultivation. River swamp forests contain bald cypress and water tupelo. This region features extensive agricultural land use. Almost all the region is in cropland. |
| MVLP | Eastern upland forests are dominated by oaks, hickories, and loblolly and shortleaf pine. To the west, there are oak–hickory and southern mesophytic forests. Agriculture is typical in the Kentucky and Tennessee portion of the region; in Arkansas, Mississippi, and Louisiana, there is a mosaic of forest, pine plantations, pasture, and cropland. |
| SCEP | Extensive loblolly and shortleaf pine in this region define the western edge of the southern coniferous pine belt. Commercial pine plantations are extensive. Timber production, livestock grazing, and oil and gas production are major land uses. The land is mostly forest or woodland, with less than 20 percent of cropland, which dominates the leveed bottomlands of the Red River. Southern floodplain forests of water oak, willow oak, swamp chestnut oak, sweetgum, blackgum, red maple, bald cypress, and water tupelo typify bottomlands. |
| SCOP | Southern floodplain forests with bald cypress, pond cypress, water tupelo, bottomland oaks, sweetgum, green ash, and water hickory. Major land uses include pine plantations and forestry, pasture for beef cattle, citrus groves, as well as parks, game refuges, and Indian reservations. |
| SEP | Floodplains include bottomland oaks, red maple, green ash, sweetgum, and American elm, along with areas of bald cypress, pond cypress, and water tupelo. The region presents a mosaic of cropland, pasture, woodland, and forestland cover. Large areas of pine plantations and successional pine and hardwood woodlands are found here. |
| SFCP | In the Everglades, sawgrass marshes are extensive, with some tree-islands of slash pine, gumbo limbo, live oak, strangler fig, and royal palm. To the west, in wet areas: Cypress, gumbo limbo, pigeon plum, live oak, and laurel oak elsewhere. The eastern coastal strip features areas of slash pine, sand pine, scrub oak, and saw palmetto. Mangrove swamps are common on the southern coast and the islands. There are some areas of sugar cane, rice, sod, and vegetables. |
| Collection Location | State(s) | Ecoregion | Month | Year |
|---|---|---|---|---|
| Vernon | TX | CGP | Nov | 2010 |
| Big Sandy Creek | TX | SCEP | Nov | 2010 |
| Huntsville | TX | SCEP | Nov | 2010 |
| Ordway-Swisher Biol. Stn. | FL | SCOP | Sep | 2010 |
| Donaldson plantation | FL | SCOP | Sep | 2010 |
| Tuscaloosa | AL | SEP | Dec | 2010 |
| Meeman-Shelby lineament | AR–TN | MVLP | Jul–Sep | 2010 |
| Reelfoot scarp | AR–TN | MAP | Jul–Sep | 2010 |
| Apopka | FL | SCOP | Jun | 2011 |
| Bald Point | FL | SCOP | Sep | 2010 |
| Vernon Merritt Island | FL | SCOP | Jun | 2008 |
| S. Florida Everglades | FL | SFCP | Nov | 2012 |
| Charleston | SC | MACP | Feb | 2010 |
| Canyon Lake George | TX | EP | Oct | 2010 |
| Bowie | MD | SEP | Jun | 2012 |
| Parker Track | NC | MACP | Jul | 2012 |
| Patuxent Refuge | MD | SEP | Jun | 2012 |
| Perquimans | NC | MACP | Jul | 2011 |
| Smithsonian Env. Res. Ctr. | MD | SEP | Oct | 2011 |
| Wallops Flight Facility | VA | MACP | Sep | 2011 |
| Including simGCHM Zeros; 0 m (ℓ = 1) Height Category | ||||||||||
| Airborne Lidar: | 90th percentile (k = 5) of Heights | 95th percentile (k = 6) of Heights | ||||||||
| Ecoregion (j) | ||||||||||
| CGP | 0.70 | 0.03 | 0.07 | 0.54 | 0.02 | 1.33 | 0.09 | 0.04 | 0.33 | 0.04 |
| EP | 8.63 | 0.02 | 0.00 | 0.90 | 0.00 | 10.43 | 0.06 | 0.00 | 0.77 | 0.02 |
| MACP | 12.79 | 0.30 | 0.00 | 0.00 | 0.13 | 16.87 | 0.23 | 0.00 | 0.00 | 0.09 |
| MAP | 6.47 | 0.53 | 0.00 | 0.00 | 0.27 | 10.05 | 0.52 | 0.00 | 0.00 | 0.23 |
| MVLP | 3.69 | 0.79 | 0.00 | 0.00 | 0.53 | 8.91 | 0.73 | 0.00 | 0.00 | 0.52 |
| SCEP | 4.38 | 0.75 | 0.03 | 0.00 | 0.28 | 8.20 | 0.71 | 0.00 | 0.00 | 0.23 |
| SCOP | 10.11 | 0.27 | 0.00 | 0.00 | 0.12 | 12.63 | 0.25 | 0.00 | 0.00 | 0.11 |
| SEP | 24.00 | −0.15 | 0.00 | 0.04 | 0.03 | 27.09 | −0.16 | 0.00 | 0.02 | 0.04 |
| SFCP | 0.03 | 0.40 | 0.99 | 0.00 | 0.23 | 1.86 | 0.39 | 0.34 | 0.00 | 0.19 |
| All | 7.00 | 0.57 | 0.00 | 0.00 | 0.35 | 9.92 | 0.57 | 0.00 | 0.00 | 0.32 |
| Excluding simGCHM Zeros; 0 m (ℓ = 1) Height Category | ||||||||||
| Airborne Lidar: | 90th percentile (k = 5) of Heights | 95th percentile (k = 6) of Heights | ||||||||
| Ecoregion (j) | ||||||||||
| CGP | −1.16 | 0.27 | 0.46 | 0.19 | 0.09 | −2.48 | 0.58 | 0.33 | 0.09 | 0.15 |
| EP | 20.88 | −1.03 | 0.00 | na | 1.00 | 26.20 | −1.28 | 0.00 | na | 1.00 |
| MACP | 8.29 | 0.52 | 0.00 | 0.00 | 0.10 | 12.87 | 0.42 | 0.00 | 0.00 | 0.08 |
| MAP | −21.90 | 1.86 | 0.00 | 0.00 | 0.75 | −17.49 | 1.82 | 0.00 | 0.00 | 0.68 |
| MVLP | −16.31 | 1.66 | 0.00 | 0.00 | 0.64 | −8.12 | 1.47 | 0.00 | 0.00 | 0.63 |
| SCEP | 1.40 | 0.89 | 0.53 | 0.00 | 0.29 | 5.32 | 0.83 | 0.02 | 0.00 | 0.25 |
| SCOP | −2.22 | 1.01 | 0.05 | 0.00 | 0.42 | 0.58 | 0.98 | 0.60 | 0.00 | 0.42 |
| SEP | 20.18 | 0.03 | 0.00 | 0.88 | 0.00 | 24.81 | −0.05 | 0.00 | 0.74 | 0.00 |
| SFCP | −0.55 | 0.43 | 0.77 | 0.00 | 0.24 | 1.38 | 0.42 | 0.51 | 0.00 | 0.20 |
| ALL | −5.37 | 1.17 | 0.00 | 0.00 | 0.55 | −3.39 | 1.22 | 0.00 | 0.00 | 0.55 |
| Ecoregion(j) | Δ(5,6) | ||||||
|---|---|---|---|---|---|---|---|
| CGP | 0.92 | 1.95 | 1.03 | −3.70 | 0.00 | −1.32 | 0.20 |
| EP | 9.06 | 11.44 | 2.37 | n.a. | n.a. | n.a. | n.a. |
| MACP | 18.87 | 21.37 | 2.50 | −3.48 | 0.00 | −4.71 | 0.00 |
| MAP | 15.09 | 8.64 | 3.55 | 7.02 | 0.00 | 5.76 | 0.00 |
| MVLP | 21.17 | 25.10 | 3.92 | 6.88 | 0.00 | 5.39 | 0.00 |
| SCEP | 20.98 | 23.72 | 0.74 | −1.12 | 0.26 | −1.57 | 0.12 |
| SCOP | 13.66 | 15.97 | 2.31 | 0.21 | 0.84 | −0.24 | 0.81 |
| SEP | 20.73 | 23.74 | 3.01 | −5.91 | 0.00 | −6.81 | 0.00 |
| SFCP | 6.11 | 7.83 | 1.72 | −5.03 | 0.00 | −4.73 | 0.00 |
| ALL | 17.19 | 19.98 | 2.79 | 5.24 | 0.00 | 6.41 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, N.-W.; Popescu, S.; Eriksson, M. Regionalization of an Existing Global Forest Canopy Height Model for Forests of the Southern United States. Remote Sens. 2021, 13, 1722. https://doi.org/10.3390/rs13091722
Ku N-W, Popescu S, Eriksson M. Regionalization of an Existing Global Forest Canopy Height Model for Forests of the Southern United States. Remote Sensing. 2021; 13(9):1722. https://doi.org/10.3390/rs13091722
Chicago/Turabian StyleKu, Nian-Wei, Sorin Popescu, and Marian Eriksson. 2021. "Regionalization of an Existing Global Forest Canopy Height Model for Forests of the Southern United States" Remote Sensing 13, no. 9: 1722. https://doi.org/10.3390/rs13091722
APA StyleKu, N.-W., Popescu, S., & Eriksson, M. (2021). Regionalization of an Existing Global Forest Canopy Height Model for Forests of the Southern United States. Remote Sensing, 13(9), 1722. https://doi.org/10.3390/rs13091722








