Airborne GNSS Reflectometry for Water Body Detection
Abstract
:1. Introduction
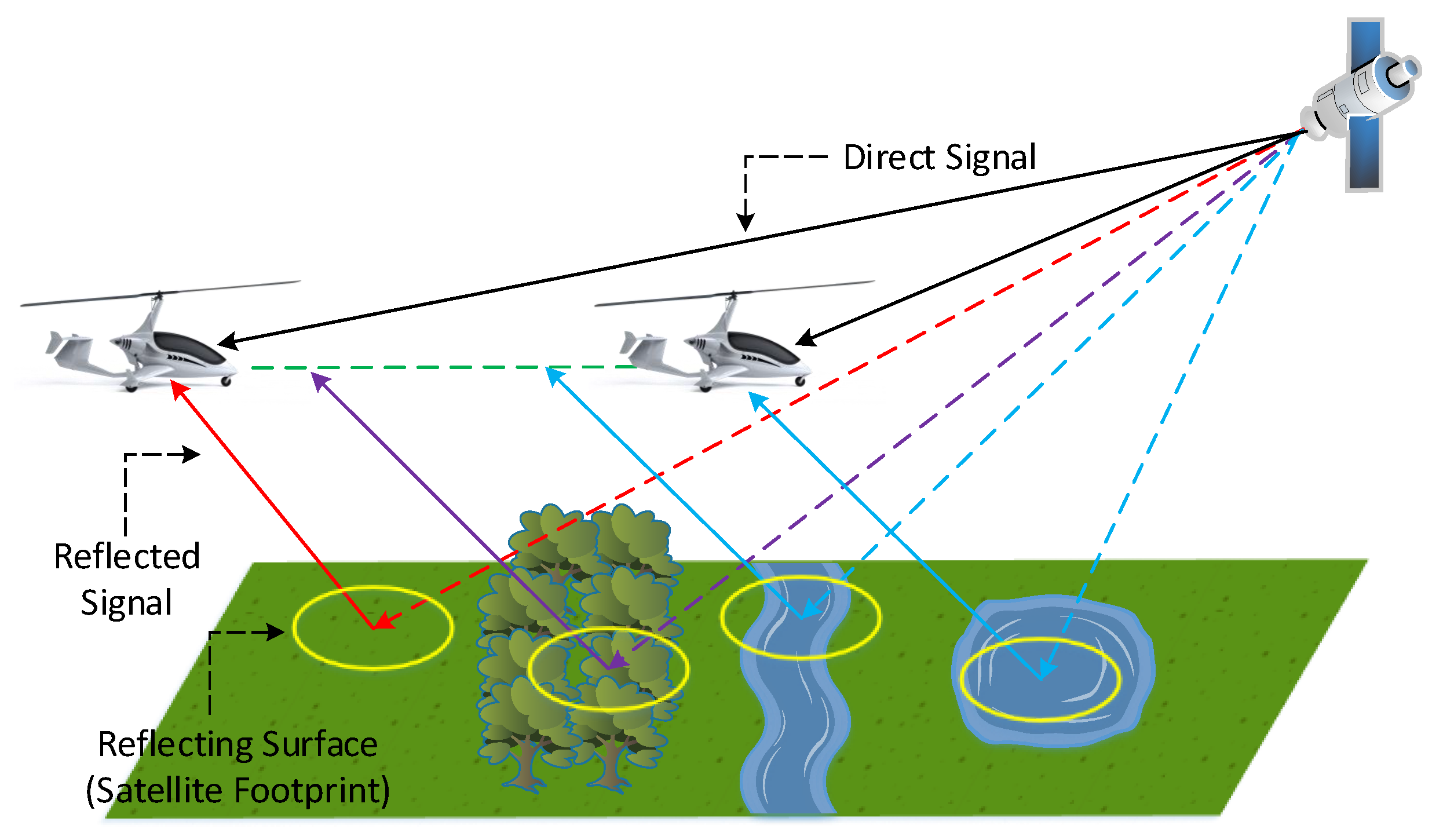
2. Airborne Bi-Static GNSS-R Configuration
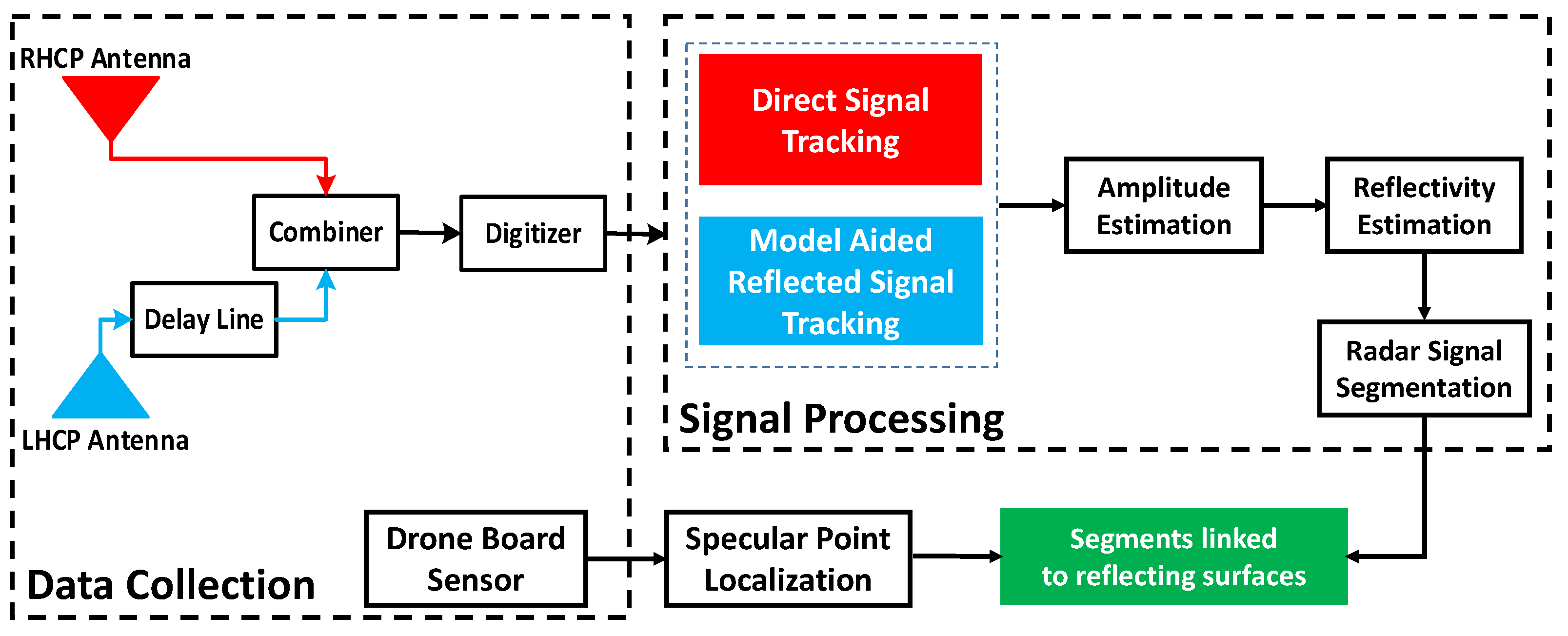
3. Airborne GNSS-R System
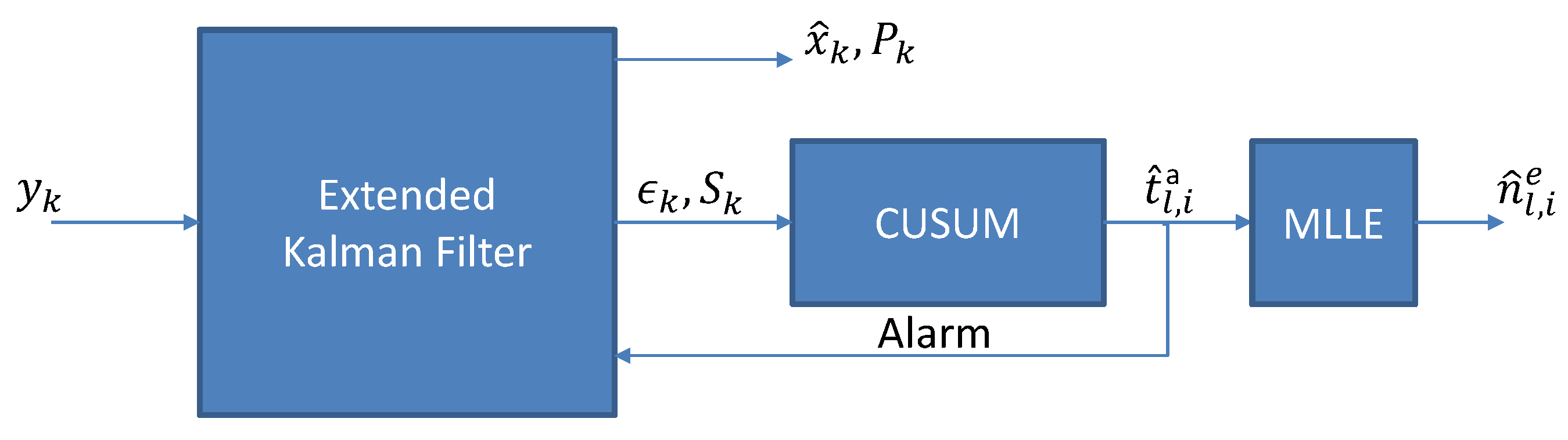
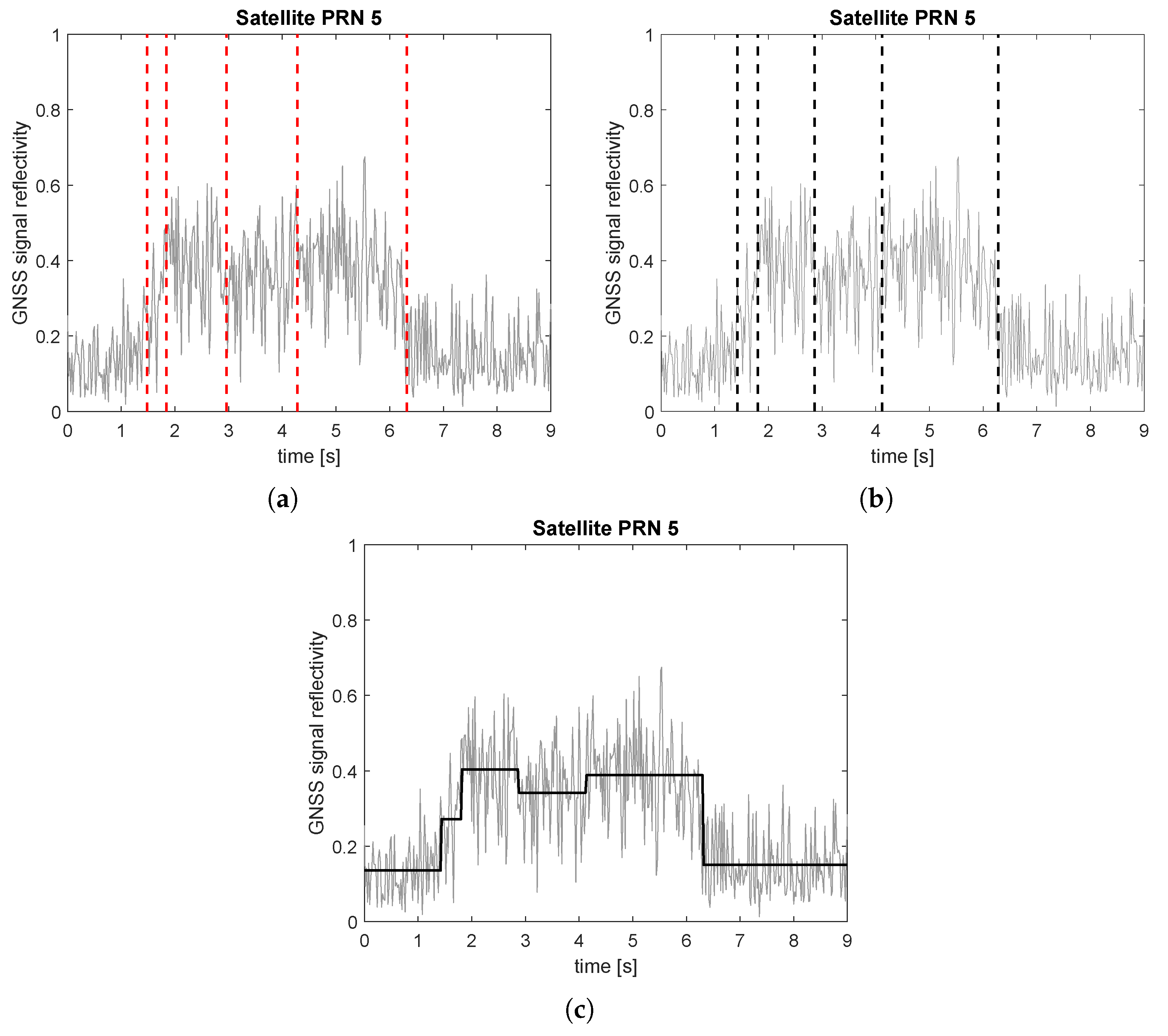
4. Segmentation of the GNSS Signal
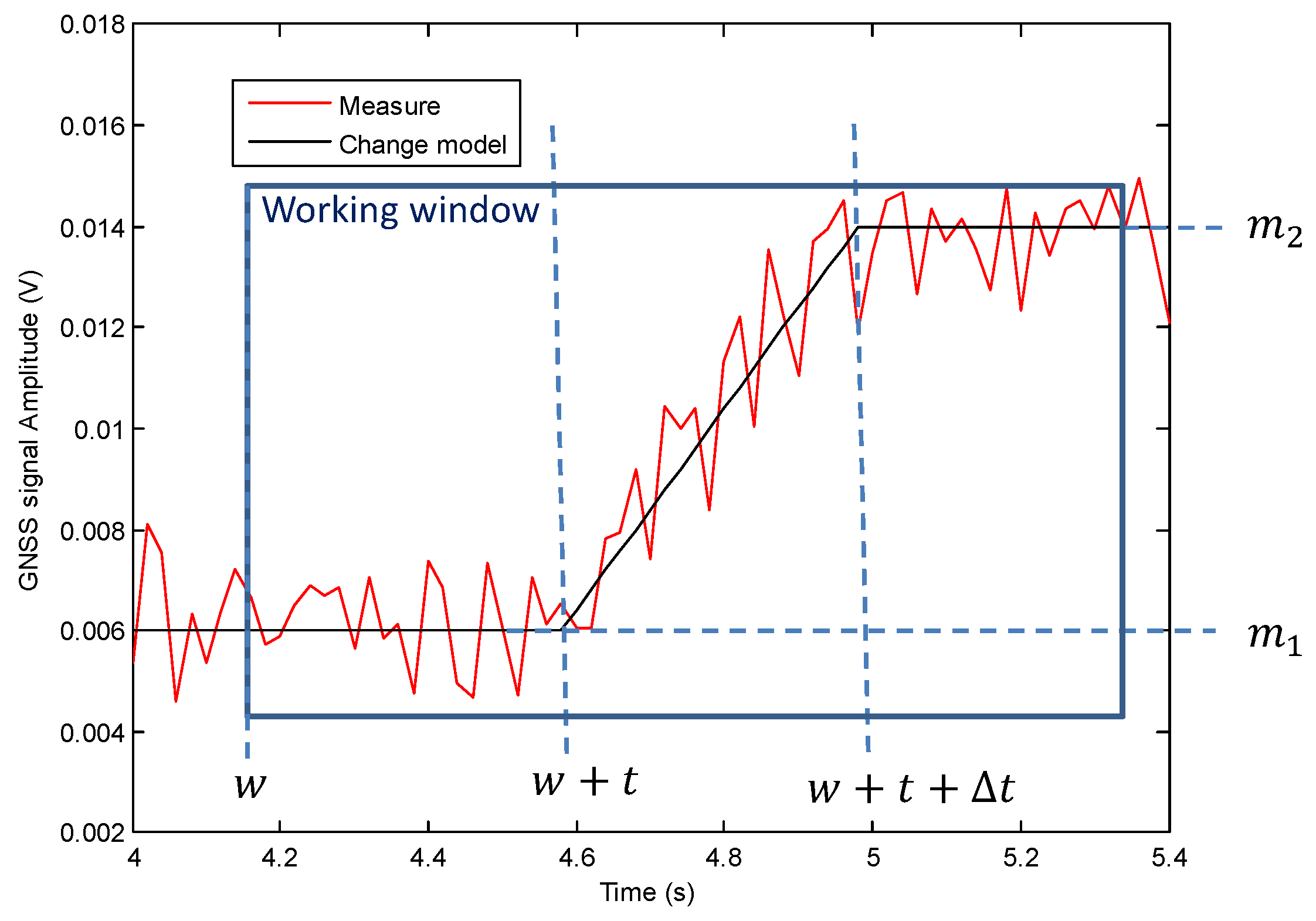
4.1. Transition Model
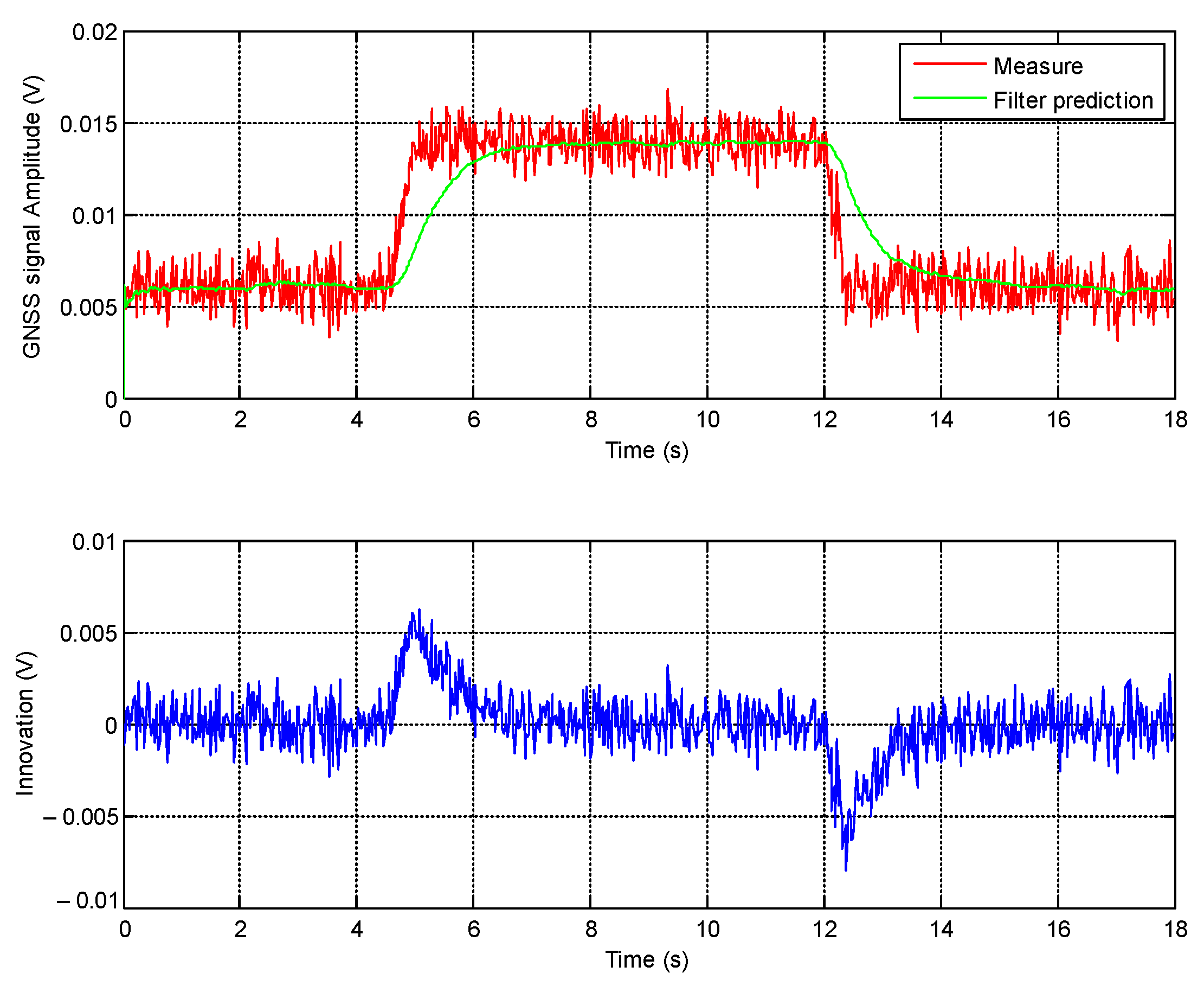
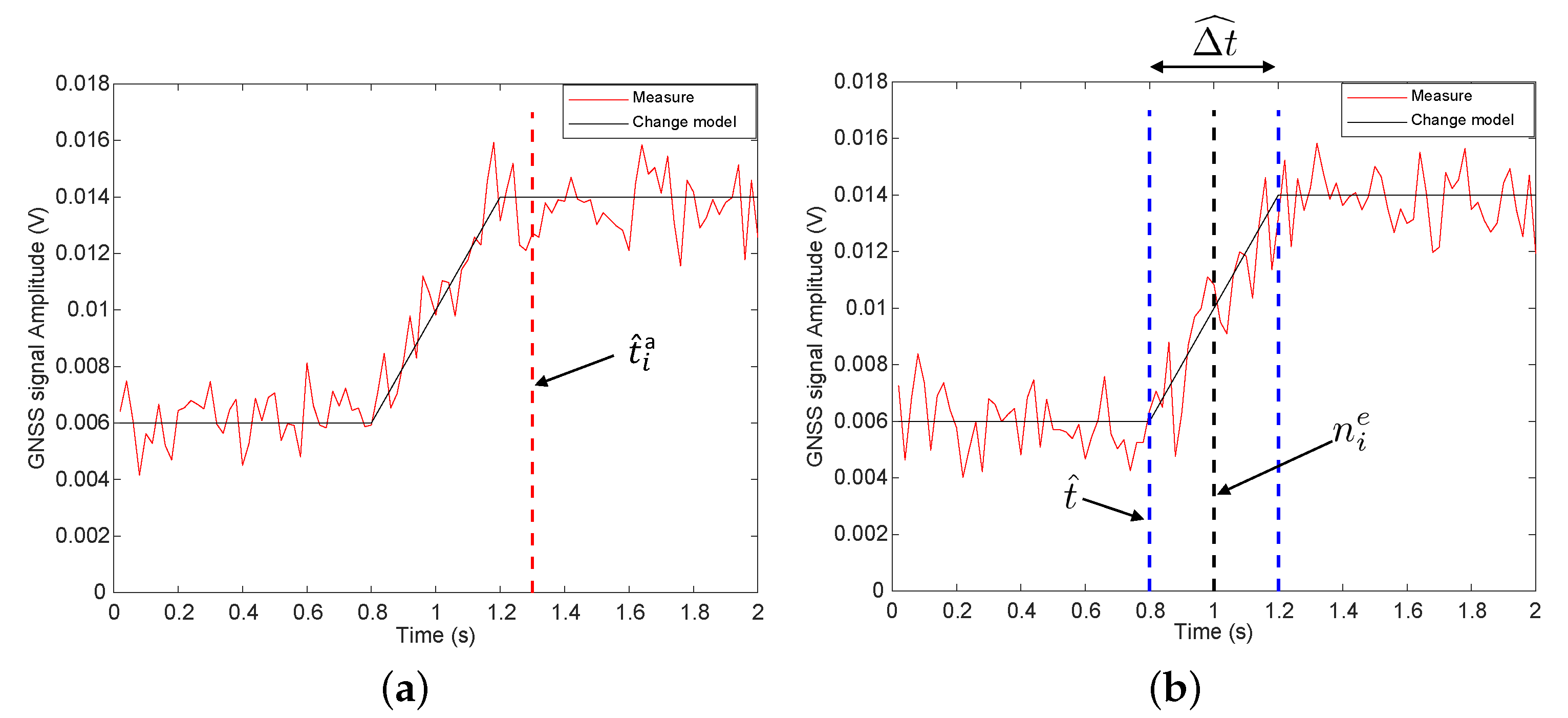
4.2. Change Detection
4.3. Change Localization
4.4. Segmentation of Airborne GNSS Measurements
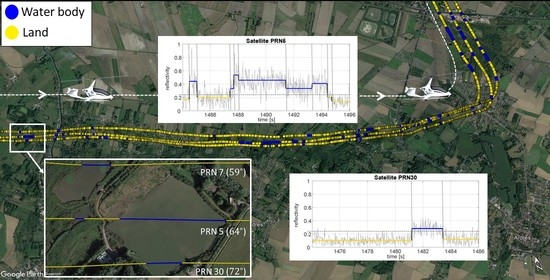
5. Flight Experimentation
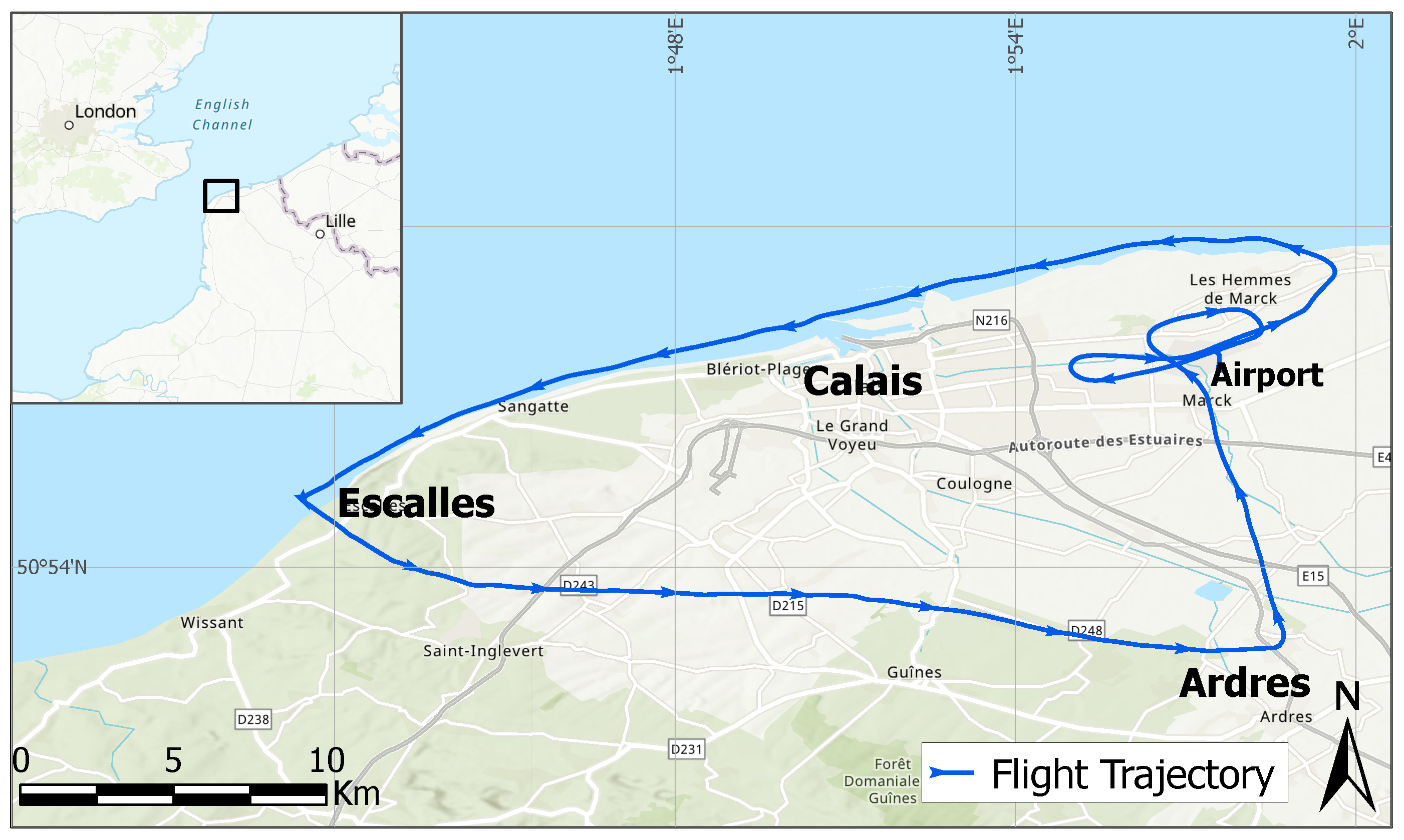
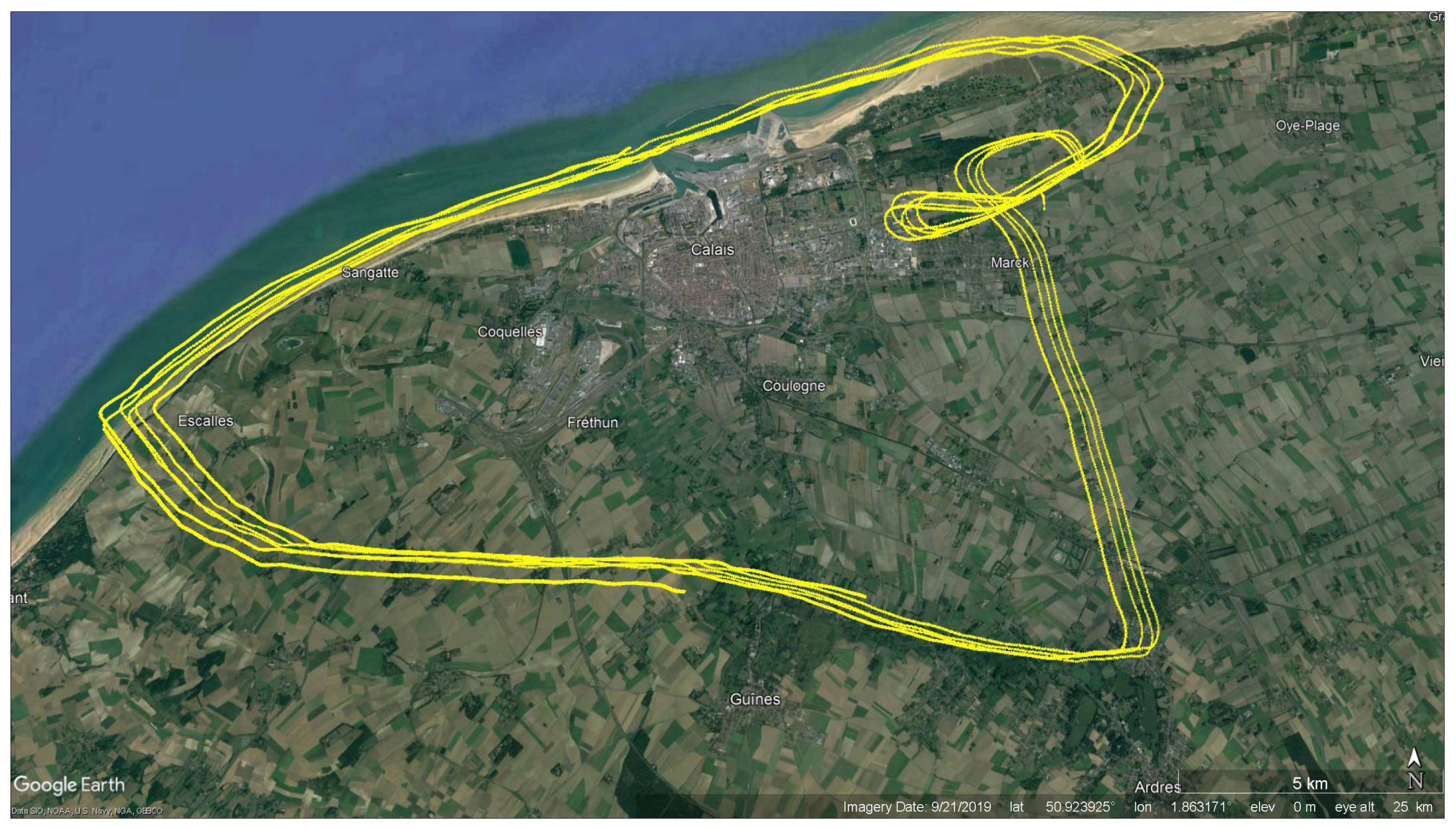
5.1. Flight Information
5.2. Flight Trajectory
6. Data Analysis
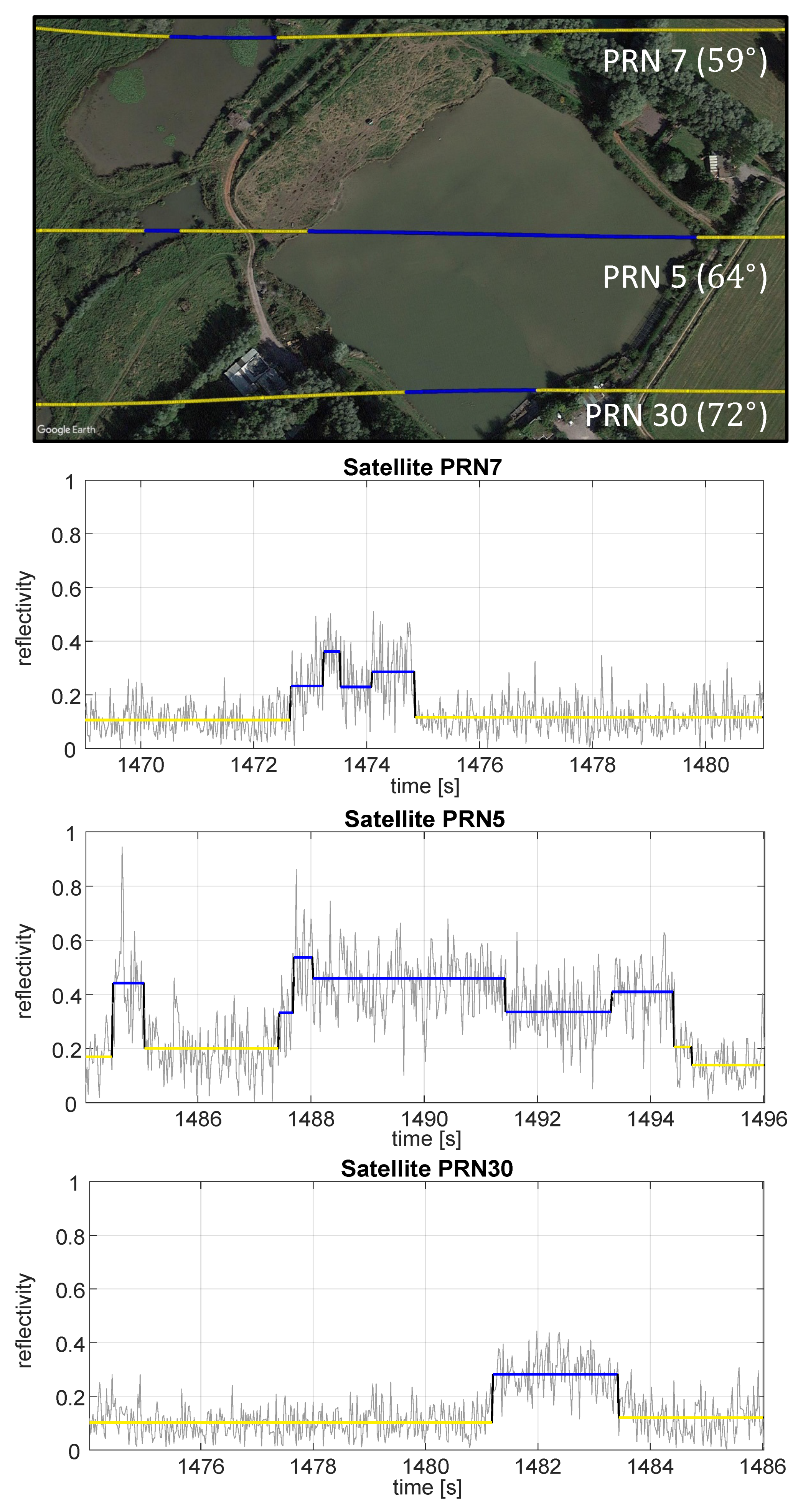
6.1. Radar Signal Segmentation
6.2. Water Body Surface Detection
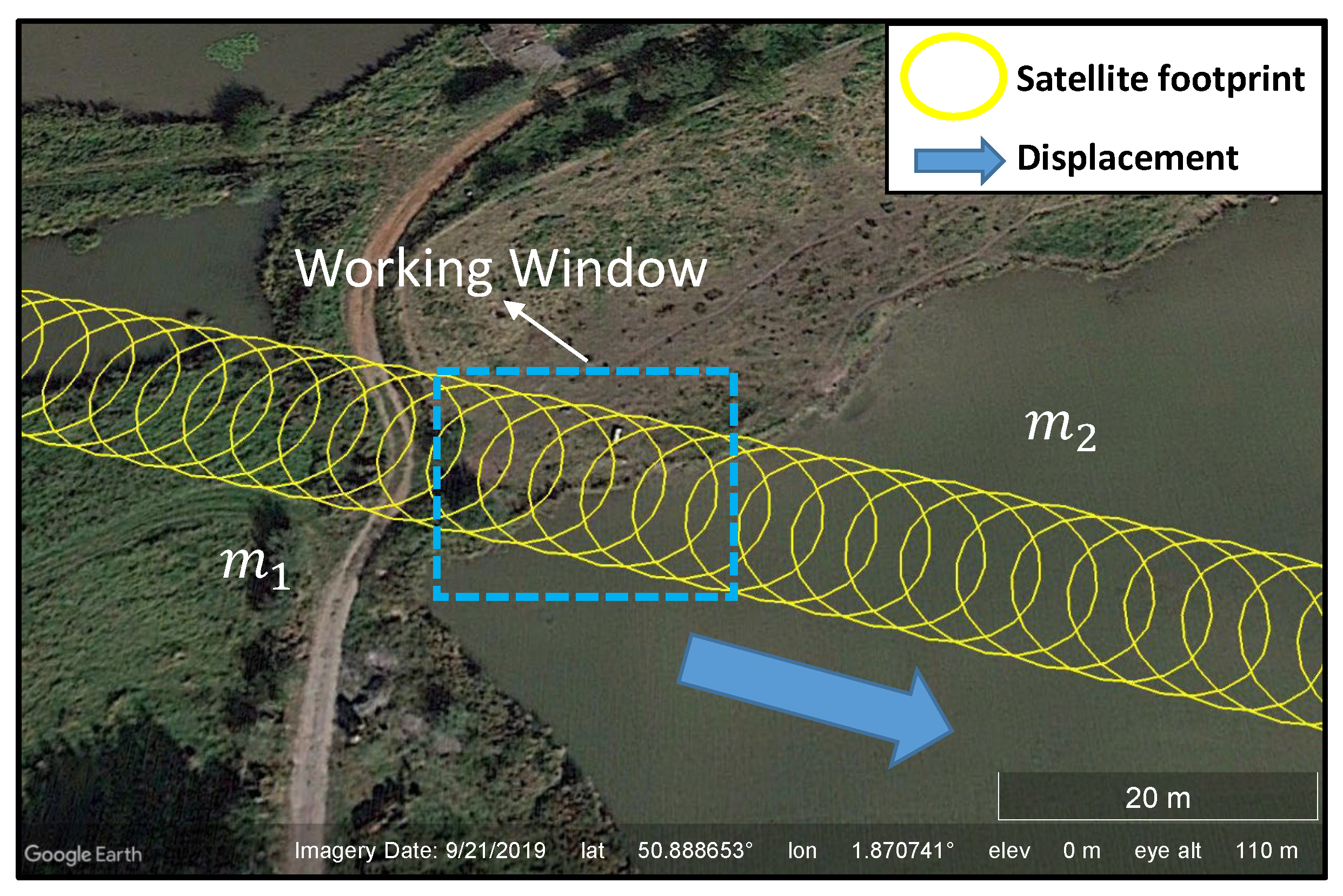
6.3. Water Body Edge Localization
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Egido, A. GNSS Reflectometry for Land Remote Sensing Applications. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2014. [Google Scholar]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.I. Hot days induced by precipitation deficits at the global scale. Proc. Natl. Acad. Sci. USA 2012, 109, 12398–12403. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Van Den Berg, M.J.; Gash, J.H.; Parinussa, R.M.; De Jeu, R.A.; Beck, H.E.; Holmes, T.R.; Jiménez, C.; Verhoest, N.E.; Dorigo, W.A.; et al. El Niño–La Niña cycle and recent trends in continental evaporation. Nat. Clim. Chang. 2014, 4, 122–126. [Google Scholar] [CrossRef]
- Masters, D.; Axelrad, P.; Katzberg, S. Initial results of land-reflected GPS bistatic radar measurements in SMEX02. Remote Sens. Environ. 2004, 92, 507–520. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Merlin, O.; Stefan, V.; Moyano, G.; Eweys, O.A.; Zribi, M.; Kamara, S.; Benahi, A.S.; Ebbe, M.A.B.; Chihrane, J.; et al. SMOS based high resolution soil moisture estimates for desert locust preventive management. Remote Sens. Appl. Soc. Environ. 2018, 11, 140–150. [Google Scholar]
- Frappart, F.; Zeiger, P.; Betbeder, J.; Gond, V.; Bellot, R.; Baghdadi, N.; Blarel, F.; Darrozes, J.; Bourrel, L.; Seyler, F. Automatic detection of inland water bodies along altimetry tracks for estimating surface water storage variations in the Congo Basin. Remote Sens. 2021, 13, 3804. [Google Scholar] [CrossRef]
- Davidson, N.; Fluet-Chouinard, E.; Finlayson, C. Global extent and distribution of wetlands: Trends and issues. Mar. Freshw. Res. 2018, 69, 620–627. [Google Scholar] [CrossRef] [Green Version]
- Acreman, M.; Holden, J. How wetlands affect floods. Wetlands 2013, 33, 773–786. [Google Scholar] [CrossRef] [Green Version]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Masters, D. Utilizing calibrated GPS reflected signals to estimate soil reflectivity and dielectric constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Jin, S.; Qian, X.; Wu, X. Sea level change from BeiDou Navigation Satellite System-Reflectometry (BDS-R): First results and evaluation. Glob. Planet. Chang. 2017, 149, 20–25. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A. A new technique to sense non-Gaussian features of the sea surface from L-band bi-static GNSS reflections. Remote Sens. Environ. 2008, 112, 2927–2937. [Google Scholar] [CrossRef]
- Garrison, J.L.; Komjathy, A.; Zavorotny, V.U.; Katzberg, S.J. Wind speed measurement using forward scattered GPS signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef] [Green Version]
- Sabia, R.; Caparrini, M.; Camps, A.; Ruffini, G. Potential synergetic use of GNSS-R signals to improve the sea-state correction in the sea surface salinity estimation: Application to the SMOS mission. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2088–2097. [Google Scholar] [CrossRef]
- Cardellach, E.; Fabra, F.; Rius, A.; Pettinato, S.; D’Addio, S. Characterization of dry-snow sub-structure using GNSS reflected signals. Remote Sens. Environ. 2012, 124, 122–134. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Aguasca, A.; Valencia, E.; Bosch-Lluis, X.; Ramos-Pérez, I.; Park, H.; Camps, A.; Vall-Llossera, M. Snow monitoring using GNSS-R techniques. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4375–4378. [Google Scholar]
- Rivas, M.B.; Maslanik, J.A.; Axelrad, P. Bistatic scattering of GPS signals off Arctic sea ice. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1548–1553. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Coastal sea ice detection using ground-based GNSS-R. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1552–1556. [Google Scholar] [CrossRef]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef] [Green Version]
- Zribi, M.; Guyon, D.; Motte, E.; Dayau, S.; Wigneron, J.P.; Baghdadi, N.; Pierdicca, N. Performance of GNSS-R GLORI data for biomass estimation over the Landes forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 150–158. [Google Scholar] [CrossRef]
- Edokossi, K.; Calabia, A.; Jin, S.; Molina, I. GNSS-Reflectometry and Remote Sensing of Soil Moisture: A Review of Measurement Techniques, Methods, and Applications. Remote Sens. 2020, 12, 614. [Google Scholar] [CrossRef] [Green Version]
- Mironov, V.L.; Fomin, S.V.; Muzalevskiy, K.V.; Sorokin, A.V.; Mikhaylov, M. The use of navigation satellites signals for determination the characteristics of the soil and forest canopy. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 7527–7529. [Google Scholar]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2016, 20, 525–537. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Malik, J.S.; Jingrui, Z.; Naqvi, N.A. Soil moisture content estimation using GNSS reflectometry (GNSS-R). In Proceedings of the 2017 Fifth International Conference on Aerospace Science & Engineering (ICASE), Islamabad, Pakistan, 14–16 November 2017; pp. 1–9. [Google Scholar]
- Egido, A.; Caparrini, M.; Ruffini, G.; Paloscia, S.; Santi, E.; Guerriero, L.; Pierdicca, N.; Floury, N. Global navigation satellite systems reflectometry as a remote sensing tool for agriculture. Remote Sens. 2012, 4, 2356–2372. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-Llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; et al. Land geophysical parameters retrieval using the interference pattern GNSS-R technique. IEEE Trans. Geosci. Remote Sens. 2010, 49, 71–84. [Google Scholar] [CrossRef]
- Arroyo, A.A.; Camps, A.; Aguasca, A.; Forte, G.F.; Monerris, A.; Rüdiger, C.; Walker, J.P.; Park, H.; Pascual, D.; Onrubia, R. Dual-polarization GNSS-R interference pattern technique for soil moisture mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1533–1544. [Google Scholar] [CrossRef]
- Jia, Y.; Savi, P.; Canone, D.; Notarpietro, R. Estimation of surface characteristics using GNSS LH-reflected signals: Land versus water. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4752–4758. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Onrubia, R.; Pascual, D.; Park, H.; Pablos, M.; Camps, A.; Rüdiger, C.; Walker, J.; Monerris, A. Single-Pass Soil Moisture Retrieval Using GNSS-R at L1 and L5 Bands: Results from Airborne Experiment. Remote Sens. 2021, 13, 797. [Google Scholar] [CrossRef]
- Egido, A.; Paloscia, S.; Motte, E.; Guerriero, L.; Pierdicca, N.; Caparrini, M.; Santi, E.; Fontanelli, G.; Floury, N. Airborne GNSS-R polarimetric measurements for soil moisture and above-ground biomass estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1522–1532. [Google Scholar] [CrossRef]
- Sánchez, N.; Alonso-Arroyo, A.; Martínez-Fernández, J.; Piles, M.; González-Zamora, Á.; Camps, A.; Vall-Llosera, M. On the synergy of airborne GNSS-R and Landsat 8 for soil moisture estimation. Remote Sens. 2015, 7, 9954–9974. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.; Savi, P.; Pei, Y.; Notarpietro, R. GNSS reflectometry for remote sensing of soil moisture. In Proceedings of the 2015 IEEE 1st International Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow (RTSI), Turin, Italy, 16–18 September 2015; pp. 498–501. [Google Scholar]
- Wan, W.; Bai, W.; Zhao, L.; Long, D.; Sun, Y.; Meng, X.; Chen, H.; Cui, X.; Hong, Y. Initial results of China’s GNSS-R airborne campaign: Soil moisture retrievals. Sci. Bull. 2015, 60, 964–971. [Google Scholar] [CrossRef] [Green Version]
- Motte, E.; Zribi, M.; Fanise, P.; Egido, A.; Darrozes, J.; Al-Yaari, A.; Baghdadi, N.; Baup, F.; Dayau, S.; Fieuzal, R.; et al. GLORI: A GNSS-R dual polarization airborne instrument for land surface monitoring. Sensors 2016, 16, 732. [Google Scholar] [CrossRef]
- Troglia Gamba, M.; Marucco, G.; Pini, M.; Ugazio, S.; Falletti, E.; Lo Presti, L. Prototyping a GNSS-based passive radar for UAVs: An instrument to classify the water content feature of lands. Sensors 2015, 15, 28287–28313. [Google Scholar] [CrossRef]
- Jia, Y.; Pei, Y. Remote Sensing in Land Applications by Using GNSS-Reflectometry. In Recent Advances and Applications in Remote Sensing; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar]
- Chew, C.; Colliander, A.; Shah, R.; Zuffada, C.; Burgin, M. The sensitivity of ground-reflected GNSS signals to near-surface soil moisture, as recorded by spaceborne receivers. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2661–2663. [Google Scholar]
- Camps, A.; Park, H.; Portal, G.; Rossato, L. Sensitivity of TDS-1 GNSS-R reflectivity to soil moisture: Global and regional differences and impact of different spatial scales. Remote Sens. 2018, 10, 1856. [Google Scholar] [CrossRef] [Green Version]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Calabia, A.; Molina, I.; Jin, S. Soil Moisture Content from GNSS Reflectometry Using Dielectric Permittivity from Fresnel Reflection Coefficients. Remote Sens. 2020, 12, 122. [Google Scholar] [CrossRef] [Green Version]
- Chew, C.; Small, E. Soil moisture sensing using spaceborne GNSS reflections: Comparison of CYGNSS reflectivity to SMAP soil moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef] [Green Version]
- Issa, H.; Stienne, G.; Reboul, S.; Semmling, M.; Raad, M.; Faour, G.; Wickert, J. A probabilistic model for on-line estimation of the GNSS carrier-to-noise ratio. Signal Process. 2021, 183, 107992. [Google Scholar] [CrossRef]
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes-Theory and Application; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1993; p. 550. [Google Scholar]
- Gustafsson, F. Adaptive Filtering and Change Detection; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2000; p. 500. [Google Scholar]
- Page, E.S. Continuous Inspection Schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]


| Description | |
|---|---|
| Date | 19 October 2020 |
| Location | North of France |
| Fight Duration | 45 min |
| Distance Covered | 71 km |
| Average Speed | 95 km/h |
| Average Height | 315 m |
| Wind Speed | 25 km/h |
| Wind Direction | North |
| Water Body | Number of Surfaces Using IGN Maps | Percentage of Detection Using Our Radar Technique |
|---|---|---|
| Lakes/Large Swamps | 20 | 100% |
| Ponds/Swamps/Wetlands | 17 | 94% |
| Rivers/Canals | 4 | 100% |
| Streams/Brooks | 6 | 83% |
| Total | 47 | 96% |
| Water Body | Wetland | Lake | River | Stream |
|---|---|---|---|---|
| Approximate size (m) | ||||
| Localization diff—Start (m) | 0 | |||
| Localization diff—End (m) | 0 | 0 | 0 | |
| Distance error—Total (m) | 0 | |||
| Automatic detection length (m) | ||||
| Manual detection length (m) |
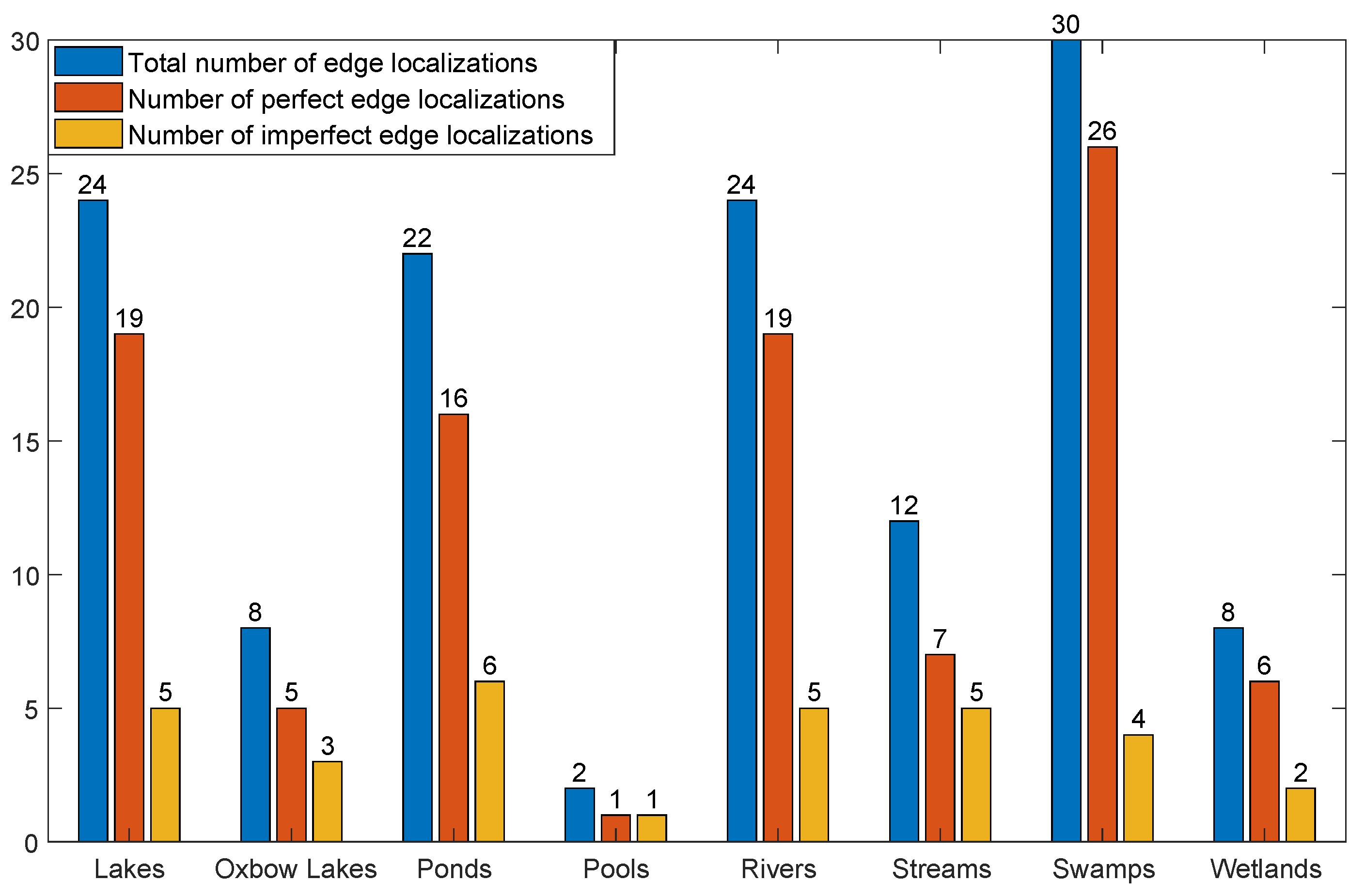
| Water Body | Number of Detections | Percentage of Perfect Edge Localization | Mean Distance Localization Error (in Meters) | Localization Difference—Std (in Meters) |
|---|---|---|---|---|
| Lakes | 12 | |||
| Oxbow Lakes | 4 | |||
| Ponds | 11 | |||
| Pools | 1 | |||
| Rivers/Canals | 12 | |||
| Streams/Brooks | 6 | |||
| Swamps | 15 | |||
| Wetlands | 4 | |||
| Total | 76.2% | 0.96 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Issa, H.; Stienne, G.; Reboul, S.; Raad, M.; Faour, G. Airborne GNSS Reflectometry for Water Body Detection. Remote Sens. 2022, 14, 163. https://doi.org/10.3390/rs14010163
Issa H, Stienne G, Reboul S, Raad M, Faour G. Airborne GNSS Reflectometry for Water Body Detection. Remote Sensing. 2022; 14(1):163. https://doi.org/10.3390/rs14010163
Chicago/Turabian StyleIssa, Hamza, Georges Stienne, Serge Reboul, Mohamad Raad, and Ghaleb Faour. 2022. "Airborne GNSS Reflectometry for Water Body Detection" Remote Sensing 14, no. 1: 163. https://doi.org/10.3390/rs14010163
APA StyleIssa, H., Stienne, G., Reboul, S., Raad, M., & Faour, G. (2022). Airborne GNSS Reflectometry for Water Body Detection. Remote Sensing, 14(1), 163. https://doi.org/10.3390/rs14010163