Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Forest Inventory Data
2.2.2. Gaofen-1 WFV Image Pre-Processing and Variable Calculation
2.2.3. Sentinel-1 Data Pre-Processing and Variable Calculation
2.2.4. Topographic Data and Preprocessing
2.3. Methods
2.3.1. Stepwise Multiple Regression Algorithm
2.3.2. Machine Learning Algorithms
2.3.3. Performance Metrics
2.3.4. Variable Selection
3. Results
3.1. Relationships between Sample Point AGB and Variables
3.2. Variable Combination and Model Construction
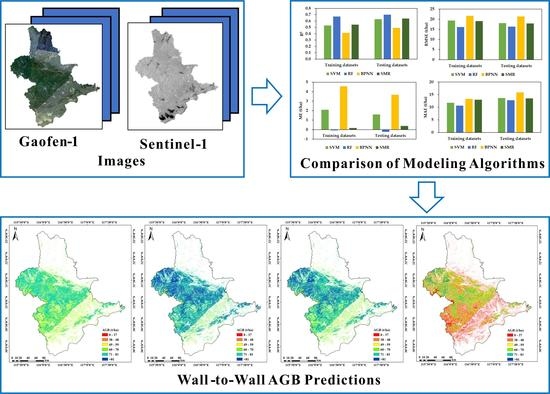
3.3. Comparison of the Estimated AGB Values among the Modeling Algorithms and Wall-to-Wall Predictions
4. Discussion
4.1. Predictors of Forest AGB Mapping
4.2. Performance of Modeling Algorithms
4.3. Limitations of Mapping AGB
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| Variable Abbreviation | Description |
|---|---|
| AGB | forest aboveground biomass |
| b1 | band 1-blue |
| b2 | band 2-green |
| b3 | band 3-red |
| b4 | band 4 near-infrared |
| NDVI | Normalized Difference Vegetation Index |
| EVI | Enhance Vegetation Index |
| RVI | Ratio Vegetation Index |
| ARVI | Atmospherically Resistant Vegetation Index |
| SAVI | Soil Adjust Vegetation Index |
| MSAVI | Modified Soil Adjust Vegetation Index |
| OSAVI | Optimized Soil Adjusted Vegetation Index |
| b3_3Con | contrast of b3 with the 3 × 3 window |
| b3_3Cor | correlation of b3 with the 3 × 3 window |
| b3_3Dis | dissimilarity of b3 with the 3 × 3 window |
| b3_3Ent | entropy of b3 with the 3 × 3 window |
| b3_3Hom | homogeneity of b3 with the 3 × 3 window |
| b3_3Mean | mean of b3 with the 3 × 3 window |
| b3_3SM | second moment of b3 with the 3 × 3 window |
| b3_3Var | variance of b3 with the 3×3 window |
| b3_5Con | contrast of b3 with the 5 × 5 window |
| b3_5Cor | correlation of b3 with the 5 × 5 window |
| b3_5Dis | dissimilarity of b3 with the 5 × 5 window |
| b3_5Ent | entropy of b3 with the 5 × 5 window |
| b3_5Hom | homogeneity of b3 with the 5 × 5 window |
| b3_5Mean | mean of b3 with the 5 × 5 window |
| b3_5SM | second moment of b3 with the 5 × 5 window |
| b3_5Var | variance of b3 with the 5 × 5 window |
| b3_7Con | contrast of b3 with the 7 × 7 window |
| b3_7Cor | correlation of b3 with the 7 × 7 window |
| b3_7Dis | dissimilarity of b3 with the 7 × 7 window |
| b3_7Ent | entropy of b3 with the 7 × 7 window |
| b3_7Hom | homogeneity of b3 with the 7 × 7 window |
| b3_7Mean | mean of b3 with the 7 × 7 window |
| b3_7SM | second moment of b3 with the 7 × 7 window |
| b3_7Var | variance of b3 with the 7 × 7 window |
| b4_3Con | contrast of b4 with the 3 × 3 window |
| b4_3Cor | correlation of b4 with the 3 × 3 window |
| b4_3Dis | dissimilarity of b4 with the 3 × 3 window |
| b4_3Ent | entropy of b4 with the 3 × 3 window |
| b4_3Hom | homogeneity of b4 with the 3 × 3 window |
| b4_3Mean | mean of b4 with the 3 × 3 window |
| b4_3SM | second moment of b4 with the 3 × 3 window |
| b4_3Var | variance of b4 with the 3 × 3 window |
| b4_5Con | contrast of b4 with the 5 × 5 window |
| b4_5Cor | correlation of b4 with the 5 × 5 window |
| b4_5Dis | dissimilarity of b4 with the 5 × 5 window |
| b4_5Ent | entropy of b4 with the 5 × 5 window |
| b4_5Hom | homogeneity of b4 with the 5 × 5 window |
| b4_5Mean | mean of b4 with the 5 × 5 window |
| b4_5SM | second moment of b4 with the 5 × 5 window |
| b4_5Var | variance of b4 with the 5 × 5 window |
| b4_7Con | contrast of b4 with the 7 × 7 window |
| b4_7Cor | correlation of b4 with the 7 × 7 window |
| b4_7Dis | dissimilarity of b4 with the 7 × 7 window |
| b4_7Ent | entropy of b4 with the 7 × 7 window |
| b4_7Hom | homogeneity of b4 with the 7 × 7 window |
| b4_7Mean | mean of b4 with the 7 × 7 window |
| b4_7SM | second moment of b4 with the 7 × 7 window |
| b4_7Var | variance of b4 with the 7 × 7 window |
| VH | vertical transmit-horizontal receive |
| VV | vertical transmit-vertical receive |
| VH/VV | VH divided by VV |
| VH_3Con | contrast of VH with the 3 × 3 window |
| VH_3Cor | correlation of VH with the 3 × 3 window |
| VH_3Dis | dissimilarity of VH with the 3 × 3 window |
| VH_3Ent | entropy of VH with the 3 × 3 window |
| VH_3Hom | homogeneity of VH with the 3 × 3 window |
| VH_3Mean | mean of VH with the 3 × 3 window |
| VH_3SM | second moment of VH with the 3 × 3 window |
| VH_3Var | variance of VH with the 3 × 3 window |
| VV_3Con | contrast of VV with the 3 × 3 window |
| VV_3Cor | correlation of VV with the 3 × 3 window |
| VV_3Dis | dissimilarity of VV with the 3 × 3 window |
| VV_3Ent | entropy of VV with the 3 × 3 window |
| VV_3Hom | homogeneity of VV with the 3 × 3 window |
| VV_3Mean | mean of VV with the 3 × 3 window |
| VV_3SM | second moment of VV with the 3 × 3 window |
| VV_3Var | variance of VV with the 3 × 3 window |
| altitude | - |
| slope | - |
| aspect | - |
References
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S. Global carbon budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Achard, F.; Eva, H.D.; Stibig, H.J.; Mayaux, P.; Gallego, J.; Richards, T.; Malingreau, J.P. Determination of deforestation rates of the world’s humid tropical forests. Science 2002, 297, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of multi-resource remotely sensed data and allometric models for forest aboveground biomass estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Ou, G.; Lv, Y.; Xu, H.; Wang, G. Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images. Remote Sens. 2019, 11, 2750. [Google Scholar] [CrossRef] [Green Version]
- Paul, K.I.; Roxburgh, S.H.; Chave, J.; England, J.R.; Zerihun, A.; Specht, A.; Lewis, T.; Bennett, L.T.; Baker, T.G.; Adams, M.A. Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Glob. Chang. Biol. 2016, 22, 2106–2124. [Google Scholar] [CrossRef] [PubMed]
- Paul, K.I.; Larmour, J.; Specht, A.; Zerihun, A.; Ritson, P.; Roxburgh, S.H.; Sochacki, S.; Lewis, T.; Barton, C.V.; England, J.R. Testing the generality of below-ground biomass allometry across plant functional types. For. Ecol. Manag. 2019, 432, 102–114. [Google Scholar] [CrossRef]
- Yu, X.; Ge, H.; Lu, D.; Zhang, M.; Lai, Z.; Yao, R. Comparative study on variable selection approaches in establishment of remote sensing model for forest biomass estimation. Remote Sens. 2019, 11, 1437. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal combination of predictors and algorithms for forest above-ground biomass mapping from Sentinel and SRTM data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Chave, J.; Davies, S.J.; Phillips, O.L.; Lewis, S.L.; Sist, P.; Schepaschenko, D.; Armston, J.; Baker, T.R.; Coomes, D.; Disney, M. Ground data are essential for biomass remote sensing missions. Surv. Geophys. 2019, 40, 863–880. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Li, M. Improving forest aboveground biomass (AGB) estimation by incorporating crown density and using landsat 8 OLI images of a subtropical forest in Western Hunan in Central China. Forests 2019, 10, 104. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest aboveground biomass mapping and estimation across multiple spatial scales using model-based inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote sensing approaches for monitoring mangrove species, structure, and biomass: Opportunities and challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Denka, S.; Cooper, H.; Mishra, D.R. Quantification of sawgrass marsh aboveground biomass in the coastal Everglades using object-based ensemble analysis and Landsat data. Remote Sens. Environ. 2018, 204, 366–379. [Google Scholar] [CrossRef]
- Foody, G.M.; Cutler, M.E.; Mcmorrow, J.; Pelz, D.; Tangki, H.; Boyd, D.S.; Douglas, I. Mapping the Biomass of Bornean Tropical Rain Forest from Remotely Sensed Data. Glob. Ecol. Biogeogr. 2001, 10, 379–387. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Cohen, W.; Kennedy, R.; Grodzki, W.; Pflugmacher, D.; Griffiths, P.; Hostert, P. Monitoring coniferous forest biomass change using a Landsat trajectory-based approach. Remote Sens. Environ. 2013, 139, 277–290. [Google Scholar] [CrossRef]
- Pham, L.T.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests—The potential of combined X-and L-band SAR data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Cutler, M.E.J.; Boyd, D.S.; Foody, G.M.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef] [Green Version]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Peng, D.; Zou, J.; Nie, S.; Qin, H. Fusion of airborne LiDAR data and hyperspectral imagery for aboveground and belowground forest biomass estimation. Ecol. Indic. 2017, 73, 378–387. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep learning based retrieval of forest aboveground biomass from combined LiDAR and landsat 8 data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef] [Green Version]
- Bortolot, Z.; Wynne, R. Estimating forest biomass using small footprint LiDAR data: An individual tree-based approach that incorporates training data. J. Photogramm. Remote Sens. 2005, 59, 342–360. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.; Innes, J.; Sheppard, S.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Lin, Y.; West, G. Reflecting conifer phenology using mobile terrestrial LiDAR: A case study of Pinus sylvestris growing under the Mediterranean climate in Perth, Australia. Ecol. Indic. 2016, 70, 1–9. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Li, G. Above-ground biomass estimation using airborne discrete-return and full-waveform LiDAR data in a coniferous forest. Ecol. Indic. 2017, 78, 221–228. [Google Scholar] [CrossRef]
- Qin, Y.; Li, S.; Vu, T.; Niu, Z.; Ban, Y. Synergistic application of geometric and radiometric features of LiDAR data for urban land cover mapping. Opt. Express 2015, 23, 13761–13775. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest biomass mapping from lidar and radar synergies. Remote Sens. Environ. 2011, 115, 2906–2916. [Google Scholar] [CrossRef] [Green Version]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Li, J.; Gong, W.; Zhao, X.; Chen, X.; Pang, X. Radiometric cross-calibration of Gaofen-1 WFV cameras using Landsat-8 OLI images: A solution for large view angle associated problems. Remote Sens. Environ. 2016, 174, 56–68. [Google Scholar] [CrossRef]
- Fu, B.; Wang, Y.; Campbell, A.; Li, Y.; Zhang, B.; Yin, S.; Xing, Z.; Jin, X. Comparison of object-based and pixel-based Random Forest algorithm for wetland vegetation mapping using high spatial resolution GF-1 and SAR data. Ecol. Indic. 2017, 73, 105–117. [Google Scholar] [CrossRef]
- Minh, D.H.T.; Ndikumana, E.; Vieilledent, G.; McKey, D.; Baghdadi, N. Potential value of combining ALOS PALSAR and Landsat-derived tree cover data for forest biomass retrieval in Madagascar. Remote Sens. Environ. 2018, 213, 206–214. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Diao, C. Synergistic retrieval model of forest biomass using the integration of optical and microwave remote sensing. J. Appl. Remote Sens. 2015, 9, 096069. [Google Scholar] [CrossRef]
- Li, L.; Zhou, X.; Chen, L.; Chen, L.; Zhang, Y.; Liu, Y. Estimating urban vegetation biomass from Sentinel-2A image data. Forests 2020, 11, 125. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E. Estimating forest attribute parameters for small areas using nearest neighbors techniques. For. Ecol. Manag. 2012, 272, 3–12. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Quegan, S.; Carreiras, J.; Persson, H.J.; Fransson, J.E.; Hoscilo, A.; Ziółkowski, D.; Stereńczak, K.; Lohberger, S.; Stängel, M. Forest biomass retrieval approaches from earth observation in different biomes. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 53–68. [Google Scholar] [CrossRef]
- Tian, X.; Yan, M.; van der Tol, C.; Li, Z.; Su, Z.; Chen, E.; Li, X.; Li, L.; Wang, X.; Pan, X. Modeling forest above-ground biomass dynamics using multi-source data and incorporated models: A case study over the qilian mountains. Agric. For. Meteorol. 2017, 246, 1–14. [Google Scholar] [CrossRef]
- Mas, J.; Flores, J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Szantoi, Z.; Escobedo, F.J.; Abd-Elrahman, A.; Pearlstine, L.; Dewitt, B.; Smith, S. Classifying spatially heterogeneous wetland communities using machine learning algorithms and spectral and textural features. Environ. Monit. Assess. 2015, 187, 262. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- KopeĿ, D.; Michalska-Hejduk, D.; Berezowski, T.; Borowski, M.; Rosadziſski, S.; Chormaſski, J. Application of multisensoral remote sensing data in the mapping of alkaline fens Natura 2000 habitat. Ecol. Indic. 2016, 70, 196–208. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Wan, R.; Wang, P.; Wang, X.; Yao, X.; Dai, X. Mapping aboveground biomass of four typical vegetation types in the Poyang Lake wetlands based on random forest modelling and landsat images. Front. Plant Sci. 2019, 10, 1281. [Google Scholar] [CrossRef]
- Zeng, N.; Ren, X.; He, H.; Zhang, L.; Zhao, D.; Ge, R.; Li, P.; Niu, Z. Estimating grassland aboveground biomass on the Tibetan Plateau using a random forest algorithm. Ecol. Indic. 2019, 102, 479–487. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A. Dynamic forest biomass carbon pools in China and their significance. J. Integr. Plant Biol. 2001, 43, 967–973. [Google Scholar]
- Fang, J.; Liu, G.; Xu, S. Biomass and net production of Forest vegetation in China. Acta Ecol. Sin. 1996, 16, 497–508. [Google Scholar]
- Ou, G.; Li, C.; Lv, Y.; Wei, A.; Xiong, H.; Xu, H.; Wang, G. Improving aboveground biomass estimation of Pinus densata forests in Yunnan using Landsat 8 imagery by incorporating age dummy variable and method comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W. Estimating forest stock volume in Hunan Province, China, by integrating in situ plot data, Sentinel-2 images, and linear and machine learning regression models. Remote Sens. 2020, 12, 186. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Liu, D. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. ISPRS J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Haralick, R. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Guitet, S.; Bailly, J.; Hérault, B.; Gond, V.; El Hajj, M.; Minh, D. Aboveground biomass mapping in French Guiana by combining remote sensing, forest inventories and environmental data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 502–514. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Wan, R.; Wang, P.; Wang, X.; Yao, X.; Dai, X. Modeling wetland aboveground biomass in the Poyang Lake National Nature Reserve using machine learning algorithms and Landsat-8 imagery. J. Appl. Remote Sens. 2018, 12, 046029. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, R.; Siqueira, P.; Hensley, S.; Bergen, K. Uncertainty of forest biomass estimates in north temperate forests due to allometry: Implications for remote sensing. Remote Sens. 2013, 5, 3007–3036. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Laurin, G.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Fleming, A.L.; Wang, G.; McRoberts, R.E. Comparison of methods toward multi-scale forest carbon mapping and spatial uncertainty analysis: Combining national forest inventory plot data and landsat TM images. Eur. J. For. Res. 2015, 134, 125–137. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Frazer, G.; Magnussen, S.; Wulder, M.; Niemann, K. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the influence of plot size and LiDAR density on forest structure attribute estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef] [Green Version]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]




| Forest Type | a | b | Sample Size (ind) | R2 |
|---|---|---|---|---|
| Picea, Abies | 0.4642 | 47.4990 | 13 | 0.98 |
| Hemlock, Cryptomeria, Keteleeria | 0.4158 | 41.3318 | 21 | 0.94 |
| Betula | 0.9644 | 0.8485 | 4 | 0.98 |
| Poplar | 0.4754 | 30.6034 | 10 | 0.93 |
| Camphor forest, Phoebe | 1.0357 | 8.0591 | 17 | 0.91 |
| Cunninghamia Lanceolata | 0.3999 | 22.5410 | 56 | 0.97 |
| Cypress | 0.6129 | 26.1451 | 11 | 0.98 |
| Quercus | 1.1453 | 8.5473 | 12 | 0.98 |
| Eucalyptus | 0.8873 | 4.5539 | 20 | 0.80 |
| Larix | 0.6096 | 33.8060 | 34 | 0.82 |
| Pinus armandii Franch | 0.5856 | 18.7435 | 9 | 0.91 |
| Pinus massoniana | 0.5034 | 20.547 | 52 | 0.87 |
| Chinese pine | 0.7554 | 5.0928 | 82 | 0.98 |
| Other pinus | 0.5168 | 33.2378 | 19 | 0.86 |
| Hard broadleaf forest | 1.1783 | 2.5585 | 17 | 0.95 |
| Soft broadleaf forest | 0.4754 | 30.603 | 16 | 0.92 |
| Coniferous and broadleaf mixed forest | 0.8136 | 18.466 | 10 | 0.99 |
| Sample Size (ind) | Min (t/ha) | Max(t/ha) | Mean(t/ha) | Median(t/ha) | Std(t/ha) | |
|---|---|---|---|---|---|---|
| Training | 260 | 12.33 | 205.54 | 72.57 | 78.75 | 28.21 |
| Testing | 66 | 9.23 | 153.20 | 71.57 | 67.57 | 29.72 |
| Total | 326 | 9.23 | 205.54 | 72.37 | 80.64 | 28.52 |
| Vegetation Indices | Formula |
|---|---|
| NDVI | |
| RVI | |
| EVI | |
| ARVI | |
| SAVI | |
| MSAVI | |
| OSAVI |
| Variables | Correlation Coefficients | Variables | Correlation Coefficients | Variables | Correlation Coefficients | Variables | Correlation Coefficients |
|---|---|---|---|---|---|---|---|
| NDVI | +0.674 ** | MSAVI | +0.544 ** | b4_3Mean | +0.387 ** | b3_3Cor | +0.209 ** |
| b1 | −0.647 ** | altitude | +0.544 ** | b4_5Mean | +0.383 ** | b4_7Hom | +0.193 ** |
| b3_3Mean | −0.615 ** | ARVI | +0.537 ** | b4_7Mean | +0.378 ** | b4_7Dis | −0.188 ** |
| b3 | −0.611 ** | b3_5Hom | +0.486 ** | b2 | −0.339 ** | VV | +0.188 ** |
| b3_5Mean | −0.602 ** | b3_7Hom | +0.485 ** | b3_3Con | −0.288 ** | b4_7Ent | −0.179 ** |
| b3_7Mean | −0.579 ** | b3_3Hom | +0.478 ** | b3_7Cor | −0.275 ** | b4_5Hom | +0.175 ** |
| b3_5SM | +0.566 ** | RVI | +0.441 ** | b3_7Var | −0.27 ** | b4_7Var | −0.173 ** |
| b3_3SM | +0.56 ** | EVI | +0.441 ** | b3_7Con | −0.26 ** | b4_5Dis | −0.168 ** |
| b3_5Ent | −0.56 ** | b3_3Dis | −0.416 ** | b3_5Con | −0.259 ** | b4_7Con | −0.168 ** |
| b3_7SM | +0.554 ** | OSAVI | +0.404 ** | VH | +0.24 ** | VV_3Mean | +0.163 ** |
| SAVI | +0.553 ** | b3_5Dis | −0.403 ** | b3_5Var | −0.235 ** | b4_3Hom | +0.152 ** |
| b3_7Ent | −0.551 ** | b3_7Dis | −0.402 ** | VH_3Mean | +0.218 ** | b4_5Con | −0.15 ** |
| b3_3Ent | −0.55 ** | b4 | +0.388 ** | b3_3Var | −0.211 ** | b4_7SM | +0.146 ** |
| Variables | Model | R2 | RMSE | MAE | ME |
|---|---|---|---|---|---|
| NDVI, b1, b3, b3_3Mean, b3_5Mean, b3_7Mean, altitude | SVM | 0.58 | 19.20 | 14.50 | 1.69 |
| RF | 0.65 | 17.51 | 13.93 | −0.98 | |
| BPNN | 0.48 | 21.33 | 15.74 | 2.34 | |
| NDVI, b1, b3, b3_3Mean, b3_5Mean, b3_7Mean | SVM | 0.53 | 20.40 | 14.92 | 2.22 |
| RF | 0.61 | 18.59 | 14.55 | −1.10 | |
| BPNN | 0.42 | 22.60 | 16.87 | 1.91 | |
| NDVI, ARVI, MSAVI, b1, b3 | SVM | 0.56 | 19.66 | 14.33 | 2.06 |
| RF | 0.61 | 18.58 | 14.36 | −1.22 | |
| BPNN | 0.37 | 23.60 | 17.47 | 5.75 | |
| NDVI, MSAVI, b3, b3_3Mean, b3_3Ent, altitude, VV_3Mean | SVM | 0.60 | 18.81 | 14.21 | 1.33 |
| RF | 0.67 | 17.16 | 13.15 | −0.38 | |
| BPNN | 0.46 | 21.83 | 16.26 | 4.61 | |
| NDVI, MSAVI, b3, b3_3Mean, b3_3Ent, altitude | SVM | 0.62 | 18.29 | 13.76 | 1.42 |
| RF | 0.70 | 16.37 | 12.81 | −0.24 | |
| BPNN | 0.51 | 20.79 | 15.51 | 3.56 | |
| NDVI, MSAVI, b3, b3_3Mean, altitude | SVM | 0.58 | 19.16 | 14.48 | 2.39 |
| RF | 0.68 | 16.83 | 13.31 | −0.50 | |
| BPNN | 0.48 | 21.45 | 15.85 | 3.22 | |
| NDVI, MSAVI, b3_3Mean, b3_3Ent, altitude | SVM | 0.66 | 18.03 | 13.65 | 1.60 |
| RF | 0.70 | 16.26 | 12.80 | −0.24 | |
| BPNN | 0.49 | 21.30 | 15.86 | 3.66 | |
| NDVI, MSAVI, b3_5Con, b3_5Dis, altitude | SVM | 0.61 | 18.34 | 14.09 | 0.04 |
| RF | 0.66 | 17.24 | 13.21 | 0.30 | |
| BPNN | 0.48 | 21.44 | 15.87 | 3.00 | |
| NDVI, MSAVI, b3_3Mean, b3_5Con, altitude | SVM | 0.58 | 19.18 | 14.23 | 2.24 |
| RF | 0.69 | 16.67 | 12.90 | 0.10 | |
| BPNN | 0.49 | 21.30 | 15.72 | 3.42 | |
| NDVI, MSAVI, b3_7Mean, b3_7Ent, altitude | SVM | 0.62 | 18.21 | 13.84 | 1.84 |
| RF | 0.66 | 17.44 | 13.70 | −0.49 | |
| BPNN | 0.47 | 21.61 | 16.09 | 4.61 | |
| …… | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Wan, R.; Li, B. Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China. Remote Sens. 2022, 14, 176. https://doi.org/10.3390/rs14010176
Han H, Wan R, Li B. Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China. Remote Sensing. 2022; 14(1):176. https://doi.org/10.3390/rs14010176
Chicago/Turabian StyleHan, Haoshuang, Rongrong Wan, and Bing Li. 2022. "Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China" Remote Sensing 14, no. 1: 176. https://doi.org/10.3390/rs14010176
APA StyleHan, H., Wan, R., & Li, B. (2022). Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China. Remote Sensing, 14(1), 176. https://doi.org/10.3390/rs14010176