Next Article in Journal
Instance Segmentation in Very High Resolution Remote Sensing Imagery Based on Hard-to-Segment Instance Learning and Boundary Shape Analysis
Previous Article in Journal
Suspected Seismo-Ionospheric Anomalies before Three Major Earthquakes Detected by GIMs and GPS TEC of Permanent Stations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 1
10.3390/rs14010022
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Validity of the AdMos, Advanced Sport Instruments, GNSS Sensor for Use in Alpine Skiing

by
Petter Andre Husevåg Jølstad
1,
Robert Cortas Reid
2,
Jon Glenn Omholt Gjevestad
3 and
Matthias Gilgien
1,2,4,*
1
Department of Physical Performance, Norwegian School of Sport Sciences, 0863 Oslo, Norway
2
Alpine Ski Team, Norwegian Ski Federation, 0855 Oslo, Norway
3
Faculty of Science and Technology, Norwegian University of Life Sciences, 1430 Ås, Norway
4
Center of Alpine Sports Biomechanics, Engadin Health and Innovation Foundation, 7503 Samedan, Switzerland
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(1), 22; https://doi.org/10.3390/rs14010022
Submission received: 10 November 2021 / Revised: 17 December 2021 / Accepted: 19 December 2021 / Published: 22 December 2021
(This article belongs to the Section Engineering Remote Sensing)
Browse Figures
Review Reports Versions Notes

Abstract

:
The AdMos receiver from Advanced Sport Instruments is a global navigation satellite system (GNSS) frequently used in alpine ski racing, with users from national and professional teams. Therefore, a validation was conducted for use of the AdMos in alpine skiing, using data from both recreational and competitive skiers. Athletes skied a total of 60 km in different measurement and skiing conditions, while carrying both an AdMos and a differential GNSS, which was used as the gold standard. From the GNSS position data, speed, acceleration, turn radius, trajectory incline and impulse were calculated as instantaneous and turn average measures for both GNSS systems and errors between the systems were calculated. The median and interquartile range (IQR) for the instantaneous errors were below 3.5 (3.5) m for horizontal plane position and below 7.0 (4.3) m for the 3D position. The median and IQR for instantaneous errors and turn average errors, respectively, were below 0.04 (0.24)/0.04 (0.16) m/s for speed, below 0.23 (1.06)/0.35 (0.63) m/s2 for acceleration, below 0.47 (5.65)/0.73 (5.3) m for turn radius, and below 0.043 (1.96)/0.42 (1.42) degrees for trajectory incline. The median and IQR for turn average impulse were 0.025 (0.099) BWs. The position error changed gradually and randomly over time, with low noise levels causing smooth trajectories of similar shape but spatially shifted from the true trajectory that allowed the position–time derivation of the performance parameters, and detection of turns with 3% median and 5% IQR error. The accuracy assessment revealed that (1) the error levels were comparable to other consumer-grade standalone GNSS units designed for sport; (2) the trajectories closely resembled the true trajectories but with a random shift that changed over time and had a low noise level; (3) there was a very low instantaneous speed error that may allow the detection of many performance aspects of skiing and other sports; and (4) there were larger instantaneous errors for the remaining performance parameters, which decreased substantially when averaged over a turn.

1. Introduction

In alpine ski racing, athletes travel from start to finish through a pre-defined course. An athlete’s performance is measured in time elapsed between start and finish, where time is a function of pathlength and speed [1,2,3]. Pathlength and speed are regulated by changes in the skier’s inertia (speed and direction). In turn, inertia is changed by the athlete’s interaction with the surroundings. The skier’s actions, including ski– and pole–snow friction forces, air drag force, snow reaction force and gravitational force [4,5,6,7], regulate speed and direction. Depending on the discipline’s course characteristics, the mean speed in male World Cup (WC) alpine ski racing ranges from 13 m/s in slalom (SL) to 26 m/s in downhill (DH) [8]. Throughout a course, however, speed varies with time as a function of turning and terrain incline [8,9,10]. In a giant slalom (GS) run, skiers change direction about 51 times and hence turn for 93% of the run time. In Super-G (SG), athletes change direction about 40 times and turn for 80% of the run time, and in DH athletes change direction for 55% of the run time [4]. Course length and altitude drop are on average 1.4 km/400 m in GS, 2.3 km/600 m in SG and 3.5 km/900 m in DH with mean terrain inclines of 18° (GS), 17° (SG), and 14° (DH) [8].
Given the dynamics, long courses, altitude drop and alpine conditions, the measurement of an athlete’s kinematics and kinetics is challenging. Historically, skier kinematics were typically captured using video-based photogrammetry [7,11,12,13,14]. Although a high level of accuracy can be obtained, video-based methods are limited to small sections of a run (a couple of turns) and can take months to process. Global navigation satellite system (GNSS) technology has the potential to revolutionize analysis methods in skiing, allowing skier kinematics to be measured over entire courses. However, implementing GNSS in alpine skiing is not without challenges: (1) mountain terrain and forests along courses limit the availability of satellite signals (blocking line-of-sight and signal multipath disturbances); (2) the high speed and frequent changes in orientation of the skier lead to continuous alterations in satellite signal availability and the multipath conditions change at a high time rate; (3) the snow surface has specific signal reflection characteristics; and (4) the large altitude differences lead to changes in GNSS signal propagation through the atmosphere.
Due to these challenges with GNSS measurements and the high accuracy demands in alpine skiing analytics, to date, scientific studies have mainly used differential GNSS (dGNSS)—also referred to as the real-time kinematic (RTK) method—where data from a stationary GNSS system (a so-called base station) are used to improve the GNSS measurements obtained on the athlete (the so-called rover). Using dGNSS measurements with geodetic high-end receivers has been shown to yield position accuracies to less than 10 cm in race-like applications in alpine skiing when the carrier phase ambiguities were fixed [15]. Due to the acceptable validity of position and position derivatives, dGNSS has been applied to measure instantaneous performance and kinematics [16,17,18,19,20,21,22,23], physical demands [4], external forces [4,5,24], the effect of equipment changes [14,17,25,26] and injury risk based on course design [8,9,10,25]. However, standalone GNSS, where only the data from a single GNSS receiver are used, provides position accuracy in the scale of meters (for high-end geodetic GNSS in standalone mode) [15] and is therefore sparsely applied in alpine skiing research. However, consumer-grade stand-alone GNSS systems are increasingly popular among practitioners since the information derived from these systems appears valuable, and since geodetic dGNSS systems are still expensive. Recently, consumer-grade receivers have been applied in scientific studies in both standalone [27,28,29,30] and differential modes [2]. To date, the consumer-grade receiver that is probably the most used in alpine skiing is the AdMos (Advanced Sport Instruments (ASI), Lausanne, Switzerland). The AdMos receiver consists of a standalone GNSS with an internal patch antenna and an inertial measurement unit (IMU). For training and performance analysis in alpine skiing, the GNSS position data are primarily used. Previous research has shown that GNSS position accuracy in dynamic alpine skiing applications can vary by up to one order of magnitude depending on the GNSS method that is applied. Three-dimensional position accuracy for kinematic carrier phase dGNSS solutions using geodetic receivers has been found to be better than 10 cm. If ambiguities could not be fixed, the position error of float solutions increased to about 1 m and for standalone solutions from a geodetic receiver, error increased to several meters [15]. Consumer-grade standalone receivers were not validated for alpine skiing, but for cross country skiing, which is also performed on snow but in less dynamic applications. Three-dimensional position error was found to be several meters and varied substantially over time for a receiver that could be considered comparable to the AdMos receiver (Catapult OptimEye S5). For the OptimEye receiver, speed—calculated as the position–time derivative—was found to have relatively small errors that allowed the assessment of speed between athletes in cross-country skiing. Given the large range in accuracies between different GNSS methods for dynamic applications, there is a need to validate and inform the user community on the possibilities and limitations of the most commonly used GNSS systems in specific sports and the parameter derivations that are relevant to specific sports. Therefore, the aim of this study was to validate the AdMos GNSS position output and skiing parameters that are derived from the GNSS position–time data to describe the dynamics of alpine skiing, such as speed, acceleration, turn radius, impulse and trajectory incline. The validation goes beyond the validation of position, since the GNSS position error characteristics have an impact on the sport-specific performance parameters, which in many cases are as important as position for the users’ applications.

2. Materials and Methods

2.1. Data Acquisition and Subjects

Three subjects were recruited for this study. Details of the subjects are presented in Table 1. All subjects gave informed written consent for participation in the study in accordance with the Declaration of Helsinki. The study was approved by the ethics committee of the Norwegian School of Sport Sciences and the Norwegian Social Science Data Services (NSD).
The data collection was split into two parts. In part one, data from competitive skiing was collected during two days of training with a European Cup skier on SG and GS courses at Juvass (Norway). The courses that were used for training were set by a coach for each training day in a different manner. In part two, data were collected in less dynamic, recreational skiing at four locations: two days at Innichen (Italy), and one day at Elsigenalp-Metsch (Switzerland), Norefjell (Norway) and Tryvann (Norway). The chosen locations spanned a variety of GNSS measurement conditions including differences in latitude, terrain orientation and GNSS signal obstruction, such as vegetation along the course.
For the data collection, no specific instructions were given to the subjects, other than that for competitive skiing the skier should conduct training as usual, and for the recreational skiing it should be treated as a leisure skiing day. The only difference for the participants in the study was that the GNSS system had to be attached to their backs prior to the session and removed afterwards.
Table 2 provides insight into the type and the number of skiing runs that were collected. A run was defined as a series of consecutive turns between the start and finish of the course for the competitive skiing sessions and freely chosen starts and stops along the slope by the recreational skiers. The slope inclines were similar for competitive and recreational skiing and on average they were 2–4 degrees flatter than terrain seen in WC competitions [8]. As expected, speeds and accelerations were lower in recreational skiing compared to competitive skiing, while the turn radii were quite similar, resembling GS and SG turns [25].

2.2. Materials

2.2.1. AdMos Receiver

The receiver tested was an AdMos (Advanced Sport Instruments (ASI), Lausanne, Switzerland) which is a small (weight: 35 g, size: 65 mm × 35 mm × 15 mm) consumer-grade sport tracking receiver consisting of GNSS, IMU and an air pressure sensor. The GNSS is connected to an antenna, which is integrated into the unit. The receiver can track the L1 signal from GPS, Galileo, GLONASS and BeiDou. The IMU and air pressure sensor are not integrated for positioning with GNSS in the sense of an inertial navigation system. Hence, we assessed the accuracy of a pure single frequency standalone consumer grade GNSS receiver. The data output rate for the GNSS is 10 Hz.
The AdMos receiver was attached on the upper back of the subject as recommended by the manufacturer (ASI). Fifteen minutes prior to the mounting of the receiver on the athlete, the receiver was turned on and placed outside in an open environment to make sure the receiver had lock on a satellite signal.

2.2.2. Ground Truth System

To provide ground truth measurements, a geodetic carrier phase differential global navigation satellite system (dGNSS) was used, which consisted of an antenna (G5Ant-2AT1, Antcom, Torrence, CA, USA) mounted on the skier’s helmet, and a GNSS receiver (Alpha-G3T Javad, San Jose, CA, USA), which was carried in a small backpack on the skier’s back. To enable differential position calculations a base station (receiver: Alpha-G3T Javad, San Jose, CA, USA; antenna: GrAnt-G3T, Javad, San Jose, CA, USA) was set up on a tripod close to where the skiing activity was conducted (0–3.5 km). Both the base station and the GNSS on the athlete tracked the GPS and GLONASS signal frequencies L1 and L2 with an output rate of 20 Hz. The ground truth receiver carried on the back was connected with a cable to the antenna attached on the helmet.
The distance from the antenna of the ground truth system (where the position of the ground truth system was measured) to the AdMos was approximately 45 ± 5 cm (three-dimensional distance), when the subjects stood in an upright position, and smaller when in a typical skiing or tuck position. Hence, the accuracy of the ground truth system with respect to the AdMos validation is the accuracy of the dGNSS when used in carrier phase differential mode with fixed ambiguities (5–10 cm) and the offset of the dGNSS ground truth system antenna to the AdMos receiver (when skiing < 45cm), a total three-dimensional distance < 0.5m. This position accuracy was sufficient since the system to be validated (AdMos) was expected to have an error that was typically one order of magnitude larger [31]. Signal analysis and parameter calculation were conducted in MATLAB R2020b (The MathWorks, Natick, MA, USA). GraphPad Prism 8 (Graph Pad Software, La Jolla, CA, USA) was used to check the data for normal distribution, measures of probability distribution and linear regression.

2.3. Data Processing

2.3.1. GNSS Processing

The ground truth system data were downloaded from the base station and rover post session, and carrier phase differential solutions were calculated using the geodetic software Justin (Javad, San Jose, CA, USA) using GLONASS and GPS L1/L2 signals. The baseline between base station and rover varied between 0 and 3.5 km for Innichen, 0–2.5 km for Elsigen–Metsch, 0–1 km for Juvass, 0–1.5 km for Tryvann and 0–3 km for Norefjell. Raw position data were filtered with a second order cubic spline filter where ambiguity status and accuracy estimates for each epoch were applied as weights in the filter [32]. From the filtered data, only epochs where the carrier phase ambiguities could be fixed were used as ground truth data to assess the accuracy of the AdMos receiver. Epochs with float solutions were discarded from the accuracy assessment (12% of the relevant data).
The GNSS processing for the AdMos was per standard procedure conducted on the receiver in real time and stored locally. The processed data were downloaded from the receiver post session and used as raw data in the accuracy assessment. Position data from both GNSS systems were transformed from WGS84 to UTM32 (Universal Transverse Mercator) coordinates.

2.3.2. Data Inclusion

GNSS data were collected from before the skiing sessions started until after the skiing sessions ended. The time periods in the datasets where skiers actually skied had to be extracted and distinguished from periods when the skiers spent time in the lift and were waiting before starting and after finishing. The algorithm that identified the time periods when skiers actually skied was based on the criteria that the skier’s vertical position dropped in altitude while speed measured with the AdMos exceeded 2 m/s. The end point of a run was defined as being when the speed decreased below 1 m/s. All the speed thresholds were chosen based on empirical tests. Runs shorter than 15 s were excluded from the analysis. Epochs with GNSS carrier phase ambiguity float solutions of the ground truth system were excluded from the analysis (12%) and a total of 105 846 GNSS epochs were used for the assessment of accuracy of the AdMos unit.

2.3.3. Calculation of Skiing Characteristics

The AdMos raw data were upsampled from 10 to 20 Hz (to the same data rate as the ground truth system), since parameters based on time derivatives (e.g., velocity and acceleration) in alpine skiing typically require a higher data rate than 10 Hz due to rapid changes in inertia. This is especially the case for the technical disciplines. Upsampling of the AdMos data from 10 to 20 Hz was conducted using second order cubic spline functions, since it has been demonstrated that cubic spline functions are suitable to interpolate alpine skiing position data [32]. To characterize the dynamics of the skiing, the following parameters were calculated from the position–time data (each skiing characteristic parameter was calculated with the same algorithm using the ground truth and the AdMos data). Speed (v) and resultant acceleration (a) were calculated as time derivatives of position using the 4 and 5 point finite central difference formulae (v: 4 point, a: 5 point) [33]. The instantaneous turn radius (turn radius) of position x at time point t (xt) was calculated in two dimensions as the radius of a circle fitting the GNSS positions {xt−3, xt, xt+3} [7]. Trajectory incline angle with respect to the horizontal plane (slope) was calculated between the instantaneous velocity vector (v) and the horizontal plane (represented by the gravity vector (g) as the surface normal of the horizontal plane (Equation (1)) [8].
α = π 2 − cos − 1 | v → · g → | v → | | g → | |
To approximate the physical load on skiers due to the sum of the external forces acting on them, the instantaneous resultant acceleration (a) was time integrated over the time of entire runs and called impulse/run [4,25]. To detect and allow splitting of the data into turns, the start and end of a turn were calculated as the deflection points between two turns. For that purpose, the velocity vector (v) was projected onto the horizontal plane and the angular velocity was calculated based on the projected velocity vector. The deflection points were then calculated for both systems as the time points at which the sign of the angular velocity switched [8] and turns were detected and split based on these deflection points. The number of turns for entire runs were calculated based on the turn’s start and end points. Skiing characteristics parameters were also calculated as averaged by turns. To be able to compare the AdMos with the ground truth system, the parameters calculated as mean for each turn used the deflection timepoints found with the ground truth system, ensuring that the same turns and time periods were compared. For these parameters only the part of the turn where the radius was below 125 m was used, as proposed in earlier studies [4,25].
Prior to parameter calculations, data from the AdMos and ground truth systems were filtered using a second order Butterworth low-pass filter in both forward and reverse directions. Position was filtered with a 5 Hz cut-off filter. After the position derivation of speed and acceleration, speed was filtered with a 5 Hz cut-off frequency. Acceleration and trajectory incline were filtered with a 3 Hz cut-off frequency. Radius was filtered with a 5 Hz cut-off frequency. The filter cut-off frequencies were based on empirical testing of the AdMos and based on one decade of user experience and sensitivity analysis with the ground truth system [34].

2.3.4. Accuracy Assessment

For the accuracy assessment only epochs for which the carrier phase ambiguities were fixed on the ground truth system [15] were used. To compare position and skiing characteristics parameter data between AdMos and the ground truth system, data were time synchronized using the receivers’ GPS times. Position and parameter data were time interpolated between the systems on the GPS time scale using cubic spline functions for position and parameter data. The positional error was calculated as the Euclidean distance between the position measured with the AdMos minus the position measured with the ground truth system in the horizontal plane (ΔXY) and in three dimensions (ΔXYZ). For the parameters of speed (Δ|v|), acceleration (Δ|a|), trajectory incline (ΔIncline) and turn radius (ΔTurn radius), the error was calculated as the parameter scalar of the AdMos minus the parameter scalar from the ground truth system. For number of turns per run and impulses per run, the error was calculated accordingly as the AdMos value minus the ground truth value.

2.3.5. Statistics

For position and skiing characteristics, median, interquartile range (IQR), 90th percentile and maximal error (Δmax) were calculated for the error between the ground truth system and the AdMos. Normal distribution, measures of probability distribution and linear regression analysis were conducted using GraphPad Prism 8 (Graph Pad Software, La Jolla, USA). Histograms were plotted to visualize the distribution of the parameter error. Bland Altman plots were created to assess the speed (Δ|v|) and acceleration (Δ|a|) dependency of the errors. The horizontal plane and three-dimensional position error were assessed for speed dependency with a regression model. Tests investigated whether the slope was significantly different from zero at the 5% significance level.

3. Results

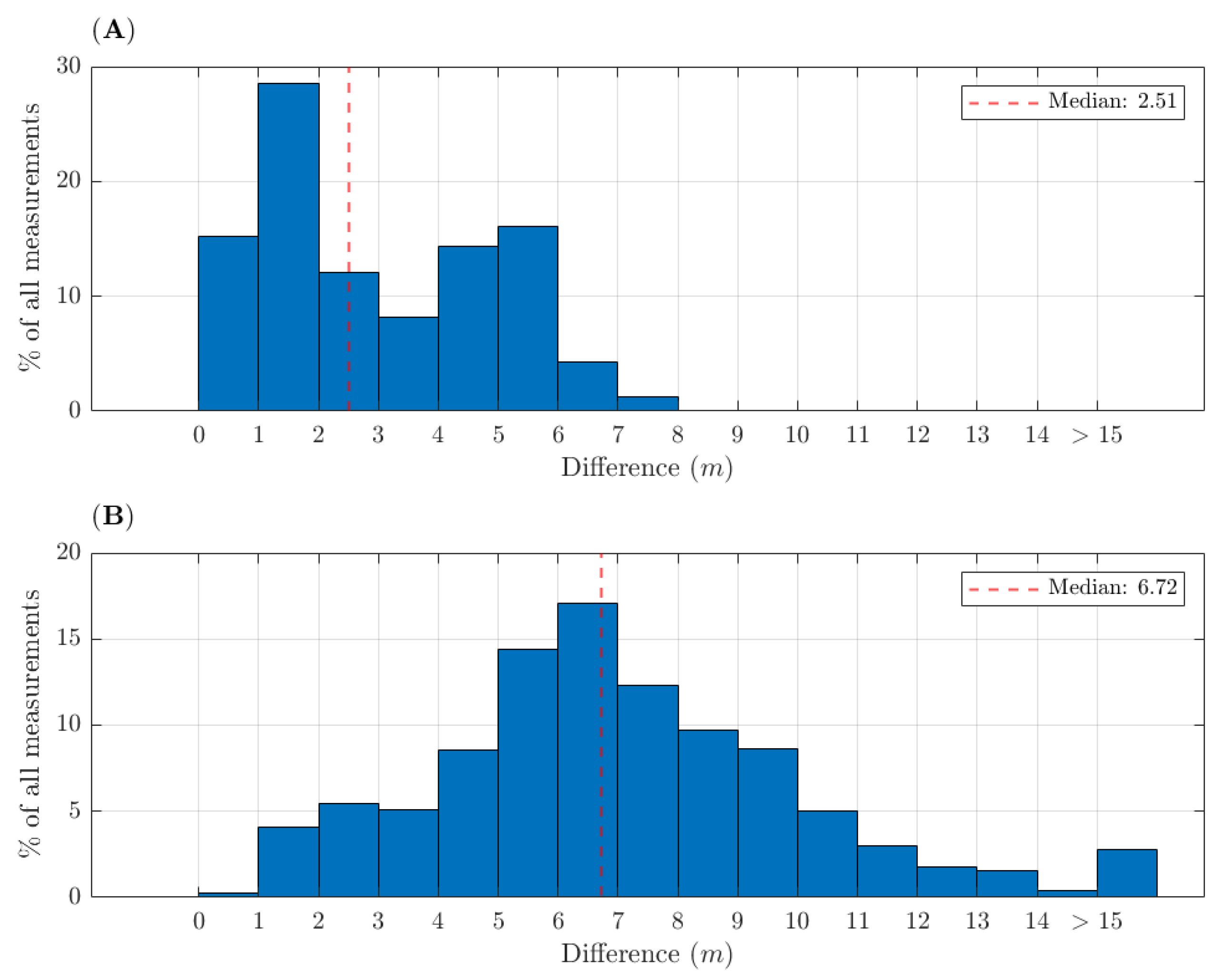
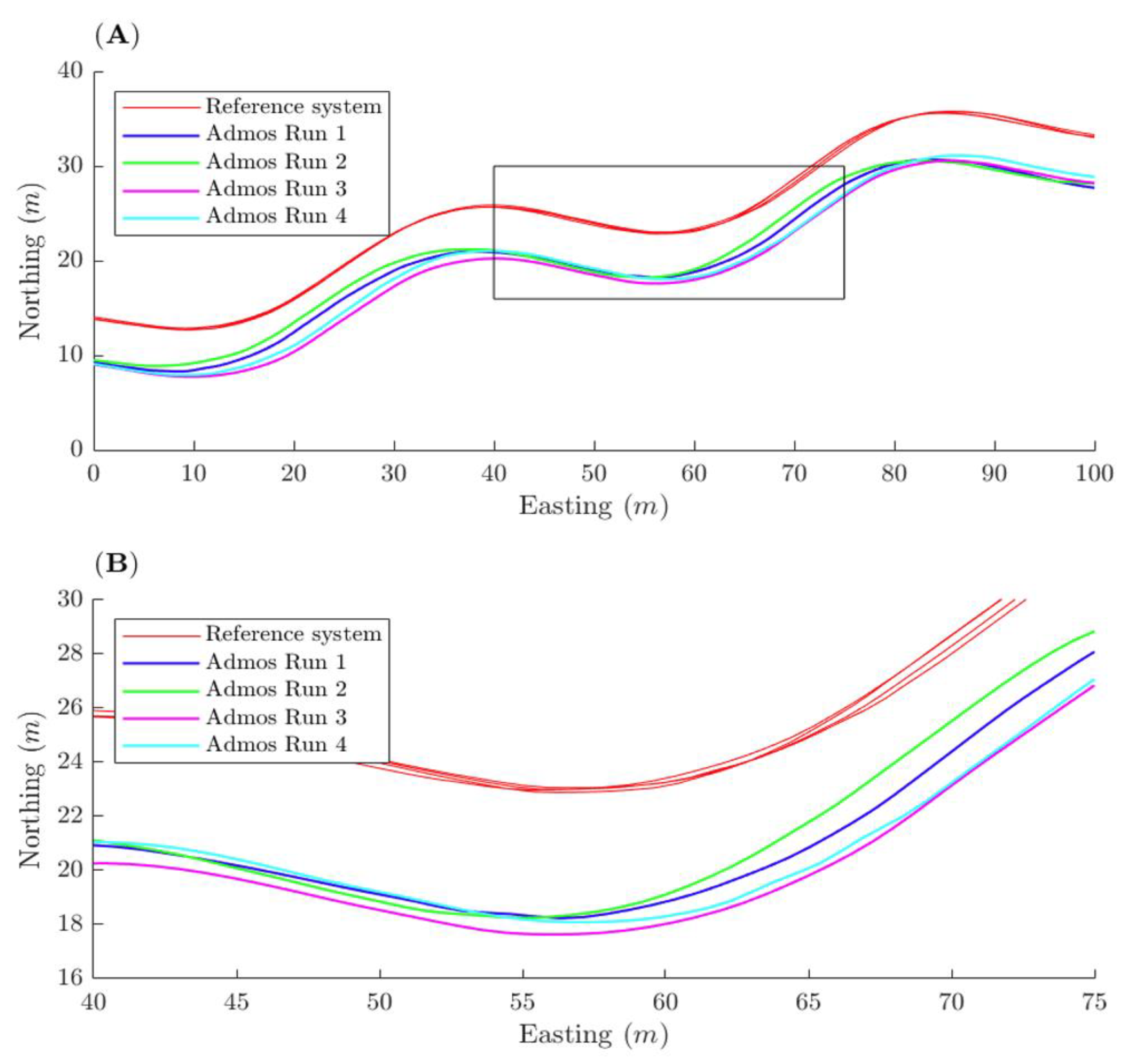
Position Errors

The results for position errors (ΔXY and ΔXYZ) are summarized in Table 3 and presented in histograms in Figure 1. The 3D position errors (ΔXYZ) were relatively large with a median of about 7 m and IQR of about 3 m. For the horizontal plane components (ΔXY) the position error was reduced to about 3 m median and 3 m IQR. Variability increased for recreational skiing, where the skiers were exposed to a larger variability in GNSS measurement conditions, compared to the competitive skiing conditions.
A small speed dependency was found for horizontal plane and 3D position error (horizontal position error (ΔXY) in competitive skiing (ΔXY = −0.03041·v + 3.771, R2 = 0.012, p < 0.001) and recreational skiing (ΔXY = 0.009486·v + 2.703, R2 = 0.000, p < 0.001), and for position error in three dimensions (ΔXYZ) in competitive skiing (ΔXYZ = 0.06622·v + 5.539, R2 = 0.051, p < 0.001) and recreational skiing (ΔXYZ = 0.09397·v + 6.715, R2 = 0.004, p < 0.001)).
Instantaneous skiing characteristics errors are summarized in Table 4 and shown in Figure 2 and Figure 3. Speed (Δ|v|) was the most valid parameter with a median overestimation of 0.1% for competitive skiing and 0.3% for recreational skiing. It had low 90th percentiles that were between −0.23 and + 0.39 m/s which are visualized in Figure 2A. Figure 3A indicates no speed dependency for the error in speed. Similar to speed, incline (ΔIncline) also shows a small median overestimation for both competitive skiing (0.3%) and recreational skiing (0.2%), but in contrast showed a substantially larger variability with 90th percentile of between −4.15 and 4.94 degrees visualized in Figure 2A,C and large maximal error. Turn radius (ΔTurn radius) had a slight underestimation (median) in competitive skiing (−0.4%) and recreational skiing (−2.3%), and a large variability with 90th percentiles of several decameters) which is visualized in Figure 2D. Acceleration error showed a small overestimation for the median (competitive skiing: 2.5%, recreational skiing: 4.3%) and large variability for both competitive skiing with 90th percentiles between −0.94 and 1.90 m/s2. Figure 3B indicates no dependency of the acceleration error on the size of acceleration.
Table 5 shows the errors for skiing characteristics for averaged turn averages within all turns from when the turn radius dropped below 125 m to when it exceeded 125 m. Turn average errors were generally smaller than their corresponding instantaneous errors (Table 4 and Figure 4). The turn average error was about half of the corresponding instantaneous error. All turn median errors were below 5% and most of them well below. Recreational skiing showed larger median errors for all parameters except for incline (ΔIncline/Turn). The smallest median, IQR and maximal errors were found for speed. Maximal errors were large for all parameters except for speed.
The detection of number of turns per run and impulse per run is summarized in Table 6. The number of turns showed a small overestimation in recreational skiing (median: 2.7%) and no median error for competitive skiing. The variability was higher for competitive skiing (IQR: 11%) than for recreational skiing (IQR: 5.4%). Impulse for the entire run showed a small median overestimation (competitive skiing: 0.3%, recreational skiing: 1.5%) and low variability (competitive skiing: 0.3%, recreational skiing: 2.1%).

4. Discussion

The aim of this study was to validate the accuracy of the position and skiing characteristics parameters describing alpine skiing for data from the AdMos GNSS output. This study found: (1) substantial position errors in the horizontal plane (ΔXY) and position errors in three dimensions (ΔXYZ); (2) median errors and variability for instantaneous speed (Δ|v|) that are small enough to make the system usable for several applications; and (3) median errors and variability for instantaneous acceleration (Δ|a|), instantaneous incline (ΔIncline) and instantaneous turn radius (ΔTurn radius) that imply they can be used with caution for specific applications. When the instantaneous parameters were averaged over turns, the median and variability of the above parameters dropped substantially. Median error and variability for impulse dropped further when averaged over runs (ΔImpulse/run).

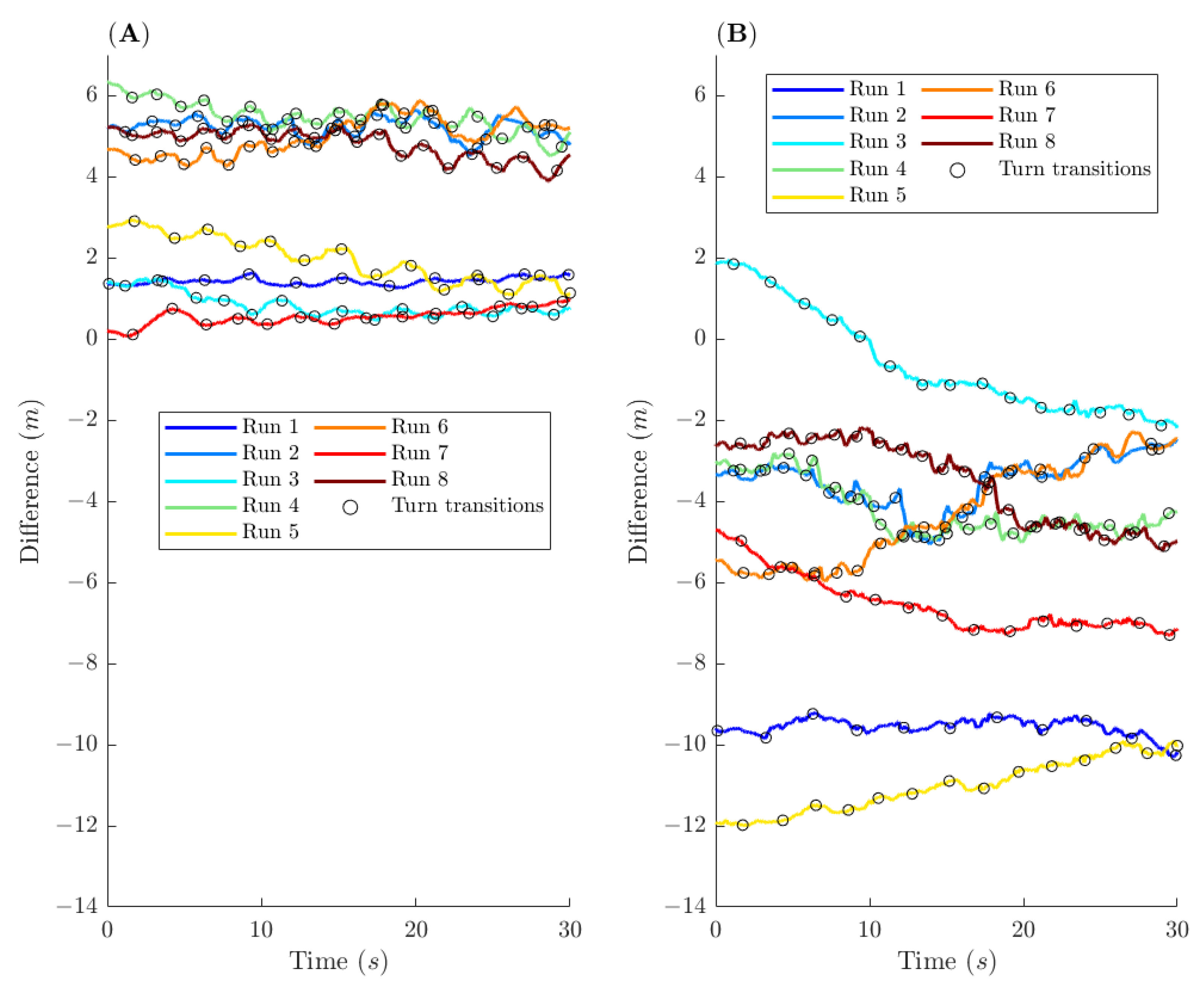
4.1. Position Errors

The position errors (ΔXY and ΔXYZ) found in this study for alpine skiing were comparable to findings from other validation studies where comparable receivers to the AdMos were used in other sports [31]. However, the position errors were substantially larger than those found for a geodetic high-end receiver measuring in standalone mode in comparable skiing conditions to the present study [15], illustrating the difference between geodetic high-end receivers and consumer-grade/affordable receivers. In accordance with the findings in other studies, the vertical component, as a consequence of satellite measurement geometry, caused the largest part of the three-dimensional position error (ΔXYZ) (Table 3) for the AdMos receiver. The position errors for recreational and competitive skiing errors were comparable, with the main difference being the smaller median position error in the horizontal plane (ΔXY) for recreational skiing. Very small speed dependency of position errors (ΔXY and ΔXYZ) was found for recreational and competitive skiing, where the speed ranged from 0 to 26 m/s (Figure 3A), with speed only explaining 0–5% of the error. Larger dependencies have been found in sport tracking with local positioning systems, where speed dependencies have been observed for a much smaller range of speed and order of magnitude smaller measurement areas [35].
To provide a broader understanding of the position error characteristics, Figure 5 and Figure 6 show data from competitive skiing in Juvass, Norway, where the skier skied repetitively through the same course from the start, around the gates to the finish. Figure 5 shows four consecutive runs on the same course with the trajectories of the ground truth system in red and the trajectories of the same runs measured with the AdMos in another color from a bird’s-eye perspective. The trajectories of the ground truth GNSS system in red show the true position and range of position error between runs with a range of decimeters. Compared to these, the AdMos trajectories (in colors) show an offset and continuous drift over time within each run compared to the ground truth trajectories. However, the shape of the AdMos trajectories and the drift over time appear to be quite smooth, which might explain the small percentage error in the first position derivatives (speed and turn radius).
The position error characteristics of the AdMos are further assessed in Figure 6, with position error in the horizontal plane (ΔXY) in Figure 6A and position error in the vertical direction (with gravity) in Figure 6B. The data represent the position errors for the competitive skiing dataset at Juvass, Norway. Each line represents the first 30 s of a total of 8 runs. The horizontal axis (time) zero point represents the start of the runs. The vertical axis shows the position error for each run. After the run, skiers skied down to the lift, went back to the start using the ski lift and started the next run about 15 min after the previous run. Hence, individual runs are time spaced by about 15 min. It appears from the graph that the global offset in the vertical direction and the horizontal plane drifted gradually over time between the runs in all dimensions. Each time the skier started from the same start location the position error had drifted several meters since the last start that was executed approximately 15 min earlier, and kept drifting during the run. This type of position offset drift over time was also observed for standalone GNSS measurements in sport applications for measurements taken at the same location but at different times during the day [31].
The global offset and drift over time may set some limitations on the validity of position applications, such as GNSS-based time difference analyses between athletes [16] or location-based comparison of mechanical characteristics of skiers [14,17]. However, it has been shown in cross-country skiing that projection of the standalone GNSS position on a true average trajectory, measured with a differential GNSS method, efficiently removes position error in the cross-track direction, which improves the GNSS-based time analysis to a sufficient level of accuracy [31]. An earlier study showed that the drifting position offset can be reduced if periodically available anchor points are used to globally shift the trajectory [27]. Figure 6A illustrates the characteristics of position error in the horizontal plane (ΔXY). The circles marked on the trajectories indicate the deflection points between turns and it appears that there is a type of cyclic change in the size of the position error in the horizontal plane (ΔXY) which is not, or is to a reduced degree, apparent in the vertical error component (Figure 6B). It is therefore likely that the cyclic change in position error in the horizontal plane (ΔXY) is related to the change in skier inertia in the plane along the snow surface and hence mainly causes artefacts in the position error in the horizontal plane (ΔXY).

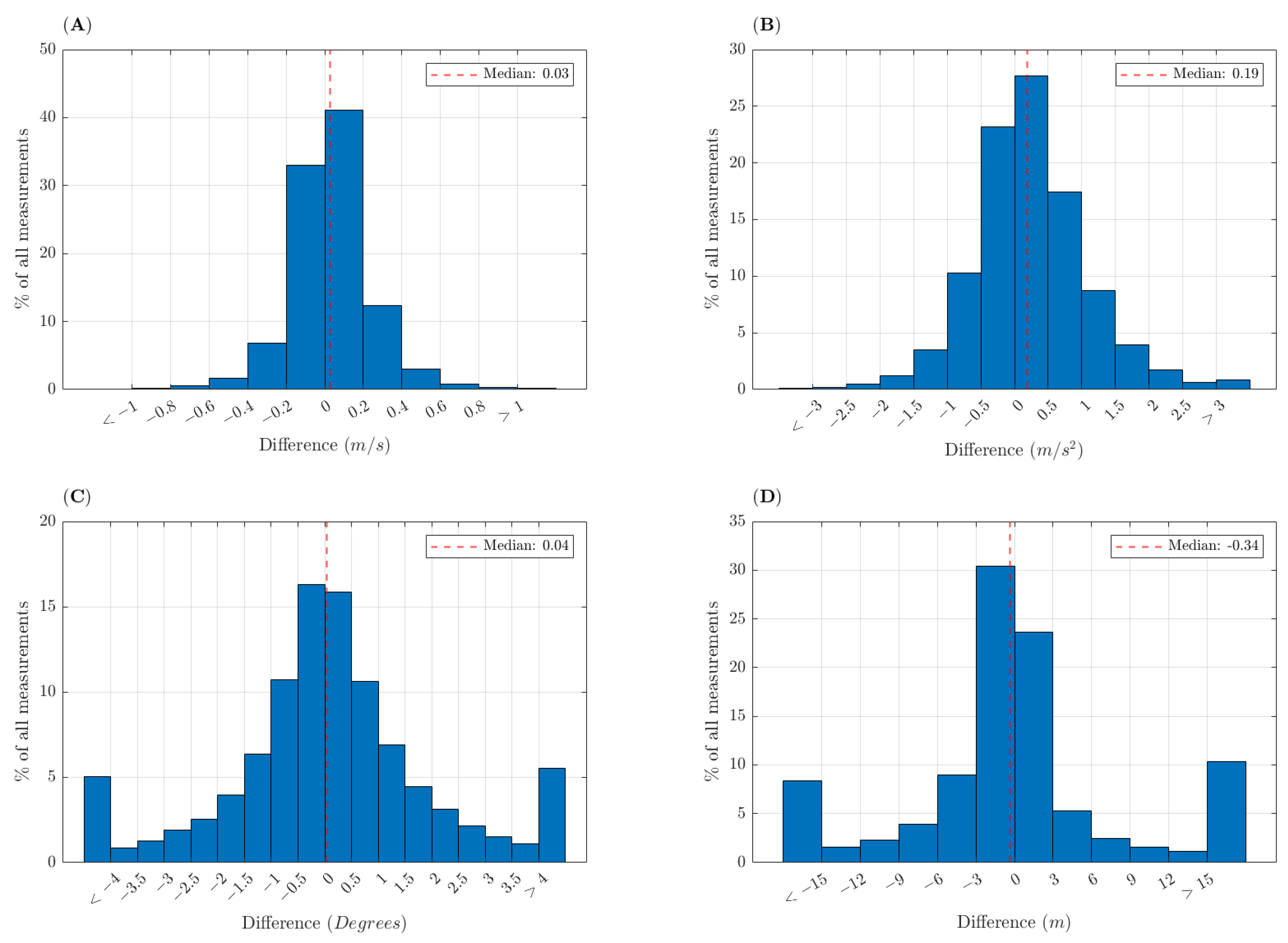
4.2. Error of Instantaneous Skiing Characteristics

In alpine skiing, speed is applied not only as a performance parameter [36] but also as a parameter related to injury risk [25,37]. The findings of the current study show that the instantaneous error in speed ranges typically from −0.3 to +0.3 m/s and differences larger than these can normally be detected. The discriminative power of the speed allows the detection of changes in turn exit speed as a function of substantial changes in course setting [9,10,11,29] and differences in turn entrance speed between high and low performing European Cup skiers [3]. Only 6.7% of the total dataset (Figure 2) had instantaneous speed errors (Δ|v|) larger than 0.4 m/s. Hence, instantaneous speed measurement as position–time derivatives, post-treated with a common 5 Hz cut-off frequency Butterworth low pass filter, obtained from AdMos position measurements, have basically good discriminative power for alpine skiing applications. However, some applications may require instantaneous measures of speed, and accuracy could probably be stabilized for most applications with additional or stronger filtering of speed, probably in the sense of a short moving average or median filter.
Good speed accuracy (Δ|v|) seems to be an effect of the AdMos internal GNSS filtering and data processing, which provides smooth trajectories with good correspondence between neighboring datapoints. This filtering seems to provide good first position derivatives but may cause drift artifacts in the global position, as were found in this study.
In alpine skiing, acceleration and force measurements are primarily undertaken to study their effect on performance, to quantify the physical demands and, connected to that, the potential injury risk due to the large forces. For measurement of the latter, inertial measurement units and force transducers are frequently used to directly measure acceleration and force in the athlete’s body frame [21,30,38,39,40]. However, storage and eventually wireless transmission of IMU data requires storage and bandwidth and therefore acceleration in this case was also derived from the dGNSS position–time data and assessed against the ground truth. When acceleration is derived from dGNSS position–time data, the accuracy of the position measurements allows expression of the resultant force, and if aerodynamic force models are applied, also its components (gravity, air drag and ski-snow friction) as vectors relative to the velocity vector and gravity [4,5,9,10,24,25]. Initial assessment of the AdMos sensor showed that the direction of the resultant acceleration and velocity vectors was not sufficiently valid for such decompositions. Instead, we validated the norm of the resultant acceleration vector. The results of the current study show that the derivation of acceleration vectors from standalone consumer-grade GNSS units (including the AdMos) position measures is not recommended due to the magnitude of error (Δ|a|). The IQR of ≈20% and maximal error of 100% for acceleration (Δ|a|) is larger than the difference of the maximal turn forces between the disciplines GS, SG and DH [25]. Hence, it is unlikely that an instantaneous acceleration norm derived from a GNSS position–time measurement from a standalone AdMos is sufficiently accurate to distinguish between skiers or equipment within the same skiing disciplines [14,25,41]. The size of the acceleration error (Δ|a|) does not allow the assessment of skiers’ kinetic laterality [42] or the effects of adjustment in course settings [9,10,43]. Hence, for instantaneous measurement of acceleration it might be better to use the IMU integrated in the AdMos.
If the resultant acceleration, calculated as GNSS position–time derivatives, is integrated over entire runs (mean ± SD: 60.6 ± 29.0 s) the accuracy can be improved to ≈2% and can be used to describe the physical load on athletes.
Trajectory incline (ΔIncline) and turn radius (ΔTurn radius) showed small median error, large variability (IQR and 90th percentile) and very large maximal errors. Since the variability and maximal error are very large, the use of these parameters for instantaneous measurements is not recommended.

4.3. Error for Turn-Average Skiing Characteristics, and for Number of Turns and Impulse per Run

The errors for the skiing characteristics parameters were much smaller when averaged over turns than the corresponding instantaneous errors. Whether or not turn average values are accurate enough to assess differences between athletes, equipment or external conditions, the respective accuracies need to be matched with the expected differences between athletes, equipment or conditions. Comparing the given skiing characteristics calculations found in this study, the AdMos receiver was adequate to distinguish turn characteristics between the disciplines GS, SG and DH with respect to speed, turn radius and impulse [25]. Average turn speed differences could also be detected between skiers from different age classes [29]. In addition, speed differences could be detected that were caused by the use of substantially different skis (35 m sidecut turn radius versus 40 m radius) for the same athletes on the same course in GS [14]. Speed differences in sharp DH turns were also detectable between DH skis with different geometries for the same skier [17].
For skiing with skis of different sidecut radius on a given GS course, the average skied turn radius changed by 11.9% when skiers switched from skis with a 35 m sidecut turn radius to a pair with a 40 m radius [14]. Such a change is unlikely to be detected with the AdMos and the suggested method for turn radius calculation. The true turn radius fluctuates much more per unit of time than the trajectory incline, especially in turn transitions when the turn radius approaches infinity. Hence the turn radius calculation method may have a substantial impact on the turn radius measure. Switching from GS skis with 35 m to 40 m sidecut radius caused a <5% change in average turn force in a GS race simulation, which is at the limit of detection with the AdMos if acceleration is derived from the GNSS position [44]. The trajectory incline error (ΔIncline) was substantially reduced when averaged over one turn and was small enough to enable description of the incline of the course as a description of terrain characteristic [8]. The turn average error for impulse (ΔImpulse) lacked a reference value from the literature and hence its applicability is unclear. The start and end of the turn were not defined at the deflection points but at the point where the turn radius was smaller than 125 m. Since the turn radius is part of the definition of the turn, the turn radius error has an effect on the time point where a turn starts and ends, and has an impact on the errors found in this study. This has a particular effect on impulse, where the values measured during a turn are not averaged but summed. Hence an offset in the turn start and end has a larger effect on the error in impulse/turn than on the other parameters. For the calculation of the impulse for an entire run, such delimitation aspects only apply to the run start, which may be the main reason for the percentagewise smaller errors than for the impulse/turn. The error in the detection of single turns was very small; hence the method can easily be used to detect turns and the number of turns in a run.
All turn median errors were smaller than 5%, while the 90th percentile errors were still substantial for acceleration (Δ|a|) and turn radius (ΔTurn radius). Hence, for these parameters, repetitive measures of the same turns executed in repetitive runs on the same course may be needed to reduce the uncertainty in single turn average values.
Recreational skiing showed larger median errors for all parameters except for incline (ΔIncline/Turn). The larger errors in recreational skiing may be caused by the greater variety in GNSS measurement conditions in the dataset for recreational skiing, which included a large variety in slope exposure, vegetation (forest) along the course and time points of measurement. The differences in error characteristics between recreational skiing and competitive skiing were small enough that the results found in this study can be regarded as representative for use in both types of alpine skiing.

4.4. Transfer of the Findings of This Study to Other Sports

The validity determined in this study was derived for alpine skiing but may have good transfer to other racing sports that are held in relatively open areas and are performed with comparable inertia (speed, and rate of change of direction). For rapid changes in direction and speed, such as in team sports, the applied filter methods may affect the position and its derivatives differently than for motions with relatively gradual changes in inertia, such as alpine skiing or endurance/racing sports. Hence for team sports, the results of this study should be applied with some caution, but for racing sports such as cycling, running, and cross-country skiing in open areas, the results may apply well, especially since no speed dependency of the error was found. Some skiing characteristic parameters are quite specific for alpine skiing, but speed, turn radius, acceleration and impulse are also very relevant for other sports. As an example, the discriminative power of speed measurement using the AdMos is sufficient to distinguish speed differences for the same skier in uphill sections of consecutive laps during a cross-country skiing race [45]. Skiers typically decrease their speed from lap to lap (positive pacing) and speed differs most in uphill sections, where resistance (due to gravity) is highest. This may also apply to other sports such as cycling and running. The discriminative power is also sufficient to detect uphill speed differences between athletes of different performance levels [46].

4.5. Limitations

This study only included data from recreational skiing, GS and SG. Further studies are therefore recommended to determine measurement validity in SL and DH, especially since the peak forces measured in SL are higher than in the other disciplines. The extension should also include alternative approaches for parameter calculations and data filtering, since these likely have an impact on the accuracy outcomes. The parameter calculations used in this study, both for the ground truth and the AdMos, were developed for use with position data from high-end geodetic receivers. It is therefore possible that different filtering and processing methods would result in more valid data from AdMos position measurements than the ones presented in this study.
Since one of the inclusion criteria for the GNSS data was for the ground truth system to have fixed ambiguities, only data from these measurement conditions were included in the analysis. It is therefore important to analyze how the AdMos receiver handles more challenging measurement conditions. The total dataset may be quite representative for alpine skiing since it covered variety in latitude for the five locations where the measurements were taken (Central Europe and Scandinavia, but not the Southern Hemisphere); variety in signal masking through mountainous terrain and its exposure including south, east, west and north faces; variety in vegetation along the course (open field, open and dense forest); and variety in GNSS conditions during vertical transportation between runs. We therefore assume that the findings of this study are reasonably representative.
The ground truth system is not a truly independent measurement system since both the ground truth and the AdMos use, to a large extent, the same measurement data, methods, and principles, but dGNSS is the most suitable and valid method to track alpine skiing over large distances. An appropriate improvement of the ground truth system would be the use of an inertial navigation system, including dGNSS for the GNSS part.
The antenna placement of the units results in a 30–60 cm position error between the AdMos and the ground truth system. The instantaneous distance between the receivers is unknown and not represented in the results. No correction of that offset was conducted since the size of the position error of the AdMos is one order of magnitude larger than the error of the ground truth system [15,24,47]. With respect to the position derivatives that are functions of change in position, the validation studies assessing the accuracy of the ground truth system applied in this study show that athlete motion is well transferred between center of mass, upper body and head in the time and amplitude domain [24,34,48] and the accuracy of the ground truth system is sufficient to assess a standalone consumer-grade GNSS along with other validation studies where the current ground truth system was applied [31].

5. Conclusions

The AdMos receiver showed substantial errors in position (ΔXY and ΔXYZ), but small median error and small variability for speed calculated as position–time derivatives, due to a smooth trajectory. Small median errors but large variability were found for acceleration, turn radius and trajectory incline. It is suggested that the use of these parameters for instantaneous measurements should be avoided, but they can be useful as turn averages since the errors are reduced substantially when averaged over time. Impulse per run as a measure of load, and the number of turns per run, are valid and can be trusted. Since no speed dependency of errors was found, the validity of the AdMos GNSS sensor may apply also for other racing sports that are held in relatively open areas with good GNSS measurement conditions, such as cycling, running and cross-country skiing.

Author Contributions

P.A.H.J., R.C.R., J.G.O.G. and M.G. designed the study; P.A.H.J. and M.G. conducted the data collection; M.G. and P.A.H.J. conducted the data analysis; P.A.H.J., R.C.R., J.G.O.G. and M.G. wrote and approved the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the institutional ethics committee at the Norwegian School of Sport Sciences.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Subjects did not provide consent to make their skiing data publicly available.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Federolf, P. Quantifying instantaneous performance in alpine ski racing. J. Sports Sci. 2012, 30, 1063–1068. [Google Scholar] [CrossRef] [Green Version]
  2. Delhaye, C.; Cross, M.R.; Bowen, M.; Samozino, P.; Hintzy, F. Influence of Line Strategy between Two Turns on Performance in Giant Slalom. Front. Sport. Act. Living 2020, 2, 175. [Google Scholar] [CrossRef] [PubMed]
  3. Spörri, J.; Kröll, J.; Schwameder, H.; Müller, E. The role of path length- and speed-related factors for the enhancement of section performance in alpine giant slalom. Eur. J. Sport Sci. 2018, 18, 911–919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Gilgien, M.; Kröll, J.; Spörri, J.; Crivelli, P.; Müller, E. Application of dGNSS in alpine ski racing: Basis for evaluating physical demands and safety. Front. Physiol. 2018, 9, 145. [Google Scholar] [CrossRef] [Green Version]
  5. Supej, M.; Saetran, L.; Oggiano, L.; Ettema, G.; Šarabon, N.; Nemec, B.; Holmberg, H.-C.C.; Saarabon, N.; Nemec, B.; Holmberg, H.-C.C. Aerodynamic drag is not the major determinant of performance during giant slalom skiing at the elite level. Scand. J. Med. Sci. Sports 2012, 23, 38–47. [Google Scholar] [CrossRef]
  6. Meyer, F. Biomechanical Analysis of Alpine Skiers Performing Giant Slalom Turns. Ph.D. Thesis, University Lausanne, Lausanne, Switzerland, 2012. [Google Scholar]
  7. Reid, R.C. A kinematic and Kinetic Study of Alpine Skiing Technique in Slalom. Ph.D. Thesis, Norwegian School of Sport Sciences, Oslo, Norway, 2010. [Google Scholar]
  8. Gilgien, M.; Crivelli, P.; Spörri, J.; Kröll, J.; Müller, E. Characterization of course and terrain and their effect on skier speed in World Cup alpine ski racing. PLoS ONE 2015, 10, e0118119. [Google Scholar] [CrossRef] [Green Version]
  9. Gilgien, M.; Crivelli, P.; Kröll, J.; Luteberget, L.S.; Müller, E.; Spörri, J. Injury prevention in Super-G alpine ski racing through course design. Sci. Rep. 2021, 11, 3637. [Google Scholar] [CrossRef]
  10. Gilgien, M.; Crivelli, P.; Kröll, J.; Luteberget, L.S.; Müller, E.; Spörri, J. Preventing injuries in alpine skiing giant slalom by shortening the vertical distance between the gates rather than increasing the horizontal gate offset to control speed. Br. J. Sports Med. 2020, 54, 1042–1046. [Google Scholar] [CrossRef]
  11. Spörri, J.; Kröll, J.; Schwameder, H.; Schiefermüller, C.; Müller, E. Course setting and selected biomechanical variables related to injury risk in alpine ski racing: An explorative case study. Br. J. Sports Med. 2012, 46, 1072–1077. [Google Scholar] [CrossRef] [Green Version]
  12. Supej, M.; Nemec, B.; Kugovnik, O. Changing conditions on the slalom ski course affect competitors’ performances. Kinesiology 2005, 37, 151–158. [Google Scholar]
  13. Schiestl, M.; Kaps, P.; Mossner, M.; Nachbauer, W. Calculation of friction and reaction forces during an alpine world cup downhill race. In The Engineering of Sport 6; Moritz, E.F., Haake, S., Eds.; Springer: New York, NY, USA, 2006; Volume 1, pp. 269–274. [Google Scholar]
  14. Spörri, J.; Kröll, J.; Gilgien, M.; Müller, E. Sidecut radius and the mechanics of turning: Equipment designed to reduce risk of severe traumatic knee injuries in alpine giant slalom ski racing. Br. J. Sports Med. 2016, 50, 14–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Gilgien, M.; Spörri, J.; Limpach, P.; Geiger, A.; Müller, E. The Effect of Different Global Navigation Satellite System Methods on Positioning Accuracy in Elite Alpine Skiing. Sensors 2014, 14, 18433–18453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Supej, M.; Holmberg, H.C. A new time measurement method using a high-end global navigation satellite system to analyze alpine skiing. Res. Q. Exerc. Sport 2011, 82, 400–411. [Google Scholar] [CrossRef] [PubMed]
  17. Gilgien, M.; Spörri, J.; Kröll, J.; Müller, E. Effect of ski geometry and standing height on kinetic energy: Equipment designed to reduce risk of severe traumatic injuries in alpine downhill ski racing. Br. J. Sports Med. 2016, 50, 8–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  18. Supej, M.; Nedergaard, N.J.; Nord, J.; Holmberg, H.C. The impact of start strategy on start performance in alpine skiing exists on flat, but not on steep inclines. J. Sports Sci. 2019, 37, 647–655. [Google Scholar] [CrossRef] [PubMed]
  19. Fasel, B.; Spörri, J.; Gilgien, M.; Boffi, G.; Chardonnens, J.; Müller, E.; Aminian, K. Three-dimensional body and centre of mass kinematics in alpine ski racing using differential GNSS and inertial sensors. Remote Sens. 2016, 8, 671. [Google Scholar] [CrossRef] [Green Version]
  20. Nemec, B.; Petrič, T.; Babič, J.; Supej, M.; Petric, T.; Babic, J.; Supej, M. Estimation of alpine skier posture using machine learning techniques. Sensors 2014, 14, 18898–18914. [Google Scholar] [CrossRef] [Green Version]
  21. Supej, M.; Ogrin, J.; Šarabon, N.; Holmberg, H.C. Asymmetries in the technique and ground reaction forces of elite alpine skiers influence their slalom performance. Appl. Sci. 2020, 10, 7288. [Google Scholar] [CrossRef]
  22. Supej, M. 3D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system. J. Sports Sci. 2010, 28, 759–769. [Google Scholar] [CrossRef]
  23. Lachapelle, G.; Morrison, A.; Ong, R. StealthTM-a-based advanced device to train Canadian olympic Skiers. Geomatica 2010, 64, 327–335. [Google Scholar]
  24. Gilgien, M.; Spörri, J.; Chardonnens, J.; Kröll, J.; Müller, E. Determination of external forces in alpine skiing using a differential global navigation satellite system. Sensors 2013, 13, 9821–9835. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Gilgien, M.; Spörri, J.; Kröll, J.; Crivelli, P.; Müller, E. Mechanics of turning and jumping and skier speed are associated with injury risk in men’s World Cup alpine skiing: A comparison between the competition disciplines. Br. J. Sports Med. 2014, 48, 742–747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. Zorko, M.; Nemec, B.; Babic, J.; Lesnik, B.; Supej, M. The Waist Width of Skis Influences the Kinematics of the Knee Joint in Alpine Skiing. J Sport. Sci. Med. 2015, 14, 606–619. [Google Scholar]
  27. Fasel, B.; Gilgien, M.; Spörri, J.; Aminian, K. A new training assessment method for alpine ski racing: Estimating center of mass trajectory by fusing inertial sensors with periodically available position anchor points. Front. Physiol. 2018, 9, 1203. [Google Scholar] [CrossRef] [PubMed]
  28. Brodie, M.; Walmsley, A.; Page, W. Fusion motion capture: A prototype system using inertial measurement units and GPS for the biomechanical analysis of ski racing. Sport. Technol. 2008, 1, 17–28. [Google Scholar] [CrossRef]
  29. Bruhin, B.; Janssen, R.J.F.; Guillaume, S.; Gander, M.; Oberle, F.; Lorenzetti, S.; Romann, M. Giant Slalom: Analysis of Course Setting, Steepness and Performance of Different Age Groups—A Pilot Study. Front. Sport. Act. Living 2020, 2, 107. [Google Scholar] [CrossRef] [PubMed]
  30. Cross, M.R.; Delhaye, C.; Morin, J.B.; Bowen, M.; Coulmy, N.; Hintzy, F.; Samozino, P. Force output in giant-slalom skiing: A practical model of force application effectiveness. PLoS ONE 2021, 16, e0244698. [Google Scholar] [CrossRef]
  31. Gløersen, Ø.; Kocbach, J.; Gilgien, M. Tracking performance in endurance racing sports: Evaluation of the accuracy offered by three commercial GNSS receivers aimed at the sports market. Front. Physiol. 2018, 9, 1425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Skaloud, J.; Limpach, P. Synergy of CP-DGPS, Accelerometry and Magnetic Sensors for Precise Trajectography in Ski Racing. In Proceedings of the Conference of the ION GPS/GNSS 2003, Portland, OR, USA, 9–12 September 2003. [Google Scholar]
  33. Gilat, A.; Subramaniam, V. Numerical Methods for Engineers and Scientists; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
  34. Gløersen, Ø.; Gilgien, M. Classification of Cross-Country Ski Skating Sub-Technique Can Be Automated Using Carrier-Phase Differential GNSS Measurements of the Head’s Position. Sensors 2021, 21, 2705. [Google Scholar] [CrossRef]
  35. Luteberget, L.; Spencer, M.; Gilgien, M. Validity of the Catapult ClearSky T6 local positioning system for team sports specific drills, in indoor conditions. Front. Physiol. 2018, 9, 115. [Google Scholar] [CrossRef] [Green Version]
  36. Supej, M.; Kipp, R.; Holmberg, H.C. Mechanical parameters as predictors of performance in alpine World Cup slalom racing. Scand. J. Med. Sci. Sports 2010, 21, e72–e81. [Google Scholar] [CrossRef]
  37. Spörri, J.; Kröll, J.; Gilgien, M.; Müller, E. How to prevent injuries in alpine ski racing: What do we know and where do we go from here? Sport. Med. 2016, 47, 599–614. [Google Scholar] [CrossRef] [Green Version]
  38. Spörri, J.; Kröll, J.; Fasel, B.; Aminian, K.; Müller, E. The use of body worn sensors for detecting the vibrations acting on the lower back in alpine ski racing. Front. Physiol. 2017, 8, 522. [Google Scholar] [CrossRef]
  39. Supej, M.; Ogrin, J.; Holmberg, H.C. Whole-body vibrations associated with alpine skiing: A risk factor for low back pain? Front. Physiol. 2018, 9, 204. [Google Scholar] [CrossRef]
  40. Nakazato, K.; Scheiber, P.; Müller, E. A comparison of ground reaction forces determined by portable force-plate and pressure-insole systems in alpine skiing. J. Sport. Sci. Med. 2011, 10, 754–762. [Google Scholar]
  41. Supej, M.; Hebert-Losier, K.; Holmberg, H.C. Impact of the Steepness of the Slope on the Biomechanics of World Cup Slalom Skiers. Int. J. Sports Physiol. Perform. 2015, 10, 361–368. [Google Scholar] [CrossRef]
  42. Ogrin, J.; Šarabon, N.; Madsen, M.K.; Kersting, U.; Holmberg, H.-C.; Supej, M. Asymmetries in Ground Reaction Forces during Turns by Elite Slalom Alpine Skiers Are Not Related to Asymmetries in Muscular Strength. Front. Physiol. 2021, 12, 431. [Google Scholar] [CrossRef] [PubMed]
  43. Spörri, J.; Kröll, J.; Schwameder, H.; Müller, E. Turn Characteristics of a Top World Class Athlete in Giant Slalom: A Case Study Assessing Current Performance Prediction Concepts. Int. J. Sport. Sci. Coach. 2012, 7, 647–660. [Google Scholar] [CrossRef]
  44. Kröll, J.; Spörri, J.; Gilgien, M.; Schwameder, H.; Müller, E. Effect of ski geometry on aggressive ski behaviour and visual aesthetics: Equipment designed to reduce risk of severe traumatic knee injuries in alpine giant slalom ski racing. Br. J. Sports Med. 2016, 50, 20–25. [Google Scholar] [CrossRef] [Green Version]
  45. Karlsson, Ø.; Gilgien, M.; Gløersen, Ø.N.; Rud, B.; Losnegard, T. Exercise Intensity During Cross-Country Skiing De-scribed by Oxygen Demands in Flat and Uphill Terrain. Front. Physiol. 2018, 9, 846. [Google Scholar] [CrossRef]
  46. Sollie, O.; Gløersen, Ø.; Gilgien, M.; Losnegard, T. Differences in pacing pattern and sub-technique selection between young and adult competitive cross-country skiers. Scand. J. Med. Sci. Sports 2020, 31, 553–563. [Google Scholar] [CrossRef] [PubMed]
  47. Yamazaki, J.; Gilgien, M.; Kleiven, S.; Mcintosh, A.S.S.; Nachbauer, W.; Müller, E.; Bere, T.; Bahr, R.; Krosshaug, T. Analysis of a severe head injury in World Cup alpine skiing. Med. Sci. Sport. Exerc. 2015, 47, 1113–1118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  48. Gilgien, M.; Spörri, J.; Chardonnens, J.; Kröll, J.; Limpach, P.; Müller, E. Determination of the centre of mass kinematics in alpine skiing using differential global navigation satellite systems. J. Sports Sci. 2015, 33, 960–969. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 14 00022 g001 550
Figure 1. Histograms for horizontal position error (A) and position error in three dimensions (B) for all skiing data (competitive skiing and recreational skiing data pooled together).
Figure 1. Histograms for horizontal position error (A) and position error in three dimensions (B) for all skiing data (competitive skiing and recreational skiing data pooled together).
Remotesensing 14 00022 g001
Remotesensing 14 00022 g002 550
Figure 2. (A) Histograms for error in speed (Δ|v|), (B) acceleration (Δ|a|), (C) trajectory incline (ΔIncline) and (D) turn radius (ΔTurn radius). The histograms use all data from recreational and competitive skiing pooled together.
Figure 2. (A) Histograms for error in speed (Δ|v|), (B) acceleration (Δ|a|), (C) trajectory incline (ΔIncline) and (D) turn radius (ΔTurn radius). The histograms use all data from recreational and competitive skiing pooled together.
Remotesensing 14 00022 g002
Remotesensing 14 00022 g003 550
Figure 3. (A) Bland–Altman plot for speed error (Δ|v|). (B) Bland–Altman plot for acceleration error. Nomenclature: standard deviation (SD).
Figure 3. (A) Bland–Altman plot for speed error (Δ|v|). (B) Bland–Altman plot for acceleration error. Nomenclature: standard deviation (SD).
Remotesensing 14 00022 g003
Remotesensing 14 00022 g004 550
Figure 4. (A) Histograms for turn error in speed (Δ|v|/Turn), (B) acceleration (Δ|a|/Turn), (C) trajectory incline (Δ Incline/Turn), (D) turn radius (Δ Turn radius/Turn), (E) impulse (Δ Impulse/Turn). The histograms use all data from recreational and competitive skiing pooled together.
Figure 4. (A) Histograms for turn error in speed (Δ|v|/Turn), (B) acceleration (Δ|a|/Turn), (C) trajectory incline (Δ Incline/Turn), (D) turn radius (Δ Turn radius/Turn), (E) impulse (Δ Impulse/Turn). The histograms use all data from recreational and competitive skiing pooled together.
Remotesensing 14 00022 g004
Remotesensing 14 00022 g005 550
Figure 5. Trajectory measurements with AdMos and the ground truth system for 4 runs over the same course. Ground truth system plotted in red and AdMos plotted in blue, green, magenta and cyan. The coordinates have been made relative for better visualization. (A) Trajectory of the last 4 turns of the course. (B) Section from A marked with a black box (turn 3).
Figure 5. Trajectory measurements with AdMos and the ground truth system for 4 runs over the same course. Ground truth system plotted in red and AdMos plotted in blue, green, magenta and cyan. The coordinates have been made relative for better visualization. (A) Trajectory of the last 4 turns of the course. (B) Section from A marked with a black box (turn 3).
Remotesensing 14 00022 g005
Remotesensing 14 00022 g006 550
Figure 6. Error measurements for the first 30 s of the 8 first runs from competitive skiing day 1 on the same course. After each run, skiers took the lift to get back to the start and appeared again in this graph with the position error illustrated over 30 s. (A) Position error in the horizontal plane (ΔXY). (B) Vertical positional error. The horizontal axis shows time from start. Time zero represents the start time point for each run. Each line represents one run. The circles indicate turn start and end, represented by the deflection points between two turns.
Figure 6. Error measurements for the first 30 s of the 8 first runs from competitive skiing day 1 on the same course. After each run, skiers took the lift to get back to the start and appeared again in this graph with the position error illustrated over 30 s. (A) Position error in the horizontal plane (ΔXY). (B) Vertical positional error. The horizontal axis shows time from start. Time zero represents the start time point for each run. Each line represents one run. The circles indicate turn start and end, represented by the deflection points between two turns.
Remotesensing 14 00022 g006
Table
Table 1. Descriptive data of the participants in the study. Nomenclature: kilograms (kg) and centimeters (cm).
Table 1. Descriptive data of the participants in the study. Nomenclature: kilograms (kg) and centimeters (cm).
Competitive SkiingRecreational Skiing *Recreational Skiing **
Performance LevelEuropa CupRetired FIS AthleteRecreational Skier
Age (years)242444
Weight (kg)867072
Height (cm)182176180
* Skier at Innichen. ** Skier at Juvass, Metsch, Norefjell and Tryvann.
Table
Table 2. Characteristics of the data acquired (all data, competitive and recreational skiing) from the ground truth measurement system. Nomenclature: speed (|v|), acceleration (|a|), trajectory incline (incline) kilometers (km), meters (m), seconds (s) and standard deviation (SD).
Table 2. Characteristics of the data acquired (all data, competitive and recreational skiing) from the ground truth measurement system. Nomenclature: speed (|v|), acceleration (|a|), trajectory incline (incline) kilometers (km), meters (m), seconds (s) and standard deviation (SD).
Competitive SkiingRecreational SkiingSum of All Skiing Data
Runs 276390
Turns 84425053349
Total distance (km) 21.7438.9160.65
Distance/run (m)Mean ± SD805 ± 327618 ± 342674 ± 347
Turns/runMean ± SD31 ± 1040 ± 1937 ± 18
Time/run (s)Mean ± SD63.2 ± 23.260.4 ± 31.060.6 ± 29.0
|v| (m/s)Mean12.7410.8511.46
SD6.983.685.07
Max27.2219.0427.22
|a| (m/s2)Mean6.105.325.97
SD4.593.593.94
Incline (degrees)Mean12.6112.3112.41
SD6.918.017.68
Turn radius (m)Mean32.7431.2231.73
SD23.9424.4725.66
Table
Table 3. Summary of position errors for competitive and recreational skiing data. Errors are reported as median with 95% confidence intervals, interquartile range (IQR) and maximal error (Δmax) for position error in the horizontal plane (ΔXY) and position error in three dimensions (ΔXYZ).
Table 3. Summary of position errors for competitive and recreational skiing data. Errors are reported as median with 95% confidence intervals, interquartile range (IQR) and maximal error (Δmax) for position error in the horizontal plane (ΔXY) and position error in three dimensions (ΔXYZ).
Competitive SkiingRecreational Skiing
ΔXY (m)Median3.54 [3.50, 3.59]2.21 [2.19, 2.24]
IQR3.503.30
90th percentile[0.69, 6.27][0.57, 5.97]
Δmax8.008.90
ΔXYZ (m)Median6.49 [6.47, 6.51]7.01 [6.99, 7.04]
IQR2.304.30
90th percentile[2.44, 10.07][2.03, 13.71]
Δmax12.4050.90
Table
Table 4. Instantaneous errors for speed (Δ|v|), acceleration (Δ|a|), trajectory incline (ΔIncline), and turn radius (ΔTurn radius), for competitive and recreational skiing. Data presented with median (with confidence intervals), interquartile range (IQR) and maximal error (Δmax) in parameter units and %. Not defined (n.d).
Table 4. Instantaneous errors for speed (Δ|v|), acceleration (Δ|a|), trajectory incline (ΔIncline), and turn radius (ΔTurn radius), for competitive and recreational skiing. Data presented with median (with confidence intervals), interquartile range (IQR) and maximal error (Δmax) in parameter units and %. Not defined (n.d).
Competitive SkiingRecreational Skiing
ValuePercentage (%)ValuePercentage (%)
Δ|v| (m/s)Median0.015 [0.013, 0.016]+0.10.037 [0.036, 0.039]+0.3
IQR0.181.40.232.0
90th percentile[−0.23, 0.34]-[−0.32, 0.39]-
Δmax0.8992.31.9369.6
Δ|a| (m/s2)Median0.119 [0.111, 0.126]+2.50.229 [0.222, 0.236]+4.3
IQR0.8217.41.0519.8
90th percentile[−0.94, 1.28]-[−1.09, 1.90]-
Δmax5.3695.25.36100
ΔIncline
(degrees)		Median0.042 [0.028, 0.053]+0.30.026 [0.014, 0.036]+0.1
IQR1.5110.81.9515.6
90th percentile[−4.15, 4.94]-[−3.99, 4.05]-
Δmaxn.dn.dn.dn.d
ΔTurn radius
(m)		Median−0.11 [−0.14, −0.08]−0.4−0.47 [−0.50, −0.44]−2.3
IQR3.914.25.6427.2
90th percentile[−19.8, 29.1]-[−30.5, 65.2]-
Δmaxn.dn.dn.dn.d
Table
Table 5. Errors for turn average values for speed (Δ|v|), acceleration (Δ|a|), trajectory incline (ΔIncline), turn radius (ΔTurn radius) and impulse (ΔImpulse/Turn) for competitive and recreational skiing. Data are presented as median (with confidence intervals), interquartile range (IQR) and maximal error (Δmax) in parameter units and %. Number of turns: competitive skiing: 599, recreational skiing: 2145. Nomenclature: bodyweight seconds (BWs), p.* = 90th percentile.
Table 5. Errors for turn average values for speed (Δ|v|), acceleration (Δ|a|), trajectory incline (ΔIncline), turn radius (ΔTurn radius) and impulse (ΔImpulse/Turn) for competitive and recreational skiing. Data are presented as median (with confidence intervals), interquartile range (IQR) and maximal error (Δmax) in parameter units and %. Number of turns: competitive skiing: 599, recreational skiing: 2145. Nomenclature: bodyweight seconds (BWs), p.* = 90th percentile.
Competitive SkiingRecreational Skiing
ValuePercentage (%)ValuePercentage (%)
Δ|v|/Turn
(m/s)		Median−0.006 [−0.013, 0.003]−0.040.039 [0.034, 0.047]0.34
IQR0.130.820.161.40
90th p.*[−0.17, 0.18]-[−0.23, 0.29]-
Δmax0.456.321.3938.9
Δ|a|/Turn
(m/s2)		Median0.070 [0.046, 0.098]0.840.346 [0.319, 0.372]4.86
IQR0.354.090.628.72
90th p.*[−0.40, 0.61]-[−0.37, 1.36]-
Δmax1.3841.64.4055.9
Δ Incline/Turn
(degrees)		Median0.138 [0.097, 0.195]0.970.071 [0.027, 0.120]0.50
IQR0.735.171.419.91
90th p.*[−1.24, 2.08]-[−2.24, 2.80]-
Δmax9.0552.719.0623
Δ Turn radius/Turn
(m)		Median−0.437 [−0.727, −0.256]−1.20−0.716 [−0.940, −0.565]−2.27
IQR3.559.765.2216.6
90th p.*[−5.38, 4.41]-[−9.82, 7.07]-
Δmax10351766.2144
Δ Impulse/Turn
(BWs)		Median0.008 [0.002, 0.013]0.300.024 [0.020, 0.028]1.57
IQR0.0863.440.0986.54
90th p.*[−0.13, 0.17]-[−0.15, 0.22]-
Δmax0.7814.10.89184
Table
Table 6. Error for number of turns per run and impulse per run. Number of runs: competitive skiing: 27, recreational skiing: 63. Nomenclature: bodyweight seconds (BWs), interquartile range (IQR), error (Δ).
Table 6. Error for number of turns per run and impulse per run. Number of runs: competitive skiing: 27, recreational skiing: 63. Nomenclature: bodyweight seconds (BWs), interquartile range (IQR), error (Δ).
Competitive SkiingRecreational Skiing
ValuePercentage (%)ValuePercentage (%)
ΔTurns/run Median0012.7
IQR31125.4
90th percentile[2.6, 6.2]-[−3, 8.2]-
ΔImpulse/run (BWs) Median0.200.30.931.5
IQR0.220.31.312.1
90th percentile[−0.01, 0.54]-[0.00, 2.62]-
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Jølstad, P.A.H.; Reid, R.C.; Gjevestad, J.G.O.; Gilgien, M. Validity of the AdMos, Advanced Sport Instruments, GNSS Sensor for Use in Alpine Skiing. Remote Sens. 2022, 14, 22. https://doi.org/10.3390/rs14010022

AMA Style

Jølstad PAH, Reid RC, Gjevestad JGO, Gilgien M. Validity of the AdMos, Advanced Sport Instruments, GNSS Sensor for Use in Alpine Skiing. Remote Sensing. 2022; 14(1):22. https://doi.org/10.3390/rs14010022

Chicago/Turabian Style

Jølstad, Petter Andre Husevåg, Robert Cortas Reid, Jon Glenn Omholt Gjevestad, and Matthias Gilgien. 2022. "Validity of the AdMos, Advanced Sport Instruments, GNSS Sensor for Use in Alpine Skiing" Remote Sensing 14, no. 1: 22. https://doi.org/10.3390/rs14010022

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop