Laboratory Research on Polarized Optical Properties of Saline-Alkaline Soil Based on Semi-Empirical Models and Machine Learning Methods
Abstract
:1. Introduction
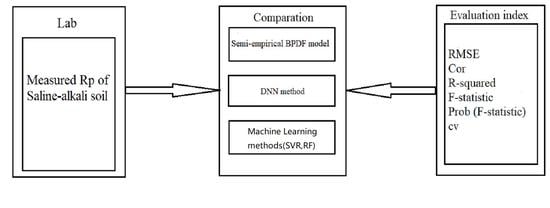
2. Introduction to Models and Algorithms
2.1. Semi-empirical BPDF Model
2.1.1. Nadal–Bréon Model
2.1.2. Litvinov Model
2.1.3. Xie–Cheng Model
- Step 1: input the azimuth, detection angle, and model parameters from the experiment to the semi-empirical BPDF model and calculate the predicted Rp.
- Step 2: compare and fit the measured Rp in the laboratory with the predicted Rp and use the root mean squared error (RMSE), correlation coefficient (Cor) and R-squared (R2) to evaluate the results.
2.2. BPDF Model Based on Machine Learning
2.2.1. Support Vector Regression (SVR)
2.2.2. Random Forest Regression
2.2.3. Deep Neural Network Regression
- Step 1: input the azimuth angle, detection angle, and solar zenith angle from the experiment into the formula to calculate the scattering angle, as one of the input variables. The Rp of the saline-alkaline soil surface measured in the laboratory was used as another input variable.
- Step 2: take 70% of the laboratory data as the experimental group to train the neural network.
- Step 3: use the remaining 30% of the laboratory data as the test group, to verify the effect of the network trained by deep learning.
2.3. Definition of the Evaluation Index
2.3.1. Root Mean Square Error (RMSE)
2.3.2. R-Squared (R2)
2.3.3. Correlation Coefficient (Cor)
2.3.4. F-Statistic
2.3.5. Coefficient of Variation (cv)
3. Data Description
3.1. Study Area
3.2. Soil Sample Processing
3.3. Spectral Measurement Process
4. Results
4.1. Spectral Measurement Results
4.2. Semi-Empirical BPDF Model Results
4.3. Machine Learning Methods Prediction Results
4.4. Comparison and Analysis of Semi-Empirical BPDF and BPDF Models Based on Machine Learning
5. Discussion
5.1. Influence of the Training Ratio on the Fitting Effect
5.2. Optimal Learning Rate of BPDF Model Based on DNN Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hassani, A.; Azapagic, A.; Shokri, N. Predicting long-term dynamics of soil salinity and sodicity on a global scale. Proc. Natl. Acad. Sci. USA 2020, 117, 33017–33027. [Google Scholar] [CrossRef]
- Abrol, I.; Yadav, J.; Massoud, F. Salt-Affected Soils and Their Management; Food & Agriculture Org: Leuven, Belgium, 1988. [Google Scholar]
- Ginn, F. The International Encyclopedia of Geography: People, The Earth, Environment and Technology; Blackwell Publishing: Boken, NJ, USA, 2017. [Google Scholar] [CrossRef] [Green Version]
- Daliakopoulos, I.N.; Tsanis, I.K.; Koutroulis, A.; Kourgialas, N.N.; Varouchakis, A.E.; Karatzas, G.P.; Ritsema, C.J. The threat of soil salinity: A European scale review. Sci. Total Environ. 2016, 573, 727–739. [Google Scholar] [CrossRef]
- Wong, V.N.L.; Greene, R.S.B.; Dalal, R.C.; Murphy, B.W. Soil carbon dynamics in saline and sodic soils: A review. Soil Use Manag. 2010, 26, 2–11. [Google Scholar] [CrossRef]
- Paix, M.J.D.L.; Lanhai, L.; Xi, C.; Varenyam, A.; Nyongesah, M.J.; Habiyaremye, G. Physicochemical properties of saline soils and aeolian dust. Land Degrad. 2013, 24, 539–547. [Google Scholar] [CrossRef]
- Singh, K. Microbial and Enzyme Activities of Saline and Sodic Soils. Land Degrad. Dev. 2016, 27, 706–718. [Google Scholar] [CrossRef]
- Rath, K.M.; Rousk, J. Salt effects on the soil microbial decomposer community and their role in organic carbon cycling: A review. Soil Biol. Biochem. 2015, 81, 108–123. [Google Scholar] [CrossRef]
- Parihar, P.; Singh, S.; Singh, R.; Singh, V.P.; Prasad, S.M. Effect of salinity stress on plants and its tolerance strategies: A review. Environ. Sci. Pollut. Res. Int. 2015, 22, 4056–4075. [Google Scholar] [CrossRef] [PubMed]
- Perri, S.; Suweis, S.; Holmes, A.; Marpu, P.R.; Entekhabi, D.; Molini, A. River basin salinization as a form of aridity. Proc. Natl. Acad. Sci. USA 2020, 117, 17635–17642. [Google Scholar] [CrossRef] [PubMed]
- Kai-shan, S. The Polarized Reflectance Characteristics of Some Soils. Sci. Geogr. Sin. 2004, 24, 357–363. [Google Scholar]
- Hassani, A.; Azapagic, A.; d Odorico, P.; Keshmiri, A.; Shokri, N. Desiccation crisis of saline lakes: A new decision-support framework for building resilience to climate change. Sci. Total Environ. 2019, 703, 134718. [Google Scholar] [CrossRef] [PubMed]
- Curran, P. The relationship between polarized visible light and vegetation amount. Remote Sens. Environ. 1981, 11, 87–92. [Google Scholar] [CrossRef]
- Bradley, C.L.; Diner, D.J.; Xu, F.; Kupinski, M.; Chipman, R.A. Spectral Invariance Hypothesis Study of Polarized Reflectance with the Ground-Based Multiangle SpectroPolarimetric Imager. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8191–8207. [Google Scholar] [CrossRef]
- Talmage, D.; Curran, P.J. Remote sensing using partially polarized light. Int. J. Remote Sens. 1986, 7, 47–64. [Google Scholar] [CrossRef]
- Peltoniemi, J.; Järvinen, J.; Zubko, N.; Gritsevich, M. Spectropolarimetric characterization of pure and polluted land surfaces. Int. J. Remote Sens. 2020, 41, 4865–4878. [Google Scholar] [CrossRef]
- Suomalainen, J.; Hakala, T.; Puttonen, E.; Peltoniemi, J. Polarised bidirectional reflectance factor measurements from vegetated land surfaces. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1044–1056. [Google Scholar] [CrossRef]
- Deuze, J.; Bréon, F.; Devaux, C.; Goloub, P.; Herman, M.; Lafrance, B.; Maignan, F.; Marchand, A.; Nadal, F.; Perry, G.; et al. Remote sensing of aerosols over land surfaces from POLDEr ADEOs 1 polarized measurements. J. Geophys. Res. 2001, 106, 4913–4926. [Google Scholar] [CrossRef] [Green Version]
- Xie, D.; Cheng, T.; Zhang, W.; Yu, J.; Li, X.; Gong, H. Aerosol type over east Asian retrieval using total and polarized remote Sensing. J. Quant. Spectrosc. Radiat. Transf. 2013, 129, 15–30. [Google Scholar] [CrossRef]
- Wang, H.; Yang, L.K.; Zhao, M.R.; Du, W.B.; Liu, P.; Sun, X.B. The Normalized Difference Vegetation Index and Angular Variation of Surface Spectral Polarized Reflectance Relationships: Improvements on Aerosol Remote Sensing Over Land. Earth Space Sci. 2019, 6, 982–989. [Google Scholar] [CrossRef] [Green Version]
- Nadal, F.; Bréon, F.M. Parameterization of surface polarized reflectance derived from POLDER spaceborne measurements. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1709–1718. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.; Fedele, E.; Bouvier, M.J.R.S.o.E. Polarized reflectances of natural surfaces: Spaceborne measurements and analytical modeling. Remote Sens. Environ. 2009, 113, 2642–2650. [Google Scholar] [CrossRef]
- Yang, B.; Zhao, H.M.; Chen, W. Modeling polarized reflectance of snow and ice surface using POLDER measurements. J. Quant. Spectrosc. Radiat. Transf. 2019, 236, 106578. [Google Scholar] [CrossRef]
- Martin, W.E.; Hesse, E.; Hough, J.H.; Sparks, W.B.; Cockell, C.S.; Ulanowski, Z.; Germer, T.A.; Kaye, P.H. Polarized optical scattering signatures from biological materials. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2444–2459. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.Q.; Wu, D.; Lv, Y.F.; Lu, S. Optical Properties of Reflected Light from Leaves: A Case Study from One Species. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4388–4406. [Google Scholar] [CrossRef]
- Nilson, T.; Kuusk, A. A reflectance model for the homogeneous plant canopy and its inversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Rondeaux, G.; Herman, M. Polarization of light reflected by crop canopies. Remote Sens. Environ. 1991, 38, 63–75. [Google Scholar] [CrossRef]
- Sun, Z.Q.; Huang, Y.H.; Bao, Y.L.; Wu, D. Polarized Remote Sensing: A Note on the Stokes Parameters Measurements from Natural and Man-Made Targets Using a Spectrometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4008–4021. [Google Scholar] [CrossRef]
- Grant, L.; Daughtry, C.S.T.; Vanderbilt, V.C. Polarized and Specular Reflectance Variation with Leaf Surface-Features. Physiologia Plantarum 1993, 88, 1–9. [Google Scholar] [CrossRef]
- Yang, B.; Knyazikhin, Y.; Lin, Y.; Yan, K.; Chen, C.; Park, T.; Choi, S.; Mottus, M.; Rautiainen, M.; Myneni, R.B.; et al. Analyses of Impact of Needle Surface Properties on Estimation of Needle Absorption Spectrum: Case Study with Coniferous Needle and Shoot Samples. Remote Sens. 2016, 8, 563. [Google Scholar] [CrossRef] [Green Version]
- Breon, F.M.; Tanre, D.; Lecomte, P.; Herman, M. Polarized Reflectance of Bare Soils and Vegetation—Measurements and Models. IEEE Trans. Geosci. Remote Sens. 1995, 33, 487–499. [Google Scholar] [CrossRef]
- Litvinov, P.; Hasekamp, O.; Cairns, B.; Mishchenko, M. Reflection models for soil and vegetation surfaces from multiple-viewing angle photopolarimetric measurements. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 529–539. [Google Scholar] [CrossRef]
- Xie, D.; Cheng, T.; Wu, Y.; Fu, H.; Zhong, R.; Yu, J. Polarized reflectances of urban areas: Analysis and models. Remote Sens. Environ. 2017, 193, 29–37. [Google Scholar] [CrossRef]
- Peltoniemi, J.I.; Gritsevich, M.; Hakala, T.; Dagsson-Waldhauserova, P.; Arnalds, O.; Anttila, K.; Hannula, H.R.; Kivekas, N.; Lihavainen, H.; Meinander, O.; et al. Soot on Snow experiment: Bidirectional reflectance factor measurements of contaminated snow. Cryosphere 2015, 9, 2323–2337. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Zhao, H.M.; Chen, W. Semi-empirical models for polarized reflectance of land surfaces: Intercomparison using space-borne POLDER measurements. J. Quant. Spectrosc. Radiat. Transf. 2017, 202, 13–20. [Google Scholar] [CrossRef]
- Vanderbilt, V.; Grant, L.J.I.T.o.G.; Sensing, R. Plant Canopy Specular Reflectance Model. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 722–730. [Google Scholar] [CrossRef]
- Diner, D.J.; Xu, F.; Martonchik, J.V.; Rheingans, B.E.; Geier, S.; Jovanovic, V.M.; Davis, A.; Chipman, R.A.; McClain, S.C. Exploration of a Polarized Surface Bidirectional Reflectance Model Using the Ground-Based Multiangle SpectroPolarimetric Imager. Atmosphere 2012, 3, 591–619. [Google Scholar] [CrossRef] [Green Version]
- Waquet, F.; Leon, J.F.; Cairns, B.; Goloub, P.; Deuze, J.L.; Auriol, F. Analysis of the spectral and angular response of the vegetated surface polarization for the purpose of aerosol remote sensing over land. Appl. Opt. 2009, 48, 1228–1236. [Google Scholar] [CrossRef] [PubMed]
- Litvinov, P.; Hasekamp, O.; Cairns, B. Models for surface reflection of radiance and polarized radiance: Comparison with airborne multi-angle photopolarimetric measurements and implications for modeling top-of-atmosphere measurements. Remote Sens. Environ. 2011, 115, 781–792. [Google Scholar] [CrossRef]
- He, Y.H.; Yang, B.; Lin, H.; Zhang, J.Q. Modeling Polarized Reflectance of Natural Land Surfaces Using Generalized Regression Neural Networks. Remote Sens. 2020, 12, 248. [Google Scholar] [CrossRef] [Green Version]
- Gilichinsky, M.; Heiskanen, J.; Barth, A.; Wallerman, J.; Egberth, M.; Nilsson, M. Histogram matching for the calibration of kNN stem volume estimates. Int. J. Remote Sens. 2012, 33, 7117–7131. [Google Scholar] [CrossRef]
- Ichii, K.; Ueyama, M.; Kondo, M.; Saigusa, N.; Kim, J.; Alberto, M.C.; Ardo, J.; Euskirchen, E.S.; Kang, M.; Hirano, T.; et al. New data-driven estimation of terrestrial CO2 fluxes in Asia using a standardized database of eddy covariance measurements, remote sensing data, and support vector regression. J. Geophys. Res. Biogeosci. 2017, 122, 767–795. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Zerrouki, N.; Harrou, F.; Sun, Y.; Hocini, L. A Machine Learning-Based Approach for Land Cover Change Detection Using Remote Sensing and Radiometric Measurements. IEEE Sens. J. 2019, 19, 5843–5850. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Di, L.P.; Zhang, L.P.; Deng, M.X.; Qin, Z.H.; Zhao, S.H.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Loozen, Y.; Rebel, K.T.; de Jong, S.M.; Lu, M.; Ollinger, S.V.; Wassen, M.J.; Karssenberg, D. Mapping canopy nitrogen in European forests using remote sensing and environmental variables with the random forests method. Remote Sens. Environ. 2020, 247, 111933. [Google Scholar] [CrossRef]
- Feret, J.B.; le Maire, G.; Jay, S.; Berveiller, D.; Bendoula, R.; Hmimina, G.; Cheraiet, A.; Oliveira, J.C.; Ponzoni, F.J.; Solanki, T.; et al. Estimating leaf mass per area and equivalent water thickness based on leaf optical properties: Potential and limitations of physical modeling and machine learning. Remote Sens. Environ. 2019, 231, 110959. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Y.; Yan, L.; Yang, B. Modeling Bidirectional Polarization Distribution Function of Land Surfaces Using Machine Learning Techniques. Remote Sens. 2020, 12, 3891. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Grafton, R.; Nelson, H.; Lambie, N.R.; Wyrwoll, P.R. Normalized Difference Vegetation Index (NDVI): Unforeseen successes in animal ecology. Clim. Res. 2012, 46, 15–27. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.C. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Wang, L.; Ma, Z.; Li, B.; Bartels, R.; Liu, C.; Zhang, X.; Dong, J. Spatially Explicit Model for Statistical Downscaling of Satellite Passive Microwave Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1182–1191. [Google Scholar] [CrossRef]
- Lin, L. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Archdeacon, T.J. Correlation and Regression Analysis: A Historian’s Guide; University of Wisconsin Press: Madison, WI, USA, 1994. [Google Scholar]
- Brown, C.E. Coefficient of variation. In Applied Multivariate Statistics in Geohydrology and Related Sciences; Springer: Berlin/Heidelberg, Germany, 1998; pp. 155–157. [Google Scholar]
- Wang, Z.M.; Song, K.S.; Zhang, B.; Liu, D.W.; Ren, C.Y.; Luo, L.; Yang, T.; Huang, N.; Hu, L.; Yang, H.J.; et al. Shrinkage and fragmentation of grasslands in the West Songnen Plain, China. Agric. Ecosyst. Environ. 2009, 129, 315–324. [Google Scholar] [CrossRef]
- He, J.; Gao, C.; Lin, Q.; Zhang, S.; Zhao, W.; Lu, X.; Wang, G. Temporal and Spatial Changes in Black Carbon Sedimentary Processes in Wetlands of Songnen Plain, Northeast of China. PLoS ONE 2015, 10, e0140834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, J.H.; Li, X.J.; Zhao, K. Quantitative analysis of relationships between crack characteristics and properties of soda-saline soils in Songnen Plain, China. Chin. Geogr. Sci. 2015, 25, 591–601. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, B.S.; Yang, Z.F. Dynamics of the soil water and solute in the sodic saline soil in the Songnen Plain, China. Environ. Earth Sci. 2009, 59, 837–845. [Google Scholar] [CrossRef]
- Yang, X.G.; Yu, Y. Estimating Soil Salinity Under Various Moisture Conditions: An Experimental Study. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2525–2533. [Google Scholar] [CrossRef]
- Xiu, L. The Alkili-saline Land and Agricultural Sustainable Development of the Western Songnen Plain in China. Sci. Geogr. Sin. 2000, 20, 51–55. [Google Scholar]
- Drake, N.A. Reflectance Spectra of Evaporite Minerals (400-2500-Nm)—Applications for Remote-Sensing. Int. J. Remote Sens. 1995, 16, 2555–2571. [Google Scholar] [CrossRef]
- Crowley, J.K. Visible and near-infrared (0.4-2.5μm) reflectance spectra of Playa evaporite minerals. J. Geophys. Res. 1991, 96, 16231–16240. [Google Scholar] [CrossRef]
- Weng, Y.L.; Gong, P.; Zhu, Z.L. Reflectance spectroscopy for the assessment of soil salt content in soils of the Yellow River Delta of China. Int. J. Remote Sens. 2008, 29, 5511–5531. [Google Scholar] [CrossRef]
- Salazar, A.; Vergara, L.; Safont, G. Generative Adversarial Networks and Markov Random Fields for oversampling very small training sets. Expert Syst. Appl. 2021, 163, 113819. [Google Scholar] [CrossRef]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]









| Semi-empirical BPDF Models | Nadal–Bréon model | ρ | 0.025 |
| β | 51.784 | ||
| Litvinov model | α | 3.366 | |
| σ2 | 0.274 | ||
| kr | 0.652 | ||
| Xie–Cheng model | A | 0.866 | |
| kr | 0.501 | ||
| Machine Learning-based BPDF Model | SVR | γ | 12.13 |
| C | 2.58 | ||
| RF | ntree | 200 | |
| DNN | number of layers | 3 | |
| learning rate (670) | 0.5 | ||
| learning rate (865) | 0.4 | ||
| number of nodes | 5,5,1 | ||
| activations | tanh | ||
| optimizer | SGD |
| Minimum | Maximum | |
|---|---|---|
| EC (ds/m) | 0.930 | 5.510 |
| pH | 8.190 | 9.490 |
| C (%) | 1.210 | 2.130 |
| N (%) | 0.014 | 0.078 |
| Band | Index | Semi-empirical BPDF Models | Machine Learning | ||||
|---|---|---|---|---|---|---|---|
| Nadal–Bréon | Litvinov Model | Xie–Cheng Model | SVR | RF | DNN | ||
| 670 nm | RMSE | 0.0372 | 0.0359 | 0.0361 | 0.0425 | 0.0384 | 0.0348 |
| Cor | 0.8935 | 0.8884 | 0.8625 | 0.9275 | 0.8785 | 0.9316 | |
| R2 | 0.6572 | 0.6700 | 0.6452 | 0.4651 | 0.6994 | 0.7521 | |
| 865 nm | RMSE | 0.0613 | 0.0579 | 0.0562 | 0.0492 | 0.0476 | 0.0451 |
| Cor | 0.9335 | 0.9336 | 0.9055 | 0.8791 | 0.8973 | 0.8917 | |
| R2 | 0.4376 | 0.4995 | 0.5127 | 0.6059 | 0.7426 | 0.7692 | |
| Index | Semi-Empirical BPDF Models | Machine Learning | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nadal–Bréon | Litvinov Model | Xie–Cheng Model | SVR | RF | DNN | |||||||
| 670 nm | 865 nm | 670 nm | 865 nm | 670 nm | 865 nm | 670 nm | 865 nm | 670 nm | 865 nm | 670 nm | 865 nm | |
| F-statistic | 1518 | 1934 | 1500 | 2052 | 1253 | 1560 | 175.7 | 185.5 | 272.3 | 296.5 | 612.9 | 353.4 |
| Prob (F-statistic) | 4.61 × 10−51 | 3.04 × 10−46 | 3.84 × 10−53 | 2.42 × 10−50 | 4.88 × 10−51 | 3.91 × 10−48 | 5.74 × 10−12 | 1.41 × 10−11 | 1.80 × 10−16 | 1.84 × 10−13 | 1.48 × 10−17 | 3.51 × 10−14 |
| cv | 0.5333 | 0.5171 | 0.5505 | 0.5301 | 0.5361 | 0.5216 | 0.1518 | 0.2616 | 0.5281 | 0.4784 | 0.5184 | 0.5246 |
| 670 nm | Machine Learning | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SVR | RF | DNN | |||||||
| Training Ratio (%) | RMSE | Cor | R2 | RMSE | Cor | R2 | RMSE | Cor | R2 |
| 10 | 0.0713 | 0.4357 | 0.0542 | 0.0552 | 0.6421 | 0.2043 | 0.0628 | 0.5123 | 0.045 |
| 20 | 0.0751 | 0.3653 | 0.1436 | 0.0622 | 0.5395 | 0.1008 | 0.0828 | 0.0103 | 0.086 |
| 30 | 0.0674 | 0.2965 | 0.2013 | 0.0445 | 0.7632 | 0.4834 | 0.0418 | 0.8231 | 0.6084 |
| 40 | 0.0703 | 0.4376 | 0.1963 | 0.0553 | 0.7038 | 0.3547 | 0.0456 | 0.8421 | 0.5455 |
| 50 | 0.0683 | 0.8632 | 0.2675 | 0.0506 | 0.7558 | 0.4896 | 0.0436 | 0.8319 | 0.6201 |
| 60 | 0.0534 | 0.8953 | 0.2141 | 0.0451 | 0.7691 | 0.5621 | 0.0339 | 0.8911 | 0.7471 |
| 70 | 0.0425 | 0.9275 | 0.4651 | 0.0384 | 0.8785 | 0.6994 | 0.0348 | 0.9316 | 0.7521 |
| 80 | 0.0458 | 0.9348 | 0.4765 | 0.0437 | 0.8566 | 0.6101 | 0.0379 | 0.9339 | 0.7068 |
| 865 nm | Machine Learning | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SVR | RF | DNN | |||||||
| Training Ratio (%) | RMSE | Cor | R2 | RMSE | Cor | R2 | RMSE | Cor | R2 |
| 10 | 0.0717 | 0.8892 | 0.2015 | 0.0586 | 0.7255 | 0.4662 | 0.0762 | 0.8026 | 0.1001 |
| 20 | 0.0745 | 0.8951 | 0.2011 | 0.0454 | 0.8495 | 0.7034 | 0.0438 | 0.8621 | 0.7232 |
| 30 | 0.0743 | 0.8901 | 0.1963 | 0.0396 | 0.8831 | 0.7717 | 0.0368 | 0.9002 | 0.7981 |
| 40 | 0.0515 | 0.8743 | 0.6028 | 0.0393 | 0.8701 | 0.7757 | 0.0352 | 0.9077 | 0.8193 |
| 50 | 0.0517 | 0.8924 | 0.6197 | 0.0471 | 0.8684 | 0.6841 | 0.0383 | 0.9038 | 0.7913 |
| 60 | 0.0551 | 0.8871 | 0.6119 | 0.0443 | 0.9085 | 0.7489 | 0.0412 | 0.9011 | 0.7833 |
| 70 | 0.0492 | 0.8791 | 0.6059 | 0.0476 | 0.8973 | 0.7426 | 0.0451 | 0.8917 | 0.7692 |
| 80 | 0.0572 | 0.9087 | 0.6211 | 0.0612 | 0.8761 | 0.5667 | 0.0541 | 0.9276 | 0.6618 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Q.; Han, Y.; Xu, Y.; Yao, H.; Niu, H.; Huang, F. Laboratory Research on Polarized Optical Properties of Saline-Alkaline Soil Based on Semi-Empirical Models and Machine Learning Methods. Remote Sens. 2022, 14, 226. https://doi.org/10.3390/rs14010226
Gu Q, Han Y, Xu Y, Yao H, Niu H, Huang F. Laboratory Research on Polarized Optical Properties of Saline-Alkaline Soil Based on Semi-Empirical Models and Machine Learning Methods. Remote Sensing. 2022; 14(1):226. https://doi.org/10.3390/rs14010226
Chicago/Turabian StyleGu, Qianyi, Yang Han, Yaping Xu, Haiyan Yao, Haofang Niu, and Fang Huang. 2022. "Laboratory Research on Polarized Optical Properties of Saline-Alkaline Soil Based on Semi-Empirical Models and Machine Learning Methods" Remote Sensing 14, no. 1: 226. https://doi.org/10.3390/rs14010226
APA StyleGu, Q., Han, Y., Xu, Y., Yao, H., Niu, H., & Huang, F. (2022). Laboratory Research on Polarized Optical Properties of Saline-Alkaline Soil Based on Semi-Empirical Models and Machine Learning Methods. Remote Sensing, 14(1), 226. https://doi.org/10.3390/rs14010226