Identifying Forest Structural Types along an Aridity Gradient in Peninsular Spain: Integrating Low-Density LiDAR, Forest Inventory, and Aridity Index
Abstract
:1. Introduction
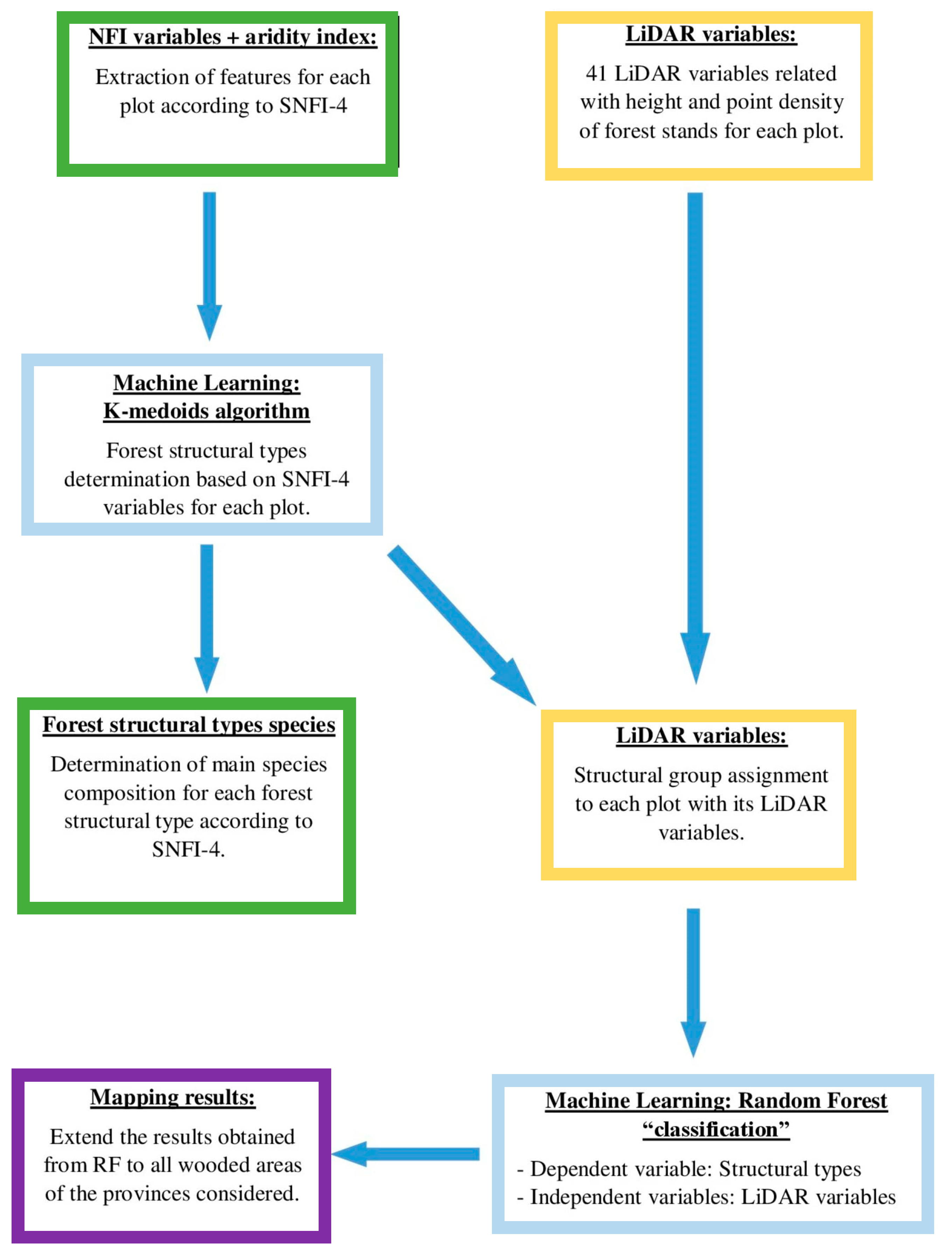
2. Materials and Methods
2.1. Sites Description and Data Gathering
2.1.1. Study Areas
2.1.2. Spanish National Forest Inventory (SNFI)
2.1.3. Airborne LiDAR Data
2.2. Determination of Structural Types from SNFI-4 Data
Discrimination of Structural Types from Airborne LiDAR Data
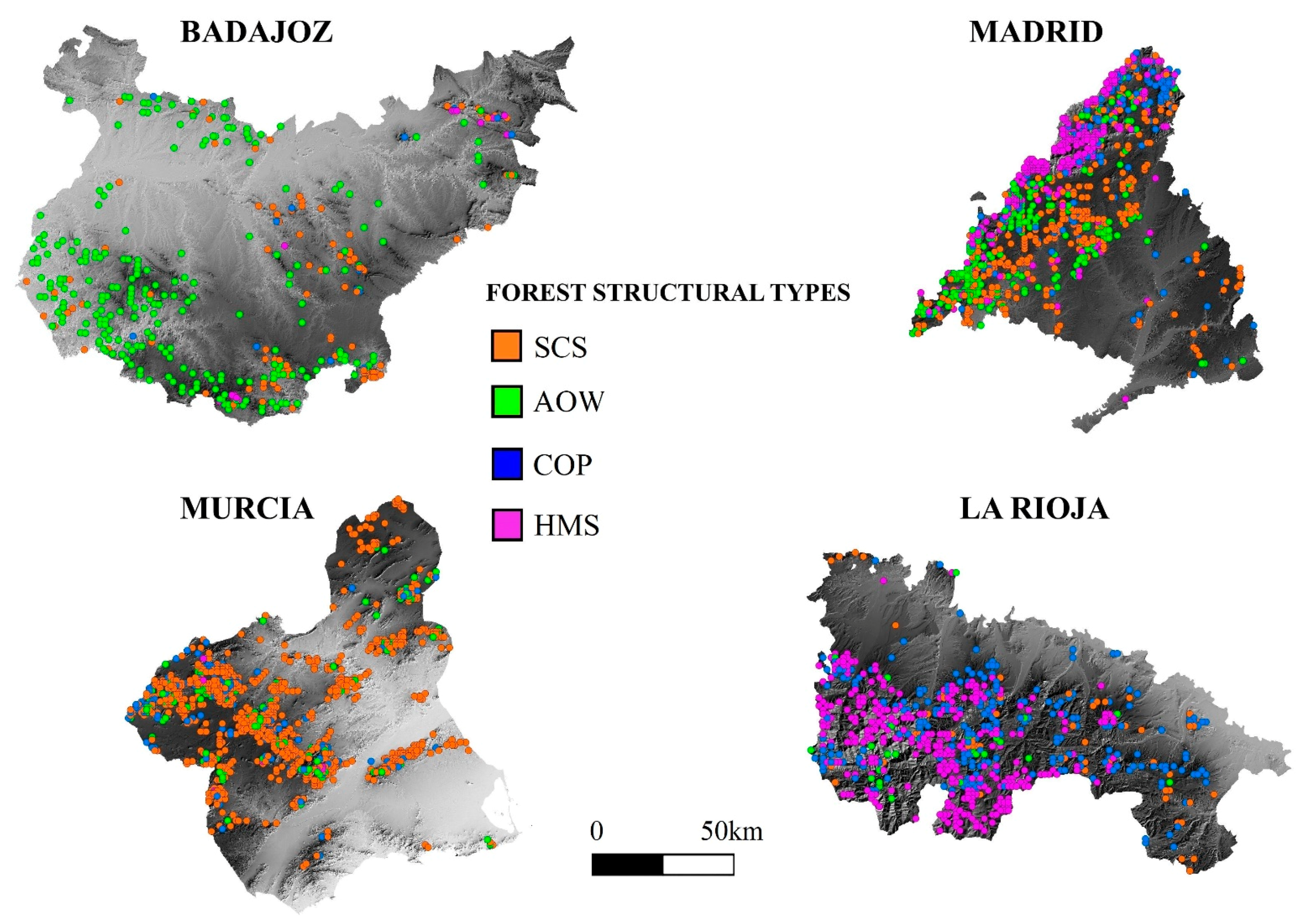
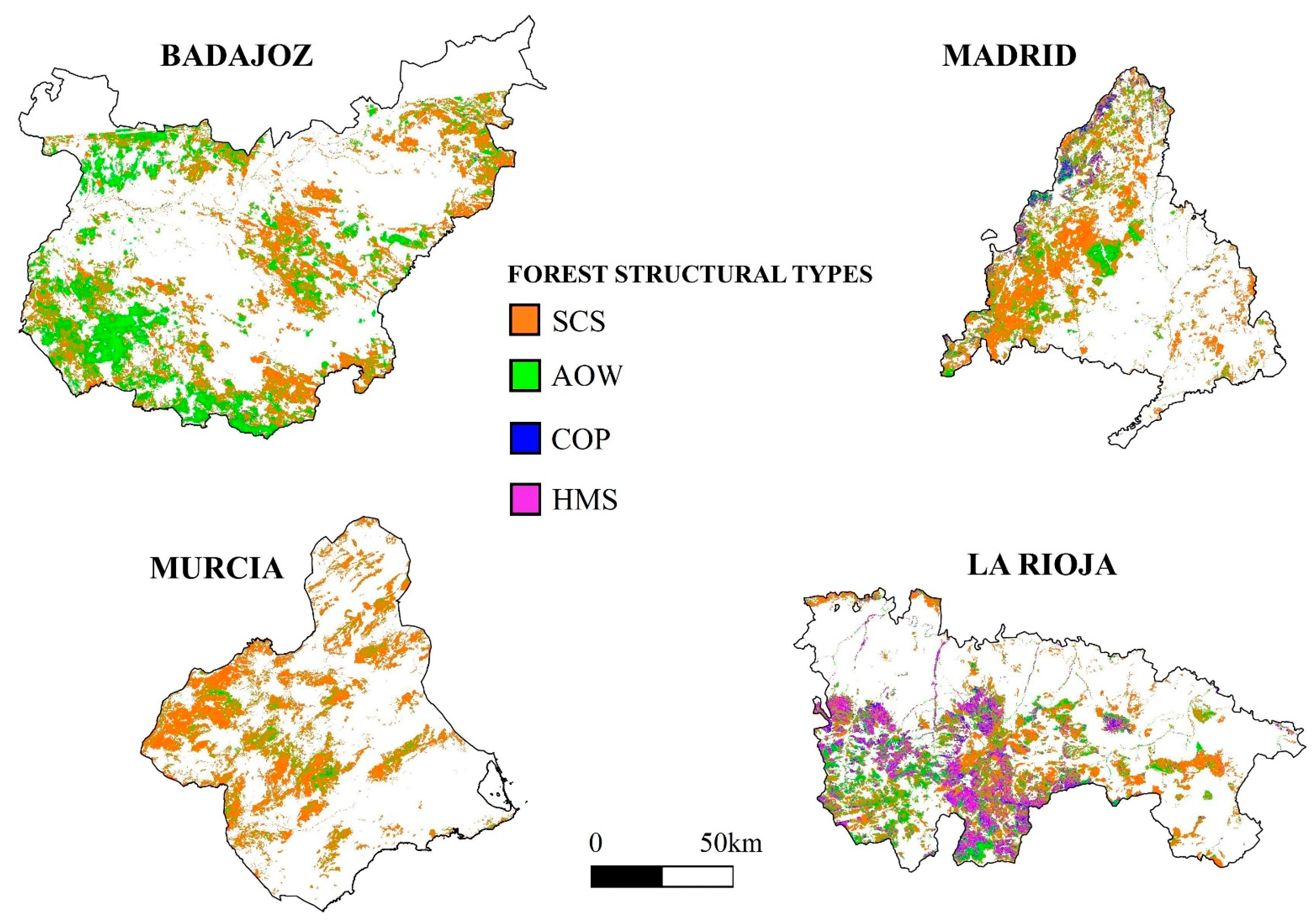
2.3. Regional Forest Structural Types Mapping
2.4. Downsampling Cloud Point Homogenizing Point Density
3. Results
3.1. Forest Structure Based on National Forest Inventories Data
3.2. Discrimination of Forest Structural Types from Airborne LiDAR Data
3.3. The Effect of Homogenizing Point Cloud Density on Model Accuracy
3.4. Species Composition and Forest Structural Types
4. Discussion
4.1. Low-Density LiDAR Data Considerations
4.2. Species Composition and Forest Structural Types
4.3. Other Methodological Remarks
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bohn, F.J.; Huth, A. The importance of forest structure to biodiversity-productivity relationships. R. Soc. Open Sci. 2017, 4, 160521. [Google Scholar] [CrossRef] [Green Version]
- Lelli, C.; Bruun, H.H.; Chiarucci, A.; Donati, D.; Frascaroli, F.; Fritz, Ö.; Goldberg, I.; Nascimbene, J.; Tøttrup, A.P.; Rahbek, C.; et al. Biodiversity response to forest structure and management: Comparing species richness, conservation relevant species and functional diversity as metrics in forest conservation. For. Ecol. Manag. 2019, 432, 707–717. [Google Scholar] [CrossRef]
- Pereira, P.; Úbeda, X.; Martin, D.; Mataix-Solera, J.; Cerdà, A.; Burguet, M. Wildfire effects on extractable elements in ash from a Pinus pinaster forest in Portugal. Hydrol. Process. 2014, 28, 3681–3690. [Google Scholar] [CrossRef]
- Gonsalves, L.; Law, B.; Blakey, R. Experimental evaluation of the initial effects of large-scale thinning on structure and biodiversity of river red gum (Eucalyptus camaldulensis) forests. Wildl. Res. 2018, 45, 397–410. [Google Scholar] [CrossRef]
- Pretzsch, H.; Bielak, K.; Block, J.; Bruchwald, A.; Dieler, J.; Ehrhart, H.-P.; Kohnle, U.; Nagel, J.; Spellmann, H.; Zasada, M.; et al. Productivity of mixed versus pure stands of oak (Quercus petraea (M att.) L iebl. and Quercus robur L.) and European beech (Fagus sylvatica L.) along an ecological gradient. Eur. J. For. Res. 2013, 132, 263–280. [Google Scholar] [CrossRef]
- Williams, A.P.; Allen, C.D.; Millar, C.I.; Swetnam, T.W.; Michaelsen, J.; Still, C.J.; Leavitt, S.W. Forest responses to increasing aridity and warmth in the southwestern United States. Proc. Natl. Acad. Sci. USA 2010, 107, 21289–21294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gómez-Aparicio, L.; García-Valdés, R.; Ruiz-Benito, P.; Zavala, M.A. Disentangling the relative importance of climate, size and competition on tree growth in Iberian forests: Implications for forest management under global change. Glob. Chang. Biol. 2011, 17, 2400–2414. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Benito, P.; Lines, E.R.; Gómez-Aparicio, L.; Zavala, M.A.; Coomes, D.A. Patterns and Drivers of Tree Mortality in Iberian Forests: Climatic Effects Are Modified by Competition. PLoS ONE 2013, 8, e56843. [Google Scholar] [CrossRef] [Green Version]
- Condés, S.; del Rio, M. Climate modifies tree interactions in terms of basal area growth and mortality in monospecific and mixed Fagus sylvatica and Pinus sylvestris forests. Eur. J. For. Res. 2015, 134, 1095–1108. [Google Scholar] [CrossRef]
- Park, J.; Kim, T.; Moon, M.; Cho, S.; Ryu, D.; Kim, H.S. Effects of thinning intensities on tree water use, growth, and resultant water use efficiency of 50-year-old Pinus koraiensis forest over four years. For. Ecol. Manag. 2018, 408, 121–128. [Google Scholar] [CrossRef]
- Seidl, R.; Schelhaas, M.-J.; Lexer, M.J. Unraveling the drivers of intensifying forest disturbance regimes in Europe. Glob. Chang. Biol. 2011, 17, 2842–2852. [Google Scholar] [CrossRef]
- Marqués, L.; Zavala, M.A.; Camarero, J.J.; Hartig, F.; Madrigal-González, J. Last-century forest productivity in a managed dry-edge Scots pine population: The two sides of climate warming. Ecol. Appl. 2018, 28, 95–105. [Google Scholar] [CrossRef]
- Madrigal-González, J.; Ballesteros-Cánovas, J.A.; Zavala, M.A.; Morales-Molino, C.; Stoffel, M. Forest stocks control long-term climatic mortality risks in Scots pine dry-edge forests. Ecosphere 2020, 11. [Google Scholar] [CrossRef]
- Astigarraga, J.; Andivia, E.; Zavala, M.A.; Gazol, A.; Cruz-Alonso, V.; Vicente-Serrano, S.M.; Ruiz-Benito, P. Evidence of non-stationary relationships between climate and forest responses: Increased sensitivity to climate change in Iberian forests. Glob. Chang. Biol. 2020, 26, 5063–5076. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.G.; Allen, C.D.; Anderson-Teixeira, K.; Aukema, B.H.; Bond-Lamberty, B.; Chini, L.; Clark, J.S.; Dietze, M.; Grossiord, C.; Hanbury-Brown, A.; et al. Pervasive shifts in forest dynamics in a changing world. Science 2020, 368. [Google Scholar] [CrossRef] [PubMed]
- Plas, F.; Ratcliffe, S.; Ruiz-Benito, P.; Scherer-Lorenzen, M.; Verheyen, K.; Wirth, C.; Zavala, M.A.; Ampoorter, E.; Baeten, L.; Barbaro, L.; et al. Continental mapping of forest ecosystem functions reveals a high but unrealised potential for forest multifunctionality. Ecol. Lett. 2018, 21, 31–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torresan, C.; Corona, P.; Scrinzi, G.; Marsal, J.V. Using classification trees to predict forest structure types from LiDAR data. Ann. For. Res. 2016, 59. [Google Scholar] [CrossRef]
- Neuville, R.; Bates, J.; Jonard, F. Estimating Forest Structure from UAV-Mounted LiDAR Point Cloud Using Machine Learning. Remote Sens. 2021, 13, 352. [Google Scholar] [CrossRef]
- Moreno-Fernández, D.; Cañellas, I.; Alberdi, I.; Montes, F. Improved stand structure characterization from nested plot designs in the Spanish National Forest Inventory. For. An Int. J. For. Res. 2021, 94, 244–257. [Google Scholar] [CrossRef]
- Scholes, R.J.; Dowty, P.R.; Caylor, K.; Parsons, D.A.B.; Frost, P.G.H.; Shugart, H.H. Trends in savanna structure and composition along an aridity gradient in the Kalahari. J. Veg. Sci. 2002, 13, 419–428. [Google Scholar] [CrossRef]
- Dodson, E.K.; Ares, A.; Puettmann, K.J. Early responses to thinning treatments designed to accelerate late successional forest structure in young coniferous stands of western Oregon, USA. Can. J. For. Res. 2012, 42, 345–355. [Google Scholar] [CrossRef]
- Restaino, C.; Young, D.J.N.; Estes, B.; Gross, S.; Wuenschel, A.; Meyer, M.; Safford, H. Forest structure and climate mediate drought-induced tree mortality in forests of the Sierra Nevada, USA. Ecol. Appl. 2019, 29, e01902. [Google Scholar] [CrossRef] [PubMed]
- Khabarov, N.; Krasovskiy, A.; Obersteiner, M.; Swart, R.; Dosio, A.; San-Miguel-Ayanz, J.; Durrant, T.; Camia, A.; Migliavacca, M. Forest fires and adaptation options in Europe. Reg. Environ. Chang. 2016, 16, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Bussotti, F.; Pollastrini, M.; Holland, V.; Brüggemann, W. Functional traits and adaptive capacity of European forests to climate change. Environ. Exp. Bot. 2015, 111, 91–113. [Google Scholar] [CrossRef]
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Chirici, G.; Winter, S.; McRoberts, R.E. National Forest Inventories: Contributions to Forest Biodiversity Assessments; Springer Science & Business Media: Cham, Switzerland, 2011; Volume 20. [Google Scholar]
- Ruiz-Benito, P.; Vacchiano, G.; Lines, E.R.; Reyer, C.P.; Ratcliffe, S.; Morin, X.; Hartig, F.; Mäkelä, A.; Yousefpour, R.; Chaves, J.E.; et al. Available and missing data to model impact of climate change on European forests. Ecol. Model. 2020, 416, 108870. [Google Scholar] [CrossRef]
- Álvarez-González, J.G.; Canellas, I.; Alberdi, I.; Gadow, K.; González, A.D.R. National Forest Inventory and forest observational studies in Spain: Applications to forest modeling. For. Ecol. Manag. 2014, 316, 54–64. [Google Scholar] [CrossRef]
- Reque, J.A.; Bravo, F. Identifying forest structure types using National Forest Inventory Data: The case of sessile oak forest in the Cantabrian range. Investig. Agrar. Sist. Recur. 2008, 17, 105. [Google Scholar] [CrossRef] [Green Version]
- Garcia, M.; Saatchi, S.; Ustin, S.; Balzter, H. Modelling forest canopy height by integrating airborne LiDAR samples with satellite Radar and multispectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 159–173. [Google Scholar] [CrossRef]
- Durán, J.V. Los inventarios forestales nacionales: Una herramienta para la gestión, la planificación y la investigación. Foresta 2013, 57, 34–41. [Google Scholar]
- Simard, M.; Pinto, N.; Fisher, J.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Coops, N.C.; Tompalski, P.; Nielsen, S.E.; Bater, C.W.; Stadt, J.J. Regional mapping of vegetation structure for biodiversity monitoring using airborne lidar data. Ecol. Inform. 2017, 38, 50–61. [Google Scholar] [CrossRef]
- Deo, R.K.; Russell, M.B.; Domke, G.M.; Woodall, C.W.; Falkowski, M.J.; Cohen, W.B. Using Landsat Time-Series and LiDAR to Inform Aboveground Forest Biomass Baselines in Northern Minnesota, USA. Can. J. Remote Sens. 2017, 43, 28–47. [Google Scholar] [CrossRef]
- Beaudoin, A.; Bernier, P.Y.; Guindon, L.; Villemaire, P.; Guo, X.J.; Stinson, G.; Bergeron, T.; Magnussen, S.; Hall, R.J. Mapping attributes of Canada’s forests at moderate resolution through kNN and MODIS imagery. Can. J. For. Res. 2014, 44, 521–532. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, L.; Recio, J.A.; Crespo-Peremarch, P.; Sapena, M. An object-based approach for mapping forest structural types based on low-density LiDAR and multispectral imagery. Geocarto Int. 2018, 33, 443–457. [Google Scholar] [CrossRef]
- Wulder, M.; White, J.; Alvarez, F.; Han, T.; Rogan, J.; Hawkes, B. Characterizing boreal forest wildfire with multi-temporal Landsat and LIDAR data. Remote Sens. Environ. 2009, 113, 1540–1555. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Tomppo, E.O. Remote sensing support for national forest inventories. Remote Sens. Environ. 2007, 110, 412–419. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Gormanson, D.D.; Walters, B. The shelf-life of airborne laser scanning data for enhancing forest inventory inferences. Remote Sens. Environ. 2018, 206, 254–259. [Google Scholar] [CrossRef]
- Pascual, A.; Guerra-Hernández, J.; Cosenza, D.N.; Sandoval-Altelarrea, V. Using enhanced data co-registration to update Spanish National Forest Inventories (NFI) and to reduce training data under LiDAR-assisted inference. Int. J. Remote Sens. 2021, 42, 126–147. [Google Scholar] [CrossRef]
- Wiggins, H.L.; Nelson, C.R.; Larson, A.J.; Safford, H.D. Using LiDAR to develop high-resolution reference models of forest structure and spatial pattern. For. Ecol. Manag. 2019, 434, 318–330. [Google Scholar] [CrossRef]
- Kane, V.R.; Bakker, J.D.; McGaughey, R.J.; Lutz, J.; Gersonde, R.F.; Franklin, J.F. Examining conifer canopy structural complexity across forest ages and elevations with LiDAR data. Can. J. For. Res. 2010, 40, 774–787. [Google Scholar] [CrossRef]
- Kane, V.R.; McGaughey, R.J.; Bakker, J.D.; Gersonde, R.F.; Lutz, J.A.; Franklin, J.F. Comparisons between field-and LiDAR-based measures of stand structural complexity. Can. J. For. Res. 2010, 40, 761–773. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Haywood, A.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Skidmore, A. Using discrete-return airborne laser scanning to quantify number of canopy strata across diverse forest types. Methods Ecol. Evol. 2016, 7, 700–712. [Google Scholar] [CrossRef]
- Woodgate, W.; Jones, S.D.; Suarez, L.; Hill, M.; Armston, J.D.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. Understanding the variability in ground-based methods for retrieving canopy openness, gap fraction, and leaf area index in diverse forest systems. Agric. For. Meteorol. 2015, 205, 83–95. [Google Scholar] [CrossRef]
- Riaño, D.; Valladares, F.; Condés, S.; Chuvieco, E. Estimation of leaf area index and covered ground from airborne laser scanner (Lidar) in two contrasting forests. Agric. For. Meteorol. 2004, 124, 269–275. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, X.; Schull, M.A.; Román-Colón, M.O.; Yao, T.; Wang, Z.; Zhang, Q.; Jupp, D.L.; Lovell, J.L.; Culvenor, D.S.; et al. Measuring effective leaf area index, foliage profile, and stand height in New England forest stands using a full-waveform ground-based lidar. Remote Sens. Environ. 2011, 115, 2954–2964. [Google Scholar] [CrossRef]
- Magnussen, S.; Nord-Larsen, T.; Riis-Nielsen, T. Lidar supported estimators of wood volume and aboveground biomass from the Danish national forest inventory (2012–2016). Remote Sens. Environ. 2018, 211, 146–153. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking lidar and forest modeling to assess biomass estimation across scales and disturbance states. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
- Silva, C.A.; Saatchi, S.; Garcia, M.; Labriere, N.; Klauberg, C.; Ferraz, A.; Meyer, V.; Jeffery, K.J.; Abernethy, K.; White, L.; et al. Comparison of Small- and Large-Footprint Lidar Characterization of Tropical Forest Aboveground Structure and Biomass: A Case Study from Central Gabon. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3512–3526. [Google Scholar] [CrossRef] [Green Version]
- Zhao, F.; Strahler, A.H.; Schaaf, C.; Yao, T.; Yang, X.; Wang, Z.; Schull, M.A.; Román, M.O.; Woodcock, C.E.; Olofsson, P.; et al. Measuring gap fraction, element clumping index and LAI in Sierra Forest stands using a full-waveform ground-based lidar. Remote Sens. Environ. 2012, 125, 73–79. [Google Scholar] [CrossRef]
- Garcia, M.; Gajardo, J.; Riano, D.; Zhao, K.; Martín, P.; Ustin, S. Canopy clumping appraisal using terrestrial and airborne laser scanning. Remote Sens. Environ. 2015, 161, 78–88. [Google Scholar] [CrossRef]
- Smith, A.; Falkowski, M.J.; Hudak, A.T.; Evans, J.; Robinson, A.; Steele, C.M. A cross-comparison of field, spectral, and lidar estimates of forest canopy cover. Can. J. Remote Sens. 2009, 35, 447–459. [Google Scholar] [CrossRef]
- Tang, H.; Armston, J.; Hancock, S.; Marselis, S.; Goetz, S.; Dubayah, R. Characterizing global forest canopy cover distribution using spaceborne lidar. Remote Sens. Environ. 2019, 231, 111262. [Google Scholar] [CrossRef]
- Valbuena, R.; Maltamo, M.; Mehtätalo, L.; Packalen, P. Key structural features of Boreal forests may be detected directly using L-moments from airborne lidar data. Remote Sens. Environ. 2017, 194, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Adnan, S.; Maltamo, M.; Coomes, D.A.; García-Abril, A.; Malhi, Y.; Manzanera, J.A.; Butt, N.; Morecroft, M.; Valbuena, R. A simple approach to forest structure classification using airborne laser scanning that can be adopted across bioregions. For. Ecol. Manage. 2019, 433, 111–121. [Google Scholar] [CrossRef]
- Jarron, L.R.; Coops, N.C.; MacKenzie, W.H.; Tompalski, P.; Dykstra, P. Detection of sub-canopy forest structure using airborne LiDAR. Remote Sens. Environ. 2020, 244, 111770. [Google Scholar] [CrossRef]
- Shoot, C.; Andersen, H.-E.; Moskal, L.; Babcock, C.; Cook, B.; Morton, D. Classifying Forest Type in the National Forest Inventory Context with Airborne Hyperspectral and Lidar Data. Remote Sens. 2021, 13, 1863. [Google Scholar] [CrossRef]
- Garcia, M.; Saatchi, S.; Ferraz, A.; Silva, C.A.; Ustin, S.; Koltunov, A.; Balzter, H. Impact of data model and point density on aboveground forest biomass estimation from airborne LiDAR. Carbon Balance Manag. 2017, 12, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Disney, M.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the impact of discrete-return lidar system and survey characteristics over young conifer and broadleaf forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
- Leitold, V.; Keller, M.; Morton, D.C.; Cook, B.D.; Shimabukuro, Y.E. Airborne lidar-based estimates of tropical forest structure in complex terrain: Opportunities and trade-offs for REDD+. Carbon Balance Manag. 2015, 10, 1–12. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the Influence of Plot Size and LiDAR Density on Forest Structure Attribute Estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef] [Green Version]
- Richardson, J.J.; Moskal, L.M. Strengths and limitations of assessing forest density and spatial configuration with aerial LiDAR. Remote Sens. Environ. 2011, 115, 2640–2651. [Google Scholar] [CrossRef]
- Pourshamsi, M.; Xia, J.; Yokoya, N.; Garcia, M.; Lavalle, M.; Pottier, E.; Balzter, H. Tropical forest canopy height estimation from combined polarimetric SAR and LiDAR using machine-learning. ISPRS J. Photogramm. Remote Sens. 2021, 172, 79–94. [Google Scholar] [CrossRef]
- Douss, R.; Ferah, I.R.; Durrieu, S.; de Boissieu, F. Regression analyses to study the benefit of Sentinel and LIDAR data fusion for forest structure. In Proceedings of the 2020 Mediterranean and Middle-East Geoscience and Remote Sensing Symposium (M2GARSS), Tunis, Tunisia, 9–11 March 2020; pp. 359–362. [Google Scholar]
- Lorite Martínez, S.; Ojeda Manrique, J.C.; Rodríguez-Cuenca, B.; González Cristóbal, E.; Muñoz, P. Procesado y distribución de nubes de puntos en el proyecto PNOA-LiDAR. In Proceedings of the XVII Congreso de la Asociación Española de Teledetección, Murcia, Spain, 4–6 October 2017; pp. 3–7. [Google Scholar]
- Gonzalez-Ferreiro, E.; Arellano-Pérez, S.; Castedo-Dorado, F.; Hevia, A.; Vega, J.A.; Vega-Nieva, D.J.; Álvarez-González, J.G.; Ruiz-González, A.D. Modelling the vertical distribution of canopy fuel load using national forest inventory and low-density airbone laser scanning data. PLoS ONE 2017, 12, e0176114. [Google Scholar] [CrossRef] [PubMed]
- Revilla, S.; Lamelas, M.; Domingo, D.; de la Riva, J.; Montorio, R.; Montealegre, A.; García-Martín, A. Assessing the Potential of the DART Model to Discrete Return LiDAR Simulation—Application to Fuel Type Mapping. Remote Sens. 2021, 13, 342. [Google Scholar] [CrossRef]
- Ekhtari, N.; Glennie, C.; Fernandez-Diaz, J.C. Classification of Airborne Multispectral Lidar Point Clouds for Land Cover Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2068–2078. [Google Scholar] [CrossRef]
- Gorgoso-Varela, J.J.; Ponce, R.A.; Rodríguez-Puerta, F. Modeling Diameter Distributions with Six Probability Density Functions in Pinus halepensis Mill. Plantations Using Low-Density Airborne Laser Scanning Data in Aragón (Northeast Spain). Remote Sens. 2021, 13, 2307. [Google Scholar] [CrossRef]
- Chan, E.P.Y.; Fung, T.; Wong, F.K.K. Estimating above-ground biomass of subtropical forest using airborne LiDAR in Hong Kong. Sci. Rep. 2021, 11, 1751. [Google Scholar] [CrossRef]
- Niemelä, J.; Haila, Y.; Punttila, P. The importance of small-scale heterogeneity in boreal forests: Variation in diversity in forest-floor invertebrates across the succession gradient. Ecography 1996, 19, 352–368. [Google Scholar] [CrossRef]
- Kuuluvainen, T.; Aakala, T.; Várkonyi, G. Dead standing pine trees in a boreal forest landscape in the Kalevala National Park, northern Fennoscandia: Amount, population characteristics and spatial pattern. For. Ecosyst. 2017, 4, 12. [Google Scholar] [CrossRef]
- Wickland, K.P.; Neff, J. Decomposition of soil organic matter from boreal black spruce forest: Environmental and chemical controls. Biogeochemistry 2008, 87, 29–47. [Google Scholar] [CrossRef]
- Bradshaw, C.; Warkentin, I.; Sodhi, N.S. Urgent preservation of boreal carbon stocks and biodiversity. Trends Ecol. Evol. 2009, 24, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Vidal-Macua, J.J.; Ninyerola, M.; Zabala, A.; Domingo-Marimon, C.; Pons, X. Factors affecting forest dynamics in the Iberian Peninsula from 1987 to 2012. The role of topography and drought. For. Ecol. Manag. 2017, 406, 290–306. [Google Scholar] [CrossRef]
- de Castro, M.; Martín-Vide, J.; Contributing, S.A.; Abaurrea, J.; Asín, J.; Barriendos, M.; Brunet, M.; Creus, J.; Galán, E.; Gaertner, M.A.; et al. Impacts of Climatic Change in Spain 1. The Climate of Spain: Past, Present and Scenarios for the 21 St Century. A Preliminary Assessment of the Impacts in Spain Due to the Effects of Climate Change; ECCE Project Report; Ministerio del Medio Ambiente: Madrid, Spain, 2005; pp. 1–62.
- Tewksbury, C.; van Miegroet, H. Soil organic carbon dynamics along a climatic gradient in a southern Appalachian spruce–fir forest. Can. J. For. Res. 2007, 37, 1161–1172. [Google Scholar] [CrossRef]
- Stegen, J.C.; Swenson, N.G.; Enquist, B.J.; White, E.P.; Phillips, O.L.; Jørgensen, P.M.; Weiser, M.D.; Monteagudo Mendoza, A.; Núñez Vargas, P. Variation in above-ground forest biomass across broad climatic gradients. Glob. Ecol. Biogeogr. 2011, 20, 744–754. [Google Scholar] [CrossRef]
- Aguirre, A.; del Rio, M.; Condés, S. Intra- and inter-specific variation of the maximum size-density relationship along an aridity gradient in Iberian pinewoods. For. Ecol. Manag. 2018, 411, 90–100. [Google Scholar] [CrossRef]
- de Martonne, E. L’indice d’aridité. Bull. Assoc. Géographes Français 1926, 3, 3–5. [Google Scholar] [CrossRef]
- Condés, S.; Aguirre, A.; del Río, M. Crown plasticity of five pine species in response to competition along an aridity gradient. For. Ecol. Manag. 2020, 473, 118302. [Google Scholar] [CrossRef]
- Pravalie, R.; Sîrodoev, I.; Peptenatu, D. Changes in the forest ecosystems in areas impacted by aridization in south-western Romania. J. Environ. Health Sci. Eng. 2014, 12, 2. [Google Scholar] [CrossRef] [Green Version]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Alberdi, I.; Sandoval, V.; Condés, S.; Cañellas, I.; Vallejo, R. El Inventario Forestal Nacional español, una herramienta para el conocimiento, la gestión y la conservación de los ecosistemas forestales arbolados. Ecosistemas 2016, 25, 88–97. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; FUSION Version 3.80; United States Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2018.
- Hastie, T.; Tibshirani, R.; Friedman, J. Data mining, inference, and prediction. In The Elements of Statistical Learning; Springer: New York, NY, USA, 2001. [Google Scholar]
- Arora, P.; Deepali; Varshney, S. Analysis of K-Means and K-Medoids Algorithm for Big Data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef] [Green Version]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Yan, M.; Ye, K. Determining the Number of Clusters Using the Weighted Gap Statistic. Biometrics 2007, 63, 1031–1037. [Google Scholar] [CrossRef] [PubMed]
- Mohajer, M.; Englmeier, K.-H.; Schmid, V.J. A comparison of Gap statistic definitions with and without logarithm function. arXiv 2011, arXiv:1103.4767 2011. [Google Scholar]
- Garcia, M.; Saatchi, S.; Casas, A.; Koltunov, A.; Ustin, S.; Ramirez, C.; Garcia-Gutierrez, J.; Balzter, H. Quantifying biomass consumption and carbon release from the California Rim fire by integrating airborne LiDAR and Landsat OLI data. J. Geophys. Res. Biogeosci. 2017, 122, 340–353. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Garcia, M.; Ferraz, A.; Keller, M.; Eitel, J.; Saatchi, S. Impacts of Airborne Lidar Pulse Density on Estimating Biomass Stocks and Changes in a Selectively Logged Tropical Forest. Remote Sens. 2017, 9, 1068. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Malley, J.; Tutz, G. An introduction to recursive partitioning: Rationale, application, and characteristics of classification and regression trees, bagging, and random forests. Psychol. Methods 2009, 14, 323. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Frazier, P.; Kumar, L. Comparative assessment of the measures of thematic classification accuracy. Remote Sens. Environ. 2007, 107, 606–616. [Google Scholar] [CrossRef]
- Detto, M.; Muller-Landau, H.; Mascaro, J.; Asner, G. Hydrological Networks and Associated Topographic Variation as Templates for the Spatial Organization of Tropical Forest Vegetation. PLoS ONE 2013, 8, e76296. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Freeman, E.A.; Moisen, G.G.; Frescino, T.S. Evaluating effectiveness of down-sampling for stratified designs and unbalanced prevalence in Random Forest models of tree species distributions in Nevada. Ecol. Model. 2012, 233, 1–10. [Google Scholar] [CrossRef]
- Pascual, C.; García-Abril, A.; García-Montero, L.; Martín-Fernández, S.; Cohen, W. Object-based semi-automatic approach for forest structure characterization using lidar data in heterogeneous Pinus sylvestris stands. For. Ecol. Manag. 2008, 255, 3677–3685. [Google Scholar] [CrossRef] [Green Version]
- Abdullahi, S.; Schardt, M.; Pretzsch, H. An unsupervised two-stage clustering approach for forest structure classification based on X-band InSAR data—A case study in complex temperate forest stands. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 36–48. [Google Scholar] [CrossRef]
- Moran, C.J.; Rowell, E.M.; Seielstad, C.A. A data-driven framework to identify and compare forest structure classes using LiDAR. Remote Sens. Environ. 2018, 211, 154–166. [Google Scholar] [CrossRef]
- Wallace, C.S.; Dale, M.B. Hierarchical clusters of vegetation types. Community Ecol. 2005, 6, 57–74. [Google Scholar] [CrossRef] [Green Version]
- de Cáceres, M.; Font, X.; Oliva, F. The management of vegetation classifications with fuzzy clustering. J. Veg. Sci. 2010, 21, 1138–1151. [Google Scholar] [CrossRef]
- Moeser, D.; Morsdorf, F.; Jonas, T. Novel forest structure metrics from airborne LiDAR data for improved snow interception estimation. Agric. For. Meteorol. 2015, 208, 40–49. [Google Scholar] [CrossRef]
- Kane, V.R.; North, M.P.; Lutz, J.; Churchill, D.J.; Roberts, S.; Smith, D.F.; McGaughey, R.J.; Kane, J.T.; Brooks, M.L. Assessing fire effects on forest spatial structure using a fusion of Landsat and airborne LiDAR data in Yosemite National Park. Remote Sens. Environ. 2014, 151, 89–101. [Google Scholar] [CrossRef]
- Karna, Y.K.; Penman, T.D.; Aponte, C.; Bennett, L.T. Assessing Legacy Effects of Wildfires on the Crown Structure of Fire-Tolerant Eucalypt Trees Using Airborne LiDAR Data. Remote Sens. 2019, 11, 2433. [Google Scholar] [CrossRef] [Green Version]
- Karna, Y.K.; Penman, T.D.; Aponte, C.; Hinko-Najera, N.; Bennett, L.T. Persistent changes in the horizontal and vertical canopy structure of fire-tolerant forests after severe fire as quantified using multi-temporal airborne lidar data. For. Ecol. Manag. 2020, 472, 118255. [Google Scholar] [CrossRef]
- Gorgens, E.; Montaghi, A.; Rodriguez, L.C. A performance comparison of machine learning methods to estimate the fast-growing forest plantation yield based on laser scanning metrics. Comput. Electron. Agric. 2015, 116, 221–227. [Google Scholar] [CrossRef]
- Görgens, E.B.; Packalen, P.; da Silva, A.G.P.; Alvares, C.A.; Campoe, O.C.; Stape, J.L.; Rodriguez, L.C. Stand volume models based on stable metrics as from multiple ALS acquisitions in Eucalyptus plantations. Ann. For. Sci. 2015, 72, 489–498. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.-P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Chen, Q.; Qi, C. Lidar remote sensing of vegetation biomass. Remote Sens. Nat. Resour. 2013, 399, 399–420. [Google Scholar]
- Huesca, M.; Roth, K.L.; García, M.; Ustin, S.L. Discrimination of Canopy Structural Types in the Sierra Nevada Mountains in Central California. Remote Sens. 2019, 11, 1100. [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A.; Harding, D.; Cohen, W.; Parker, G.; Shugart, H. Surface Lidar Remote Sensing of Basal Area and Biomass in Deciduous Forests of Eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Fang, J.; Wang, X.; Liu, Y.; Tang, Z.; White, P.S.; Sanders, N.J. Multi-scale patterns of forest structure and species composition in relation to climate in northeast China. Ecography 2012, 35, 1072–1082. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. For. Int. J. For. Res. 2012, 85, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Ediriweera, S.; Pathirana, S.; Danaher, T.; Nichols, D. LiDAR remote sensing of structural properties of subtropical rainforest and eucalypt forest in complex terrain in North-eastern Australia. J. Trop. For. Sci. 2014, 26, 397–408. [Google Scholar]
- Falkowski, M.J.; Smith, A.M.; Gessler, P.E.; Hudak, A.T.; Vierling, L.A.; Evans, J.S. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens. 2008, 34, S338–S350. [Google Scholar] [CrossRef]
- Jeronimo, S. LiDAR Individual Tree Detection for Assessing Structurally Diverse Forest Landscapes. Doctoral Dissertation. 2015. Available online: https://digital.lib.washington.edu/researchworks/handle/1773/35211 (accessed on 1 November 2021).
- Hayashi, R.; Weiskittel, A.; Sader, S. Assessing the Feasibility of Low-Density LiDAR for Stand Inventory Attribute Predictions in Complex and Managed Forests of Northern Maine, USA. Forests 2014, 5, 363–383. [Google Scholar] [CrossRef] [Green Version]
- Wulder, M.; Bater, C.W.; Coops, N.; Hilker, T.; White, J. The role of LiDAR in sustainable forest management. For. Chron. 2008, 84, 807–826. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Fernández, D.; Hernández, L.; Sánchez-González, M.; Cañellas, I.; Montes, F. Space–time modeling of changes in the abundance and distribution of tree species. For. Ecol. Manag. 2016, 372, 206–216. [Google Scholar] [CrossRef]
- Aldea, J.; Bravo, F.; Vázquez-Piqué, J.; Ruíz-Peinado, R.; del Río, M. Differences in stem radial variation between Pinus pinaster Ait. and Quercus pyrenaica Willd. may release inter-specific competition. For. Ecol. Manag. 2021, 481, 118779. [Google Scholar] [CrossRef]
- Garilleti, R.; Calleja, J.A.; Lara, F. Vegetación Ribereña de los Ríos y Ramblas de la España Meridional (Península y Archipiélagos); Ministerio de Agricultura, Alimentación y Medio Ambiente, Centro de Publicaciones: Madrid, Spain, 2012. [Google Scholar]
- de Andrés, E.G.; Camarero, J.J.; Blanco, J.A.; Imbert, J.B.; Lo, Y.-H.; Sangüesa-Barreda, G.; Castillo, F.J. Tree-to-tree competition in mixed European beech-Scots pine forests has different impacts on growth and water-use efficiency depending on site conditions. J. Ecol. 2018, 106, 59–75. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Fernández, D.; Ledo, A.; Martín-Benito, D.; Canellas, I.; Gea-Izquierdo, G. Negative synergistic effects of land-use legacies and climate drive widespread oak decline in evergreen Mediterranean open woodlands. For. Ecol. Manag. 2019, 432, 884–894. [Google Scholar] [CrossRef]
- Pasalodos-Tato, M.; Alberdi, I.; Canellas, I.; González, M.S. Towards assessment of cork production through National Forest Inventories. For. An Int. J. For. Res. 2018, 91, 110–120. [Google Scholar] [CrossRef] [Green Version]
- del Castillo, E.; Tejedor, E.; Serrano-Notivoli, R.; Novak, K.; Saz, M.Á.; Longares, L.A.; de Luis, M. Contrasting patterns of tree growth of mediterranean pine species in the iberian peninsula. Forests 2018, 9, 416. [Google Scholar] [CrossRef] [Green Version]
- Quinto, L.; Navarro-Cerrillo, R.M.; Palacios-Rodriguez, G.; Ruiz-Gómez, F.; Duque-Lazo, J. The current situation and future perspectives of Quercus ilex and Pinus halepensis afforestation on agricultural land in Spain under climate change scenarios. N. For. 2021, 52, 145–166. [Google Scholar] [CrossRef]
- Pacheco, A.; Camarero, J.J.; Ribas, M.; Gazol, A.; Gutierrez, E.; Carrer, M. Disentangling the climate-driven bimodal growth pattern in coastal and continental Mediterranean pine stands. Sci. Total Environ. 2018, 615, 1518–1526. [Google Scholar] [CrossRef]
- Tiscar, P.A.; Linares, J.C. Pinus nigra subsp. salzmannii forests from Southeast Spain: Using structure and process information to guide management. In Pine Forests: Types, Threats and Management; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2011; pp. 1–27. [Google Scholar]
- Sánchez-Salguero, R.; Navarro-Cerrillo, R.M.; Camarero, J.J.; Fernández-Cancio, A. Selective drought-induced decline of pine species in southeastern Spain. Clim. Chang. 2012, 113, 767–785. [Google Scholar] [CrossRef]
- Linares, A.M. Forest planning and traditional knowledge in collective woodlands of Spain: The dehesa system. For. Ecol. Manag. 2007, 249, 71–79. [Google Scholar] [CrossRef]
- López Estébanez, N.; Gomez Mediavilla, G.; Gómez Mendoza, J.; de Lomana, G.; Sáez Pombo, E. Forest dynamics in the Spanish central mountain range. End Tradit. 2010, 8, 119. [Google Scholar]
- Arnáez, J.; Oserin, M.; Ortigosa, L.; Martínez, T.L. Cambios en la cubierta vegetal y usos del suelo en el Sistema Ibérico noroccidental entre 1956 y 2001: Los Cameros (La Rioja, España). Boletín Asoc. Geógrafos Españoles 2008, 47, 195–211. [Google Scholar]
- Scarascia-Mugnozza, G.; Oswald, H.; Piussi, P.; Radoglou, K. Forests of the Mediterranean region: Gaps in knowledge and research needs. For. Ecol. Manag. 2000, 132, 97–109. [Google Scholar] [CrossRef]
- Seidler, R. Patterns of Biodiversity Change in Anthropogenically Altered Forests. In Encyclopedia of Biodiversity; Elsevier: Amsterdam, The Netherlands, 2013; pp. 446–458. [Google Scholar] [CrossRef]
- Zhao, D.; Bullock, B.P.; Montes, C.R.; Wang, M. Rethinking maximum stand basal area and maximum SDI from the aspect of stand dynamics. For. Ecol. Manag. 2020, 475, 118462. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; González, G.M.; del Rio, M. Biomass models to estimate carbon stocks for hardwood tree species. For. Syst. 2012, 21, 42–52. [Google Scholar] [CrossRef]
- de Cáceres, M.; Martín-Alcón, S.; Olabarria, J.R.G.; Coll, L. A general method for the classification of forest stands using species composition and vertical and horizontal structure. Ann. For. Sci. 2019, 76, 40. [Google Scholar] [CrossRef] [Green Version]
- Jaskierniak, D.; Lane, P.N.; Robinson, A.; Lucieer, A. Extracting LiDAR indices to characterise multilayered forest structure using mixture distribution functions. Remote Sens. Environ. 2011, 115, 573–585. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Coops, N.; Culvenor, D.S. Assessment of forest structure with airborne LiDAR and the effects of platform altitude. Remote Sens. Environ. 2006, 103, 140–152. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef] [Green Version]
- Lasch, P.; Lindner, M.; Erhard, M.; Suckow, F.; Wenzel, A. Regional impact assessment on forest structure and functions under climate change—the Brandenburg case study. For. Ecol. Manag. 2002, 162, 73–86. [Google Scholar] [CrossRef]
- Bennett, J.M.; Cunningham, S.C.; Connelly, C.A.; Clarke, R.H.; Thomson, J.R.; Mac Nally, R. The interaction between a drying climate and land use affects forest structure and above-ground carbon storage. Glob. Ecol. Biogeogr. 2013, 22, 1238–1247. [Google Scholar] [CrossRef]
- Palace, M.; Sullivan, F.B.; Ducey, M.; Herrick, C. Estimating Tropical Forest Structure Using a Terrestrial Lidar. PLoS ONE 2016, 11, e0154115. [Google Scholar] [CrossRef]
- Bastin, J.; Rutishauser, E.; Kellner, J.R.; Saatchi, S.; Pélissier, R.; Hérault, B.; Slik, F.; Bogaert, J.; de Cannière, C.; Marshall, A.R.; et al. Pan-tropical prediction of forest structure from the largest trees. Glob. Ecol. Biogeogr. 2018, 27, 1366–1383. [Google Scholar] [CrossRef]
- Ministerio de Medio Ambiente y Medio Rural y Marino. Anuario de Estadística Agraria y Agroalimentaria 2010. Available online: http://www.mapa.es/es/estadistica/pags/anuario/introduccion.htm (accessed on 1 November 2021).
- Barbati, A.; Marchetti, M.; Chirici, G.; Corona, P. European Forest Types and Forest Europe SFM indicators: Tools for monitoring progress on forest biodiversity conservation. For. Ecol. Manag. 2014, 321, 145–157. [Google Scholar] [CrossRef] [Green Version]



| Province | SNFI Plots | Temperature (°C) | Precipitation (mm) | M |
|---|---|---|---|---|
| Murcia | 905 | 13.71 (1.7) | 397.25 (65.1) | 17.04 (4.2) |
| Badajoz | 363 | 15.26 (0.9) | 562.81 (78.3) | 22.27 (3.1) |
| Madrid | 887 | 11.66 (2.3) | 502.59 (194.3) | 24.48 (13.1) |
| La Rioja | 615 | 9.04 (1.5) | 620.01 (105.0) | 33.16 (3.1) |
| Province | Zone ID | Flight Start | Flight End | Points/m2 | Tile Size |
|---|---|---|---|---|---|
| Murcia | MUR-LM-ALI | 8/2016 | 3/2017 | 0.5 | 2 × 2 km |
| Badajoz | EXT-S | 7/2018 | 4/2019 | 1 | 2 × 2 km |
| Madrid | MAD | 8/2016 | 9/2016 | 1 | 1 × 1 km |
| La Rioja | RIO | 8/2016 | 9/2016 | 2 | 2 × 2 km |
| Structural Type | BA | N | DBH | HM | M |
|---|---|---|---|---|---|
| SCS | 7.91 (4.8) | 314 (205.8) | 21.3 (5.76) | 7.99 (1.52) | 18 (4.81) |
| AOW | 9.59 (6.5) | 151 (174.2) | 41.2 (13.8) | 8.07 (1.41) | 21.1 (5.31) |
| COP | 22.1 (10.3) | 1229 (564.5) | 17.5 (5.23) | 9.61 (1.81) | 26 (8.13) |
| HMS | 29.1 (12.7) | 654 (420.6) | 30.5 (10.4) | 13.8 (2.95) | 36.6 (12.38) |
| CONTINGENCY TABLE (Training Set: 70% of Total Observations) | |||||||
|---|---|---|---|---|---|---|---|
| Predicted | Observed | USER’S ACCURACY (%) | COMISSION ERROR (%) | ||||
| SCS | AOW | COP | HMS | TOTAL | |||
| SCS | 649 | 197 | 123 | 51 | 216 | 45.37 | 54.63 |
| AOW | 71 | 158 | 18 | 28 | 275 | 57.45 | 42.55 |
| COP | 32 | 18 | 98 | 68 | 1020 | 63.63 | 36.37 |
| HMS | 33 | 40 | 84 | 270 | 427 | 63.23 | 36.77 |
| TOTAL | 785 | 413 | 323 | 417 | 1938 | ||
| PRODUCER’S ACCURACY (%) | 82.68 | 38.26 | 30.34 | 64.75 | TOTAL ACCURACY (%) | 60.63 | |
| OMISSION ERROR (%) | 17.32 | 61.74 | 69.66 | 35.25 | TOTAL ERROR (%) | 39.37 | |
| CONTINGENCY TABLE (Validation Set: 30% of Total Observations) | |||||||
|---|---|---|---|---|---|---|---|
| Predicted | Observed | USER’S ACCURACY (%) | COMISSION ERROR (%) | ||||
| SCS | AOW | COP | HMS | TOTAL | |||
| SCS | 293 | 83 | 54 | 17 | 83 | 62.65 | 37.35 |
| AOW | 35 | 75 | 5 | 13 | 128 | 58.59 | 41.41 |
| COP | 6 | 5 | 52 | 20 | 447 | 65.55 | 34.45 |
| HMS | 11 | 16 | 33 | 114 | 174 | 65.52 | 34.48 |
| TOTAL | 345 | 179 | 144 | 164 | 832 | ||
| PRODUCER’S ACCURACY (%) | 84.93 | 41.90 | 36.11 | 69.51 | TOTAL ACCURACY (%) | 64.18 | |
| OMISSION ERROR (%) | 15.07 | 58.10 | 63.89 | 30.49 | TOTAL ERROR (%) | 35.82 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tijerín-Triviño, J.; Moreno-Fernández, D.; Zavala, M.A.; Astigarraga, J.; García, M. Identifying Forest Structural Types along an Aridity Gradient in Peninsular Spain: Integrating Low-Density LiDAR, Forest Inventory, and Aridity Index. Remote Sens. 2022, 14, 235. https://doi.org/10.3390/rs14010235
Tijerín-Triviño J, Moreno-Fernández D, Zavala MA, Astigarraga J, García M. Identifying Forest Structural Types along an Aridity Gradient in Peninsular Spain: Integrating Low-Density LiDAR, Forest Inventory, and Aridity Index. Remote Sensing. 2022; 14(1):235. https://doi.org/10.3390/rs14010235
Chicago/Turabian StyleTijerín-Triviño, Julián, Daniel Moreno-Fernández, Miguel A. Zavala, Julen Astigarraga, and Mariano García. 2022. "Identifying Forest Structural Types along an Aridity Gradient in Peninsular Spain: Integrating Low-Density LiDAR, Forest Inventory, and Aridity Index" Remote Sensing 14, no. 1: 235. https://doi.org/10.3390/rs14010235
APA StyleTijerín-Triviño, J., Moreno-Fernández, D., Zavala, M. A., Astigarraga, J., & García, M. (2022). Identifying Forest Structural Types along an Aridity Gradient in Peninsular Spain: Integrating Low-Density LiDAR, Forest Inventory, and Aridity Index. Remote Sensing, 14(1), 235. https://doi.org/10.3390/rs14010235







