A Novel Flickering Multi-Target Joint Detection Method Based on a Biological Memory Model
Abstract
:1. Introduction
- Detection of the target with flickering characteristics under low SCR. This paper proposes a memory weight DP merit function integral operator. The theory of biological memory is introduced into DP integration to study the appearance and blanking state of targets with flickering characteristics in sea clutter. The merit function effectively integrates the correlation of flickering characteristic targets’ states among different frames. Therefore, the method achieves accurate detection for flickering characteristic targets with a low SCR.
- Multi-target detection is employed without pre-target number information, and the computational cost is reduced. Usually, when using DP to solve multi-target detection problems, the target’s high-dimensional state is difficult to calculate due to the uncertain number of targets. However, the target number being known is inconsistent with practical applications. Therefore, we choose a simple and effective way to achieve the suboptimal solution of multi-target detection. We use a lower global threshold in the DP process and discretize the areas with candidate targets to simplify the high-dimensional maximization to multiple low-dimensional maximization, meaning that the computational cost is reduced.
2. DP Model
2.1. Target Motion Model
2.2. Multi-Frame Joint Target Detection
2.2.1. Initialization
2.2.2. Multi-Frame Joint Integration
2.2.3. Target Detection
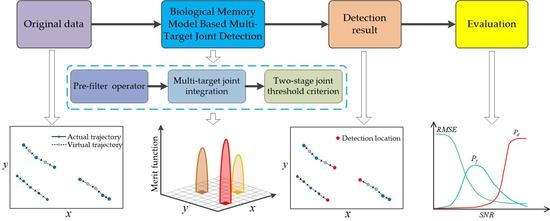
3. Biological Memory Model Based Multi-Target Joint Detection Method
3.1. Biological Memory Theory for the Flickering Characteristics Target
3.1.1. Definition of Memory and Forgetting
- Memory

- Forgetting
3.1.2. The Memory Model for the Flickering Characteristics Target
3.2. Process of BM-DP-MJD Method
3.2.1. Pre-Filter Operator
3.2.2. Multi-Target Joint Integration
- 1.
- Initialization
- 2.
- Multi-frame joint accumulation
- 3.
- Progressive loop integration
3.2.3. Two-Stage Joint Threshold Criterion
3.3. Assumptions for Special Situations of Flickering Characteristics Multi-Target Detection
4. Results and Discussion
4.1. Simulation Data Results
4.1.1. Demonstration of Simulation Data Detection Results
4.1.2. Simulation Data Detection Performance of BMM-DP-MJD
- Detection performance of three types of target
- Detection performance in special assumed situations
- Comparison of the detection performance of three algorithms on simulation data
4.2. Experimental Data Detection Performance of BMM-DP-MJD
4.3. Detection Performance Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huo, W.; Tuo, X.; Zhang, Y. Balanced Tikhonov and Total Variation Deconvolution Approach for Radar Forward-Looking Super-Resolution Imaging. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3505805. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, J.; Li, J. Fast Inverse-Scattering Reconstruction for Airborne High-Squint Radar Imagery Based on Doppler Centroid Compensation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5205517. [Google Scholar] [CrossRef]
- Hao, C.P.; Li, J.; Hou, C.H. A Study on CFAR Detection Method of Weighted Cell Averaging and Fuzzy Rules. Modern Radar 2009, 31, 44–46. [Google Scholar]
- De Maio, A.; Foglia, G.; Conte, E. CFAR behavior of adaptive detectors: An experimental analysis. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 233–251. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Yang, K.; Zou, H. A bilateral CFAR algorithm for ship detection in SAR images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1536–1540. [Google Scholar] [CrossRef]
- Miao, K.; Leng, X.; Zhao, L.; Ji, K. A modified faster R-CNN based on CFAR algorithm for SAR ship detection. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017; pp. 1–4. [Google Scholar]
- Fang, X.U.; Jing-Hong, L. Ship detection and extraction using visual saliency and histogram of oriented gradient. IEEE Geosci. Remote Sens. Lett. 2016, 12, 473–477. [Google Scholar]
- Chen, Y.; Xin, Y. An efficient infrared small target detection method based on visual contrast mechanism. IEEE Geosci. Remote Sens. Lett. 2016, 13, 962–966. [Google Scholar] [CrossRef]
- Han, J.; Yong, M.; Bo, Z.; Fan, F.; Liang, K.; Yu, F. A robust infrared small target detection algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2168–2172. [Google Scholar]
- Chen, S.; Wang, H.; Xu, F. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Y.; Liu, W.; Orlando, D.; Li, H. Training data assisted anomaly detection of multi-pixel targets in hyperspectral imagery. IEEE Trans. Signal Proc. 2020, 68, 3022–3032. [Google Scholar] [CrossRef]
- Lang, H.; Jie, Z.; Xi, Z.; Meng, J. Ship classification in SAR image by joint feature and classifier selection. IEEE Geosci. Remote Sens. Lett. 2015, 13, 212–216. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C. Adaptive ship detection in SAR images using variance WIE-based method. Signal Image Video Processing 2016, 10, 1219–1224. [Google Scholar] [CrossRef]
- Tao, W.; Guang-Shun, H.; Jing, G. Energy consumption and economic growth in China’s marine economic zones-an estimation based on partial linear model. Energy 2020, 205, 118028. [Google Scholar] [CrossRef]
- Gini, F.; Greco, M.V.; Diani, M.; Verrazzani, L. Performance analysis of two adaptive radar detectors against non-Gaussian real sea clutter data. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 1429–1439. [Google Scholar]
- Xu, S.; Zhu, J.; Jiang, J. Sea-surface floating small target detection by multifeature detector based on isolation forest. IEEE J. Sel. Top. Appl. Eart. Observ. Remote Sens. 2020, 14, 704–715. [Google Scholar] [CrossRef]
- Xu, X.K. Low observable targets detection by joint fractal properties of sea clutter: An experimental study of IPIX OHGR datasets. IEEE Trans. Ant. Prop. 2010, 58, 1425–1429. [Google Scholar]
- Shi, S.N.; Shui, P.L.; Liu, M. Subband adaptive coherent detection of weak moving targets in K-distributed sea clutter. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Shui, P.L.; Li, D.C.; Xu, S.W. Tri-feature-based detection of floating small targets in sea clutter. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1416–1430. [Google Scholar] [CrossRef]
- Xu, S.; Zheng, J.; Jia, P.; Shui, P. Sea-surface floating small target detection based on polarization features. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1505–1509. [Google Scholar] [CrossRef]
- Shi, S.; Shui, P. Sea-surface floating small target detection by one-class classifier in time-frequency feature space. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6395–6411. [Google Scholar] [CrossRef]
- Li, Y.; Xie, P.; Tang, Z.; Jiang, T.; Qi, P. SVM-based sea-surface small target detection: A false-alarm-rate-controllable approach. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1225–1229. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.X.; Shui, P.L. Anomaly Based Sea-Surface Small Target Detection Using K-Nearest Neighbor Classification. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4947–4964. [Google Scholar] [CrossRef]
- Li, D.; Shui, P. Floating small target detection in sea clutter via normalised Hurst exponent. Electron. Lett. 2014, 50, 1240–1242. [Google Scholar] [CrossRef]
- Barniv, Y.; Kella, O. Dynamic programming solution for detecting dim moving targets part II: Analysis. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 776–788. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Yi, W. A distributed asynchronous recursive filtering fusion algorithm via DP-TBD. J. Radars 2018, 7, 254–262. [Google Scholar]
- Gao, J.; Du, J.; Wang, W. Radar detection of fluctuating targets under heavy-tailed clutter using track before detect. Sensors 2018, 18, 2241. [Google Scholar] [CrossRef] [Green Version]
- Yi, W.; Morelande, M.R.; Kong, L.J.; Yang, J.Y. An efficient particle filter for multi-target tracking using an independence assumption. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 2378–2385. [Google Scholar]
- Jiang, H.; Yi, W.; Cui, G.; Kong, L.; Yang, X. Tracking targets in K clutter via particle filter. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 0350–0355. [Google Scholar]
- Huo, W.; Pei, J.; Huang, Y. A new maritime moving target detection and tracking method for airborne forward-looking scanning radar. Sensors 2019, 19, 1586. [Google Scholar] [CrossRef] [Green Version]
- Si, W.; Zhu, H.; Qu, Z. Robust Poisson multi-Bernoulli filter with unknown clutter rate. IEEE Access 2019, 7, 117871–117882. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Z.; Li, C.; Wang, J. Study on dim target detection and discrimination from sea clutter. China Ocean Eng. 2013, 27, 183–192. [Google Scholar] [CrossRef]
- Grossi, E.; Lops, M.; Venturino, L. A novel dynamic programming algorithm for track-before-detect in radar systems. IEEE Trans. Signal Proc. 2013, 61, 2608–2619. [Google Scholar] [CrossRef]
- Orlando, D.; Ricci, G.; Bar-Shalom, Y. Track-before-detect algorithms for targets with kinematic constraints. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1837–1849. [Google Scholar]
- Huang, D.; Xue, A.; Guo, Y. Penalty dynamic programming algorithm for dim targets detection in sensor systems. Sensors 2012, 12, 5028–5046. [Google Scholar] [CrossRef]
- Buzzi, S.; Lops, M.; Venturino, L.; Ferri, M. Track-before-detect procedures in a multi-target environment. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1135–1150. [Google Scholar]
- Orlando, D.; Venturino, L.; Lops, M. Track-before-detect strategies for STAP radars. IEEE Trans. Signal Proc. 2009, 58, 933–938. [Google Scholar]
- Jiang, H.; Yi, W.; Cui, G. Knowledge-Based Track-Before-Detect Strategies for Fluctuating Targets in K-Distributed Clutter. IEEE Sens. 2016, 16, 7124–7132. [Google Scholar] [CrossRef]
- Morimoto, B.H.; Koshland, D.E. Short-term and long-term memory in single cells. FASEB 1991, 5, 2061–2067. [Google Scholar] [CrossRef] [PubMed]
- Gao, G.; Liu, L.; Zhao, L. An adaptive and fast CFAR algorithm based on automatic censoring for target detection in high-resolution SAR images. Trans. Geosci. Remote Sens. 2008, 47, 1685–1697. [Google Scholar]
- Cam, L.; Neyman, J.; Scott, E.L. Probability Theory; University of California Press: Berkeley, CA, USA, 1972. [Google Scholar]











| Parameter | Value |
|---|---|
| K distribution scale parameter | |
| Number of frames | 10 |
| False alarm probability | 0.02 |
| Target appearance’s probability of binomial distribution | 0.7 |
| The size of simulation data | |
| Target position random noise |
| Target Number | SCR | Distribution |
|---|---|---|
| Target 1 | 5 dB | Swerling I distribution |
| Target 2 | 10 dB | Uniform distribution |
| Target 3 | 10 dB | Uniform distribution |
| Target 4 | 5 dB | Swerling I distribution |
| Target 5 | 10 dB | Uniform distribution |
| Target Number | Distribution |
|---|---|
| Target 1, Target 4 | Binomial distribution |
| Target 2, Target 5 | Swerling I distribution |
| Target 3, Target 6 | Uniform distribution targets |
| Target Number | Distribution |
|---|---|
| Target 1 | The target disappearance probability is 0.2 |
| Target 2 | Binomial distribution |
| Target 3 | The target disappearance probability is 0.3 |
| Target 4 | Binomial distribution |
| Target 5 | Binomial distribution |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Wave band | X band | Main lobe of the azimuth | 5.1° |
| Scanning speed | 72°/s | Bandwidth | 75 MHz |
| PRF | 200 Hz | Image size |
| Method | RMSE (Cell) | ||
|---|---|---|---|
| DP-TBD | 0.4 | 0 | 11.3 of |
| Two stage DP-TBD | 0.8 | 0.4 | 14.3 of |
| BMM-DP-MJD | 1 | 0 | 1.7 of |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Huo, W.; Pei, J.; Zhang, Y.; Yang, J.; Huang, Y. A Novel Flickering Multi-Target Joint Detection Method Based on a Biological Memory Model. Remote Sens. 2022, 14, 39. https://doi.org/10.3390/rs14010039
Zhang Q, Huo W, Pei J, Zhang Y, Yang J, Huang Y. A Novel Flickering Multi-Target Joint Detection Method Based on a Biological Memory Model. Remote Sensing. 2022; 14(1):39. https://doi.org/10.3390/rs14010039
Chicago/Turabian StyleZhang, Qian, Weibo Huo, Jifang Pei, Yongchao Zhang, Jianyu Yang, and Yulin Huang. 2022. "A Novel Flickering Multi-Target Joint Detection Method Based on a Biological Memory Model" Remote Sensing 14, no. 1: 39. https://doi.org/10.3390/rs14010039
APA StyleZhang, Q., Huo, W., Pei, J., Zhang, Y., Yang, J., & Huang, Y. (2022). A Novel Flickering Multi-Target Joint Detection Method Based on a Biological Memory Model. Remote Sensing, 14(1), 39. https://doi.org/10.3390/rs14010039