A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction
Abstract
:1. Introduction
2. Signal Model
2.1. Signal Model of LFM Radar
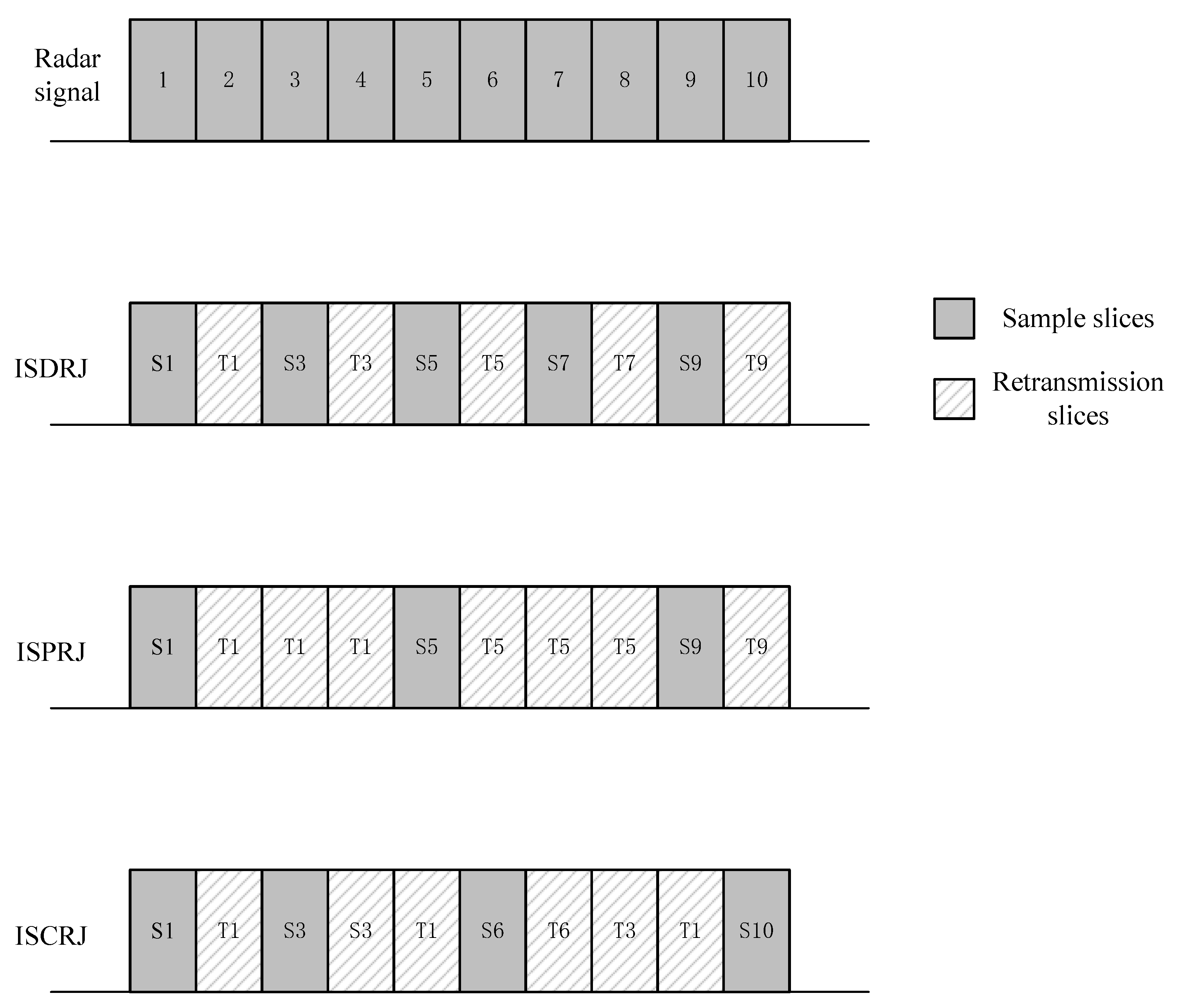
2.2. Mechanism of ISRJ
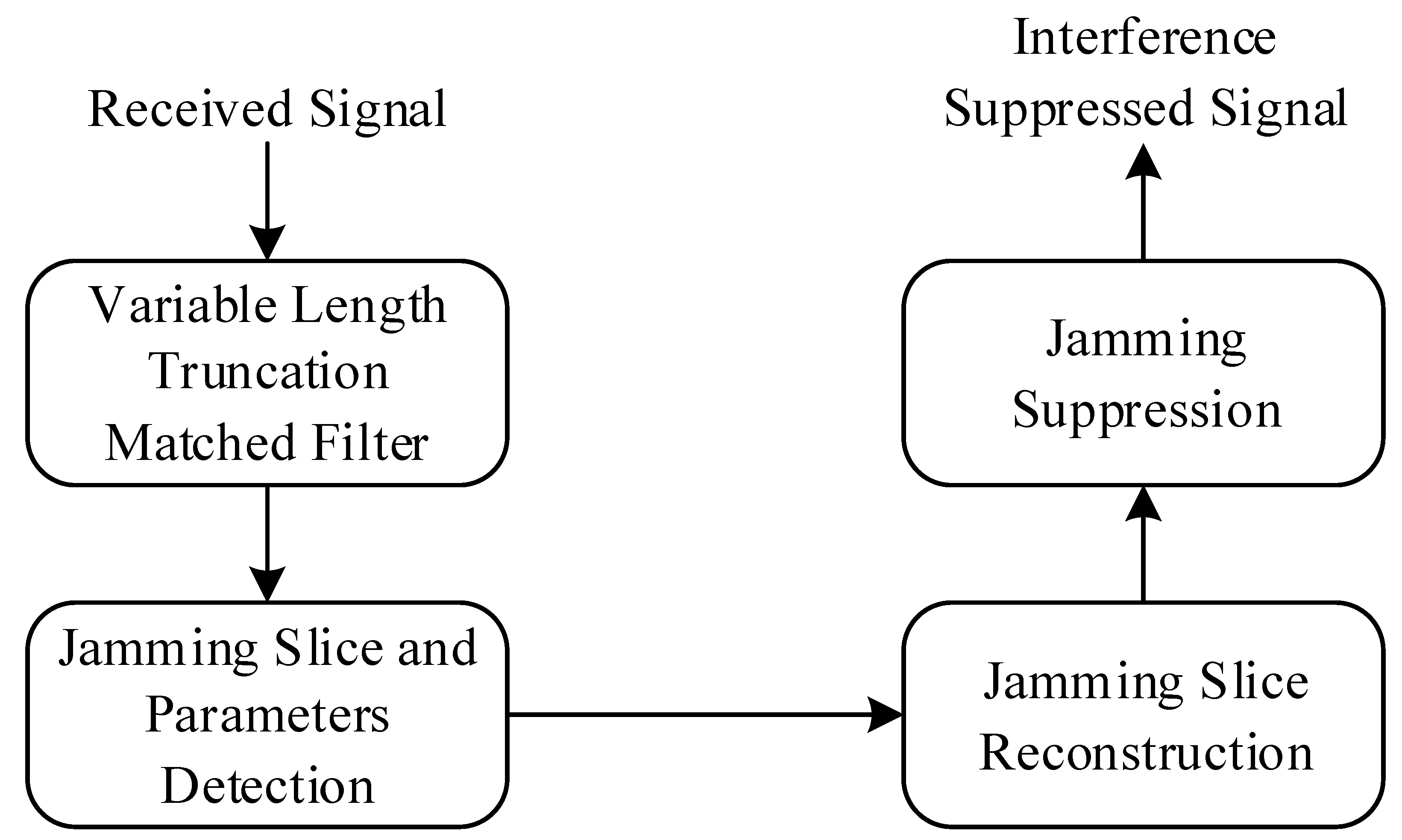
3. Truncated Matched Filter for ISRJ Suppression
3.1. Truncated Matched Filter
3.2. Extraction and Reconstruction of Jamming Slice
| Algorithm 1: Truncated Matched Filter Method for jamming slice extraction. |
Input: The max-peak function , the transmitting cycle time T, echo signal Output: The reconstructed jamming signal
|
4. Simulation
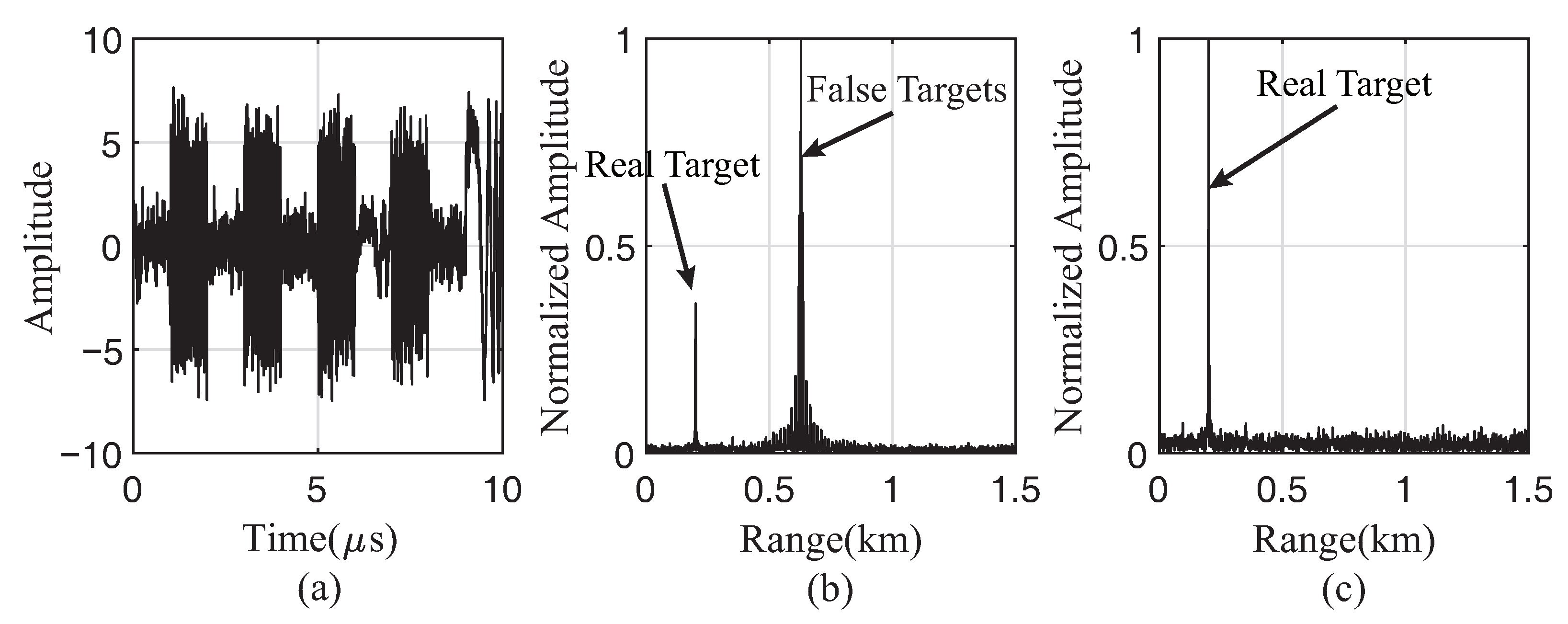
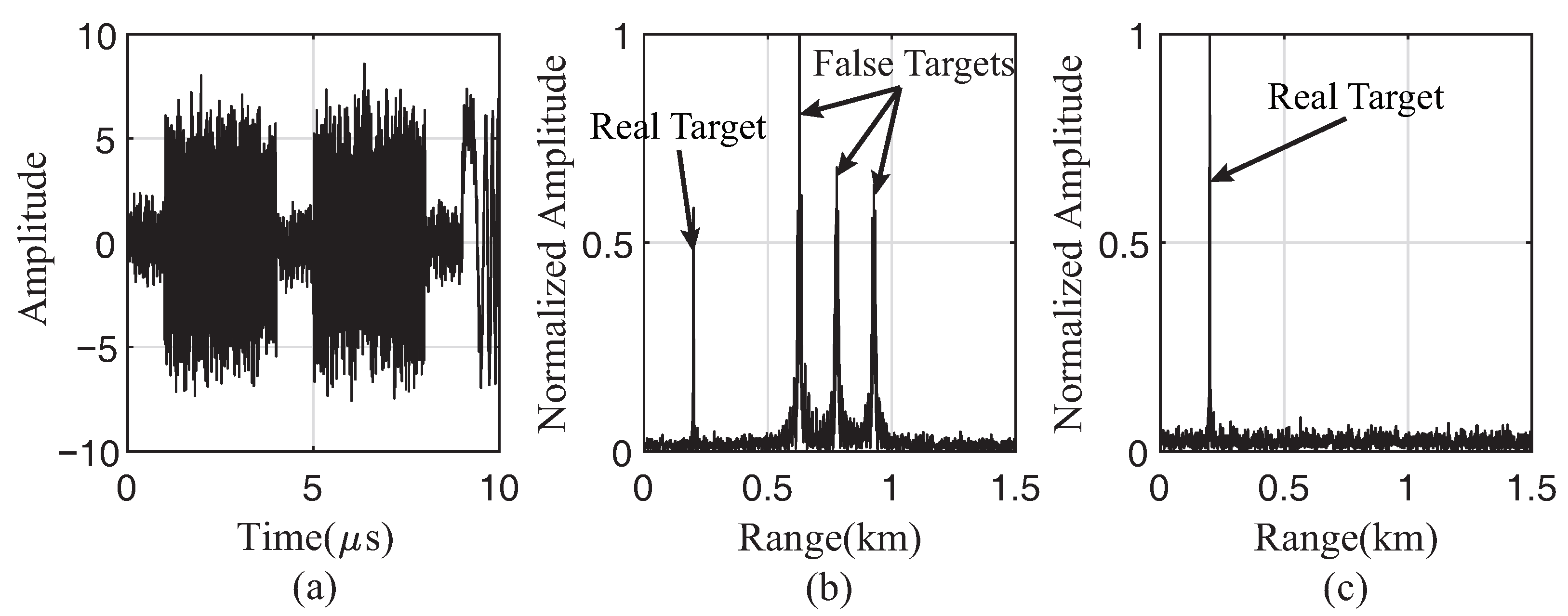
4.1. Interference Suppression Based on TMF
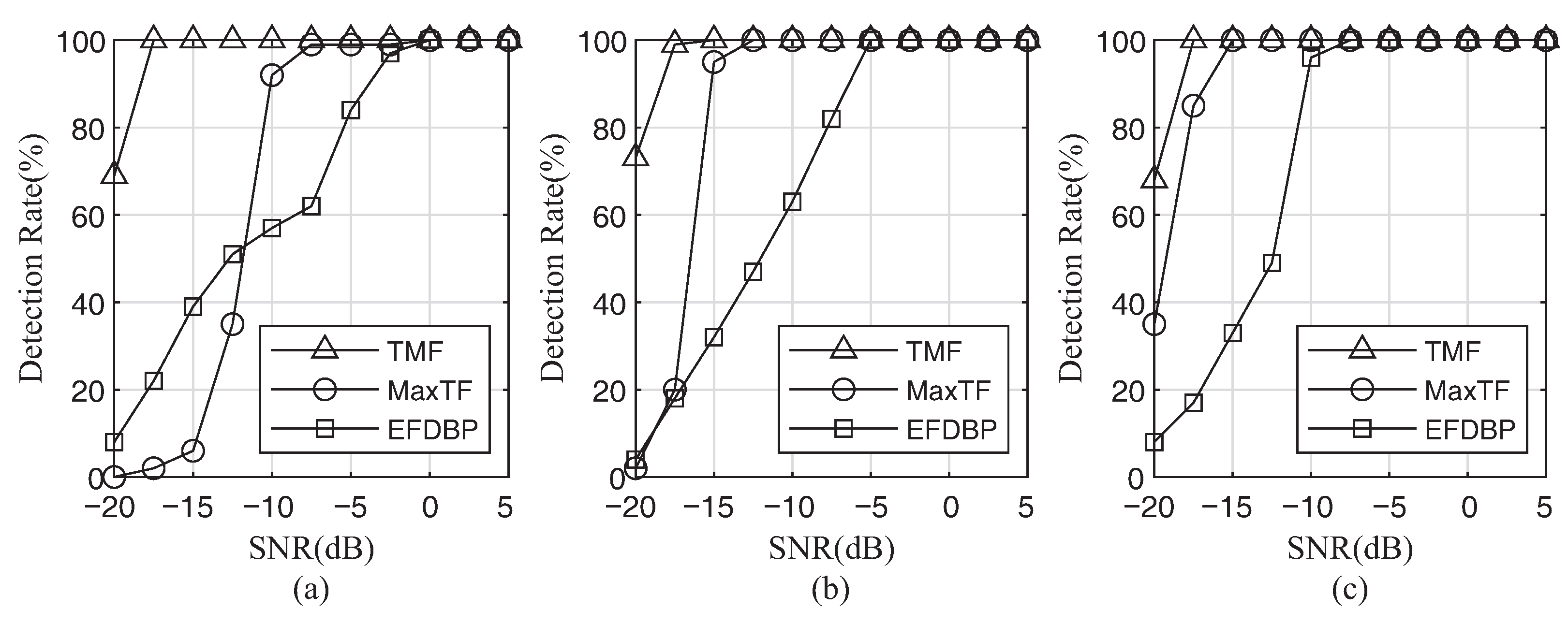
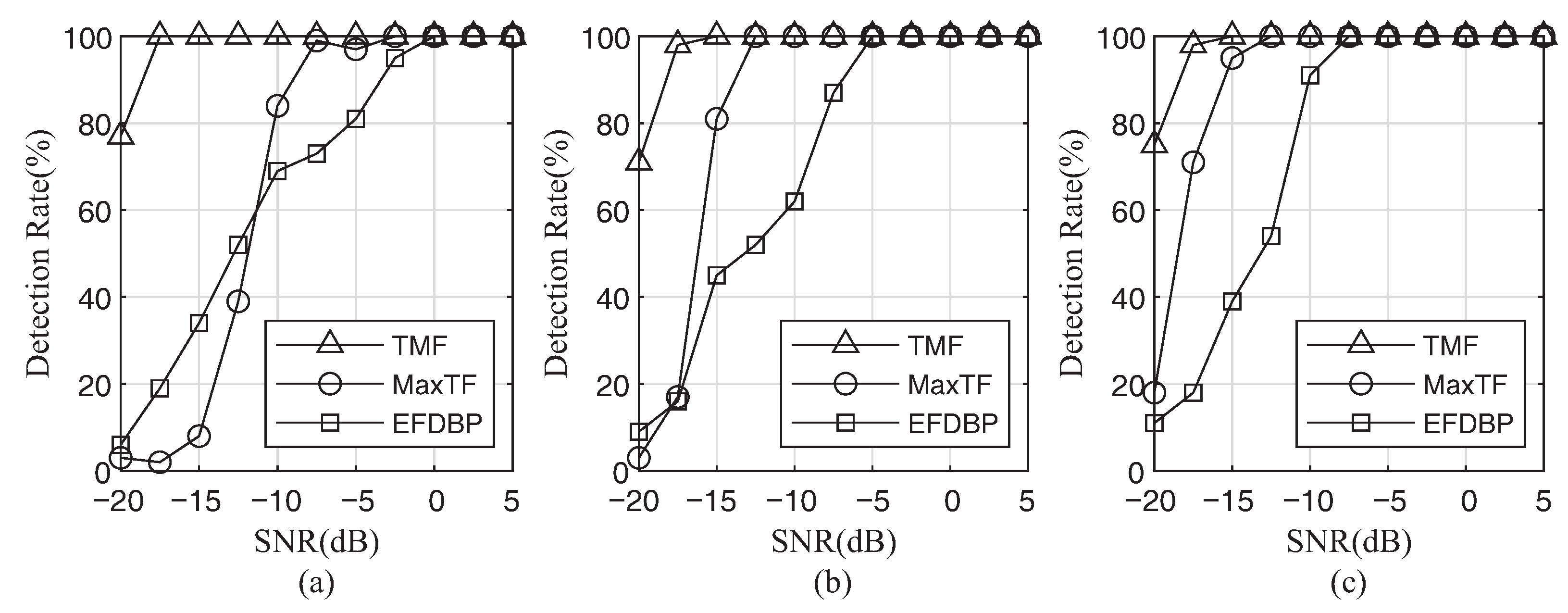
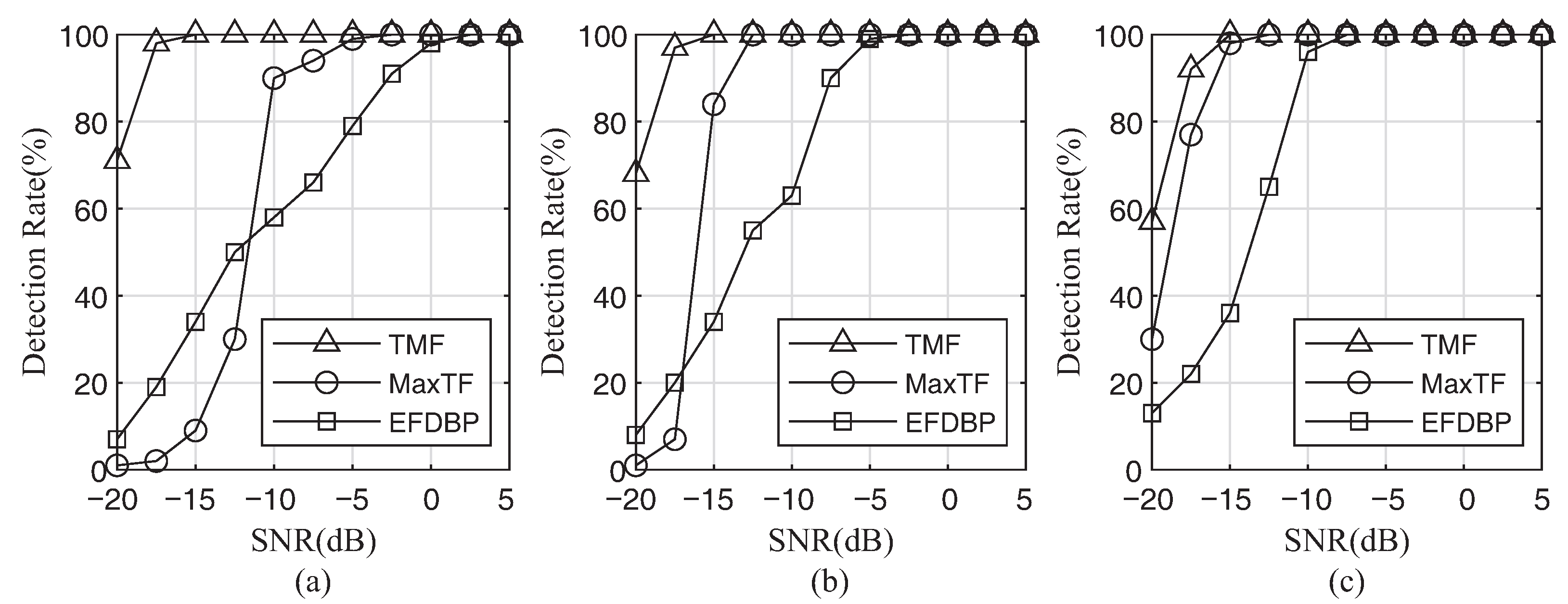
4.2. Monte-Carlo Simulations and Results
- (i)
- Under the three jamming suppression methods, the probability of target detection will improve with the increase of SNR and JSR. The reason is that, when SNR and JSR rise, the distinction between jamming and true target signals becomes increasingly clear, which makes it easier to extract interference-free segments for MaxTF and EFDBP methods. In the TMF method, higher SNR and JSR mean higher jamming-noise ratio (JNR) and better recovery of jamming signals, which improves interference suppression.
- (ii)
- The TMF method shows better performance in lower SNR and JSR compared with other methods. The other two methods rely on the extraction of interference-free segments, whereas their extraction performance in the low SNR and JSR regimes is poor. In addition, the TMF method is to recover jamming signals directly. When the SNR and JSR are low, the JNR is still high enough to ensure the recovery of jamming signals, resulting in a greater interference suppression effect.
- (iii)
- For the same jamming type, the performance of the three jamming suppression methods increases with the SNR raising. For the same jamming suppression method, the performance under the three jamming types show the similar improvement characteristic. The other two methods are not sensitive to jamming types because they rely on identifying interference-free segments. The TMF method provides great interference suppression for them because it recovers each independent jamming slice, and all three types of jamming are based on the combination of multiple jamming slices.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Liu, J.; Zhang, W.; Fu, Q.; Liu, Z.; Xie, X. Mathematic principles of interrupted-sampling repeater jamming (ISRJ). Sci. China Ser. F Inf. Sci. 2007, 50, 113–123. [Google Scholar] [CrossRef]
- Feng, D.; Xu, L.; Pan, X.; Wang, X. Jamming wideband radar using interrupted-sampling repeater. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1341–1354. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.S.; Liu, J.C.; Wang, G.; Xiao, S. Jamming technique of interrupted-sampling and periodic repeater based on digital radio frequency memory. Acta Armamentarii 2008, 29, 405–410. [Google Scholar]
- Zhong, L. Jamming Technique for Countering LFM Pulse Compression Radar Based on Digital Radio Frequency Memory. Ph.D. Dissertation, National University of Defense Technology, Changsha, China, 2006. [Google Scholar]
- Li, H.; Zhao, G.; Yang, Y.; Gao, H. The performance analysis of multi-false target jamming of part copying Radar pulse. Electron. Inf. Warf. Technol. 2010, 25, 39–44. [Google Scholar]
- Yang-rui, Z.; Yun-jie, L.; Man-ling, L.; Mei-guo, G.; Xiong-jun, F. Suppress Jamming Technique of Multiple False Targets on Interrupted-Sampling and Non-Uniform Periodic Repeater. Acta Electron. Sin. 2016, 44, 46–53. [Google Scholar] [CrossRef]
- Ping, Z.; Qingsheng, Z.; Yanbin, L.; Nan, H.; Wenqing, X. Intermittent Sampling Repeater Jamming Technique Based on Multi-waveform Modulation. Mod. Radar 2020, 42, 77–83. [Google Scholar] [CrossRef]
- Li, C.Z.; Su, W.M.; Gu, H.; Ma, C.; Chen, J.L. Improved interrupted sampling repeater jamming based on DRFM. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014; pp. 254–257. [Google Scholar]
- Jianzhong, Z.; Heqiang, M.; Shuliang, W.; Yanbing, L.; Hongwei, G. Anti-Intermittent Sampling Repeater Jamming Method Based on LFM Segmented Pulse Compression. J. Electron. Inf. Technol. 2019, 41, 1712–1720. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Q.; Chen, X. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer. IET Radar Sonar Navig. 2018, 12, 56–63. [Google Scholar] [CrossRef]
- Xiong, W.; Zhang, G.; Liu, W. Efficient filter design against interrupted sampling repeater jamming for wideband radar. EURASIP J. Adv. Signal Process. 2017, 2017, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hanbali, S.B.S.; Kastantin, R. Technique to counter active echo cancellation of self-protection ISRJ. Electron. Lett. 2017, 53, 680–681. [Google Scholar] [CrossRef]
- Zhou, K.; Li, D.; Quan, S.; Liu, T.; Su, Y.; He, F. SAR Waveform and Mismatched Filter Design for Countering Interrupted-Sampling Repeater Jamming. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Yu, M.; Dong, S.; Duan, X.; Liu, S. A novel interference suppression method for interrupted sampling repeater jamming based on singular spectrum entropy function. Sensors 2019, 19, 136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, K.; Li, D.; Su, Y.; Liu, T. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming. IEEE Signal Process. Lett. 2020, 27, 1610–1614. [Google Scholar] [CrossRef]
- Hanbali, S.B.S. Technique to counter improved active echo cancellation based on ISRJ with frequency shifting. IEEE Sens. D 2019, 19, 9194–9199. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, C. Interrupted Sampling Repeater Jamming Suppression Method based on Hybrid Modulated Radar Signal. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Zhou, C.; Liu, F.; Liu, Q. An adaptive transmitting scheme for interrupted sampling repeater jamming suppression. Sensors 2017, 17, 2480. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Luo, X.; Duan, X.; Wang, W.; Ou, J. A Novel Radar Waveform Design for Anti-Interrupted Sampling Repeater Jamming via Time-Frequency Random Coded Method. Prog. Electromagn. Res. M 2020, 98, 89–99. [Google Scholar] [CrossRef]
- Mu-yao, Y.; Sheng-bo, D.; Xiang-yu, D. An Interference Suppression Algorithm of Multiple False Targets for Pulse Doppler Radar. J. Signal Process. 2017, 33, 1578–1584. [Google Scholar] [CrossRef]
- Chen, J.; Wu, W.; Xu, S.; Chen, Z.; Zou, J. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis. IET Radar Sonar Navig. 2019, 13, 1646–1654. [Google Scholar] [CrossRef]
- Chao, Z.; Quan-hua, L.; Tao, Z. Research on DRFM Repeater Jamming Recognition. J. Signal Process. 2017, 33, 911–917. [Google Scholar] [CrossRef]
- Wei, Y.; Lu, Z.; Yuan, G.; Fang, Z.; Huang, Y. Sparsity adaptive matching pursuit detection algorithm based on compressed sensing for radar signals. Sensors 2017, 17, 1120. [Google Scholar] [CrossRef]
- Hui, Y.; Chunyang, W.; Lei, A.; Xin, L. ECCM scheme against interrupted-sampling repeater jamming based on compressed sensing signal reconstruction. Syst. Eng. Electron. 2018, 40, 717–725. [Google Scholar] [CrossRef]
- Zhao, Y.; Gini, F.; Greco, M.; Tang, B. Radar ECCM based on phase-aid distributed compressive sensing. Signal Image Video Process. 2018, 12, 1497–1504. [Google Scholar] [CrossRef]
- Huan, S.; Dai, G.; Luo, G.; Ai, S. Bayesian compress sensing based countermeasure scheme against the interrupted sampling repeater jamming. Sensors 2019, 19, 3279. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Chaoxuan, S.; Zhuangzhi, H.; Ning, H.; Hui, X. Fractional Fourier Transform and Compressed Sensing Adaptive Countering Smeared Spectrum Jamming. J. Electron. Inf. Technol. 2019, 41, 1047–1054. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.; Zhang, X.; Li, S.; Xin, T. Interrupted-sampling repeater jamming adaptive suppression algorithm based on fractional dictionary. Syst. Eng. Electron. 2020, 42, 1439–1448. [Google Scholar] [CrossRef]
- Fang, B.; Huang, G.; Gao, J. Sub-Nyquist sampling and reconstruction model of LFM signals based on blind compressed sensing in FRFT domain. Circuits Syst. Signal Process. 2015, 34, 419–439. [Google Scholar] [CrossRef]
- Tuncay, P.; Kartal, M. A new method for Doppler centroid estimation based on block processing. In Proceedings of the 2013 6th IEEE International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 12–14 June 2013; pp. 417–420. [Google Scholar]

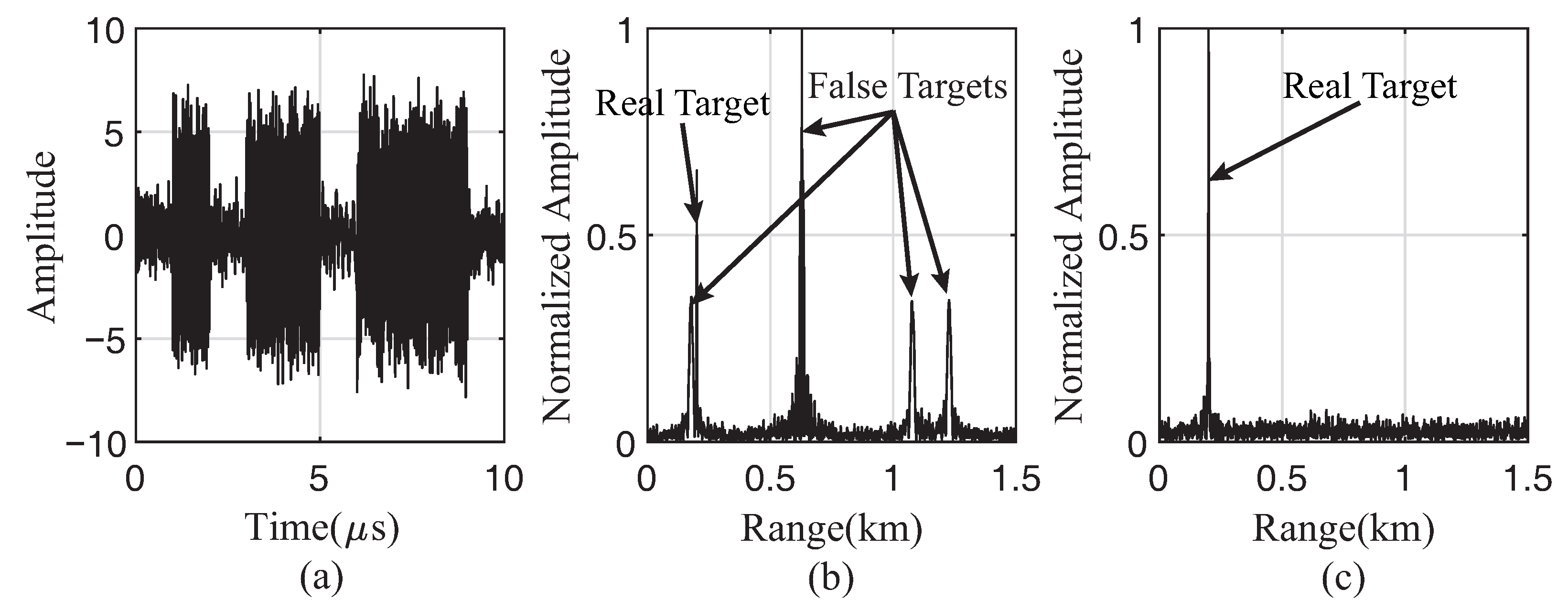
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Signal-to-noise ratio | dB | 0 | |
| Jamming-to-signal ratio | dB | 15 | |
| Radar signal cycle | T | s | 10 |
| Radar signal band width | B | MHz | 100 |
| Radar receiver complex sampling frequency | MHz | 150 | |
| Target location | m | 200 | |
| Main false target location | m | 678 | |
| ISRJsampling pulse width | s | 1 | |
| Pulse repetition interval of ISPRJ | s | 2 | |
| Slice number of ISPRJ | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Gao, M. A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction. Remote Sens. 2022, 14, 97. https://doi.org/10.3390/rs14010097
Lu L, Gao M. A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction. Remote Sensing. 2022; 14(1):97. https://doi.org/10.3390/rs14010097
Chicago/Turabian StyleLu, Lu, and Meiguo Gao. 2022. "A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction" Remote Sensing 14, no. 1: 97. https://doi.org/10.3390/rs14010097
APA StyleLu, L., & Gao, M. (2022). A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction. Remote Sensing, 14(1), 97. https://doi.org/10.3390/rs14010097






