Quantifying the Contributions of Climate Change and Human Activities to Water Volume in Lake Qinghai, China
Abstract
:1. Introduction
2. Materials and Methods
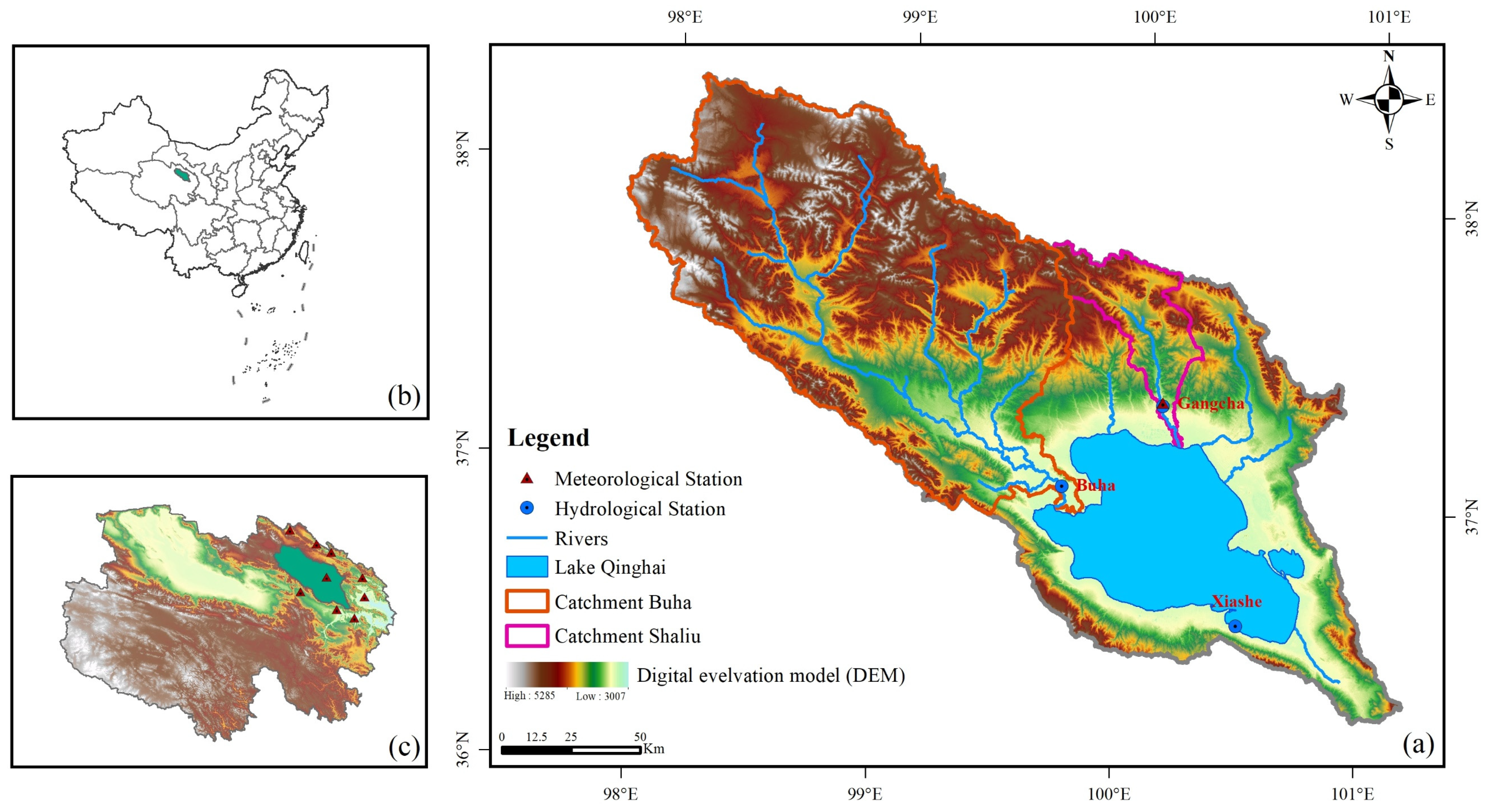
2.1. Study Area
2.2. Data Collection and Preprocessing
2.2.1. Datasets of the Lake Area and Lake Level
2.2.2. Meteorological Data
2.2.3. Other Data
- Digital elevation model (DEM) data were downloaded from the Geospatial Data Cloud (http://www.gscloud.cn/, accessed on 11 April 2021), the spatial resolution of the data is 30 m.
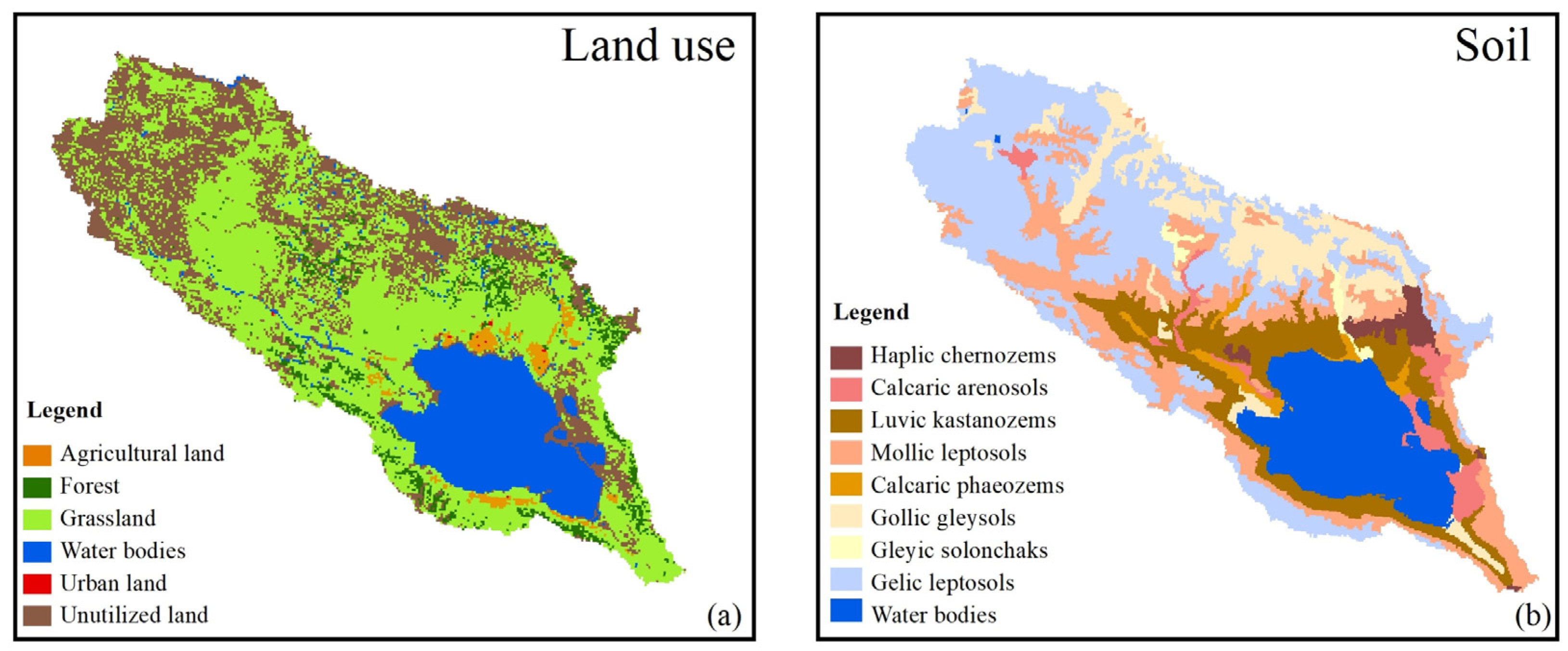
- Land use data with a spatial resolution of 1 km from the 1980s, 1990s, 2000s, and 2010s (Figure 2a) were downloaded from the Resource and Environment Science and Data Center (http://www.resdc.cn/, accessed on 11 April 2021). The original land use classification system was based on the Food and Agriculture Organization (FAO) classification system, which includes six first-level classifications, and they were converted into the corresponding land use types embedded in the SWAT. The final land use types were agricultural land (AGRL), forest (FRST), grassland (PAST), water body (WATR), urban land (URBN), and unutilized land (BARR).
- A soil dataset derived from HWSD1.1 (Figure 2b) with a spatial resolution of 1 km was acquired from the National Science and Technology Infrastructure website (https://data.tpdc.ac.cn/, accessed on 11 April 2021). The soil was reclassified into eight types, and relevant parameters, such as the soil moisture density, soil effective water holding capacity and other soil parameters, were formatted according to the requirements of the SWAT model.
- Monthly average observed surface runoff data for the Gangcha and Buha stations from 1975 to 2014 were provided by the Data Center for Eco-Environment Protection in the Qinghai Lake catchment. The data were used to analyze the surface runoff change into lake and calibration and validation for the SWAT model.
2.3. Methods
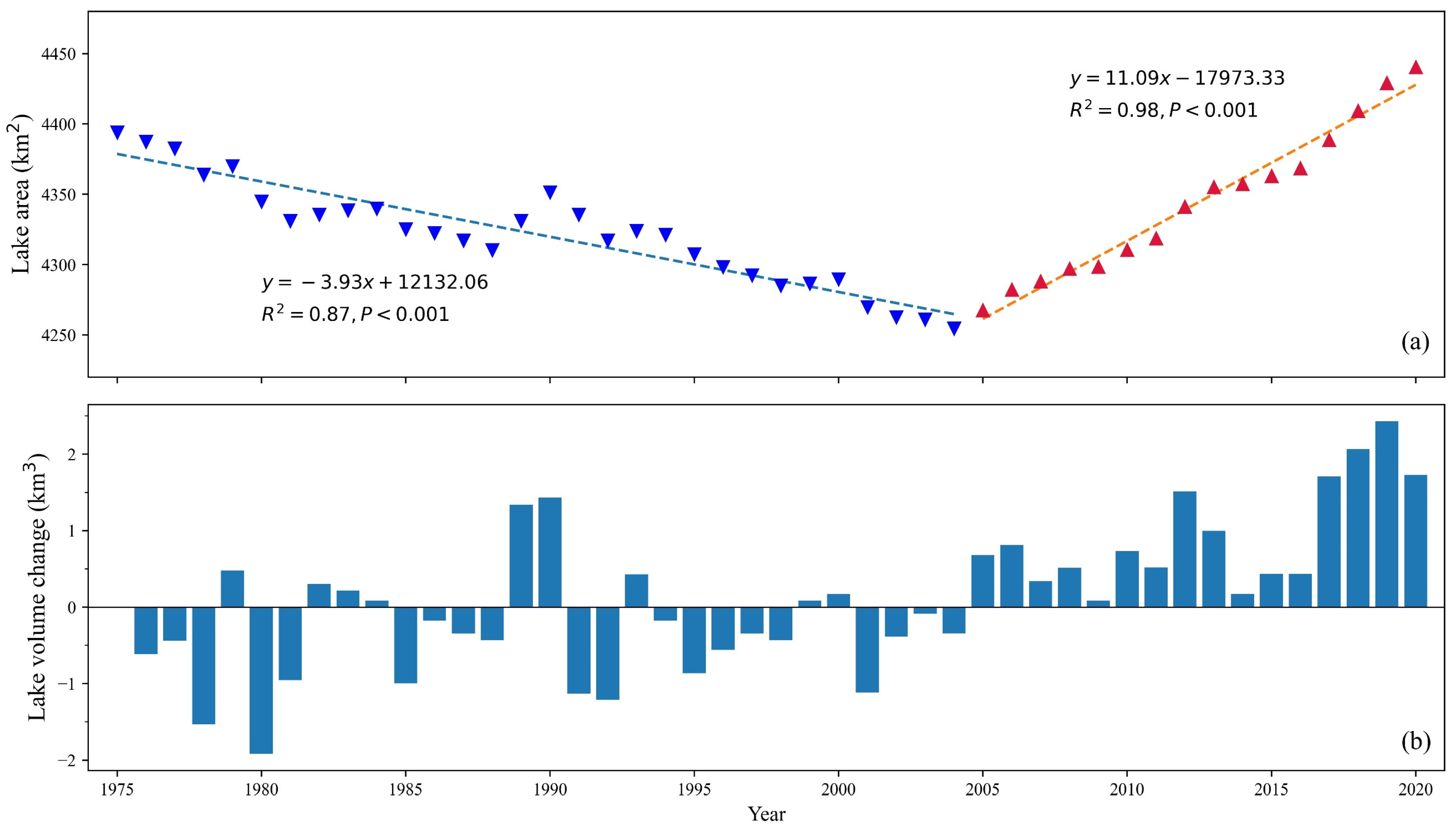
2.3.1. Estimation of the Water Volume in Lake Qinghai
- Variations in lake water volume
- 2.
- Lake water balance model
2.3.2. Diagnostic Methods for Climate Trends
- Pettitt’s Test
- 2.
- Sen’s slope analysis
2.3.3. Setup and Scenario Design of the SWAT Model
- Model setup
- 2.
- Scenario simulation
- 3.
- Model calibration and validation
3. Results
3.1. The Water Volume Change in Lake Qinghai
3.2. Climate Change and Land Use Change
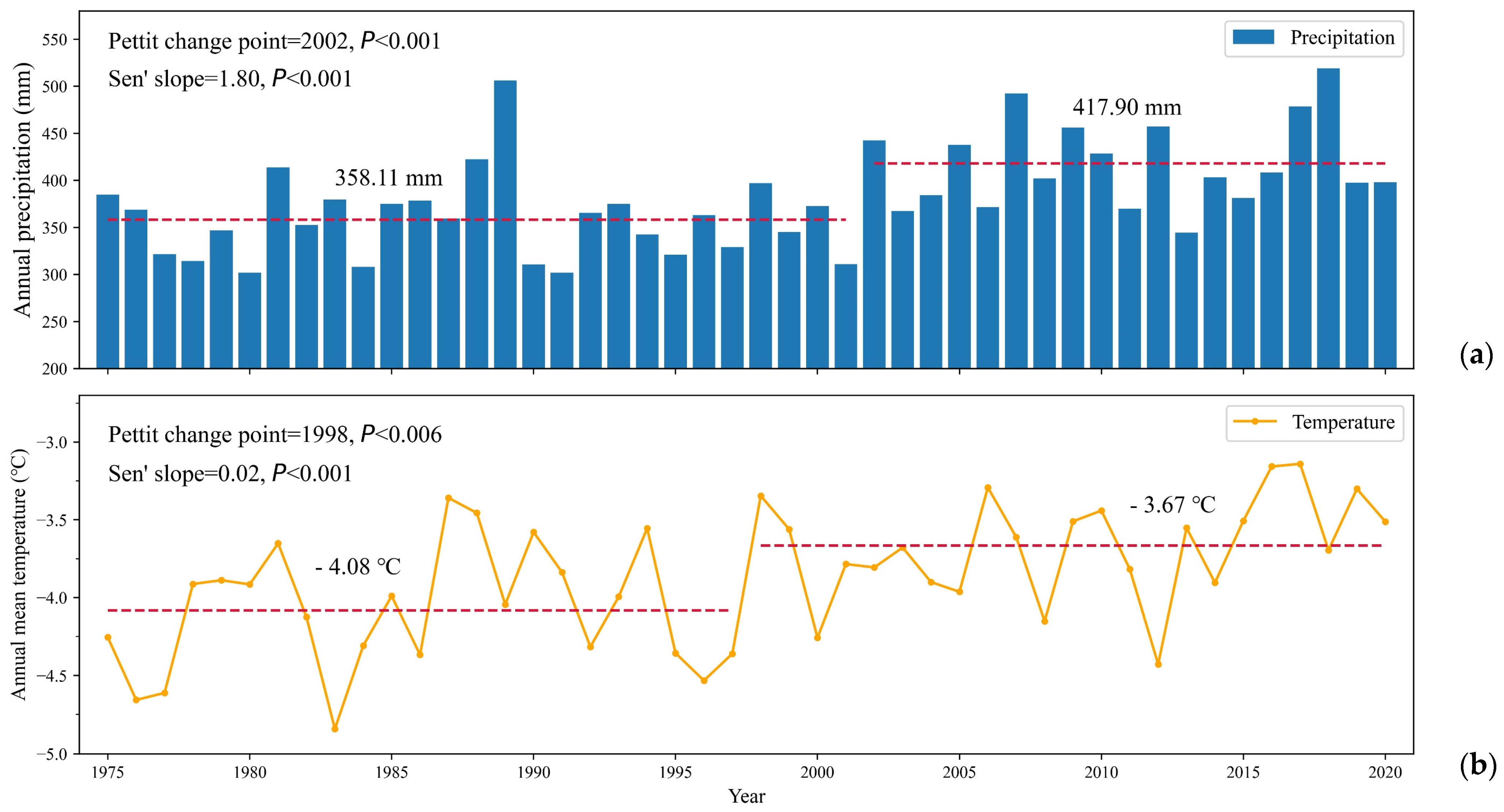
3.2.1. Climate Change in Lake Qinghai Catchment
3.2.2. Land Use Change in Lake Qinghai Catchment
3.3. Simulation of Surface Runoff Based on the SWAT Model
3.3.1. Calibration and Validation of Simulations
3.3.2. Simulated Surface Runoff Results for Different Scenarios
3.3.3. Contributions of Land Use and Climate Change to Surface Runoff
3.3.4. Land Use and Climate Change Interactions
3.4. Other Components That Influence Water Volume Change in Lake
4. Discussion
4.1. Uncertainty Analysis of the SWAT Model
4.2. Water Balance Calculation
4.3. Mechanism of Lake Variation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, R.; Yang, G.; Duan, H.; Jiang, J.; Wang, S.; Feng, X.; Li, A.; Kong, F.; Xue, B.; Wu, J.; et al. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2010, 54, 283–289. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Zhang, K.; Zhu, F. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 59, 3010–3021. [Google Scholar] [CrossRef]
- Ma, R.; Duan, H.; Hu, C.; Feng, X.; Li, A.; Ju, W.; Jiang, J.; Yang, G. A half-century of changes in China’s lakes: Global warming or human influence? Geophys. Res. Lett. 2010, 37, L24106. [Google Scholar] [CrossRef]
- Huang, L.; Liu, J.; Shao, Q.; Liu, R. Changing inland lakes responding to climate warming in Northeastern Tibetan Plateau. Clim. Chang. 2011, 109, 479–502. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Micklin, P. The Aral Sea Disaster. Annu. Rev. Earth Planet. Sci. 2007, 35, 47–72. [Google Scholar] [CrossRef] [Green Version]
- Wurtsbaugh, W.A.; Miller, C.; Null, S.E.; DeRose, R.J.; Wilcock, P.; Hahnenberger, M.; Howe, F.; Moore, J. Decline of the world’s saline lakes. Nat. Geosci. 2017, 10, 816–821. [Google Scholar] [CrossRef]
- Schulz, S.; Darehshouri, S.; Hassanzadeh, E.; Tajrishy, M.; Schüth, C. Climate change or irrigated agriculture–what drives the water level decline of Lake Urmia. Sci. Rep. 2020, 10, 236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, L.; Zheng, M. The response of lake variations to climate change in the past forty years: A case study of the northeastern Tibetan Plateau and adjacent areas, China. Quat. Int. 2015, 371, 31–48. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, J.; Xu, C.Y.; Zhou, Y.; Wu, Y.; Chen, X.; Jiang, S.; Duan, Z. The response of lake area and vegetation cover variations to climate change over the Qinghai-Tibetan Plateau during the past 30years. Sci. Total Environ. 2018, 635, 443–451. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Xu, B. Quantifying the contribution of glacier meltwater in the expansion of the largest lake in Tibet. J. Geophys. Res. Atmos. 2016, 121, 11158–11173. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Yu, Z.; Liang, Z.; Chen, L.; Acharya, K. Climate change driven water budget dynamics of a Tibetan inland lake. Glob. Planet. Change 2017, 150, 70–80. [Google Scholar] [CrossRef]
- Wanjuan, Y.; Xiaoyan, L.; Buli, C.; Yujun, M. Climate Change and Impact on Water Level of the Qinghai Lake Watershed. J. Arid Mereorol. 2010, 28, 375–383. [Google Scholar]
- Bai, A.; Huang, R.; Cheng, Z. Change of water level of the Qinghai Lake under Climate change. Arid Zone Res. 2014, 31, 792–797. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Tian, S.; Yi, D. Water level variation of Lake Qinghai from satellite and in situ measurements under climate change. J. Appl. Remote Sens. 2011, 5, 053532. [Google Scholar] [CrossRef]
- Wan, W.; Xiao, P.; Feng, X.; Li, H.; Ma, R.; Duan, H.; Zhao, L. Monitoring lake changes of Qinghai-Tibetan Plateau over the past 30 years using satellite remote sensing data. Chin. Sci. Bull. 2014, 59, 1021–1035. [Google Scholar] [CrossRef]
- Cui, B.-L.; Xiao, B.; Li, X.-Y.; Wang, Q.; Zhang, Z.-H.; Zhan, C.; Li, X.-D. Exploring the geomorphological processes of Qinghai Lake and surrounding lakes in the northeastern Tibetan Plateau, using Multitemporal Landsat Imagery (1973–2015). Glob. Planet. Chang. 2017, 152, 167–175. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Li, X.; Sun, Y. Climatic change in the Lake Qinghai watershed in recent 47 years. Arid Meteorol. 2007, 6, 25. [Google Scholar]
- Li, X.; Cui, B. The impact of climate changes on water level of Qinghai Lake in China over the past 50 years. Hydrol. Res. 2016, 47, 532–542. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.; Song, C.; Li, W.; Liu, K.; Cheng, J.; Fu, C.; Chen, T.; Ke, L.; Wang, J. What drives the rapid water-level recovery of the largest lake (Qinghai Lake) of China over the past half century? J. Hydrol. 2021, 593, 125921. [Google Scholar] [CrossRef]
- Qing, B.; Shi, Y. The hydrological characteristics and the cause of the declining of water level in Qinghai lake. Acta Geogr. Sin. 1992, 47, 267–273. [Google Scholar]
- Yan, H.; Jia, S. Water balance and water resources allocation of Qinghai Lake. J. Lake Sci. 2003, 15, 35–40. [Google Scholar]
- Tang, L.; Duan, X.; Kong, F.; Zhang, F.; Zheng, Y.; Li, Z.; Mei, Y.; Zhao, Y.; Hu, S. Influences of climate change on area variation of Qinghai Lake on Qinghai-Tibetan Plateau since 1980s. Sci. Rep. 2018, 8, 7331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, J.; Li, Q.; Liu, X.; Wen, D. Hydrological Characteristics of Qinghai Lake, 1956–2017. J. Hydroecol. 2020, 41, 27–33. [Google Scholar] [CrossRef]
- Lei, X.; Gao, L.; Wei, J.; Ma, M.; Xu, L.; Fan, H.; Li, X.; Gao, J.; Dang, H.; Chen, X.; et al. Contributions of climate change and human activities to runoff variations in the Poyang Lake Basin of China. Phys. Chem. Earth Parts A/B/C 2021, 123, 103019. [Google Scholar] [CrossRef]
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Yin, J.; He, F.; Xiong, Y.J.; Qiu, G.Y. Effects of land use/land cover and climate changes on surface runoff in a semi-humid and semi-arid transition zone in northwest China. Hydrol. Earth Syst. Sci. 2017, 21, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Lyu, J.; Luo, P.; Mo, S.; Zhou, M.; Shen, B.; Fan, L.; Nover, D. Towards sustainable water regulation based on a distributed hydrological model for a heavily polluted urban river, northwest China. Hydrol. Res. 2019, 50, 961–973. [Google Scholar] [CrossRef]
- Yuetan, L.; Xiaoyan, L.; Buli, C.; Haiying, P. Trend of streamflow in Lake Qinghai basin during the past 50 years(1956–2007)—Take Buha River and Shaliu River for examples. J. Lake Sci. 2010, 22, 757–766. [Google Scholar]
- Wang, Z.; Zhang, F.; Li, X.; Cao, Y.; Hu, J.; Wang, H.; Lu, H.; Li, T.; Liu, W. Changes in the depth of Lake Qinghai since the last deglaciation and asynchrony between lake depth and precipitation over the northeastern Tibetan Plateau. Glob. Planet. Chang. 2020, 188, 103156. [Google Scholar] [CrossRef]
- Water Resources Department of Qinghai Province; Bureau of Statistics of Qinghai Province. The communique of first Water Resource Census of Qinghai Province. Qinghai Daily, 28 May 2013; 1–10. [Google Scholar]
- Crétaux, J.F.; Abarca-del-Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef] [Green Version]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. Appl. Stat. 1979, 28. [Google Scholar] [CrossRef]
- Mallakpour, I.; Villarini, G. A simulation study to examine the sensitivity of the Pettitt test to detect abrupt changes in mean. Hydrol. Sci. J. 2016, 61, 245–254. [Google Scholar] [CrossRef] [Green Version]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment. J. Am. Water Rescour. Aaaoxiat. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Mekonnen, D.F.; Duan, Z.; Rientjes, T.; Disse, M. Analysis of combined and isolated effects of land-use and land-cover changes and climate change on the upper Blue Nile River basin’s streamflow. Hydrol. Earth Syst. Sci. 2018, 22, 6187–6207. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, K.; Vaghefi, S.; Srinivasan, R. A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference. Water 2018, 10, 6. [Google Scholar] [CrossRef] [Green Version]
- Guzman, J.A.; Shirmohammadi, A.; Sadeghi, A.M.; Wang, X.; Chu, M.L.; Jha, M.; Parajuli, P.B.; Harmel, R.D.; Khare, Y.; Hernandez, J.E. Uncertainty Considerations in Calibration and Validation of Hydrologic and Water Quality Models. Trans. ASABE 2015, 58, 1745–1762. [Google Scholar] [CrossRef]
- Mehan, S.; Neupane, R.P.; Kumar, S. Coupling of SUFI 2 and SWAT for Improving the Simulation of Streamflow in an Agricultural Watershed of South Dakota. Hydrol. Curr. Res. 2017, 8, 1000280. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; VanLiew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Zhangdong, J.; Fei, Z. The reasons of rising water level in Lake Qinghai since 2005. J. Earth Environ. 2013, 4, 1355–1362. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Fang, W.; Jia, L.; Huayun, Y. Analysis on hydrological process ofwater balance factors in Qinghai Lake. J. Hydraul. Eng. 2008, 39, 1229–1238. [Google Scholar] [CrossRef]
- Duku, C.; Rathjens, H.; Zwart, S.J.; Hein, L. Towards ecosystem accounting: A comprehensive approach to modelling multiple hydrological ecosystem services. Hydrol. Earth Syst. Sci. 2015, 19, 4377–4396. [Google Scholar] [CrossRef] [Green Version]
- Shafeeque, M.; Luo, Y.; Wang, X.; Sun, L. Altitudinal Distribution of Meltwater and Its Effects on Glacio-Hydrology in Glacierized Catchments, Central Asia. JAWRA J. Am. Water Resour. Assoc. 2020, 56, 30–52. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Xinghe, S.; Shengchen, L.; Di, A.; Dongliang, L.; Zhongcheng, S. A Study of the Change of Qinghai Lake Evaporation. Clim. Environ. Res. 2010, 15, 787–796. [Google Scholar]
- Zhang, M.; Song, Y.; Dong, H. Hydrological trend of Qinghai Lake over the last 60 years: Driven by climate variations or human activities? J. Water Clim. Chang. 2019, 10, 524–534. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sens. 2018, 10, 829. [Google Scholar] [CrossRef] [Green Version]
- Gossel, W. GIS-MODFLOW: Ein kleines OpenSource-Werkzeug zur Anbindung von GIS-Daten an MODFLOW. Grundwasser 2013, 18, 99–102. [Google Scholar] [CrossRef]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Mu, Y.; Wang, S.; Zhu, W.; Mishra, B.K.; Huo, A.; Zhou, M.; Lyu, J.; Hu, M.; Duan, W.; et al. Exploring sustainable solutions for the water environment in Chinese and Southeast Asian cities. Ambio 2021. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, C. Trends in precipitation recycling over the Qinghai–Xizang Plateau in last decades. J. Hydrol. 2014, 517, 826–835. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, C.; Chen, D. Recent Changes in the Moisture Source of Precipitation over the Tibetan Plateau. J. Clim. 2017, 30, 1807–1819. [Google Scholar] [CrossRef]




| Scenario | Land Use/Cover | Climate | Remark |
|---|---|---|---|
| P0 | 1980 | 1975–1984 | Base period |
| P1 | 1990 | 1985–1994 | Influence of land use and climate changes |
| P2 | 2000 | 1994–2004 | |
| P3 | 2010 | 2005–2014 | |
| SL1 | 1990 | 1975–1984 | Influence of land use change |
| SL2 | 2000 | 1975–1984 | |
| SL3 | 2010 | 1975–1984 | |
| SC1 | 1980 | 1985–1994 | Influence of climate change |
| SC2 | 1980 | 1994–2004 | |
| SC3 | 1980 | 2005–2014 |
| Simulation Performance | R2 | NSE | PBIAS (%) |
|---|---|---|---|
| Very good | 0.85 < R2 ≤ 1.00 | 0.80 < NSE ≤ 1.00 | |PBIAS| ≤ 5 |
| Good | 0.75 < R2 ≤ 0.85 | 0.70 < NSE ≤ 0.80 | 5 < |PBIAS| ≤ 10 |
| Satisfactory | 0.60 < R2 ≤ 0.75 | 0.50 < NSE ≤ 0.70 | 10 < |PBIAS| ≤ 15 |
| Unsatisfactory | R2 ≤ 0.60 | NSE ≤ 0.50 | |PBIAS| > 15 |
| Classes | 1980 | 1990 | 2000 | 2010 | ||||
|---|---|---|---|---|---|---|---|---|
| Area (km2) | Area (%) | Area (km2) | Area (%) | Area (km2) | Area (%) | Area (km2) | Area (%) | |
| AGRL | 487 | 1.64% | 486 | 1.64% | 539 | 1.82% | 565 | 1.91% |
| FRST | 1377 | 4.65% | 1377 | 4.65% | 1373 | 4.63% | 1366 | 4.61% |
| PAST | 14,526 | 49.01% | 14,562 | 49.13% | 14,523 | 49.00% | 14,506 | 48.94% |
| WATR | 5121 | 17.28% | 4782 | 16.14% | 4765 | 16.08% | 4764 | 16.07% |
| URBN | 17 | 0.06% | 18 | 0.06% | 19 | 0.06% | 19 | 0.06% |
| BARR | 8110 | 27.36% | 8413 | 28.39% | 8419 | 28.41% | 8418 | 28.40% |
| Parameter | Definition | Initial Range | Calibration Result | Sensitivity Priority | ||
|---|---|---|---|---|---|---|
| Gangcha | Buha | Gangcha | Buha | |||
| r__CN2 | Initial SCS runoff curve number for moisture condition II | −0.2–0.2 | 0.05 | 0.16 | 1 | 1 |
| v__ALPHA_BF | Baseflow alpha factor | 0–1 | 0.58 | 3 | ||
| v__GW_DELAY | Groundwater delay time | 0–500 | 162.79 | 7 | ||
| v__GW_REVAP | Groundwater “revap” coefficient | 0.02–0.2 | 0.07 | 10 | ||
| v__RCHRG_DP | Deep aquifer percolation fraction | 0–1 | 0.25 | 0.05 | 8 | 4 |
| v__CH_N2 | Manning’s “n” value for the main channel | 0–0.3 | 0.25 | 0.24 | 9 | 6 |
| v__CH_K2 | Effective hydraulic conductivity in main channel alluvium | 0–150 | 122.21 | 8 | ||
| v__SURLAG | Surface runoff lag time | 1–24 | 20.31 | 2.18 | 6 | 2 |
| v__SLSUBBSN | Average slope length | 10–150 | 23.12 | 96.07 | 3 | 10 |
| v__ESCO | Soil evaporation compensation factor | 0.01–1 | 0.51 | 0.06 | 2 | 5 |
| v__EPCO | Plant uptake compensation factor | 0.01–1 | 0.65 | 9 | ||
| v__SMFMX | Maximum melt rate for snow during year | 0–10 | 7.44 | 0.03 | 4 | 7 |
| v__SFTMP | Snowfall temperature | −5–5 | 0.63 | 11 | ||
| r__SOL_AWC | Available water capacity of the soil layer | −0.5–0.5 | −0.5 | 5 | ||
| Period | Land Use | Climate | Simulation (m3/s) | Variation (m3/s) | Percentage (%) |
|---|---|---|---|---|---|
| P0 | 1980 | 1975–1984 | 32.156 | - | - |
| P1 | 1990 | 1985–1994 | 41.331 | 9.175 | 28.53 |
| P2 | 2000 | 1994–2004 | 34.005 | 1.849 | 5.75 |
| P3 | 2010 | 2005–1914 | 44.722 | 12.566 | 39.08 |
| Mean | 40.019 | 7.864 | 24.45 |
| Period | Land Use | Climate | Simulation (m3/s) | Variation (m3/s) | Percentage (%) |
|---|---|---|---|---|---|
| SL1 | 1990 | 1975–1984 | 32.467 | 0.311 | 3.39% |
| SL2 | 2000 | 1975–1984 | 32.462 | 0.306 | 16.56% |
| SL3 | 2010 | 1975–1984 | 32.461 | 0.305 | 2.43% |
| Mean | 32.463 | 0.308 | 7.46% |
| Period | Land use | Climate | Simulation (m3/s) | Variation (m3/s) | Percentage (%) |
|---|---|---|---|---|---|
| SC1 | 1980 | 1985–1994 | 41.053 | 8.897 | 96.96% |
| SC2 | 1980 | 1994–2004 | 33.729 | 1.573 | 85.07% |
| SC3 | 1980 | 2005–1914 | 44.389 | 12.233 | 97.35% |
| Mean | 39.724 | 7.568 | 93.13% |
| Lake Water Volume Change | Supply | Loss | |||
|---|---|---|---|---|---|
| R | P | G | E | H | |
| −0.83 | 17.61 | 16.13 | 7.67 | 41.45 | 0.73 |
| Index | Calibration | Validation | ||
|---|---|---|---|---|
| Gangcha | Buha | Gangcha | Buha | |
| P-factor | 0.83 | 0.71 | 0.89 | 0.69 |
| R-factor | 0.94 | 0.68 | 0.95 | 0.76 |
| Study Period | Water Balance Terms | Source | ||||
|---|---|---|---|---|---|---|
| R | P | G | E | H | ||
| 1958–1986 | 16.0 | 18.09 | 4.56 | 42.44 | 0.88 | Qing et al. [21] |
| 1959–2000 | 15.26 | 15.61 | 6.03 | 40.50 | Yan et al. [22] | |
| 1965–2002 | 14.57 | 16.62 | 7.64 | 40.93 | 0.73 | Wang et al. [46] |
| 1956–2017 | 17.62 | 16.32 | 6.56 | 41.94 | Du et al. [24] | |
| 1975–2014 | 17.61 | 16.13 | 7.67 | 41.45 | 0.73 | Our study |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Zhang, M.; Xie, Z.; Li, J.; Ma, M.; Lai, P.; Wang, J. Quantifying the Contributions of Climate Change and Human Activities to Water Volume in Lake Qinghai, China. Remote Sens. 2022, 14, 99. https://doi.org/10.3390/rs14010099
Yang G, Zhang M, Xie Z, Li J, Ma M, Lai P, Wang J. Quantifying the Contributions of Climate Change and Human Activities to Water Volume in Lake Qinghai, China. Remote Sensing. 2022; 14(1):99. https://doi.org/10.3390/rs14010099
Chicago/Turabian StyleYang, Guoqing, Miao Zhang, Zhenghui Xie, Jiyuan Li, Mingguo Ma, Peiyu Lai, and Junbang Wang. 2022. "Quantifying the Contributions of Climate Change and Human Activities to Water Volume in Lake Qinghai, China" Remote Sensing 14, no. 1: 99. https://doi.org/10.3390/rs14010099
APA StyleYang, G., Zhang, M., Xie, Z., Li, J., Ma, M., Lai, P., & Wang, J. (2022). Quantifying the Contributions of Climate Change and Human Activities to Water Volume in Lake Qinghai, China. Remote Sensing, 14(1), 99. https://doi.org/10.3390/rs14010099









