Insect Migration Flux Estimation Based on Statistical Hypothesis for Entomological Radar
Abstract
:1. Introduction
2. Methods
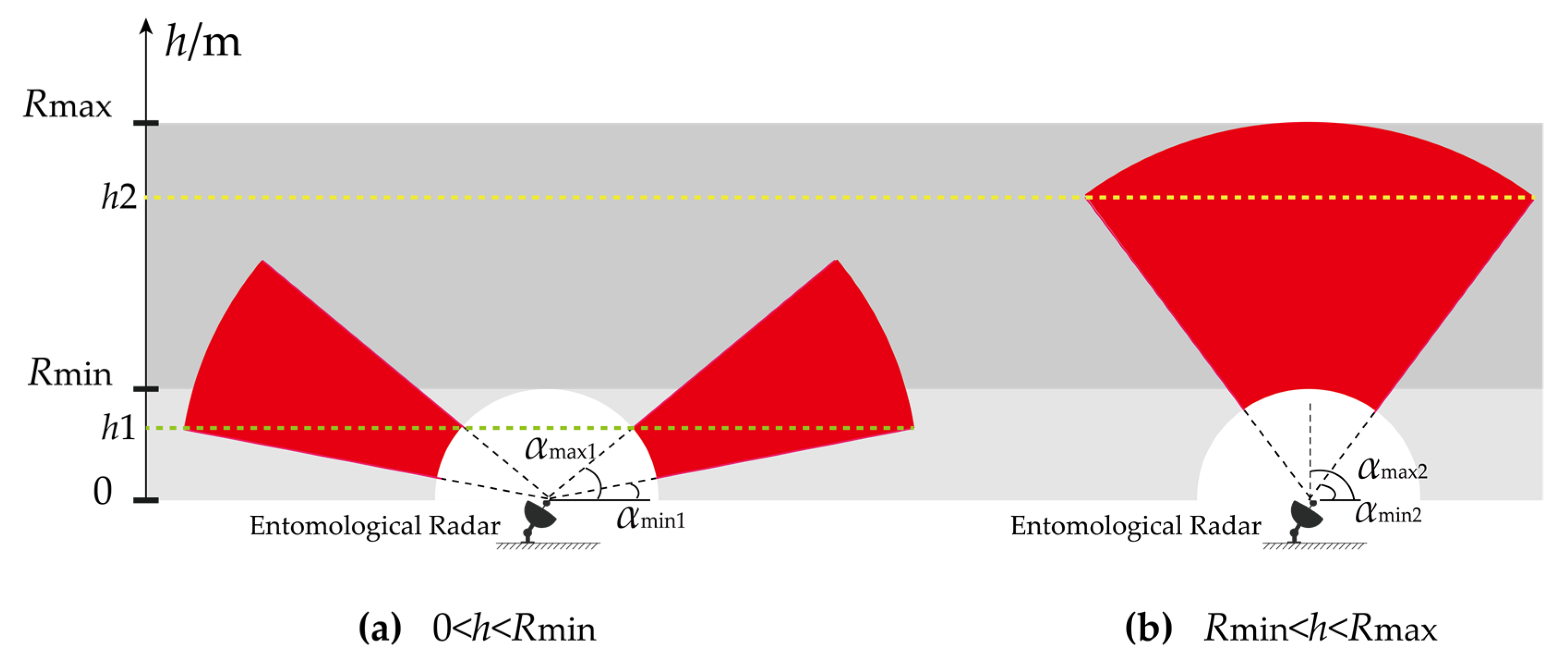
2.1. Fixed-Beam Vertical Looking Mode
2.2. Fixed-Beam Arbitrary Pointing Mode
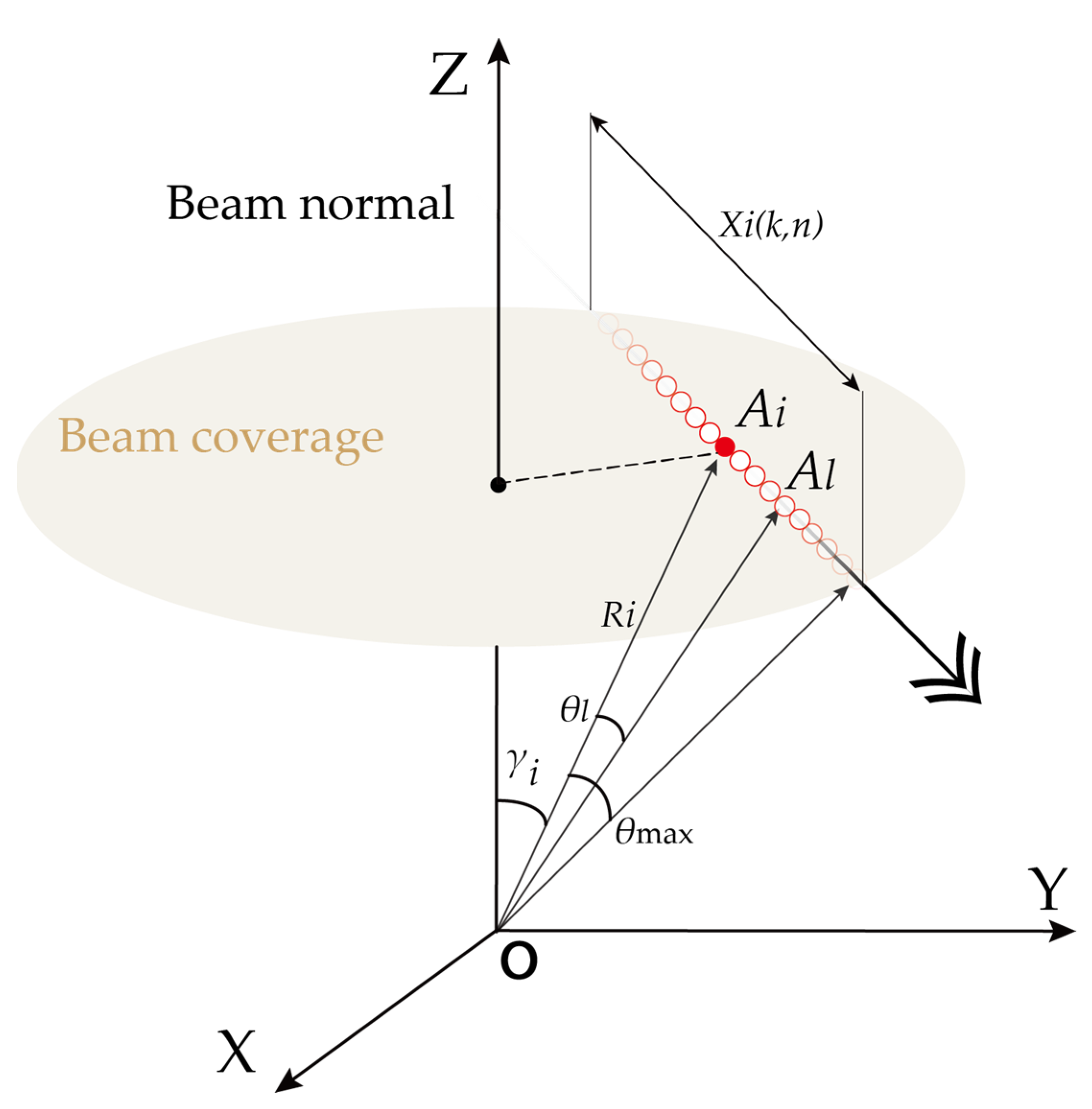
2.3. Scanning Mode
2.3.1. Scanning Mode Description
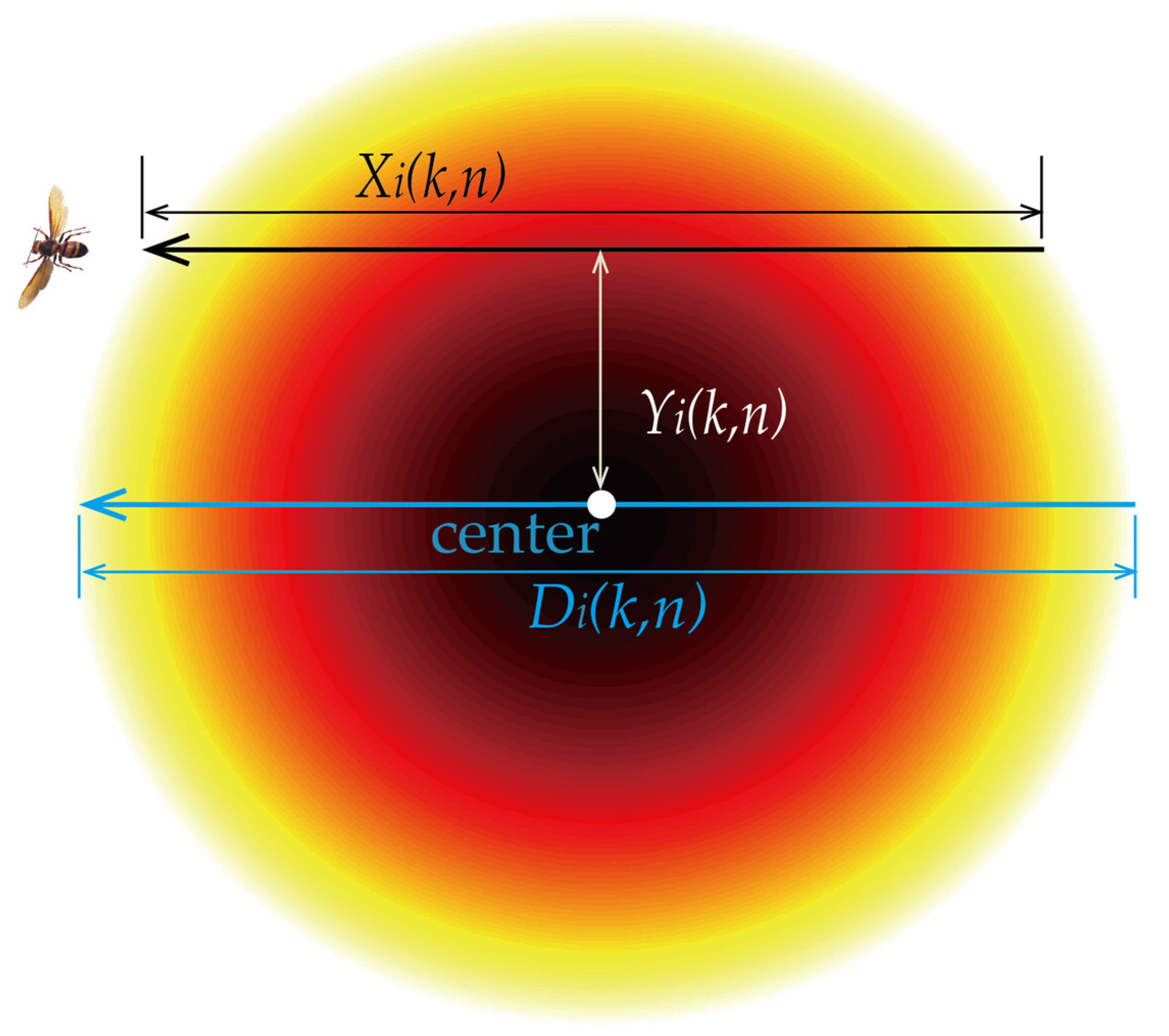
2.3.2. Flux Estimation Method for Scanning Mode
- (1)
- Statistical time gap
- (2)
- Migration flux calculation
3. Results
3.1. Simulation Analysis
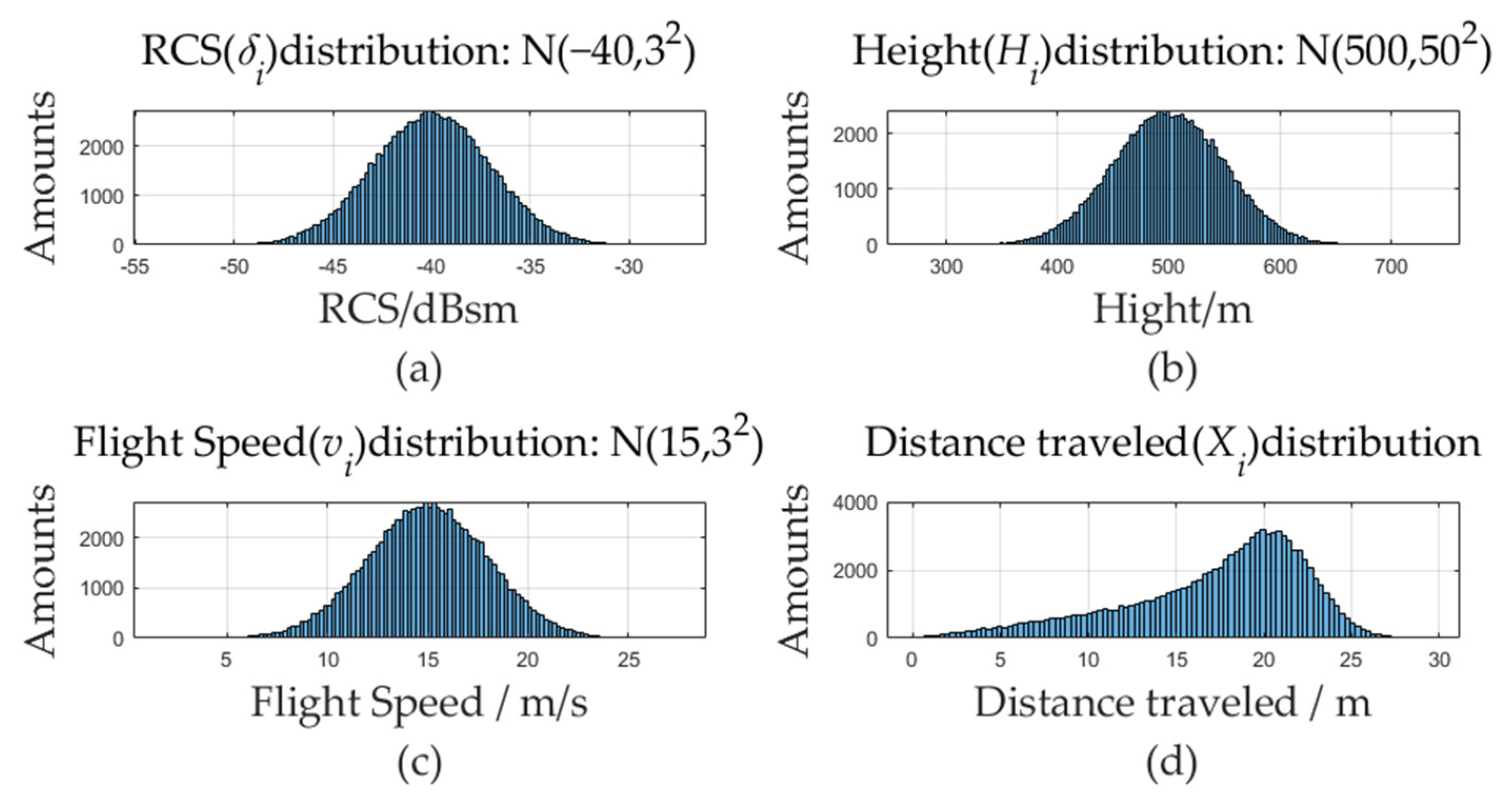
3.1.1. Method Simulation under Ideal Conditions
- (1)
- Theoretical migration flux results
- (2)
- Migration flux calculated by the traditional method
- (3)
- Migration flux by the proposed method
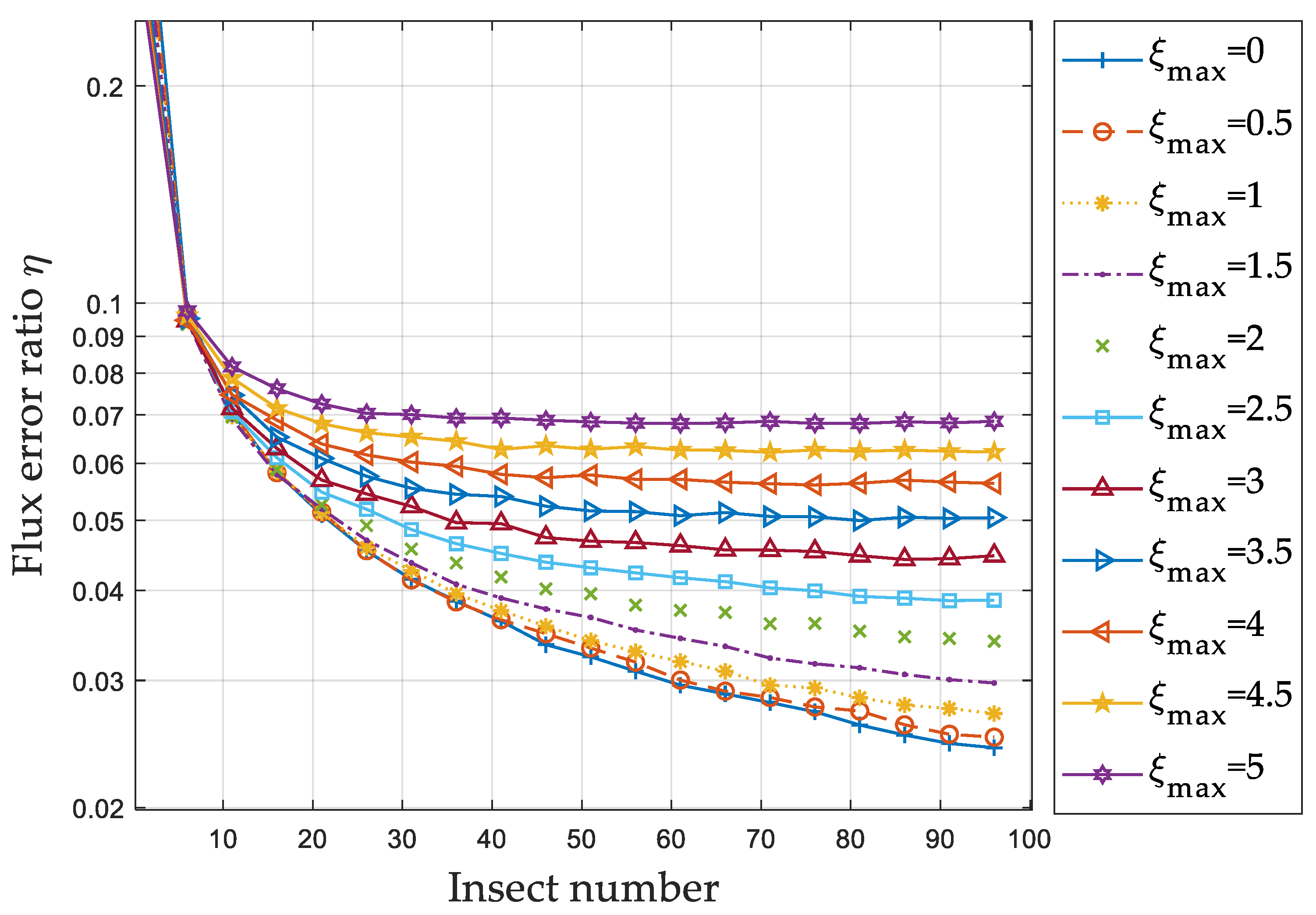
3.1.2. Influence of Number of Statistical Samples and RCS Measurement Error on Migration Flux Estimation
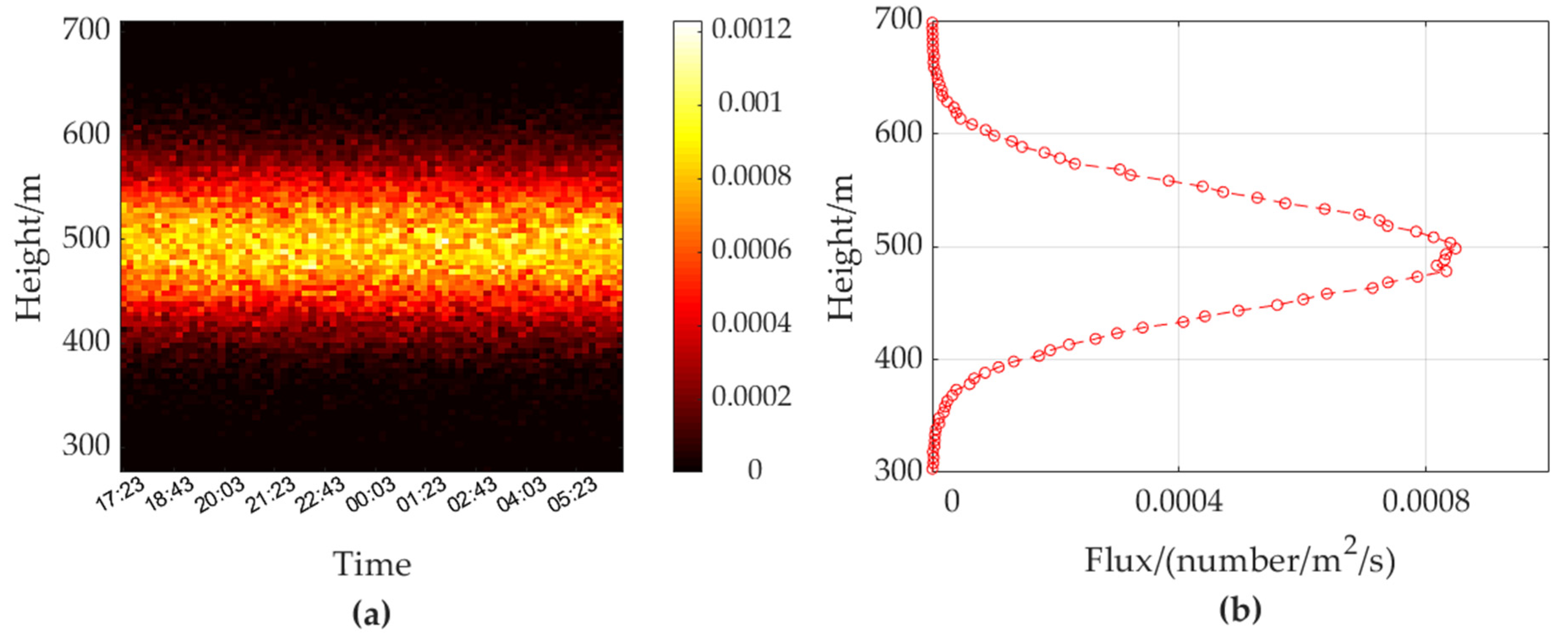
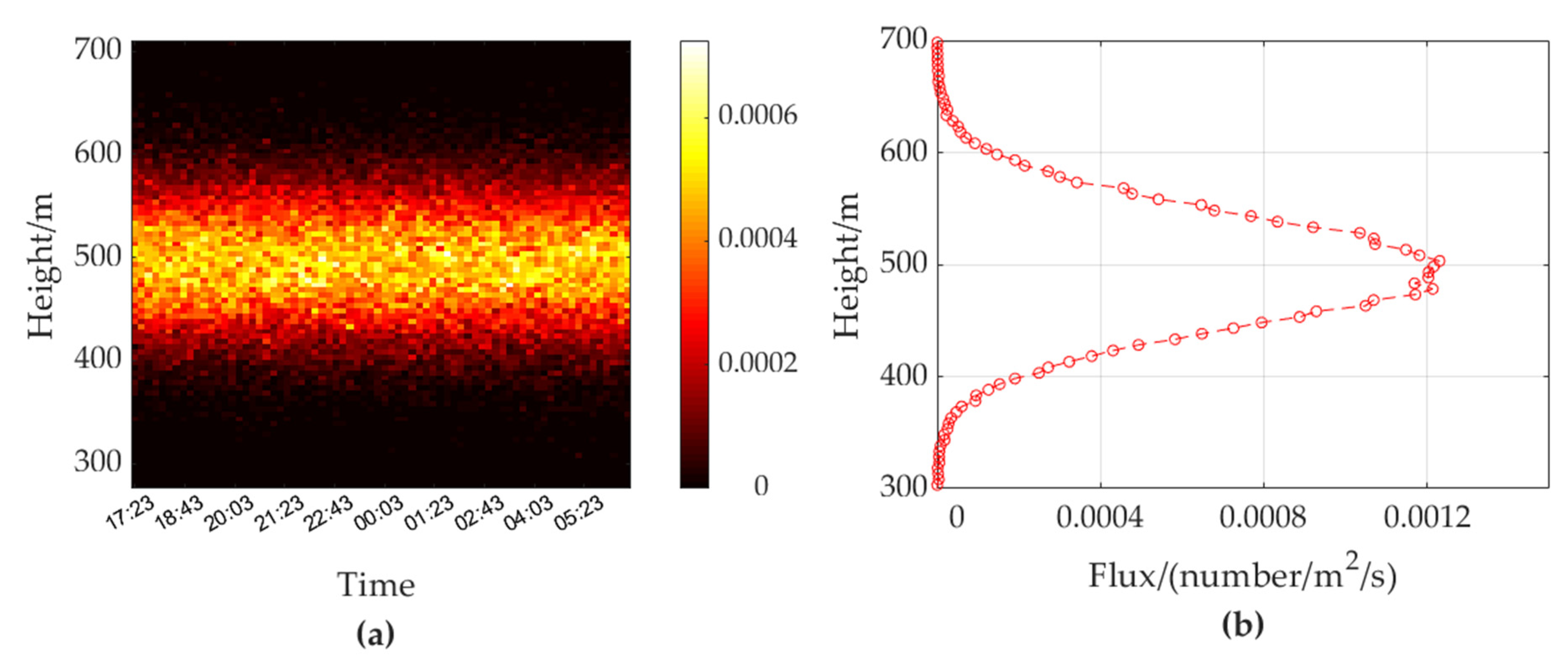
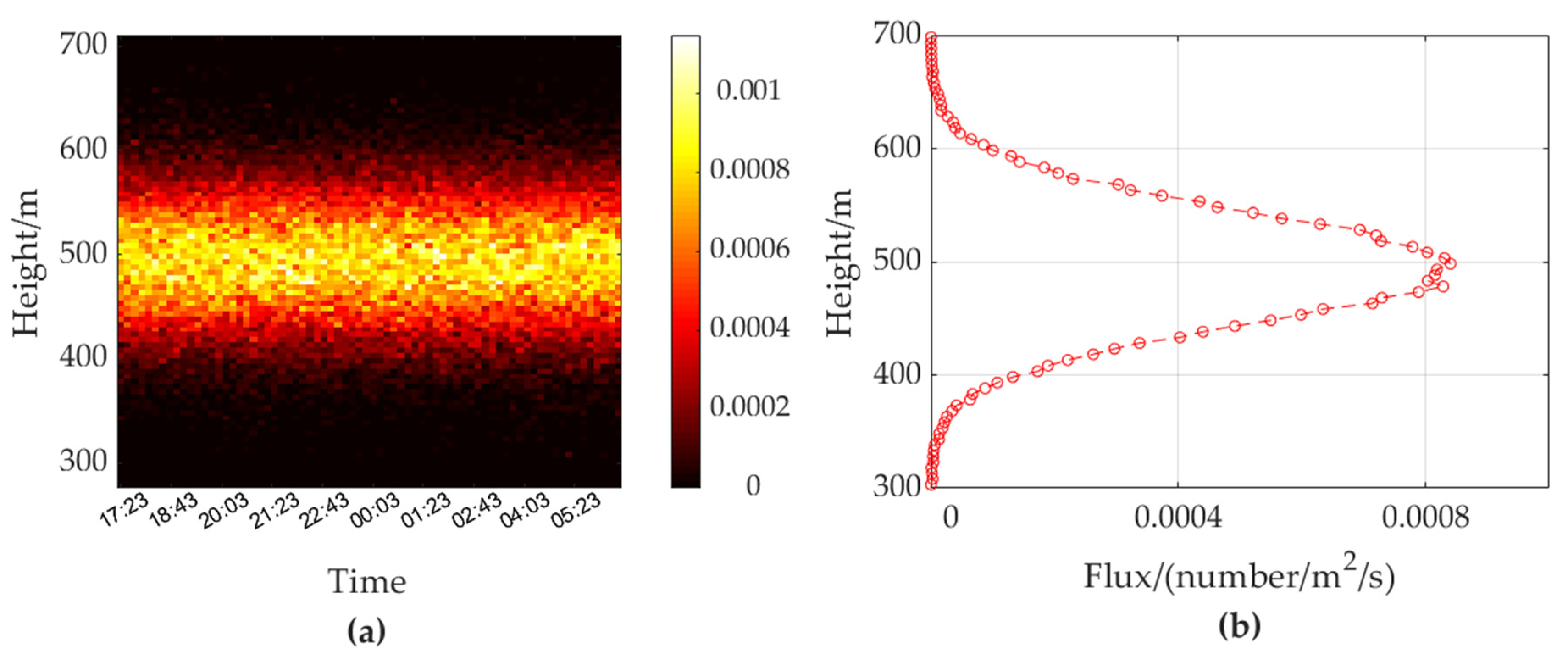
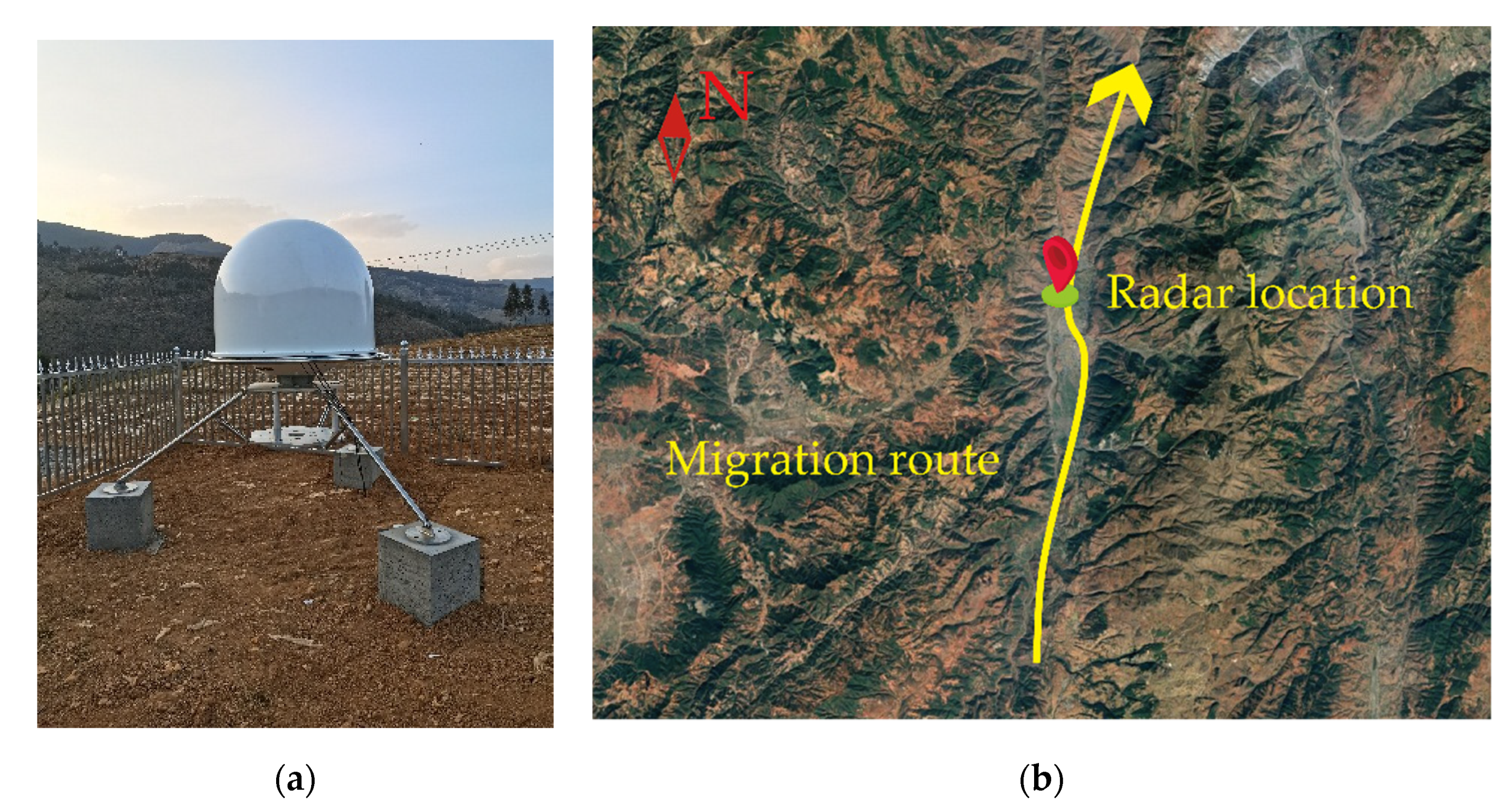
3.2. Experimental Verification
- (1)
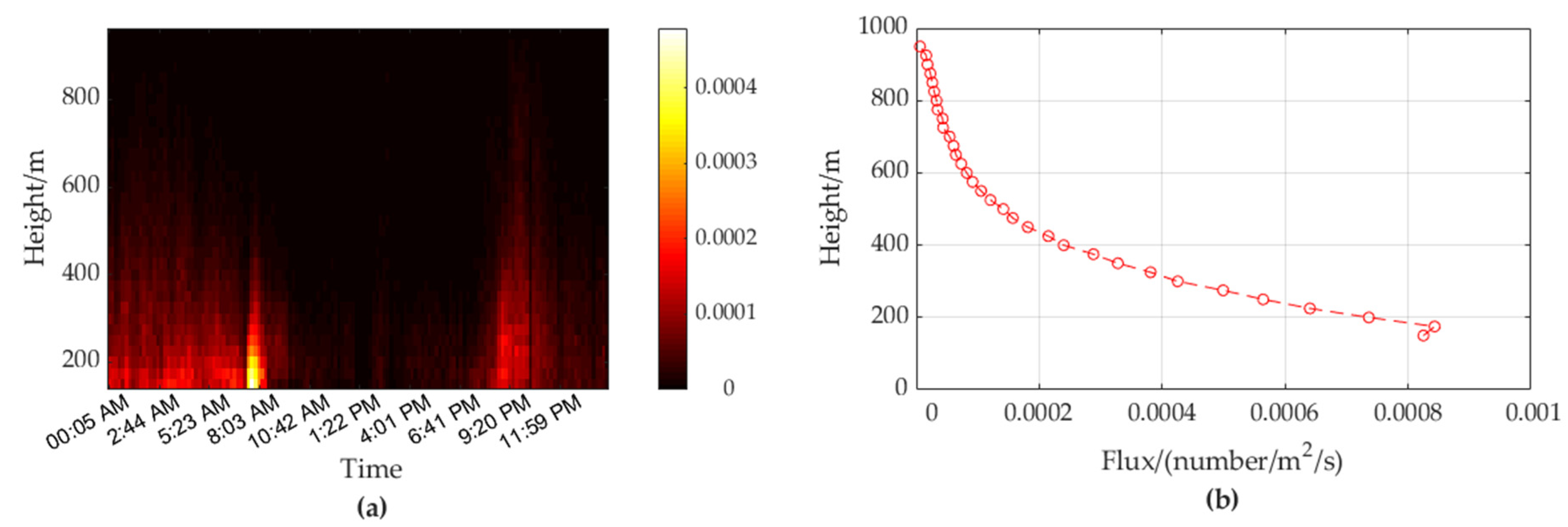
- Verification results in fixed-beam vertical-looking mode
- (2)
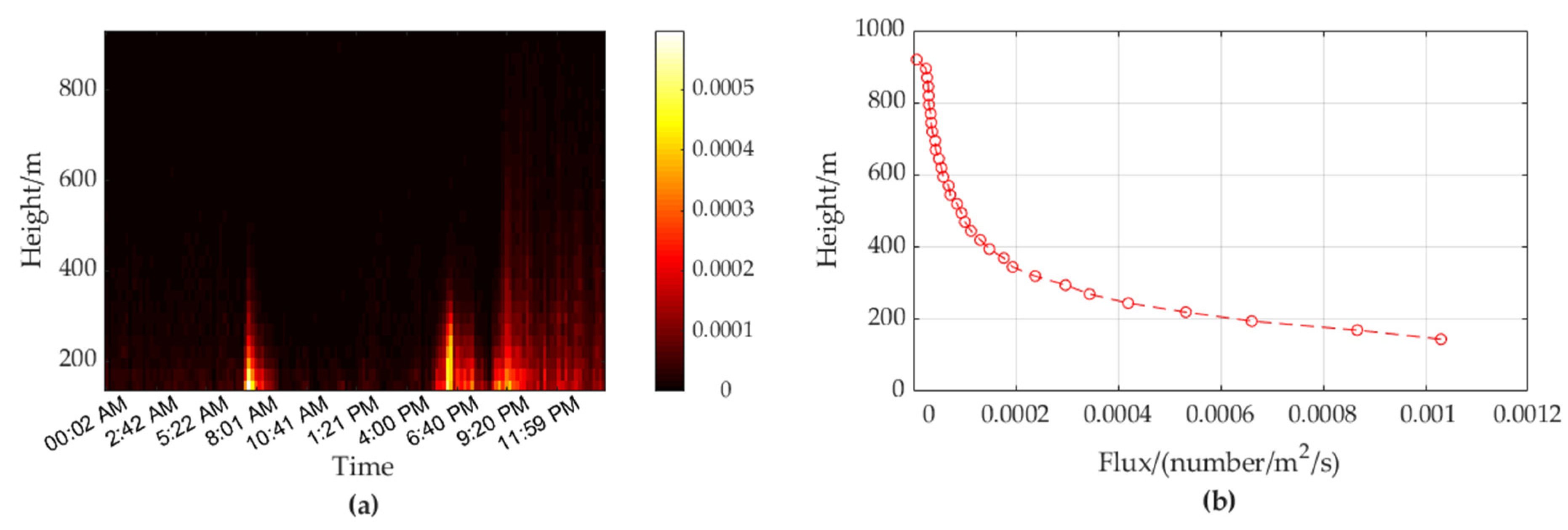
- Verification results in fixed-beam arbitrary pointing mode
- (3)
- Verification results in scanning mode
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chapman, J.; Smith, A.; Woiwod, I.; Reynolds, D.; Riley, J. Development of vertical-looking radar technology for monitoring insect migration. Comput. Electron. Agric. 2002, 35, 95–110. [Google Scholar] [CrossRef]
- Cai, J.; Yuan, Q.; Wang, R.; Liu, C.; Zhang, T. Insect detection and density estimation based on a Ku-band scanning entomological radar. J. Eng. 2019, 2019, 7636–7639. [Google Scholar] [CrossRef]
- Zhai, B.P. Entomological Radar: From Research to Practice. J. Remote Sens. 2001, 5, 240. [Google Scholar]
- Cheng, D.F.; Wu, K.M.; Tian, Z.; Wen, L.P.; Shen, Z.R. Acquisition and analysis of migration data from the digitised display of a scanning entomological radar. Comput. Electron. Agric. 2002, 35, 63–75. [Google Scholar] [CrossRef]
- Drake, V.A. Quantitative Observation and Analysis Procedures for a Manually Operated Entomological Radar; CSIRO: Melbourne, Australia, 1981. [Google Scholar]
- Hu, C.; Kong, S.; Wang, R.; Zhang, F.; Wang, L. Insect Mass Estimation Based on Radar Cross Section Parameters and Support Vector Regression Algorithm. Remote Sens. 2020, 12, 1903. [Google Scholar] [CrossRef]
- Long, T.; Hu, C.; Wang, R.; Zhang, T.; Zeng, T. Entomological radar overview: System and signal processing. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–32. [Google Scholar] [CrossRef]
- Hu, C.; Kong, S.; Wang, R.; Long, T.; Fu, X. Identification of Migratory Insects from their Physical Features using a Decision-Tree Support Vector Machine and its Application to Radar Entomology. Sci. Rep. 2018, 8, 5449. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Mao, H.; Hu, C.; Zeng, T.; Long, T. Joint association and registration in a multiradar system for migratory insect track observation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4028–4043. [Google Scholar] [CrossRef]
- Yu, T.; Li, M.; Li, W.; Mao, H.; Wang, R.; Hu, C.; Long, T. Polarimetric Calibration Technique for a Fully Polarimetric Entomological Radar Based on Antenna Rotation. Remote Sens. 2022, 14, 1551. [Google Scholar] [CrossRef]
- Hu, C.; Li, W.; Wang, R.; Li, Y.; Li, W.; Zhang, T. Insect flight speed estimation analysis based on a full-polarization radar. Sci. China Inf. Sci. 2018, 61, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Kong, S.; Wang, R.; Zhang, F. Radar Measurements of Morphological Parameters and Species Identification Analysis of Migratory Insects. Remote Sens. 2019, 11, 1977. [Google Scholar] [CrossRef] [Green Version]
- Chao, Z.; Rui, W.; Hu, C. Equivalent point estimation for small target groups tracking based on MLE. Sci. China Inf. Sci. 2019, 63, 8. [Google Scholar]
- Li, W.; Hu, C.; Wang, R.; Kong, S.; Zhang, F. Comprehensive analysis of polarimetric radar cross-section parameters for insect body width and length estimation. Sci. China Inf. Sci. 2021, 64, 11. [Google Scholar] [CrossRef]
- Chapman, J.W.; Reynolds, D.R.; Smith, A.D. Vertical-Looking Radar: A New Tool for Monitoring High-Altitude Insect Migration. BioScience 2003, 53, 503–511. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Wang, R.; Li, M.; Hu, C. Research on the design and calibration of wideband fully polarized vertical insect radar. J. Signal Process. 2021, 37, 222–233. [Google Scholar]
- Wang, R.; Li, W.; Hu, C.; Li, M.; Mao, H. Insect Biological Parameters Estimation Method and Field Quantitative Experiment Verification for Fully Polarimetric Entomological Radar. J. Signal Process. 2021, 37, 199–208. [Google Scholar]
- Wang, R.; Cai, J.; Hu, C.; Zhou, C.; Zhang, T. A Novel Radar Detection Method for Sensing Tiny and Maneuvering Insect Migrants. Remote Sens. 2020, 12, 3238. [Google Scholar] [CrossRef]
- Reynolds, D.R.; Smith, A.D.; Chapman, J.W. A radar study of emigratory flight and layer formation by insects at dawn over southern Britain. Bull. Entomol. Res. 2008, 98, 35–52. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T.; Taylor, L.R. Diurnal periodicity of flight by insects. Trans. R. Entomol. Soc. Lond. 1965, 116, 393–435. [Google Scholar] [CrossRef]









| Number | Parameter Symbols | Parameter Value | Unit |
|---|---|---|---|
| 1 | dBsm | ||
| 2 | m | ||
| 3 | m/s | ||
| 4 | - | ||
| 5 | Monte Carlo times | - | |
| 6 | Maximum error of amplitude measurement | dB | |
| 7 | Amplitude measurement error | dB | |
| 8 | Statistical sample size | 1~100 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Li, M.; Li, W.; Cai, J.; Wang, R.; Hu, C. Insect Migration Flux Estimation Based on Statistical Hypothesis for Entomological Radar. Remote Sens. 2022, 14, 2298. https://doi.org/10.3390/rs14102298
Yu T, Li M, Li W, Cai J, Wang R, Hu C. Insect Migration Flux Estimation Based on Statistical Hypothesis for Entomological Radar. Remote Sensing. 2022; 14(10):2298. https://doi.org/10.3390/rs14102298
Chicago/Turabian StyleYu, Teng, Muyang Li, Weidong Li, Jiong Cai, Rui Wang, and Cheng Hu. 2022. "Insect Migration Flux Estimation Based on Statistical Hypothesis for Entomological Radar" Remote Sensing 14, no. 10: 2298. https://doi.org/10.3390/rs14102298
APA StyleYu, T., Li, M., Li, W., Cai, J., Wang, R., & Hu, C. (2022). Insect Migration Flux Estimation Based on Statistical Hypothesis for Entomological Radar. Remote Sensing, 14(10), 2298. https://doi.org/10.3390/rs14102298









