Automated Glacier Snow Line Altitude Calculation Method Using Landsat Series Images in the Google Earth Engine Platform
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Analyzed Data
2.2.1. Landsat Series Data
2.2.2. NASADEM
2.2.3. Glacier Data
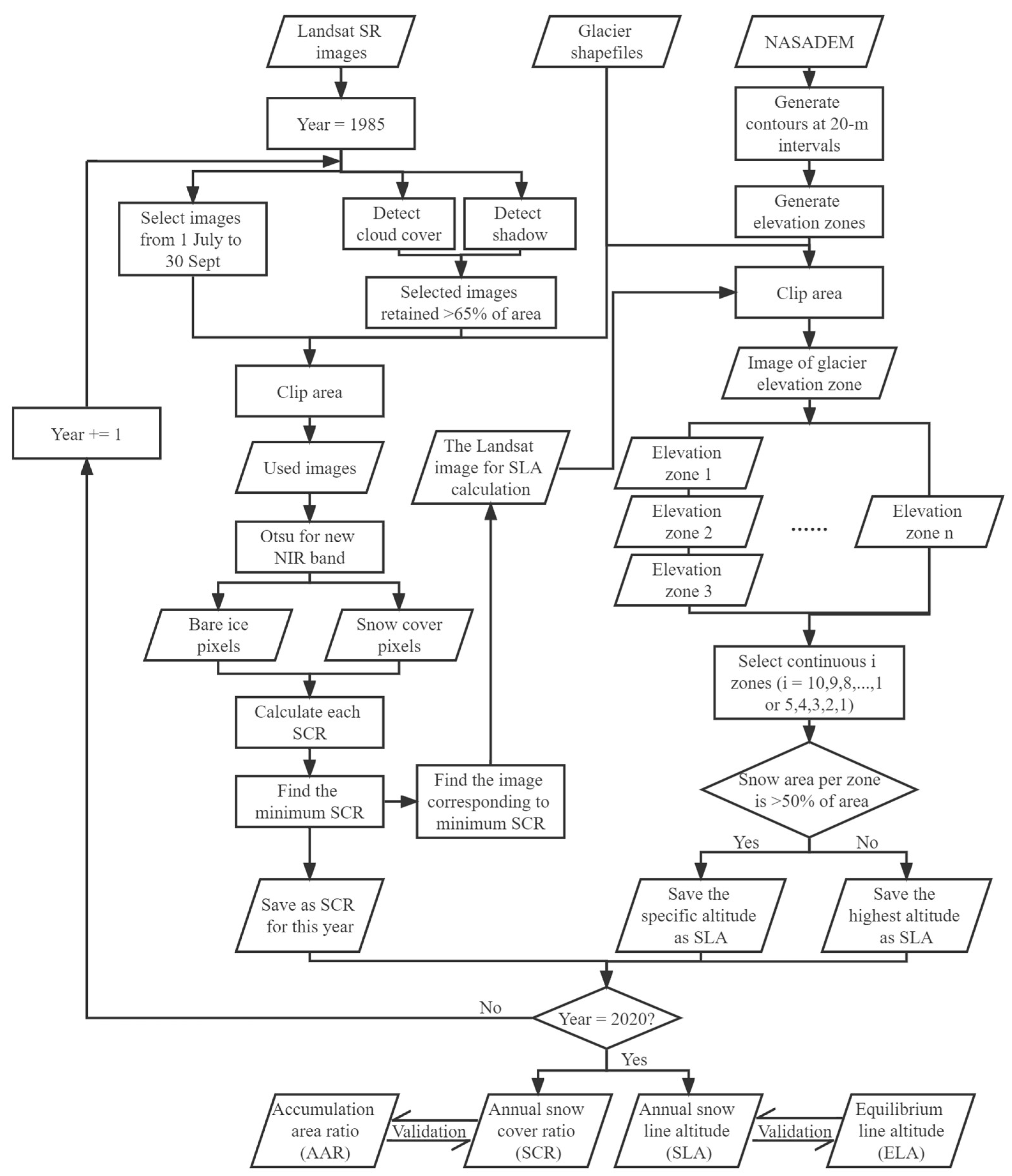
3. Methods
3.1. Preprocessing
3.1.1. Rename Landsat Bands
3.1.2. Cloud Cover and Shadow Detection
3.2. Generate Used Images
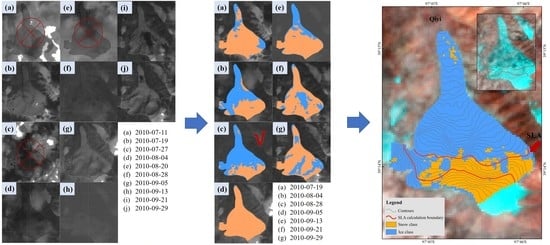
3.3. Glacier Surface Classification and Snow Cover Ratio (SCR) Calculation
3.4. Snow Line Altitude (SLA) Calculation
3.5. Uncertainty Estimates
4. Results
4.1. Glacier Snow Cover Ratio (SCR) Time Series
4.2. Snow Line Altitude (SLA) Time Series
5. Discussion
5.1. Snow Line Altitude (SLA)-Equilibrium Line Altitude (ELA) Comparison
5.2. Algorithm Discussion
5.2.1. Glacier Outline Impact on the Snow Line Altitude (SLA) Calculation
5.2.2. Algorithm Limitation
5.2.3. Landsat Series Images Impact on the Snow Line Altitude (SLA) Calculations
5.3. Further Works
- (a)
- Debris-covered glaciers’ SLA calculation should be researched. For global mountain glaciers, debris-covered glaciers over 7.3% of Earth’s mountain glacier area, presenting a significant factor contributing to the variability of glacier response to climate changes in different regions [42,43,44,45]. Debris-covered area and thickness affect the glacier ablation process, affecting the calculation of AAR and ELA. Besides, the composition of debris will also affect the snow ablation process, leading to impacts on SCR and SLA. Therefore, the relationship between SCR-AAR and SLA-ELA needs further research on debris-covered glaciers.
- (b)
- Quantifying the impact of the limitations on SCR and SLA should be researched. This article analyzed the total effect of mentioned limitations and factors between the SCR-AAR and SLA-ELA relationship. It is still difficult to quantify how each factor affects the SCR and SLA calculation individually.
- (c)
- Multiple satellite datasets should be incorporated into the algorithm to reduce images’ temporal resolution, leading to the true days of SLA closed to the day of ELA. We are trying to add some Sentinel-2 images in Landsat series images to do further testing.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Joswiak, D. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.; Bierkens, M.F.P.; Lutz, A.F.; Immerzeel, W.W. Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 2017, 549, 257–260. [Google Scholar] [CrossRef] [PubMed]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Cogley, J.G. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Meier, M.F. Proposed definitions for glacier mass budget terms. J. Glaciol. 1962, 4, 252–263. [Google Scholar] [CrossRef] [Green Version]
- Cogley, J.G. Geodetic and direct mass-balance measurements: Comparison and joint analysis. Ann. Glaciol. 2009, 50, 96–100. [Google Scholar] [CrossRef] [Green Version]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Barandun, M.; Huss, M.; Usubaliev, R.; Azisov, E.; Berthier, E.; Kääb, A.; Bolch, T.; Hoelzle, M. Multi-decadal mass balance series of three Kyrgyz glaciers inferred from modelling constrained with repeated snow line observations. Cryosphere 2018, 12, 1899–1919. [Google Scholar] [CrossRef] [Green Version]
- Rabatel, A.; Bermejo, A.; Loarte, E.; Soruco, A.; Gomez, J.; Leonardini, G.; Sicart, J.E. Can the snowline be used as an indicator of the equilibrium line and mass balance for glaciers in the outer tropics? J. Glaciol. 2012, 58, 1027–1036. [Google Scholar] [CrossRef] [Green Version]
- Rabatel, A.; Dedieu, J.P.; Vincent, C. Spatio-temporal changes in glacier-wide mass balance quantified by optical remote sensing on 30 glaciers in the French Alps for the period 1983–2014. J. Glaciol. 2016, 62, 1153–1166. [Google Scholar] [CrossRef] [Green Version]
- Dozier, J. Spectral signature of alpine snow cover from the Landsat Thematic Mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Girona-Mata, M.; Miles, E.S.; Ragettli, S.; Pellicciotti, F. High-resolution snowline delineation from Landsat imagery to infer snow cover controls in a Himalayan catchment. Water Resour. Res. 2019, 55, 6754–6772. [Google Scholar] [CrossRef] [Green Version]
- Verbyla, D.; Hegel, T.; Nolin, A.W.; Van de Kerk, M.; Kurkowski, T.A.; Prugh, L.R. Remote sensing of 2000–2016 alpine spring snowline elevation in dall sheep mountain ranges of Alaska and Western Canada. Remote Sens. 2017, 9, 1157. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Ormsby, J.P.; Bindschadler, R.A.; Siddalingaiah, H. Characterization of snow and ice reflectance zones on glaciers using Landsat Thematic Mapper data. Ann. Glaciol. 1987, 9, 104–108. [Google Scholar] [CrossRef] [Green Version]
- Racoviteanu, A.E.; Rittger, K.; Armstrong, R. An automated approach for estimating snowline altitudes in the Karakoram and eastern Himalaya from remote sensing. Front. Earth Sci. 2019, 7, 220. [Google Scholar] [CrossRef] [Green Version]
- Dumont, M.; Brun, E.; Picard, G.; Michou, M.; Libois, Q.; Petit, J.R.; Josse, B. Contribution of light-absorbing impurities in snow to Greenland’s darkening since 2009. Nat. Geosci. 2014, 7, 509–512. [Google Scholar] [CrossRef]
- Matzl, M.; Schneebeli, M. Measuring specific surface area of snow by near-infrared photography. J. Glaciol. 2006, 52, 558–564. [Google Scholar] [CrossRef] [Green Version]
- Davaze, L.; Rabatel, A.; Dufour, A.; Hugonnet, R.; Arnaud, Y. Region-wide annual glacier surface mass balance for the European Alps from 2000 to 2016. Front. Earth Sci. 2020, 8, 149. [Google Scholar] [CrossRef]
- Hu, Z.; Dietz, A.J.; Kuenzer, C. Deriving regional snow line dynamics during the ablation seasons 1984–2018 in European Mountains. Remote Sens. 2019, 11, 933. [Google Scholar] [CrossRef] [Green Version]
- Davaze, L.; Rabatel, A.; Arnaud, Y.; Sirguey, P.; Six, D.; Letreguilly, A.; Dumont, M. Monitoring glacier albedo as a proxy to derive summer and annual surface mass balances from optical remote-sensing data. Cryosphere 2018, 12, 271–286. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Geng, L.; Shen, B.; Wu, Y.; Chen, A.; Wang, N. Spatiotemporal variability in the glacier snowline altitude across high mountain asia and potential driving factors. Remote Sens. 2021, 13, 425. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, N.; Shen, B.; Gu, Z.; Wu, Y.; Chen, A. Recent Spatiotemporal Trends in Glacier Snowline Altitude at the End of the Melt Season in the Qilian Mountains, China. Remote Sens. 2021, 13, 4935. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, N.; Wu, H.; Wu, Y.; Wu, X.; Li, Q. Variations in firn line altitude and firn zone area on Qiyi Glacier, Qilian Mountains, over the period of 1990 to 2011. Arct. Antarct. Alp. Res. 2015, 47, 293–300. [Google Scholar] [CrossRef] [Green Version]
- Krajčí, P.; Holko, L.; Perdigão, R.A.; Parajka, J. Estimation of regional snowline elevation (RSLE) from MODIS images for seasonally snow covered mountain basins. J. Hydrol. 2014, 519, 1769–1778. [Google Scholar] [CrossRef]
- Mernild, S.H.; Pelto, M.; Malmros, J.K.; Yde, J.C.; Knudsen, N.T.; Hanna, E. Identification of snow ablation rate, ELA, AAR and net mass balance using transient snowline variations on two Arctic glaciers. J. Glaciol. 2013, 59, 649–659. [Google Scholar] [CrossRef] [Green Version]
- Pellitero, R.; Rea, B.R.; Spagnolo, M.; Bakke, J.; Hughes, P.; Ivy-Ochs, S.; Ribolini, A. A GIS tool for automatic calculation of glacier equilibrium-line altitudes. Comput. Geosci. 2015, 82, 55–62. [Google Scholar] [CrossRef]
- Oien, R.P.; Rea, B.R.; Spagnolo, M.; Barr, I.D.; Bingham, R.G. Testing the area–altitude balance ratio (AABR) and accumulation–area ratio (AAR) methods of calculating glacier equilibrium-line altitudes. J. Glaciol. 2022, 68, 357–368. [Google Scholar] [CrossRef]
- Rastner, P.; Prinz, R.; Notarnicola, C.; Nicholson, L.; Sailer, R.; Schwaizer, G.; Paul, F. On the automated mapping of snow cover on glaciers and calculation of snow line altitudes from multi-temporal landsat data. Remote Sens. 2019, 11, 1410. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zhang, R.; Zuo, Z. Impact of Eurasian spring snow decrement on East Asian summer precipitation. J. Clim. 2017, 30, 3421–3437. [Google Scholar] [CrossRef]
- Zhang, Q.; Kang, S. Glacier snowline altitude variations in the Pamirs, Tajikistan, 1998–2013: Insights from remote sensing images. Remote Sens. Lett. 2017, 8, 1220–1229. [Google Scholar] [CrossRef]
- Li, C.; Su, F.; Yang, D.; Tong, K.; Meng, F.; Kan, B. Spatiotemporal variation of snow cover over the Tibetan Plateau based on MODIS snow product, 2001–2014. Int. J. Climatol. 2018, 38, 708–728. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A systematic, regional assessment of high mountain Asia glacier mass balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef] [Green Version]
- Dehecq, A.; Gourmelen, N.; Gardner, A.S.; Brun, F.; Goldberg, D.; Nienow, P.W.; Trouvé, E. Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 2019, 12, 22–27. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef]
- Bettiol, G.M.; Ferreira, M.E.; Motta, L.P.; Cremon, É.H.; Sano, E.E. Conformity of the NASADEM_HGT and ALOS AW3D30 DEM with the Altitude from the Brazilian Geodetic Reference Stations: A Case Study from Brazilian Cerrado. Sensors 2021, 21, 2935. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Helmer, E.H. An automatic method for screening clouds and cloud shadows in optical satellite image time series in cloudy regions. Remote Sens. Environ. 2018, 214, 135–153. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Automated cloud, cloud shadow, and snow detection in multitemporal Landsat data: An algorithm designed specifically for monitoring land cover change. Remote Sens. Environ. 2014, 152, 217–234. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D., Jr.; Beckmann, T.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef] [Green Version]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Van De Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Paul, F.; Barrand, N.E.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Winsvold, S. On the accuracy of glacier outlines derived from remote-sensing data. Ann. Glaciol. 2013, 54, 171–182. [Google Scholar] [CrossRef] [Green Version]
- Herreid, S.; Pellicciotti, F. The state of rock debris covering Earth’s glaciers. Nat. Geosci. 2020, 13, 621–627. [Google Scholar] [CrossRef]
- Holobâcă, I.H.; Tielidze, L.G.; Ivan, K.; Elizbarashvili, M.; Alexe, M.; Germain, D.; Gaprindashvili, G. Multi-sensor remote sensing to map glacier debris cover in the Greater Caucasus, Georgia. J. Glaciol. 2021, 67, 685–696. [Google Scholar] [CrossRef]
- Tielidze, L.G.; Wheate, R.D. The greater caucasus glacier inventory (Russia, Georgia and Azerbaijan). Cryosphere 2018, 12, 81–94. [Google Scholar] [CrossRef] [Green Version]
- Tielidze, L.G.; Nosenko, G.A.; Khromova, T.E.; Paul, F. Strong acceleration of glacier area loss in the Greater Caucasus between 2000 and 2020. Cryosphere 2022, 16, 489–504. [Google Scholar] [CrossRef]











| Name | Central Lon | Central Lat | Region | Area/km2 | Zmin/m a.s.l. | Zmax/m a.s.l. | Aspect/° | Slope/° | Lmax/m | Published Observe Period |
|---|---|---|---|---|---|---|---|---|---|---|
| Helm | 123.00°W | 49.97°N | Western Canada | 0.80 | 1700 | 1900 | 306 | 12.4 | 2143 | 1975–2019 |
| Place | 122.60°W | 50.40°N | Western Canada | 3.98 | 1800 | 2610 | 9 | 11.1 | 3589 | 1965–2019 |
| Peyto | 116.53°W | 51.67°N | Western Canada | 11.40 | 2100 | 2640 | 29 | 12.7 | 5387 | 1966–2019 |
| Silvretta | 10.08°E | 46.85°N | Alps | 2.70 | 2470 | 3070 | 292 | 12.9 | 3151 | 1919–2020 |
| Gries | 8.34°E | 46.44°N | Alps | 4.40 | 2430 | 3010 | 41 | 11.8 | 5652 | 1961–2020 |
| Careser | 10.70°E | 46.45°N | Alps | 1.90 | 2880 | 3278 | 176 | 10.6 | 2305 | 1967–2020 |
| Djankuat | 42.77°E | 43.20°N | Caucasus | 2.69 | 2700 | 3750 | 322 | 21.9 | 3043 | 1968–2009 |
| Abramov | 71.56°E | 39.61°N | HMA | 24 | 3650 | 5000 | 10 | 27.0 | 8572 | 2010–2019 |
| VNF * | 10.82°E | 46.88°N | Alps | 8.80 | 2770 | 3630 | 165 | 14.7 | 3087 | 1965–2019 |
| KWF * | 10.79°E | 46.84°N | Alps | 3.90 | 2700 | 3500 | 123 | 11.6 | 4202 | 1953–2020 |
| HEF * | 10.77°E | 46.80°N | Alps | 7.80 | 2507 | 3739 | 71 | 16.2 | 7178 | 1953–2020 |
| Tsentralniy | 77.08°E | 43.05°N | HMA | 2.30 | 3478 | 4219 | 359 | 19.1 | 3131 | 1958–2019 |
| Urumqi No.1 | 86.82°E | 43.08°N | HMA | 1.65 | 3743 | 4484 | 33 | 20.6 | 1946 | 1959–2020 |
| Qiyi | 97.76°E | 39.24°N | HMA | 2.76 | 4304 | 5159 | 2 | 19.2 | 3007 | 1958–2016 |
| Glacier Name | Selected Images | Glacier Name | Selected Images | Glacier Name | Selected Images |
|---|---|---|---|---|---|
| Helm | 273 | Careser | 110 | Hintereisferner | 213 |
| Place | 231 | Djankuat | 241 | Tsentralniy | 97 |
| Peyto | 197 | Abramov | 252 | Urumqi No.1 | 116 |
| Silvretta | 331 | Vernagtferner | 136 | Qiyi | 125 |
| Gries | 213 | Kesselwandferner | 149 | Total | 2684 |
| Dataset | Temporal Extent | Spatial Extent | Pixel Size | Horizontal Accuracy | Vertical Accuracy |
|---|---|---|---|---|---|
| NASADEM | 2000-02-11 to 2000-02-21 | 60°N to 56°S, 180°W to 180°E | 30 m | 20 m | 16 m |
| Landsat-5 | Landsat-7 | Landsat-8 | Image Collection |
|---|---|---|---|
| B1 | B1 | B2 | Blue |
| B2 | B2 | B3 | Green |
| B3 | B3 | B4 | Red |
| B4 | B4 | B5 | Nir |
| B5 | B5 | B6 | Swir1 |
| B7 | B8 | B7 | Swir2 |
| QA_PIXEL | QA_PIXEL | QA_PIXEL | QA |
| Glacier Name | Very Good Fit | Good Fit | Fit | Unfit | Glacier Name | Very Good Fit | Good Fit | Fit | Unfit |
|---|---|---|---|---|---|---|---|---|---|
| Helm | 5 | 7 | 12 | 6 | Abramov | 4 | 2 | 2 | 0 |
| Place | 5 | 3 | 7 | 8 | VNF * | 4 | 6 | 9 | 3 |
| Peyto | 4 | 3 | 8 | 10 | KWF * | 8 | 5 | 10 | 4 |
| Silvretta | 5 | 8 | 11 | 8 | HEF * | 7 | 5 | 6 | 8 |
| Gries | 4 | 9 | 6 | 12 | Djankuat | 6 | 3 | 7 | 3 |
| Careser | 4 | 2 | 3 | 16 | Qiyi | 7 | 5 | 5 | 9 |
| Tsentralniy | 1 | 5 | 6 | 4 | Urumqi No.1 | 8 | 5 | 4 | 8 |
| Glacier Name | Average ELA-SLA Deviation (1985–1999)/m | Average ELA-SLA Deviation (2000–2020)/m | Glacier Name | Average ELA-SLA Deviation (1985–1999)/m | Average ELA-SLA Deviation (2000–2020)/m |
|---|---|---|---|---|---|
| Helm | 59.07 | 44.50 | VNF * | 55.89 | 35.16 |
| Place | 53.09 | 36.14 | KWF * | 64.15 | 18.43 |
| Peyto | 125.69 | 110.42 | HEF * | −8.58 | 11.50 |
| Silvretta | 17.17 | −15.40 | Tsentralniy | 37.00 | 21.06 |
| Gries | 61.53 | 67.41 | Urumqi No.1 | 59.60 | 39.25 |
| Djankuat | 48.46 | 58.33 | Qiyi | 29.10 | 75.56 |
| Abramov | NA | 13.50 | Total Average | 50.18 | 39.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, N.; Wu, Y. Automated Glacier Snow Line Altitude Calculation Method Using Landsat Series Images in the Google Earth Engine Platform. Remote Sens. 2022, 14, 2377. https://doi.org/10.3390/rs14102377
Li X, Wang N, Wu Y. Automated Glacier Snow Line Altitude Calculation Method Using Landsat Series Images in the Google Earth Engine Platform. Remote Sensing. 2022; 14(10):2377. https://doi.org/10.3390/rs14102377
Chicago/Turabian StyleLi, Xiang, Ninglian Wang, and Yuwei Wu. 2022. "Automated Glacier Snow Line Altitude Calculation Method Using Landsat Series Images in the Google Earth Engine Platform" Remote Sensing 14, no. 10: 2377. https://doi.org/10.3390/rs14102377
APA StyleLi, X., Wang, N., & Wu, Y. (2022). Automated Glacier Snow Line Altitude Calculation Method Using Landsat Series Images in the Google Earth Engine Platform. Remote Sensing, 14(10), 2377. https://doi.org/10.3390/rs14102377