Backtracking Reconstruction Network for Three-Dimensional Compressed Hyperspectral Imaging
Abstract
:1. Introduction
2. CATF Spectral Imager
3. Methodology
3.1. Design Inspiration and Representation
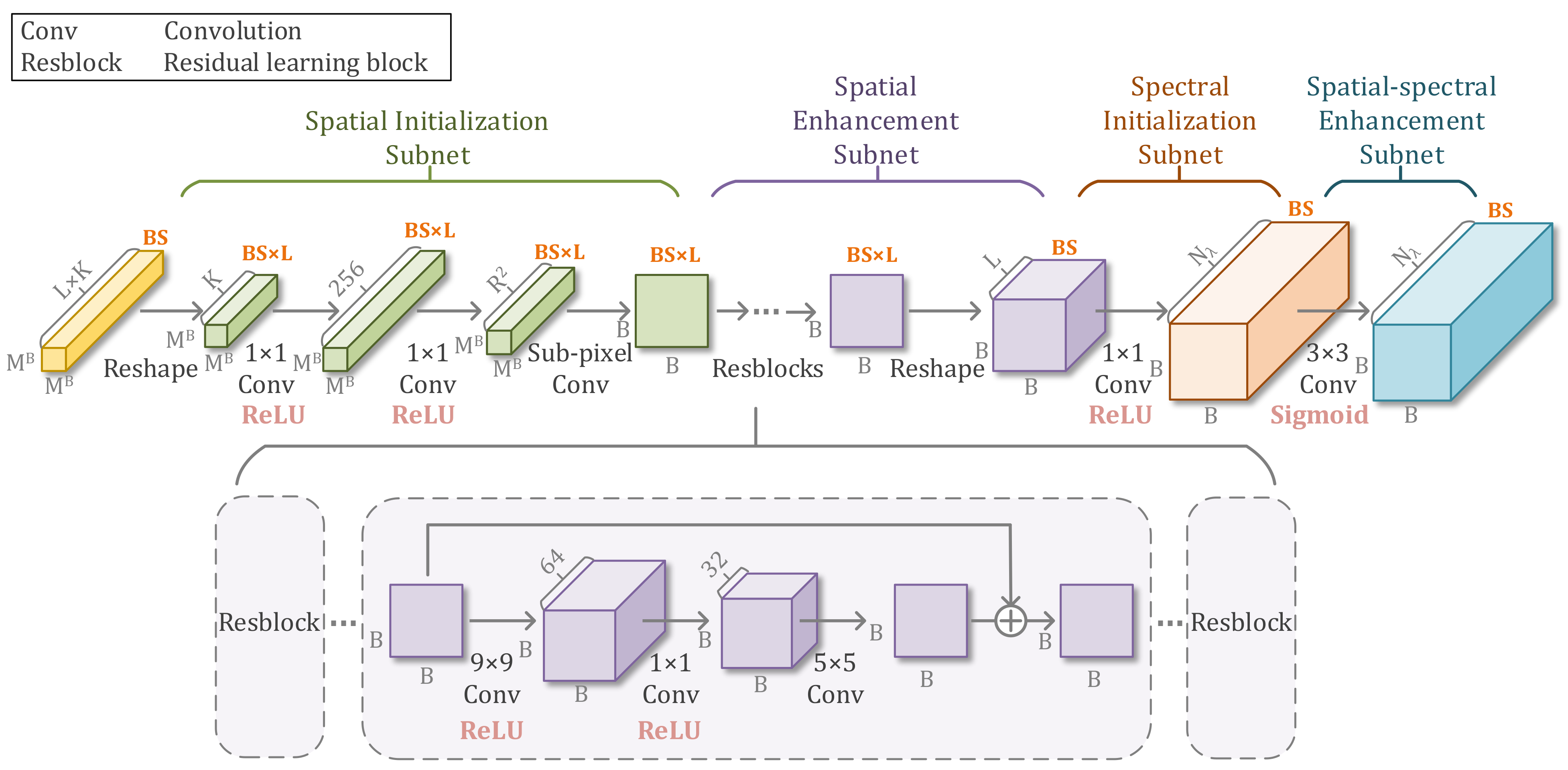
3.2. BTR-Net Architecture
3.3. Loss Function
4. Results
4.1. Dataset and Evaluation Metrics
4.2. Comparison with Iterative Algorithms
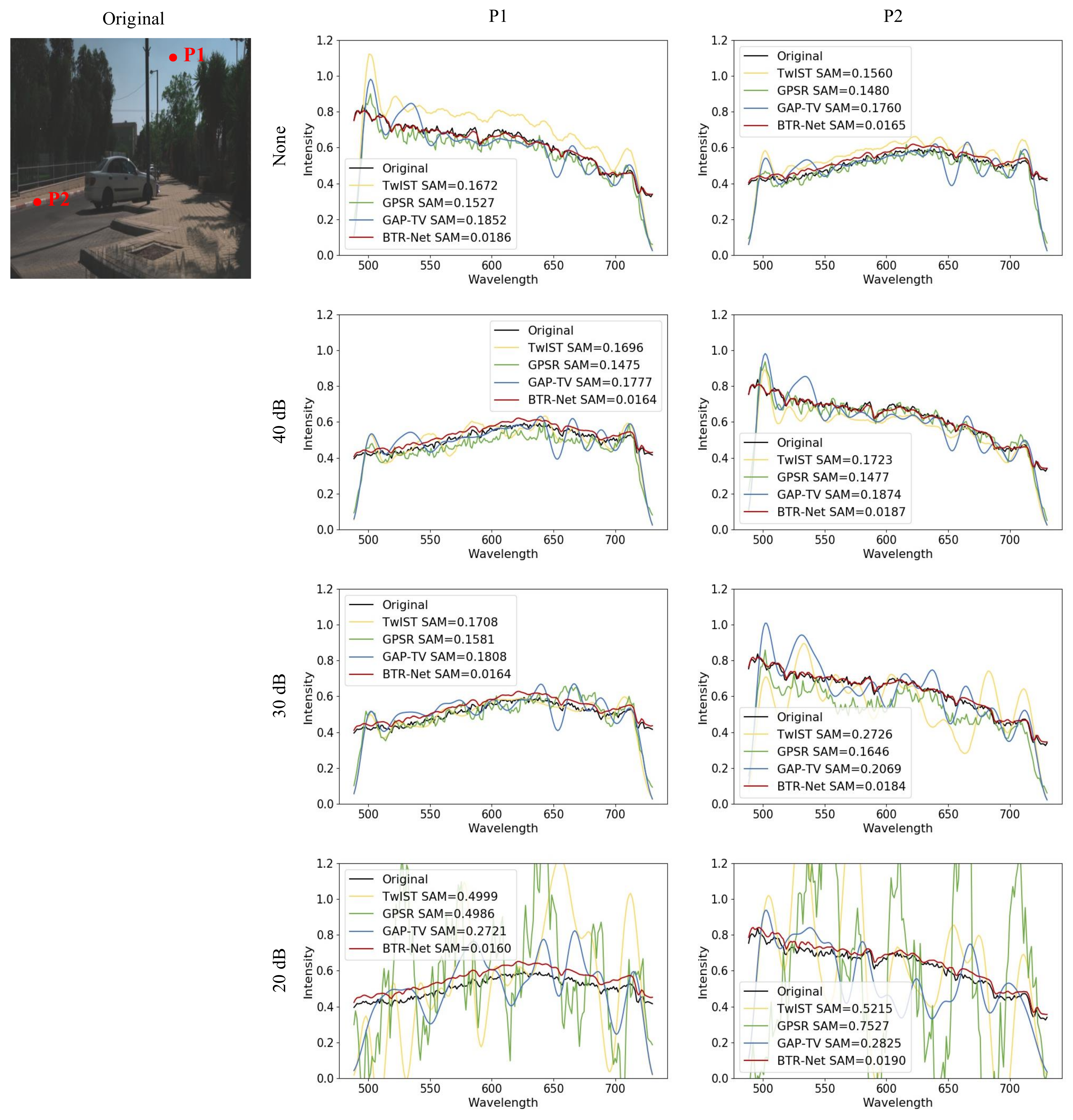
4.3. Real Experiments
5. Discussion
5.1. Effect of Up-Sampling Methods
5.2. Effect of Resblock Number
5.3. Effect of Kernel Size in Resblock
5.4. Cross-Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HS | hyperspectral |
| CS | compressed sensing |
| BTR-Net | backtracking reconstruction network |
| CATF | coded aperture tunable filter |
| LCTF | liquid crystal tunable filter |
| DMD | digital micromirror device |
| CNN | convolution neural network |
| CASSI | coded aperture snapshot spectral imaging |
| BCS | block compressed sensing |
| TV | total variation |
| MS | multispectral |
| Resblock | residual learning block |
| MPSNR | mean peak signal to noise ratio |
| MSSIM | mean structural similarity index measure |
| MRAE | mean relative absolute error |
| MSAM | mean spectral angle mapper |
References
- Zhang, B.; Wu, D.; Zhang, L.; Jiao, Q.; Li, Q. Application of hyperspectral remote sensing for environment monitoring in mining areas. Environ. Earth Sci. 2012, 65, 649–658. [Google Scholar] [CrossRef]
- Roberts, D.A.; Quattrochi, D.A.; Hulley, G.C.; Hook, S.J.; Green, R.O. Synergies between VSWIR and TIR data for the urban environment: An evaluation of the potential for the Hyperspectral Infrared Imager (HyspIRI) Decadal Survey mission. Remote Sens. Environ. 2012, 117, 83–101. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. A survey on representation-based classification and detection in hyperspectral remote sensing imagery. Pattern Recognit. Lett. 2016, 83, 115–123. [Google Scholar] [CrossRef]
- Jay, S.; Guillaume, M.; Minghelli, A.; Deville, Y.; Chami, M.; Lafrance, B.; Serfaty, V. Hyperspectral remote sensing of shallow waters: Considering environmental noise and bottom intra-class variability for modeling and inversion of water reflectance. Remote Sens. Environ. 2017, 200, 352–367. [Google Scholar] [CrossRef]
- Yu, C.; Yang, J.; Song, N.; Sun, C.; Wang, M.; Feng, S. Microlens array snapshot hyperspectral microscopy system for the biomedical domain. Appl. Opt. 2021, 60, 1896–1902. [Google Scholar] [CrossRef]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Neifeld, M.A.; Ke, J. Optical architectures for compressive imaging. Appl. Opt. 2007, 46, 5293–5303. [Google Scholar] [CrossRef] [PubMed]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Liu, Y.; Wu, J.; Dai, Q. Spatial-spectral encoded compressive hyperspectral imaging. ACM Trans. Graph. 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Z.; Shi, G.; Wu, F.; Zeng, W. Adaptive Nonlocal Sparse Representation for Dual-Camera Compressive Hyperspectral Imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2104–2111. [Google Scholar] [CrossRef]
- Ren, W.; Fu, C.; Wu, D.; Xie, Y.; Arce, G.R. Channeled compressive imaging spectropolarimeter. Opt. Express 2019, 27, 2197–2211. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Ma, X.; Xu, T.; Arce, G.R. Compressive spectral imaging system based on liquid crystal tunable filter. Opt. Express 2018, 26, 25226–25243. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, T.; Wang, X.; Pan, C.; Hao, J.; Huang, C. Real-time adaptive coded aperture: Application to the compressive spectral imaging system. In Proceedings of the Optics, Photonics and Digital Technologies for Imaging Applications VI, Online, 6–10 April 2020; Schelkens, P., Kozacki, T., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11353, pp. 280–289. [Google Scholar]
- Xu, C.; Xu, T.; Yan, G.; Ma, X.; Zhang, Y.; Wang, X.; Zhao, F.; Arce, G.R. Super-resolution compressive spectral imaging via two-tone adaptive coding. Photon. Res. 2020, 8, 395–411. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for Image Restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [Green Version]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2539–2543. [Google Scholar]
- Wagadarikar, A.A.; Pitsianis, N.P.; Sun, X.; Brady, D.J. Spectral image estimation for coded aperture snapshot spectral imagers. In Proceedings of the Image Reconstruction from Incomplete Data V, San Francisco, CA, USA, 28 August 2008; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2008; Volume 7076, pp. 9–23. [Google Scholar]
- Mousavi, A.; Baraniuk, R.G. Learning to invert: Signal recovery via Deep Convolutional Networks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2272–2276. [Google Scholar]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. From Denoising to Compressed Sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Wang, L.; Feng, Y.; Gao, Y.; Wang, Z.; He, M. Compressed Sensing Reconstruction of Hyperspectral Images Based on Spectral Unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1266–1284. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction. Remote Sens. 2019, 11, 193. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Huang, T.; He, W.; Yokoya, N.; Zhao, X. Hyperspectral Image Compressive Sensing Reconstruction Using Subspace-Based Nonlocal Tensor Ring Decomposition. IEEE Trans. Image Process. 2020, 29, 6813–6828. [Google Scholar] [CrossRef]
- Takeyama, S.; Ono, S.; Kumazawa, I. A Constrained Convex Optimization Approach to Hyperspectral Image Restoration with Hybrid Spatio-Spectral Regularization. Remote Sens. 2020, 12, 3541. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In Proceedings of the Computer Vision—ECCV 201, 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 525–542. [Google Scholar]
- Moeskops, P.; Viergever, M.A.; Mendrik, A.M.; de Vries, L.S.; Benders, M.J.N.L.; Išgum, I. Automatic Segmentation of MR Brain Images With a Convolutional Neural Network. IEEE Trans. Med. Imaging 2016, 35, 1252–1261. [Google Scholar] [CrossRef] [Green Version]
- Liskowski, P.; Krawiec, K. Segmenting Retinal Blood Vessels With Deep Neural Networks. IEEE Trans. Med. Imaging 2016, 35, 2369–2380. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhang, G.; Qiao, H.; Bao, F.; Deng, Y.; Wu, J.; He, Y.; Yun, J.; Lin, X.; Xie, H.; et al. Unsupervised content-preserving transformation for optical microscopy. Light. Sci. Appl. 2021, 10, 44. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Song, H.; He, X.; Huang, L.; Zhang, X.; Zheng, J.; Shen, W.; Hao, X.; Liu, X. Deeply learned broadband encoding stochastic hyperspectral imaging. Light. Sci. Appl. 2021, 10, 108. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, T.; Fu, Y.; Huang, H. HyperReconNet: Joint Coded Aperture Optimization and Image Reconstruction for Compressive Hyperspectral Imaging. IEEE Trans. Image Process. 2019, 28, 2257–2270. [Google Scholar] [CrossRef] [PubMed]
- Miao, X.; Yuan, X.; Pu, Y.; Athitsos, V. lambda-Net: Reconstruct Hyperspectral Images From a Snapshot Measurement. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 4058–4068. [Google Scholar]
- Wang, L.; Sun, C.; Fu, Y.; Kim, M.H.; Huang, H. Hyperspectral Image Reconstruction Using a Deep Spatial-Spectral Prior. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8024–8033. [Google Scholar]
- Wang, L.; Sun, C.; Zhang, M.; Fu, Y.; Huang, H. DNU: Deep Non-Local Unrolling for Computational Spectral Imaging. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1658–1668. [Google Scholar]
- Yang, Y.; Xie, Y.; Chen, X.; Sun, Y. Hyperspectral Snapshot Compressive Imaging with Non-Local Spatial-Spectral Residual Network. Remote Sens. 2021, 13, 1812. [Google Scholar] [CrossRef]
- Gedalin, D.; Oiknine, Y.; Stern, A. DeepCubeNet: Reconstruction of spectrally compressive sensed hyperspectral images with deep neural networks. Opt. Express 2019, 27, 35811–35822. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Gan, L. Block Compressed Sensing of Natural Images. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, Wales, UK, 1–4 July 2007; pp. 403–406. [Google Scholar]
- Yao, H.; Dai, F.; Zhang, S.; Zhang, Y.; Tian, Q.; Xu, C. DR2-Net: Deep Residual Reconstruction Network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef] [Green Version]
- Alsallakh, B.; Kokhlikyan, N.; Miglani, V.; Yuan, J.; Reblitz-Richardson, O. Mind the Pad–CNNs can Develop Blind Spots. arXiv 2020, arXiv:2010.02178. [Google Scholar]
- Arad, B.; Ben-Shahar, O. Sparse Recovery of Hyperspectral Signal from Natural RGB Images. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 19–34. [Google Scholar]











| Methods | Metrics | Scene 1 | Scene 2 | Scene 3 | Scene 4 | Scene 5 | Scene 6 | Scene 7 | Scene 8 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| TwIST | MPSNR | 25.9461 | 25.3603 | 29.0709 | 26.4064 | 25.9091 | 23.3570 | 25.3866 | 25.7167 | 25.8941 |
| MSSIM | 0.7651 | 0.7555 | 0.8446 | 0.7913 | 0.7389 | 0.5745 | 0.7795 | 0.7741 | 0.7529 | |
| MRAE | 0.1440 | 0.1618 | 0.1548 | 0.1531 | 0.1400 | 0.1304 | 0.1730 | 0.1696 | 0.1533 | |
| MSAM | 0.1925 | 0.1779 | 0.3029 | 0.1903 | 0.1701 | 0.1683 | 0.2730 | 0.3021 | 0.2221 | |
| GPSR | MPSNR | 27.7491 | 26.6125 | 30.9366 | 28.0081 | 28.1142 | 25.4694 | 26.6935 | 27.0328 | 27.5770 |
| MSSIM | 0.8587 | 0.8359 | 0.9056 | 0.8754 | 0.8525 | 0.7100 | 0.8544 | 0.8451 | 0.8422 | |
| MRAE | 0.1012 | 0.1294 | 0.1106 | 0.1130 | 0.1018 | 0.1053 | 0.1312 | 0.1358 | 0.1160 | |
| MSAM | 0.1473 | 0.1422 | 0.2434 | 0.1415 | 0.1341 | 0.1469 | 0.2113 | 0.2525 | 0.1774 | |
| GAP-TV | MPSNR | 27.0290 | 26.0617 | 29.6778 | 27.3291 | 27.1311 | 26.1558 | 25.3088 | 25.8458 | 26.8174 |
| MSSIM | 0.8977 | 0.8728 | 0.9032 | 0.8977 | 0.8959 | 0.9187 | 0.8442 | 0.8459 | 0.8845 | |
| MRAE | 0.1445 | 0.1582 | 0.1781 | 0.1526 | 0.1368 | 0.1230 | 0.1959 | 0.1920 | 0.1601 | |
| MSAM | 0.2090 | 0.1938 | 0.3237 | 0.2079 | 0.1861 | 0.1830 | 0.2947 | 0.3230 | 0.2402 | |
| BTR-Net | MPSNR | 31.4361 | 29.2063 | 35.0696 | 30.2514 | 32.4901 | 33.7753 | 30.2386 | 29.9614 | 31.5536 |
| MSSIM | 0.9354 | 0.9065 | 0.9682 | 0.9242 | 0.9356 | 0.9485 | 0.9160 | 0.9009 | 0.9294 | |
| MRAE | 0.0473 | 0.0786 | 0.0544 | 0.0679 | 0.0454 | 0.0254 | 0.0724 | 0.0780 | 0.0587 | |
| MSAM | 0.0257 | 0.0337 | 0.0458 | 0.0316 | 0.0225 | 0.0199 | 0.0371 | 0.0491 | 0.0332 |
| Methods | TwIST | GPSR | GAP-TV | BTR-Net |
|---|---|---|---|---|
| Running time(s) CPU/GPU | – | – | – |
| Methods | Metrics | None | 40 dB | 30 dB | 20 dB |
|---|---|---|---|---|---|
| TwIST | MPSNR | 25.8941 | 25.2734 | 22.7043 | 15.9897 |
| MSSIM | 0.7529 | 0.7225 | 0.5942 | 0.2820 | |
| MRAE | 0.1533 | 0.1625 | 0.2048 | 0.4066 | |
| MSAM | 0.2221 | 0.2277 | 0.2617 | 0.4585 | |
| GPSR | MPSNR | 27.5770 | 27.4652 | 25.8821 | 12.0305 |
| MSSIM | 0.8422 | 0.8385 | 0.7816 | 0.1633 | |
| MRAE | 0.1160 | 0.1175 | 0.1245 | 0.5493 | |
| MSAM | 0.1774 | 0.1779 | 0.1893 | 0.6204 | |
| GAP-TV | MPSNR | 26.8174 | 26.6058 | 25.3251 | 20.5241 |
| MSSIM | 0.8845 | 0.8736 | 0.8011 | 0.5357 | |
| MRAE | 0.1601 | 0.1755 | 0.1889 | 0.2654 | |
| MSAM | 0.2402 | 0.2418 | 0.2512 | 0.3299 | |
| BTR-Net | MPSNR | 31.5536 | 31.5209 | 31.3158 | 29.9170 |
| MSSIM | 0.9294 | 0.9294 | 0.9292 | 0.9278 | |
| MRAE | 0.0587 | 0.0594 | 0.0625 | 0.0820 | |
| MSAM | 0.0332 | 0.0332 | 0.0332 | 0.0334 |
| Methods | MPSNR(dB) | MSSIM | MRAE | MSAM |
|---|---|---|---|---|
| Sub-pixel Convolution | 31.5536 | 0.9294 | 0.0586 | 0.0332 |
| Bilinear Interpolation | 30.6836 | 0.9226 | 0.0706 | 0.0362 |
| Kernel Size | MPSNR(dB) | MSSIM | MRAE | MSAM | Time Complexity |
|---|---|---|---|---|---|
| 11-1-7 | 31.6100 | 0.9302 | 0.0585 | 0.0333 | |
| 9-1-5 | 31.5536 | 0.9294 | 0.0586 | 0.0332 | |
| 7-1-3 | 31.3566 | 0.9269 | 0.0605 | 0.0332 |
| Testing Set | MPSNR | MSSIM | MRAE | MSAM |
|---|---|---|---|---|
| 1 | 30.9160 | 0.9173 | 0.0563 | 0.0316 |
| 2 | 30.8934 | 0.9116 | 0.0589 | 0.0315 |
| 3 | 30.9825 | 0.9136 | 0.0568 | 0.0327 |
| 4 | 31.6278 | 0.9209 | 0.0518 | 0.0289 |
| 5 | 31.5536 | 0.9294 | 0.0587 | 0.0332 |
| Average | 31.1947 | 0.9186 | 0.0565 | 0.0316 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xu, T.; Zhang, Y.; Fan, A.; Xu, C.; Li, J. Backtracking Reconstruction Network for Three-Dimensional Compressed Hyperspectral Imaging. Remote Sens. 2022, 14, 2406. https://doi.org/10.3390/rs14102406
Wang X, Xu T, Zhang Y, Fan A, Xu C, Li J. Backtracking Reconstruction Network for Three-Dimensional Compressed Hyperspectral Imaging. Remote Sensing. 2022; 14(10):2406. https://doi.org/10.3390/rs14102406
Chicago/Turabian StyleWang, Xi, Tingfa Xu, Yuhan Zhang, Axin Fan, Chang Xu, and Jianan Li. 2022. "Backtracking Reconstruction Network for Three-Dimensional Compressed Hyperspectral Imaging" Remote Sensing 14, no. 10: 2406. https://doi.org/10.3390/rs14102406
APA StyleWang, X., Xu, T., Zhang, Y., Fan, A., Xu, C., & Li, J. (2022). Backtracking Reconstruction Network for Three-Dimensional Compressed Hyperspectral Imaging. Remote Sensing, 14(10), 2406. https://doi.org/10.3390/rs14102406







