Next Article in Journal
Remote Sensing of Surface Water Dynamics in the Context of Global Change—A Review
Next Article in Special Issue
Spatiotemporal Dynamics of Terrestrial Vegetation and Its Driver Analysis over Southwest China from 1982 to 2015
Previous Article in Journal
An Extended Watershed-Based AHP Model for Flood Hazard Estimation: Constraining Runoff Converging Indicators via MFD-Derived Sub-Watershed by Maximum Zonal Statistical Method
Previous Article in Special Issue
Analysis of Water Yield Changes from 1981 to 2018 Using an Improved Mann-Kendall Test
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 10
10.3390/rs14102474
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dynamics of the Evaporation of Intercepted Precipitation during the Last Two Decades over China

by
Lingyun Yan
1,2,†,
Jilong Chen
1,†,
Lei He
3,
Yongyue Ji
1,2,
Qingqing Tang
1,2,
Yuanchao Fan
4 and
Daming Tan
5,*
1
Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing 401122, China
2
University of Chinese Academy of Sciences, Beijing 100049, China
3
School of Tourism and Urban Management, Jiangxi University of Finance and Economics, Nanchang 330013, China
4
Department of Earth and Planetary Sciences, Harvard University, Cambridge, MA 02138, USA
5
Institute of Agricultural Resources and Environment, Tibet Academy of Agricultural and Animal Husbandry Science, Lhasa 850000, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Remote Sens. 2022, 14(10), 2474; https://doi.org/10.3390/rs14102474
Submission received: 20 April 2022 / Revised: 16 May 2022 / Accepted: 19 May 2022 / Published: 21 May 2022
(This article belongs to the Special Issue Remotely Monitoring Terrestrial Carbon, Water and Energy Fluxes in Ecologically Sensitive Areas)
Browse Figures
Versions Notes

Abstract

:
The evaporation of intercepted precipitation (Ei) is an important component of evapotranspiration. Investigating the spatial and temporal variations of Ei and its driving factors can improve our understanding of water and energy balance in the context of China’s greening. This study investigated the spatial and temporal variation of Ei across China during 2001−2020 using PML ET product with a temporal resolution of 8 days and a spatial resolution of 500 m. The results showed that Ei generally decreased from southeast to northwest, which was contributed by the coupled effect of precipitation and vegetation coverage variation across China. Generally, Ei showed an increasing trend over the last two decades with an average changing rate of 0.45 mm/year. The changing rate varied greatly among different regions, with the most obvious change occurring in tropical and humid regions. Precipitation was the most important climatic factor driving the interannual change of Ei over the past two decades, with an average contribution rate of 30.18~37.59%. Relative humidity was the second most important climatic factor following precipitation. Temperature showed contracting contribution in different thermal regions. The contribution rates of NDVI and LAI followed a similar spatial pattern. Both the contribution rates of NDVI and LAI generally increased along the moisture gradient from east to west and generally increased from south to north.

1. Introduction

As an indicator to quantify the coupling between the water and energy balance, as well as an important component of evapotranspiration (ET), the evaporation of the intercepted precipitation (Ei) of the ecosystem is typically referred to as the precipitation that was intercepted by branches, leaves and stalks of vegetation and returned to the atmosphere in the form of evaporation [1]. Therefore, that part of precipitation does not undergo surface and underground water cycling. Ei is the initial process of redistributing the precipitation, which affects the spatial and temporal distribution of regional and even global precipitation, as well as the changes in sensible heat flux and latent heat flux [2]. Investigating the spatial and temporal variation of Ei and its driving factors is essential to understanding the interaction between vegetation dynamics and water and energy exchange in future climate change [3].
Two methods were generally employed to measure Ei at the field scale, one is the classic water wiping method [4], and the other is the water balance method [5], where precipitation, throughfall, and stemflow were measured with rain gauges and collectors, and Ei was calculated by subtracting throughfall and stemflow from the precipitation. While Ei was usually obtained with a modeling approach at a regional scale [6], these models can be classified into the empirical model, semi-empirical model, and theoretical model. Empirical models are widely studied due to their simplicity yet reasonable accuracy; however, they are site-dependent and cannot be applied to other places [7]. Semi-empirical models were developed by adding the principle of interception to empirical models, such as the Gash model [8] and the Rutter model [9]. Since canopy coverage, leaf area index, canopy closure, and other indexes can be obtained and parameterized with remote sensing technology, semi-empirical models are widely used to investigate the dynamic of Ei at a regional scale [10]. The theoretical model can simulate the physical process of the Ei [11]; however, it is not only complex but also data-intensive, such as the detailed information on vegetation canopy, which limits the applications of the theoretical model [12].
Remote sensing can provide information on land surface and vegetation at multiple spatial and temporal scales. Coupled with the Ei simulation models, particularly the semi-empirical models, it provides an approach to investigating the spatial-temporal variation of Ei at a regional scale [11]. Zhang et al. [13] investigated the changing trend of Ei throughout the world using the Penman–Monteith–Leuning (PML) model and MODIS data during 2003–2017 and found that vegetation change resulted in an average increase of Ei by 0.8 ± 3.9 mm/year. Shen et al. [14] used the Shuttleworth–Wallace (SW) model to estimate ET components and found that Ei accounted for about 10% of ET. Song et al. [15] estimated the maximum Ei of conservation forest in Danjiangkou Reservoir blocking river basin in China based on the canopy interception model and Landsat ETM + Remote Sensing fusion data. The results showed that the spatial variation of maximum Ei had a strong relationship with vegetation cover. Duan et al. [16] added the canopy interception model to the PML model to simulate the ET at Wangdu station in China. The results showed that Ei accounted for 3.14% and 4.37% of the ET and precipitation, respectively.
Many previous observations and studies showed that Ei was greatly affected by vegetation canopy status and precipitation [7,13,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. The status of the vegetation canopy can affect the amount and characteristics of precipitation undertaken by leaves. Ei is closely related to vegetation coverage (Fcov) and leaf area index (LAI) [18,19]. Zhang et al. [13] studied global land underlying conditions from 2003 to 2017 and found that shrub degradation and ice melting were the main reasons for the significant decline of Ei and vegetation transpiration. In addition, in the latitude zones of 70°N~80°N and 20°S~30°S, vegetation change led vegetation transpiration and Ei to increase by about 10~15%, respectively. Vegetation greening led to a significant increase of Ei in northern America, Europe, eastern China, southern Africa, and northeastern Australia, where LAI significantly increased. Similar results were also observed in Moso Bamboo, where Ei increased with the increase of LAI mainly due to the reduction of rain penetration contributed by the increase of LAI [20]. Deng et al. [21] used the coupled model ssib4t/triffid to analyze the variation of ET components in two tributaries in the Yangtze River Basin. The results showed a positive correlation between Fcov and Ei. Fan et al. [22] reported similar results for grassland in the Hulun Lake Basin in China.
Precipitation is considered the most important factor influencing Ei [7,23]. Asdak et al. [24] estimated the Ei of tropical rain forests in India. The result indicated that the Ei of tropical rain forests accounted for an average of 8.5% of rainfall, which was lower than 11~35% for the tropical areas of China [25]. Ei could account for more than 80% of precipitation when the precipitation amount and precipitation intensity were low [5]. Previous observations and analysis showed that Ei was positively correlated with precipitation intensity and precipitation duration [26,27,28], while Ei was negatively correlated with the frequency of rainstorms with large seasonal variations [29]. Ei increased with the increase of precipitation intensity and reached a saturation state [30], and an exponential relationship between Ei and precipitation intensity was observed for two desert shrubs [29]. Yang [31] found that the canopy interception capacity and interception rate varied among different grassland communities under the same precipitation intensity.
Except for the vegetation canopy and precipitation, Ei was regulated not only by the feature of vegetation, other climatological variables, and environmental conditions but also by the interactions among these factors [32,33]. The features of vegetation included vegetation type, plant age, and vegetation thinning density [26,34,35]. Ufoegbune et al. [36] found that the Ei of pine and cypress plants was generally higher than that of broad-leaved plants, which was mainly due to the different leaf shapes of different vegetation. Based on the long-term observations and studies, Pypker et al. [37] reported that the Ei of young trees differed greatly from that of the older trees, mainly due to the change of canopy structure with the increase of tree age. Yu et al. [38] studied the Ei of alpine meadows and found that the interception capacity of meadows varied with the change of meadow density, and the Ei of the slightly degraded, moderately degraded, and significantly degraded alpine meadows was 0.612 mm, 0.289 mm, and 0.217 mm, respectively. Other climatological variables included air temperature, sunshine duration, relative humidity, and wind speed [39,40]. Many studies reported that Ei was negatively correlated with humidity and temperature, while it did not show an obvious relationship with wind speed, evaporation rate, solar radiation, and other meteorological factors [19,23,41].
Fleischbein et al. [42] found that the dominant driving factors were different and depended on the scale of the study. Meteorological factors such as precipitation characteristics, wind speed, and evaporation played a leading role on a large scale. At the same time, the characteristics of the vegetation community were the leading factors on a small scale. Song et al. [15] analyzed the sensitivity of Ei to climatic factors and detected the essential roles of temperature and precipitation affecting the variation of Ei for the Loess Plateau in China.
More and more studies and remote sensing observations showed a widespread increase in LAI across China (greening), which is mainly due to the global warming, ecological projects, and land use and management policies since the 1980s [43]. LAI was an important indicator quantifying the status of the vegetation canopy; the vegetation greening reflected the change of vegetation canopy structure [44], which will affect the spatially and temporal variation of Ei. However, it was still not clear how the Ei changed spatially and temporally under the influence of China’s greening and climate change.
Therefore, this study was carried out to fill the lack of knowledge. The main objectives of this study were to (1) characterize the spatial distribution of Ei across China; (2) investigate the temporal variation of Ei from 2001 to 2020; and (3) quantify the contribution of climate change and vegetation dynamics to the temporal changes of Ei. The work can help us to understand the effect of China’s greening and climate change on water and energy exchange.

2. Materials and Methods

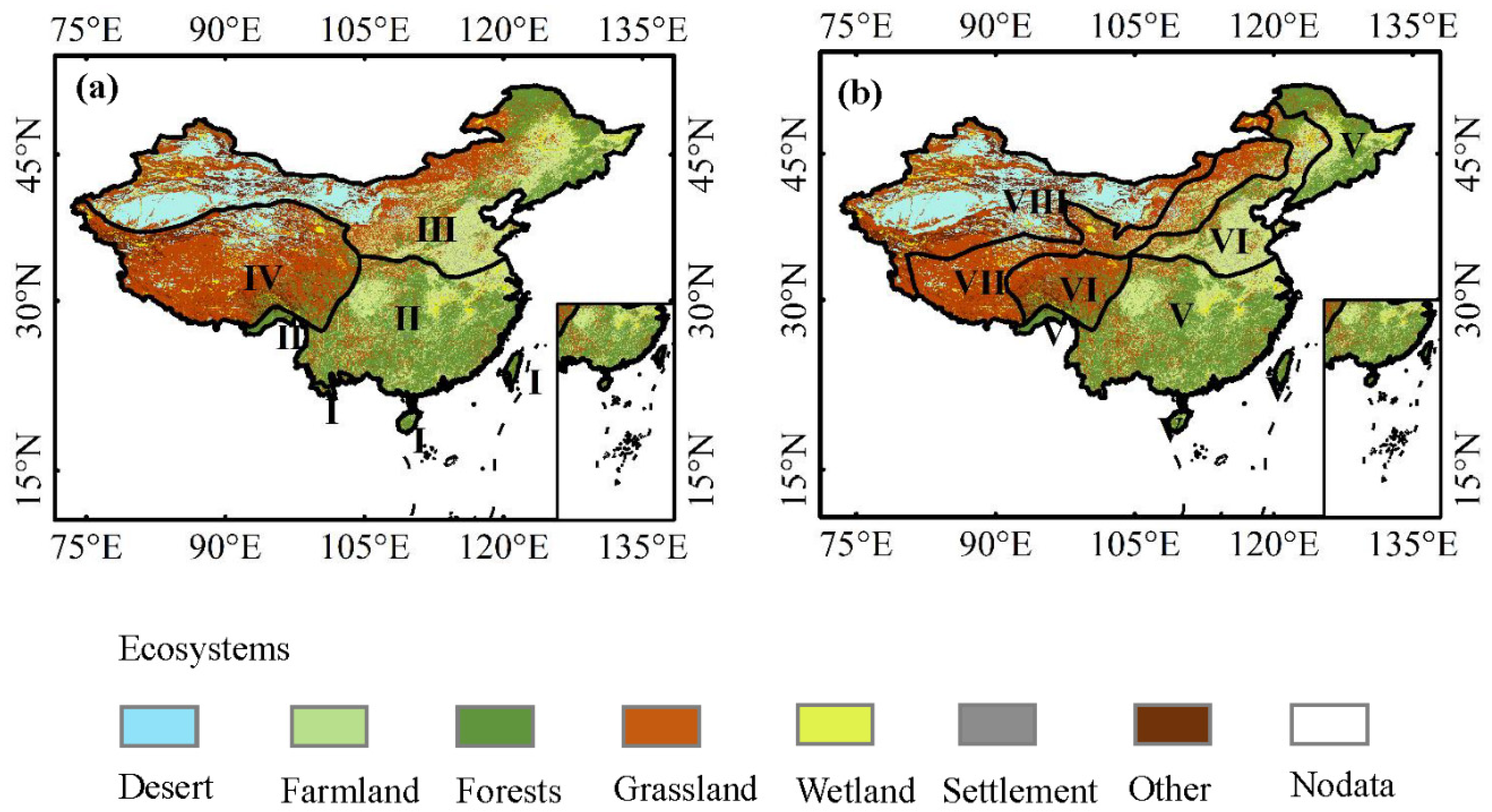
2.1. Data Collection

The subdatasets of Ei from the PML ET datasets were used to investigate the spatial and temporal variation of Ei across China in the current study. The PML model was presented by Leuning et al. [45,46] and Zhang et al. [47] based on the Penman–Monteith (PM) model. This model was later modified by Gan et al. [2] and Zhang et al. [48] by introducing a canopy conductance model. The PML model can simulate Ei, vegetation transpiration, and soil evaporation simultaneously. Combined with MODIS product data, including LAI, NDVI, land use, reflectance, emissivity, and GLDAS meteorological datasets, including temperature, rainfall, and radiation, the PML model was used to estimate ET components datasets globally. The performance of the PML model and datasets was validated at 95 flux towers globally, with the RMSE of 0.69 mm/day [49]. It was also evaluated across China, and the results suggested that the datasets can be used to study the spatial and temporal distribution of Ei at regional scales [50,51,52]. In this study, the subdatasets of Ei with 500 m and 8-day resolution covering China during 2001–2020 were downloaded from the Google Earth Engine (https://developers.google.com/earth-engine/datasets, accessed on 12 November 2021).
Five meteorological variables data, including wind speed (m/s), temperature (°C), precipitation (mm), relative humidity, and sunshine duration (h), were obtained from the daily dataset of surface climatic data at the National Meteorological Information Centre of China (NMIC) (http://data.cma.cn/en, accessed on 20 November 2021). The quality of meteorological data was checked by the NMIC, while meteorological data still contained errors due to occasional voltage instability and equipment errors [47]. Therefore, the meteorological data was further checked following the criteria presented by Feng et al. [17] and Tang et al. [31].
MODIS product data, including LAI (MOD15A2H) and NDVI (MYD13A1) with the same coverage and spatial and temporal resolution as the PML data, were collected from the National Aeronautics and Space Administration (NASA) earth data search center (https://search.earthdata.nasa.gov/, accessed on 15 November 2021). The pixel with missing data was not excluded from the dataset.
The physical geographic division data of China, including the thermal regions and moisture regions, were obtained from the Resource and Environment Science and Data Center, Chinese Academy of Sciences (https://www.resdc.cn, accessed on 20 November 2021). The thermal regions were determined using the ≥10 °C accumulated temperature, and moisture regions were determined using precipitation and evapotranspiration. Continental China was divided into 4 thermal regions, including temperate, subtropical, tropical, and plateau climate regions, and 4 moisture regions, including humid, semi-humid, semi-arid, and arid regions. The physical geographic division is presented in Figure 1.

2.2. Methods

The linear regression model was employed to analyze the changing trend [53] of Ei across China during 2001–2020. The changing trend was calculated as:
K = n ∑ j = 1 n j × E i j ¯ − ∑ j = 1 n j × E i j ¯ ∑ j = 1 n j 2 − ( ∑ j = 1 n j ) 2
where K is the linear regression slope of the time-series data, n is the length of time series, Eij is the Ei of the jth year, and E i j ¯ is the multi-year average of Ei. K > 0 implies an increasing trend, while K < 0 implies a decreasing trend.
F-test was used to measure the significance of the linear trend:
F = U Q / ( n − 2 ) ~ F ( 1 ,   n − 2 )
U = ∑ i = 1 n ( E i i ^ − E i ¯ ) 2
Q = ∑ i = 1 n ( E i i − E i i ^ ) 2
where U and Q are the sum of regression squares and the sum of residual squares, respectively, n is the sample size, E i i is the Ei from PML product, E i i ^ is the estimated Ei by the linear regression model, and E i ¯ is the average Ei.
The contribution of climate change and vegetation dynamics to the interannual variation of Ei was investigated using the sensitivity analysis method. Climate change includes the interannual changes in precipitation, relative humidity, air temperature, sunshine duration, and wind speed. The vegetation dynamic was measured by LAI and NDVI. The sensitivity of Ei to driving factors [54,55] was defined as:
S v i = lim Δ v i → 0 ( Δ E i / E i Δ v i / v i ) = ∂ E i ∂ v i × v i E i
where vi is the influencing factor for the ith year, ∆Ei is the changes of Ei, and ∆vi are the changes of the influencing factor.
The contribution rate (Cvi) of the influencing factor was defined as [56]:
C v i = Δ v i v i × S v i × 100 % .  

3. Results

3.1. Spatial Variation of Ei across China

The spatial distribution of Ei across China during 2001–2020 is shown in Figure 2. As can be seen, Ei presented obvious spatial variation toward the changes in temperature and moisture. It generally decreased from southeast to northwest. The spatial variation of Ei was similar to those of LAI and NDVI over China. As can be seen from Figure 3, LAI and NDVI had a similar spatial distribution which generally decreased from southeast to northwest [57]. LAI and NDVI can explain 46.9% and 42.03% spatial variance of Ei, respectively.
As far as the climatic region was concerned, the maximum Ei was observed in the tropical region with the annual mean Ei varying between 98.63 mm and 139.03 mm, following that in the subtropical region with the annual mean Ei varying between 78.85 mm and 111.42 mm. At the same time, the lowest Ei occurred in the plateau climate region, with the annual mean Ei varying between 8.23 mm and 13.94 mm. The simulated result from the PML model found that the average annual Ei was 46.6 ± 77.2 mm at the global level, and the Ei in most areas of China was in the range of 0~50 mm [13] which was consistent with the results in this study. The Ei of the tropical region was similar to that of the tropical rain forests in India [24]. The average Ei of southeast Asia, central Africa, and northern South America was about 250 mm/year [54], much higher than that across China, while Ei in other regions was basically at the same level as that of China [58,59,60,61,62,63,64,65,66].
Higher Ei in the tropical region was probably because this region was dominated by tropical rainforests with higher LAI. Satellite observations showed that the average LAI of tropical rainforests could reach as high as more than six in China [67,68], which was higher than that of subtropical evergreen broad-leaved forests in the subtropical region [69,70] and the grassland in temperature regions [71]. While in the plateau climate region, vegetation was dominant by grassland with lower vegetation coverage and LAI [72], resulting in lower Ei compared to other thermal regions.
Precipitation was another critical factor regulating the spatial distribution pattern of Ei [73]. As can be seen from Figure 4, precipitation showed an obvious spatial variation which was similar to the spatial distribution of Ei across China. Precipitation can explain the 33.64% spatial variance of Ei.
Ei showed a decreasing trend along the moisture gradient from east to west. The maximum Ei was presented in the humid region, with the annual mean Ei varying between 68.92 mm and 96.64 mm, which was mainly contributed by the abundant precipitation. Long-term observation showed that the annual mean precipitation was more than 800 mm in this region, which was much higher than that in the semi-humid region, semi-arid region, and arid region [74]. The annual mean Ei in the semi-humid region was about 30% lower than that in the humid region. At the same time, the annual mean Ei in the semi-arid and arid regions were only 6.24~10.25 mm and 1.29~1.9 mm, respectively, which were much lower than those in humid and semi-humid regions. This was mainly contributed by the low level of precipitation coupled with the lower vegetation coverage [75]. The vegetation from the humid area to the arid area gradually transited from forest to grassland to desert, and the vegetation coverage gradually decreased [76,77]. The results suggested that coupled effect of precipitation and vegetation coverage variation resulted in the spatial distribution of Ei from humid region to arid region.

3.2. Temporal Variation of Ei during 2001–2020

The spatial distribution of changing rate of Ei during 2001−2020 is shown in Figure 5. Generally, Ei changed dramatically over the last two decades across China, with an average changing rate of 0.45 mm/year, while the changing rate varied greatly among different regions. A large portion of the area showed an upward trend, which accounted for 53.85% of continental China. Ei significantly (p < 0.05) increased in most areas of the sub-tropical region, tropical region, eastern humid region, and central semi-humid region (Figure 6), accounting for 39.65% of continental China. In contrast, Ei showed a downward trend at 46.15% of the area of China, with a significantly (p < 0.05) decreasing trend occurring in western China and the southern part of the plateau climate region, which only accounted for 3.35% of continental China.
The temporal trends of Ei for four thermal regions during 2001−2020 are shown in Figure 7. The results indicated a significantly increasing trend of Ei for all thermal regions, and the most obvious change occurred in the tropical region with a changing rate of 1.45 mm/year. The changing rate of Ei for the temperate region was similar to that for the subtropical region, while the plateau climatic region had the lowest increasing rate of 0.22 mm/year. As far as the moisture region was concerned, Ei increased significantly (p < 0.05) in all regions (Figure 8), and the increasing rate generally decreased along the moisture gradient from east to west. The most obvious change occurred in the humid region with a changing rate of 1.11 mm/year which was much higher than that in semi-humid regions. The arid region had the lowest changing rate of 0.02 mm/year, which was much lower than that in a semi-arid region.

3.3. Contribution of Influencing Factors to the Temporal Variation of Ei

3.3.1. Climatic Factors

The spatial distribution of the contribution rate of climatic factors to the interannual change of Ei during 2001–2020 is presented in Figure 9, and the contribution rates for four thermal regions and four moisture regions are shown in Figure 10. As can be seen, the contribution rate varied obviously from region to region. On average, precipitation contributed mostly to the interannual change of Ei over China, with an average contribution rate of 30.18~37.59%; this suggested that precipitation was the most important climatic factor driving the interannual change of Ei over the past two decades, confirming the previous finding that the variation of precipitation was the main reason responsible for the change of Ei [78]. Zhang et al. [79] investigated the Ei of single sand fixing shrub caragana and semi shrub Artemisia annua crown in 210 precipitation events from 2004~2014 and concluded that precipitation could better explain the variance of Ei than canopy structure.
The most dominant contribution of precipitation was observed in the humid and semi-humid regions, where precipitation contributed about 40% of the interannual change of Ei (Figure 10b).
The contribution rate in the semi-arid region was slightly higher than that in the arid region, and they were 4.94~5.85% lower than those in the humid and semi-humid regions. The contribution rates of precipitation ranged from 31.51% to 35.59% among different thermal regions (Figure 10), indicating that precipitation contributed equally approximately to the interannual change of Ei in different thermal regions.
Relative humidity contributed negatively to the interannual change of Ei, probably due to the fact that a decrease in relative humidity increased the atmospheric demand for evapotranspiration [80]. This was another important factor affecting the interannual change of Ei following precipitation. The average contribution rate varied between −40.19~−18.06% in different regions, with the most pronounced contribution occurring in the humid region and tropical region, where relative humidity negatively contributed about 40% interannual change of Ei.
The contribution rate of temperature changed greatly among different thermal regions. Temperature contributed negatively to the interannual change of Ei in tropical, subtropical, humid, and arid regions, while a positive contribution was observed in other regions.
The increase in wind speed would cause an increase in the evaporation rate, leading to an increase in Ei [81]. The contribution rate of wind speed ranged from 8.78% to 19.39%, with the most obvious effect observed in the humid region, while wind speed contributed almost equally to the interannual change of Ei in the semi-humid region, arid region, and semi-arid region. Wind speed also contributed nearly equally to the interannual change of Ei in tropical and subtropical regions, and the contribution rate of wind speed was slightly higher than that in the plateau climatic region. Similarly, the contribution rate of sunshine duration also varied obviously among different moisture regions, with a positive contribution in the humid region and semi-humid region, while providing a negative contribution in the arid region and semi-arid region.

3.3.2. Vegetation Dynamic

The spatial distribution for the contribution rate of vegetation dynamic to the interannual variation of Ei during 2001–2020 was presented in Figure 11. The contribution rates of NDVI and LAI followed a similar spatial pattern, mainly that LAI was retrieved from NDVI, and they showed similar spatial distribution. On average, LAI contributed 46.9% of the interannual change of Ei, which was slightly higher than 42.04% for NDVI, indicating that the interannual change of Ei was significantly affected by vegetation dynamic; the result agreed well with many previous studies. Zhang et al. [13] studied global land underlying conditions from 2003 to 2017 and concluded that LAI was the main controlling factor affecting the change of Ei. Increasing LAI led to a significant increase in Ei in many regions globally. Similar results were also observed in Moso Bamboo, where Ei increased with the increase of LAI mainly because the increase of LAI reduced the amount of rain penetration [48]. Deng et al. [21] reported that there was a positive correlation between the interannual change of LAI and Ei in the Yangtze River Basin.
Both the contribution rates of NDVI and LAI generally increased along the moisture gradient from east to west, with a maximum of 44.7% and 55.78% in the arid region, respectively, and minimum contribution rates appeared in the humid region (40.69%) and humid regions (43.05%), respectively. The results suggested that the effect of vegetation dynamic on the interannual change of Ei was more pronounced in arid regions than that in humid regions.

4. Discussions

The evaporation of the intercepted precipitation (Ei) presented similar spatial distribution decreasing from southeast to northwest to LAI, NDVI and precipitation across China. LAI, NDVI and precipitation can explain 46.9%, 42.03%, and 33.64% variance of Ei, respectively, which confirmed the previous finding that Ei was greatly affected by vegetation canopy status and precipitation conditions [44] and was consistent with many studies on the relationship between the spatial distribution of Ei and LAI, NDVI. For example, Min [58] studied the ET of forest ecosystems in the north–south transect of eastern China and found that the Ei and LAI decreased with the increase of latitude. Li [59] analyzed the precipitation interception characteristics of the Tianlaochi watershed in the upper reaches of the Heihe River in China. The result showed similar spatial distribution of Ei with LAI and NDVI for shrubs. Véliz-Chávez et al. [60] investigated the spatial and temporal dynamic of NDVI and surface ET of banyan forest in southern Africa and reported that the components of ET and NDVI followed the general pattern of periodic seasonal changes. They also presented similar spatial variations in different geographical regions, and Ei showed a positive correlation with precipitation. Moreover, many studies reported that Ei was positively correlated with LAI [60,61,62]. For example, Liu et al. [20] investigated the Ei of larch forest in Liupan Mountain in China and concluded that the seasonal variation of LAI was the main factor affecting the spatial and temporal variation of Ei. Sun et al. [63] analyzed the rainfall interception capacity and spatial and temporal variation characteristics of a vegetation canopy in Guangdong Province in China from 2004 to 2016 and found a positive correlation between LAI and Ei. Zheng et al. [64] conducted a field experiment on the Ei dynamic of corn during the growing season from 2015 to 2017, and the results confirmed an obvious relationship between Ei and LAI in all rainfall events. For precipitation, Zhang et al. [72] investigated the Ei distribution pattern and its influencing factors of the main shelter forest types in northern Jiangsu province in China. The results revealed an obvious positive correlation between Ei and precipitation. Jing et al. [34] observed and analyzed the Ei of the soil and water conservation forests in the black soil area and found that Ei was closely related to precipitation. Zhang et al. [48] studied the relationship between the Ei and precipitation of the Quercus acutissima forest on Zijin Mountain and observed that Ei increased with the increase of precipitation in a power function manner. Zhang et al. [71] analyzed the Ei characteristics of maize canopy in China’s main production areas based on the observation at 13 agro-meteorological stations and also found a positive correlation between Ei and rainfall.
Ei has changed dramatically over the last two decades across China, with an average changing rate of 0.45 mm/year. The changing rate of Ei throughout China was similar to those in some regions of North America [17]. Cesar et al. [76] investigated the interannual variation of Ei for deciduous banyan trees in Querétaro city in Mexico and reported an average changing rate of 2.44 mm/year which was higher than those across different climatic and moisture regions. Zhang et al. [13] investigated the changing trend of Ei over the world during 2003–2017 and found the vegetation change resulted in an average increase of Ei by 0.8 ± 3.9 mm/y. The changing rate in some regions in North America and Europe was similar to that of the similar latitude regions in China [65].
Precipitation contributed about 40% of the interannual change of Ei over China, which suggested that precipitation was the most important climatic factor driving the interannual change of Ei over the past two decades. Higher contribution rates appeared in tropical, subtropical, humid, and semi-humid regions, which were mainly contributed by the larger LAI, higher vegetation coverage, and more abundant precipitation. The areas were dominated by subtropical evergreen broad-leaved forest and temperate deciduous broad-leaved forest with wide leaves and larger LAI [74]. Furthermore, tropical, subtropical, humid, and semi-humid regions had abundant precipitation throughout the year. On the contrary, the coupled effect of low level of precipitation and lower vegetation coverage and LAI contributed to the relatively lower contribution rate in other regions. In particular, temperature contributed negatively to the interannual change of Ei in tropical, subtropical, humid, and arid regions, while a positive contribution was observed in other regions. The contracting contribution of temperature to the variation of Ei was probably due to the different climate change patterns across different thermal regions [82]. Long term observation showed that the average temperature in tropical regions and most areas of the Yangtze River basin in subtropical regions presented a decreasing trend, while precipitation significantly increased over the last two decades [56]. Precipitation dominated the variation of Ei in humid and arid regions where increased precipitation contributed to the increase of Ei, which resulted in the negative contribution of temperature to the change of Ei. While both air temperature and precipitation increased in temperate regions [83], it resulted in the positive contribution of temperature to the change of Ei. In the Tibet Plateau region, which featured extremely cold temperatures, most of the water intercepted by the canopy appeared in the form of snow and ice, and evaporation increased with the increase of temperature [84], which contributed to the positive relationship between temperature and Ei in this region.
LAI contributed a 46.9% interannual change of Ei, which was slightly higher than 42.04% for NDVI. The effect of vegetation dynamic on the interannual change of Ei was more pronounced in arid regions than that in humid regions. The contribution rates of NDVI and LAI generally increased from south to north, with the maximum in the temperate region (Figure 11c). The spatial changing pattern was generally opposite that of NDVI and LAI, which decreased from south to north. The results indicated that the contribution of vegetation dynamic to the interannual change of Ei was more pronounced in the region with lower LAI under the similar precipitation, probably due to the saturation effect of Ei at higher LAI [85]. In arid regions and western China, which were dominated by grassland with lower vegetation coverage and LAI, Ei increased with the increase of LAI [27], while in the humid and tropical regions, which were dominated by vegetation with higher LAI, Ei did not significantly increase with the increase of LAI [86]. This saturation effect was also observed in other regions around the world. Liu et al. [20] found a significant positive correlation between Ei and LAI, while Ei did not increase significantly with the increase of LAI at higher values. Fischer et al. [86] analyzed the water use efficiency of poplar in the Czech Republic. The results showed that the relative respiration rate and transpiration increased with the increase of LAI and reached saturation at higher LAI.

5. Conclusions

This study investigated the spatial and temporal variation of Ei for different thermal regions and moisture regions across China during 2001–2020 using PML ET product and analyzed the contribution of climate change and vegetation dynamics to the interannual variation of Ei. The results showed that Ei generally decreased from southeast to northwest. The spatial variation was similar to those of LAI, NDVI and precipitation across China. As far as the climatic region was concerned, the maximum Ei was observed in tropical regions, probably due to the dominant landscape of the tropical rainforest. Ei showed a decreasing trend along the moisture gradient from east to west, mainly contributed by the precipitation. The results suggested that the coupled effect of precipitation and vegetation coverage resulted in the spatial distribution of Ei across China. Generally, Ei showed an increasing trend over the last two decades, with an average changing rate of 0.45 mm/year. As far as the climatic region was concerned, the most obvious change occurred in the tropical region with a changing rate of 1.45 mm/year, and the increasing rate generally decreased along the moisture gradient from east to west, with the most obvious change occurring in the humid region with a changing rate of 1.11 mm/year. Precipitation was the most important climatic factor driving the interannual change of Ei over the past two decades, with an average contribution rate of 30.18~37.59%, with a higher contribution rate occurring in the humid and semi-humid regions, while precipitation contributed equally approximately to the interannual change of Ei in four thermal regions. Relative humidity was another important factor affecting the interannual change of Ei following precipitation. Temperature showed a negative contribution in the four thermal regions. The contribution rates of NDVI and LAI followed a similar spatial pattern. Both the contribution rates of NDVI and LAI generally increased along the moisture gradient from east to west and generally increased from south to north.

Author Contributions

Conceptualization, L.Y.; Data curation, L.H. and Y.J.; Formal analysis, Y.J.; Funding acquisition, D.T. and J.C.; Methodology, L.Y. and L.H.; Software, L.H. and Y.F.; Supervision, Q.T. and D.T.; Visualization, Q.T. and Y.F.; Writing—original draft, L.Y.; Writing—review and editing, J.C. All authors will be informed about each step of manuscript processing including submission, revision, revision reminder, etc. via emails from our system or assigned Assistant Editor. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Central Guidance on Local Science and Technology Development Fund of Chongqing Municipality (No. 2021000069), the Youth Innovation Promotion Association (No. 2018417 and 2021385), the National Natural Science Foundation of China (No. 41901130, 42005130 and 42061015), Chongqing Municipal Bureau of Water Resources (No. 5000002021BF40001), and the Institute of Agricultural Resources and Environment, Tibet Academy of Agricultural and Animal Husbandry Science (No. 2020ZZKT-01).

Data Availability Statement

PML ET, MOD15A2H, and MYD13A1 used in this paper can be downloaded from Google Earth Engine. The physical geographic division data of China can be collected from the Resource and Environment Science and Data Center, Chinese Academy of Sciences (https://www.resdc.cn, accessed on 20 November 2021). Meteorological variables data were obtained from the daily dataset of surface climatic data at the National Meteorological Information Centre of China (NMIC) (http://data.cma.cn/en, accessed on 20 November 2021).

Acknowledgments

We acknowledge the research environment provided by Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Guo, J. Research progress of plant interception of precipitation. J. Appl. Meteorol. 2020, 31, 641–652. [Google Scholar]
  2. Gan, R.; Zhang, Y.; Shi, H.; Yang, Y.; Eamus, D.; Cheng, L.; Chiew, F.H.S.; Yu, Q. Use of satellite leaf area index estimating evapotranspiration and gross assimilation for Australian ecosystems. Ecohydrology 2018, 11, e1974. [Google Scholar] [CrossRef]
  3. Zheng, C.; Jia, L. Global canopy rainfall interception loss derived from satellite earth observations. Ecohydrology 2020, 13, e2186. [Google Scholar] [CrossRef] [Green Version]
  4. Wang, Q.; Kang, Y. Canopy interception and dissipation of Winter Wheat. Agric. Res. Arid Areas 2005, 23, 6. [Google Scholar]
  5. Boulet, G.; Delogu, E.; Chebbi, W.; Rafi, Z.; Merlin, O. Evapotranspiration and Evaporation/Transpiration Retrieval Using Dual-Source Surface Energy Balance Models Integrating VIS/NIR/TIR Data with Satellite Surface Soil Moisture Information. In IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
  6. Cortés, S.S.; Juan, I.W.; Eduardo, L.P.; Diego, E.G.; Patricio, N.M. Changes in rainfall partitioning caused by the replacement of native dry forests of Lithraea molleoides by exotic plantations of Pinus elliottii in the dry Chaco mountain forests, central Argentina. J. Arid Land 2020, 12, 717–729. [Google Scholar] [CrossRef]
  7. Davies-Barnard, T.; Valdes, P.J.; Jones, C.D.; Singarayer, J.S. Sensitivity of a coupled climate model to canopy interception capacity. Clim. Dyn. 2014, 42, 1715–1732. [Google Scholar] [CrossRef]
  8. Gash, J.H.C.; Lloyd, C.R.; Lachaud, G. Estimating sparse forest rainfall interception with an analytical model. J. Hydrol. 1995, 170, 79–86. [Google Scholar] [CrossRef]
  9. Rutter, A.J.; Kershaw, K.A.; Robins, P.C.; Morton, A.J. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
  10. Fan, Y.; Tim, J. Reconciling Canopy Interception Parameterization and Rainfall Forcing Frequency in the Community Land Model for Simulating Evapotranspiration of Rainforests and Oil Palm Plantations in Indonesia. J. Adv. Modeling Earth Syst. 2019, 11, 732–751. [Google Scholar] [CrossRef] [Green Version]
  11. Ghilain, D.; Arboleda, A.; Barrios, J.M.; Gellens, F. Water interception by canopies for remote sensing based evapotranspiration models. Int. J. Remote Sens. 2020, 41, 2934–2945. [Google Scholar] [CrossRef]
  12. Yu, L.; Xue, Y.; Diallo, I. Vegetation greening in China and its effect on summer regional climate. Sci. Bull. 2020, 66, 13–17. [Google Scholar] [CrossRef]
  13. Zhang, Y.; Zou, B.; Luo, J. Impact of vegetation change on global land surface evapotranspiration from 2003 to 2017. Acta Geogr. Sin. 2021, 76, 11. [Google Scholar]
  14. Shen, J.; Zhang, M.; Xiao, W.; Wen, X.; Liu, S.; Li, X. Resolution and characteristics of evapotranspiration components of Qianyanzhou plantation in China based on improved SW model. J. Ecol. 2016, 36, 11. [Google Scholar]
  15. Song, W.; Yang, S.; Lu, J.; Liu, C.; Wang, S. Simulation and analysis of large-scale vegetation canopy interception precipitation in the middle reaches of the Yellow River. Acta Geogr. Sin. 2014, 69, 80–89. [Google Scholar]
  16. Duan, H.; Kang, W. Effects of canopy interception on Evapotranspiration and energy distribution of PML model. China Rural Water Hydropower 2021, 3, 80–84. [Google Scholar]
  17. Neto, A.; Niu, G.; Roy, T.; Tyler, S.; Troch, P. Interactions between snow cover and evaporation lead to higher sensitivity of streamflow to temperature. Commun. Earth Environ. 2020, 1, 1234567890. [Google Scholar]
  18. Chao, L.; Zhang, K.; Wang, J.; Feng, J.; Zhang, M. A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sens. 2021, 13, 2414. [Google Scholar] [CrossRef]
  19. Hao, L.; Wang, S.; Cui, X.; Zhai, Y. Spatiotemporal Dynamics of Vegetation Net Primary Productivity and Its Response to Climate Change in Inner Mongolia from 2002 to 2019. Sustainability 2021, 13, 13310. [Google Scholar] [CrossRef]
  20. Liu, Z.; Wang, Y.; Tian, A.; Liu, Y.; Deng, X.; Wang, X.; Wang, Y.; Peng, Y. Spatial-temporal Variation and Scale Effect of Canopy Interception on a Larix principis-rupprechtii Plantation Slope in Liupan Mountains, Ningxia, China. J. Soil Water Conserv. 2017, 31, 9. [Google Scholar]
  21. Deng, H. Simulation and analysis of the impact of vegetation cover change on runoff and evaporation in Watershed. J. Geosci. 2012, 2, 16. [Google Scholar]
  22. Fan, C.; Li, C.; Jia, K.; Sun, B.; Gao, H. Canopy interception of grassland vegetation in Hulun Lake Basin under different grazing systems. J. Ecol. 2015, 35, 9. [Google Scholar]
  23. Sharma, M.; Bangotra, P.; Gautam, A.; Gautam, S. Sensitivity of normalized difference vegetation index (NDVI) to land surface temperature, soil moisture and precipitation over district Gautam Buddh Nagar, UP, India. Stoch. Environ. Res. Risk Assess. 2021, 36, 1779–1789. [Google Scholar] [CrossRef] [PubMed]
  24. Asdak, C.; Jarvis, P.; Gardingen, P.; Fraser, A. Rainfall interception loss in unlogged and logged forest areas of Central Kalimantan, Indonesia. J. Hydrol. 1998, 206, 237–244. [Google Scholar] [CrossRef] [Green Version]
  25. Fei, M.; Sun, H.; Yang, H. Research Progress in Dry/wet Climate Zoning. Prog. Geogr. Sci. 2011, 30, 17–26. [Google Scholar]
  26. Sun, X.; Wang, G.; Wu, Y.; Liu, L.; Liu, G. Hydrologic regime of interception for typical forest ecosystem at subalpine of Western Sichuan, China. J. Ecol. 2013, 33, 501–508. [Google Scholar]
  27. Sadeghi, S.M.M.; Attarod, P.; Pypker, T.G.; Dunikerley, D. Is canopy interception increased in semiarid tree plantations? Evidence from a field investigation in Tehran, Iran. Turk. J. Agric. For. 2014, 38, 792–806. [Google Scholar] [CrossRef]
  28. Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  29. Zhang, G.; Zeng, G.; Jiang, Y.; Huang, G.H.; Zhang, X. Modelling and measurement of two-layer-canopy interception losses in a subtropical evergreen forest of central-south China. Hydrol. Earth Syst. Sci. 2006, 10, 65–77. [Google Scholar] [CrossRef] [Green Version]
  30. Zhi, L.I.; Wang, Y.; Wang, Z.; Li, W. Spatiotemporal Variation of Evaporation and Transpiration from 1982—2012 in the Arid Valley Region in Northwest China. J. Irrig. Drain. 2018, 36, 112–115. [Google Scholar]
  31. Qiong, L.; Luo, Z.; Zhong, B.; Zhou, H. An Improved Approach for Evapotranspiration Estimation Using Water Balance Equation: Case Study of Yangtze River Basin. Water 2018, 10, 812. [Google Scholar]
  32. Silva, N.G.D.; Alves, R.J.V. The eradication of feral goats and its impact on plant biodiversity—A milestone in the history of Trindade Island, Brazil. Rodriguésia 2019, 62, 717–719. [Google Scholar] [CrossRef] [Green Version]
  33. Xia, H.; Yang, Y.; Ding, F. Recursive Least-squares Estimation for Multivariable Systems Based on the Maximum Likelihood Principle. Int. J. Control Autom. Syst. 2020, 18, 503–512. [Google Scholar] [CrossRef]
  34. Wang, Z. Interception of Vapor Flow near Soil Surface for Water Conservation and Drought Alleviation. In Proceedings of the AGU Fall Meeting Abstracts, Cambridge, MA, USA, 14–18 December 2015. [Google Scholar]
  35. Fathizadeh, O.; Hosseini, S.; Alexander, Z.; Keim, R.; Boloorani, A. Estimating linkages between forest structural variables and rainfall interception parameters in semi-arid deciduous oak forest stands. Sci. Total Environ. 2017, 601–602, 1824–1837. [Google Scholar] [CrossRef] [PubMed]
  36. Ufoegbune, G.C.; Ogunyemi, O.; Eruola, A.O.; Awomeso, J.A. Variation of interception loss with different plant species at the University of Agriculture, Abeokuta, Nigeria. Afr. J. Environ. Sci. Technol. 2010, 4, 831–844. [Google Scholar]
  37. Pypker, T.G.; Barbara, J.B.; Timothy, E.L.; Danny, G.M. The importance of canopy structure in controlling the interception loss of rainfall: Examples from a young and an old-growth Douglas-fir forest. Agric. For. Meteorol. 2005, 130, 113–129. [Google Scholar] [CrossRef]
  38. Yu, K. Effects of species composition on rainfall interception capacity of alpine meadow vegetation canopy. J. Ecol. 2011, 31, 9. [Google Scholar]
  39. Herwitz, S.R.; Slye, R.E. Three-dimensional modeling of canopy tree interception of wind-driven rainfall. J. Hydrol. 1995, 168, 205–226. [Google Scholar] [CrossRef]
  40. Marin, C.T. Gross rainfall and its partitioning into throughfall, stemflow and evaporation of intercepted water in four forest ecosystems in western Amazonia. J. Hydrol. 2000, 237, 40–57. [Google Scholar] [CrossRef]
  41. Xiao, Q.; Mcpherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Processes 2015, 14, 763–784. [Google Scholar] [CrossRef]
  42. Fleischbein, K.; Wilcke, W.; Goller, R.; Boy, J.; Valarezo, C.; Zech, W.; Knoblich, K. Rainfall interception in a lower montane forest in Ecuador: Effects of canopy properties. Hydrol. Processes 2005, 19, 1355–1371. [Google Scholar] [CrossRef]
  43. Zhu, X.; Wu, T.; Ni, J. Increased extreme warming events and the differences in the observed hydrothermal responses of the active layer to these events in China’s permafrost regions. Clim. Dyn. 2022, 1–20. [Google Scholar] [CrossRef]
  44. Niu, X. Dynamic Changes of Leaf Area Index of Typical Vegetation in Water and Wind Erosion Ecotone and Its Influence on Canopy Interception. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]
  45. Kang, W.; Deng, X.; Zhao, Z. Effects of canopy interception on energy conversion processes in a Chinese fir plantation ecosystem. Front. For. China 2008, 3, 264–270. [Google Scholar] [CrossRef]
  46. Leuning, R.; Cleugh, H.A.; Zegelin, S.J.; Hughes, D. Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: Measurements and comparison with MODIS remote sensing estimates. Agric. For. Meteorol. 2005, 129, 151–173. [Google Scholar] [CrossRef]
  47. Zhang, Y.; Kang, S.; Ward, E.J.; Ding, R.; Xin, Z.; Rui, Z. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China: Dynamics and influential factors. Agric. Water Manag. 2011, 98, 1207–1214. [Google Scholar] [CrossRef]
  48. Zhang, Z.S.; Roy, M.B.; Roy, P.K. Gross rainfall amount and maximum rainfall intensity in 60-minute influence on interception loss of shrubs: A 10-year observation in the Tengger Desert. Sci. Rep. 2016, 6, 26030. [Google Scholar] [CrossRef] [Green Version]
  49. Zhang, Y.; Kengni, L.; Tematio, P.; Manefouet, I.B.; Kenfack, J.V. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
  50. Lu, J.; Wang, G.; Gong, T.; Hagan, D.; Su, B. Changes of actual evapotranspiration and its components in the Yangtze River valley during 1980–2014 from satellite assimilation product. Theor. Appl. Climatol. 2019, 138, 1493–1510. [Google Scholar] [CrossRef]
  51. Xiao, Q.; Mcpherson, E. Rainfall interception of three trees in Oakland, California. Urban Ecosyst. 2011, 14, 755–769. [Google Scholar] [CrossRef]
  52. Zheng, J.; Fan, J.; Zhang, F.; Zhuang, Q. Evapotranspiration partitioning and water productivity of rainfed maize under contrasting mulching conditions in Northwest China. Agric. Water Manag. 2021, 243, 106473. [Google Scholar] [CrossRef]
  53. Sun, H.; Bai, Y.; Lu, M.; Wang, J.; Ye, T.; Yan, D. Drivers of the water use efficiency changes in China during 1982–2015. Sci. Total Environ. 2021, 799, 149145. [Google Scholar] [CrossRef]
  54. Rowe, L.K. Rainfall interception by an evergreen beech forest, Nelson, New Zealand. J. Hydrol. 1983, 66, 143–158. [Google Scholar] [CrossRef]
  55. Zheng, C.; Li, J. Global rainfall interception loss derived from multi-source satellite earth observations. In Proceedings of the IGARSS 2016-2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
  56. Carlyle-Moses, D.E.; Price, A.G. Modelling canopy interception loss from a Madrean pine-oak stand, northeastern Mexico. Hydrol. Processes 2010, 21, 2572–2580. [Google Scholar] [CrossRef]
  57. Liu, H.; Deng, Y.; Liu, X. The contribution of forest and grassland change was greater than that of cropland in human-induced vegetation greening in China, especially in regions with high climate variability. Sci. Total Environ. 2021, 792, 148408. [Google Scholar] [CrossRef] [PubMed]
  58. Min, C. Study on Forest Ecosystem Evapotranspiration in North-South Transect of Eastern China Based on RS and GIS; Hubei University: Wuhan, China, 2012. [Google Scholar]
  59. Li, W. Rainfall Interception Characteristics of Shrub in Tianlaochi Watershed in the Upper Reaches of Heihe River in China; Lanzhou University: Lanzhou, China, 2015. [Google Scholar]
  60. Véliz-Chávez, C.; Mastachi-Loza, C.A.; González-Sosa, E.; Becerril-Piña., R.; Ramos-Salinas, N.M. Canopy Storage Implications on Interception Loss Modeling. Am. J. Plant Sci. 2014, 5, 3032–3048. [Google Scholar] [CrossRef] [Green Version]
  61. McJannet, D.; Vertessy, R. McJannet and Vertessy, Effects of thinning on wood production, leaf area index, transpiration and canopy interception of a plantation subject to drought. Tree Physiol. 2001, 21, 1001–1008. [Google Scholar] [CrossRef] [Green Version]
  62. Lu, S.; Tian, F. Spatiotemporal variations of agricultural water use efficiency and its response to the Grain to Green Program during 1982–2015 in the Chinese Loess Plateau. Phys. Chem. Earth Parts A/B/C 2021, 121, 102975. [Google Scholar] [CrossRef]
  63. Azida, A.B.A.; Syahidah, A.M.N.; Lee, W.K. The effects of rainfall intensity to floor interception of Axonopus Compressus (Dwaft) under controlled condition. IOP Conf. Ser. Earth Environ. Sci. 2021, 646, 012041. [Google Scholar] [CrossRef]
  64. Sun, C.; Jetten, V.G. Rainfall interception simulation and temporal and spatial variation characteristics of vegetation canopy in Guangdong Province from 2004 to 2016 in China. J. Ecol. 2020, 40, 15. [Google Scholar]
  65. Dimitriadou, S.; Nikolakopoulos, K.G. Evapotranspiration Trends and Interactions in Light of the Anthropogenic Footprint and the Climate Crisis: A Review. Hydrology 2021, 8, 163. [Google Scholar] [CrossRef]
  66. Siles, P.; Vaast, P.; Dreyer, E.; Harmand, J.M. Rainfall partitioning into throughfall, stemflow and interception loss in a coffee (Coffea arabica L.) monoculture compared to an agroforestry system with Inga densiflora. J. Hydrol. 2010, 395, 39–48. [Google Scholar] [CrossRef] [Green Version]
  67. Ling, B.; Liu, S.; Qu, Y.; Zhou, G.; He, X. Analysis of changes in Amazon tropical rain forest from 1982 to 2012 using glass Lai data. J. Remote Sens. 2016, 20, 8. [Google Scholar]
  68. Golubeva, E.I.; Zimin, M.V.; Tutubalina, O.V.; Timokhina, Y.I.; Azarova, A.S. Leaf Area Index: Methods of Field Instrumental Measurements and Using Remote Sensing Materials; Southern Scientific Center of the Russian Academy of Sciences Rostov on Don: Moscow, Russia, 2020. [Google Scholar]
  69. Hu, L.; Chen, Y.; Mao, J. Effects of different spatial resolutions of remote sensing images on the estimation of effective leaf area index of evergreen broad-leaved forest in mountainous areas of Southwest Sichuan in China. J. Sichuan Agric. Univ. 2016, 34, 8. [Google Scholar]
  70. Hu, L. Dynamic analysis of vegetation in key ecological functional areas of wind prevention and sand fixation in recent 20 years. J. Ecol. 2021, 41, 11. [Google Scholar]
  71. Zhang, Y.; Liu, T.; Wang, Y.; Zhang, M.; Zheng, Y. Vegetation variation trend and its influencing factors in Urad Grassland over remote sensing. MATEC Web Conf. 2021, 336, 06028. [Google Scholar] [CrossRef]
  72. Zhang, J.; Liu, T.; Wang, Y.; Zhang, M.; Zheng, Y. Study on the characteristics of rainfall interception by the canopy of the seawall shelter forest in Northern Jiangsu in China. J. Nanjing For. Univ. 1996, 39, 17. [Google Scholar]
  73. Tan, S.; Ni, X.; Yue, K.; Liao, S.; Wu, F. Increased precipitation differentially changed soil CO2 efflux in arid and humid areas. Geoderma 2021, 388, 114946. [Google Scholar] [CrossRef]
  74. Ma, P.; LREIS. Validation and analysis of musyq leaf area index products—A case study of China. J. Remote Sens. 2018, 23, 131. [Google Scholar]
  75. Zhang, Y.; Chiew, F.; Zhang, L.; Li, H. Use of Remotely Sensed Actual Evapotranspiration to Improve Rainfall-Runoff Modeling in Southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
  76. Cesar. Canopy Interception. In Dictionary Geotechnical Engineering/Wörterbuch Geotechnik; Springer: Berlin/Heidelberg, Germany, 2014; p. 188. [Google Scholar]
  77. Richter, F.; Ring, J.; Panferov, O.; Spank, U.; Bernhofer, C. How to predict hydrological effects of local land use change: How the vegetation parameterisation for short rotation coppices influences model results. Hydrol. Earth Syst. Sci. 2015, 19, 3457–3474. [Google Scholar] [CrossRef] [Green Version]
  78. Zhang, Y.F.; Wang, X.; Hu, R.; Pan, Y.; Paradeloc, M. Rainfall partitioning into throughfall, stemflow and interception loss by two xerophytic shrubs within a rain-fed re-vegetated desert ecosystem, northwestern China. J. Hydrol. 2015, 527, 1084–1095. [Google Scholar] [CrossRef]
  79. Mccarthy, M.P.; Toumi, R. Observed Interannual Variability of Tropical Troposphere Relative Humidity. J. Clim. 2004, 17, 3181–3191. [Google Scholar] [CrossRef]
  80. Davarzani, H.; Smits, K.; Tolene, R.M.; Illangasekare, T. Study of the effect of wind speed on evaporation from soil through integrated modeling of the atmospheric boundary layer and shallow subsurface. Water Resour. Res. 2014, 50, 661–680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  81. Chen, J.; Gao, D.; Xu, Q.; Hao, Y.; Zhang, B. Characteristics of δD and δ18O in summer precipitation in the West Ordos Desert and its water vapor sources. For. Res. 2016, 29, 911–918. [Google Scholar]
  82. Li, C. LUCC-Driven Changes in Gross Primary Production and Actual Evapotranspiration in Northern China. J. Geophys. Res. Atmos. 2020, 125, e2019JD031705. [Google Scholar] [CrossRef]
  83. Rogers, C.A.; Chen, J.M.; Gonsamo, A.; Luo, X.; Staebler, R. Daily leaf area index from photosynthetically active radiation for long term records of canopy structure and leaf phenology. Agric. For. Meteorol. 2021, 304–305, 108407. [Google Scholar] [CrossRef]
  84. Dayisaba, F.N.; Guo, H.; Isabwe, A.; Bao, A.; Nahayo, L.; Khan, G. Inter-Annual Vegetation Changes in Response to Climate Variability in Rwanda. J. Environ. Prot. 2017, 8, 464. [Google Scholar] [CrossRef] [Green Version]
  85. Jitka, K.; Václav ípek, Š.; Hnilica, J.; Vlek, L.; Tesa, M. Canopy interception estimates in a Norway spruce forest and their importance for hydrological modelling. Hydrol. Sci. J. 2021, 66, 1233–1247. [Google Scholar]
  86. Fischer, M.; Zenone, T.; Trnka, M.; Orság, M.; Montagnani, L.; Ward, E.J.; Tripathi, A.M.; Hlavinka, P.; Seufert, G.; Žalud, Z.; et al. Water requirements of short rotation poplar coppice: Experimental and modelling analyses across Europe. Agric. For. Meteorol. 2018, 250, 343–360. [Google Scholar] [CrossRef]
Remotesensing 14 02474 g001 550
Figure 1. The physical geographic division of China. (a) Thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (b) moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Figure 1. The physical geographic division of China. (a) Thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (b) moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Remotesensing 14 02474 g001
Remotesensing 14 02474 g002 550
Figure 2. The spatial distribution of Ei across China during 2001–2020. (a) The spatial distribution of Ei; (b) the average Ei of different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (c) the average Ei of different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Figure 2. The spatial distribution of Ei across China during 2001–2020. (a) The spatial distribution of Ei; (b) the average Ei of different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (c) the average Ei of different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Remotesensing 14 02474 g002
Remotesensing 14 02474 g003 550
Figure 3. The spatial variation of NDVI (a) and LAI (b) across China during 2001–2020.
Figure 3. The spatial variation of NDVI (a) and LAI (b) across China during 2001–2020.
Remotesensing 14 02474 g003
Remotesensing 14 02474 g004 550
Figure 4. The spatial variation of precipitation across China during 2001–2020.
Figure 4. The spatial variation of precipitation across China during 2001–2020.
Remotesensing 14 02474 g004
Remotesensing 14 02474 g005 550
Figure 5. The spatial distribution of Ei changing trend across China during 2001−2020. (a) The spatial distribution of changing trend (K); (b) the average K of different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (c) the average K of different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Figure 5. The spatial distribution of Ei changing trend across China during 2001−2020. (a) The spatial distribution of changing trend (K); (b) the average K of different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (c) the average K of different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Remotesensing 14 02474 g005
Remotesensing 14 02474 g006 550
Figure 6. The spatial distribution of significance for the interannual change of Ei across China during 2001−2020.
Figure 6. The spatial distribution of significance for the interannual change of Ei across China during 2001−2020.
Remotesensing 14 02474 g006
Remotesensing 14 02474 g007 550
Figure 7. The temporal variation of Ei for different thermal regions during 2001−2020. (a) Tropical region; (b) subtropical region; (c) temperate region; (d) plateau climate region.
Figure 7. The temporal variation of Ei for different thermal regions during 2001−2020. (a) Tropical region; (b) subtropical region; (c) temperate region; (d) plateau climate region.
Remotesensing 14 02474 g007
Remotesensing 14 02474 g008 550
Figure 8. The temporal variation of Ei for different moisture regions during 2001−2020. (a) Humid region; (b) semi-humid region; (c) semi-arid region; (d) arid region.
Figure 8. The temporal variation of Ei for different moisture regions during 2001−2020. (a) Humid region; (b) semi-humid region; (c) semi-arid region; (d) arid region.
Remotesensing 14 02474 g008
Remotesensing 14 02474 g009 550
Figure 9. The spatial distribution of the contribution rates of climatic factors to the interannual change of Ei during 2001−2020. (a) Wind speed; (b) temperature; (c) precipitation; (d) relative humidity; (e) sunshine duration.
Figure 9. The spatial distribution of the contribution rates of climatic factors to the interannual change of Ei during 2001−2020. (a) Wind speed; (b) temperature; (c) precipitation; (d) relative humidity; (e) sunshine duration.
Remotesensing 14 02474 g009
Remotesensing 14 02474 g010 550
Figure 10. The average contribution rates of climatic factors for different climatic and moisture regions during 2001−2020. (a) The average contribution rates of climate change for different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (b) the average contribution rates of climate change for different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Figure 10. The average contribution rates of climatic factors for different climatic and moisture regions during 2001−2020. (a) The average contribution rates of climate change for different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (b) the average contribution rates of climate change for different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions, and arid regions, respectively.
Remotesensing 14 02474 g010
Remotesensing 14 02474 g011 550
Figure 11. The spatial distribution for the contribution rates of vegetation dynamic to the interannual change of Ei during 2001–2020. (a) The spatial distribution for the contribution rates of NDVI; (b) the spatial distribution for the contribution rates of LAI; (c) I average contribution rates of vegetation dynamic for different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (d) the average contribution rates of vegetation dynamic for different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions and arid regions, respectively.
Figure 11. The spatial distribution for the contribution rates of vegetation dynamic to the interannual change of Ei during 2001–2020. (a) The spatial distribution for the contribution rates of NDVI; (b) the spatial distribution for the contribution rates of LAI; (c) I average contribution rates of vegetation dynamic for different thermal regions. I, II, III, and IV are tropical regions, subtropical regions, temperate regions, and plateau climate regions, respectively; (d) the average contribution rates of vegetation dynamic for different moisture regions. V, VI, VII, and VIII are humid regions, semi-humid regions, semi-arid regions and arid regions, respectively.
Remotesensing 14 02474 g011
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Yan, L.; Chen, J.; He, L.; Ji, Y.; Tang, Q.; Fan, Y.; Tan, D. Dynamics of the Evaporation of Intercepted Precipitation during the Last Two Decades over China. Remote Sens. 2022, 14, 2474. https://doi.org/10.3390/rs14102474

AMA Style

Yan L, Chen J, He L, Ji Y, Tang Q, Fan Y, Tan D. Dynamics of the Evaporation of Intercepted Precipitation during the Last Two Decades over China. Remote Sensing. 2022; 14(10):2474. https://doi.org/10.3390/rs14102474

Chicago/Turabian Style

Yan, Lingyun, Jilong Chen, Lei He, Yongyue Ji, Qingqing Tang, Yuanchao Fan, and Daming Tan. 2022. "Dynamics of the Evaporation of Intercepted Precipitation during the Last Two Decades over China" Remote Sensing 14, no. 10: 2474. https://doi.org/10.3390/rs14102474

APA Style

Yan, L., Chen, J., He, L., Ji, Y., Tang, Q., Fan, Y., & Tan, D. (2022). Dynamics of the Evaporation of Intercepted Precipitation during the Last Two Decades over China. Remote Sensing, 14(10), 2474. https://doi.org/10.3390/rs14102474

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop