Measuring PM2.5 Concentrations from a Single Smartphone Photograph
Abstract
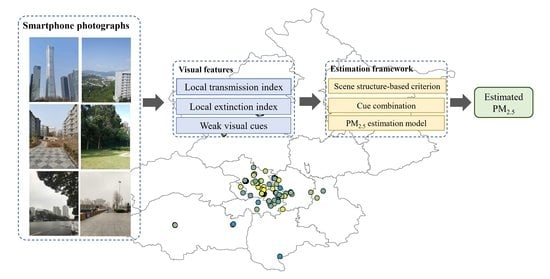
:1. Introduction
2. Materials and Methods
2.1. Weak Cues from a Single Smartphone Photograph
2.1.1. Sky Discoloration
2.1.2. Luminance Gradients
2.1.3. Structural Information Loss
2.2. Local Transmission Index
2.3. Local Extinction Coefficient
2.3.1. Depth Map
2.3.2. Scene Segmentation
2.3.3. Refined Local Extinction Index
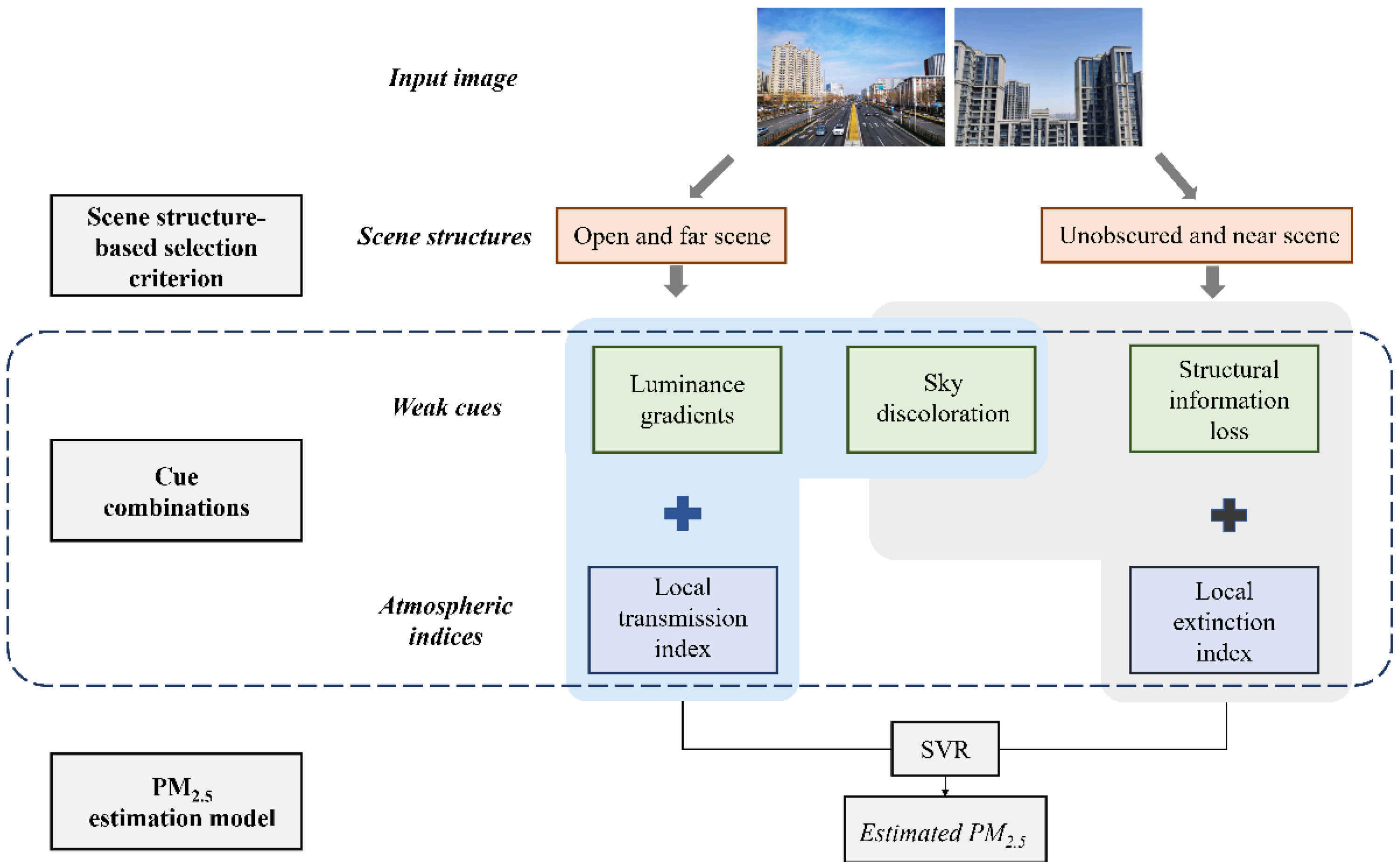
2.4. PM2.5 Estimation Framework
2.4.1. Scene Structure-Based Selection Criterion
- For an obscured view, where the VPs are located outside the photograph or are located on objects, and objects (i.e., buildings) dominate the photograph, the local extinction index [LEI] should be selected.
- For an open view, where the VPs are located far away, typically near the horizon, the local transmission index [LTI] should be selected.
2.4.2. Cue Combination
2.4.3. PM2.5 Estimation Model
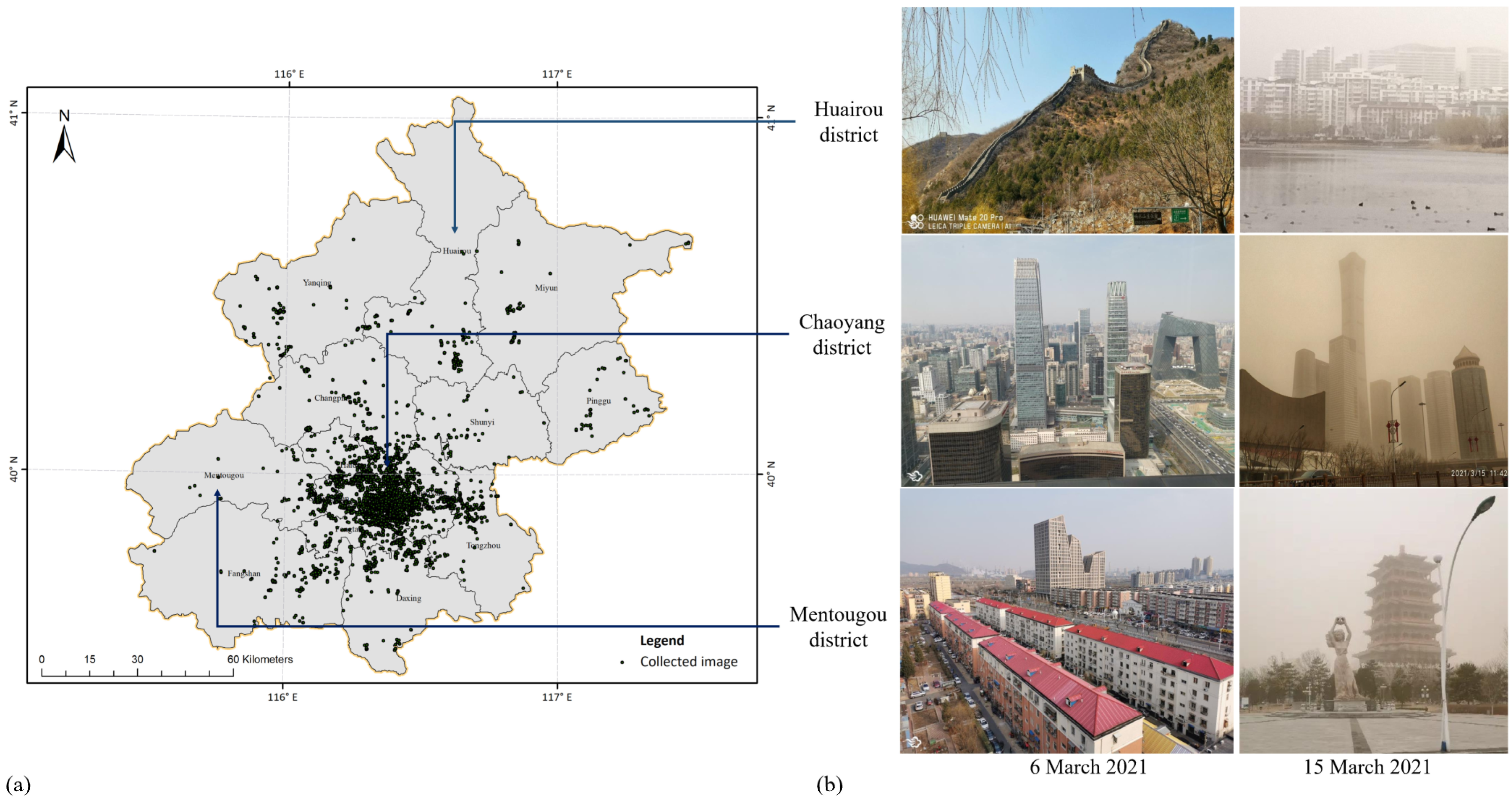
2.5. Experimental Data
2.5.1. PhotoPM-Daytime Dataset
2.5.2. Crowdsourced Photographs from the Internet
3. Results
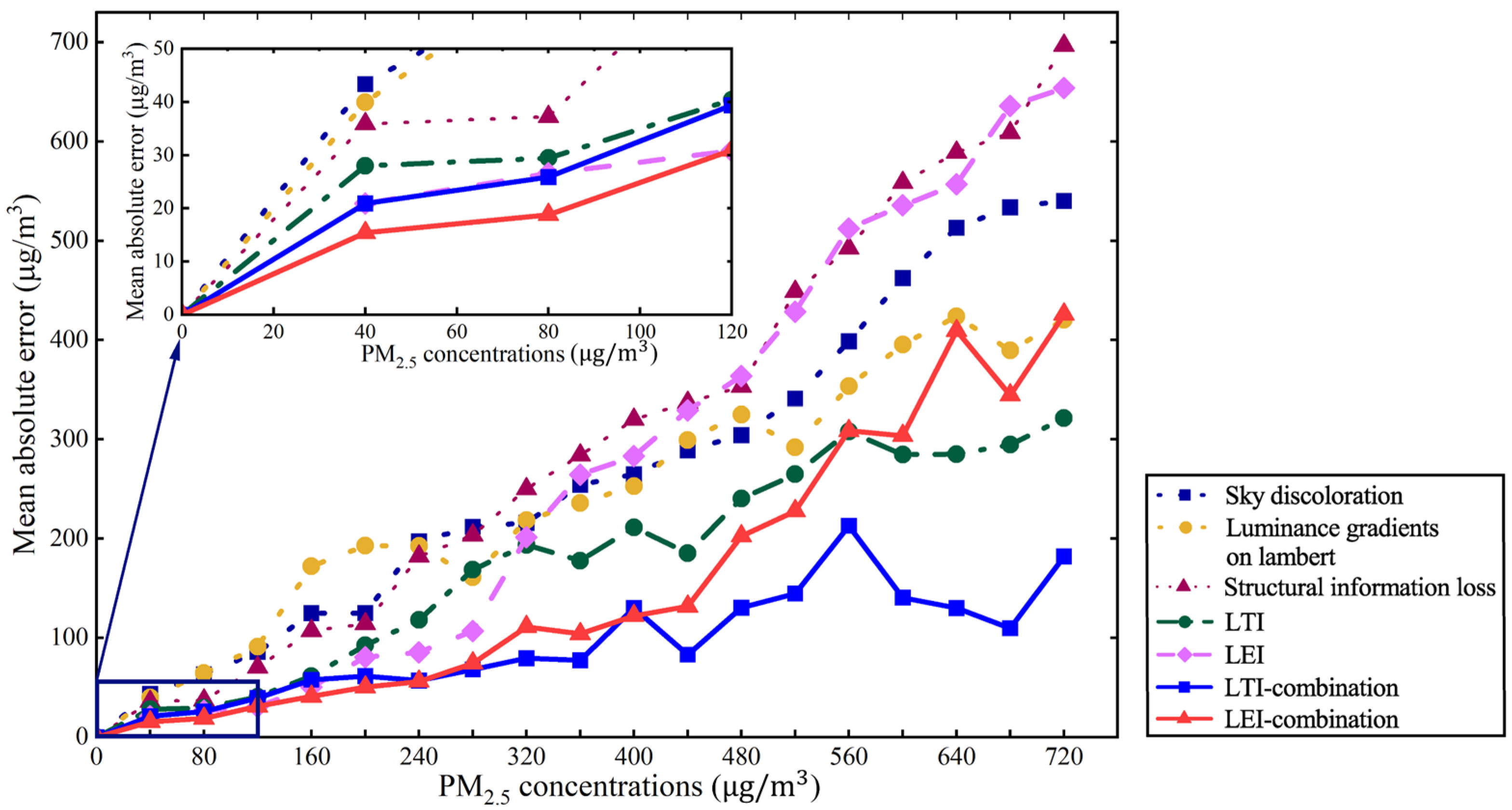
3.1. Evaluation of the Cue Combinations for PM2.5 Estimation
3.2. Validation of the PM2.5 Estimation Model
3.2.1. Performance of the Estimation Model
3.2.2. Performance under Different Outdoor Sceneries
3.3. PM2.5 Estimation for Beijing
4. Discussion
4.1. Comparison with Other Methods Using the PhotoPM-Daytime Dataset
4.2. Transferability of the PM2.5 Estimation Model Based on Other Datasets
4.3. Limitations and Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Ambient Air Pollution: A Global Assessment of Exposure and Burden of Disease; World Health Organization: Geneva, Switzerland, 2016; ISBN 978-92-4-151135-3.
- Song, Y.M.; Huang, B.; He, Q.Q.; Chen, B.; Wei, J.; Rashed, M. Dynamic Assessment of PM2·5 Exposure and Health Risk Using Remote Sensing and Geo-spatial Big Data. Environ. Pollut. 2019, 253, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Yue, H.; He, C.; Huang, Q.; Yin, D.; Bryan, B.A. Stronger Policy Required to Substantially Reduce Deaths from PM2.5 Pollution in China. Nat. Commun. 2020, 11, 1462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ministry of Ecology and Environment the People’s Republic of China. The State Council Issues Action Plan on Prevention and Control of Air Pollution Introducing Ten Measures to Improve Air Quality. Available online: http://english.mee.gov.cn/News_service/infocus/201309/t20130924_260707.shtml (accessed on 4 January 2021).
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.W.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The Changing Paradigm of Air Pollution Monitoring. Environ. Sci. Technol. 2013, 47, 11369–11377. [Google Scholar] [CrossRef] [PubMed]
- Milà, C.; Salmon, M.; Sanchez, M.; Ambrós, A.; Bhogadi, S.; Sreekanth, V.; Nieuwenhuijsen, M.; Kinra, S.; Marshall, J.D.; Tonne, C. When, Where, and What? Characterizing Personal PM2.5 Exposure in Periurban India by Integrating GPS, Wearable Camera, and Ambient and Personal Monitoring Data. Environ. Sci. Technol. 2018, 52, 13481–13490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, Q.; Huang, B. Satellite-Based Mapping of Daily High-Resolution Ground PM2.5 in China via Space-Time Regression Modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Fan, W.; Qin, K.; Cui, Y.; Li, D.; Bilal, M. Estimation of Hourly Ground-Level PM2.5 Concentration Based on Himawari-8 Apparent Reflectance. IEEE Trans. Geosci. Remote Sens. 2021, 59, 76–85. [Google Scholar] [CrossRef]
- Yue, G.; Gu, K.; Qiao, J. Effective and Efficient Photo-Based PM2.5 Concentration Estimation. IEEE Trans. Instrum. Meas. 2019, 68, 3962–3971. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, F.; Tian, R. A Deep Learning and Image-Based Model for Air Quality Estimation. Sci. Total Environ. 2020, 724, 138178. [Google Scholar] [CrossRef]
- Gu, K.; Qiao, J.; Li, X. Highly Efficient Picture-Based Prediction of PM2.5 Concentration. IEEE Trans. Ind. Electron. 2019, 66, 3176–3184. [Google Scholar] [CrossRef]
- Pudasaini, B.; Kanaparthi, M.; Scrimgeour, J.; Banerjee, N.; Mondal, S.; Skufca, J.; Dhaniyala, S. Estimating PM2.5 from Photographs. Atmos. Environ. X 2020, 5, 100063. [Google Scholar] [CrossRef]
- Liaw, J.-J.; Huang, Y.-F.; Hsieh, C.-H.; Lin, D.-C.; Luo, C.-H. PM2.5 Concentration Estimation Based on Image Processing Schemes and Simple Linear Regression. Sensors 2020, 20, 2423. [Google Scholar] [CrossRef] [PubMed]
- Babari, R.; Hautière, N.; Dumont, É.; Paparoditis, N.; Misener, J. Visibility Monitoring Using Conventional Roadside Cameras—Emerging Applications. Transp. Res. Part C Emerg. Technol. 2012, 22, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Qin, H. Image-Based Dedicated Methods of Night Traffic Visibility Estimation. Appl. Sci. 2020, 10, 440. [Google Scholar] [CrossRef] [Green Version]
- Koschmieder, H. Theorie Der Horizontalen Sichtweite. Beitr. Zur Phys. Der Freien Atmosphare 1924, 12, 33–53. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar]
- Jian, M.; Kun, L.; Han, Y.H. Image-based PM2.5 Estimation and its Application on Depth Estimation. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Rijal, N.; Gutta, R.T.; Cao, T.; Lin, J.; Bo, Q.; Zhang, J. Ensemble of Deep Neural Networks for Estimating Particulate Matter from Images. In Proceedings of the 2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 733–738. [Google Scholar]
- Eldering, A.; Hall, J.R.; Hussey, K.J.; Cass, G.R. Visibility Model Based on Satellite-Generated Landscape Data. Environ. Sci. Technol. 1996, 30, 361–370. [Google Scholar] [CrossRef]
- Groen, I.I.A.; Silson, E.H.; Baker, C.I. Contributions of Low- and High-Level Properties to Neural Processing of Visual Scenes in the Human Brain. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160102. [Google Scholar] [CrossRef] [Green Version]
- Landy, M.S.; Maloney, L.T.; Johnston, E.B.; Young, M. Measurement and Modeling of Depth Cue Combination: In Defense of Weak Fusion. Vis. Res. 1995, 35, 389–412. [Google Scholar] [CrossRef] [Green Version]
- Arcaro, M.J.; Honey, C.J.; Mruczek, R.E.; Kastner, S.; Hasson, U. Widespread Correlation Patterns of FMRI Signal across Visual Cortex Reflect Eccentricity Organization. eLife 2015, 4, e03952. [Google Scholar] [CrossRef] [Green Version]
- Grill-Spector, K.; Malach, R. The Human Visual Cortex. Annu. Rev. Neurosci. 2004, 27, 649–677. [Google Scholar] [CrossRef] [Green Version]
- Zavagno, D. Some New Luminance-Gradient Effects. Perception 1999, 28, 835–838. [Google Scholar] [CrossRef] [PubMed]
- Giesel, M.; Gegenfurtner, K.R. Color Appearance of Real Objects Varying in Material, Hue, and Shape. J. Vis. 2010, 10, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, J.; Dong, Y.; Su, H.; Yu, S.X. Learning Non-Lambertian Object Intrinsics Across ShapeNet Categories. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1685–1694. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Simoncelli, E.P. Structural Approaches to Image Quality Assessment. In Handbook of Image and Video Processing; Elsevier: Amsterdam, The Netherlands, 2005; pp. 961–974. ISBN 978-0-12-119792-6. [Google Scholar]
- Cozman, F.; Krotkov, E. Depth from Scattering. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997. [Google Scholar]
- Swinehart, D.F. The Beer–Lambert Law. J. Chem. Educ. 1962, 39, 3. [Google Scholar] [CrossRef]
- Zhu, Q.; Mai, J.; Shao, L. A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar]
- Wang, H.; Yuan, X.; Wang, X.; Zhang, Y.; Dai, Q. Real-Time Air Quality Estimation Based on Color Image Processing. In Proceedings of the 2014 IEEE Visual Communications and Image Processing Conference, Valletta, Malta, 7–10 December 2014; pp. 326–329. [Google Scholar]
- Zamir, A.R.; Sax, A.; Shen, W.; Guibas, L.; Malik, J.; Savarese, S. Taskonomy: Disentangling Task Transfer Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 3712–3722. [Google Scholar]
- Fattal, R. Single Image Dehazing. ACM Trans. Graph. 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Lalonde, J.-F.; Efros, A.; Narasimhan, S. Estimating Natural Illumination Conditions from a Single Outdoor Image. Int. J. Comput. Vis. 2012, 98, 123–145. [Google Scholar] [CrossRef]
- Chaudhury, K.; DiVerdi, S.; Ioffe, S. Auto-Rectification of User Photos. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 3479–3483. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Xiao, J.; Hays, J.; Ehinger, K.A.; Oliva, A.; Torralba, A. SUN Database: Large-Scale Scene Recognition from Abbey to Zoo. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3485–3492. [Google Scholar]
- Larson, S.M.; Cass, G.R.; Hussey, K.J.; Luce, F. Verification of Image Processing Based Visibility Models. Environ. Sci. Technol. 1988, 22, 629–637. [Google Scholar] [CrossRef]
- Gui, K.; Yao, W.; Che, H.; An, L.; Zheng, Y.; Li, L.; Zhao, H.; Zhang, L.; Zhong, J.; Wang, Y.; et al. Two Mega Sand and Dust Storm Events over Northern China in March 2021: Transport Processes, Historical Ranking and Meteorological Drivers. Atmos. Chem. Phys. Discuss. 2021; in review. [Google Scholar] [CrossRef]
- Bo, Q.; Yang, W.; Rijal, N.; Xie, Y.; Feng, J.; Zhang, J. Particle Pollution Estimation from Images Using Convolutional Neural Network and Weather Features. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 3433–3437. [Google Scholar]
- Liu, C.; Tsow, F.; Zou, Y.; Tao, N. Particle Pollution Estimation Based on Image Analysis. PLoS ONE 2016, 11, e0145955. [Google Scholar] [CrossRef]
- Rayleigh, L. XXXIV. On the Transmission of Light through an Atmosphere Containing Small Particles in Suspension, and on the Origin of the Blue of the Sky. Lond.Edinb. Dublin Philos. Mag. J. Sci. 1899, 47, 375–384. [Google Scholar] [CrossRef] [Green Version]
- Middleton, W.E.K. Vision through the Atmosphere. In Geophysik II/Geophysics II; Bartels, J., Ed.; Handbuch der Physik/Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 1957; pp. 254–287. ISBN 978-3-642-45881-1. [Google Scholar]
- Liu, X.; Song, Z.; Ngai, E.; Ma, J.; Wang, W. PM2:5 Monitoring Using Images from Smartphones in Participatory Sensing. In Proceedings of the 2015 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Hong Kong, 26 April–1 May 2015; pp. 630–635. [Google Scholar]
- Solar Light Company Solarmeter. Available online: https://www.solarmeter.com/ (accessed on 18 November 2021).
- Lalonde, J.-F.; Efros, A.; Narasimhan, S. Estimating Natural Illumination from a Single Outdoor Image. In Proceedings of the IEEE 12th International Conference on Computer Vision, ICCV 2009, Kyoto, Japan, 27 September–4 October 2009; p. 190. [Google Scholar]



| Atmospheric Index Combination | Outdoor Man-Made | Outdoor Natural | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 (Transportation) | C2 (Sports Fields) | C3 (Buildings) | C4 (Water) | C5 (Mountains) | C6 (Man-Made Elements) | |||||||
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| LTI-combination | 0.791 | 72.484 | 0.815 | 57.110 | 0.321 | 195.225 | 0.535 | 43.462 | 0.623 | 45.699 | 0.628 | 52.469 |
| LEI-combination | 0.529 | 111.053 | 0.527 | 91.582 | 0.857 | 63.792 | 0.261 | 58.540 | 0.383 | 54.595 | 0.558 | 56.355 |
| Selected combination | 0.830 | 64.420 | 0.871 | 47.761 | 0.872 | 58.112 | 0.669 | 36.129 | 0.678 | 44.048 | 0.789 | 39.239 |
| Numbers of photos | 314 | 915 | 849 | 502 | 107 | 258 | ||||||
| Name | Method | RMSE | MAE | Pearson r |
|---|---|---|---|---|
| Rijal et al. [19] | Deep learning based | 45.199 | 77.765 | 0.817 |
| Jian et al. [18] | 70.260 | 85.719 | 0.559 | |
| Gu et al. [11] | Image analysis and distribution based | 94.996 | 116.448 | 0.237 |
| Our proposed algorithm | Image analysis based | 29.896 | 50.523 | 0.923 |
| Dataset | Method | RMSE | Pearson r | R2 |
|---|---|---|---|---|
| Shanghai-1954 | SBFS [42] | 13.65 | 0.836 | 0.700 |
| Resnet [41] | 10.11 | 0.934 | 0.871 | |
| Resnet & weather [40] | 10.09 | 0.934 | 0.872 | |
| Our algorithm | 10.003 | 0.935 | 0.874 | |
| Beijing-1460 | VGG-16 [19] | 60.44 | 0.733 | 0.537 |
| Inception-V3 [19] | 64.32 | 0.681 | 0.464 | |
| Resnet-50 [19] | 53.63 | 0.792 | 0.627 | |
| Our algorithm | 48.969 | 0.831 | 0.691 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Wang, F.; Huang, B. Measuring PM2.5 Concentrations from a Single Smartphone Photograph. Remote Sens. 2022, 14, 2572. https://doi.org/10.3390/rs14112572
Yao S, Wang F, Huang B. Measuring PM2.5 Concentrations from a Single Smartphone Photograph. Remote Sensing. 2022; 14(11):2572. https://doi.org/10.3390/rs14112572
Chicago/Turabian StyleYao, Shiqi, Fei Wang, and Bo Huang. 2022. "Measuring PM2.5 Concentrations from a Single Smartphone Photograph" Remote Sensing 14, no. 11: 2572. https://doi.org/10.3390/rs14112572
APA StyleYao, S., Wang, F., & Huang, B. (2022). Measuring PM2.5 Concentrations from a Single Smartphone Photograph. Remote Sensing, 14(11), 2572. https://doi.org/10.3390/rs14112572