Machine-Learning for Mapping and Monitoring Shallow Coral Reef Habitats
Abstract
:1. Introduction
2. Machine-Learning Algorithms Applied to Coral Reef Benthic Mapping Using Multispectral Satellite Imagery
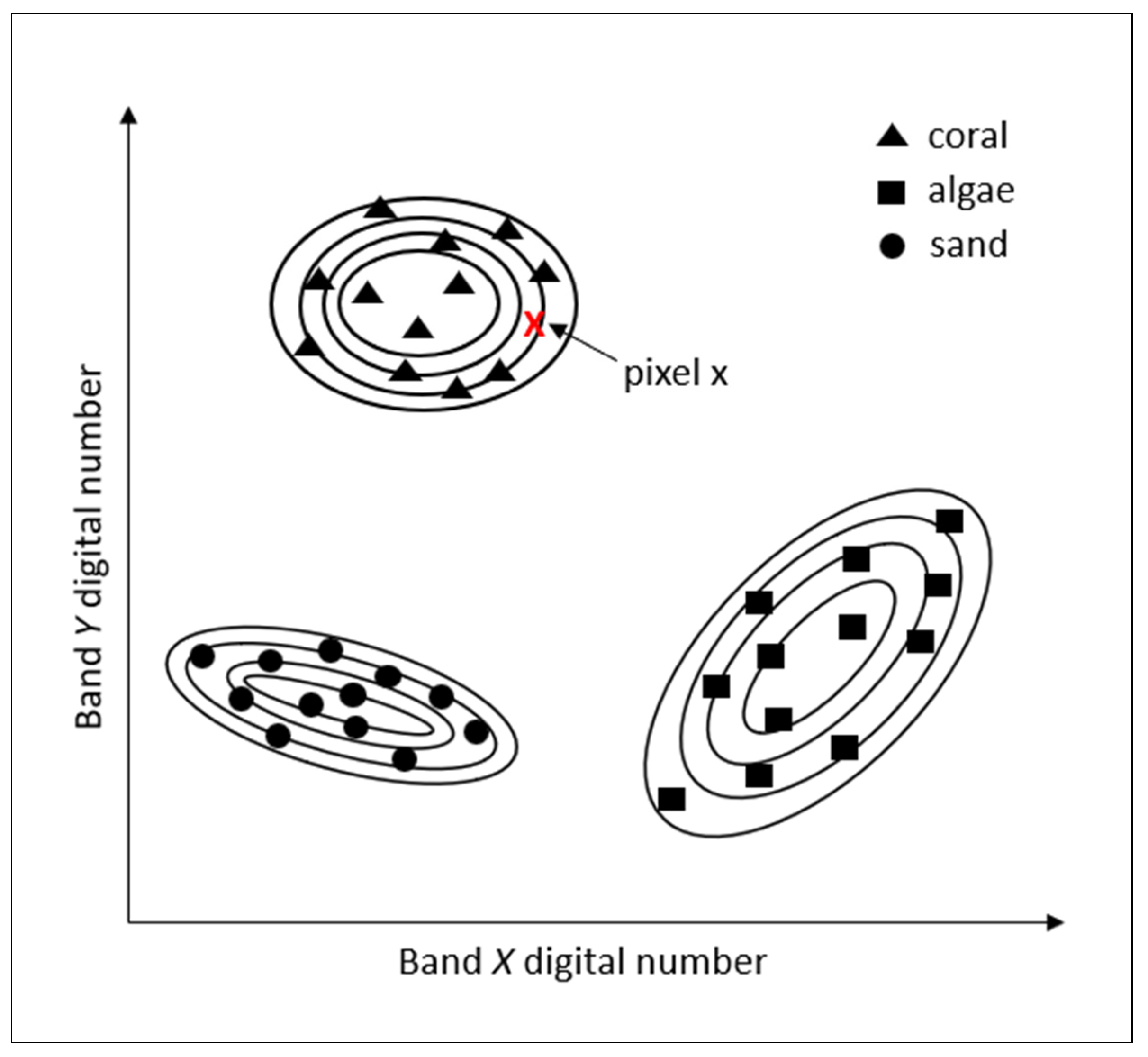
2.1. Pixel-Based Machine-Learning Classification Algorithms
| Authors | Sensor/Spatial Resolution | Pixel or Object-Based | Classification Algorithm(s) | Supervised or Unsupervised | Number of Benthic Habitat Classes | Accuracy (Overall Accuracy) |
|---|---|---|---|---|---|---|
| [39] | WorldView-3 (1.2 m). | Pixel-based. | SVM. | Supervised. | 15 | 79% |
| [37] | QuickBird (2.4 m). | Pixel-based. | MLC, MD, k-NN, Parallelepiped classification (PP), and Fisher (F); then ensemble. Classification using Majority Voting (MV), Simple Averaging (SA), and Mode Combination (MC). | Supervised. | 4 | 55% (MLC), 53% (MD), 54% (KNN), 41% (PP), 47% (F), 83% (MV), 71% (SA), and 68% (MC). |
| [8] | WorldView-2 (1.9 m). | Pixel-based. | MLC, RF. | Supervised. | 2–26 | 74.01–22.15% (mean MLC), 95.97–76.83% (mean RF). |
| [40] | PlanetScope (3.7 m). | Pixel-based. | RF. | Supervised. | 4 | 78% (Cemara Islands based on 500 trees), 61% (Gelang Island based on 500 trees); 79% (Cemara Islands based using Log and Entropy function), 61% (Geland Island using Square Root and Gini function). |
| [41] | Landsat-8 OLI (30 m). | Pixel-based. | Linear Discriminant Analysis (LDA). | Supervised. | 4 | 80% (Palmyara Atoll), 79% (Kingman Reef), 69% (Howland Island), 71% (Baker Island Atoll), and 74% (Combined). |
| [42] | Planet Dove (4.7 m). | Pixel-based. | ISODATA classification. | Unsupervised. | 8 | 63% |
| [38] | Landsat-8 (30 m). | Pixel-based. | MLC, SVM, ANN. | Supervised. | 4 | Lizard Island; 72% (ANN), 67% SVM, 67% MLC; Qeshm and Larak Islands; 58% (ANN), 68% (SVM), 66% (MLC). |
| [43] | IKONOS (4 m). | Pixel-based. | MLC. | Supervised. | 6 | 82% |
| [10] | QuickBird-2 (2.4 m) local. | Pixel-based. | MDM. | Supervised. | 21 | Suva site: 69% (photo transect), 65% (spot check). |
| [44] | IKONOS (4 m). | Pixel-based. | MLC. | Supervised. | 9 | 89% (Bawe) and 80% (Chumbe). |
| [45] | QuickBird (2.4 m). | Pixel-based. | MLC. | Supervised. | 6 | 67% (no water column correction), 89% (with water column correction. |
| [46] | Landsat-7 ETM+ (30 m). | Pixel-based. | Ensemble of hybrid SVM Classifiers. | Supervised. | 5 | 89% |
| [47] | QuickBird-2 (2.4 m), Landsat 5 TM (30 m). | Pixel-based. | MDM. | Supervised. | 10–21 | 25–62% |
| [48] | Landsat 5 TM (30 m). | Pixel-based. | MLC. | Supervised. | 7 | 76% |
| [7] | IKONOS (4 m). | Pixel-based. | MLC. | Supervised. | 4, 8, 13 | 75% (4 classes), ~65% (8 classes), and 50% (13 classes). |
| [49] | Landsat TM (30 m). | Pixel-based. | MLC followed by contextual editing. | Supervised. | 4, 8, and 13 | ~60%, ~40%, and ~25%, respectively. |
| [4] | Landsat TM (30 m). | Pixel-based. | MLC. | Supervised. | 4, 6, 9 | ~57% (4 classes), ~53% (6 classes), and ~50% (9 classes). |
Object-Based Image Analysis
| Authors | Sensor/Spatial Resolution | Pixel or Object-Based | Classification Algorithm(s) | Supervised or Unsupervised | Number of Benthic Habitat Classes | Accuracy (Overall Accuracy) |
|---|---|---|---|---|---|---|
| [58] | Sentinel-2 (10 m). | Object-based. | OBIA–RF followed by expert-driven membership rulesets. | Supervised. | 4 | 62% |
| [70] | Sentinel-2 (10 m). | Object-based. | Mean Texture Analysis followed by either RF or SVM. | Supervised. | 4 | 71% (RF, highest), 73 (SVM, highest). |
| [59] | Worldview-2 (1.9 m), Planet Dove (5 m), Sentinel-2 (10 m), Landsat-8 (15 m). | Pixel-based and object-based. | Pixel-based RF and OBIA–RF followed by expert-driven membership rulesets. | Supervised. | 8 | 78% (mean). |
| [17] | Landsat OLI (15 m). | Object-based. | OBIA followed by expert-driven membership rulesets. | Supervised. | 6 | 50% |
| [31] | WorldView-2 (1.9 m), Sentinel-2 (10 m). | Object-based. | LAPDANN. | Supervised. | 10 | 86% (trained/tested on same reef), 47% (trained/tested on data from Indian Ocean and Pacific Ocean simultaneously). |
| [32] | WorldView-2 (1.9 m), PlanetScope (3.7 m). | Object-based and pixel-based. | FCN–KNN, VGG16–FCN, DeepLab, SharpMask. | Supervised. | 9 | WorldView-2 imagery: 84% (FCN–KNN), 80% (VGG16–FCN), 81% (DeepLab), 80% (SharpMask); PlanetScope imagery: 73% (FCN–KNN), 73% (VGG16–FCN), 73% (DeepLab), 71% (SharpMask); Generalisation tests: 85% (FCN–KNN), 83% (VGG16–FCN), 78% (DeepLab), 82% (SharpMask). |
| [80] | WorldView-2 (1.9 m), Gaofen-2 (3.2 m). | Object-based. | CNN–SVM, CNN–RF, CNN, RF, SVM. | Supervised. | 4 | WorldView-2 data set 1: 92% (CNN–SVM), 91% (CNN–RF), 91% (CNN), 90% (RF), 89% (SVM); WorldView-2 data set 2: 86% (CNN_SVM), 85% (CNN–RF), 85% (CNN), 82% (RF), 84% (SVM) Gaofen-2 data set: 91% (CNN–SVM), 88% (CNN–RF), 89% (CNN), 87% (RF), 88% (SVM). |
| [33] | QuickBird (0.6 m) (benthic), GeoEye-1 (0.5 m) (seagrass). | Object-based. | CNN. | Supervised. | 7 benthic, 4 seagrass. | 90% (benthic), 91% (seagrass). |
| [67] | Sentinel-2 (10 m). | Object-based. | MD followed by post-classification filtering. | Supervised. | 17 (incl. 5 non-coral reef benthic classes (i.e., mangroves, beach). | 77% |
| [72] | WorldView-2 (1.9 m). | Object-based. | MLC, Neural Network (NN), SVM. | Supervised. | 5 | 86% (MLC), 87%(NN), 93% (SVM). |
| [15] | WorldView-2 (1.9–2.4 m). | Object-based. | OBIA followed by manual class assignment. | Expert-derived. | Atlantic sites: 7 (aggregated Benthic cover type and geomorphology classes (i.e., Fore Reef Sediment with Algae), Non-Atlantic sites: 16. | 81% (Atlantic sites), 90% (non-Atlantic sites). |
| [60] | WorldView-2 (1.9 m). | Object-based. | OBIA–RF, OBIA–Classification Tree Analysis (OBIA–CTA), OBIA–SVM. | Supervised. | 14 | 89% (RF), 78% (CTA), 76% (SVM). |
| [61] | Planet Dove (3 m). | Object-based. | OBIA–KNN. | Supervised. | 11 | 82% |
| [57] | GeoEye-1 (2 m). | Object-based. | OBIA and Jeffries–Matusita distance measure. | Supervised. | 175 | 72% |
| [21] | QuickBird-2 (2.4 m). | Object-based. | OBIA–KNN. | Supervised. | 7 | 62% |
| [68] | QuickBird (2.4 m). | Object-based. | Bag of Features (BOF) followed by either Bagging (BAG), KNN, or SVM then lastly a Weighted Majority Voting (WMV). | Supervised. | 4 | 80% (BAG), 81% (KNN), 86% (SVM), 89% (WMV). |
| [71] | WorldView-2 (1.9 m). | Object-based. | SVM. | Supervised. | 5 | 78% |
| [16] | Sentinel-2 (10 m). | Object-based. | OBIA with expert-driven membership rulesets. | Supervised. | 6 | 49% |
| [19] | Landsat 8 (15 m). | Object-based. | OBIA with expert-driven membership rulesets. | Supervised. | 5 | 33% |
| [69] | Landsat 7 ETM+ (30 m), Landsat 8 (30 m). | Object-based. | Seed pixel regional growing. | Supervised. | 3 coral reef benthic and 2 non-benthic (i.e., land and human habitats). | 75–99.7% based on 10 sites. |
| [20] | WorldView-2 (1.9 m). | Object-based. | OBIA with expert-driven membership rulesets. | Supervised. | 4 | 76% |
| [62] | WorldView-2 (1.9 m). | Object-based. | OBIA-multinomial logistic discrete choice models. | Supervised. | 8 benthic and 3 non-benthic (i.e., terrestrial vegetation). | 85% (Vanua Vatu site). |
| [63] | Landsat 8 OLI (30 m). | Object-based. | OBIA–SVM, OBIA–RT, OBIA–DT, OBIA–KNN, OBIA–Bayesian. | Supervised. | 7 | 73% (OBIA–SVM), 68% (OBIA–RT), 67% (OBIA–KNN), 66% (OBIA–Bayesian), and 56% (OBIA–DT). |
| [18] | QuickBird-2 (2.4 m), IKONOS (4 m). | Object-based. | OBIA with expert-driven membership rulesets. | Supervised. | 14–17 (individual reefs), 20–30 (reef systems). | 52–75%. |
| [9] | QuickBird-2 (2.4 m). | Pixel-based and object based. | OBIA with expert-driven membership rulesets; pixel-based MDM. | Supervised. | Heron Reef: 13 Ngderack Reef: 11 Navakavu Reef: 17. | 78% (Heron Reef, object-based), 52% (Ngderack Reef, object-based), 65%, 57% (Navakavu Reef, object-based and pixel-based, respectively). |
| [64] | QuickBird-2 (2.4 m), IKONOS (4 m). | Object-based. | OBIA with expert-driven membership rulesets. | Supervised | 22 benthic and 3 non-benthic (i.e., cloud). | 67%. |
| [6] | QuickBird (0.6 m Pan-sharpened). | Pixel-based and object-based. | Pixel-based MLC and contextual editing; OBIA–NN. | Supervised. | 5, 7, and 11. | 59–77% (MLC), 61–76% (contextual editing), and 81–90% (OBIA–NN). |
| [66] | Landsat TM (30 m). | Object-based. | Unsupervised ISODATA Classification. | Unsupervised. | 7 | 74% |
| [5] | IKONOS (4 m), Landsat 7 ETM+ (30 m). | Object-based (unsupervised segments and ground-truthed polygons). | Unsupervised segmentation followed by expert class assignment (applied to 2 reefs); MLC (applied to 7 reefs). | Unsupervised (2 reefs) and supervised (7 reefs). | 4–5, 7–8, 9–11, >13. | 77% (4–5 classes), 71% (7–8 classes), 65% (9–11 classes), and 53% (> 13 classes). |
| [65] | IKONOS (4 m). | Object-based. | MLC. | Supervised. | 5 | 90% (Half Moon Bay), 89% (Tabyana Bay). |
2.2. Convolutional Neural Networks
2.2.1. Fully Convolutional Neural Networks
2.2.2. Convolutional and Fully Convolutional Neural Networks Applied to Coral Reef Benthic Composition Mapping
2.3. Change Detection
2.3.1. Coral Reef Benthic Change Detection Methods
| Authors | Pixel or Object-Based | Time-Series | Classification Method | Supervised or Unsupervised | Number of Classes Mapped | Change Detection Method |
|---|---|---|---|---|---|---|
| [121] | Pixel-based. | 2015–2016 | Radiometric normalization with pseudo invariant features (PIFs), multi-temporal depth invariant indices (DII), followed by SVM. | Supervised. | 1 (bleached coral). | PCCCD. |
| [122] | Object-based. | 2017–2019 | Unsupervised ISODATA classification. | Unsupervised. | 4 | PCCCD. |
| [23] | Pixel-based. | 2000–2014, 2002–2014, 2001–2015 | Pixel-based-SVM. | Supervised. | 2 | PCCCD. |
| [112] | Pixel-based. | 2009–2015 | Spectral linear unmixing using IDL CONSTRAINED_MIN optimization algorithm followed by assigning class thresholds. | Supervised. | 13 | PCCCD. |
| [113] | Object-based. | 2001–2015 | Manual polygon delineation. | Supervised. | 8 (habitat scenario trajectories). | PCCCD. |
| [114] | Object-based | 2014–2016 | Unsupervised IRMAD to detect areas of change, OBIA–RF to classify classes, overlaying images to perform supervised change detection. | Unsupervised and Supervised. | 10 habitat classes and 5 classes of change type. | PCCCD. |
| [115] | Object-based (multiresolution segmentation) and pixel-based. | 2013–2015 | OBIA–RF change prediction, pixel-based-RF change prediction. | Supervised. | 5 change types (i.e., reef sediments extension). | MT-OBCD. |
| [123] | Pixel-based. | 1994–2014 | Unsupervised Iterative self-organizing class analysis (ISOCLASS) followed by supervised reclassification based on visual interpretation. | Unsupervised and Supervised. | 5 | PCCCD. |
| [110] | Pixel-based. | 2001–2014 | SVM | Supervised. | 11 | PCCCD. |
| [22] | Pixel-based. | 1987–2013 | ISODATA clustering followed by unsupervised k-means classification; MLC. | Unsupervised and Supervised. | 10 unsupervised, 5 supervised. | PCCCD. |
| [124] | Pixel-based. | 2005–2008 | MLC for mapping 5 classes then ‘differences in reflectance values between two images within the coral classes were used to detect bleached corals. | Supervised. | 5 | PCCCD. |
| [24] | Object-based (manually delineated polygons). | 1972–2007 | Photo-interpretation based on manual polygon delineation. | Supervised. | 3, 19, and 42 (based on level 1, 2, and 3 maps). | PCCCD. |
| [105] | Pixel-based and object-based. | 2002–2004 | Post-cyclone coral community structure maps: Photo-interpretation based on manual polygon delineation, pixel-based MLC, OBIA-MLC; Pre-cyclone community maps: post-cyclone coral community structure classes were used to label pre-cyclone polygons based on consistent colour and texture visible on the images, and also accounting for proximity [105].’ | Supervised. | 20 | PCCCD. |
| [111] | Pixel-based. | 1991–2002 | Parallelepiped classification. | Supervised. | 6 | PCCCD. |
| [14] | Object-based (manually delineated polygons). | 1973–2007 | Photo-interpretation based on manual polygon delineation. | Supervised. | 15 | PCCCD. |
| [106] | Pixel-based. | 1984–2002 | Mahalanobis distance classification. | Supervised. | 4 | PCCCD. |
| [116] | Object-based (timed automata model), Pixel-based (minimum distance classification). | 2002–2004 | A combined generic timed automata model of reef habitat trajectories and classified remotely sensed imagery based on MD classification. | Supervised. | 36 (habitat classes). | PCCCD, Modelling (generic timed automata). |
| [119] | Pixel-based. | 1990–2001 | Unsupervised ISODATA classification followed by calculating the median coefficient of variation (COV). Images were then segmented by habitat to create habitat masks and also segmented by representative quadrants. The median COV for each habitat and quadrat were calculated before performing a Kruskall–Wallis nonparametric test to determine whether differences between the median COV values were significant at the 0.05 level. | Unsupervised and Supervised. | 6 class habitat map, test for significant differences. | PCCCD, statistical analysis. |
| [125] | Pixel-based. | 1987–2000 | Multi-component change detection: image differencing to determine areas of significant change followed by MLC. Images were then ‘combined’ to create a ‘from-to change map.’ | Supervised. | 4 benthic classes each with 6 possible change types. | PCCCD. |
| [126] | Pixel-based. | 1991–2003, 2000–2001 | Unsupervised K-means clustering followed by PCA. | Unsupervised. | 3 | PCCCD. |
| [117] | Pixel-based. | 1984–2000 | Radiative transfer simulation and also an image normalisation method [127] followed by digital number comparison. | Supervised. | 2 (radiative transfer simulation: bleached coral, healthy coral), 2 (normalisation method: slightly or non-bleached, severely bleached). | PCCCD (normalisation method), Modelling (radiative transfer simulation). |
| [109] | Pixel-based. | 1984–2000 | Mahalanobis Distance classifier. | Supervised. | 4 | PCCCD. |
| [108] | Pixel-based. | 1981–2000 | Mahalanobis Distance classifier. | Supervised. | 4 | PCCCD. |
| [128] | Pixel-based. | 1998 (February)–1998 (August) | Image differencing based on mean (3 × 3) filtering, PCA, difference between local variation calculated as a standard deviation in a 3 × 3 neighbourhood. | Supervised. | 1 (bleaching detection). | PCCCD. |
| [118] | Pixel-based. | 1994–1996 | Getis Statistic. | Supervised. | Test for significant difference. | PCCCD—Spatial autocorrelation. |
| [107] | Pixel-based. | 1984–1999 | Mahalanobis Distance classification. | Supervised. | 4 | PCCCD. |
2.3.2. Recurrent Neural Networks Applied to Land Cover Change Detection Using Multispectral Satellite Imagery
3. Conclusions
3.1. Coral Reef Benthic Mapping
3.1.1. Coral Reef Benthic Change Detection
3.1.2. Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hedley, J.D.; Roelfsema, C.M.; Chollett, I.; Harborne, A.R.; Heron, S.F.; Weeks, S.; Skirving, W.J.; Strong, A.E.; Eakin, C.M.; Christensen, T.R.L.; et al. Remote Sensing of Coral Reefs for Monitoring and Management: A Review. Remote Sens. 2016, 8, 118. [Google Scholar] [CrossRef] [Green Version]
- Caras, T.; Hedley, J.; Karnieli, A. Implications of sensor design for coral reef detection: Upscaling ground hyperspectral imagery in spatial and spectral scales. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 68–77. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Atkinson, M.J.; Andréfouët, S. Spectral reflectance of coral reef bottom-types worldwide and implications for coral reef remote sensing. Remote Sens. Environ. 2003, 85, 159–173. [Google Scholar] [CrossRef]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. Coral reef habitat mapping: How much detail can remote sensing provide? Mar. Biol. 1997, 130, 193–202. [Google Scholar] [CrossRef]
- Andréfouët, S.; Kramer, P.; Torres-Pulliza, D.; Joyce, K.; Hochberg, E.J.; Garza-Pérez, R.; Mumby, P.J.; Riegl, B.; Yamano, H.; White, W.H.; et al. Multi-site evaluation of IKONOS data for classification of tropical coral reef environments. Remote Sens. Environ. 2003, 88, 128–143. [Google Scholar] [CrossRef]
- Benfield, S.L.; Guzman, H.M.; Mair, J.M.; Young, J.A.T. Mapping the distribution of coral reefs and associated sublittoral habitats in Pacific Panama: A comparison of optical satellite sensors and classification methodologies. Int. J. Remote Sens. 2007, 28, 5047–5070. [Google Scholar] [CrossRef]
- Mumby, P.J.; Edwards, A.J. Mapping marine environments with IKONOS imagery: Enhanced spatial resolution can deliver greater thematic accuracy. Remote Sens. Environ. 2002, 82, 248–257. [Google Scholar] [CrossRef]
- Wicaksono, P.; Aryaguna, P.A. Analyses of inter-class spectral separability and classification accuracy of benthic habitat mapping using multispectral image. Remote Sens. Appl. Soc. Environ. 2020, 19, 100335. [Google Scholar] [CrossRef]
- Phinn, S.R.; Roelfsema, C.M.; Mumby, P.J. Multi-scale, object-based image analysis for mapping geomorphic and ecological zones on coral reefs. Int. J. Remote Sens. 2012, 33, 3768–3797. [Google Scholar] [CrossRef]
- Roelfsema, C. Integrating field data with high spatial resolution multispectral satellite imagery for calibration and validation of coral reef benthic community maps. J. Appl. Remote Sens. 2010, 4, 043527. [Google Scholar] [CrossRef] [Green Version]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Hochberg, E.; Andrefouet, S.; Tyler, M. Sea surface correction of high spatial resolution ikonos images to improve bottom mapping in near-shore environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Chavez, P.S. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Scopélitis, J.; Andréfouët, S.; Phinn, S.; Chabanet, P.; Naim, O.; Tourrand, C.; Done, T. Changes of coral communities over 35 years: Integrating in situ and remote-sensing data on Saint-Leu Reef (la Réunion, Indian Ocean). Estuar. Coast. Shelf Sci. 2009, 84, 342–352. [Google Scholar] [CrossRef]
- Purkis, S.J.; Gleason, A.C.R.; Purkis, C.R.; Dempsey, A.C.; Renaud, P.G.; Faisal, M.; Saul, S.; Kerr, J.M. High-resolution habitat and bathymetry maps for 65,000 sq. km of Earth’s remotest coral reefs. Coral Reefs 2019, 38, 467–488. [Google Scholar] [CrossRef] [Green Version]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.; Barrilero, O.; Laporte, J.; Koetz, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Roelfsema, C.M.; Kovacs, E.M.; Ortiz, J.C.; Callaghan, D.P.; Hock, K.; Mongin, M.; Johansen, K.; Mumby, P.J.; Wettle, M.; Ronan, M.; et al. Habitat maps to enhance monitoring and management of the Great Barrier Reef. Coral Reefs 2020, 39, 1039–1054. [Google Scholar] [CrossRef]
- Roelfsema, C.; Phinn, S.; Jupiter, S.; Comley, J.; Albert, S. Mapping coral reefs at reef to reef-system scales, 10s–1000s km2, using object-based image analysis. Int. J. Remote Sens. 2013, 34, 6367–6388. [Google Scholar] [CrossRef]
- Roelfsema, C.; Kovacs, E.; Ortiz, J.C.; Wolff, N.; Callaghan, D.; Wettle, M.; Ronan, M.; Hamylton, S.; Mumby, P.; Phinn, S. Coral reef habitat mapping: A combination of object-based image analysis and ecological modelling. Remote Sens. Environ. 2018, 208, 27–41. [Google Scholar] [CrossRef]
- Selgrath, J.C.; Roelfsema, C.; Gergel, S.E.; Vincent, A.C.J. Mapping for coral reef conservation: Comparing the value of participatory and remote sensing approaches. Ecosphere 2016, 7, e01325. [Google Scholar] [CrossRef] [Green Version]
- Roelfsema, C.; Kovacs, E.; Roos, P.; Terzano, D.; Lyons, M.; Phinn, S. Use of a semi-automated object based analysis to map benthic composition, Heron Reef, Southern Great Barrier Reef. Remote Sens. Lett. 2018, 9, 324–333. [Google Scholar] [CrossRef]
- El-Askary, H.; El-Mawla, S.H.A.; Li, J.; El-Hattab, M.; El-Raey, M. Change detection of coral reef habitat using Landsat-5 TM, Landsat 7 ETM+ and Landsat 8 OLI data in the Red Sea (Hurghada, Egypt). Int. J. Remote Sens. 2014, 35, 2327–2346. [Google Scholar] [CrossRef]
- Gapper, J.J.; El-Askary, H.; Linstead, E.; Piechota, T. Coral Reef Change Detection in Remote Pacific Islands Using Support Vector Machine Classifiers. Remote Sens. 2019, 11, 1525. [Google Scholar] [CrossRef] [Green Version]
- Scopélitis, J.; Andréfouët, S.; Phinn, S.; Done, T.; Chabanet, P. Coral colonisation of a shallow reef flat in response to rising sea level: Quantification from 35 years of remote sensing data at Heron Island, Australia. Coral Reefs 2011, 30, 951–965. [Google Scholar] [CrossRef]
- Planet Labs. 2021. Available online: https://www.planet.com/products/monitoring/ (accessed on 10 November 2021).
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 2. [Google Scholar]
- Guirado, E.; Tabik, S.; Alcaraz-Segura, D.; Cabello, J.; Herrera, F. Deep-learning Versus OBIA for Scattered Shrub Detection with Google Earth Imagery: Ziziphus Lotus as Case Study. Remote Sens. 2017, 9, 1220. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Abd-Elrahman, A.; Morton, J.; Wilhelm, V.L. Comparing fully convolutional networks, random forest, support vector machine, and patch-based deep convolutional neural networks for object-based wetland mapping using images from small unmanned aircraft system. GISci. Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
- Zhang, D.; Pan, Y.; Zhang, J.; Hu, T.; Zhao, J.; Li, N.; Chen, Q. A generalized approach based on convolutional neural networks for large area cropland mapping at very high resolution. Remote Sens. Environ. 2020, 247, 111912. [Google Scholar] [CrossRef]
- Akbari Asanjan, A.; Das, K.; Li, A.; Chirayath, V.; Torres-Perez, J.; Sorooshian, S. Learning Instrument Invariant Characteristics for Generating High-Resolution Global Coral Reef Maps. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, 23–27 August 2020. [Google Scholar]
- Li, A.S.; Chirayath, V.; Segal-Rozenhaimer, M.; Torres-Perez, J.L.; Bergh, J.V.D. NASA NeMO-Net’s Convolutional Neural Network: Mapping Marine Habitats with Spectrally Heterogeneous Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5115–5133. [Google Scholar] [CrossRef]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Semiautomated Mapping of Benthic Habitats and Seagrass Species Using a Convolutional Neural Network Framework in Shallow Water Environments. Remote Sens. 2020, 12, 4002. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning Spectral-Spatial-Temporal Features via a Recurrent Convolutional Neural Network for Change Detection in Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 924–935. [Google Scholar] [CrossRef] [Green Version]
- Goodman, J.A.; Purkis, S.; Phinn, S.R. Coral Reef Remote Sensing. A Guide for Mapping, Monitoring and Management; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1. [Google Scholar]
- Hossain, M.S.; Muslim, A.M.; Nadzri, M.I.; Teruhisa, K.; David, D.; Khalil, I.; Mohamad, Z. Can ensemble techniques improve coral reef habitat classification accuracy using multispectral data? Geocarto Int. 2020, 35, 1214–1232. [Google Scholar] [CrossRef]
- Chegoonian, A.M.; Mokhtarzade, M.; Zoej, M.J.V. A comprehensive evaluation of classification algorithms for coral reef habitat mapping: Challenges related to quantity, quality, and impurity of training samples. Int. J. Remote Sens. 2017, 38, 4224–4243. [Google Scholar] [CrossRef]
- da Silveira, C.B.L.; Strenzel, G.M.R.; Maida, M.; Gaspar, A.L.B.; Ferreira, B.P. Coral Reef Mapping with Remote Sensing and Machine Learning: A Nurture and Nature Analysis in Marine Protected Areas. Remote Sens. 2021, 13, 2907. [Google Scholar] [CrossRef]
- Wicaksono, P.; Lazuardi, W. Random Forest Classification Scenarios for Benthic Habitat Mapping using Planetscope Image. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2019. [Google Scholar] [CrossRef]
- Gapper, J.J.; El-Askary, H.; Linstead, E.; Piechota, T. Evaluation of Spatial Generalization Characteristics of a Robust Classifier as Applied to Coral Reef Habitats in Remote Islands of the Pacific Ocean. Remote Sens. 2018, 10, 1774. [Google Scholar] [CrossRef] [Green Version]
- Asner, G.P.; Martin, R.E.; Mascaro, J. Coral reef atoll assessment in the South China Sea using Planet Dove satellites. Remote Sens. Ecol. Conserv. 2017, 3, 57–65. [Google Scholar] [CrossRef]
- Zapata-Ramírez, P.A.; Blanchon, P.; Olioso, A.; Hernandez-Nuñez, H.; Sobrino, J.A. Accuracy of IKONOS for mapping benthic coral-reef habitats: A case study from the Puerto Morelos Reef National Park, Mexico. Int. J. Remote Sens. 2012, 34, 3671–3687. [Google Scholar] [CrossRef]
- Knudby, A.; LeDrew, E.; Brenning, A. Predictive mapping of reef fish species richness, diversity and biomass in Zanzibar using IKONOS imagery and machine-learning techniques. Remote Sens. Environ. 2010, 114, 1230–1241. [Google Scholar] [CrossRef]
- Nurlidiasari, M.; Budiman, S. Mapping Coral Reef Habitat with and without Water Column Correction Using Quickbird Image. Int. J. Remote Sens. Earth Sci. (IJReSES) 2010, 2, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Henriques, A.P.; Neto, A.D.D.; Amaral, R.F. Classification of multispectral images in coral environments using a hybrid of classifier ensembles. Neurocomputing 2010, 73, 1256–1264. [Google Scholar] [CrossRef]
- Roelfsema, C.; Phinn, S. Evaluating eight field and remote sensing approaches for mapping the benthos of three different coral reef environments in Fiji. Proc. Remote Sens. Inland Coast. Ocean. Waters 2008, 7150, 71500. [Google Scholar] [CrossRef] [Green Version]
- Purkis, S.J.; Pasterkamp, R. Integrating in situ reef-top reflectance spectra with Landsat TM imagery to aid shallow-tropical benthic habitat mapping. Coral Reefs 2004, 23, 5–20. [Google Scholar] [CrossRef]
- Mumby, P.J.; Clark, C.D.; Green, E.P.; Edwards, A.J. Benefits of water column correction and contextual editing for mapping coral reefs. Int. J. Remote Sens. 1998, 19, 203–210. [Google Scholar] [CrossRef]
- Blaschke, T.; Lang, S.; Lorup, E.; Strobl, J.; Zeil, P. Object-Oriented Image Processing in an Integrated GIS/Remote Sensing Environment and Perspectives for Environmental Applications. Environ. Inf. Plan. Politics Public 2000, 2, 555–570. [Google Scholar]
- Blaschke, T. Object Based Image Analysis for Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Brodrick, P.G.; Davies, A.B.; Asner, G.P. Uncovering Ecological Patterns with Convolutional Neural Networks. Trends Ecol. Evol. 2019, 34, 734–745. [Google Scholar] [CrossRef]
- Hay, G.J.; Castilla, G. Geographic Object-Based Image Analysis (GEOBIA): A new name for a new discipline. In Object-Based Image Analysis; Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2008; pp. 75–89. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J. Object-Oriented Image Analysis and Scale-Space: Theory and Methods for Modeling and Evaluating Multiscale Landscape Structure. Int. Arch. Photogramm. Remote Sens. 2001, 34, 22–29. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Kettig, R.L.; Landgrebe, D.A. Classification of Multispectral Image Data by Extraction and Classification of Homogeneous Objects. IEEE Trans. Geosci. Electron. 1976, 14, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Ampou, E.E.; Ouillon, S.; Andréfouët, S. Challenges in rendering Coral Triangle habitat richness in remotely sensed habitat maps: The case of Bunaken Island (Indonesia). Mar. Pollut. Bull. 2018, 131, 72–82. [Google Scholar] [CrossRef]
- Roelfsema, C.M.; Lyons, M.B.; Castro-Sanguino, C.; Kovacs, E.M.; Callaghan, D.; Wettle, M.; Markey, K.; Borrego-Acevedo, R.; Tudman, P.; Roe, M.; et al. How Much Shallow Coral Habitat Is There on the Great Barrier Reef? Remote Sens. 2021, 13, 4343. [Google Scholar] [CrossRef]
- Lyons, M.B.; Roelfsema, C.; Kennedy, E.; Kovacs, E.M.; Borrego-Acevedo, R.; Markey, K.; Roe, M.; Yuwono, D.M.; Harris, D.L.; Phinn, S.R.; et al. Mapping the world’s coral reefs using a global multiscale earth observation framework. Remote Sens. Ecol. Conserv. 2020, 6, 557–568. [Google Scholar] [CrossRef] [Green Version]
- Wicaksono, P.; Aryaguna, P.A.; Lazuardi, W. Benthic Habitat Mapping Model and Cross Validation Using Machine-Learning Classification Algorithms. Remote Sens. 2019, 11, 1279. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Schill, S.R.; Knapp, D.E.; Asner, G.P. Object-Based Mapping of Coral Reef Habitats Using Planet Dove Satellites. Remote Sens. 2019, 11, 1445. [Google Scholar] [CrossRef] [Green Version]
- Saul, S.; Purkis, S. Semi-Automated Object-Based Classification of Coral Reef Habitat using Discrete Choice Models. Remote Sens. 2015, 7, 15894–15916. [Google Scholar] [CrossRef] [Green Version]
- Wahidin, N.; Siregar, V.P.; Nababan, B.; Jaya, I.; Wouthuyzen, S. Object-based Image Analysis for Coral Reef Benthic Habitat Mapping with Several Classification Algorithms. Procedia Environ. Sci. 2015, 24, 222–227. [Google Scholar] [CrossRef] [Green Version]
- Roelfsema, C.; Phinn, S.; Jupiter, S.; Comley, J.; Beger, M.; Paterson, E. The application of object based analysis of high spatial resolution imagery for mapping large coral reef systems in the West Pacific at geomorphic and benthic community spatial scales. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 15–30 July 2010. [Google Scholar] [CrossRef]
- Maeder, J.; Narumalani, S.; Rundquist, D.C.; Perk, R.L.; Schalles, J.; Hutchins, K.; Keck, J. Classifying and Mapping General Coral-Reef Structure Using Ikonos Data. Photogramm. Eng. Remote Sens. 2002, 68, 1297–1306. [Google Scholar]
- Call, K.A.; Hardy, J.T.; Wallin, D.O. Coral reef habitat discrimination using multivariate spectral analysis and satellite remote sensing. Int. J. Remote Sens. 2003, 24, 2627–2639. [Google Scholar] [CrossRef]
- Mateos-Molina, D.; Antonopoulou, M.; Baldwin, R.; Bejarano, I.; Burt, J.A.; García-Charton, J.A.; Al-Ghais, S.M.; Walgamage, J.; Taylor, O.J. Applying an integrated approach to coastal marine habitat mapping in the north-western United Arab Emirates. Mar. Environ. Res. 2020, 161, 105095. [Google Scholar] [CrossRef]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Assessment of Machine Learning Algorithms for Automatic Benthic Cover Monitoring and Mapping Using Towed Underwater Video Camera and High-Resolution Satellite Images. Remote Sens. 2018, 10, 773. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.S.; Bujang, J.S.; Zakaria, M.H.; Hashim, M. Marine and human habitat mapping for the Coral Triangle Initiative region of Sabah using Landsat and Google Earth imagery. Mar. Policy 2016, 72, 176–191. [Google Scholar] [CrossRef]
- Lazuardi, W.; Wicaksono, P.; Marfai, M.A. Remote sensing for coral reef and seagrass cover mapping to support coastal management of small islands. IOP Conf. Ser. Earth Environ. Sci. 2021, 686, 012031. [Google Scholar] [CrossRef]
- Kabiri, K.; Rezai, H.; Moradi, M. Mapping of the corals around Hendorabi Island (Persian Gulf), using WorldView-2 standard imagery coupled with field observations. Mar. Pollut. Bull. 2018, 129, 266–274. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Liu, Z.; Zhu, J.; Lu, X.; Liu, Q. Classification of Coral Reef Benthos around Ganquan Island Using WorldView-2 Satellite Imagery. J. Coast. Res. 2019, 93, 466–474. [Google Scholar] [CrossRef]
- Arbiol, R.; Zhang, Y.; Palà, V. Advanced Classification Techniques: A Review; Revista Catalana de Geografia: Enschede, The Netherlands, 2006; pp. 292–296. [Google Scholar]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J. Discriminatory Analysis Nonparametric Discrimination: Small Sample Performance; Project No. 21-49-004, Report No. 11, Contract No. AF 41(129)-31; USAF School of Aviation: Randolph Field, TX, USA, 1952. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Bhattacharya, G.; Ghosh, K.; Chowdhury, A.S. KNN Classification with an Outlier Informative Distance Measure. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2017; Volume 10597. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Shelter Island, NY, USA, 2017. [Google Scholar]
- Wan, J.; Ma, Y. Multi-scale Spectral-Spatial Remote Sensing Classification of Coral Reef Habitats Using CNN–SVM. J. Coast. Res. 2020, 102, 11–20. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. Springer Series in Statistics the Elements of Statistical Learning; Springer: New York, NY, USA, 2009; Volume 27. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef] [Green Version]
- Kleinberg, E.M. Stochastic discrimination. Ann. Math. Artif. Intell. 1990, 1, 207–239. [Google Scholar] [CrossRef]
- Kleinberg, E.M. An overtraining-resistant stochastic modeling method for pattern recognition. Ann. Stat. 1996, 24, 2319–2349. [Google Scholar] [CrossRef]
- Kleinberg, E.M. On the algorithmic implementation of stochastic discrimination. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 473–490. [Google Scholar] [CrossRef]
- Deng, Z.; Sun, H.; Zhou, S.; Zhao, J.; Lei, L.; Zou, H. Multi-scale object detection in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2018, 145, 3–22. [Google Scholar] [CrossRef]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks. arXiv 2015, arXiv:1508.00092. [Google Scholar]
- Wagner, F.H.; Sanchez, A.; Tarabalka, Y.; Lotte, R.G.; Ferreira, M.P.; Aidar, M.P.; Gloor, E.; Phillips, O.L.; Aragao, L.E. Using the U-net convolutional network to map forest types and disturbance in the Atlantic rainforest with very high resolution images. Remote Sens. Ecol. Conserv. 2019, 5, 360–375. [Google Scholar] [CrossRef] [Green Version]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the ICML 2010—Proceedings, 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. Proc. J. Mach. Learn. Res. 2011, 15, 315–323. [Google Scholar]
- Cireşan, D.C.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 4. [Google Scholar]
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning Hierarchical Features for Scene Labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef] [Green Version]
- Pinheiro, P.O.; Collobert, R. Recurrent Convolutional Neural Networks for Scene Labeling. In Proceedings of the 31st International Conference on Machine Learning, ICML 2014, Beijing, China, 21–26 June 2014; Volume 1. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9351. [Google Scholar]
- Flood, N.; Watson, F.; Collett, L. Using a U-net convolutional neural network to map woody vegetation extent from high resolution satellite imagery across Queensland, Australia. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101897. [Google Scholar] [CrossRef]
- Stoian, A.; Poulain, V.; Inglada, J.; Poughon, V.; Derksen, D. Land Cover Maps Production with High Resolution Satellite Image Time Series and Convolutional Neural Networks: Adaptations and Limits for Operational Systems. Remote Sens. 2019, 11, 1986. [Google Scholar] [CrossRef] [Green Version]
- Clark, A.; McKechnie, J. Detecting Banana Plantations in the Wet Tropics, Australia, Using Aerial Photography and U-Net. Appl. Sci. 2020, 10, 2017. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2016; Volume 2016-December. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation. In Proceedings of the Proceedings—30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–27 July 2017; Volume 2017-January. [Google Scholar]
- Kemker, R.; Salvaggio, C.; Kanan, C. Algorithms for semantic segmentation of multispectral remote sensing imagery using deep learning. ISPRS J. Photogramm. Remote Sens. 2018, 145, 60–77. [Google Scholar] [CrossRef] [Green Version]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Denton, E.; Chintala, S.; Szlam, A.; Fergus, R. Deep Generative Image Models Using a Laplacian Pyramid of Adversarial Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 2015-January. [Google Scholar]
- Scopélitis, J.; Andréfouët, S.; Phinn, S.; Arroyo, L.; Dalleau, M.; Cros, A.; Chabanet, P. The next step in shallow coral reef monitoring: Combining remote sensing and in situ approaches. Mar. Pollut. Bull. 2010, 60, 1956–1968. [Google Scholar] [CrossRef] [PubMed]
- Palandro, D.A.; Andréfouët, S.; Hu, C.; Hallock, P.; Müller-Karger, F.E.; Dustan, P.; Callahan, M.K.; Kranenburg, C.; Beaver, C.R. Quantification of two decades of shallow-water coral reef habitat decline in the Florida Keys National Marine Sanctuary using Landsat data (1984–2002). Remote Sens. Environ. 2008, 112, 3388–3399. [Google Scholar] [CrossRef]
- Palandro, D.; Andrefouet, S.; Muller-Karger, F.; Dustan, P. Coral reef change detection using Landsats 5 and 7: A case study using Carysfort Reef in the Florida Keys. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Sydney, NSW, Australia, 9–13 July 2001; Volume 2, pp. 625–627. [Google Scholar] [CrossRef]
- Palandro, D.; Andréfouët, S.; Dustan, P.; Muller-Karger, F.E. Change detection in coral reef communities using Ikonos satellite sensor imagery and historic aerial photographs. Int. J. Remote Sens. 2003, 24, 873–878. [Google Scholar] [CrossRef] [Green Version]
- Palandro, D.; Andréfouët, S.; Muller, P.H.; Dustan, P.; Hu, C.; Hallock, P. Detection of changes in coral reef communities using Landsat-5 TM and Landsat-7 ETM+ data. Can. J. Remote Sens. 2003, 29, 201–209. [Google Scholar] [CrossRef]
- Iovan, C.; Ampou, E.; Andrefouet, S.; Ouillon, S.; Gaspar, P. Change Detection of Coral Reef Habitats from Multi-Temporal and Multi-Source Satellite Imagery in Bunaken, Indonesia. In Proceedings of the 2015 8th International Workshop on the Analysis of Multitemporal Remote Sensing Images, Multi-Temp, Annecy, France, 22–24 July 2015. [Google Scholar]
- Nurlidiasari, M.; Budiman, S. Coral Reef Habitat Changing Assessment of Derawan Islands, East Kalimantan, Using Remote Sensing Data. Int. J. Remote Sens. Earth Sci. (IJReSES) 2010, 2, 32–44. [Google Scholar] [CrossRef] [Green Version]
- Bajjouk, T.; Mouquet, P.; Ropert, M.; Quod, J.-P.; Hoarau, L.; Bigot, L.; Le Dantec, N.; Delacourt, C.; Populus, J. Detection of changes in shallow coral reefs status: Towards a spatial approach using hyperspectral and multispectral data. Ecol. Indic. 2019, 96, 174–191. [Google Scholar] [CrossRef]
- Ampou, E.E.; Ouillon, S.; Iovan, C.; Andréfouët, S. Change detection of Bunaken Island coral reefs using 15 years of very high resolution satellite images: A kaleidoscope of habitat trajectories. Mar. Pollut. Bull. 2018, 131, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Ben-Romdhane, H.; Al-Musallami, M.; Marpu, P.R.; Ouarda, T.B.M.J.; Ghedira, H. Change detection using remote sensing in a reef environment of the UAE during the extreme event of El Niño 2015–2016. Int. J. Remote Sens. 2018, 39, 6358–6382. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, L.; Fu, T.; Zhang, G.; Yao, M.; Li, M. Change Detection in Coral Reef Environment Using High-Resolution Images: Comparison of Object-Based and Pixel-Based Paradigms. ISPRS Int. J. Geo-Inf. 2018, 7, 441. [Google Scholar] [CrossRef] [Green Version]
- Scopélitis, J.; Andréfouët, S.; Largouët, C. Modelling coral reef habitat trajectories: Evaluation of an integrated timed automata and remote sensing approach. Ecol. Model. 2007, 205, 59–80. [Google Scholar] [CrossRef]
- Yamano, H.; Tamura, M. Detection limits of coral reef bleaching by satellite remote sensing: Simulation and data analysis. Remote Sens. Environ. 2004, 90, 86–103. [Google Scholar] [CrossRef]
- LeDrew, E.F.; Wulder, M.; Holden, H. Change Detection of Satellite Imagery for Reconnaissance of Stressed Tropical Corals. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000; Volume 6. [Google Scholar]
- Schuyler, Q.; Dustan, P.; Dobson, E. Remote Sensing of Coral Reef Community Change on a Remote Coral Atoll: Karang Kapota, Indonesia. In Proceedings of the 10th International Coral Reef Symposium (ICRS), Okinawa, Japan, 28 June–2 July 2004; Japanese Coral Reef Society: Tokyo, Japan, 2006; pp. 1763–1770. [Google Scholar]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, J.; Wang, F.; Chen, Y.; Lee, Z. Detection of Coral Reef Bleaching Based on Sentinel-2 Multi-Temporal Imagery: Simulation and Case Study. Front. Mar. Sci. 2021, 8, 268. [Google Scholar] [CrossRef]
- Wicaksono, P.; Wulandari, S.A.; Lazuardi, W.; Munir, M. Sentinel-2 images deliver possibilities for accurate and consistent multi-temporal benthic habitat maps in optically shallow water. Remote Sens. Appl. Soc. Environ. 2021, 23, 100572. [Google Scholar] [CrossRef]
- Haya, L.O.M.Y.; Fujii, M. Mapping the change of coral reefs using remote sensing and in situ measurements: A case study in Pangkajene and Kepulauan Regency, Spermonde Archipelago, Indonesia. J. Oceanogr. 2017, 73, 623–645. [Google Scholar] [CrossRef]
- Kabiri, K.; Pradhan, B.; Samimi-Namin, K.; Moradi, M. Detecting coral bleaching, using QuickBird multi-temporal data: A feasibility study at Kish Island, the Persian Gulf. Estuar. Coast. Shelf Sci. 2013, 117, 273–281. [Google Scholar] [CrossRef]
- Vanderstraete, T.; Goossens, R.; Ghabour, T.K. The use of multi-temporal Landsat images for the change detection of the coastal zone near Hurghada, Egypt. Int. J. Remote Sens. 2006, 27, 3645–3655. [Google Scholar] [CrossRef]
- Shapiro, A.C.; Rohmann, S.O. Summit-to-sea mapping and change detection using satellite imagery: Tools for conservation and management of coral reefs. Proc. Rev. Biol. Trop. 2005, 53, 185–193. [Google Scholar]
- Yamano, H.; Tamura, M. Use of Landsat TM Data and Radiative Transfer Models for Monitoring Coral Reef Bleaching. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Sydney, NSW, Australia, 9–13 July 2001; Volume 5. [Google Scholar]
- Ammenberg, P.; Lindell, T. Automated Change Detection of Bleached Coral Reefs. In Proceedings of the 7th International Conference, Remote Sensing for Marine and Coastal Environments, Miami, FL, USA, 20–22 May 2002. [Google Scholar]
- Andréfouët, S.; Guillaume, M.M.M.; Delval, A.; Rasoamanendrika, F.M.A.; Blanchot, J.; Bruggemann, J.H. Fifty years of changes in reef flat habitats of the Grand Récif of Toliara (SW Madagascar) and the impact of gleaning. Coral Reefs 2013, 32, 757–768. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Roelfsema, C.M.; Lyons, M.; Murray, N.; Kovacs, E.M.; Kennedy, E.; Markey, K.; Borrego-Acevedo, R.; Ordoñez Alvarez, A.; Say, C.; Tudman, P.; et al. Workflow for the Generation of Expert-Derived Training and Validation Data: A View to Global Scale Habitat Mapping. Front. Mar. Sci. 2021, 8, 1–13. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burns, C.; Bollard, B.; Narayanan, A. Machine-Learning for Mapping and Monitoring Shallow Coral Reef Habitats. Remote Sens. 2022, 14, 2666. https://doi.org/10.3390/rs14112666
Burns C, Bollard B, Narayanan A. Machine-Learning for Mapping and Monitoring Shallow Coral Reef Habitats. Remote Sensing. 2022; 14(11):2666. https://doi.org/10.3390/rs14112666
Chicago/Turabian StyleBurns, Christopher, Barbara Bollard, and Ajit Narayanan. 2022. "Machine-Learning for Mapping and Monitoring Shallow Coral Reef Habitats" Remote Sensing 14, no. 11: 2666. https://doi.org/10.3390/rs14112666
APA StyleBurns, C., Bollard, B., & Narayanan, A. (2022). Machine-Learning for Mapping and Monitoring Shallow Coral Reef Habitats. Remote Sensing, 14(11), 2666. https://doi.org/10.3390/rs14112666







