Multi-Prior Twin Least-Square Network for Anomaly Detection of Hyperspectral Imagery
Abstract
:1. Introduction
- To change the preconceptions of anomaly detection with insufficient samples, we propose a multi-prior strategy to reliably and adaptively generate prior dictionaries. Specifically, we calculate a series of multi-scale covariance matrices rather than traditional one-order statistics, taking advantage of second-order statistics to naturally model the distribution with integrated spectral and spatial information.
- The twin least-square loss in both the feature and image domains and differential expansion loss are jointly introduced into the architecture to fit the characteristics of high-dimensional and complex HSI data, which can overcome the gradient vanishing and training stability problem.
- To lease the generation ability of the model and reduce the false-alarm rate by an order of magnitude, we design a weakly supervised training pattern to enlarge the distribution diversity between background regions and anomalies, aiming to distinguish between background and anomalies in reconstruction. Experimental results illustrate that the AUC score of in MPN is one order of magnitude lower than other compared methods.
2. Related Work
2.1. Hyperspectral Anomaly Detection
2.2. Generative Adversarial Networks (GANs)
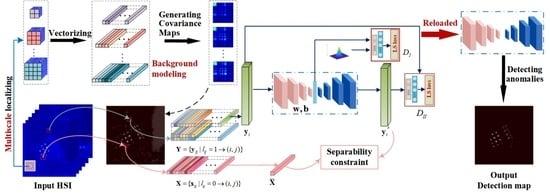
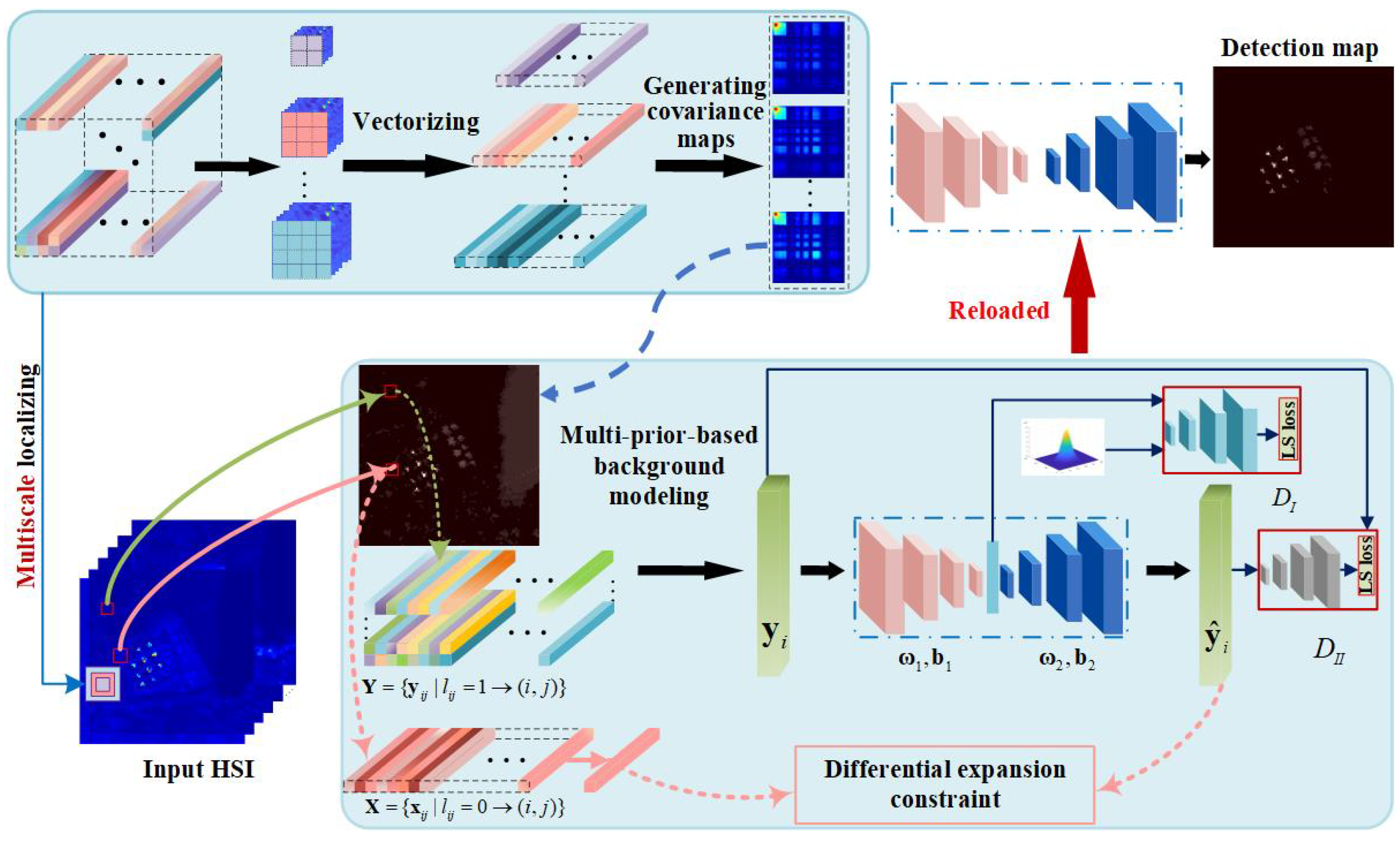
3. Proposed Method
3.1. Network Architecture
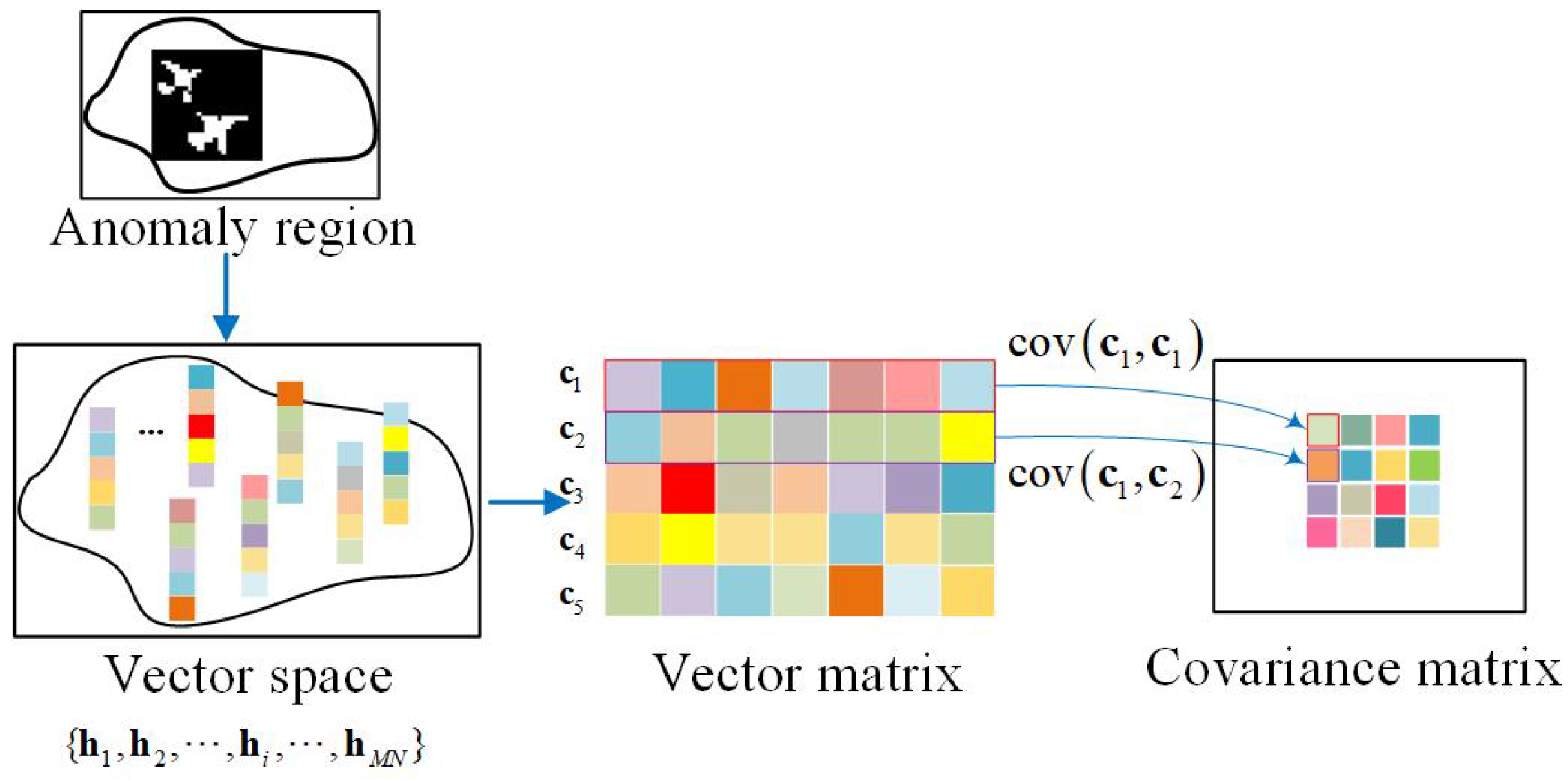
3.2. Multi-Prior for Background Construction
3.2.1. Multi-Scale Localizing
3.2.2. Generating Covariance Maps
3.3. Two-Branch Cascaded Architecture with Least-Square Losses
3.3.1. Stability Branch
3.3.2. Separability Branch
3.4. Solving the Cascaded Model
- Minimize by updating parameters of .
- Minimize by updating parameters of .
- Minimize by updating parameters of and the decoder .
4. Experimental Results and Discussion
4.1. Datasets Description
4.1.1. HYDICE
4.1.2. Airport–Beach–Urban (ABU) Database
4.1.3. Grand Island
4.1.4. EI Segundo
4.2. Evaluation Metrics
4.3. Experiment Setup
4.4. Ablation Study
4.5. Discussion
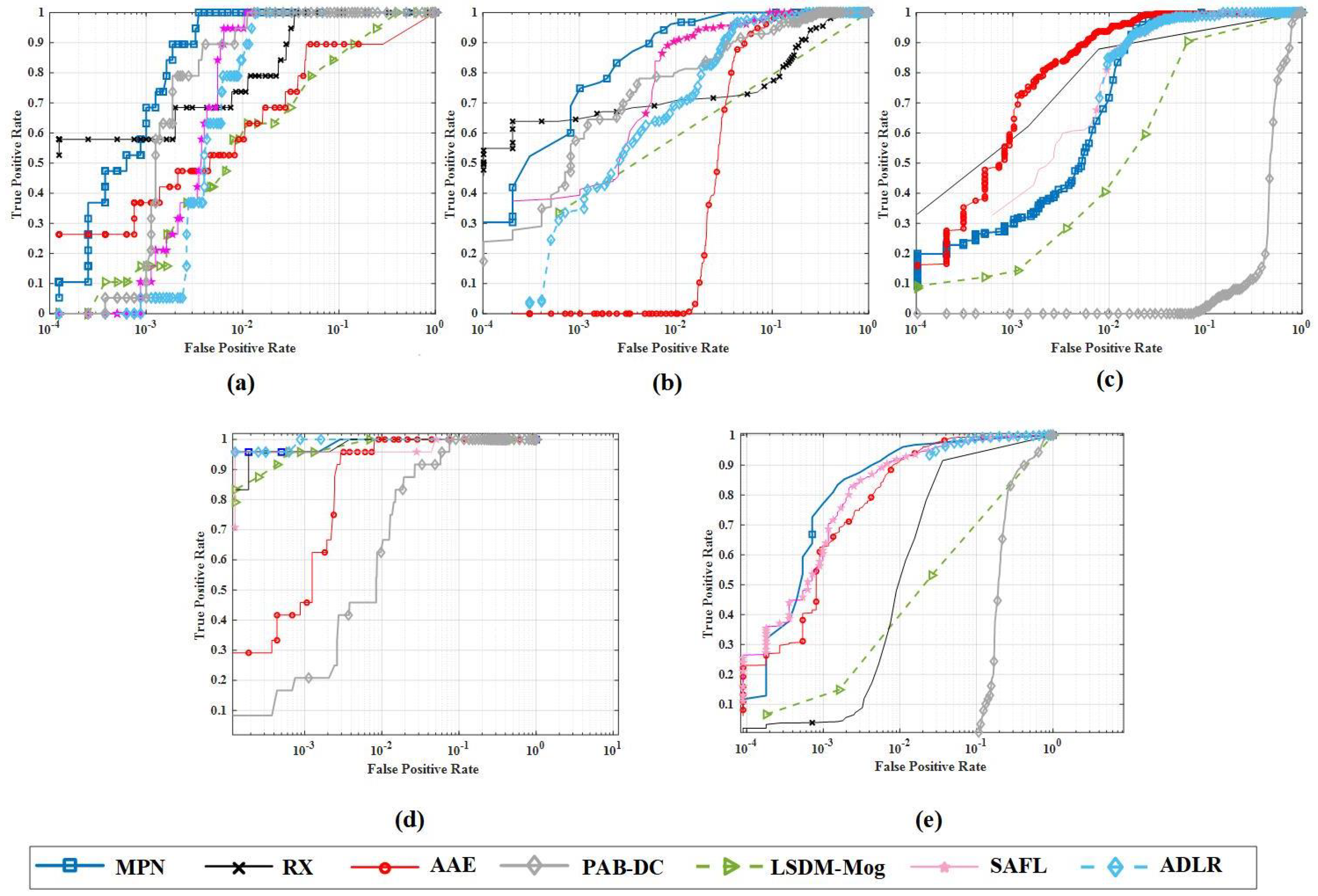
4.5.1. Baseline Methods
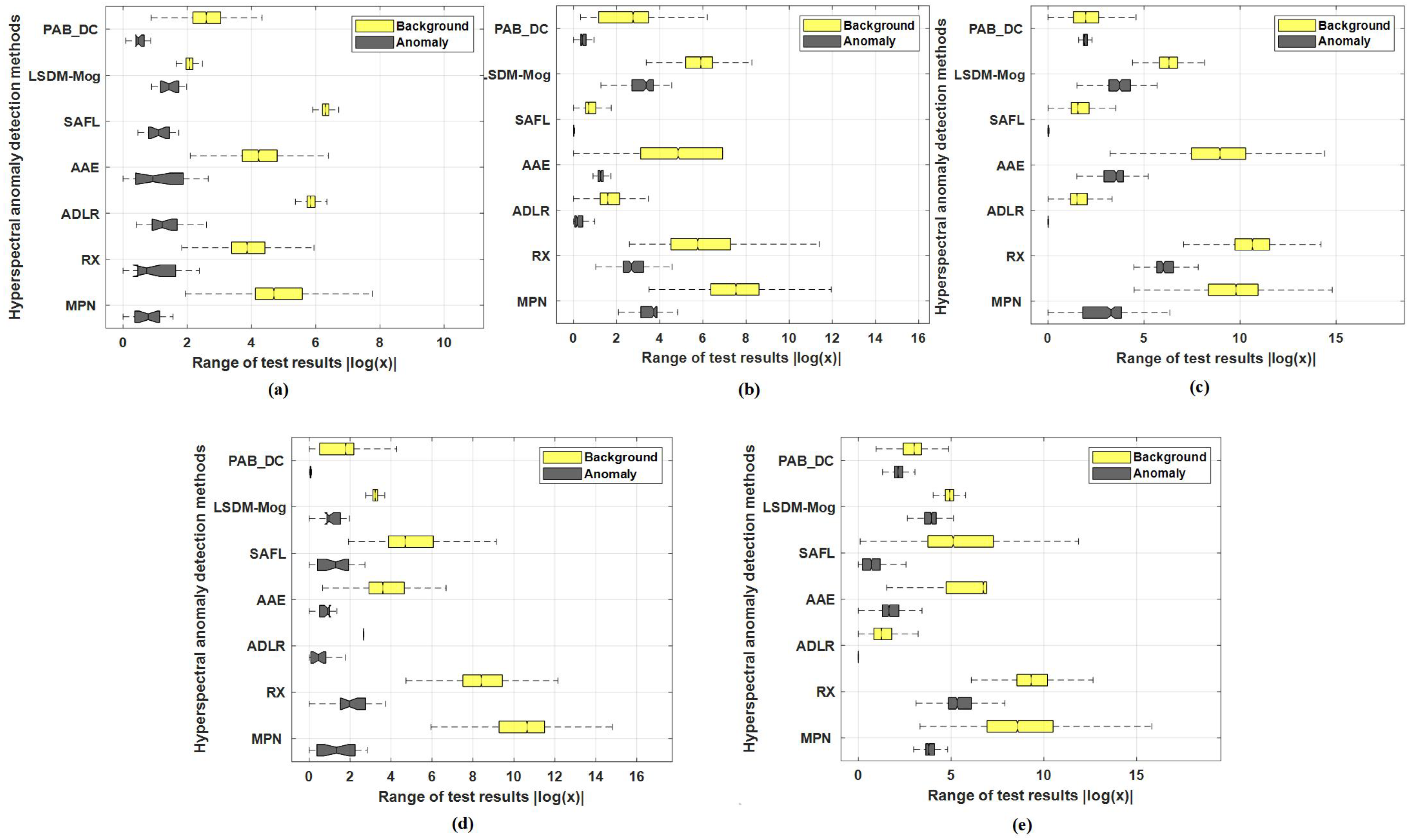
4.5.2. Quantitative Comparison
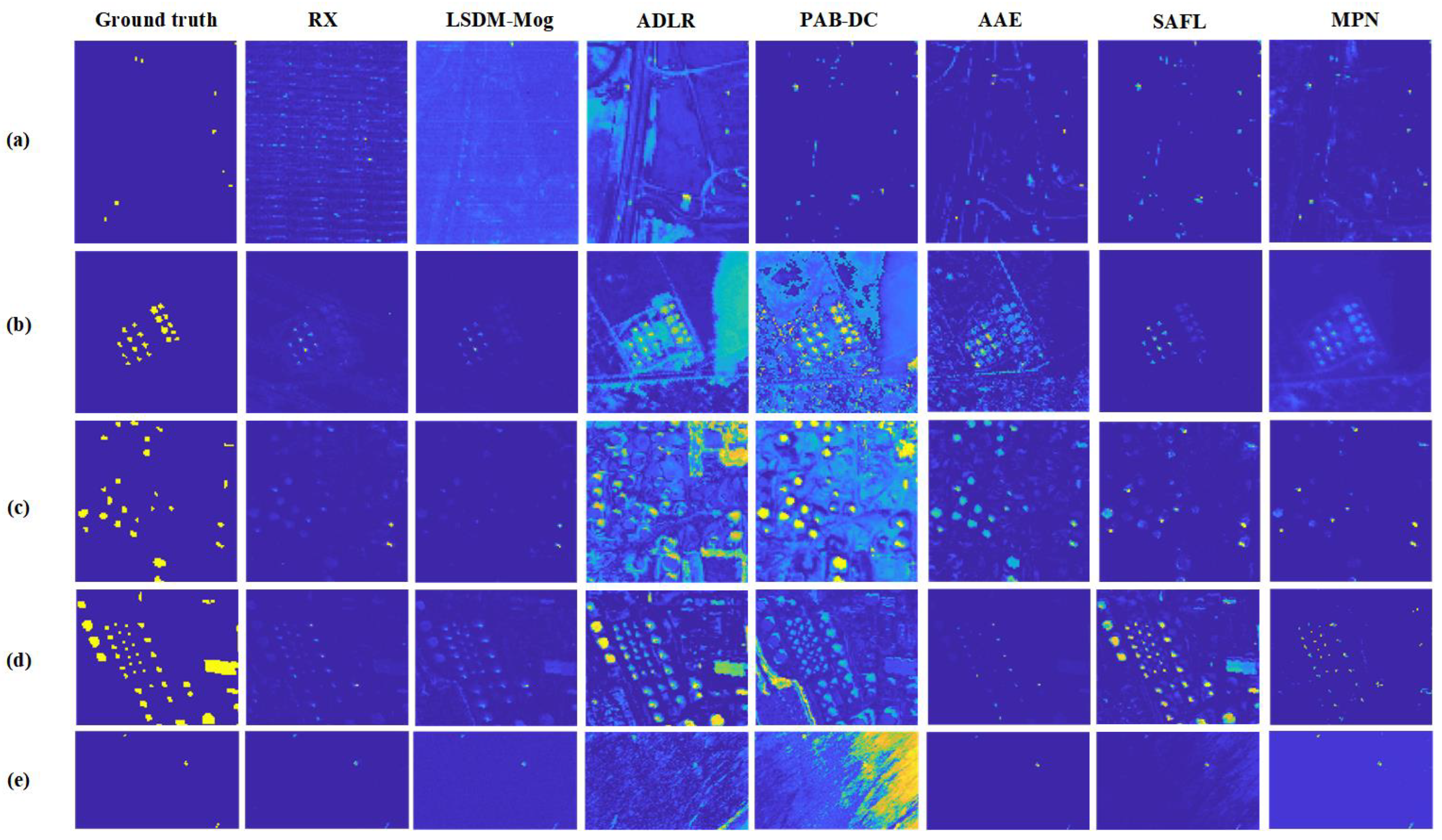
4.5.3. Qualitative Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GANs | generative adversarial networks |
| HSI | hyperspectral imagery |
| MCMs | multi-scale covariance maps |
| KNN | K nearest neighbors |
| MSE | mean squared error |
| ROC | the receiver operating characteristic curve |
References
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J. Advances in hyperspectral image classifification: Earth monitoring with statistical learning methods. IEEE Signal Process. Mag. 2013, 31, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Okwuashi, O.; Christopher, E. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103, 107298. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, H.; Xu, X.; Hu, X.; Heng, P. Learning semantic context from normal samples for unsupervised anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Virtual, 8 February 2021; p. 425. [Google Scholar]
- Abati, D.; Porrello, A.; Calderara, S.; Rita, C. Latent space autoregression for novelty detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 481–490. [Google Scholar]
- Ma, M.; Mei, S.; Wan, S.; Hou, J.; Wang, Z.; Feng, D. Video summarization via block sparse dictionary selection. Neorocomputing 2020, 378, 197–209. [Google Scholar] [CrossRef]
- Luo, W.; Liu, W.; Lian, D.; Tang, J.; Gao, S. Video anomaly detection with sparse coding inspired deep neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 1070–1084. [Google Scholar] [CrossRef]
- Stanislaw, J.; Maciej, S.; Stanislav, F.; Devansh, A.; Jacek, T.; Kyunghyun, C.; Krzysztof, G. The break-even point on optimization trajectories of deep neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Eyal, G.; Aryeh, K.; Sivan, S.; Ofer, B.; Oded, S. Temporal anomaly detection: Calibrating the surprise. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Honolulu, HI, USA, 27 January–1 February 2019; pp. 689–692. [Google Scholar]
- Wen, T.; Keyes, R. Time series anomaly detection using convolutional neural networks and transfer learning. In Proceedings of the International Joint Conference on Artifificial Intelligence (IJCAI), Macao, China, 10–16 August 2019. [Google Scholar]
- Ansari, A.; Scarlett, J.; Soh, H. A characteristic function approach to deep implicit generative modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7478–7487. [Google Scholar]
- Villa, A.; Chanussot, J.; Benediktsson, J.; Jutten, C.; Dambreville, R. Unsupervised methods for the classifification of hyperspectral images with low spatial resolution. Pattern Recognit. 2013, 46, 1556–1568. [Google Scholar] [CrossRef]
- Fowler, J.; Du, Q. Anomaly detection and reconstruction from random projections. IEEE Trans. Image Process. 2011, 21, 184–195. [Google Scholar] [CrossRef] [Green Version]
- Gong, Z.; Zhong, P.; Hu, W. Statistical loss and analysis for deep learning in hyperspectral image classifification. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 322–333. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Cheng, B. A stacked autoencoders-based adaptive subspace model for hyperspectral anomaly detection. Infrared Phys. Technol. 2019, 96, 52–60. [Google Scholar] [CrossRef]
- Erfani, S.; Rajasegarar, S.; Karunasekera, S.; Leckie, S.; Leckie, C. High dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning. Pattern Recognit. 2016, 58, 121–134. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Z.; Shi, G.; Wu, F.; Zeng, W. Adaptive nonlocal sparse representation for dual-camera compressive hyperspectral imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 2104–2111. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Forero, S.; Angulo, J. Classification of hyperspectral images by tensor modeling and additive morphological decomposition. Pattern Recognit. 2013, 46, 566–577. [Google Scholar] [CrossRef] [Green Version]
- Malpica, J.; Rejas, J.; Alonsoa, M. A projection pursuit algorithm for anomaly detection in hyperspectral imagery. Pattern Recognit. 2008, 41, 3313–3327. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Guo, Y.; Fang, L.; Wang, S. Data-uncertainty guided multiphase learning for semi-supervised object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Taghipour, A.; Ghassemian, H. Unsupervised hyperspectral target detection using spectral residual of deep autoencoder networks. In Proceedings of the International Conference on Pattern Recognition and Image Analysis (IPAS), Tehran, Iran, 6–7 March 2019; pp. 52–57. [Google Scholar]
- Liu, Y.; Li, Z.; Zhou, C.; Jiang, Y.; Sun, J.; Wang, M.; He, X. Generative adversarial active learning for unsupervised outlier detection. IEEE Trans. Knowl. Data Eng. 2019, 32, 1517–1528. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Dong, M.; Wang, Z.; Gao, L.; Zhang, L.; Xue, J. Data-augmented matched subspace detector for hyperspectral subpixel target detection. Pattern Recognit. 2020, 106, 107464. [Google Scholar] [CrossRef]
- Ergen, T.; Kozat, S. Unsupervised anomaly detection with LSTM neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3127–3141. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Prasad, S. Semi-supervised deep learning using pseudo labels for hyperspectral image classifification. IEEE Trans. Image Process. 2018, 27, 1259–1270. [Google Scholar] [CrossRef]
- Antonio, P.; Atli, B.; Jason, B.; Lorenzo, B.; Gustavo, C.; Jocelyn, C.; Mathieu, F.; Paolo, G.; Anthony, G. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar]
- Yang, X.; Deng, C.; Zheng, F.; Yan, J.; Liu, W. Deep spectral clustering using dual autoencoder network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4066–4075. [Google Scholar]
- Dincalp, U.; G zel, M.; Sevine, O.; Bostanci, E.; Askerzade, I. Anomaly based distributed denial of service attack detection and prevention with machine learning. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–4. [Google Scholar]
- Wang, R.; Guo, H.; Davis, L.; Dai, Q. Covariance discriminative learning: A natural and efficient approach to image set classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2496–2503. [Google Scholar]
- He, N.; Paoletti, M.; Haut, J.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature extraction with multiscale covariance maps for hyperspectral image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 755–769. [Google Scholar] [CrossRef]
- Li, A.; Miao, Z.; Cen, Y.; Zhang, X.-P.; Zhang, L.; Chen, S. Abnormal event detection in surveillance videos based on low-rank and compact coefficient dictionary learning. Pattern Recognit. 2020, 108, 107355. [Google Scholar] [CrossRef]
- Fang, L.; He, N.; Li, S.; Plaza, A.; Plaza, J. A new spatial-spectral feature extraction method for hyperspectral images using local covariance matrix representation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3534–3546. [Google Scholar] [CrossRef]
- Reed, I.; Yu, X. Adaptive multiple band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, W.; Guo, R.; Ayhan, B.; Kwan, C.; Vance, S.; Qi, H. Hyperspectral anomaly detection through spectral unmixing and dictionary-based low-rank decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4391–4405. [Google Scholar] [CrossRef]
- Huyan, N.; Zhang, X.; Zhou, H.; Jiao, L. Hyperspectral anomaly detection via background and potential anomaly dictionaries construction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2263–2276. [Google Scholar] [CrossRef] [Green Version]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Du, Q.; Tao, R. Low-rank and sparse decomposition with mixture of gaussian for hyperspectral anomaly detection. IEEE Trans. Cybern. 2020, 51, 4363–4372. [Google Scholar] [CrossRef]
- Xie, W.; Lei, J.; Liu, B.; Li, Y.; Jia, X. Spectral constraint adversarial autoencoders approach to feature representation in hyperspectral anomaly detection. Neural Netw. 2019, 119, 222–234. [Google Scholar] [CrossRef]
- Xie, W.; Liu, B.; Li, Y.; Lei, J.; Chang, C.-I.; He, G. Spectral adversarial feature learning for anomaly detection in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2352–2365. [Google Scholar] [CrossRef]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.K.; Wang, Z.; Paul Smolley, S. Least squares generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2794–2802. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; p. 27. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4401–4410. [Google Scholar]
- Brock, A.; Donahue, J.; Simonyan, K. Large scale GAN training for high fidelity natural image synthesis. arXiv 2018, arXiv:1809.11096. [Google Scholar]
- Carreira, J.; Caseiro, R.; Batista, J.; Sminchisescu, C. Free-form region description with second-order pooling. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1177–1189. [Google Scholar] [CrossRef]
- Chen, D.; Yue, L.; Chang, X.; Xu, M.; Jia, T. NM-GAN: Noisemodulated generative adversarial network for video anomaly detection. Pattern Recognit. 2021, 116, 107969. [Google Scholar] [CrossRef]

| Configuration | HYDICE | Urban-1 | Urban-2 | Grand Island | EI Segundo | Average |
|---|---|---|---|---|---|---|
| Scene | 0.99716 | 0.99839 | 0.99234 | 0.99940 | 0.98943 | 0.99534 |
| Scene | 0.99804 | 0.99805 | 0.99305 | 0.99990 | 0.98816 | 0.99544 |
| Scene | 0.99790 | 0.99778 | 0.99302 | 0.99991 | 0.99372 | 0.99654 |
| MPN | 0.99945 | 0.99816 | 0.99312 | 0.99991 | 0.99982 | 0.99809 |
| Configuration | HYDICE | Urban-1 | Urban-2 | Grand Island | EI Segundo | Average |
|---|---|---|---|---|---|---|
| Scene | 0.02059 | 0.00193 | 0.00090 | 0.00311 | 0.00207 | 0.00572 |
| Scene | 0.02169 | 0.00124 | 0.00159 | 0.00071 | 0.00246 | 0.00554 |
| Scene | 0.01965 | 0.00146 | 0.00088 | 0.00257 | 0.00178 | 0.00525 |
| MPN | 0.01540 | 0.002 | 0.00145 | 0.00069 | 0.00218 | 0.00518 |
| Dataset | MPN | ADLR | LSDM–MoG | RX | AAE | PAB_DC | SAFL |
|---|---|---|---|---|---|---|---|
| HYDICE | 0.99945 | 0.99471 | 0.95643 | 0.97637 | 0.92185 | 0.99760 | 0.99621 |
| Urban-1 | 0.99816 | 0.98774 | 0.99321 | 0.99463 | 0.96806 | 0.98327 | 0.99800 |
| Urban-2 | 0.99312 | 0.99284 | 0.97504 | 0.98874 | 0.99284 | 0.54635 | 0.97188 |
| Grand Island | 0.99991 | 0.99993 | 0.99989 | 0.99990 | 0.99940 | 0.98768 | 0.99804 |
| EI Segundo | 0.99982 | 0.99145 | 0.96798 | 0.97826 | 0.99260 | 0.75911 | 0.99231 |
| Average | 0.99809 | 0.99321 | 0.97851 | 0.98757 | 0.97495 | 0.85480 | 0.99141 |
| Dataset | MPN | ADLR | LSDM–MoG | RX | AAE | PAB_DC | SAFL |
|---|---|---|---|---|---|---|---|
| HYDICE | 0.01540 | 0.00316 | 0.18799 | 0.03798 | 0.00962 | 0.10525 | 0.00310 |
| Urban-1 | 0.00200 | 0.08011 | 0.04555 | 0.01351 | 0.04229 | 0.16974 | 0.00216 |
| Urban-2 | 0.00145 | 0.07451 | 0.01338 | 0.01140 | 0.06192 | 0.32350 | 0.01045 |
| Grand Island | 0.00069 | 0.00079 | 0.02848 | 0.00738 | 0.04818 | 0.06799 | 0.01126 |
| EI Segundo | 0.00218 | 0.09622 | 0.14127 | 0.00952 | 0.04355 | 0.10506 | 0.01864 |
| Average | 0.00518 | 0.05096 | 0.08333 | 0.01596 | 0.0328 | 0.15431 | 0.00912 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, J.; Li, Y.; Xie, W.; Lei, J.; Jia, X. Multi-Prior Twin Least-Square Network for Anomaly Detection of Hyperspectral Imagery. Remote Sens. 2022, 14, 2859. https://doi.org/10.3390/rs14122859
Zhong J, Li Y, Xie W, Lei J, Jia X. Multi-Prior Twin Least-Square Network for Anomaly Detection of Hyperspectral Imagery. Remote Sensing. 2022; 14(12):2859. https://doi.org/10.3390/rs14122859
Chicago/Turabian StyleZhong, Jiaping, Yunsong Li, Weiying Xie, Jie Lei, and Xiuping Jia. 2022. "Multi-Prior Twin Least-Square Network for Anomaly Detection of Hyperspectral Imagery" Remote Sensing 14, no. 12: 2859. https://doi.org/10.3390/rs14122859
APA StyleZhong, J., Li, Y., Xie, W., Lei, J., & Jia, X. (2022). Multi-Prior Twin Least-Square Network for Anomaly Detection of Hyperspectral Imagery. Remote Sensing, 14(12), 2859. https://doi.org/10.3390/rs14122859