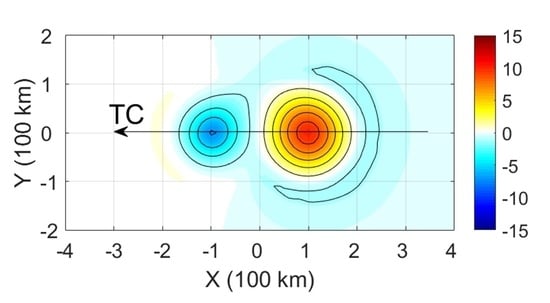
Response of a Mesoscale Dipole Eddy to the Passage of a Tropical Cyclone: A Case Study Using Satellite Observations and Numerical Modeling
Abstract
:1. Introduction
2. Data, Model, and Method
2.1. Data
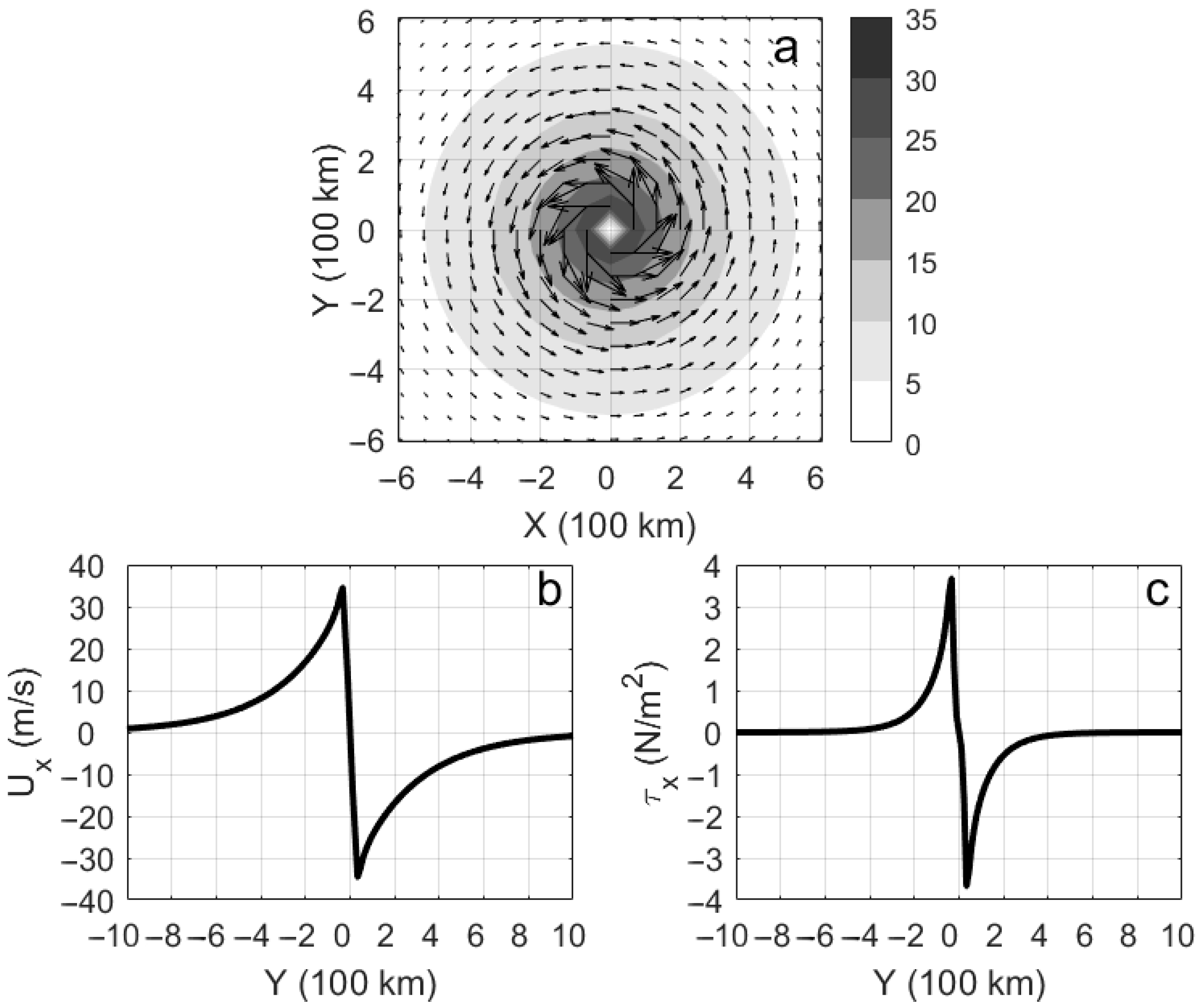
2.2. Model Settings
2.3. Method
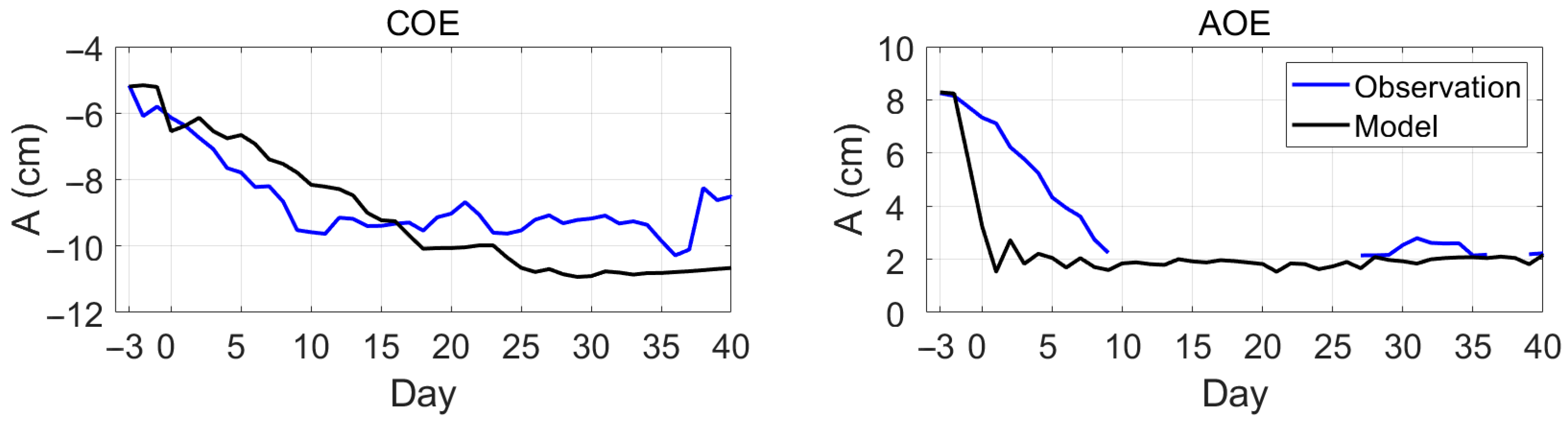
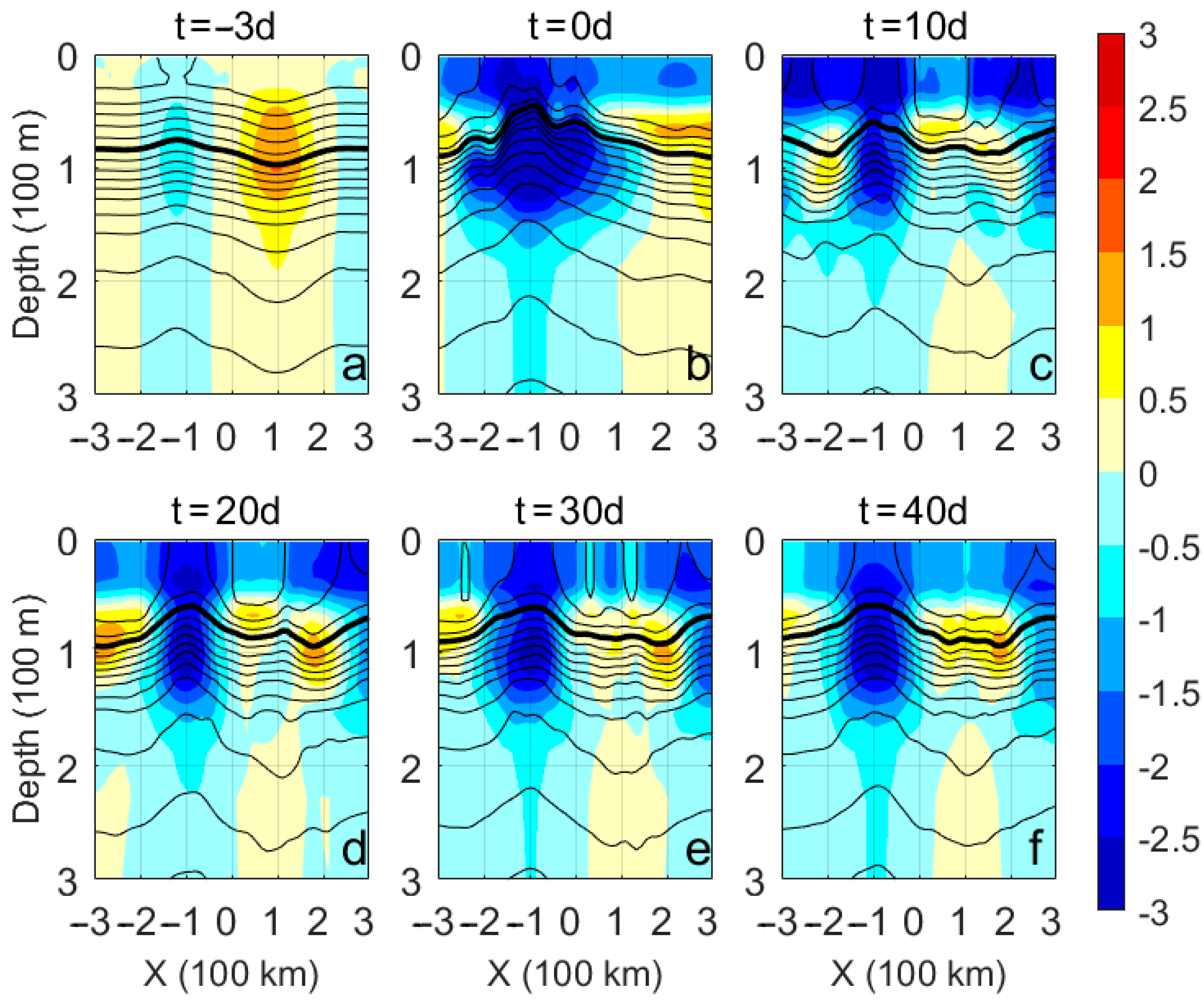
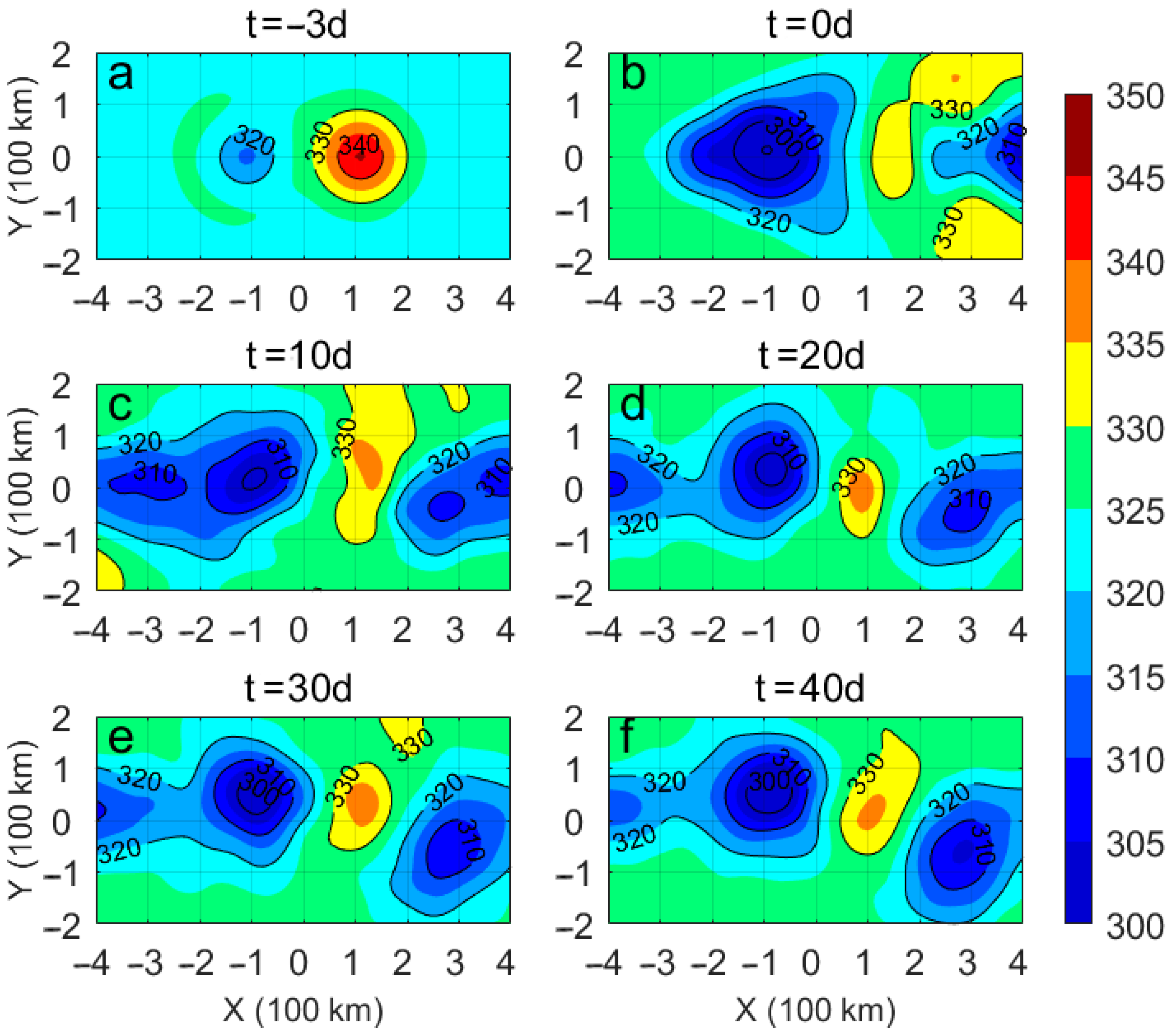
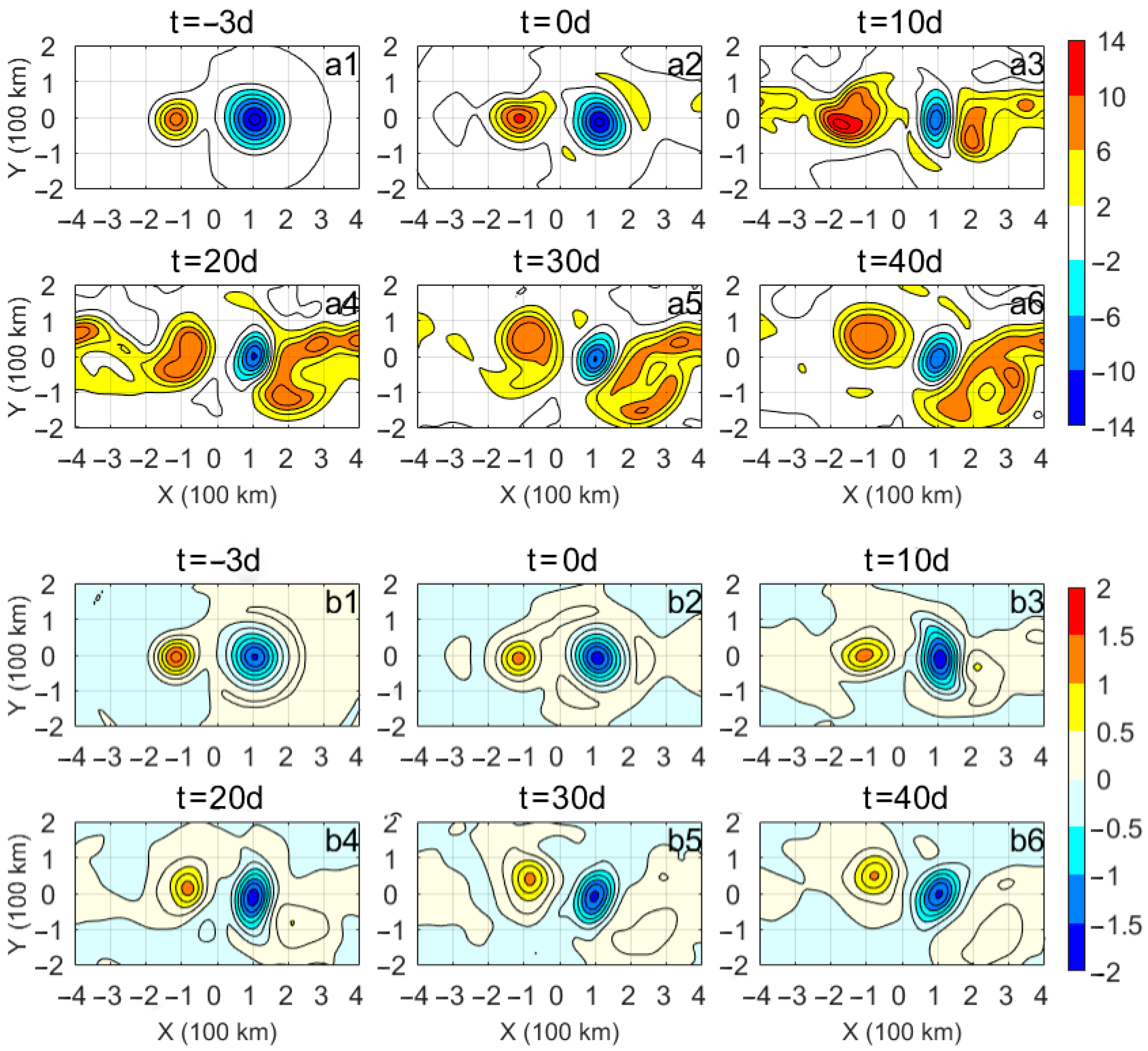
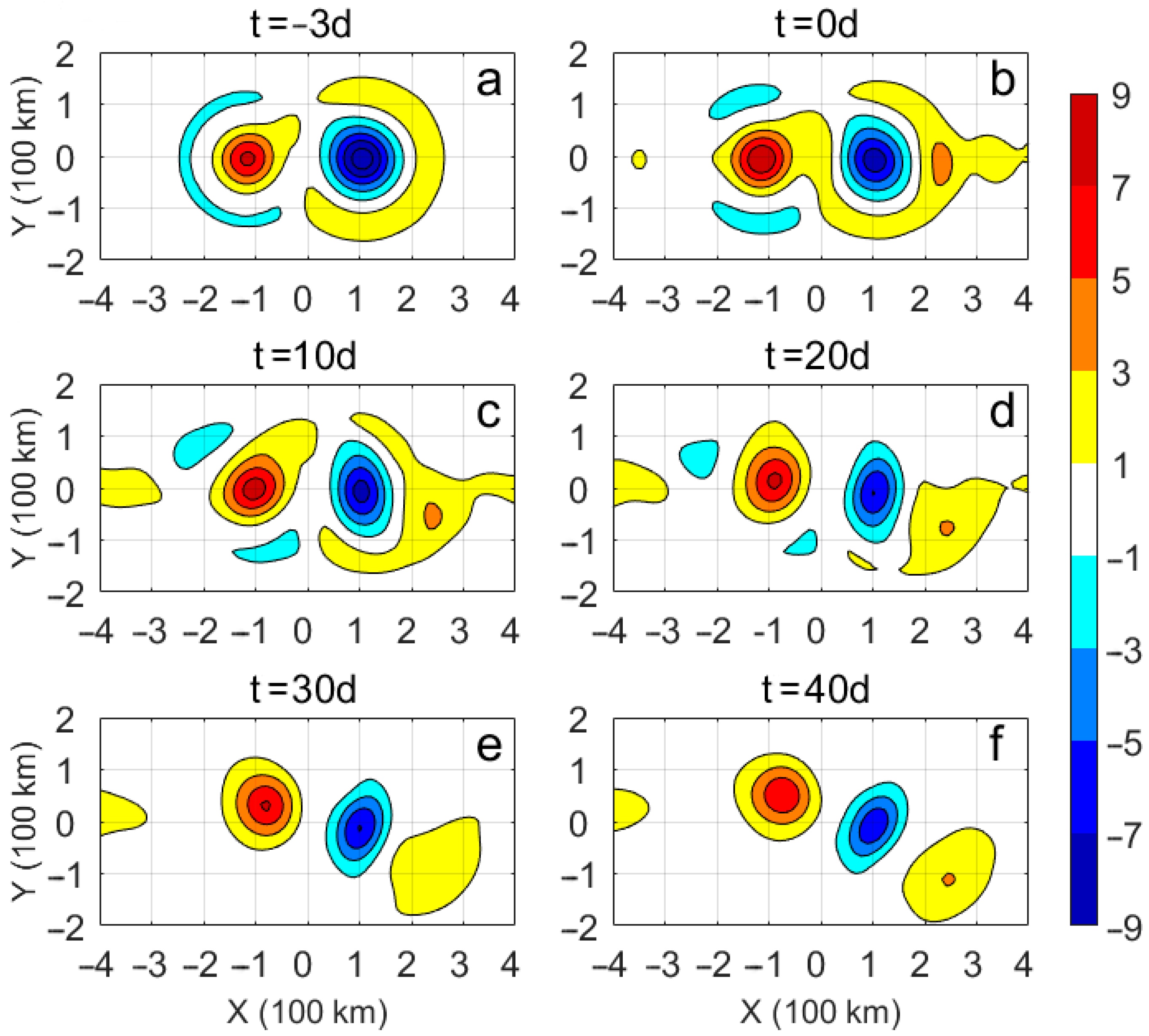
3. Results
3.1. Evolution of Dipole Structure after TC Passage
3.2. Dynamics of Dipole after the TC
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ikeda, M.; Mysak, L.A.; Emery, W.J. Observation and Modeling of Satellite-Sensed Meanders and Eddies off Vancouver Island. J. Phys. Oceanogr. 1984, 14, 3–21. [Google Scholar] [CrossRef] [Green Version]
- Hughes, C.W.; Miller, P.I. Rapid Water Transport by Long-Lasting Modon Eddy Pairs in the Southern Midlatitude Oceans. Geophys. Res. Lett. 2017, 44, 12375–12384. [Google Scholar] [CrossRef] [Green Version]
- Ni, Q.; Zhai, X.; Wang, G.; Hughes, C.W. Widespread Mesoscale Dipoles in the Global Ocean. J. Geophys. Res. Ocean. 2020, 125, e2020JC016479. [Google Scholar] [CrossRef]
- Flierl, G.R.; Stern, M.E.; Whitehead, J.A. The Physical Significance of Modons: Laboratory Experiments and General Integral Constraints. Dyn. Atmos. Ocean. 1983, 7, 233–263. [Google Scholar] [CrossRef]
- Hooker, S.B.; Brown, J.W.; Kirwan, A.D.; Lindemann, G.J.; Mied, R.P. Kinematics of a Warm-Core Dipole Ring. J. Geophys. Res. Ocean. 1995, 100, 24797–24809. [Google Scholar] [CrossRef]
- Mied, R.P.; Lindemann, G.J.; McWilliams, J.C. The Generation and Evolution of Mushroom-like Vortices. J. Phys. Oceanogr. 1991, 21, 489–510. [Google Scholar] [CrossRef] [Green Version]
- Pidcock, R.; Martin, A.; Allen, J.; Painter, S.C.; Smeed, D. The Spatial Variability of Vertical Velocity in an Iceland Basin Eddy Dipole. Deep. Sea Res. Part Oceanogr. Res. Pap. 2013, 72, 121–140. [Google Scholar] [CrossRef]
- Roberts, M.J.; Ternon, J.-F.; Morris, T. Interaction of Dipole Eddies with the Western Continental Slope of the Mozambique Channel. Deep Sea Res. Part II Top. Stud. Oceanogr. 2014, 100, 54–67. [Google Scholar] [CrossRef]
- Arruda, W.Z.; da Silveira, I.C.A. Dipole-Induced Central Water Extrusions South of Abrolhos Bank (Brazil, 20.5° S). Cont. Shelf Res. 2019, 188, 103976. [Google Scholar] [CrossRef]
- Leweke, T.; Le Dizès, S.; Williamson, C.H.K. Dynamics and Instabilities of Vortex Pairs. Annu. Rev. Fluid Mech. 2016, 48, 507–541. [Google Scholar] [CrossRef] [Green Version]
- Apango-Figueroa, E.; Sánchez-Velasco, L.; Lavín, M.F.; Godínez, V.M.; Barton, E.D. Larval Fish Habitats in a Mesoscale Dipole Eddy in the Gulf of California. Deep Sea Res. Part Oceanogr. Res. Pap. 2015, 103, 1–12. [Google Scholar] [CrossRef]
- Durán-Campos, E.; Monreal-Gómez, M.A.; de León, D.A.S.; Coria-Monter, E. Zooplankton Functional Groups in a Dipole Eddy in a Coastal Region of the Southern Gulf of California. Reg. Stud. Mar. Sci. 2019, 28, 100588. [Google Scholar] [CrossRef]
- Walker, N.D.; Leben, R.R.; Balasubramanian, S. Hurricane-Forced Upwelling and Chlorophyll a Enhancement within Cold-Core Cyclones in the Gulf of Mexico. Geophys. Res. Lett. 2005, 32, L18610. [Google Scholar] [CrossRef]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a Warm Oceanic Feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Lin, I.-I.; Wu, C.-C.; Emanuel, K.A.; Lee, I.-H.; Wu, C.-R.; Pun, I.-F. The Interaction of Supertyphoon Maemi (2003) with a Warm Ocean Eddy. Mon. Weather Rev. 2005, 133, 2635–2649. [Google Scholar] [CrossRef]
- Jaimes, B.; Shay, L.K. Mixed Layer Cooling in Mesoscale Oceanic Eddies during Hurricanes Katrina and Rita. Mon. Weather Rev. 2009, 137, 4188–4207. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Wang, G.; Xiong, X.; Hui, Z.; Hu, X.; Ling, Z.; Yu, L.; Yang, G.; Guo, Y.; Ju, X.; et al. Impact of Warm Mesoscale Eddy on Tropical Cyclone Intensity. Acta Oceanol. Sin. 2020, 39, 1–13. [Google Scholar] [CrossRef]
- Jaimes, B.; Shay, L.K.; Halliwell, G.R. The Response of Quasigeostrophic Oceanic Vortices to Tropical Cyclone Forcing. J. Phys. Oceanogr. 2011, 41, 1965–1985. [Google Scholar] [CrossRef]
- Sun, L.; Yang, Y.-J.; Xian, T.; Wang, Y.; Fu, Y.-F. Ocean Responses to Typhoon Namtheun Explored with Argo Floats and Multiplatform Satellites. Atmosphere-Ocean 2012, 50, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Wang, G.; Shang, X. Response of a Preexisting Cyclonic Ocean Eddy to a Typhoon. J. Phys. Oceanogr. 2016, 46, 2403–2410. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Chen, D.; Qiu, B.; Wang, W. Strengthening of the Kuroshio Current by Intensifying Tropical Cyclones. Science 2020, 368, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Wang, G.; Shang, X. Strength and Spatial Structure of the Perturbation Induced by a Tropical Cyclone to the Underlying Eddies. J. Geophys. Res. Ocean. 2020, 125, e2020JC016097. [Google Scholar] [CrossRef]
- Wang, G.; Chen, D.; Su, J. Generation and Life Cycle of the Dipole in the South China Sea Summer Circulation. J. Geophys. Res. 2006, 111, C06002. [Google Scholar] [CrossRef] [Green Version]
- Eden, C.; Dietze, H. Effects of Mesoscale Eddy/Wind Interactions on Biological New Production and Eddy Kinetic Energy. J. Geophys. Res. 2009, 114, C05023. [Google Scholar] [CrossRef] [Green Version]
- Chelton, D.; Xie, S.-P. Coupled Ocean-Atmosphere Interaction at Oceanic Mesoscales. Oceanography 2010, 23, 52–69. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Eddy-Mean Flow Interaction in the Decadally Modulating Kuroshio Extension System. Deep Sea Res. Part II Top. Stud. Oceanogr. 2010, 57, 1098–1110. [Google Scholar] [CrossRef]
- Vic, C.; Roullet, G.; Capet, X.; Carton, X.; Molemaker, M.J.; Gula, J. Eddy-topography interactions and the fate of the Persian Gulf Outflow. J. Geophys. Res. Oceans 2015, 120, 6700–6717. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.G.; Frajka-Williams, E.; Naveira Garabato, A.C.; Polzin, K.L.; Forryan, A. Mesoscale Eddy Dissipation by a “Zoo” of Submesoscale Processes at a Western Boundary. J. Geophys. Res. Ocean. 2020, 125, e2020JC016246. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global Observations of Nonlinear Mesoscale Eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, W.; Huang, R.X. Universal Structure of Mesoscale Eddies in the Ocean. Geophys. Res. Lett. 2013, 40, 3677–3681. [Google Scholar] [CrossRef] [Green Version]
- Shchepetkin, A.F.; McWilliams, J.C. The Regional Oceanic Modeling System (ROMS): A Split-Explicit, Free-Surface, Topography-Following-Coordinate Oceanic Model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Dong, C.; Lin, X.; Liu, Y.; Nencioli, F.; Chao, Y.; Guan, Y.; Chen, D.; Dickey, T.; McWilliams, J.C. Three-Dimensional Oceanic Eddy Analysis in the Southern California Bight from a Numerical Product. J. Geophys. Res. Ocean. 2012, 117, C00H14. [Google Scholar] [CrossRef] [Green Version]
- Vic, C.; Roullet, G.; Carton, X.; Capet, X. Mesoscale Dynamics in the Arabian Sea and a Focus on the Great Whirl Life Cycle: A Numerical Investigation Using ROMS. J. Geophys. Res. Ocean. 2014, 119, 6422–6443. [Google Scholar] [CrossRef] [Green Version]
- Mellor, G.L.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Price, J.F. Internal Wave Wake of a Moving Storm. Part I. Scales, Energy Budget and Observations. J. Phys. Oceanogr. 1983, 13, 949–965. [Google Scholar] [CrossRef] [Green Version]
- Willoughby, H.E.; Darling, R.W.R.; Rahn, M.E. Parametric Representation of the Primary Hurricane Vortex. Part II: A New Family of Sectionally Continuous Profiles. Mon. Weather Rev. 2006, 134, 1102–1120. [Google Scholar] [CrossRef] [Green Version]
- Emanuel, K. A Statistical Analysis of Tropical Cyclone Intensity. Mon. Weather Rev. 2000, 128, 1139–1152. [Google Scholar] [CrossRef]
- Lajoie, F.; Walsh, K. A Technique to Determine the Radius of Maximum Wind of a Tropical Cyclone. Weather Forecast. 2008, 23, 1007–1015. [Google Scholar] [CrossRef]
- Chavas, D.R.; Lin, N.; Emanuel, K. A Model for the Complete Radial Structure of the Tropical Cyclone Wind Field. Part I: Comparison with Observed Structure. J. Atmos. Sci. 2015, 72, 3647–3662. [Google Scholar] [CrossRef]
- Large, W.G.; Pond, S. Open Ocean Momentum Flux Measurements in Moderate to Strong Winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Wang, F.; Li, Y.; Lin, P. Mesoscale Eddies in the Northwestern Subtropical Pacific Ocean: Statistical Characteristics and Three-Dimensional Structures. J. Geophys. Res. Ocean. 2013, 118, 1906–1925. [Google Scholar] [CrossRef]
- Shay, L.K.; Mariano, A.J.; Jacob, S.D.; Ryan, E.H. Mean and Near-Inertial Ocean Current Response to Hurricane Gilbert. J. Phys. Oceanogr. 1998, 28, 858–889. [Google Scholar] [CrossRef]
- Ling, Z.; Chen, Z.; Wang, G.; He, H.; Chen, C. Recovery of Tropical Cyclone Induced SST Cooling Observed by Satellite in the Northwestern Pacific Ocean. Remote Sens. 2021, 13, 3781. [Google Scholar] [CrossRef]
- Shay, L.K. Upper Ocean Structure: Responses to Strong Atmospheric Forcing Events. In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 86–96. ISBN 978-0-12-813082-7. [Google Scholar]
- Sun, L.; Li, Y.-X.; Yang, Y.-J.; Wu, Q.; Chen, X.-T.; Li, Q.-Y.; Li, Y.-B.; Xian, T. Effects of Super Typhoons on Cyclonic Ocean Eddies in the Western North Pacific: A Satellite Data-Based Evaluation between 2000 and 2008. J. Geophys. Res. Ocean. 2014, 119, 5585–5598. [Google Scholar] [CrossRef]
- Pilo, G.S.; Oke, P.R.; Coleman, R.; Rykova, T.; Ridgway, K. Patterns of Vertical Velocity Induced by Eddy Distortion in an Ocean Model. J. Geophys. Res. Ocean. 2018, 123, 2274–2292. [Google Scholar] [CrossRef]
- Early, J.J.; Samelson, R.M.; Chelton, D.B. The Evolution and Propagation of Quasigeostrophic Ocean Eddies. J. Phys. Oceanogr. 2011, 41, 1535–1555. [Google Scholar] [CrossRef]
- Prakash, K.R.; Nigam, T.; Pant, V.; Chandra, N. On the interaction of mesoscale eddies and a tropical cyclone in the Bay of Bengal. Nat. Hazards 2021, 106, 1981–2001. [Google Scholar] [CrossRef]
- Kumar, A.U.; Brüggemann, N.; Smith, R.K.; Marotzke, J. Response of a tropical cyclone to a subsurface ocean eddy and the role of boundary layer dynamics. Q. J. R. Meteorol. Soc. 2021, 148, 378–402. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Wang, G. Response of a Mesoscale Dipole Eddy to the Passage of a Tropical Cyclone: A Case Study Using Satellite Observations and Numerical Modeling. Remote Sens. 2022, 14, 2865. https://doi.org/10.3390/rs14122865
Huang X, Wang G. Response of a Mesoscale Dipole Eddy to the Passage of a Tropical Cyclone: A Case Study Using Satellite Observations and Numerical Modeling. Remote Sensing. 2022; 14(12):2865. https://doi.org/10.3390/rs14122865
Chicago/Turabian StyleHuang, Xiaorong, and Guihua Wang. 2022. "Response of a Mesoscale Dipole Eddy to the Passage of a Tropical Cyclone: A Case Study Using Satellite Observations and Numerical Modeling" Remote Sensing 14, no. 12: 2865. https://doi.org/10.3390/rs14122865
APA StyleHuang, X., & Wang, G. (2022). Response of a Mesoscale Dipole Eddy to the Passage of a Tropical Cyclone: A Case Study Using Satellite Observations and Numerical Modeling. Remote Sensing, 14(12), 2865. https://doi.org/10.3390/rs14122865