Dynamic Antenna Selection for Colocated MIMO Radar
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Methodology
1.3. Main Contributions
2. System Model
2.1. Signal Model
2.2. Target Dynamics
2.3. Measurement Model
3. Cramér–Rao Lower Bound of Joint Velocity and DOA
4. Dynamic Antenna Configuration Strategy
4.1. Objective Function Establishment
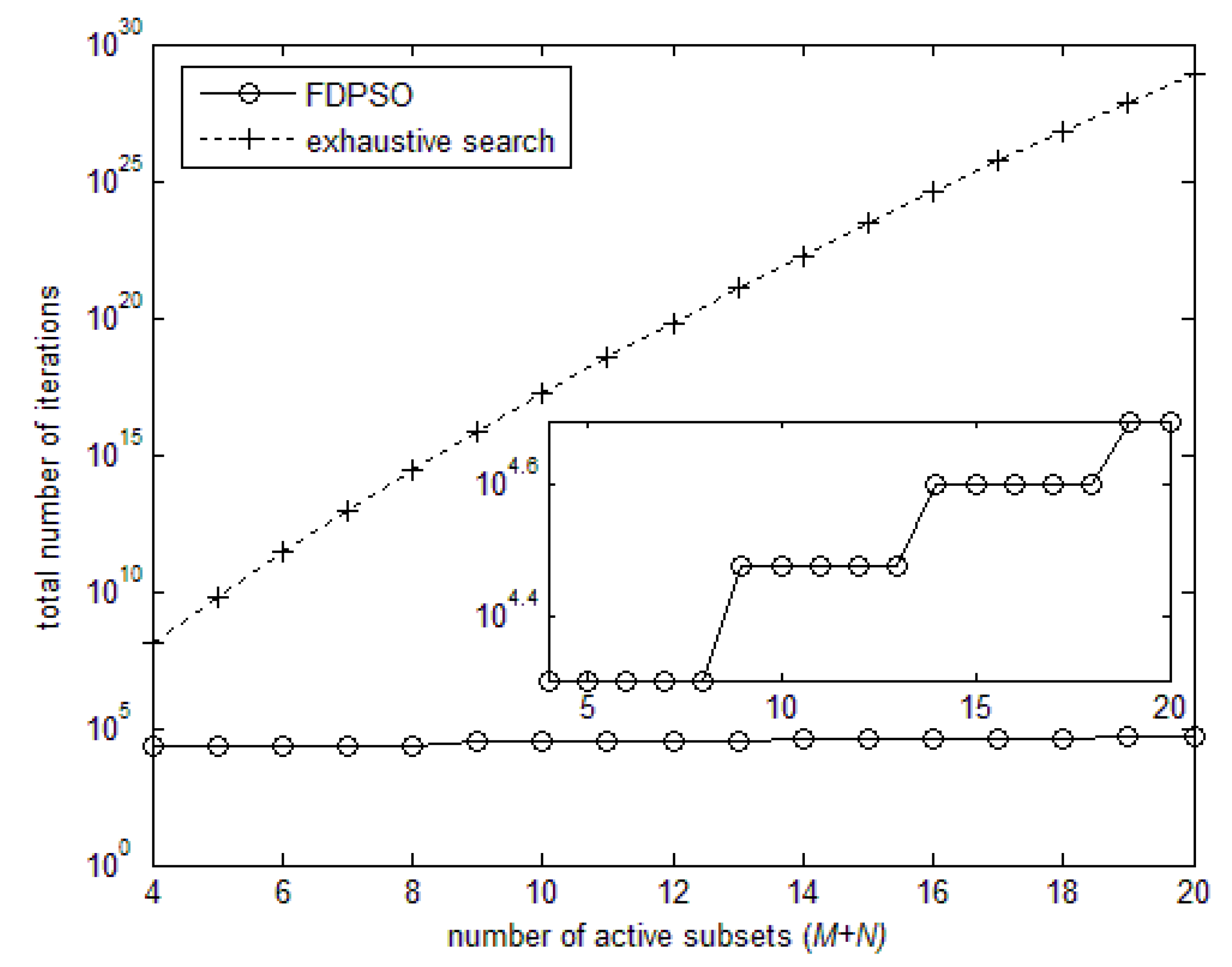
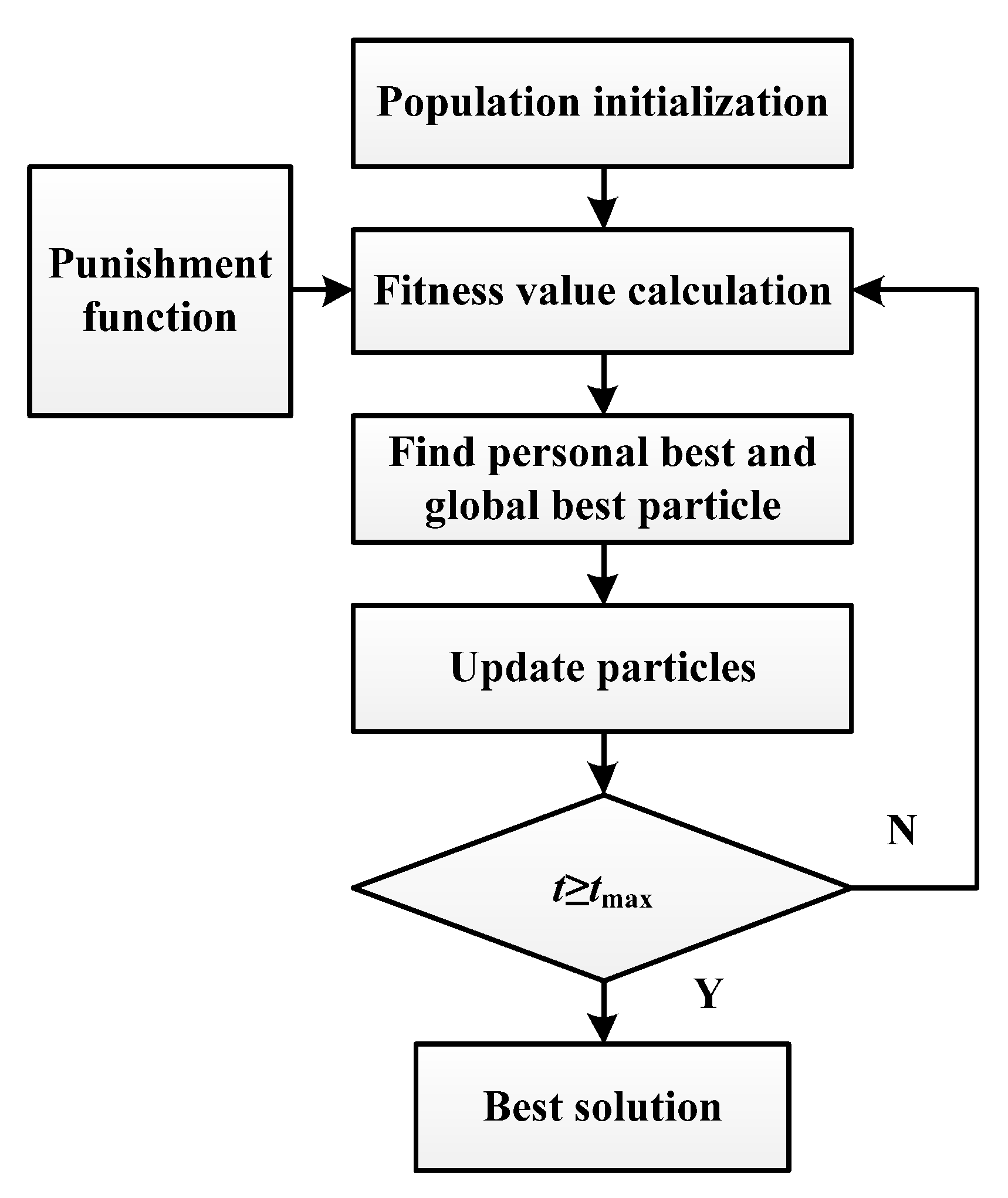
4.2. FDPSO Algorithm
4.3. Computational Complexity Analysis
4.4. Closed-Loop Feedback System for Target Tracking
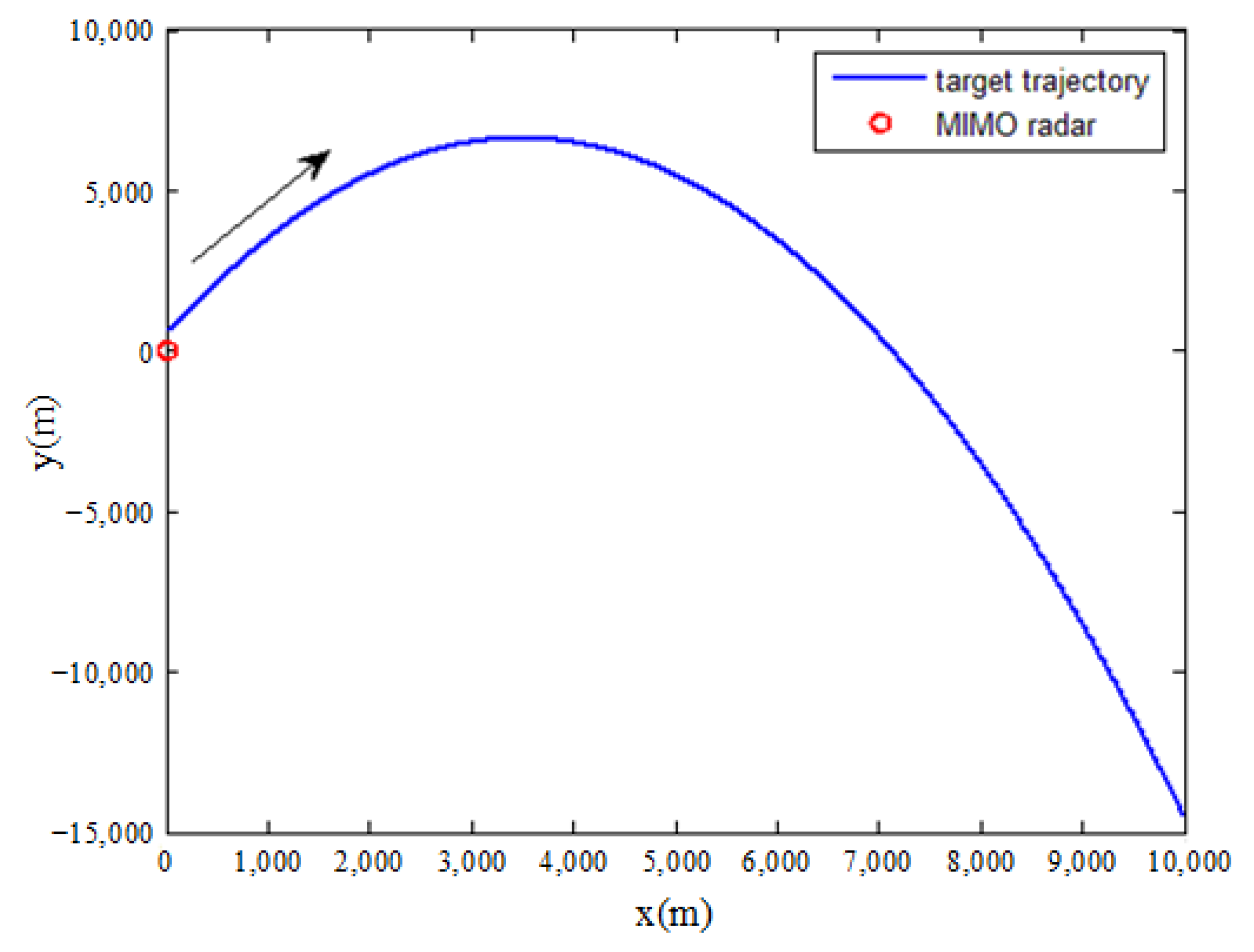
5. Simulations and Results
5.1. Determining Variable α
- (1)
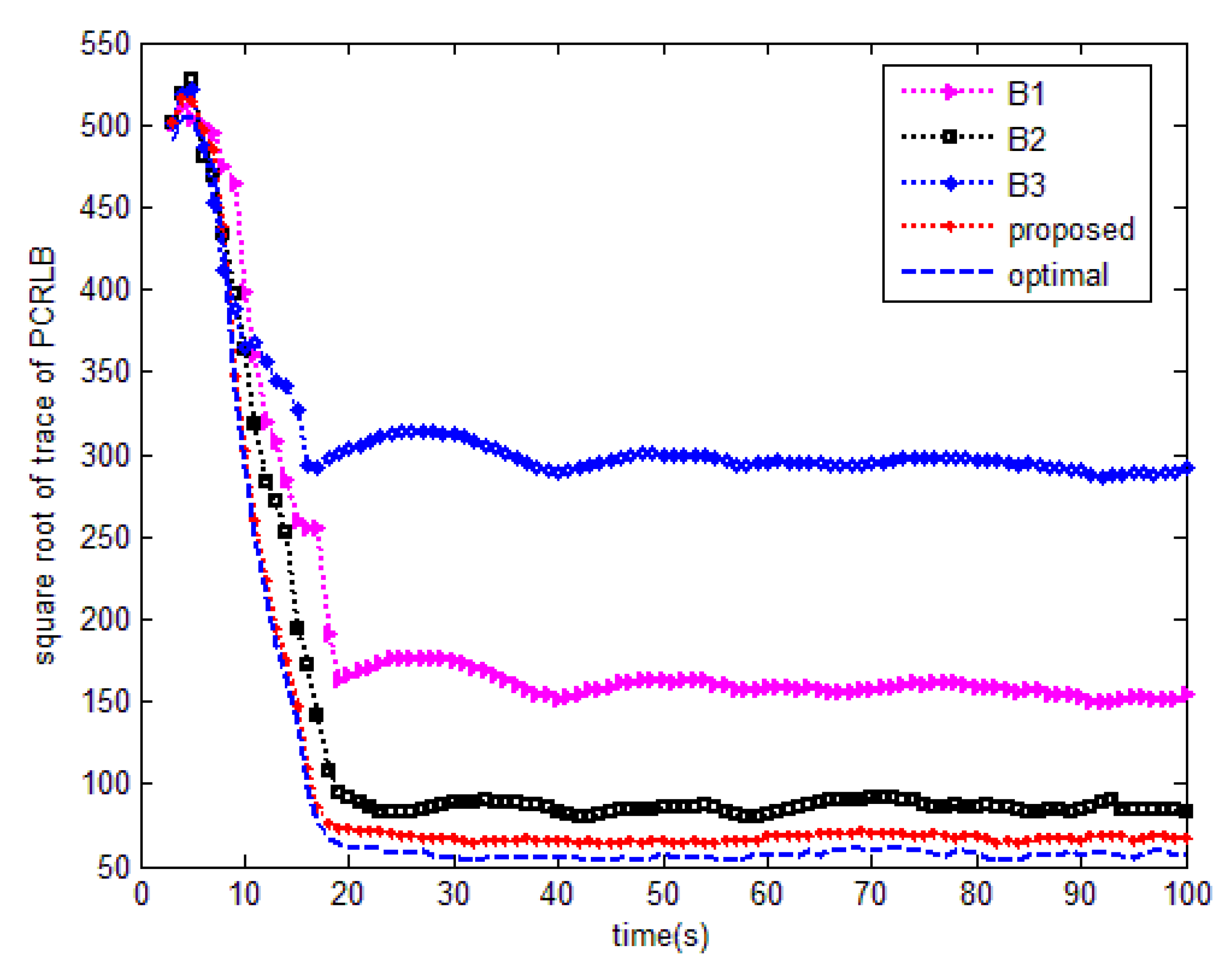
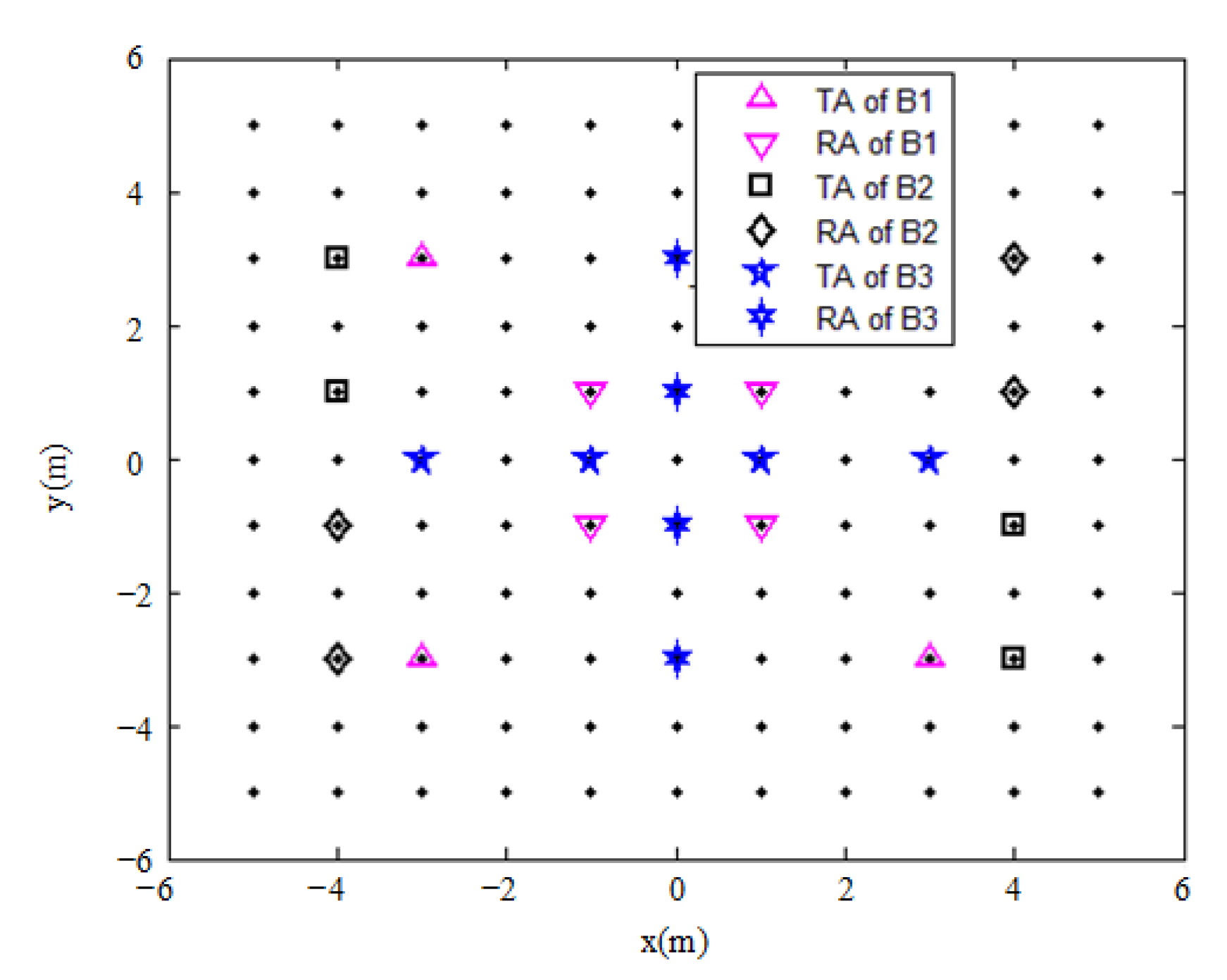
- Case of SNR = −20 dB
| Time Epoch | bt1 | bt2 | bt3 | bt4 | br1 | br2 | br3 | br4 |
|---|---|---|---|---|---|---|---|---|
| 3 | (−3,−2) | (0,−3) | (5,0) | (0,1) | (2,1) | (2,−1) | (−4,4) | (−2,0) |
| 4 | (−3,2) | (−3,4) | (5,2) | (1,−4) | (4,−3) | (1,0) | (−4,1) | (−1,−2) |
| 5 | (−4,0) | (−4,5) | (5,−4) | (−3,−3) | (2,1) | (−1,−1) | (0,1) | (5,1) |
| 6 | (2,1) | (−5,2) | (−1,−5) | (5,−1) | (4,1) | (1,0) | (−2,−1) | (−4,3) |
| 7 | (−5,3) | (0,4) | (4,3) | (−4,−3) | (4,−1) | (3,−2) | (−3,0) | (1,−4) |
| … | … | … | … | … | … | … | … | … |
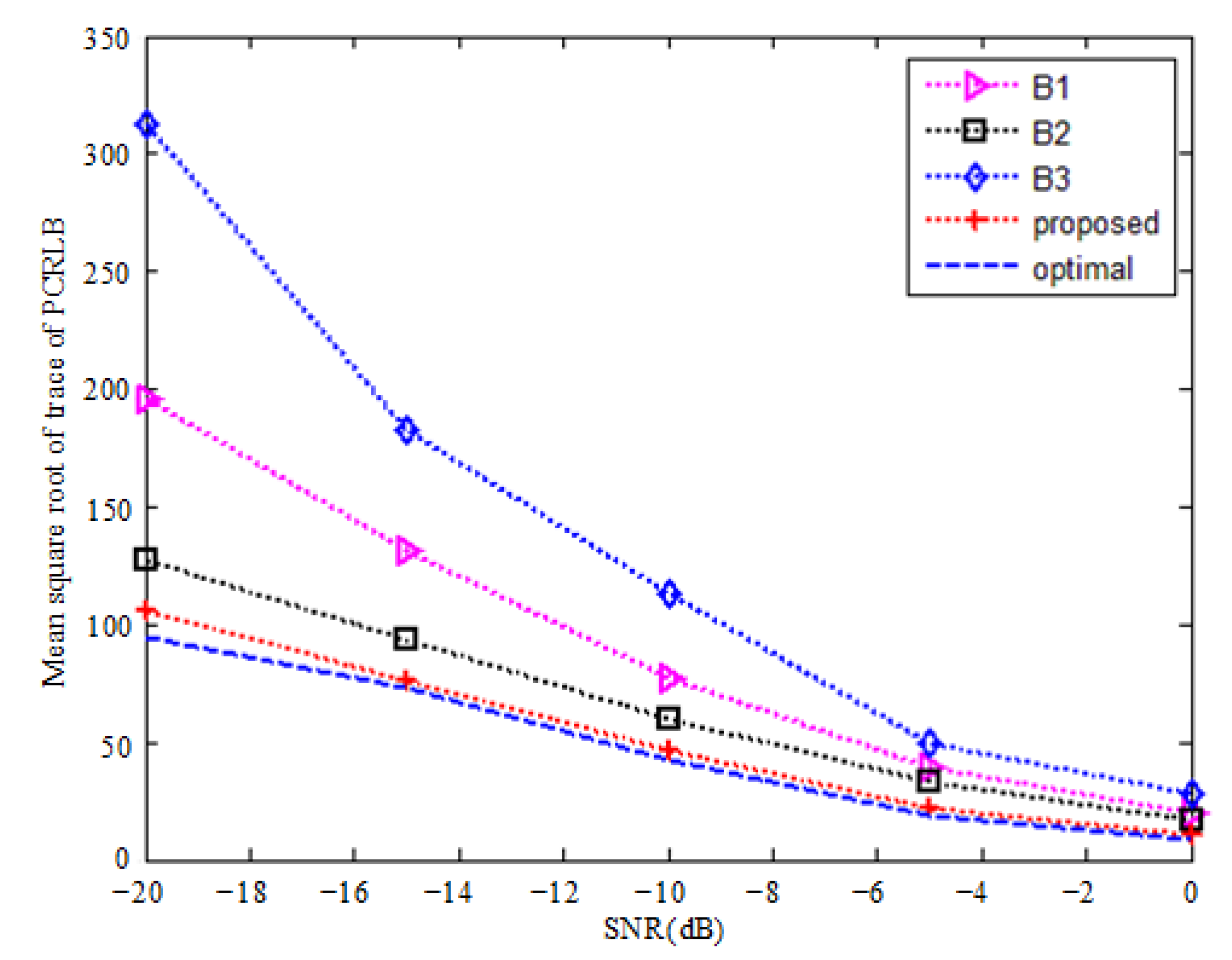
| Algorithms | Optimal | Proposed | B1 | B2 | B3 |
|---|---|---|---|---|---|
| Mean square root of trace of PCRLB | 94.3481 | 105.7771 | 196.2323 | 127.2541 | 312.7999 |
| Algorithms | Proposed | Optimal | Common Convex Optimizer |
|---|---|---|---|
| Average runtime | 354.92 | 9.32 × 106 | 50~200 |
- (2)
- Influence of SNR
5.2. Random Variable α
- (1)
- Case of SNR = −20 dB
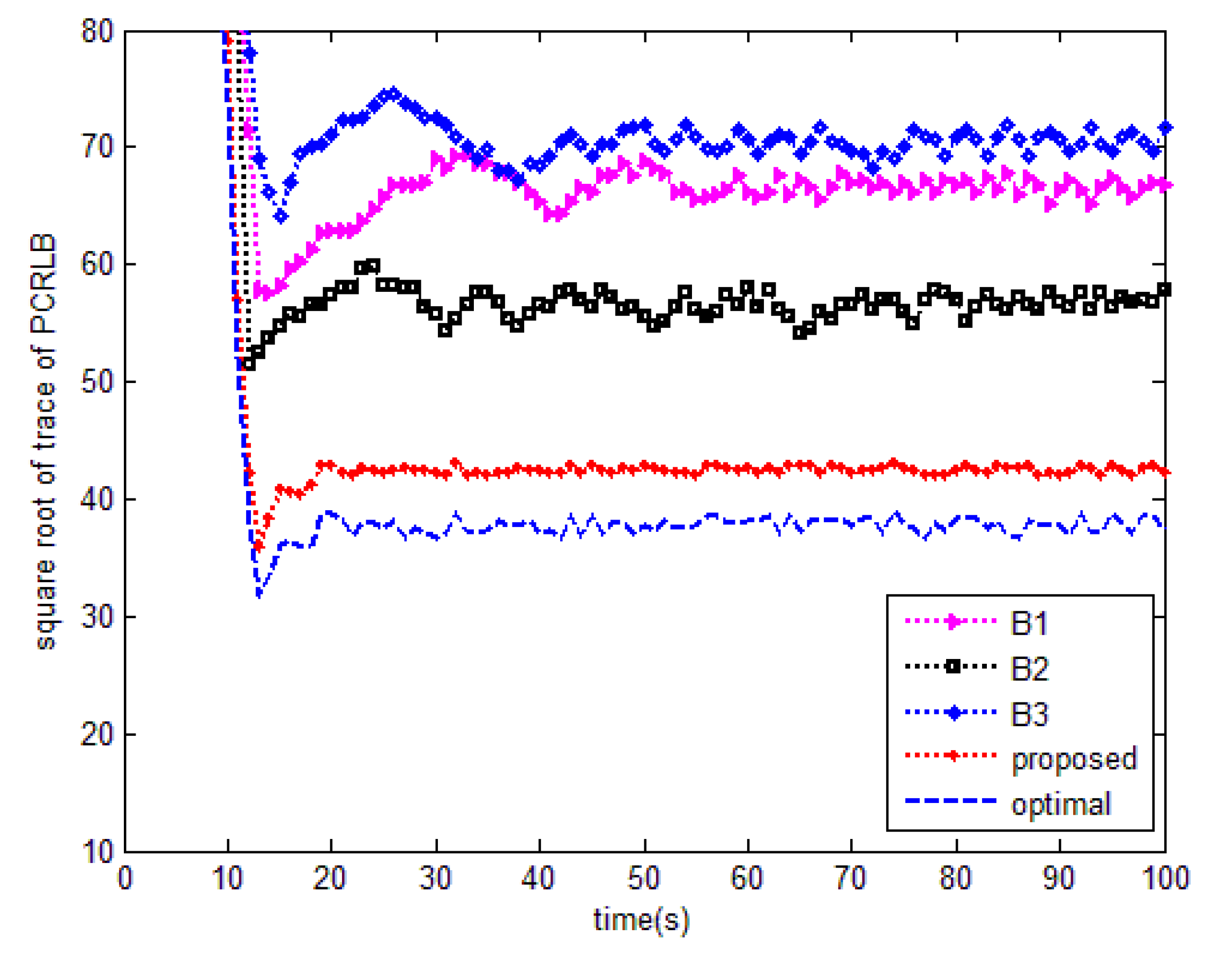
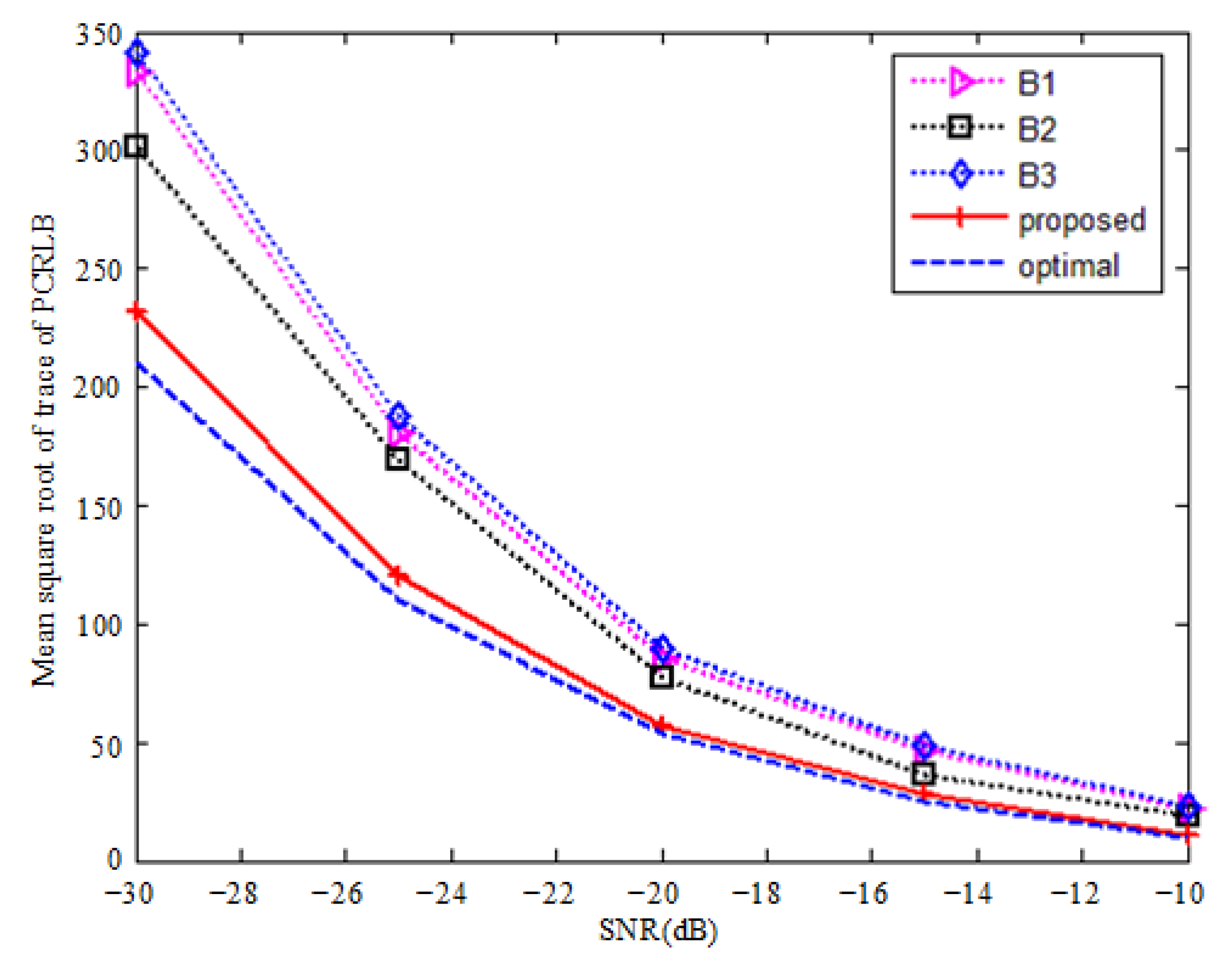
| Algorithms | Optimal | Proposed | B1 | B2 | B3 |
|---|---|---|---|---|---|
| Mean square root of trace of PCRLB | 53.2463 | 57.0236 | 85.7477 | 77.4903 | 89.4255 |
- (2)
- Influence of SNR
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of R-1 in Swerling I Type
- (1)
- Case 1 for Determining Variable α
- (2)
- Case 2 for Random Variable α
References
- Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, L.J.; Chizhik, D.; Valenzuela, R.A. Spatial diversity in radars: Models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Jian, L.; Stoica, P. MIMO radar with colocated antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar]
- Xu, L.; Li, J.; Stoica, P. Target detection and parameter estimation for MIMO radar systems. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 927–939. [Google Scholar]
- Yu, Y.; Sun, S.; Madan, R.N.; Petropulu, A. Power Allocation and Waveform Design for the Compressive Sensing Based MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 898–909. [Google Scholar] [CrossRef]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- Li, J.; Xu, L.; Stoica, P.; Forsythe, K.W.; Bliss, D.W. Range compression and waveform optimization for MIMO radar: A Cramer-Rao bound based study. IEEE Trans. Signal Process. 2008, 56, 218–232. [Google Scholar]
- Gorji, A.A.; Tharmarasa, R.; Kirubarajan, K. Optimal Antenna Allocation in MIMO Radars with Collocated Antennas. IEEE Trans. Aerosp. Electron. Syst. 2012, 50, 542–558. [Google Scholar] [CrossRef] [Green Version]
- Gorji, A.A.; Tharmarasa, R.; Blair, W.D.; Kirubarajan, T. Multiple unresolved target localization and tracking using collocated MIMO radars. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2498–2517. [Google Scholar] [CrossRef]
- Yan, J.; Jiu, B.; Liu, H.; Chen, B.; Bao, Z. Prior knowledge based simultaneous multibeam power allocation algorithm for cognitive multiple targets tracking in clutter. IEEE Trans. Signal Process. 2015, 63, 512–527. [Google Scholar] [CrossRef]
- Yan, J.; Liu, H.; Jiu, B.; Chen, B.; Liu, Z.; Bao, Z. Simultaneous multibeam resource allocation scheme for multiple target tracking. IEEE Trans. Signal Process. 2015, 63, 3110–3122. [Google Scholar] [CrossRef]
- Ming, J.; Liao, G.; Li, J. Joint DOD and DOA estimation for bistatic MIMO radar. Signal Process. 2009, 89, 244–251. [Google Scholar]
- Tichavsky, P.; Muravchik, C.; Nehorai, A. Posterior Cramer-Rao bounds for discrete-time nonlinear filtering. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef] [Green Version]
- Xie, M.; Yi, W.; Kong, L.; Kirubarajan, T. Receive-beam resource allocation for multiple target tracking with distributed MIMO radars. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2421–2436. [Google Scholar] [CrossRef]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.; Doğançay, K.; Pathirana, P.N. Optimality analysis of sensor-target localization geometries. Automatica 2010, 46, 479–492. [Google Scholar] [CrossRef]
- Tharmarasa, R.; Kirubarajan, T.; Hernandez, M.L. Large-scale optimal sensor array management for multitarget tracking. IEEE Trans. Syst. Man Cybern. 2007, 37, 803–814. [Google Scholar] [CrossRef]
- Tharmarasa, R.; Kirubarajan, T.; Hernandez, M.L.; Sinha, A. PCRLB-based multisensor array management for multitarget tracking. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 539–555. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. A combinatorial optimization framework for subset selection in distributed multiple-radar architectures. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Sensor selection in distributed multiple-radar architectures for localization: A knapsack problem formulation. IEEE Trans. Signal Process. 2012, 60, 247–260. [Google Scholar] [CrossRef]
- He, Q.; Blum, R.S.; Godrich, H.; Haimovich, A.M. Target velocity estimation and antenna placement for MIMO radar with widely separated antennas. IEEE J. Sel. Top. Signal Process. 2010, 4, 79–100. [Google Scholar] [CrossRef]
- Song, X.; Zheng, N.; Bai, T. Resource Allocation Schemes for Multiple Targets Tracking in Distributed MIMO Radar Systems. Int. J. Antenn. Propag. 2017, 2017, 7241281. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S.; Zia, A.; Xue, Y.; Arasaratnam, I. Control theoretic approach to tracking radar: First step towards cognition. Digit. Signal Process. 2011, 21, 576–585. [Google Scholar] [CrossRef]
- Huleihel, W.; Tabrikian, J.; Shavit, R. Optimal Adaptive waveform design for cognitive MIMO radar. IEEE Trans. Signal Process. 2013, 61, 5075–5089. [Google Scholar] [CrossRef]
- Chavali, P.; Nehorai, A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking. IEEE Trans. Signal Process. 2012, 60, 715–729. [Google Scholar] [CrossRef]
- Garcia, N.; Haimovich, A.M.; Coulon, M.; Lops, M. Resource allocation in MIMO radar with multiple targets for non-coherent localization. IEEE Trans. Signal Process. 2014, 62, 2656–2666. [Google Scholar] [CrossRef] [Green Version]
- Martello, S.; Toth, P. Knapsack Problems: Algorithms and Computer Implementations; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4 November 1995. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE Icnn95-international Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Rong, L.; Zhang, L.; Du, B. A novel endmember extraction method for hyperspectral Imagery based on quantum-behaved particle swarm optimization. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1610–1631. [Google Scholar]
- Liu, L.; Qi, M.S.; Zhou, F. A Novel Non-Uniform Rotational Motion Estimation and Compensation Method for Maneuvering Targets ISAR Imaging Utilizing Particle Swarm Optimization. IEEE Sens. J. 2018, 18, 299–309. [Google Scholar] [CrossRef]
- Behnamian, J. Heterogeneous networked cooperative scheduling with anarchic particle swarm optimization. IEEE Trans. Eng. Manag. 2017, 64, 166–178. [Google Scholar] [CrossRef]
- Yu, Z.; Xiao, L.; Li, H.; Zhu, X.; Huai, R. Model Parameter Identification for Lithium Batteries Using the Coevolutionary Particle Swarm Optimization Method. IEEE Trans. Ind. Electron. 2017, 64, 5690–5700. [Google Scholar] [CrossRef]
- Meza, J.; Espitia, H.; Montenegro, C.; Giménez, E.; González-Crespo, R. González-Crespo, MOVPSO: Vortex multi-objective particle swarm optimization. Appl. Soft. Comput. 2017, 52, 1042–1057. [Google Scholar] [CrossRef]
- Valdez, F.; Vazquez, J.C.; Melin, P.; Castillo, O. Comparative study of the use of fuzzy logic in improving particle swarm optimization variants for mathematical functions using co-evolution. Appl. Soft. Comput. 2017, 52, 1070–1083. [Google Scholar] [CrossRef]
- Tsai, H.C. Unified particle swarm delivers high efficiency to particle swarm optimization. Appl. Soft. Comput. 2017, 55, 371–383. [Google Scholar] [CrossRef]
- Ouyang, H.B.; Gao, L.Q.; Li, S.; Kong, X.Y. Improved global-best-guided particle swarm optimization with learning operation for global optimization problems. Appl. Soft. Comput. 2017, 52, 987–1008. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Ensemble particle swarm optimizer. Appl. Soft. Comput. 2017, 55, 533–548. [Google Scholar] [CrossRef]
- Gou, J.; Lei, Y.X.; Guo, W.P.; Wang, C.; Cai, Y.Q.; Luo, W. A novel improved particle swarm optimization algorithm based on individual difference evolution. Appl. Soft. Comput. 2017, 57, 468–481. [Google Scholar] [CrossRef]
- Kao, Y.T.; Zahara, E. A hybrid GA and particle swarm optimization for multimodal functions. Appl. Soft. Comput. 2008, 8, 849–857. [Google Scholar] [CrossRef]
- Cheng, S.; Zhan, H.; Shu, Z. An innovative hybrid multi-objective particle swarm optimization with or without constraints handling. Appl. Soft. Comput. 2016, 47, 370–388. [Google Scholar] [CrossRef]
- Tan, C.; Chang, S.Q.; Liu, L. Hierarchical genetic-particle swarm optimization for bistable permanent magnet actuators. Appl. Soft. Comput. 2017, 61, 1–7. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Glass, J.D.; Smith, L.D. MIMO radar resource allocation using posterior Cramer-Rao lower bounds. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3 May 2011. [Google Scholar]
- Zhang, H.; Xie, J.; Ge, J.; Lu, W.; Zong, B. Adaptive Strong Tracking Square-Root Cubature Kalman Filter for Maneuvering Aircraft Tracking. IEEE Access 2018, 6, 10052–10061. [Google Scholar] [CrossRef]
- Cui, B.; Chen, X.; Tang, X. Improved cubature Kalman filter for GNSS/INS based on transformation of posterior sigma-points error. IEEE Trans. Signal Process. 2017, 65, 2975–2987. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Z.; Lu, W.; Xie, J. Joint target assignment and power allocation in multiple distributed MIMO radar networks. IEEE Syst. J. 2021, 15, 694–704. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Shi, J.; Fei, T.; Zong, B. Joint detection threshold optimization and illumination time allocation strategy for cognitive tracking in a networked radar system. IEEE Trans. Signal Process. 2022, to be published. [Google Scholar]
| Algorithms | Exhaustive Search | FDPSO |
|---|---|---|
| Computational complexity | O (2Mtot+Ntot) | O (Npoptmax) |
| Ts = 1 s | M = 4 | dmin = 2 m | bL = 5 m | Npop = 100 | γ = 0.2 | Ntot = 121 |
| TP = 0.01 s | N = 4 | dmax = 12 m | bU = 5 m | tmax = 100 | ρ = 0.95 | |
| nf = 1 | L = 128 | λ = 0.2 m | Δd = 1 m | β = 0.5 | Mtot = 121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Xie, J.; Zhang, H.; Li, Z.; Qi, C. Dynamic Antenna Selection for Colocated MIMO Radar. Remote Sens. 2022, 14, 2912. https://doi.org/10.3390/rs14122912
Zhang G, Xie J, Zhang H, Li Z, Qi C. Dynamic Antenna Selection for Colocated MIMO Radar. Remote Sensing. 2022; 14(12):2912. https://doi.org/10.3390/rs14122912
Chicago/Turabian StyleZhang, Gangsheng, Junwei Xie, Haowei Zhang, Zhengjie Li, and Cheng Qi. 2022. "Dynamic Antenna Selection for Colocated MIMO Radar" Remote Sensing 14, no. 12: 2912. https://doi.org/10.3390/rs14122912
APA StyleZhang, G., Xie, J., Zhang, H., Li, Z., & Qi, C. (2022). Dynamic Antenna Selection for Colocated MIMO Radar. Remote Sensing, 14(12), 2912. https://doi.org/10.3390/rs14122912







