Drying–Wetting Changes of Surface Soil Moisture and the Influencing Factors in Permafrost Regions of the Qinghai-Tibet Plateau, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Preparing
2.2.1. Observation Data
2.2.2. Soil Moisture Estimate Data
2.2.3. Meteorological and Vegetation Data
2.3. Methods
2.3.1. Accuracy Evaluation
2.3.2. Mann–Kendall Trend Test
2.3.3. Ensemble Empirical Mode Decomposition
3. Results
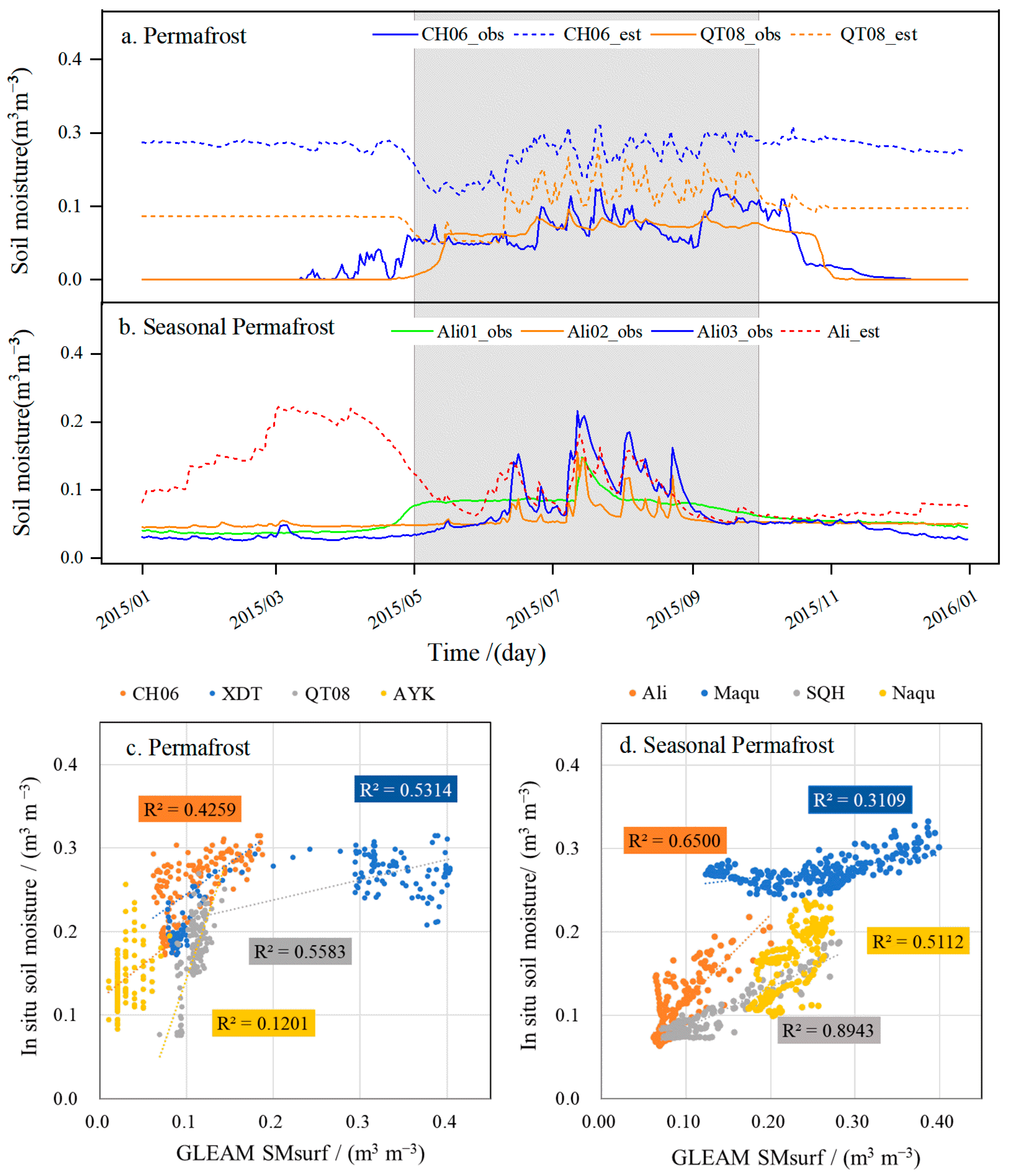
3.1. Accuracy Evaluation of GLEAM SM Products
3.1.1. Comparison of GLEAM SM Products and Observation Data
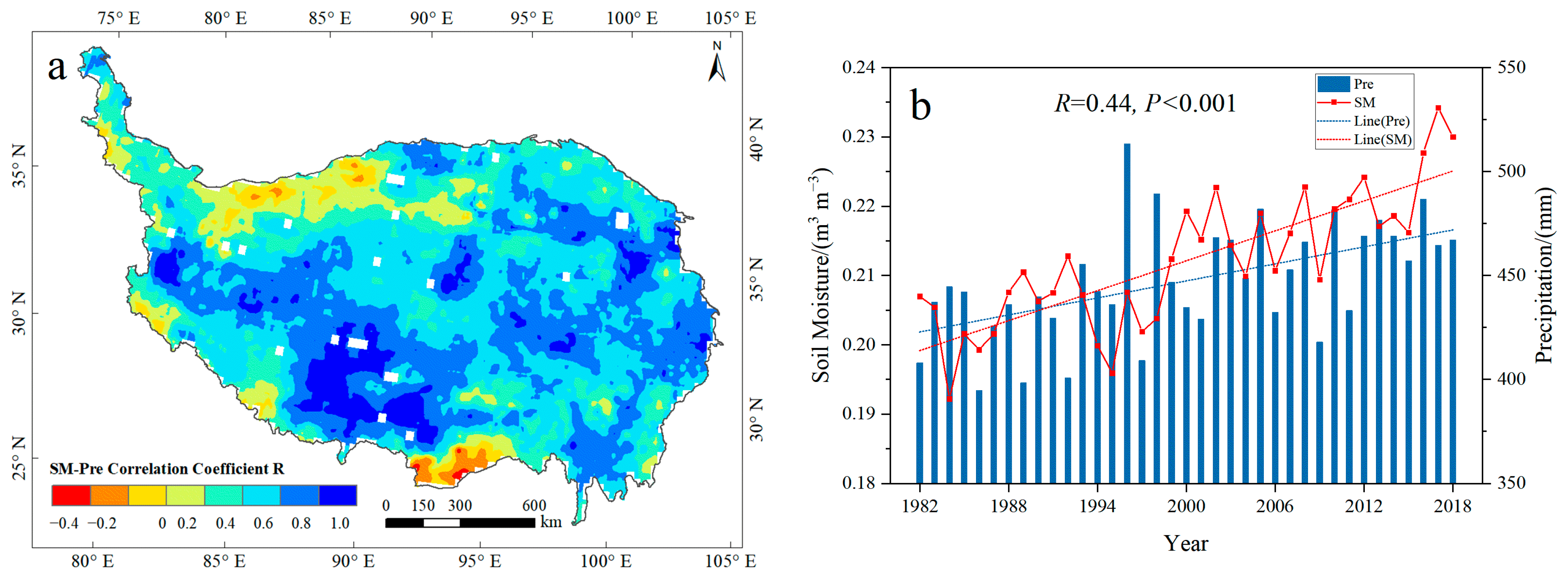
3.1.2. Comparison of Hydrological Characteristics of GLEAM SM and Precipitation
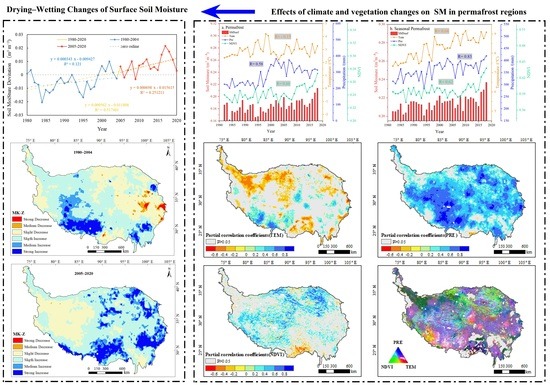
3.2. Trend Characteristics and Spatial Heterogeneity of Soil Moisture
3.2.1. Dynamic Trends of Soil Moisture
3.2.2. Spatial Heterogeneity of Soil Moisture Dynamics Trends
3.2.3. Soil Moisture Dynamics under Different Vegetation Conditions
4. Discussion
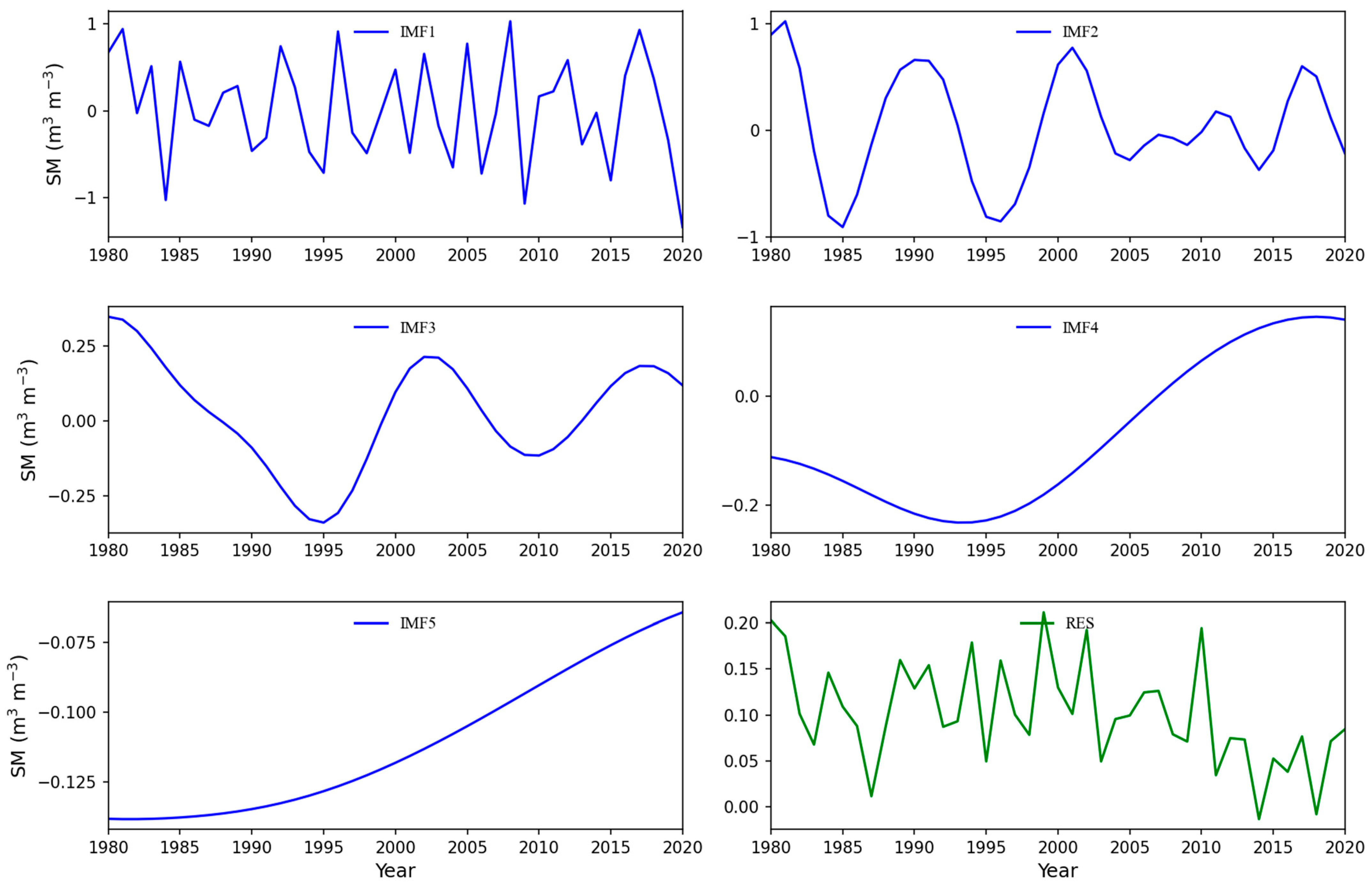
4.1. Trend Analysis Based on EEMD
4.2. Analysis of the Causes of Soil Wetting Trends
4.2.1. Synergistic Effects of Soil Wetting with Climate and Vegetation Change
4.2.2. Effects of Climate and Vegetation Changes on Soil Moisture
4.2.3. Quantitative Analysis of the Causes of Soil Moisture Changes in Permafrost Regions
5. Conclusions
- (1)
- GLEAM SM products can better reflect SM changes in the Qinghai-Tibet Plateau in the warm season. The average correlation coefficient with measured SM, Bias, and average ubRMSE in the permafrost region were 0.619, 0.079 m3 m−3, and 0.049 m3 m−3, respectively. In the seasonal permafrost region, the average correlation coefficient with measured SM was 0.809 with a maximum of 0.946, the Bias was 0.025 m3 m−3, and the average ubRMSE was 0.033 m3 m−3. Overall, there is some overestimation of the GLEAM SM product in the warm season; however, it is closer to the real SM in the seasonal permafrost region than in the permafrost region, and the data accuracy is higher than other SM products.
- (2)
- In the past 40 years, the QTP SM has shown a significant wetting trend, with an average rate of 0.573 × 10−3 m3 m−3 yr−1. Under the influence of global warming, this rising trend accelerated after 2005. The area showing significant wetting accounts for 64.31% of the QTP, mainly distributed in the perennial permafrost distribution area. Soil wetting is faster in dry areas such as the alpine desert, meadow, and steppe dry areas, while the SM rises more slowly in wet areas such as woodlands. However, the wetting trend of SM on the QTP does not have a long-term continuity of more than 20 years and is dominated by interannual and interdecadal oscillations, showing the variation process of “wetting–drying–wetting”, in which the oscillations are more significant in seasonal permafrost regions.
- (3)
- Soil wetting trends on the QTP are jointly determined by temperature, precipitation, and vegetation, and the combined explanatory power of the three is over 65%; however, there is apparent spatial heterogeneity in different permafrost regions and vegetation cover conditions. In the permafrost region, the combined explanatory power of the three was 51%, and precipitation had the highest contribution of 47.2%. In the seasonal permafrost region, the combined explanatory power was 69.1%, and the contribution of both precipitation and vegetation exceeded 41%, with vegetation being the key factor of SM changes on the QTP. Overall, with global climate change, the synergistic effect of soil moisture–vegetation–climate on the QTP tends to become more pronounced in the seasonal permafrost region.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.A.M.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwingshackl, C.; Hirschi, M.; Seneviratne, S.I. Quantifying Spatiotemporal Variations of Soil Moisture Control on Surface Energy Balance and Near-Surface Air Temperature. J. Clim. 2017, 30, 7105–7124. [Google Scholar] [CrossRef]
- Meng, X.; Li, R.; Luan, L.; Lyu, S.; Zhang, T.; Ao, Y.; Han, B.; Zhao, L.; Ma, Y. Detecting hydrological consistency between soil moisture and precipitation and changes of soil moisture in summer over the Tibetan Plateau. Clim. Dyn. 2018, 51, 4157–4168. [Google Scholar] [CrossRef] [Green Version]
- Nicolai-Shaw, N. Climate Research Applications of Remote-Sensing Based Soil Moisture: Spatial Representativeness, Predictability and Drought Response; ETH Zurich: Zurich, Switzerland, 2016. [Google Scholar]
- Wang, C.; Dong, W.; Wei, Z. Anomaly feature of seasonal frozen soil variationson the Qinghai-Tibet Plateau. J. Geogr. Sci. 2002, 12, 102–110. [Google Scholar]
- Jiang, K.; Pan, Z.; Pan, F.; Wang, J.; Han, G.; Song, Y.; Zhang, Z.; Huang, N.; Ma, S.; Chen, X. Influence patterns of soil moisture change on surface-air temperature difference under different climatic background. Sci. Total Environ. 2022, 822, 153607. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Peng, F.; Xue, X.; You, Q.; Lai, C.; Zhang, W.; Cheng, Y. Productivity and Quality of Alpine Grassland Vary with Soil Water Availability under Experimental Warming. Front. Plant Sci. 2018, 9, 1790. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Gao, J.; Zhao, L.; Xu, X.; Ouyang, H. Linking thaw depth with soil moisture and plant community composition: Effects of permafrost degradation on alpine ecosystems on the Qinghai-Tibet Plateau. Plant Soil 2012, 367, 687–700. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.; Yang, W.; Sun, Z.; Zhao, J. Variation in soil hydrological properties on shady and sunny slopes in the permafrost region, Qinghai–Tibetan Plateau. Environ. Earth Sci. 2019, 78, 100. [Google Scholar] [CrossRef]
- Jiang, P.; Ding, W.; Yuan, Y.; Ye, W. Diverse response of vegetation growth to multi-time-scale drought under different soil textures in China’s pastoral areas. J. Environ. Manag. 2020, 274, 110992. [Google Scholar] [CrossRef]
- Gallego-Elvira, B.; Taylor, C.M.; Harris, P.P.; Ghent, D.; Veal, K.L.; Folwell, S.S. Global observational diagnosis of soil moisture control on the land surface energy balance. Geophys. Res. Lett. 2016, 43, 2623–2631. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.P.; Meng, X.; McCabe, M.F. Land surface albedo and vegetation feedbacks enhanced the millennium drought in south-east Australia. Hydrol. Earth Syst. Sci. 2017, 21, 409–422. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Huang, J. Enhanced soil moisture drying in transitional regions under a warming climate. J. Geophys. Res. Atmos. 2016, 121, 2542–2555. [Google Scholar] [CrossRef]
- Schuur, E.A.; Mack, M.C. Ecological Response to Permafrost Thaw and Consequences for Local and Global Ecosystem Services. Annu. Rev. Ecol. Evol. Syst. 2018, 49, 279–301. [Google Scholar] [CrossRef]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Zou, D.; Hu, G.; Du, E.; Pang, Q.; Xiao, Y.; Li, R.; Sheng, Y.; Wu, X.; Sun, Z.; et al. Changing climate and the permafrost environment on the Qinghai–Tibet (Xizang) plateau. Permafr. Periglac. Processes 2020, 31, 396–405. [Google Scholar] [CrossRef]
- Cheng, G.; Wu, Q.; Li, R.; Li, X.; Sheng, Y.; Hu, G.; Zhao, L.; Jin, H.; Zou, D.; Wu, X. Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau. Chin. Sci. Bull. 2019, 64, 2783–2795. [Google Scholar]
- Jianping, L.I.; Fei, Z.; Cheng, S.U.; Juan, F.; Jing, W. Pathways of Influence of the Northern Hemisphere Mid–high Latitudes on East Asian Climate: A Review. Adv. Atmos. Sci. 2019, 36, 902–921. [Google Scholar]
- Wang, K.; Zhang, T.; Mu, C.; Zhong, X.; Peng, X.; Cao, B.; Lu, L.; Zheng, L.; Wu, X.; Liu, J. From the Third Pole to the Arctic: Changes and impacts of the climate and cryosphere. J. Glaciol. Geocryol. 2020, 42, 104–123. [Google Scholar]
- Ma, Q.; Jin, H.; Bense, V.F.; Luo, D.; Marchenko, S.S.; Harris, S.A.; Lan, Y. Impacts of degrading permafrost on streamflow in the source area of Yellow River on the Qinghai-Tibet Plateau, China. Adv. Clim. Change Res. 2019, 10, 225–239. [Google Scholar] [CrossRef]
- Chen, S.; Liu, W.; Qin, X.; Liu, Y.; Zhang, T.; Chen, K.; Hu, F.; Ren, J.; Qin, D. Response characteristics of vegetation and soil environment to permafrost degradation in the upstream regions of the Shule River Basin. Environ. Res. Lett. 2012, 7, 45406. [Google Scholar] [CrossRef] [Green Version]
- Kuang, X.; Jiao, J.J. Review on climate change on the Tibetan Plateau during the last half century. J. Geophys. Res. Atmos. 2016, 121, 3979–4007. [Google Scholar] [CrossRef]
- Wu, P.; Liang, S.; Wang, X.-S.; Feng, Y.; McKenzie, J. A New Assessment of Hydrological Change in the Source Region of the Yellow River. Water 2018, 10, 877. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Dong, Z.; Zhou, Z. Effect of decreasing soil frozen depth on vegetation growth in the source region of the Yellow River for 1982–2015. Theor. Appl. Climatol. 2020, 140, 1185–1197. [Google Scholar] [CrossRef]
- Jin, X.; Jin, H.; Iwahana, G.; Marchenko, S.S.; Luo, D.; Li, X.; Liang, S. Impacts of climate-induced permafrost degradation on vegetation: A review. Adv. Clim. Change Res. 2021, 12, 29–47. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Env. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Chen, H.; Wu, J.; Li, C.; Li, Z.; Qin, G. Applicability evaluation of satellite soil moisture products in Qinghai-Tibet Plateau. Acta Ecol. Sin. 2020, 40, 9195–9207. [Google Scholar]
- Luo, D.; Jin, H.; Bense, V.F.; Jin, X.; Li, X. Hydrothermal processes of near-surface warm permafrost in response to strong precipitation events in the Headwater Area of the Yellow River, Tibetan Plateau. Geoderma 2020, 376, 114531. [Google Scholar] [CrossRef]
- Wang, W.; Wu, T.; Zhao, L.; Li, R.; Zhu, X.; Wang, W.; Yang, S.; Qin, Y.; Hao, J. Exploring the ground ice recharge near permafrost table on the central Qinghai-Tibet Plateau using chemical and isotopic data. J. Hydrol. 2018, 560, 220–229. [Google Scholar] [CrossRef]
- Fu, W.; Zhang, X.; Zhao, J.; Du, S.; Horton, R.; Hou, M. Artificial warming-mediated soil freezing and thawing processes can regulate soybean production in Northeast China. Agric. For. Meteorol. 2018, 262, 249–257. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Luo, G.; Wu, L.; Cao, Y.; Li, H.; Li, C.; Yang, Y.; Hu, Z.; et al. Variation trend of global soil moisture and its cause analysis. Ecol. Indic. 2020, 110, 105939. [Google Scholar] [CrossRef]
- Fan, K.; Zhang, Q.; Shi, P.; Sun, P.; Yu, H. Evaluation of remote sensing and reanalysis soil moisture products on the Tibetan Plateau. Acta Geogr. Sin. 2018, 73, 1778–1791. [Google Scholar]
- Deng, Y.; Wang, S.; Bai, X.; Wu, L.; Cao, Y.; Li, H.; Wang, M.; Li, C.; Yang, Y.; Hu, Z.; et al. Comparison of soil moisture products from microwave remote sensing, land model, and reanalysis using global ground observations. Hydrol. Processes 2020, 34, 836–851. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, Z.; van der Velde, R.; Wang, L.; Xu, K.; Wang, X.; Wen, J. Blending Satellite Observed, Model Simulated, and In Situ Measured Soil Moisture over Tibetan Plateau. Remote Sens. 2016, 8, 268. [Google Scholar] [CrossRef] [Green Version]
- Fan, K.; Zhang, Q.; Sun, P.; Song, C.; Zhu, X.; Yu, H.; Shen, Z. Variation, causes and future estimation of surface soil moisture on the Tibetan Plateau. Acta Ecol. Sinica 2019, 74, 520–533. [Google Scholar]
- Gao, Z.; Niu, F.; Lin, Z.; Luo, J.; Yin, G.; Wang, Y. Evaluation of thermokarst lake water balance in the Qinghai-Tibet Plateau via isotope tracers. Sci. Total Environ. 2018, 636, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Su, F.; Zhang, L.; Ou, T.; Chen, D.; Yao, T.; Tong, K.; Qi, Y. Hydrological response to future climate changes for the major upstream river basins in the Tibetan Plateau. Glob. Planet. Chang. 2016, 136, 82–95. [Google Scholar] [CrossRef]
- Gao, Y.; Li, X.; Leung, R.L.; Chen, D.; Xu, J. Aridity changes in the Tibetan Plateau in a warming climate. Environ. Res. Lett. 2015, 10, 34013. [Google Scholar] [CrossRef]
- Li, C.; Lu, H.; Yang, K.; Han, M.; Wright, J.; Chen, Y.; Yu, L.; Xu, S.; Huang, X.; Gong, W. The Evaluation of SMAP Enhanced Soil Moisture Products Using High-Resolution Model Simulations and In-Situ Observations on the Tibetan Plateau. Remote Sens. 2018, 10, 535. [Google Scholar] [CrossRef] [Green Version]
- Niu, F.; Gao, Z.; Lin, Z.; Luo, J.; Fan, X. Vegetation influence on the soil hydrological regime in permafrost regions of the Qinghai-Tibet Plateau, China. Geoderma 2019, 354, 113892. [Google Scholar] [CrossRef]
- Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sens. Environ. 2006, 100, 190–199. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; Rosnay, P.D.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of its Specifications, Validation Results, and Emerging Applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Gruber, A.; de Jeu, R.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Beaudoing, H.; Rodell, M.; Nasa/Gsfc/Hsl. GLDAS Noah Land Surface Model L4 3 Hourly 0.25 × 0.25 Degree, Version 2.1; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2020. [Google Scholar]
- Su, Z.; Wen, J.; Dente, L.; van der Velde, R.; Wang, L.; Ma, Y.; Yang, K.; Hu, Z. The Tibetan Plateau observatory of plateau scale soil moisture and soil temperature (Tibet-Obs) for quantifying uncertainties in coarse resolution satellite and model products. Hydrol. Earth Syst. Sci. 2011, 15, 2303–2316. [Google Scholar] [CrossRef] [Green Version]
- Su, Z.; de Rosnay, P.; Wen, J.; Wang, L.; Zeng, Y. Evaluation of ECMWF’s soil moisture analyses using observations on the Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 5304–5318. [Google Scholar] [CrossRef] [Green Version]
- Xing, Z.; Fan, L.; Zhao, L.; de Lannoy, G.; Frappart, F.; Peng, J.; Li, X.; Zeng, J.; Al-Yaari, A.; Yang, K.; et al. A first assessment of satellite and reanalysis estimates of surface and root-zone soil moisture over the permafrost region of Qinghai-Tibet Plateau. Remote Sens. Environ. 2021, 265, 112666. [Google Scholar] [CrossRef]
- Yuan, X.; Ma, Z.; Pan, M.; Shi, C. Microwave remote sensing of short-term droughts during crop growing seasons. Geophys. Res. Lett. 2015, 42, 4394–4401. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, H.; Tong, C.; Liu, W.; Du, B. Evaluation of ESA Active, Passive and Combined Soil Moisture Products Using Upscaled Ground Measurements. Sensors 2019, 19, 2718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, M.; Zhong, L.; Ma, Y.; Zou, M.; Hu, Y. A Study on the Assessment of Multi-Source Satellite Soil Moisture Products and Reanalysis Data for the Tibetan Plateau. Remote Sens. 2019, 11, 1196. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, B.; Zheng, D. A discussion on the boundary and area of the Tibetan Plateau in China. Geogr. Res. 2002, 21, 1–8. [Google Scholar]
- Immerzeel, W.W.; Bierkens, M.F.P. Asian water towers: More on monsoons—Response. Science 2010, 330, 585. [Google Scholar] [CrossRef]
- Zhao, L.; Ding, Y.J.; Liu, G.Y.; Wang, S.L.; Jin, H.J. Estimates of the Reserves of Ground Ice in Permafrost Regions on the Tibetan Plateau. J. Glaciol. Geocryol. 2010, 32, 1–9. [Google Scholar]
- Chang, J.; Wang, G.X.; Chunjie, L.I.; Mao, T.X. Seasonal dynamics of suprapermafrost groundwater and its response to the freeing-thawing processes of soil in the permafrost region of Qinghai-Tibet Plateau. Sci. China Earth Sci. 2015, 58, 727–738. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, G.; Zou, D.; Wu, X.; Liu, S. Permafrost Changes and Its Effects on Hydrological Processes on Qinghai-Tibet Plateau. Bull. Chin. Acad. Sci. (Chin. Version) 2019, 34, 1233–1246. [Google Scholar]
- Duan, H.; Xue, X.; Wang, T.; Kang, W.; Liao, J.; Liu, S. Spatial and Temporal Differences in Alpine Meadow, Alpine Steppe and All Vegetation of the Qinghai-Tibetan Plateau and Their Responses to Climate Change. Remote Sens. 2021, 13, 669. [Google Scholar] [CrossRef]
- Zhang, P.; Zheng, D.; van der Velde, R.; Wen, J.; Zeng, Y.; Wang, X.; Wang, Z.; Chen, J.; Su, Z. A 10-Year (2009–2019) Surface Soil Moisture Dataset Produced Based on in situ Measurements Collected from the Tibet-Obs; 4TU.ResearchData: Delft, The Netherlands, 2020. [Google Scholar]
- Zhang, P.; Zheng, D.; van der Velde, R.; Wen, J.; Zeng, Y.; Wang, X.; Wang, Z.; Chen, J.; Su, Z. Status of the Tibetan Plateau observatory (Tibet-Obs) and a 10-year (2009–2019) surface soil moisture dataset. Earth Syst. Sci. Data 2021, 13, 3075–3102. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Wu, T.; Du, E.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A synthesis dataset of permafrost thermal state for the Qinghai–Tibet (Xizang) Plateau, China. Earth Syst. Sci. Data 2021, 13, 4207–4218. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, G.; Zou, D.; Wu, T.; Erji, D.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A Synthesis Dataset of Permafrost for the Qinghai-Xizang (Tibet) Plateau, China (2002–2018); National Tibetan Plateau Data Center: Beijing, China, 2021. [Google Scholar]
- Ren, L.; Wei, L.; Jiang, S.; Shi, J.; Yuan, F.; Zhang, L.; Liu, R. Drought monitoring utility assessment of CHIRPS and GLEAM satellite products in China. Transl. Chin. Soc. Agric. Eng. 2019, 35, 146–154. [Google Scholar]
- Jiang, B.; Tian, J.; Su, H. Estimation of monthly evapotranspiration and soil moisture in the Central Asia. Prog. Geogr. 2020, 39, 433–442. [Google Scholar] [CrossRef]
- Li, H.; Zhang, C.; Wang, S.; Ma, W.; Liu, F.; Chen, Q.; Zhou, Q.; Xia, X.; Niu, B. Response of vegetation dynamics to hydrothermal conditions on the Qinghai-Tibetan Plateau in the last 40 years. Acta Ecol. Sin. 2022, 42, 1–14. [Google Scholar]
- Hou, X. 1:1 Million Vegetation Map of China; National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Zhao, L. A new map of permafrost distribution on the Tibetan Plateau (2017); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Pan, M.; Sahoo, A.K.; Wood, E.F. Improving soil moisture retrievals from a physically-based radiative transfer model. Remote Sens. Environ. 2014, 140, 130–140. [Google Scholar] [CrossRef]
- Song, E.; Liu, S.; He, R.; Cai, J.; Luo, K. Forward modeling on the seasonal frozen soil region detection by ground penetrating radar. Geophys. Geochem. Explor. 2018, 42, 962–969. [Google Scholar]
- Du, E.; Zhao, L.; Wu, T.; Li, R.; Yue, G.; Wu, X.; Li, W.; Jiao, Y.; Hu, G.; Qiao, Y.; et al. The relationship between the ground surface layer permittivity and active-layer thawing depth in a Qinghai–Tibetan Plateau permafrost area. Cold Reg. Sci. Technol. 2016, 126, 55–60. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Theil–Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical model decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Qin, Z.; Zou, X.; Weng, F. Comparison between linear and nonlinear trends in NOAA-15 AMSU-A brightness temperatures during 1998–2010. Clim. Dyn. 2012, 39, 1763–1779. [Google Scholar] [CrossRef]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition. Geoderma 2018, 330, 136–161. [Google Scholar] [CrossRef]
- Huang, N.E. An Adaptive Data Analysis Method for Nonlinear and Nonstationary Time Series: The Empirical Mode Decomposition and Hilbert Spectral Analysis. In Wavelet Analysis and Applications; Qian, T., Vai, M.I., Xu, Y., Eds.; Birkhäuser: Basel, Switzerland, 2007; pp. 363–376. ISBN 978-3-7643-7777-9. [Google Scholar]
- Wu, Z.; Huang, N.E.; Wallace, J.M.; Smoliak, B.V.; Chen, X. On the time-varying trend in global-mean surface temperature. Clim. Dyn. 2011, 37, 759. [Google Scholar] [CrossRef] [Green Version]
- Hao, H.; Yu, F.; Li, Q. Soil Temperature Prediction Using Convolutional Neural Network Based on Ensemble Empirical Mode Decomposition. IEEE Access 2021, 9, 4084–4096. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Huang, N.E. Ensemble empirical mode decomposition: A noise assisted dataanalysis method Center for Ocean land Atmosphere Studies. In Handbook of Systemic Autoimmune Diseases; World Scientific: Singapore, 2006; Volume 85. [Google Scholar]
- Xu, Z.X.; Gong, T.L.; Li, J.Y. Decadal trend of climate in the Tibetan Plateau-regional temperature and precipitation. Hydrol. Processes 2008, 22, 3056–3065. [Google Scholar] [CrossRef]
- Fan, K.; Zhang, Q.; Sun, P.; Song, C.; Yu, H.; Zhu, X.; Shen, Z. Effect of soil moisture variation on near-surface air temperature over the Tibetan Plateau. Acta Geogr. Sin. 2020, 75, 82–97. [Google Scholar]
- Zhang, S.; Yang, H.; Yang, D.; Jayawardena, A.W. Quantifying the effect of vegetation change on the regional water balance within the Budyko framework. Geophys. Res. Lett. 2016, 43, 1140–1148. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Liu, H.; Randerson, J.T.; Yu, G.; Tieszen, L.L. Impacts of precipitation seasonality and ecosystem types on evapotranspiration in the Yukon River Basin, Alaska. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ohata, T.; Kadota, T. Land-surface hydrological processes in the permafrost region of the eastern Tibetan Plateau. J. Hydrol. 2003, 283, 41–56. [Google Scholar] [CrossRef]
- Chang, Y.; Qin, D.; Ding, Y.; Zhao, Q.; Zhang, S. A modified MOD16 algorithm to estimate evapotranspiration over alpine meadow on the Tibetan Plateau, China. J. Hydrol. 2018, 561, 16–30. [Google Scholar] [CrossRef]
- Qin, Y.; Wu, T.; Wu, X.; Li, R.; Xie, C.; Qiao, Y.; Hu, G.; Zhu, X.; Wang, W.; Shang, W. Assessment of reanalysis soil moisture products in the permafrost regions of the central of the Qinghai–Tibet Plateau. Hydrol. Processes 2017, 31, 4647–4659. [Google Scholar] [CrossRef]
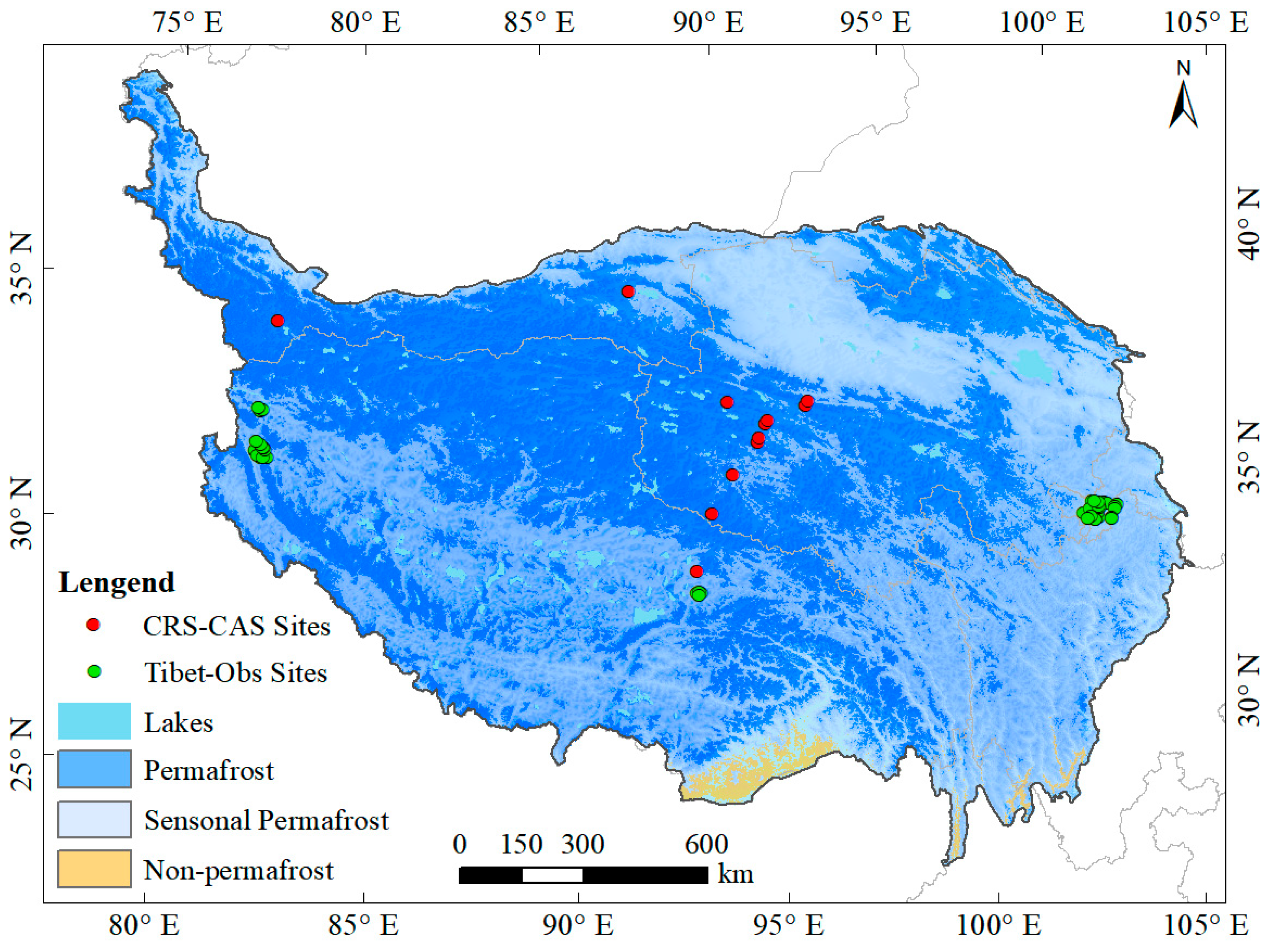




| Region | Site | Elevation/m | Vegetation Type | Soil Type |
|---|---|---|---|---|
| Permafrost | QT09 | 4449 | Alpine meadow | Aridisols |
| QT06 | 4739 | Alpine Steppe | Inceptisols | |
| QT08 | 4617 | Alpine meadow | Aridisols | |
| AYK | 4285 | Alpine Desert | Inceptisols | |
| Seasonal Permafrost | SQH | 4306 | Alpine Desert | Sand |
| Naqu | 4509 | Alpine meadow | Loamy sand | |
| MaQu | 3441 | Alpine meadow | Silt loam | |
| Ali | 4266 | Alpine Steppe | Loamy sand |
| Data | Data Type | Temporal Coverage | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| Tibet-Obs | observation data | 2009–2019 | – | 15 min |
| CRS-CAS | observation data | 2008–2016 | – | 30 min |
| GLEAM SM | Reanalysis | 1980–2020 | 0.25° | 1 d |
| Permafrost | Simulated data | – | 1 km | – |
| Precipitation and Temperature | Reanalysis | 1979–2018 | 0.1° | Monthly |
| NDVI | Reanalysis | 1982–2020 | 0.083° | 15 d |
| Permafrost Map | Map | 2017 | – | – |
| Region | Site | R | RMSE | Bias | ubRMSE | p-Value |
|---|---|---|---|---|---|---|
| Permafrost | Ch06 | 0.652 | 0.146 | 0.143 | 0.031 | 0.000 |
| XDT | 0.729 | 0.095 | −0.002 | 0.095 | 0.000 | |
| QT08 | 0.747 | 0.072 | 0.061 | 0.039 | 0.000 | |
| AYK | 0.347 | 0.118 | 0.114 | 0.031 | 0.000 | |
| Seasonal Permafrost | Ali | 0.769 | 0.031 | 0.021 | 0.023 | 0.000 |
| Maqu | 0.824 | 0.049 | −0.006 | 0.049 | 0.000 | |
| SQH | 0.946 | 0.044 | 0.031 | 0.031 | 0.000 | |
| Naqu | 0.662 | 0.060 | 0.054 | 0.027 | 0.000 |
| IMF Components | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | Res |
|---|---|---|---|---|---|---|
| Cycle/a | 3.42 | 8.20 | 20.5 | 39.05 | 0 | - |
| Variance contribution rate/% | 36.24 | 24.91 | 3.24 | 1.86 | 0.06 | 33.69 |
| Correlation coefficient | 0.79 | 0.79 | 0.51 | 0.20 | 0.09 | 0.09 |
| Significance | 0.000 | 0.000 | 0.001 | 0.213 | 0.594 | 0.286 |
| Region | Partial Correlation Coefficient | Stepwise Regression | Standard α, β and γ | ||
|---|---|---|---|---|---|
| Pre (x1) | Tem (x2) | NDVI(x3) | |||
| QTP | 0.774 *** | 0.269 *** | 0.751 *** | y = 0.803x1 − 0.001x2 + 0.132x3 + 0.37, R2 = 0.654 | 0.491, −0.047, 0.382 |
| Permafrost | 0.686 *** | 0.096 *** | 0.636 *** | y = 0.903x1 − 0.002x2 + 0.119x3 + 0.546, R2 = 0.51 | 0.472, −0.046, 0.301 |
| Seasonal Permafrost | 0.790 *** | 0.157 *** | 0.779 *** | y = 0.776x1 + 0.143x3, R2 = 0.691 | 0.464, −0.414 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, F.; Zhang, S.; Zhang, C.; Zhang, C.; Ma, W.; Luo, J. Drying–Wetting Changes of Surface Soil Moisture and the Influencing Factors in Permafrost Regions of the Qinghai-Tibet Plateau, China. Remote Sens. 2022, 14, 2915. https://doi.org/10.3390/rs14122915
Li H, Liu F, Zhang S, Zhang C, Zhang C, Ma W, Luo J. Drying–Wetting Changes of Surface Soil Moisture and the Influencing Factors in Permafrost Regions of the Qinghai-Tibet Plateau, China. Remote Sensing. 2022; 14(12):2915. https://doi.org/10.3390/rs14122915
Chicago/Turabian StyleLi, Hongying, Fenggui Liu, Shengpeng Zhang, Chaokun Zhang, Cungui Zhang, Weidong Ma, and Jing Luo. 2022. "Drying–Wetting Changes of Surface Soil Moisture and the Influencing Factors in Permafrost Regions of the Qinghai-Tibet Plateau, China" Remote Sensing 14, no. 12: 2915. https://doi.org/10.3390/rs14122915
APA StyleLi, H., Liu, F., Zhang, S., Zhang, C., Zhang, C., Ma, W., & Luo, J. (2022). Drying–Wetting Changes of Surface Soil Moisture and the Influencing Factors in Permafrost Regions of the Qinghai-Tibet Plateau, China. Remote Sensing, 14(12), 2915. https://doi.org/10.3390/rs14122915