Abstract
The refractive index structure constant () is a key parameter used in describing the influence of turbulence on laser transmissions in the atmosphere. Three different methods for estimating were analyzed in detail. A new method that uses a combination of these methods for continuous profiling with both high temporal and spatial resolution is proposed and demonstrated. Under the assumption of the Kolmogorov “2/3 law”, the profile can be calculated by using the wind field and turbulent kinetic energy dissipation rate (TKEDR) measured by coherent Doppler wind lidar (CDWL) and other meteorological parameters derived from a microwave radiometer (MWR). In a horizontal experiment, a comparison between the results from our new method and measurements made by a large aperture scintillometer (LAS) is conducted. The correlation coefficient, mean error, and standard deviation between them in a six-day observation are 0.8073, 8.18 × 10−16 m−2/3 and 1.27 × 10−15 m−2/3, respectively. In the vertical direction, the continuous profiling results of and other turbulence parameters with high resolution in the atmospheric boundary layer (ABL) are retrieved. In addition, the limitation and uncertainty of this method under different circumstances were analyzed, which shows that the relative error of estimation normally does not exceed 30% under the convective boundary layer (CBL).
1. Introduction
Turbulence analysis is meaningful in many fields, such as astronomy [1], aviation safety [2], optical communication technology [3], laser weapon [4], wind field retrieval [5], air pollution [6], oceanography [7], etc. In astronomy, due to the existence of atmospheric turbulence, the star images seen in astronomical observations often jitter and flicker, and increasing the aperture of the telescope in ground-based observations cannot achieve the expected results. To reduce the effects, researchers need to seek sites with high altitudes or locations such Dome A in Antarctica [1], where the atmospheric boundary layer (ABL) is thin. In addition, in areas of Free-Space Optical (FSO) communications and laser ranging, the fluctuation of the refractive index caused by atmospheric turbulence will affect the coherence of the laser beam through the optical angle-of-arrival fluctuation, laser beam wander and scintillation [8], etc. These phenomena will bring uncertain variances and reduce the detection efficiency of these systems.
There are several parameters normally used to describe the turbulence from the aspect of dynamics or thermodynamics, for example, the Reynolds number, turbulence kinetic energy, Richardson number, integral scale, temperature structure constant, refractive index structure constant, etc. Among all these parameters, the refractive index structure constant is the one that contains both dynamics and thermodynamics information and most directly represents the fluctuation intensity of the spatial refractive index, which makes it unique and vital, especially in optical turbulence research. At present, there are some common methods for detection.
For instance, in areas of astronomy and satellite-ground laser communication, profiles can be obtained by Slope Detection and Ranging (SLODAR) [9], Coupled Slope and Scintillation Detection and Ranging (CO-SLIDAR) [10], etc. [11,12,13]. The empirical models that represent the average characteristics of different regions are normally used for comparison, such as the Hufnagel-Valley (HV) profile model [14,15,16,17].
In addition, using the Radiosonde and sounding balloon, turbulence profile can be acquired at high spatial resolutions [18,19,20,21,22]. In the near-surface, researchers mostly use the relationship between and the temperature structure constant [23,24,25]. A large aperture scintillometer (LAS) can measure the path-averaged within a certain distance in high time resolution, which is also a common instrument using the intensity scintillation principle [26,27,28].
Moreover, by adjusting the focal length and remaining at each height to reduce the variance of the distribution of lidar profiles, imaging methods that use the differential image motion monitor (DIMM) are effective methods for detecting turbulence intensity profiles [29,30,31,32,33,34,35]. Using atmospheric backscattering amplification phenomena by measuring the intensity of laser echo signal amplification effects can also calculate under certain conditions [36,37,38].
However, there are some limitations with respect to these methods in effectively detecting rapidly changing atmospheric turbulence within its integral length scale and time scale. For example, it normally takes a long period of time when using balloon methods; the optical scintillation becomes saturation when detecting long distances; it is difficult for imaging methods to improve spatial resolution; the response to temperature fluctuation is not sensitive enough using the Raman lidar [39]. Consequently, it is necessary to seek a method that can detect turbulence profiles with high temporal and spatial resolution simultaneously.
Coherent Doppler wind lidar (CDWL) obtains radial wind speed information by retrieving the frequency shift of the received signal after passing through a distance in the atmosphere [40,41,42]. Its reliable performance has been verified in various areas, such as the following: turbulence parameters [43,44,45,46,47], aircraft wake vortices [48], boundary layer height [49,50,51], cloud seeding [52], gravity waves [53,54], low-level jets (LLJs) [44,55,56], simultaneous wind and rainfall detection [57], identifying different atmospheric environments [58], and others [59,60]. Therefore, using CDWL is a promising method for detecting the dynamic part of turbulence with high resolution.
A microwave radiometer (MWR) can provide profiles of temperature, water vapor density, relative humidity, etc. [61], which supplement the thermodynamics part of turbulence for retrieval. Consequently, profiling with high temporal and spatial resolution can be achieved by using a combination of CDWL and MWR.
This paper begins with a principle to estimate in Section 2. In Section 3, a horizontal comparison experiment with LAS is carried out firstly. The results of different methods are discussed. The limitation and its uncertainty are analyzed next. Then, the continuous observation results of profiles are retrieved vertically. Later, several turbulence parameters such as the buoyancy term, gradient Richardson number, perturbations of temperature and wind, variance of the fluctuations of vertical wind, and flux of potential temperature are estimated to analyze turbulence characteristics. After that, five typical sets of 12 min continuous turbulent profiles representing different periods of daytime and night-time are analyzed and compared with the turbulence model. The uncertainty of this method is also calculated in the vertical experiment. Finally, conclusions and discussion are provided in Section 4.
2. Principle
2.1. Stable Stratification
In the “inertial sub-region” (between inner scale l0 and outer scale L0), where the refractive index structure function obeys the Kolmogorov “2/3 law” () [62], turbulent energy propagates from the outer scale to the inner scale without dissipation. According to Tatarskii’s theory [63], under stable stratification, by combining wind field data or the outer scale of turbulence L0 with meteorological parameters, can be calculated by Equation (1) [64]:
where is a constant, usually takes the experimental empirical value of 2.8, and M is the vertical gradient of generalized potential refractive index. Km is the eddy viscosity (coefficient of mixing of momentum), and is the wind shear of the horizontal wind vector in the vertical direction. In the latter method, the calculation of L0 is quite difficult. Usually, it is estimated by different outer scale models [65,66] based on Tatarskii’s theory, such as the Colman–Vernin (C-V) model [66], which expresses L0 as a function of altitude only within 2–17 km. Moreover, the Dewan model [67] considers the effect of both altitude and wind shear of the horizontal wind, which has different expressions in the troposphere and stratosphere of the following:
where z is the height (m), and is the intensity of the wind shear.
Most of these models are related to height, wind shear intensity, and temperature gradient. Empirical models are normally obtained from long-term statistical averaged data with an in situ sounding balloon, which is hard for reflecting local atmospheric features in different areas. In addition, wind shear and temperature gradient cannot be measured directly, and they are closely related to the scale chosen for calculation. It would be more robust when choosing a larger scale, but it might lose detailed messages and would be more sensitive on the contrary. In order to reduce errors, it is necessary to avoid using these parameters for calculation as much as possible.
Therefore, the former part of Equation (1) is mainly discussed and adopted in this paper under stable stratification conditions. From the simplified turbulence kinetic energy (TKE) budget equation for steady states, the following expression is described [68]:
Term Ⅰ is a positive contribution to TKE caused by wind shear, where , , and are fluctuations of the wind component in zonal, meridional, and vertical directions. Term Ⅱ is the buoyant production or consumption term depending on the sign of the vertical heat flux (positive during the daytime or negative at night). Here, g denotes gravity acceleration, and is the averaged potential temperature. is the fluctuation of potential temperature. The angle bracket means spatial average. Finally, ε is the turbulent kinetic energy dissipation rate (TKEDR), which is always a loss term.
When using the K-theory, the vertical flux of a turbulent scale quantity can be related to its local mean gradient [68]. Then, the fluxes of wind component and potential temperature have the following expression:
where Kθ is the coefficient of mixing of heat. Therefore, combining Equations (3)–(6), ε can be rewritten as follows:
where , which can be calculated by the following equation:
and N2 is the square of the buoyancy frequency.
Then, by using the relationship between Km and Kθ, Equation (7) has a new expression of the following [69]:
where ( is the turbulent Prandtl number) and is the gradient Richardson number. From the definition, one can see that the Rrt is an indicator of discrepancy between turbulent transport by heat and momentum. With gradient Richardson number Rg and flux Richardson number Rf, Rrt can be shown as follows:
Under stable conditions, Rrt grows nearly linear with increasing Rg and has an empirical function of the following [70,71,72]:
where is the turbulent Prandtl number under neutral conditions. is the maximum flux Richardson number.
Next, substituting Equation (10) into Equation (1) yields the following:
From Equation (13), one can find that the result of is affected by both dynamics and thermodynamics. In addition, ε can be calculated by matching the measured radial velocity and azimuth structure function with the theoretical structure function [56]. Moreover, M has the expression of the following [63]:
where q is the specific humidity (), and θ is the potential temperature:
where T represents temperature (K). P means pressure (hPa). However, since humidity contributions are expected to be insignificant in the optical range [69], parameter M for dry air can be rewritten as follows [67]:
In order to simplify the calculation and analyze the effects of temperature and pressure gradients, merging Equations (15) and (16) yields the following:
If the hydrostatic hypothesis is used and pressure data are unavailable, can be simplified into the following [73]:
where .
From Equation (13) to Equation (18), one can see that, with the TKEDR and wind profiles measured from CDWL in the inertial subrange and temperature and pressure profiles derived from MWR and the barometric formula, the refractive index structure constant can be estimated under stable stratification circumstances.
2.2. Convective Boundary Layer
When temperature stratification is unstable under the convective boundary layer (CBL), especially within the well-mixed part (, where zi is the height of CBL), the source of turbulence becomes mainly buoyancy-driven. Then, due to the non-local large-eddy heat flux, Equations (4)–(6) and (10) that are based on K- theory failed to deal with the “zero/counter-gradient” region, where while [68,74]. Likewise, temperature structure constant and refractive index structure constant are not proportional to and M2 anymore. Therefore, should not be calculated with Equation (13) within CBL.
In the optical range, structure characteristics and are related by the following equation:
In the surface layer and lower portion of CBL, where is approximately a constant and decreases with , can be estimated by the following [69]:
where is a constant, is the von Kármán’s constant, β is a dimensional parameter (), and all the rest are the same as before. The entire numerical coefficient is found to be around 0.7; thus, the equation can be rewritten as follows:
Accordingly, in the near-surface layer has the following expression:
In addition, to correct Equation (6) in the well-mixed area of CBL, a positive “counter-gradient term” is provided and Equation (6) becomes the following [74,75]:
One commonly used expression of is as follows:
where and are the variances of the fluctuations of the vertical wind component and potential temperature. Then, temperature structure constant can be estimated from and ε [76].
Substituting Equation (25) into Equation (19) yields the following:
Therefore, in the near-surface () and well-mixed () part of CBL can be estimated with Equations (22) and (26), respectively. The area above of CBL and under the conditions of stable stratification is then calculated with Equation (13).
3. Experiments
A horizontal verification experiment is carried out on the University of Science and Technology of China (USTC) campus in Hefei City, Anhui Province (31°50′10″N, 117°16′10″E), to discover a suitable method for retrieval. After that, the vertical field experiment is conducted on the Xilin Gol Prairie in Inner Mongolia (43°54′N, 115°58′E) to test the behavior of this method in profiling. The two experimental sites are shown on the left of Figure 1.
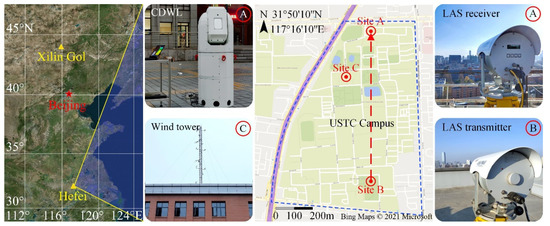
Figure 1.
Illustration of two experiment sites in the satellite map and the instruments layout in the horizontal experiment (USTC, Hefei City).
3.1. Instruments
The CDWL applied in this paper (Site A of Figure 1, right.) uses an eye-safe 1.55 μm wavelength in the transmitting system, the single pulse energy of the laser is 200 μJ, and repetition frequency is 10 kHz. In the experiment, CDWL adopts a velocity azimuth display (VAD) scanning mode, and the elevation angle is fixed at 60 degrees. The step length of the scanning azimuth angle is 5 degrees, and the scanning period is 147 s, which is the same as the temporal resolution of the retrieved wind field.
The lidar has a pulse width of 200 ns, which has a blind zone of around 30 m. Thus, in the vertical direction of 0.03–2.20 km, 2.20–4.79 km, and 4.79–11.29 km, the spatial resolutions are 30 m, 60 m, and 150 m, respectively. In addition, lidar adopts an all-fiber structure and temperature control system in order to ensure stability. The specific parameters of CDWL are listed in Table 1.

Table 1.
Key Parameters of CDWL.
The ground-based MWR used in the experiment has a time resolution of 2 min. In the vertical direction of 0–0.5 km, 0.5–2 km, and 2–10 km, the spatial resolution is as follows: 50 m, 100 m, and 250 m, respectively. Ground surface measurements contain temperature, humidity, pressure, and cloud base height, and vertical observation results can provide profiles of temperature, water vapor density, relative humidity, and liquid water content within 0–10 km. There are more specific introductions and applications about MWR in [61].
Under the assumption of horizontally homogeneous, LAS (Kipp&Zonen LAS MKII, Figure 1, right.) can retrieve path-averaged by detecting the light intensity fluctuations of signals in the receiving end that pass through a distance in the atmosphere. LAS was chosen for the verification experiment due to its mature theory and reliable results. It can provide information at a temporal resolution of 1 s. In this experiment, a 10 min time interval is adopted to reduce data fluctuations.
3.2. Verification Experiment
In the horizontal direction verification experiment, as shown in the right of Figure 1, CDWL and the weather station (DAVIS6162: Wireless Vantage Pro2 Plus [77]) are placed at site A. The receiving and transmitting ends of LAS are located at the height of 55 m at site A and site B, respectively. Its detection path (in the direction of the red arrow) is a south–north direction in order to avoid the influence of sunlight. The two sites are 900 m apart, which is within the best detection range of LAS to avoid scintillation saturation or aperture averaging effects [78]. The wind tower is placed on the top of a 6-story building about 30 m high at site C to record the continuous data of temperature and for the calculation of temperature gradient.
As shown in Figure 2, six days of continuous observations were carried out from 00:00 on 26 September to 24:00 on 1 October 2020, local time. Figure 2a–e represent wind field and TKEDR results obtained from the CDWL, Figure 2f is the temperature data recorded at the height of 2 m, 8 m, and 18 m of the wind tower and the temperature gradient result calculated by linear fitting. Figure 2g shows the variances of vertical wind component fluctuation and the heat flux of potential temperature. The results of log10 that are estimated by different methods introduced in the principle part are drawn in Figure 2h. Since the height of the wind tower is about 18 m and near the ground, which represents the changes in a local area of the surface, the calculated temperature gradient can vary widely every day. In addition, the method used to estimate is suitable for stable conditions. Therefore, to reduce errors, in the process of calculating in the horizontal experiment, the temperature gradient is taken as the empirical value in the troposphere: −0.0065 K/m; the pressure gradient is −0.10 hPa/m.
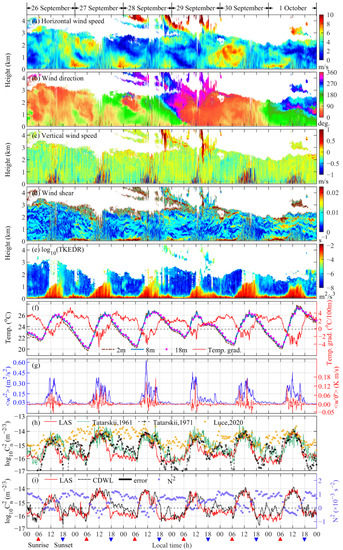
Figure 2.
The horizontal wind speed (a), wind direction (b), vertical wind speed (c), wind shear (d), log10(TKEDR) (e), temperature and its gradient (f), variances in vertical wind fluctuation and flux of potential temperature (g), log10 estimated by different methods (h), Brunt–Väisälä frequency squared, log10 and its shaded area error bar (i) retrieved from CDWL, wind tower, and LAS in the observations from 26 September to 1 October 2020, local time.
Combining with the daily trend of the temperature gradient in Figure 2f, it can be observed that it has a strong negative correlation with the result detected by LAS and the temperature gradient. Obviously, there is a strong temperature inversion in the surface layer from afternoon to night every day. On the one hand, when the temperature gradient changes from negative to positive around 16:00 in the afternoon, the convection activities weaken instantly and drops rapidly [79,80]. It can also be verified from the vertical wind speed in Figure 2c that it becomes more stable and approaches zero when temperature inversion develops.
On the other hand, with an increase in temperature gradient, a stratified structure begins to form. This can be proved by the Brunt–Väisälä frequency, which is a common method for estimating the stability of atmosphere stratification [53,81,82,83] (Equation (9)). When , the stratification structure is stable, and it becomes unstable when due to the inversion of density. The continuous time profile of N2 calculated from the wind tower is shown in Figure 2i. It can be found that N2 also turns from negative to positive after around 16:00, similarly to the temperature gradient, which means that atmosphere stratification becomes more stable and the laminar flow grows.
LLJs can often be found at the night, especially on 26, 27, and 30 September. The occurrence of low-level jet (LLJ) usually leads to an increase in wind shear, which in turn breaks the stability of the atmosphere and generates turbulent flow. However, unlike the daytime, the increase in wind shear did not cause a wide range of turbulence due to the suppressing effect of the Brunt–Väisälä frequency. Instead, only small fluctuations occurred on the edge of LLJ, which can be found in the slight variations of at night.
In addition, from the discrepancy of estimated by different methods (Figure 2h), some interesting phenomena can be found. When the variances of vertical wind fluctuation is neglectable at night-time, the flux of potential temperature is also near zero due to the lack of vertical motion. While during the daytime, with the increase in convective activities driven by surface heating, the potential temperature heat flux becomes positive (meaning upwards). At the same time, the temperature gradient and corresponding N2 drop to near zero and can even approach negative values. Thus, the method derived from stable stratification is no longer applicable. It can be proved from the shown in Figure 2h that it becomes unstable and fluctuates around 1–2 orders of magnitude during these periods.
The result of that applies to the surface layer and lower portion of CBL shows a fine consistency with LAS during the daytime. Moreover, it is normally underestimated during the nighttime due to the decline of temperature and TKEDR.
Similarly, the method for estimating is mainly suitable for the well-mixed area of CBL during the daytime; thus, the restrictions for using this method in near-surface detection are stricter. For the rest of the time when temperature stratifications are stable, is able to overestimate results from the small variances of potential temperature fluctuations.
Therefore, considering the limitations of different methods, a combination of them should be applied for continuous retrieval. In our horizontal near-surface experiment, the method for estimating is mostly adopted before sunrise and after sunset. After sunrise, is used due to the variance of vertical wind fluctuation over a threshold value ( is taken in this paper). If is still satisfied after sunset, then this method is used until is smaller than . The combination of these methods and its comparison with LAS are shown in Figure 2i.
The statistical analyses of the results in six-day continuous observations from LAS and CDWL are shown in Figure 3c. The results of and are plotted in black dots and green circles, respectively. By comparing the orders of magnitude of , one can find that their results are quite consistent every day.
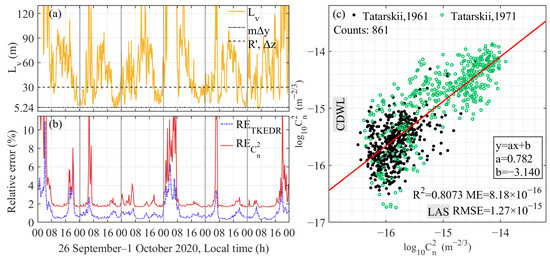
Figure 3.
The integral scale Lv (a), relative error of the estimation of TKEDR and (b), and comparative statistical analysis of LAS and CDWL observation results (c) from 26 September to 1 October 2020, local time.
The that conducted estimations during nighttime is mainly distributed around and and within to during the daytime. The correlation coefficient, mean error, and standard deviation RMSE between the new combination method and LAS are 0.8073, , and , respectively.
3.3. Limitation and Uncertainty Analysis
To make this new method more practical and convincing, testifying the applicability and estimating its uncertainty under different circumstances are significant procedures.
Integral scale Lv is an indicator reflecting the rationality of the turbulence parameters retrieval [46]. The Kolmogorov “2/3 law” holds, and the lidar measurement is within an inertial subrange when the longitudinal and transverse dimensions of the sensing volume do not exceed the upper boundary of the inertial subrange (, Δy is the spatial distance between the centers of two neighbouring probing volumes, Δz is the longitudinal dimension of the probing volume, and m and 60 m in the vertical direction of 0.03–2.20 km and 2.20–4.79 km, respectively). It can be calculated from the radial velocity variance averaged over all azimuth angles () and TKEDR [84]:
where has the following expression:
where , , , and are the variances of the fluctuations of zonal, meridional, and vertical wind components. On the one hand, when distance is additionally satisfied ( in the horizontal experiment and grows with height in the vertical observation), it indicates that TKEDR can be obtained within the inertial subregion of turbulence. Normally, is smaller than mΔy, especially in the vertical measurement (in our experiment setup, holds when the height is above 297.7 m). On the other hand, if the radius of the scanning cone at a certain height ( at the height of 60 m and grows with height in the vertical observation) is comparable with or is smaller than Lv, the relative error of estimation of TKEDR () becomes larger.
From the results of Lv in Figure 3a, one can observe that it is bigger than Δy, Δz, and lΔy in most cases, which means that TKEDR and are measured and retrieved within the inertial subrange most of the time during the experiment. During the transition period around 16:00–20:00, the integral scale of turbulence Lv drops to the scale smaller than Δz. Similarly to the results shown in the temperature gradient and N2, this verified the prominent motion state of atmosphere changes from convective to laminar flow and the sensing volume exceeding the integral scale of turbulence. Thus, the spatial resolution of CDWL Δz needs to be improved in near-surface observations in future studies. In addition, the results also indicate that it is reliable to use the criterion in measuring the credibility of the new method.
To estimate the relative error of , the method for calculating TKEDR should be explained first because it is a key parameter in retrieval. When using CDWL to estimate the wind field, the averaged azimuth structure function has the following expression [43,84]:
where is the number of conical scans used for averaging, and M is the number of radial velocity estimates in one conical scan. describes the fluctuations of radial velocity, with Rk being the distance from the lidar to the center of the sensing volume, is the azimuth angle, and Δθ is the azimuth angle resolution. and . In addition, function can be expressed as follows:
where the following is obtained.
is the longitudinal transfer function of the low-pass filter, and is the transverse transfer function of the low-pass filter. , , , and is the pulse duration. , c is the speed of light, and TW is the temporal window width. is the transverse size of the sensing volume.
With the equation of , the difference of is equal to . Then, ε can be obtained from the difference of the averaged azimuth structure function of radial velocity.
Next, the relative error of the estimation of (, in real value, rather than logarithmic scale) is calculated according to Equations (13), (22), and (26) as follows:
where is estimated based on lidar system parameters, the value of TKEDR, and the instrumental error of the radial velocity () [43,84]. is mainly affected by CNR, and it is calculated by the model of Cramer–Rao lower bound (CRLB) with an assumption of a Gaussian laser pulse [85,86,87]. The expression of is complicated (Equations (11)–(12)); nonetheless, it has asymptotical behaviors (close to 0.75) when . Thus, the uncertainty caused by is relatively small considering that it is used in stable stratification (takes ±0.01 at 0.75 here). can be derived from the sum of the relative error of horizontal wind in different altitudes divided by the distance between two layers. According to Equation (17), is estimated by the relative error of temperature () and pressure (). In this paper, takes ±1 K at 280 K and takes ±1 hPa at 800 hPa.
When using Equation (22) to estimate , we obtain the following:
and when is adopted, the following is obtained.
Finally, is calculated by using the same combination method as in Figure 2i. The six-day continuous results of and are plotted in Figure 3b. Since the height in the horizontal experiment is near the surface layer, CNR is high and the instrumental error of estimation of the wind field is quite small. Therefore, the relative errors of TKEDR and are within 10% most of the time, which demonstrates the robustness of this method. is also shown in Figure 2i with a shaded area error bar. Since is usually pictured on a log scale, a 10% relative error is not obvious in the figure.
3.4. Continuous Observation of Profile
Based on the results of the horizontal verification experiment, the results of the continuous field experiment conducted on the Xilin Gol Prairie in Inner Mongolia (43°54′N, 115°58′E) in September 2019 are analyzed and discussed. Different from cities, the topography of the grassland makes the atmosphere in CBL more likely to meet homogeneous assumptions.
Figure 4a–c,e–g show the wind field and TKEDR results retrieved from CDWL in two continuous days from 10:00 on 6 September to 24:00 on 7 September 2019, local time. The quality of data is affected by carrier-to-noise (CNR), which is the ratio of total signal power to the noise power, and it is the main parameter that determines the accuracy of wind field retrieval. In this paper, the data with CNR above −35 dB were selected for retrieving radial wind speed [59]. Due to the effect of turbulence, the boundary layer height is uplifted during the daytime; thus, CNR can be detected at higher values accordingly. A sudden increase in CNR above 2.2 km is caused by a change in spatial resolution (Figure 4a during the nighttime). In addition, the horizontal wind direction defines the north wind as 0° and the degree increases in the clockwise direction.
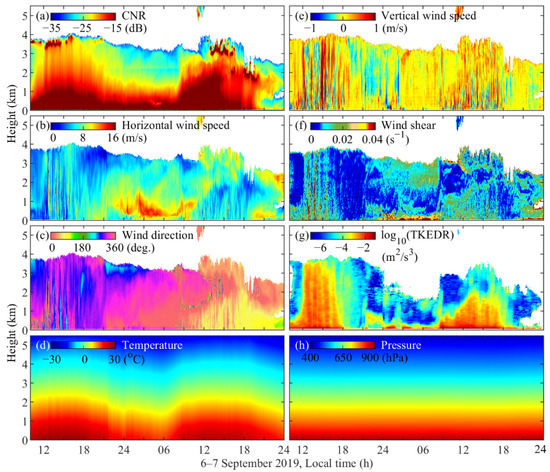
Figure 4.
The CNR (a), horizontal wind speed (b), wind direction (c), vertical wind speed (e), wind shear (f), and log10(TKEDR) (g) derived from CDWL. The temperature (d) and pressure (h) retrieved from MWR and the barometric formula in the observations from 6 September to 7 September 2019, local time.
Similarly to the results observed in the horizontal verification experiment, the fluctuations of horizontal wind speed and direction remain small, and vertical motion is neglectable mostly at night except for an LLJ that can be discovered around 0.6 km (Figure 4b). Therefore, the stratification of the atmosphere is stable at nighttime. After sunrise, when the air is warmed and the ground is unevenly heated, convection activities begin to occur. This can be verified from the vertical wind speeds, which differ from the stable state that approaches zero most of the time during the night, and it changes quickly between positive and negative numbers (negative means upward). The stable stratification structure and LLJ that occurred at night also gradually vanished, as shown in the horizontal wind speed and wind direction during the day. Correspondingly, the calculated horizontal wind shear is smaller compared with those observed during nighttime.
The results of temperature and pressure profiles in 0–5 km derived from MWR are shown in Figure 4d,h. Obviously diurnal variations can be observed from the continuous results of the temperature profile. It should be mentioned that because MWR does not have pressure profile data, considering that atmospheric pressure normally decreases monotonously and rapidly with height, we used the barometric formula to calculate the pressure profile under the assumption that the temperature gradient is constant within a certain height range. The pressure in the height of hi can be derived by using the following equation:
where and are the temperature (K) and pressure (hPa) in , respectively. k is the temperature gradient (K/m) between the height of hi and ; g is gravitational acceleration (9.8 m/s2); M is the molar mass of Earth’s air (0.029 kg/mol); R is the universal gas constant (8.314 J/(mol·K)). Using the temperature profile measured by MWR and the recorded surface pressure, the pressure profile can be calculated from the bottom (the experimental site is 1160 m above sea level) to the top by using the differential method.
Then, according to wind field information derived from CDWL and meteorological data recorded by MWR, two-day continuous observation results of profiles can be retrieved by using different methods, as shown in Figure 5c–e. The variances in the fluctuations of vertical wind component and the instantaneous vertical flux of potential temperature are also drawn here for comparison (Figure 5a,b).
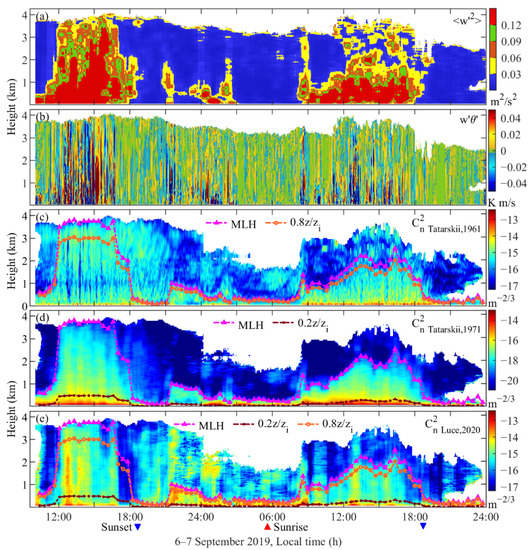
Figure 5.
The results of the variances of vertical wind fluctuation (a), instantaneous flux of potential temperature (b), log10 estimated by (c), (d), and (e) in the observations from 6 September to 7 September 2019, local time.
Considering that the threshold value of is taken as in the horizontal experiment, an area with is depicted in blue. Clearly, after sunset and before sunrise, is smaller than most of the time except for the area around LLJ (Figure 4b). Thus, atmospheric stratification can be assumed as stable overall during the night-time. In addition, the heat flux of the potential temperature that is mainly close to zero can also prove this observation. In order to compare with CBL, the mixing layer heights (MLHs) are also drawn here using a threshold method of [45,51]. On the contrary, holds throughout the daytime, especially under CBL. Moreover, the well-mixed part is mainly within . Meanwhile, from Figure 5b, one can observe that is normally larger than zero under due to the surface heating effect, and it becomes negative in the entrainment zone (>).
From the result of (Figure 5c), some layer structures can be found above CBL, especially after sunset. However, when dealing within CBL during the daytime, it can fluctuate quickly about 1–2 orders of magnitude with both time (6 September) and height (7 September), as revealed in the horizontal experiment (Figure 2h). Moreover, there is a sudden decreasing layer at around 1 km that can be found in during the daytime on 6 September. The reason for these phenomena can be analyzed by using Equations (13) and (16). The gradient terms can become unstable when wind shear fluctuates quickly (Figure 4f) and the potential temperature gradient drops to zero and can even approach negative values in the well-mixed region. Therefore, this method is not suitable for retrieval when stratification is unstable during daytime periods.
The method for calculating that is applied for the surface layer and lower portion of CBL shows a clear negative correlation with height (Figure 5d). Notice that the lower limit of this color bar is much smaller than the others; thus, this method would become highly underestimated above . To deal with that, should be considered within the well-mixed part of CBL (Figure 5e). The decline rate with height is much lower than , and it shows the characteristic of CBL where the strongest turbulence activities are mainly within [76]. However, when above , begins to overestimate due to the near-zero variance of potential temperature fluctuations.
Therefore, a combination of these methods is also needed in the vertical detection. In this paper, is used before sunrise, after sunset, and in the region above of CBL during the daytime. is considered within and is adopted in the well-mixed part of . The combined result is shown in Figure 6d.
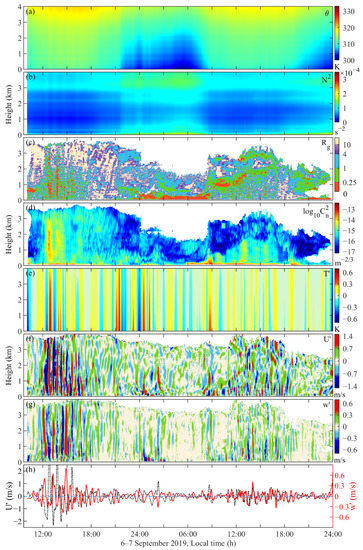
Figure 6.
The potential temperature (a), Brunt–Väisälä frequency squared (b), gradient Richardson number (c), log10 (d) profiles, perturbations of temperature (e), horizontal wind speed (f), vertical wind speed (g), and averaged wind speed perturbations within 1–2 km (h) derived from CDWL and MWR in the observations on 6–7 September 2019, local time.
By performing comparisons with the TKEDR profile (Figure 4g), it is obvious that there are similar trends between them due to the fact that they are both key parameters used to describe the intensity of turbulence. Nevertheless, the profile reveals more details on the time and space scale because it contains information on both the wind field and meteorological parameters. When temperature stratification is stable during the night-time, the instability of turbulence is mainly driven by wind shear. Moreover, layer structures can be found near the strong wind shear layer (00:00–07:00, 7 September Figure 4f). Correspondingly, during the period around 00:00–03:00, with the increasing intensity of wind shear generated by LLJ, activities in the vertical direction increase (Figure 5a), which causes to rise during the night. In CBL, quickly drops with in the near-surface layer and then decreases slowly with height in the well-mixed portion.
3.5. Results Analysis
In order to analyze turbulence characteristics in a more comprehensive manner, several key dynamics and thermodynamics parameters are shown in Figure 6. In the profile of the potential temperature (Figure 6a), it increases with height most of the time. In addition, the Brunt–Väisälä frequency squared (Figure 6b) is positive throughout the experiment; however, it is close to zero under CBL during the daytime. By combining these features, we can assume that the atmosphere stratification is stable overall above the CBL and becomes unstable within the CBL.
The gradient Richardson number is also an important and comprehensive turbulence parameter that contains both dynamics and thermodynamics information [56,88,89]. It is a dimensionless number that considers both the effects of buoyancy and wind shear (), which provides a reference for judging the intensity of atmospheric instability.
If , turbulence is strengthened due to the domination of wind shear. If , turbulence is suppressed by the buoyancy term. There is a critical gradient Richardson number (Rc) of 0.25 in order to refer to [90,91]. When , this indicates the small-scale perturbation of turbulence. We point out that Rg is used in stably stratified turbulence, and it becomes much less meaningful when . Therefore, the calculation of Rg in this paper using the “bubble sort” algorithm proposed by Thorpe is meant to re-sort potential temperatures in a monotonically increasing order. Moreover, one should mainly focus on stable stratification conditions. The result of Rg is shown in Figure 6c. Similarly to N2, it also has a stably stratified structure outside of CBL and increases after night falls. Significantly, the overall distribution features are quite consistent with .
Figure 6e–g show the perturbations of temperature, horizontal wind speed, and vertical wind speed, respectively. They are derived from the following procedures. Firstly, the mean background of these parameters is calculated by a moving average with a window of 1 h. Secondly, the original perturbation is the difference between raw data and mean background. Thirdly, to reduce high-frequency noises, the original perturbation is smoothed by a moving average of three points. To analyze the wave structures more intuitively, horizontal and vertical wind speeds within the height of 1–2 km are averaged, and then the procedures above are used to obtain the perturbations (Figure 6h).
In the result of (Figure 6d), stratified structures similar to N2 and Ri can be found outside of CBL, especially on 6 September. In addition, there are several vertical structures in the daytime of on 6 September. By performing comparisons with Figure 6e–h, one can find that they are closely related to the wave structures of , , and . Unlike gravity waves, these waves are more likely driven by the cloud’s ability to block solar radiation, which causes temperature fluctuations. When , then , indicating that the atmosphere is depositional; on the contrary, the atmosphere is uplifting. These phenomena generate the perturbation of TKEDR directly, which in turn affects the value of .
In Figure 4b, an LLJ with a maximum speed of around 14 m/s formed below 1 km after 21:00 on the sixth, which leads to an increase in wind shear and around it and also the perturbation of temperature. However, what is interesting is that although wind shear is still high after 03:00 and , a large value of N2 indicates that stratification is quite stable. Therefore, the buoyancy term suppresses the generation of convective activity (vertical wind perturbation is near to zero) and results in a reduction in . In addition, in the area above 1 km from 9:00 to 12:00 on the seventh, the discrepancy between and Rg can also be better understood by the stationary .
When estimating Rg and , since the spatial resolution of MWR is lower than CDWL, the original temperature profile is interpolated according to the spatial resolution of CDWL first. The profiles of potential temperature and potential temperature gradient at different times acquired from MWR on 6–7 September are shown in Figure 7a,b,e, and f. The thin lines in Figure 7e,f represent the original profiles of potential temperature gradient calculated by adjacent points. Thick lines represent the potential temperature gradient profiles that are estimated by the moving linear fit in a height range of 200 m. Using these thick lines, the profiles of Brunt–Väisälä frequency squared are shown in Figure 7c,d, which all have a similar characteristic with potential temperature gradient results, as excepted. Then, the gradient Richardson number profiles are depicted in Figure 7g,h.
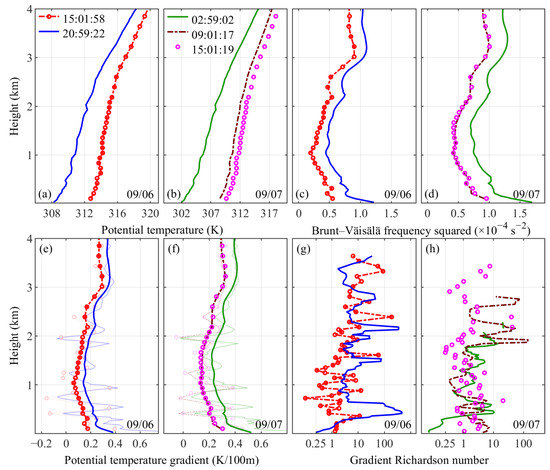
Figure 7.
The results of potential temperature (a,b), potential temperature gradient (e,f), Brunt–Väisälä frequency squared (c,d), and gradient Richardson number (g,h) profiles derived from CDWL, MWR, and the barometric formula at different times on 6–7 September 2019, local time.
From the profiles of and N2 during the daytime, one can observe that they are normally small and close to zero in the well-mixed part of CBL (Figure 7e,f). Meanwhile, the Rg profiles also have a relatively small value that is less than 1. On the contrary, , N2, and Rg usually have a larger number at night, except for the region where LLJ occurred (Figure 7g,h).
In addition, MWR uses a remote sensing method to obtain the temperature profiles and it has limitations in detecting strong temperature gradient layers [92]. This phenomenon often occurs at the tropopause, the top of the boundary layer, and the inversion layer, particularly at night. In order to analyze these layers more accurately, the spatial resolution of both the MWR and CDWL needs to be highly improved.
Then, the relative error of estimation of TKEDR, combined , and integral scale Lv are calculated vertically in Figure 8. The region with a relative error greater than 50% is marked in light yellow in Figure 8a,b. From the results, it can be observed that when using this combination method to obtain the profiles, a small relative error (Figure 8b, where is mostly within 30%) can be maintained under CBL. In the meantime, Lv is under 1 km in this area; thus, is satisfied mostly, which results in a low (Figure 8a). After 18:00, with a decrease in the height of the boundary layer, TKEDR drops rapidly at high altitudes, and Lv becomes larger than 2 km. As a result, the calculated and also grow, as shown in the figure. During the period of atmosphere changes from convection to laminar flow (around 18:00 to 21:00), a sudden increase in relative error can be observed, similarly to the horizontal experiment. After the atmosphere stabilized at night, the relative error of TKEDR and began to gradually decrease, but this occurred mainly within the mixing layer.
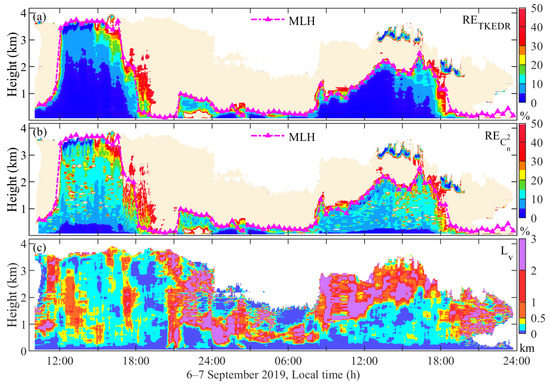
Figure 8.
The relative error of the estimation of TKEDR (a), combined (b), mixing layer height (MLH, (a,b)), and integral scale Lv (c) calculated from CDWL and MWR in the observations from 6 September to 7 September 2019, local time.
To observe different profile characteristics during the day and night, from 15:00 on the sixth to 15:00 on the seventh, five sets of continuous profiles were selected every 6 h for analysis. As shown in Figure 9, each group has six consecutive profiles for a total period of around 12 min. The raw data in original spatial resolution are depicted in black dashed lines, and the blue and red lines represent the results after 100 m and 200 m moving average in the range of 0.03–2.20 km and >2.20 km of the original profiles, respectively. In addition, results drawn in the second and third-row represent the profiles of night, which are represented with blue lines, and the remaining rows are the profiles of day, which are depicted as red lines. is also drawn in every profile with the same color and with a shaded area error bar. The seventh column shows the results of Lv, lΔy, and profiles averaged in 12 min of the corresponding row. Δz profiles are not drawn here because they are smaller than lΔy when the height is above 297.7 m.
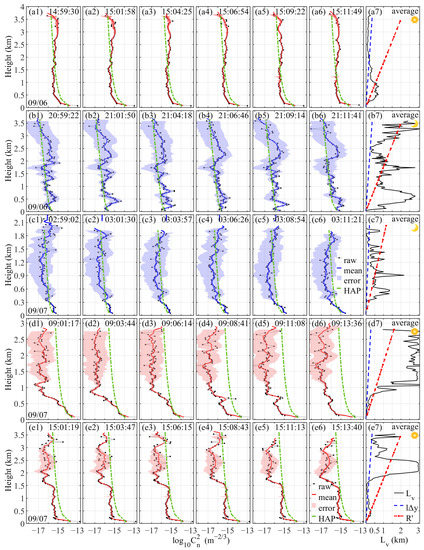
Figure 9.
Profiles of log10 in raw data that are distance averaged and show a shaded area error bar, calculated from the HAP model and time averaged integral scale Lv (a7–e7) during the period of 14:59:30–15:11:49 (a1–a6) and 20:59:22–21:11:41 (b1–b6) on 6 September and 02:59:02–03:11:21 (c1–c6), 09:01:17–09:13:36 (d1–d6), and 15:01:19–15:13:40 (e1–e6) on 7 September 2019, local time.
As analyzed above, this new combination method holds and has a relatively small uncertainty mostly within CBL. Moreover, strong turbulence activities normally occur in CBL, especially during the daytime. Therefore, to conduct comparisons, the Hufnagel/Andrews/Phillips (HAP) model [27,93] is drawn as green dot-dash lines in Figure 9. The model is a modification of the HV model, which takes into account the power-law relationship with height near the ground, which is more suitable in our experiments considering that is applied within . It can be calculated by the following equation:
where M is a scaling factor that is related to local characteristics ( is applied in this paper), hs is the height above the sea level, w is the average wind speed in high-altitude (normally 21 m/s), and h0 and are the height above the ground of the instrument and the measured , respectively. Power law p typically takes 2/3 at night, and it varies around 4/3 depending on the time during the day (the same as ).
Firstly, it is not hard to find that the profiles at adjacent moments, especially at night, have a strong correlation and continuity. Secondly, by observing the colored lines, most results at night are one to two orders of magnitude lower than that during the daytime at the same height. In addition, the results of these profiles also show a good agreement with the HAP model, especially within 1.5 km. Similarly to the HAP model, the intensity of decreases distinctly with height, and it drops faster during the day than at night near the ground. Considering that the model is the averaged profile, it is reasonable that the results fluctuate near the profile most of the time. As for the differences in the fourth row, these are mainly due to the boundary layer being uplifted at this moment. In the meantime, the development process of turbulence at different heights can be observed via the high temporal and spatial resolution results of raw data.
In the order of time series, the mean intensity of is the highest around 15:00. After sunset, decreases to the minimum near 03:00. Around 09:00 in the morning, grows from the surface at first but the upper region still remains low. At noon, the profile becomes unstable when reaches the maximum again. All these characteristics reflect the credibility of the results.
By comparing and Lv profiles, one can observe that the criterion is satisfied under normal conditions, which indicates the credibility of this method in profiling. The in lower altitudes (especially with CBL) is relatively small due to the high value of CNR, TKEDR, and the low instrumental error of the radial velocity. In these regions, condition is usually satisfied, especially during the daytime. In contrast, in the second and third rows or the high altitude in the fourth and fifth rows, when is comparable with or smaller than Lv, the relative error of the estimation of can increase dramatically. can fluctuate between two orders of magnitude above CBL, as shown in the figure.
4. Conclusions and Discussion
To analyze atmospheric turbulence in high resolution, we considered and analyzed three different methods that might be suitable for continuous retrieval. A contrastive experiment was conducted horizontally with LAS to study the characteristics of these methods. By conducting a comparison of a six-day result, it turns out that the methods of , , and are suitable for stable stratification (outside the CBL), near-surface and lower part of CBL (), and well-mixed part of CBL (), respectively. A combination of these three methods is then used to work in different circumstances.
Based on the results, we simultaneously obtained the continuous turbulence profiles with high temporal and spatial resolutions. The features and limitations of these methods are also discussed in detail in the vertical experiment. In addition, the dynamic parameters such as TKEDR and perturbations of wind were obtained from CDWL. Moreover, MWR can provide the thermodynamic terms such as buoyancy term and the perturbation of temperature. Later, the gradient Richardson number and combined , which contain both dynamics and thermodynamics information, were derived by combining the advantages of CDWL and MWR.
This is significant for studying complex and fast-changing atmospheric environments. Due to the difficulty of profiling with high temporal and spatial resolutions using the existing method, the vertical comparison experiment is hard to achieve. Currently, most researchers adopt the sounding balloon with a radiosonde in the vertical observation; nevertheless, it normally takes a long period of time and its position changes with altitude all the time. Therefore, it is not very suitable for our new method with high temporal and spatial resolutions. More analyses are required in the future for vertical comparison experiments.
We discovered stable stratified structures at night by conducting an analysis of the buoyancy term and gradient Richardson number. The process of demonstrated how turbulence developed from the surface and gradually decreased with height during the day. Moreover, the wave structures were found in the daytime due to the perturbation of temperature and wind speed. Next, by observing continuous typical profiles, the rationality of the results near the surface was verified by comparing them with the HAP turbulence profile model.
Due to the use of CDWL and MWR, there are some limitations of this method that need to be explained. When detecting weak turbulence regions, small-scale turbulence is hard to capture because the volume averaging effect of CDWL can only be corrected to a certain limit. In addition, MWR has difficulties in detecting strong temperature gradient layers. Therefore, the viability of this method in regions such as the tropopause, top of the boundary layer, and inversion layer remains to be further confirmed.
When retrieving vertical profiles, we assumed, most of the time, that the region below CBL satisfies the Kolmogorov “2/3 law” [63]. By performing calculations of the relative error and comparisons between integral scale Lv, , lΔy, and , we analyzed the uncertainty and limitations when using this method at different time periods and altitudes. In the horizontal results, the criterion was proven valid in measuring the credibility of the new method. The compared results showed a great agreement between them most of the time in the six-day experiment, except for the period when the integral scale of turbulence Lv reduces to a value smaller than Δz or lΔy. In the vertical profiles, can be estimated within the inertial subrange and with a low relative error under CBL. Moreover, Lv grows when TKEDR decreases with height, which leads to a larger in high altitudes. Therefore, to meet the criterion and to reduce uncertainties as much as possible, the most appropriate scan angle resolution and spatial resolution of CDWL and MRW should be analyzed and adjusted according to the landscape, season, and even time period of the experimental site.
Author Contributions
Conceptualization, H.X. and P.J.; methodology, P.J. and L.W.; experiment, J.Y. and P.J.; data curation, L.W., J.Y., P.J. and K.W.; formal analysis, P.J. and L.W.; writing—original draft preparation, P.J.; writing—review and editing, P.J., K.W., L.W., J.Y. and H.X.; visualization, P.J. and H.X.; supervision, H.X.; project administration, H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Strategic Priority Research Program of Chinese Academy of Sciences, grant number XDA22040601.
Data Availability Statement
All data mentioned in the paper can be downloaded from https://figshare.com/articles/dataset/Turbulence_detection_experiments/16607306 (accessed on 16 June 2022).
Acknowledgments
We thank Hao Liu from the atmospheric boundary layer physics laboratory of USTC for providing data for the wind tower.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, B.; Shang, Z.; Hu, Y.; Hu, K.; Wang, Y.; Yang, X.; Ashley, M.C.B.; Hickson, P.; Jiang, P. Night-time measurements of astronomical seeing at Dome A in Antarctica. Nature 2020, 583, 771–774. [Google Scholar] [CrossRef] [PubMed]
- Storer, L.N.; Williams, P.D.; Gill, P.G. Aviation Turbulence: Dynamics, Forecasting, and Response to Climate Change. Pure Appl. Geophys. 2019, 176, 2081–2095. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, H.; Xie, G.; Ahmed, N.; Yan, Y.; Erkmen, B.I.; Chandrasekaran, N.; Lavery, M.P.J.; Steinhoff, N.K.; Tur, M.; et al. Atmospheric turbulence effects on the performance of a free space optical link employing orbital angular momentum multiplexing. Opt. Lett. 2013, 38, 4062–4065. [Google Scholar] [CrossRef] [PubMed]
- Extance, A. Laser weapons get real. Nature 2015, 521, 408–410. [Google Scholar] [CrossRef] [PubMed]
- Kumer, V.-M.; Reuder, J.; Dorninger, M.; Zauner, R.; Grubsic, V. Turbulent kinetic energy estimates from profiling wind LiDAR measurements and their potential for wind energy applications. Renew. Energy 2016, 99, 898–910. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, H.; Cai, X.; Song, Y.; Bian, Y.; Xiao, K.; Zhang, H. Influence of Intermittent Turbulence on Air Pollution and Its Dispersion in Winter 2016/2017 over Beijing, China. J. Meteorol. Res. 2020, 34, 176–188. [Google Scholar] [CrossRef]
- Nootz, G.; Jarosz, E.; Dalgleish, F.R.; Hou, W. Quantification of optical turbulence in the ocean and its effects on beam propagation. Appl. Opt. 2016, 55, 8813–8820. [Google Scholar] [CrossRef]
- Libich, J.; Perez, J.; Zvanovec, S.; Ghassemlooy, Z.; Nebuloni, R.; Capsoni, C. Combined effect of turbulence and aerosol on free-space optical links. Appl. Opt. 2017, 56, 336–341. [Google Scholar] [CrossRef]
- Butterley, T.; Wilson, R.W.; Sarazin, M. Determination of the profile of atmospheric optical turbulence strength from SLODAR data. Mon. Not. R. Astron. Soc. 2006, 369, 835–845. [Google Scholar] [CrossRef]
- Voyez, J.; Robert, C.; Conan, J.-M.; Mugnier, L.M.; Samain, E.; Ziad, A. First on-sky results of the CO-SLIDAR Cn2 profiler. Opt. Express 2014, 22, 10948–10967. [Google Scholar] [CrossRef]
- Fusco, T.; Costille, A. Impact of Cn2 profile structure on Wide Field AO performance. Adapt. Opt. Syst. II 2010, 7736. [Google Scholar] [CrossRef]
- Voyez, J.; Robert, C.; Michau, V.; Conan, J.-M.; Fusco, T. Accurate measurement of Cn2 profile with Shack-Hartmann data. Adapt. Opt. Syst. III 2010, 7736, 77360J. [Google Scholar] [CrossRef]
- Otoniel Canuet, L.F. Atmospheric Turbulence Profile Modeling for Satellite-Ground Laser Communication; UPC, Escola d’Enginyeria de Telecomunicació i Aeroespacial de Castelldefels: Barcelona, Spain, 2015. [Google Scholar]
- Beland, R.R. Propagation through Atmospheric Optical Turbulence; SPIE: New York, NY, USA, 1993. [Google Scholar]
- Andrews, L.C.; Phillips, R.L.; Wayne, D.; Leclerc, T.; Sauer, P.; Crabbs, R.; Kiriazes, J. Near-ground vertical profile of refractive-index fluctuations. Proc. SPIE—Int. Soc. Opt. Eng. 2009, 7324, 732402–732412. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Sun, G.; Liu, Q.; Zhu, W.; Weng, N. Analysis of an optical turbulence profile using complete ensemble empirical mode decomposition. Appl. Opt. 2016, 55, 9932–9938. [Google Scholar] [CrossRef]
- Wu, S.; Wu, X.; Su, C.; Yang, Q.; Xu, J.; Luo, T.; Huang, C.; Qing, C. Reliable model to estimate the profile of the refractive index structure parameter (Cn2) and integrated astroclimatic parameters in the atmosphere. Opt. Express 2021, 29, 12454–12470. [Google Scholar] [CrossRef] [PubMed]
- Barletti, R.; Ceppatelli, G.; Moroder, E.; Paterno, L.; Righini, A. A vertical profile of turbulence in atlantic air mass measured by balloon-borne radiosondes. J. Geophys. Res. 1974, 79, 4545–4549. [Google Scholar] [CrossRef]
- Martini, E.; Freni, A.; Cuccoli, F.; Facheris, L. Derivation of clear-air turbulence parameters from high-resolution radiosonde data. J. Atmos. Ocean. Technol. 2017, 34, 277–293. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.D.; Huang, C.M.; Huang, K.M.; Gong, Y.; Gan, Q.; Zhang, Y.H. Latitudinal and topographical variabilities of free atmospheric turbulence from high-resolution radiosonde data sets. J. Geophys. Res. Atmos. 2019, 124, 4283–4298. [Google Scholar] [CrossRef]
- Ko, H.C.; Chun, H.Y.; Wilson, R.; Geller, M.A. Characteristics of atmospheric turbulence retrieved from high vertical-resolution radiosonde data in the United States. J. Geophys. Res. Atmos. 2019, 124, 7553–7579. [Google Scholar] [CrossRef]
- He, Y.; Sheng, Z.; He, M. The First Observation of Turbulence in Northwestern China by a Near-Space High-Resolution Balloon Sensor. Sensors 2020, 20, 677. [Google Scholar] [CrossRef]
- Vyhnalek, B.E. Path Profiles of Cn2 Derived from Radiometer Temperature Measurements and Geometrical Ray Tracing. In Free-Space Laser Communication and Atmospheric Propagation XXIX; SPIE: New York, NY, USA, 2017; Volume 10096. [Google Scholar] [CrossRef]
- van Iersel, M.; Paulson, D.A.; Wu, C.; Ferlic, N.A.; Rzasa, J.R.; Davis, C.C.; Walker, M.; Bowden, M.; Spychalsky, J.; Titus, F. Measuring the turbulence profile in the lower atmospheric boundary layer. Appl. Opt. 2019, 58, 6934–6941. [Google Scholar] [CrossRef] [PubMed]
- Odintsov, S.L.; Gladkikh, V.A.; Kamardin, A.P.; Nevzorova, I.V. Determination of the Structural Characteristic of the Refractive Index of Optical Waves in the Atmospheric Boundary Layer with Remote Acoustic Sounding Facilities. Atmosphere 2019, 10, 711. [Google Scholar] [CrossRef]
- Ting-i, W.; Ochs, G.R.; Clifford, S.F. A saturation-resistant optical scintillometer to measure Cn2. J. Opt. Soc. Am. 1978, 68, 334–338. [Google Scholar]
- Andrews, L.C.; Phillips, R.L.; Crabbs, R.; Wayne, D.; Leclerc, T.; Sauer, P. Creating a Cn2 Profile as a Function of Altitude Using Scintillation Measurements Along a Slant Path. In High Energy/Average Power Lasers and Intense Beam Applications VI Atmospheric and Oceanic Propagation of Electromagnetic Waves VI; SPIE: New York, NY, USA, 2012; Volume 8238. [Google Scholar] [CrossRef]
- Han, Y.; Gao, P.; Huang, J.; Zhang, T.; Zhuang, J.; Hu, M.; Wu, Y. Ground-based synchronous optical instrument for measuring atmospheric visibility and turbulence intensity: Theories, design and experiments. Opt. Express 2018, 26, 6833–6850. [Google Scholar] [CrossRef] [PubMed]
- Belen’kii, M.S.; Roberts, D.W.; Stewart, J.M.; Gimmestad, G.G.; Dagle, W.R. Experimental validation of the differential image motion lidar concept. Laser Radar Technol. Appl. VI 2001, 4377, 307–316. [Google Scholar] [CrossRef]
- Gimmestad, G.; Roberts, D.; Stewart, J.; Wood, J. Development of a lidar technique for profiling optical turbulence. Opt. Eng. 2012, 51, 101713. [Google Scholar] [CrossRef]
- Brown, D.M.; Juarez, J.C.; Brown, A.M. Laser differential image-motion monitor for characterization of turbulence during free-space optical communication tests. Appl. Opt. 2013, 52, 8402–8410. [Google Scholar] [CrossRef]
- Jing, X.; Hou, Z.; Wu, Y.; Qin, L.A.; He, F.; Tan, F. Development of a differential column image motion light detection and ranging for measuring turbulence profiles. Opt. Lett. 2013, 38, 3445–3447. [Google Scholar] [CrossRef]
- Cheng, Z.; Tan, F.; Jing, X.; He, F.; Qin, L.A.; Hou, Z. Retrieval of Cn2 profile from differential column image motion lidar using the regularization method. Chin. Opt. Lett. 2017, 15, 020101. [Google Scholar] [CrossRef]
- Aristidi, E.; Ziad, A.; Chabe, J.; Fantei-Caujolle, Y.; Renaud, C.; Giordano, C. A generalized differential image motion monitor. arXiv 2019, arXiv:1904.07093. [Google Scholar] [CrossRef]
- Chabe, J.; Aristidi, E.; Ziad, A.; Lanteri, H.; Fantei-Caujolle, Y.; Giordano, C.; Borgnino, J.; Marjani, M.; Renaud, C. PML: A generalized monitor of atmospheric turbulence profile with high vertical resolution. Appl. Opt. 2020, 59, 7574–7584. [Google Scholar] [CrossRef] [PubMed]
- Banakh, V.A.; Razenkov, I.A. Refractive turbulence strength estimation based on the laser echo signal amplification effect. Opt. Lett. 2016, 41, 4429–4432. [Google Scholar] [CrossRef]
- Banakh, V.A.; Razenkov, I.A. Lidar measurements of atmospheric backscattering amplification. Opt. Spectrosc. 2016, 120, 326–334. [Google Scholar] [CrossRef]
- Razenkov, I.A. Turbulent Lidar: II-Experiment. Atmos. Ocean. Opt. 2018, 31, 281–289. [Google Scholar] [CrossRef]
- Whiteman, D.N.; Venable, D.; Landulfo, E. Comments on “Accuracy of Raman lidar water vapor calibration and its applicability to long-term measurements”. Appl. Opt. 2011, 50, 2170–2176. [Google Scholar] [CrossRef]
- Shangguan, M.; Xia, H.; Wang, C.; Qiu, J.; Lin, S.; Dou, X.; Zhang, Q.; Pan, J.-W. Dual-frequency Doppler lidar for wind detection with a superconducting nanowire single-photon detector. Opt. Lett. 2017, 42, 3541–3544. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Xia, H.; Wu, Y.; Dong, J.; Wei, T.; Wang, L.; Dou, X. Meter-scale spatial-resolution-coherent Doppler wind lidar based on Golay coding. Opt. Lett. 2019, 44, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, Y.; Xia, H. Spatial resolution enhancement of coherent Doppler wind lidar using differential correlation pair technique. Opt. Lett. 2021, 46, 5550–5553. [Google Scholar] [CrossRef]
- Banakh, V.A.; Smalikho, I.N.; Falits, A.V. Estimation of the turbulence energy dissipation rate in the atmospheric boundary layer from measurements of the radial wind velocity by micropulse coherent Doppler lidar. Opt. Express 2017, 25, 22679–22692. [Google Scholar] [CrossRef]
- Banakh, V.A.; Smalikho, I.N.; Falits, A.V. Wind-Temperature Regime and Wind Turbulence in a Stable Boundary Layer of the Atmosphere: Case Study. Remote Sens. 2020, 12, 955. [Google Scholar] [CrossRef]
- Banakh, V.A.; Smalikho, I.N.; Falits, A.V. Estimation of the height of the turbulent mixing layer from data of Doppler lidar measurements using conical scanning by a probe beam. Atmos. Meas. Tech. 2021, 14, 1511–1524. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A. Effect of Wind Transport of Turbulent Inhomogeneities on Estimation of the Turbulence Energy Dissipation Rate from Measurements by a Conically Scanning Coherent Doppler Lidar. Remote Sens. 2020, 12, 2802. [Google Scholar] [CrossRef]
- Banakh, V.A.; Smalikho, I.N.; Falits, A.V.; Sherstobitov, A.M. Estimating the Parameters of Wind Turbulence from Spectra of Radial Velocity Measured by a Pulsed Doppler Lidar. Remote Sens. 2021, 13, 2071. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A.; Falits, A.V.; Sukharev, A.A. Experimental Study of Aircraft Wake Vortices on the Airfield of Tolmachevo Airport in 2018. Atmos. Ocean. Opt. 2020, 33, 124–133. [Google Scholar] [CrossRef]
- Wang, C.; Jia, M.; Xia, H.; Wu, Y.; Wei, T.; Shang, X.; Yang, C.; Xue, X.; Dou, X. Relationship analysis of PM2.5 and boundary layer height using an aerosol and turbulence detection lidar. Atmos. Meas. Tech. 2019, 12, 3303–3315. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, S.; Wang, L.; Gao, Z.; Zhang, Y.; Zou, H.; Miao, S.; Li, Y.; Huang, M.; Yim, S.H.L.; et al. Diurnal Evolution of the Wintertime Boundary Layer in Urban Beijing, China: Insights from Doppler Lidar and a 325-m Meteorological Tower. Remote Sens. 2020, 12, 3935. [Google Scholar] [CrossRef]
- Wang, L.; Qiang, W.; Xia, H.; Wei, T.; Yuan, J.; Jiang, P. Robust Solution for Boundary Layer Height Detections with Coherent Doppler Wind Lidar. Adv. Atmos. Sci. 2021, 38, 1920–1928. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, K.; Wei, T.; Wang, L.; Shu, Z.; Yang, Y.; Xia, H. Cloud Seeding Evidenced by Coherent Doppler Wind Lidar. Remote Sens. 2021, 13, 3815. [Google Scholar] [CrossRef]
- Jia, M.; Yuan, J.; Wang, C.; Xia, H.; Wu, Y.; Zhao, L.; Wei, T.; Wu, J.; Wang, L.; Gu, S.-Y.; et al. Long-lived high-frequency gravity waves in the atmospheric boundary layer: Observations and simulations. Atmos. Chem. Phys. 2019, 19, 15431–15446. [Google Scholar] [CrossRef]
- Cao, C.; Xinzhao, C.; Jian, Z.; Roberts, B.R.; Zhibin, Y.; Weichun, F.; Xian, L.; Smith, J.A. Lidar observations of persistent gravity waves with periods of 3-10 h in the Antarctic middle and upper atmosphere at McMurdo (77.83degS, 166.67degE). J. Geophys. Res. Space Phys. 2016, 121, 1483–1502. [Google Scholar] [CrossRef]
- Tuononen, M.; O’Connor, E.J.; Sinclair, V.A.; Vakkari, V. Low-Level Jets over Uto, Finland, Based on Doppler Lidar Observations. J. Appl. Meteorol. Climatol. 2017, 56, 2577–2594. [Google Scholar] [CrossRef]
- Banakh, V.A.; Smalikho, I.N. Lidar Studies of Wind Turbulence in the Stable Atmospheric Boundary Layer. Remote Sens. 2018, 10, 1219. [Google Scholar] [CrossRef]
- Wei, T.; Xia, H.; Hu, J.; Wang, C.; Shangguan, M.; Wang, L.; Jia, M.; Dou, X. Simultaneous wind and rainfall detection by power spectrum analysis using a VAD scanning coherent Doppler lidar. Opt. Express 2019, 27, 31235–31245. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Xia, H.; Wei, T.; Wang, L.; Yue, B.; Wu, Y. Identifying cloud, precipitation, windshear, and turbulence by deep analysis of the power spectrum of coherent Doppler wind lidar. Opt. Express 2020, 28, 37406–37418. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Xia, H.; Shangguan, M.; Wu, Y.; Wang, L.; Zhao, L.; Qiu, J.; Zhang, R. 1.5 µm polarization coherent lidar incorporating time-division multiplexing. Opt. Express 2017, 25, 20663–20674. [Google Scholar] [CrossRef] [PubMed]
- Wei, T.; Xia, H.; Wu, Y.; Yuan, J.; Wang, C.; Dou, X. Inversion probability enhancement of all-fiber CDWL by noise modeling and robust fitting. Opt. Express 2020, 28, 29662–29675. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Zhang, S.; Li, Q.; Ma, L.; Jiang, S.; Lei, L.; Lyu, W.; Wang, Z. Analysis of convective instability data derived from a ground-based microwave radiometer before triggering operations for artificial lightning. Atmos. Res. 2020, 243, 105005. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Tatarskii, V.I. Wave Propagation in a Turbulent Medium; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE: New York, NY, USA, 2005. [Google Scholar]
- Han, Y.; Wu, X.; Luo, T.; Qing, C.; Yang, Q.; Jin, X.; Liu, N.; Wu, S.; Su, C. New Cn2 statistical model based on first radiosonde turbulence observation over Lhasa. J. Opt. Soc. Am. A—Opt. Image Sci. Vis. 2020, 37, 995–1001. [Google Scholar] [CrossRef]
- Coulman, C.E.; Vernin, J.; Coqueugniot, Y.; Caccia, J.L. Outer scale of turbulence appropriate to modeling refractive-index structure profiles. Appl. Opt. 1988, 27, 155–160. [Google Scholar] [CrossRef]
- Dewan, E.M.; Beland, R.; Brown, J. A Model for Cn2 (Optical Turbulence) Profiles Using Radiosonde Data; Directorate of Geophysics: Hanscom Air Force Base, MA, USA, 1993. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Dordrecht, The Netherlands; Kluwer Academic: Alphen aan den Rijn, The Netherlands, 1988. [Google Scholar]
- Tatarskii, V.I. The Effects of the Turbulent Atmosphere on Wave Propagation; Israel Program for Scientific Translations: Jerusalem, Palestine, 1971. [Google Scholar]
- Venayagamoorthy, S.K.; Stretch, D.D. On the turbulent Prandtl number in homogeneous stably stratified turbulence. J. Fluid Mech. 2010, 644, 359–369. [Google Scholar] [CrossRef]
- Kantha, L.; Luce, H. Mixing Coefficient in Stably Stratified Flows. J. Phys. Oceanogr. 2018, 48, 2649–2665. [Google Scholar] [CrossRef]
- Li, D. Turbulent Prandtl number in the atmospheric boundary layer—where are we now? Atmos. Res. 2019, 216, 86–105. [Google Scholar] [CrossRef]
- Luce, H.; Kantha, L.; Hashiguchi, H.; Lawrence, D. Estimation of Turbulence Parameters in the Lower Troposphere from ShUREX (2016–2017) UAV Data. Atmosphere 2019, 10, 384. [Google Scholar] [CrossRef]
- Ghannam, K.; Duman, T.; Salesky, S.T.; Chamecki, M.; Katul, G. The non-local character of turbulence asymmetry in the convective atmospheric boundary layer. Q. J. R. Meteorol. Soc. 2017, 143, 494–507. [Google Scholar] [CrossRef]
- Deardorff, J.W. The Counter-Gradient Heat Flux in the Lower Atmosphere and in the Laboratory. J. Atmos. Sci. 1966, 23, 503–506. [Google Scholar] [CrossRef]
- Luce, H.; Kantha, L.; Hashiguchi, H.; Doddi, A.; Lawrence, D.; Yabuki, M. On the Relationship between the TKE Dissipation Rate and the Temperature Structure Function Parameter in the Convective Boundary Layer. J. Atmos. Sci. 2020, 77, 2311–2326. [Google Scholar] [CrossRef]
- DAVIS6162: Wireless Vantage Pro2 Plus Support Documents. Available online: https://cdn.shopify.com/s/files/1/0515/5992/3873/files/07395.234_Manual_VP2__RevZ_web.pdf?v=1647548782 (accessed on 16 June 2022).
- LAS MkII Scintillometer—Manual. Available online: https://www.kippzonen.com/Download/598/LAS-MkII-Scintillometer-Manual (accessed on 16 June 2022).
- Olofson, K.F.G.; Andersson, P.U.; Hallquist, M.; Ljungstrom, E.; Tang, L.; Chen, D.; Pettersson, J.B.C. Urban aerosol evolution and particle formation during wintertime temperature inversions. Atmos. Environ. 2009, 43, 340–346. [Google Scholar] [CrossRef]
- Guo, J.; Chen, X.; Su, T.; Liu, L.; Zheng, Y.; Chen, D.; Li, J.; Xu, H.; Lv, Y.; He, B.; et al. The Climatology of Lower Tropospheric Temperature Inversions in China from Radiosonde Measurements: Roles of Black Carbon, Local Meteorology, and Large-Scale Subsidence. J. Clim. 2020, 33, 9327–9350. [Google Scholar] [CrossRef]
- Sorbjan, Z.; Balsley, B.B. Microstructure of turbulence in the stably stratified boundary layer. Bound.-Layer Meteorol. 2008, 129, 191–210. [Google Scholar] [CrossRef]
- Friedrich, K.; Lundquist, J.K.; Aitken, M.; Kalina, E.A.; Marshall, R.F. Stability and turbulence in the atmospheric boundary layer: A comparison of remote sensing and tower observations. Geophys. Res. Lett. 2012, 39, L03801. [Google Scholar] [CrossRef]
- Balsley, B.B.; Lawrence, D.A.; Fritts, D.C.; Wang, L.; Wan, K.; Werne, J. Fine Structure, Instabilities, and Turbulence in the Lower Atmosphere: High-Resolution In Situ Slant-Path Measurements with the DataHawk UAV and Comparisons with Numerical Modeling. J. Atmos. Ocean. Technol. 2018, 35, 619–642. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A. Measurements of wind turbulence parameters by a conically scanning coherent Doppler lidar in the atmospheric boundary layer. Atmos. Meas. Tech. 2017, 10, 4191–4208. [Google Scholar] [CrossRef]
- Frehlich, R.; Hannon, S.M.; Henderson, S.W. Performance of a 2-µm Coherent Doppler Lidar for Wind Measurements. J. Atmos. Ocean. Technol. 1994, 11, 1517–1528. [Google Scholar] [CrossRef]
- Rye, B.J.; Hardesty, R.M. Discrete spectral peak estimation in incoherent backscatter heterodyne lidar. I. Spectral accumulation and the Cramer-Rao lower bound. IEEE Trans. Geosci. Remote Sens. 1993, 31, 16–27. [Google Scholar] [CrossRef]
- Rye, B.J.; Hardesty, R.M. Discrete spectral peak estimation in incoherent backscatter heterodyne lidar. II. Correlogram accumulation. IEEE Trans. Geosci. Remote Sens. 1993, 31, 28–35. [Google Scholar] [CrossRef]
- Venayagamoorthy, S.K.; Koseff, J.R. On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 2016, 798, R1. [Google Scholar] [CrossRef]
- Banakh, V.A.; Smalikho, I.N.; Falits, A.V. Remote Sensing of Stable Boundary Layer of Atmosphere. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2020; p. 06015. [Google Scholar]
- Miles, J.W. On the stability of heterogeneous shear flows. J. Fluid Mech. 1961, 10, 496–508. [Google Scholar] [CrossRef]
- Stull, R. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998; p. 176. [Google Scholar]
- Xu, G.; Xi, B.; Zhang, W.; Cui, C.; Dong, X.; Liu, Y.; Yan, G. Comparison of atmospheric profiles between microwave radiometer retrievals and radiosonde soundings. J. Geophys. Res. 2015, 120, 10313–10323. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Crabbs, R.; Wayne, D.; Leclerc, T.; Sauer, P. Atmospheric Channel Characterization for ORCA Testing at NTTR. In Atmospheric and Oceanic Propagation of Electromagnetic Waves IV; Korotkova, O., Ed.; SPIE: New York, NY, USA, 2010; Volume 7588. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).