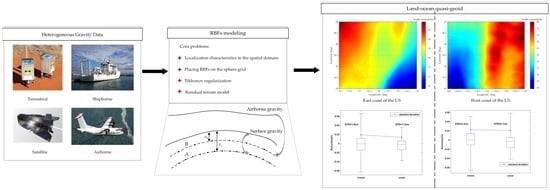
Unified Land–Ocean Quasi-Geoid Computation from Heterogeneous Data Sets Based on Radial Basis Functions
Abstract
:1. Introduction
2. Data and Method
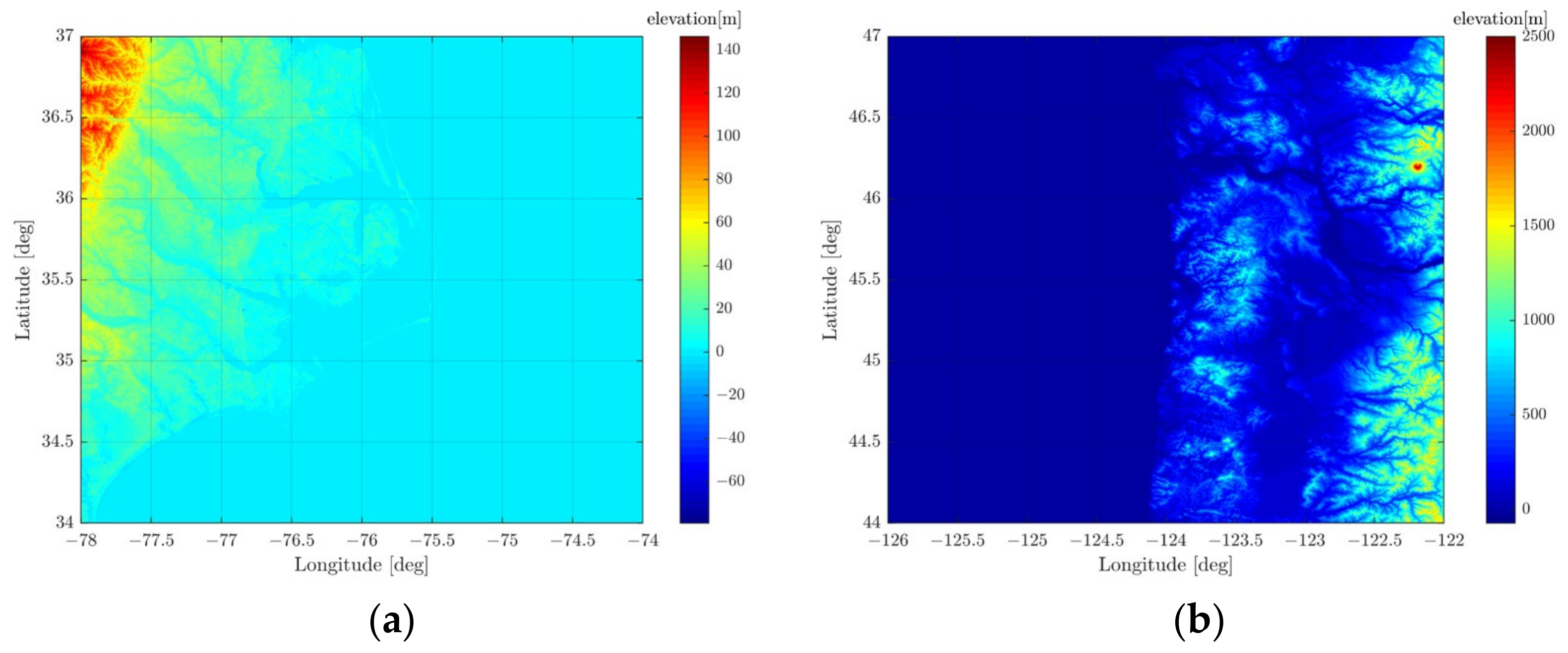
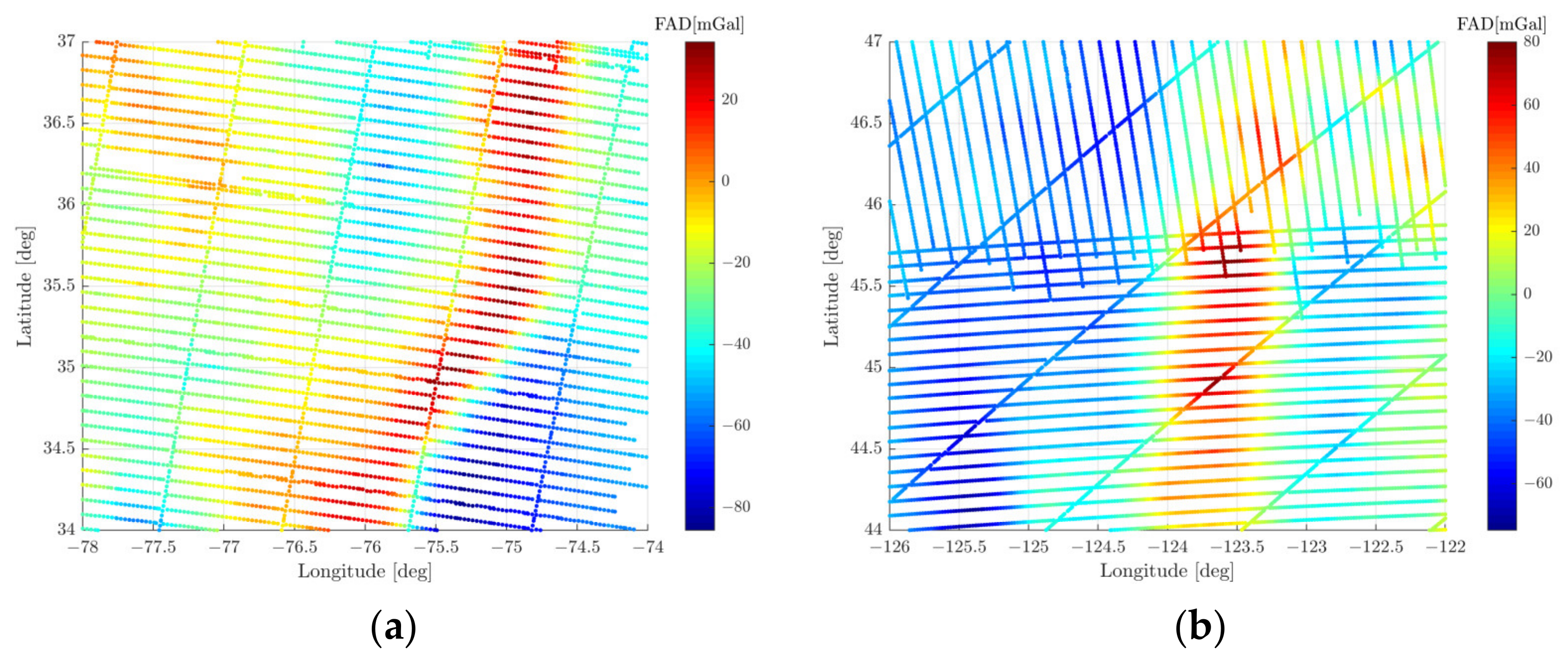
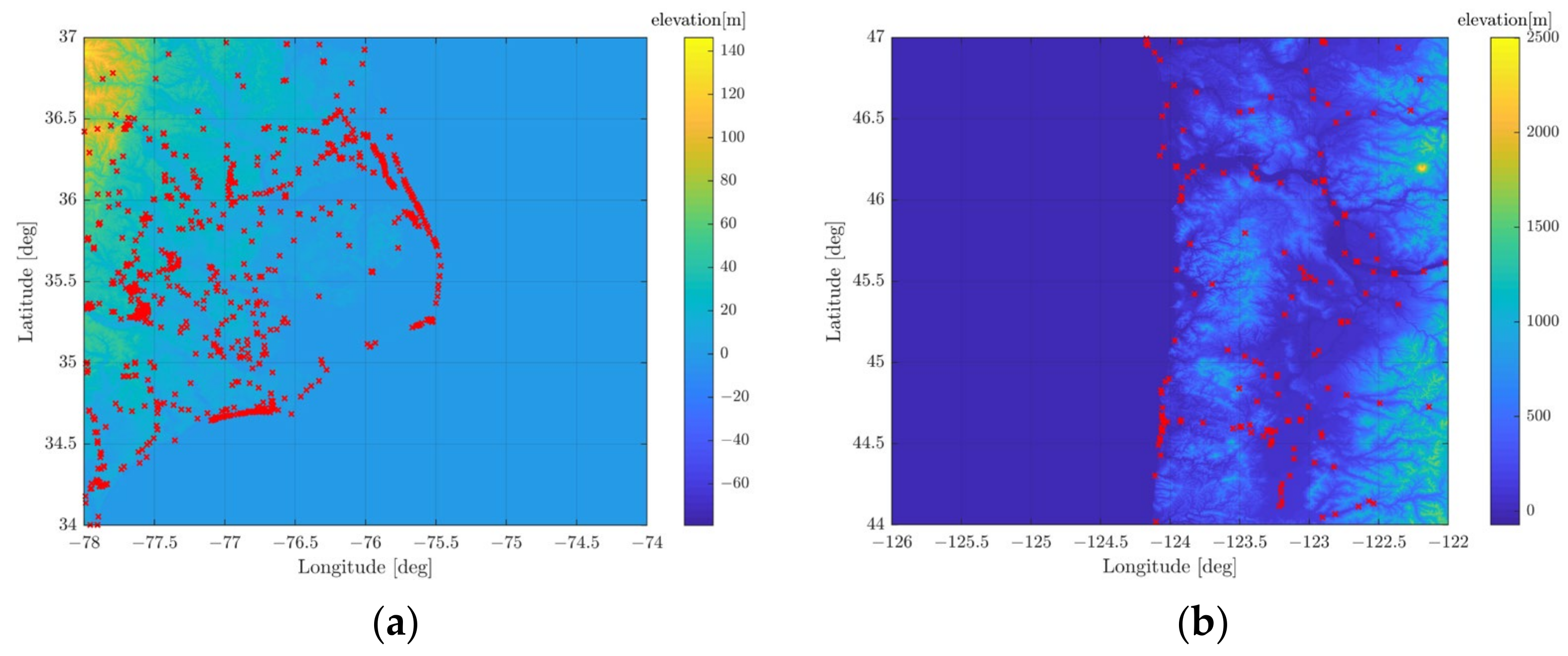
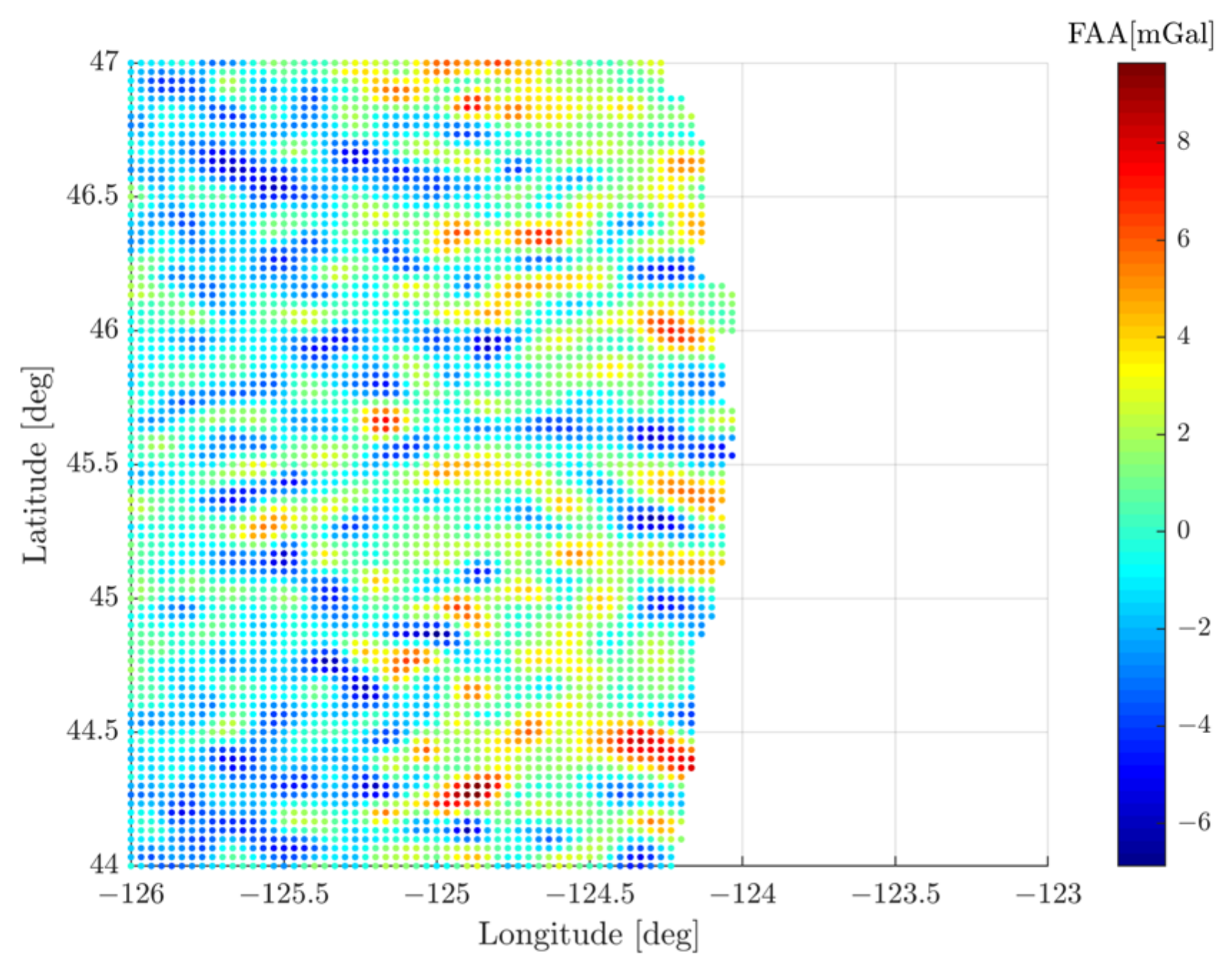
2.1. Data Preparation
2.2. RBF Modeling Strategies
- GGM and RTM are removed from the terrestrial, shipborne and satellite altimetry observations to obtain residual gravity anomalies, . The RBF network A is determined by the STD minimization. After the three kinds of gravity data are fused to calculate the RBF model parameters, the airborne gravity points are taken as prediction points and the corresponding model gravity disturbance will be calculated.
- Remove GGM and from the airborne gravity to obtain residual gravity disturbances, . The RBF network B is determined by STD minimization and then the corresponding RBF model parameters will be calculated.
- Based on the RBF networks A and B, the height anomalies on unknown points are computed, respectively, and added together. Then GGM and RTM signals are restored then to obtain the final quasi-geoid.
2.3. RBF Modeling Methodology
2.3.1. Characteristics of RBFs in the Spatial Domain
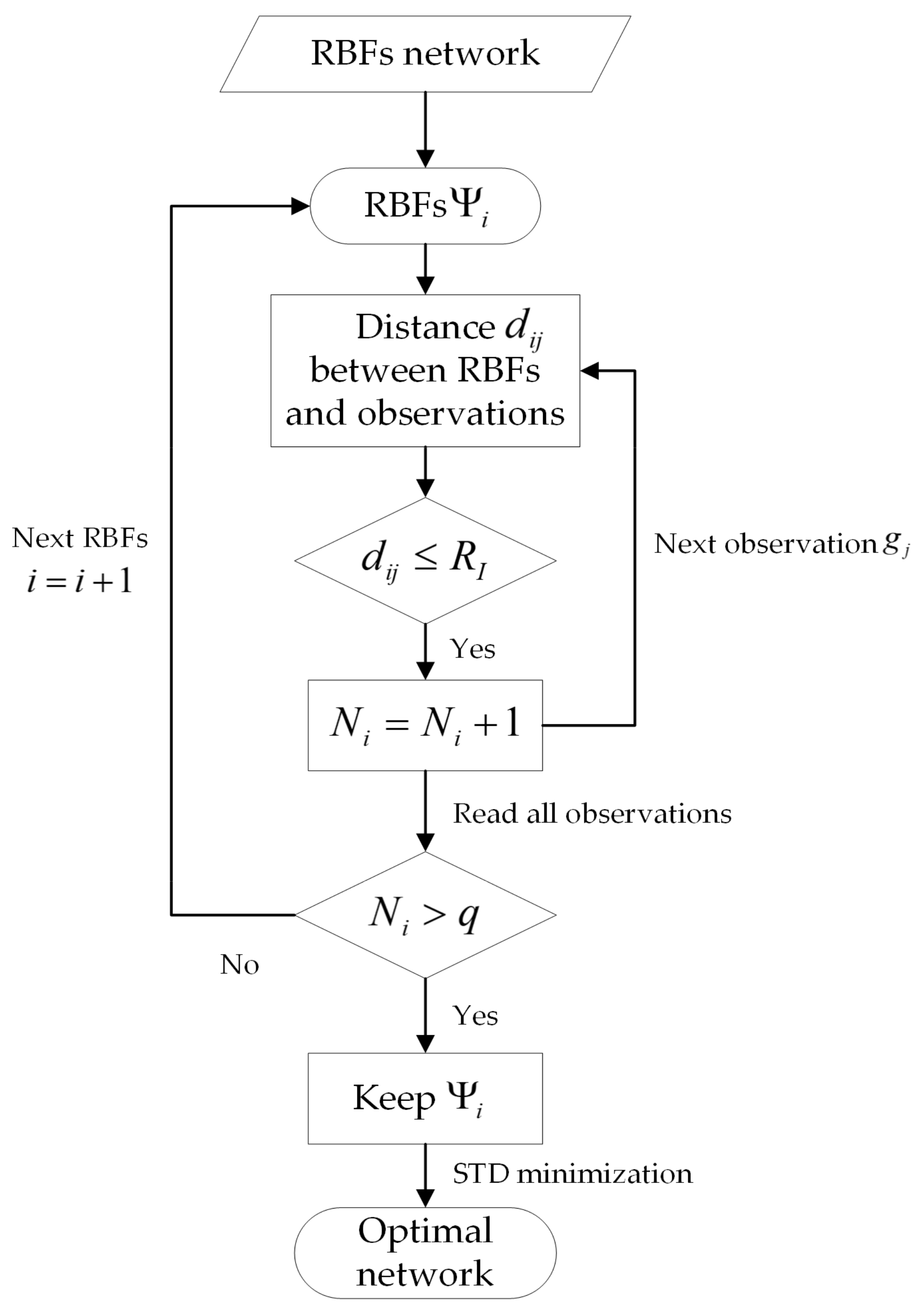
2.3.2. RBF Networks
2.3.3. Tikhonov Regularization Technique
2.3.4. Residual Terrain Model
3. Results
3.1. The East Coast Experiment Area of the USA
3.2. The West Coast Experiment Area of the USA
4. Discussion
- (1)
- The RBF used to calculate the land–ocean quasi-geoid in this article is the IMQ kernel, which has simpler function forms than the Poisson kernel, the radial multipoles kernel and the Poisson wavelets kernel. It can be seen from Figure 9 that the first-order Poisson wavelets kernel has the strongest localization characteristics when the depth is 300 km. However, the buried depth of RBFs will not be so deep generally when dealing with the measured data. When the buried depth is less than 100 km, the localization characteristics of various RBFs are all strong and their differences are quite small. By further analyzing the spectrum characteristics of RBFs, as shown in Figure 25, it can be seen that the Poisson kernel, the radial multipoles kernel and the Poisson wavelets kernel all have band-pass characteristics, while the IMQ kernel presents the characteristics of low-pass filtering. We have carried out some experiments to compare the modeling accuracy of the four RBFs. We preliminarily find that the low-pass characteristics of the IMQ kernel can help it filter out more high-frequency noise when dealing with the terrestrial gravity, making its modeling results slightly better than the other RBFs. The specific experimental results will not be presented in this article. Theoretically, the band-pass characteristics can help the RBFs simulate gravity signals more accurately. In this paper, the IMQ kernel is used to calculate the quasi-geoid for the time being, and the modeling differences between various RBFs will be more comprehensively analyzed in the future.
- (2)
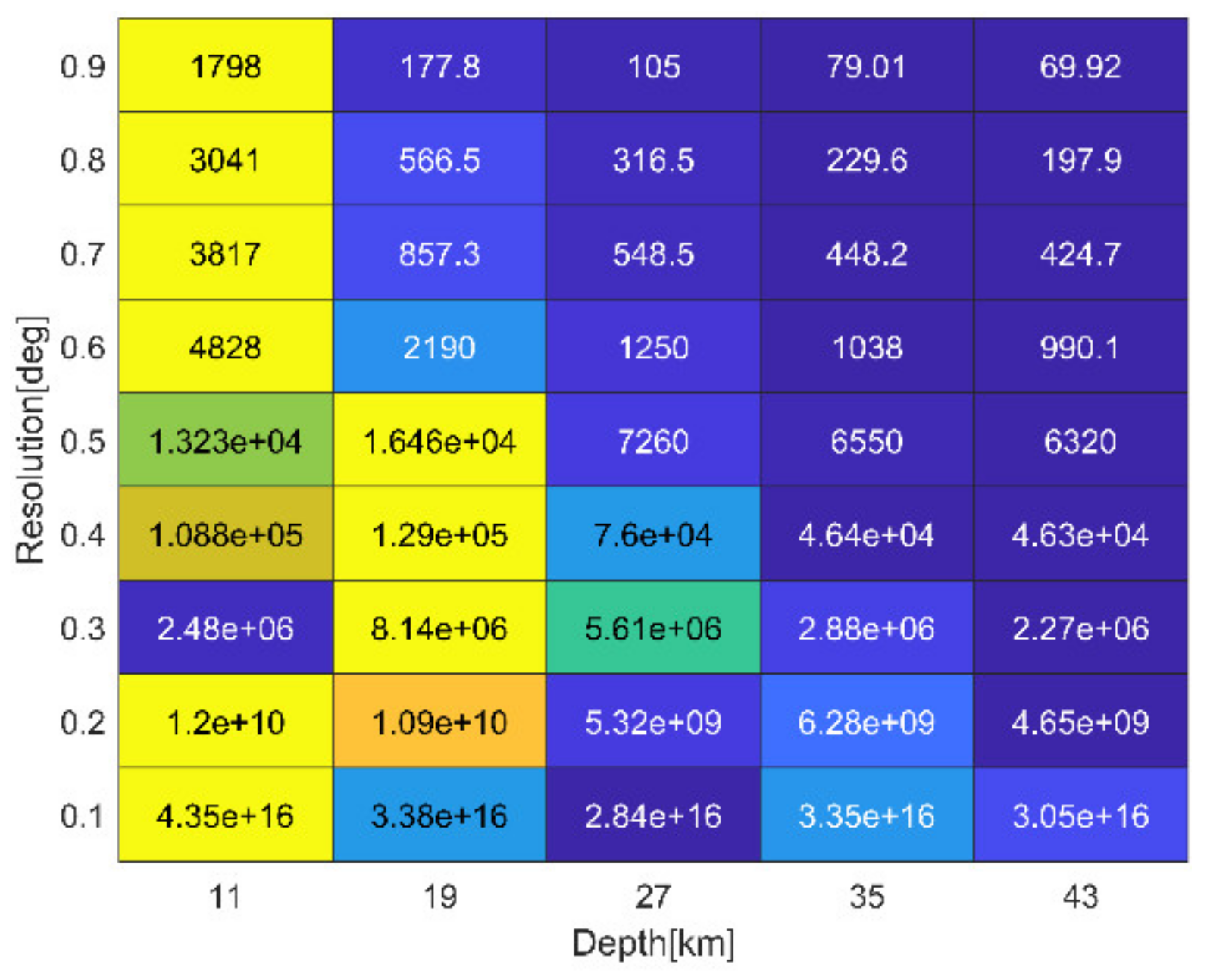
- The STD minimization technique used to determine the optimal RBF network lacks a strictly theoretical basis, which is a compromise method in view of the lack of other more effective strategies. The reason why it is difficult to determine the RBF networks is that it is difficult to directly determine the appropriate positions of RBFs based on the prior information of discrete observations. If the gravity signals are gridded before modeling, we may directly determine the spatial position of the RBF points according to the resolution and height of the gravity grid. However, our goal is to model using discrete observations. The STD minimization technique can obtain good modeling results by screening lots of RBF networks, but it increases too much redundant calculations, which hinders the solution efficiency of the RBF model to a great extent. So, it is very important to develop a rigorous and logical method to determine the RBF networks.
- (3)
- The accuracy of the quasi-geoid fusing terrestrial, shipborne and DTU15 data is quite high, but the improvement is not obvious after adding airborne gravity. The main reason is that the gravity signals on airborne points simulated by network A is insufficient, resulting in little change in residual gravity disturbances after removing , as shown in Table 2 and Table 5. Theoretically, if the result of is significantly reduced, the function of the network B will be more obvious. In the future, we can further improve the multi-layer RBF network and try to set more layers of RBF grids, simulating the gravity signals more accurately.
5. Conclusions
- (1)
- The behavior of four types of RBFs—the IMQ kernel, the Poisson kernel, radial multipoles and Poisson wavelets—is analyzed in the spatial domain. The figures show that RBFs have significant localization characteristics in the spatial domain, which is helpful to concentrate more gravity signals in local gravity field approximation. Placing RBFs on the geographic or the Reuter grid, the optimal RBF network, i.e., the optimal grid resolution and depth can be effectively determined based on the STD minimization technique.
- (2)
- The ill condition of the design matrix may occur due to the uneven distribution of observations and the excessive number of RBFs. Using the Tikhonov regularization technique, the accuracy of the ill-conditioned model is greatly improved to the centimeter level. The regularization parameters determined by the MSE and L-curve methods are basically the same. RTM calculated based on the prism integral algorithm can effectively simulate the high-frequency gravity signals implied by terrain masses and compensate for the omission errors existing in EIGEN-6C4. In the west coast experiment area, the compensation effect can reach approximately 74%. Therefore, in areas with large topographic relief, it is necessary to consider the influence of terrain masses on geoid calculations.
- (3)
- The local gravity quasi-geoids with a 1′ resolution are calculated by setting up multi-layer RBF networks based on the IMQ kernel, respectively, on the east and west coast of the United States. The results show that the accuracy of the quasi-geoid computed by fusing the terrestrial, shipborne, satellite altimetry and airborne gravity data in the east coast experimental area is 1.9 cm inland and 1.3 cm on coast after internal verification. The accuracy of the quasi-geoid calculated in the west coast experimental area is 2.2 cm inland and 2.1 cm on coast.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Forsberg, R. Modelling the Fine-Structure of the Geoid: Methods, Data Requirements and Some Results. Surv. Geophys. 1993, 14, 403–418. [Google Scholar] [CrossRef]
- Alberts, B.; Klees, R. A Comparison of Methods for the Inversion of Airborne Gravity Data. J. Geodesy 2004, 78, 55–56. [Google Scholar] [CrossRef]
- Sabri, L.M.; Sudarsono, B.; Pahlevi, A. Geoid of South East Sulawesi from Airborne Gravity Using Hotine Approach. IOP Conf. Ser. Earth Environ. Sci. 2021, 731, 012014. [Google Scholar] [CrossRef]
- Strykowski, G.; Forsberg, R. Operational Merging of Satellite, Airborne and Surface Gravity Data by Draping Techniques. In Geodesy on the Move; Forsberg, R., Feissel, M., Dietrich, R., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 1998; Volume 119, pp. 243–248. [Google Scholar] [CrossRef]
- Knudsen, P.; Andersen, O.B. Improved Recovery of the Global Marine Gravity Field from the GEOSAT and the ERS-1 Geodetic Mission Altimetry. In Gravity, Geoid and Marine Geodesy; Segawa, J., Fujimoto, H., Okubo, S., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 1997; Volume 117, pp. 429–436. [Google Scholar] [CrossRef]
- Eppelbaum, L.; Katz, Y. A New Regard on the Tectonic Map of the Arabian–African Region Inferred from the Satellite Gravity Analysis. Acta Geophys. 2017, 65, 607–626. [Google Scholar] [CrossRef]
- Braitenberg, C.; Ebbing, J. New Insights into the Basement Structure of the West Siberian Basin from Forward and Inverse Modeling of GRACE Satellite Gravity Data. J. Geophys. Res. Earth Surf. 2009, 114, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Neyman, Y.M.; Li, J. Modification of Stokes and Vening-Meinesz Formulas for the Inner Zone of Arbitrary Shape by Minimization of Upper Bound Truncation Errors. J. Geod. 1996, 70, 410–418. [Google Scholar] [CrossRef]
- Abbak, R.A.; Sjöberg, L.E.; Ellmann, A.; Ustun, A. A Precise Gravimetric Geoid Model in a Mountainous Area with Scarce Gravity Data: A Case Study in Central Turkey. Stud. Geophys. Geod. 2012, 56, 909–927. [Google Scholar] [CrossRef]
- Featherstone, W.E. Deterministic, Stochastic, Hybrid and Band-Limited Modifications of Hotine’s Integral. J. Geodesy 2013, 87, 487–500. [Google Scholar] [CrossRef] [Green Version]
- Wichiengaroen, C. A Comparison of Gravimetric Undulations Computed by the Modified Molodensky Truncation Method and the Method of Least Squares Spectral Combination by Optimal Integral Kernels. J. Geodesique 1984, 58, 494–509. [Google Scholar] [CrossRef]
- Nahavandchi, H.; Sjöberg, L.E. Precise Geoid Determination over Sweden Using the Stokes-Helmert Method and Improved Topographic Corrections. J. Geodesy 2001, 75, 74–88. [Google Scholar] [CrossRef]
- Tscherning, C.C.; Rapp, R.H. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations, and Deflections of the Vertical Implied by Anomaly Degree Variance Models; Scientific Interim Report Ohio State University: Columbus, GA, USA, 1974. [Google Scholar]
- Rapp, R.H. Gravity Anomalies and Sea Surface Heights Derived from a Combined GEOS3/Seasat Altimeter Data Set. J. Geophys. Res. 1986, 91, 4867. [Google Scholar] [CrossRef]
- Hwang, C. Analysis of Some Systematic Errors Affecting Altimeter-Derived Sea Surface Gradient with Application to Geoid Determination over Taiwan. J. Geod. 1997, 71, 113–130. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.; Deng, X.; Hsu, H.-Y.; Liu, Y. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data. J. Geodesy 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Olesen, A.V.; Andersen, O.B.; Tscherning, C.C. Merging of Airborne Gravity and Gravity Derived from Satellite Altimetry: Test Cases Along the Coast of Greenland. Stud. Geophys. Geod. 2002, 46, 387–394. [Google Scholar] [CrossRef]
- Stein, E.M.; Weiss, G. Introduction to Fourier Analysis on Euclidean Spaces (PMS-32); Princeton University Press: Princeton, NJ, USA, 2016; Volume 32. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric Equations of Topography and Other Irregular Surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Reilly, J.P.; Herbrechtsmeier, E.H. A Systematic Approach to Modeling the Geopotential with Point Mass Anomalies. J. Geophys. Res. 1978, 83, 841. [Google Scholar] [CrossRef]
- Barthelmes, F. Local Gravity Field Approximation by Point Masses with Optimized Positions. In Proceedings of the 6th International Symposium “Geodesy and Physics of the Earth”, Potsdam, Germany, 22–27 August 1988. [Google Scholar] [CrossRef]
- Lehmann, R. The Method of Free-Positioned Point Masses—Geoid Studies on the Gulf of Bothnia. Bull. Géodésique 1993, 67, 31–40. [Google Scholar] [CrossRef]
- Marchenko, A.N.; Barthelmes, F.; Meyer, U.; Schwintzer, P. Regional Geoid Determination: An Application to Airborne Gravity Data in the Skagerrak. 2001, pp. 1–48. Available online: https://gfzpublic.gfz-potsdam.de/rest/items/item_8522_3/component/file_8521/content (accessed on 1 March 2021).
- Holschneider, M.; Iglewska-Nowak, I. Poisson Wavelets on the Sphere. J. Fourier Anal. Appl. 2007, 13, 405–419. [Google Scholar] [CrossRef]
- Schmidt, M.; Fengler, M.; Mayer-Gürr, T.; Eicker, A.; Kusche, J.; Sánchez, L.; Han, S.-C. Regional Gravity Modeling in Terms of Spherical Base Functions. J. Geod. 2006, 81, 17–38. [Google Scholar] [CrossRef] [Green Version]
- Freeden, W. Spherical Spline Interpolation—Basic Theory and Computational Aspects. J. Comput. Appl. Math. 1984, 11, 367–375. [Google Scholar] [CrossRef] [Green Version]
- Tenzer, R.; Klees, R. The Choice of the Spherical Radial Basis Functions in Local Gravity Field Modeling. Stud. Geophys. Geod. 2008, 52, 287–304. [Google Scholar] [CrossRef] [Green Version]
- Bentel, K.; Schmidt, M.; Gerlach, C. Different Radial Basis Functions and Their Applicability for Regional Gravity Field Representation on the Sphere. Int. J. Geomath. 2013, 4, 67–96. [Google Scholar] [CrossRef]
- Wu, Y.; Zhong, B.; Luo, Z. Investigation of the Tikhonov Regularization Method in Regional Gravity Field Modeling by Poisson Wavelets Radial Basis Functions. J. Earth Sci. 2018, 29, 1349–1358. [Google Scholar] [CrossRef]
- Liu, Q.; Schmidt, M.; Sánchez, L.; Willberg, M. Regional Gravity Field Refinement for (Quasi-) Geoid Determination Based on Spherical Radial Basis Functions in Colorado. J. Geod. 2020, 94, 99. [Google Scholar] [CrossRef]
- Liu, Q.; Schmidt, M.; Pail, R.; Willberg, M. Determination of the Regularization Parameter to Combine Heterogeneous Observations in Regional Gravity Field Modeling. Remote Sens. 2020, 12, 1617. [Google Scholar] [CrossRef]
- Eicker, A. Gravity Field Refinement by Radial Basis Functions from In-Situ Satellite Data; Bonn University: Bonn, Germany, 2008. [Google Scholar]
- Klees, R.; Wittwer, T. A Data-Adaptive Design of a Spherical Basis Function Network for Gravity Field Modelling. In Dynamic Planet; Tregoning, P., Rizos, C., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2007; Volume 130, pp. 322–328. [Google Scholar] [CrossRef]
- Tenzer, R.; Klees, R.; Wittwer, T. Local Gravity Field Modelling in Rugged Terrain Using Spherical Radial Basis Functions: Case Study for the Canadian Rocky Mountains. In Geodesy for Planet Earth; Kenyon, S., Pacino, M.C., Marti, U., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2012; Volume 136, pp. 401–409. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A Discussion on the Approximations Made in the Practical Implementation of the Remove–Compute–Restore Technique in Regional Geoid Modelling. J. Geodesy 2005, 78, 645–653. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Lou, L. Efficient Estimation of Variance and Covariance Components: A Case Study for GPS Stochastic Model Evaluation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 203–210. [Google Scholar] [CrossRef]
- Wittwer, T. Regional Gravity Field Modelling with Radial Basis Functions; Netherlands Geodetic Commission: Delft, The Netherlands, 2009. [Google Scholar]
- Kusche, J.; Klees, R. Regularization of Gravity Field Estimation from Satellite Gravity Gradients. J. Geodesy 2002, 76, 359–368. [Google Scholar] [CrossRef]
- Hirt, C.; Kuhn, M. Band-limited Topographic Mass Distribution Generates Full-spectrum Gravity Field: Gravity Forward Modeling in the Spectral and Spatial Domains Revisited. J. Geophys. Res. Solid Earth. 2014, 119, 3646–3661. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C. RTM Gravity Forward-Modeling Using Topography/Bathymetry Data to Improve High-Degree Global Geopotential Models in the Coastal Zone. Mar. Geodesy 2013, 36, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.; Kuhn, M.; Claessens, S.; Pail, R.; Seitz, K.; Gruber, T. Study of the Earth׳s Short-Scale Gravity Field Using the ERTM2160 Gravity Model. Comput. Geosci. 2014, 73, 71–80. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.; Yang, M.; Kuhn, M.; Bucha, B.; Kurzmann, A.; Pail, R. SRTM2gravity: An Ultrahigh Resolution Global Model of Gravimetric Terrain Corrections. Geophys. Res. Lett. 2019, 46, 4618–4627. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.; Rexer, M. Earth2014: 1 Arc-Min Shape, Topography, Bedrock and Ice-Sheet Models—Available as Gridded Data and Degree-10,800 Spherical Harmonics. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 103–112. [Google Scholar] [CrossRef] [Green Version]



















| Mean | Min | Max | Std | Rms | |
|---|---|---|---|---|---|
| 0.579 | −7.563 | 9.946 | 1.982 | 0.579 | |
| 3.697 | −5.449 | 12.058 | 2.109 | 4.257 | |
| 2.385 | −26.723 | 30.875 | 5.261 | 2.385 | |
| −0.314 | −14.073 | 14.717 | 2.724 | −0.314 |
| Mean | Min | Max | Std | Rms | |
|---|---|---|---|---|---|
| 2.040 | −13.427 | 11.490 | 3.184 | 3.781 | |
| 1.679 | −14.825 | 11.158 | 3.022 | 3.457 |
| Mean | Min | Max | Std | Rms | ||
|---|---|---|---|---|---|---|
| inland | Terrestrial + DTU15 + shipborne + airborne | −0.2 | −6.3 | 6.6 | 1.9 | 1.9 |
| Terrestrial + shipborne + airborne | −0.3 | −7.2 | 6.4 | 1.9 | 2.0 | |
| coast | Terrestrial + DTU15 + shipborne + airborne | −0.3 | −3.8 | 3.5 | 1.3 | 1.4 |
| Terrestrial + shipborne + airborne | −0.2 | −4.1 | 3.1 | 1.2 | 1.2 |
| Mean | Min | Max | Std | Rms | |
|---|---|---|---|---|---|
| −7.663 | −78.808 | 50.652 | 15.983 | −7.663 | |
| 1.585 | −22.311 | 33.455 | 4.134 | 1.585 | |
| 4.591 | −8.221 | 23.001 | 4.009 | 4.591 | |
| 0.049 | −6.878 | 9.645 | 2.354 | 0.049 |
| Mean | Min | Max | Std | Rms | |
|---|---|---|---|---|---|
| 2.126 | −5.884 | 14.753 | 2.321 | 3.147 | |
| −0.190 | −7.867 | 11.710 | 2.394 | 2.402 |
| Mean | Min | Max | Std | Rms | ||
|---|---|---|---|---|---|---|
| inland | Terrestrial + DTU15 + shipborne + airborne | 0.0 | −6.6 | 5.1 | 2.2 | 2.2 |
| Terrestrial + shipborne + airborne | −0.2 | −6.9 | 4.0 | 2.0 | 2.0 | |
| coast | Terrestrial + DTU15 + shipborne + airborne | −0.3 | −4.2 | 5.8 | 2.1 | 2.0 |
| Terrestrial + shipborne + airborne | −0.5 | −4.6 | 5.6 | 2.1 | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Lou, L. Unified Land–Ocean Quasi-Geoid Computation from Heterogeneous Data Sets Based on Radial Basis Functions. Remote Sens. 2022, 14, 3015. https://doi.org/10.3390/rs14133015
Liu Y, Lou L. Unified Land–Ocean Quasi-Geoid Computation from Heterogeneous Data Sets Based on Radial Basis Functions. Remote Sensing. 2022; 14(13):3015. https://doi.org/10.3390/rs14133015
Chicago/Turabian StyleLiu, Yusheng, and Lizhi Lou. 2022. "Unified Land–Ocean Quasi-Geoid Computation from Heterogeneous Data Sets Based on Radial Basis Functions" Remote Sensing 14, no. 13: 3015. https://doi.org/10.3390/rs14133015
APA StyleLiu, Y., & Lou, L. (2022). Unified Land–Ocean Quasi-Geoid Computation from Heterogeneous Data Sets Based on Radial Basis Functions. Remote Sensing, 14(13), 3015. https://doi.org/10.3390/rs14133015