Evaluation of Vegetation Indexes and Green-Up Date Extraction Methods on the Tibetan Plateau
Abstract
:1. Introduction
2. Study Area and Data Sources
2.1. Study Area
2.2. Data Sources
2.2.1. Land Surface Reflectance Products
2.2.2. Ground-Observed GUD Data
2.2.3. Snow Cover Product
2.2.4. Land Cover Type Data
3. Methods
3.1. Calculation of VIs
3.1.1. NDVI
3.1.2. EVI
3.1.3. NDII
3.1.4. PI
3.1.5. NDPI
3.1.6. NDGI
3.2. Determination of Vegetation GUD
3.2.1. Method 1: βmax
3.2.2. Method 2: CCRmax
3.2.3. Method 3: G20
3.2.4. Method 4: RCmax
3.3. Calculation of SCED
3.4. Analysis
3.4.1. Trend Analysis
3.4.2. Accuracy Assessment
4. Results
4.1. Spatiotemporal Variation of GUD
4.2. Performance of VIs in GUD Extraction
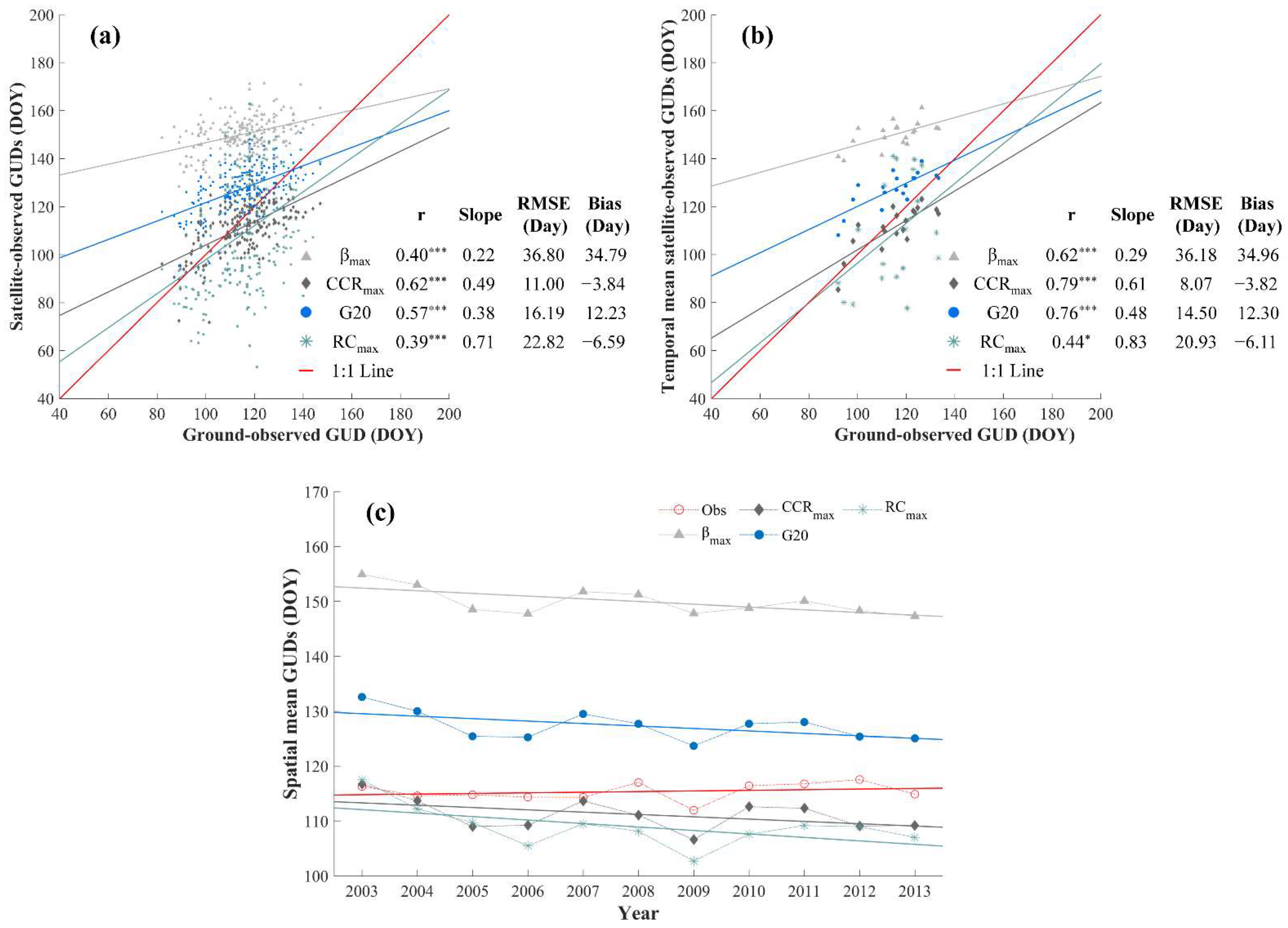
4.3. Performance of GUD Extraction Methods
5. Discussion
5.1. Applicability of Snow-Free VIs on the TP
5.2. Impact of Extraction Methods on GUD Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Temperature Zone | Humidity Region | Eco-Geographical Region |
|---|---|---|
| HI Plateau sub-cold zone | B Sub-humid region | HIB1 Golog-Naqu hummocky plateau shrub-meadow region |
| C Semi-arid region | HIC1 South Qinghai plateau wide valley meadow-steppe region | |
| HIC2 Qiangtang plateau lake basin steppe region | ||
| D Arid region | HID1 Kunlun high mountain plateau desert region | |
| HII Plateau temperate zone | A/B Humid/sub-humid region | HIIA/B1 West Sichuan and east Tibet high mountain and deep valley coniferous forest region |
| C Semi-arid region | HIIC1 Qilian Mountains of east Qinghai coniferous forest-steppe region | |
| HIIC2 South Tibet Mountain shrub-steppe region | ||
| D Arid region | HIID1 Qaidam basin desert region | |
| HIID2 North wing of Kunlun Mountain desert region | ||
| HIID3 Ngari Mountain desert region | ||
| V Middle subtropical zone | A Humid region | VA6 South wing of east Himalaya Mountain seasonal rainforest evergreen broad-leaved forest region |
References
- Qiu, J. The third pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, M.; Jiang, Y.; Zheng, C.; Zhang, D. Trends in the thermal growing season throughout the Tibetan Plateau during 1960–2009. Agric. For. Meteorol. 2012, 166–167, 201–206. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Keenan, T.F.; Gray, J.; Friedl, M.A.; Toomey, M.; Bohrer, G.; Hollinger, D.Y.; Munger, J.W.; O’Keefe, J.; Schmid, H.P.; SueWing, I.; et al. Net carbon uptake has increased through warming-induced changes in temperate forest phenology. Nat. Clim. Chang. 2014, 4, 598–604. [Google Scholar] [CrossRef]
- Zha, T.S.; Barr, A.G.; van der Kamp, G.; Black, T.A.; McCaughey, J.H.; Flanagan, L.B. Interannual variation of evapotranspiration from forest and grassland ecosystems in Western Canada in relation to drought. Agric. For. Meteorol. 2010, 150, 1476–1484. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Wolkovich, E.M.; Cook, B.I.; Allen, J.M.; Crimmins, T.M.; Betancourt, J.L.; Travers, S.E.; Pau, S.; Regetz, J.; Davies, T.J.; Kraft, N.J.; et al. Warming experiments underpredict plant phenological responses to climate change. Nature 2012, 485, 494–497. [Google Scholar] [CrossRef]
- Wingate, L.; Ogee, J.; Cremonese, E.; Filippa, G.; Mizunuma, T.; Migliavacca, M.; Moisy, C.; Wilkinson, M.; Moureaux, C.; Wohlfahrt, G.; et al. Interpreting canopy development and physiology using a European phenology camera network at flux sites. Biogeosciences 2015, 12, 5995–6015. [Google Scholar] [CrossRef] [Green Version]
- Berra, E.F.; Gaulton, R.; Barr, S. Assessing spring phenology of a temperate woodland: A multiscale comparison of ground, unmanned aerial vehicle and Landsat satellite observations. Remote Sens. Environ. 2019, 223, 229–242. [Google Scholar] [CrossRef]
- Wu, C.Y.; Chen, J.M.; Black, T.A.; Price, D.T.; Kurz, W.A.; Desai, A.R.; Gonsamo, A.; Jassal, R.S.; Gough, C.M.; Bohrer, G.; et al. Interannual variability of net ecosystem productivity in forests is explained by carbon flux phenology in autumn. Global Ecol. Biogeogr. 2013, 22, 994–1006. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Chen, M.; Gray, J.M.; Johnston, M.R.; Keenan, T.F.; Klosterman, S.T.; Kosmala, M.; et al. Tracking vegetation phenology across diverse North American biomes using PhenoCam imagery. Sci. Data 2018, 5, 24. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.J.; Schimel, D.; Frankenberg, C.; Drewry, D.T.; Fisher, J.B.; Verma, M.; Berry, J.A.; Lee, J.E.; Joiner, J. Application of satellite solar-induced chlorophyll fluorescence to understanding large-scale variations in vegetation phenology and function over northern high latitude forests. Remote Sens. Environ. 2017, 190, 178–187. [Google Scholar] [CrossRef]
- Guo, L.; An, N.; Wang, K. Reconciling the discrepancy in ground- and satellite-observed trends in the spring phenology of winter wheat in China from 1993 to 2008. J. Geophys. Res. Atmos. 2016, 121, 1027–1042. [Google Scholar] [CrossRef] [Green Version]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS; Freden, S.C., Mercanti, E.P., Becker, M., Eds.; NASA: Washington, DC, USA, 1973; pp. 309–317.
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G.Y. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to topographic effects: A case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [Green Version]
- Shen, M.; Sun, Z.; Wang, S.; Zhang, G.; Kong, W.; Chen, A.; Piao, S. No evidence of continuously advanced green-up dates in the Tibetan Plateau over the last decade. Proc. Natl. Acad. Sci. USA 2013, 110, E2329. [Google Scholar] [CrossRef] [Green Version]
- Delbart, N.; Kergoat, L.; Le Toan, T.; Lhermitte, J.; Picard, G. Determination of phenological dates in boreal regions using normalized difference water index. Remote Sens. Environ. 2005, 97, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Gonsamo, A.; Chen, J.M.; Price, D.T.; Kurz, W.A.; Wu, C. Land surface phenology from optical satellite measurement and CO2 eddy covariance technique. J. Geophys. Res. Biogeosci. 2012, 117, 18. [Google Scholar] [CrossRef]
- Peckham, S.D.; Ahl, D.E.; Serbin, S.P.; Gower, S.T. Fire-induced changes in green-up and leaf maturity of the Canadian boreal forest. Remote Sens. Environ. 2008, 112, 3594–3603. [Google Scholar] [CrossRef]
- Yang, W.; Kobayashi, H.; Wang, C.; Shen, M.; Chen, J.; Matsushita, B.; Tang, Y.; Kim, Y.; Bret-Harte, M.S.; Zona, D.; et al. A semi-analytical snow-free vegetation index for improving estimation of plant phenology in tundra and grassland ecosystems. Remote Sens. Environ. 2019, 228, 31–44. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Wu, J.; Tang, Y.; Shi, P.; Black, T.A.; Zhu, K. A snow-free vegetation index for improved monitoring of vegetation spring green-up date in deciduous ecosystems. Remote Sens. Environ. 2017, 196, 1–12. [Google Scholar] [CrossRef]
- Cao, R.Y.; Feng, Y.; Liu, X.L.; Shen, M.G.; Zhou, J. Uncertainty of vegetation green-up date estimated from vegetation indices due to snowmelt at northern middle and high latitudes. Remote Sens. 2020, 12, 190. [Google Scholar] [CrossRef] [Green Version]
- Gan, L.; Cao, X.; Chen, X.; Dong, Q.; Cui, X.; Chen, J. Comparison of MODIS-based vegetation indices and methods for winter wheat green-up date detection in Huanghuai region of China. Agric. For. Meteorol. 2020, 288–289, 108019. [Google Scholar] [CrossRef]
- Zeng, L.L.; Wardlow, B.D.; Xiang, D.X.; Hu, S.; Li, D.R. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 20. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Yu, H.; Luedeling, E.; Xu, J. Winter and spring warming result in delayed spring phenology on the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2010, 107, 22151–22156. [Google Scholar] [CrossRef] [Green Version]
- Tan, B.; Morisette, J.T.; Wolfe, R.E.; Gao, F.; Ederer, G.A.; Nightingale, J.; Pedelty, J.A. An enhanced TIMESAT algorithm for estimating vegetation phenology metrics from MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 361–371. [Google Scholar] [CrossRef]
- Lu, L.L.; Wang, C.Z.; Guo, H.D.; Li, Q.T. Detecting winter wheat phenology with SPOT-VEGETATION data in the North China Plain. Geocarto Int. 2014, 29, 244–255. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Zhou, L.M.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology in China’s temperate vegetation. Global Change Biol. 2006, 12, 672–685. [Google Scholar] [CrossRef]
- Zheng, Z.T.; Zhu, W.Q. Uncertainty of remote sensing data in monitoring vegetation phenology: A comparison of MODIS C5 and C6 vegetation index products on the Tibetan Plateau. Remote Sens. 2017, 9, 1288. [Google Scholar] [CrossRef] [Green Version]
- Keatley, M.R.; Hudson, I.L. Phenological Research Methods for Environmental and Climate Change Analysis Introduction and Overview; Hudson, I.L., Keatley, M.R., Eds.; Springer: New York, NY, USA, 2010; pp. 1–22. [Google Scholar] [CrossRef]
- de Beurs, K.M.; Henebry, G.M. Spatio-Temporal Statistical Methods for Modelling Land Surface Phenology; Hudson, I.L., Keatley, M.R., Eds.; Springer: New York, NY, USA, 2010; pp. 177–208. [Google Scholar] [CrossRef]
- Sakamoto, T.; Wardlow, B.D.; Gitelson, A.A.; Verma, S.B.; Suyker, A.E.; Arkebauer, T.J. A Two-Step Filtering approach for detecting maize and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2010, 114, 2146–2159. [Google Scholar] [CrossRef]
- Pan, Z.K.; Huang, J.F.; Zhou, Q.B.; Wang, L.M.; Cheng, Y.X.; Zhang, H.K.; Blackburn, G.A.; Yan, J.; Liu, J.H. Mapping crop phenology using NDVI time-series derived from HJ-1 A/B data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 188–197. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.M.; Conrad, C.; Doktor, D. Optimising phenological metrics extraction for different crop types in Germany using the Moderate Resolution Imaging Spectrometer (MODIS). Remote Sens. 2017, 9, 254. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.L.; Wardlow, B.D.; Wang, R.; Shan, J.; Tadesse, T.; Hayes, M.J.; Li, D.R. A hybrid approach for detecting corn and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2016, 181, 237–250. [Google Scholar] [CrossRef]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
- Wang, H.J.; Dai, J.H.; Ge, Q.S. Comparison of satellite and ground-based phenology in China’s temperate monsoon area. Adv. Meteorol. 2014, 2014, 10. [Google Scholar] [CrossRef]
- Zhang, X.X.; Cui, Y.P.; Qin, Y.C.; Xia, H.M.; Lu, H.L.; Liu, S.J.; Li, N.; Fu, Y.M. Evaluating the accuracy of and evaluating the potential errors in extracting vegetation phenology through remote sensing in China. Int. J. Remote Sens. 2020, 41, 3592–3613. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Z.; Liu, Y.; Wu, J.; Han, Y. Trend analysis of vegetation dynamics in Qinghai–Tibet Plateau using Hurst Exponent. Ecol. Indic. 2012, 14, 28–39. [Google Scholar] [CrossRef]
- Wu, S.; Yang, Q.; Du, Z. Delineation of eco-geographic regional system of China. J. Geog. Sci. 2003, 13, 309–315. [Google Scholar] [CrossRef]
- Pu, Z.; Xu, L.; Salomonson, V.V. MODIS/Terra observed seasonal variations of snow cover over the Tibetan Plateau. Geophys. Res. Lett. 2007, 34, 6. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E.F.; Roger, J.C.; Ray, J.P. MODIS Surface Reflectance Collection 6 User’s Guide. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD09_UserGuide_v1.4.pdf (accessed on 8 December 2020).
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Shen, M.G.; Zhang, G.X.; Cong, N.; Wang, S.P.; Kong, W.D.; Piao, S.L. Increasing altitudinal gradient of spring vegetation phenology during the last decade on the Qinghai-Tibetan Plateau. Agric. For. Meteorol. 2014, 189, 71–80. [Google Scholar] [CrossRef]
- Zhang, X.; Tarpley, D.; Sullivan, J.T. Diverse responses of vegetation phenology to a warming climate. Geophys. Res. Lett. 2007, 34, 5. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, H.X.; Yu, B.L.; Wu, J.P.; Kang, E.L.; Xu, M.; Wang, S.J.; Klein, A.; Chen, Y.N. Improving MODIS snow products with a HMRF-based spatio-temporal modeling technique in the Upper Rio Grande Basin. Remote Sens. Environ. 2018, 204, 568–582. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, J.; Xu, J.; Zhao, Y.; Yu, B.; Liu, H.; Wang, S.; Xu, W.; Wu, J.; Zheng, Z. HMRFS-TP: Long-term daily gap-free snow cover products over the Tibetan Plateau from 2002 to 2021 based on Hidden Markov Random Field model. Earth Syst. Sci. Data Discuss. 2022; in review. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Klemas, V.; Smart, R.M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Helman, D. Land surface phenology: What do we really ‘see’ from space? Sci. Total Environ. 2018, 618, 665–673. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Long, D.; Hong, Y.; Hao, X.; Hou, A. Climatology of snow phenology over the Tibetan plateau for the period 2001–2014 using multisource data. Int. J. Climatol. 2018, 38, 2718–2729. [Google Scholar] [CrossRef]
- Guo, H.; Wang, X.Y.; Guo, Z.C.; Chen, S.Y. Assessing snow phenology and its environmental driving factors in Northeast China. Remote Sens. 2022, 14, 262. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. In Henri Theil’s Contributions to Economics and Econometrics: Econometric Theory and Methodology; Raj, B., Koerts, J., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 345–381. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.; Tagesson, T.; Brandt, M.; Wang, L.; Chen, N.; Zu, J.; Jin, H.; Cai, Z.; Tong, X.; et al. The confounding effect of snow cover on assessing spring phenology from space: A new look at trends on the Tibetan Plateau. Sci. Total Environ. 2021, 756, 144011. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Cao, R.; Chen, J.; Shen, M.; Tang, Y. An improved logistic method for detecting spring vegetation phenology in grasslands from MODIS EVI time-series data. Agric. For. Meteorol. 2015, 200, 9–20. [Google Scholar] [CrossRef]
- Shang, R.; Liu, R.; Xu, M.; Liu, Y.; Zuo, L.; Ge, Q. The relationship between threshold-based and inflexion-based approaches for extraction of land surface phenology. Remote Sens. Environ. 2017, 199, 167–170. [Google Scholar] [CrossRef]
- Li, N.; Zhan, P.; Pan, Y.Z.; Zhu, X.F.; Li, M.Y.; Zhang, D.J. Comparison of remote sensing time-series smoothing methods for grassland spring phenology extraction on the Qinghai-Tibetan Plateau. Remote Sens. 2020, 12, 3383. [Google Scholar] [CrossRef]
- Delbart, N.; Le Toan, T.; Kergoat, L.; Fedotova, V. Remote sensing of spring phenology in boreal regions: A free of snow-effect method using NOAA-AVHRR and SPOT-VGT data (1982–2004). Remote Sens. Environ. 2006, 101, 52–62. [Google Scholar] [CrossRef]
- Hamunyela, E.; Verbesselt, J.; Roerink, G.; Herold, M. Trends in spring phenology of Western European deciduous forests. Remote Sens. 2013, 5, 6159–6179. [Google Scholar] [CrossRef] [Green Version]


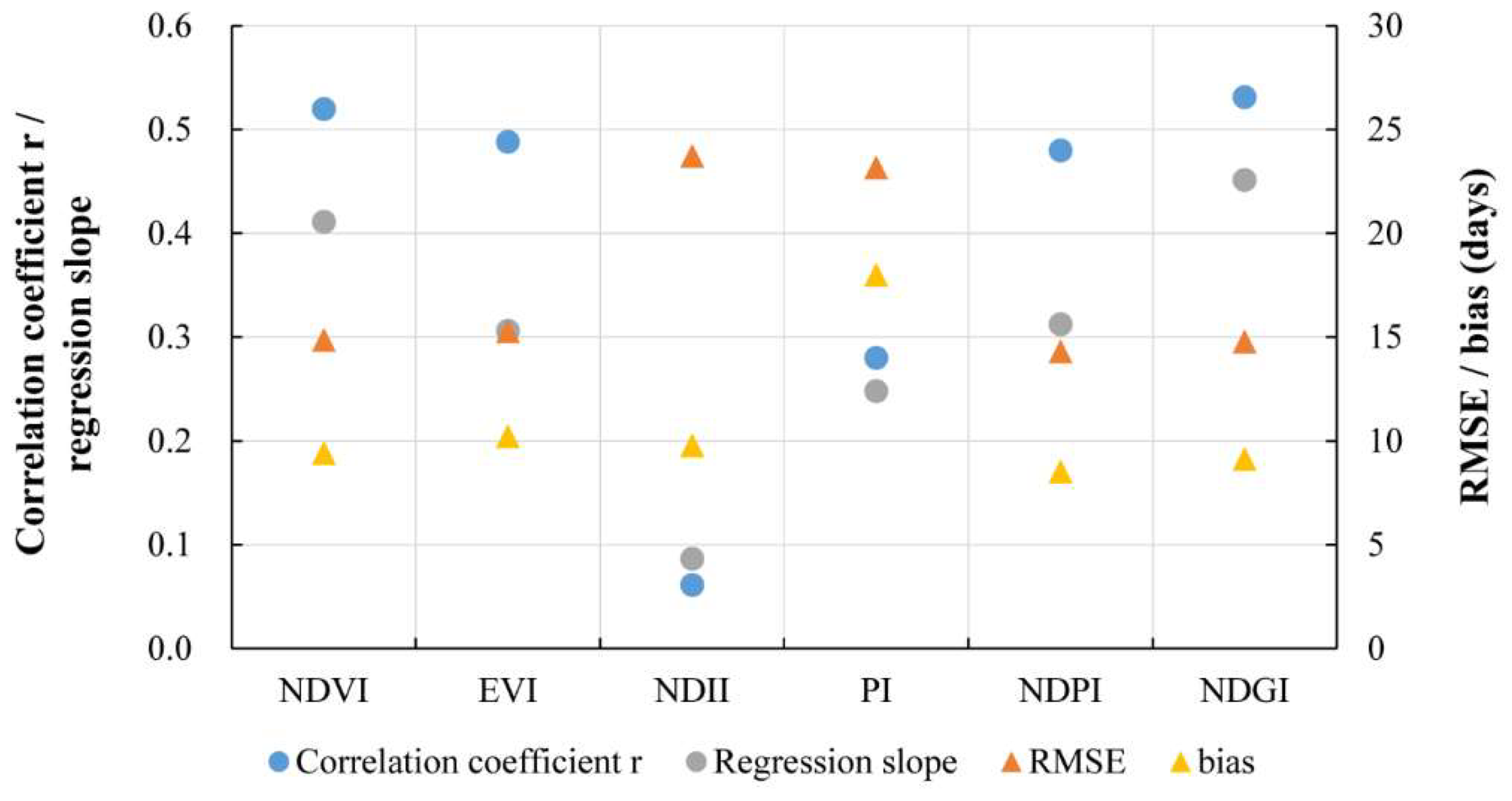

| VI | Without Preseason Snow Cover | With Preseason Snow Cover | ||||||
|---|---|---|---|---|---|---|---|---|
| r | Slope | RMSE (Day) | Bias (Day) | r | Slope | RMSE (Day) | Bias (Day) | |
| NDVI | 0.58 *** | 0.53 | 14.03 | −8.70 | 0.72 *** | 0.46 | 14.46 | −10.72 |
| EVI | 0.52 *** | 0.40 | 13.96 | −8.30 | 0.63 *** | 0.42 | 12.48 | −6.25 |
| NDII | 0.28 *** | 0.39 | 24.02 | −15.33 | −0.34 * | −0.90 | 50.23 | −24.25 |
| PI | 0.29 *** | 0.30 | 16.90 | 7.80 | 0.38 ** | 0.27 | 15.87 | 7.95 |
| NDPI | 0.57 *** | 0.48 | 12.78 | −6.81 | 0.57 *** | 0.35 | 12.38 | −4.66 |
| NDGI | 0.60 *** | 0.49 | 11.06 | −3.80 | 0.71 *** | 0.44 | 10.69 | −4.05 |
| VI | Whether to Calibrate Snow | r | Slope | RMSE (Day) | Bias (Day) |
|---|---|---|---|---|---|
| NDVI | uncalibrated | 0.18 ** | 0.27 | 23.23 | −10.95 |
| snow-calibrated | 0.60 *** | 0.53 | 14.10 | −9.02 | |
| EVI | uncalibrated | 0.11 | 0.16 | 23.12 | −9.81 |
| snow-calibrated | 0.54 *** | 0.41 | 13.73 | −7.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Tang, Y.; Xu, J.; Chen, J.; Bai, K.; Shu, S.; Yu, B.; Wu, J.; Huang, Y. Evaluation of Vegetation Indexes and Green-Up Date Extraction Methods on the Tibetan Plateau. Remote Sens. 2022, 14, 3160. https://doi.org/10.3390/rs14133160
Xu J, Tang Y, Xu J, Chen J, Bai K, Shu S, Yu B, Wu J, Huang Y. Evaluation of Vegetation Indexes and Green-Up Date Extraction Methods on the Tibetan Plateau. Remote Sensing. 2022; 14(13):3160. https://doi.org/10.3390/rs14133160
Chicago/Turabian StyleXu, Jingyi, Yao Tang, Jiahui Xu, Jin Chen, Kaixu Bai, Song Shu, Bailang Yu, Jianping Wu, and Yan Huang. 2022. "Evaluation of Vegetation Indexes and Green-Up Date Extraction Methods on the Tibetan Plateau" Remote Sensing 14, no. 13: 3160. https://doi.org/10.3390/rs14133160
APA StyleXu, J., Tang, Y., Xu, J., Chen, J., Bai, K., Shu, S., Yu, B., Wu, J., & Huang, Y. (2022). Evaluation of Vegetation Indexes and Green-Up Date Extraction Methods on the Tibetan Plateau. Remote Sensing, 14(13), 3160. https://doi.org/10.3390/rs14133160







