A New Coherence Detection Method for Mapping Inland Water Bodies Using CYGNSS Data
Abstract
:1. Introduction
2. Data and Methods
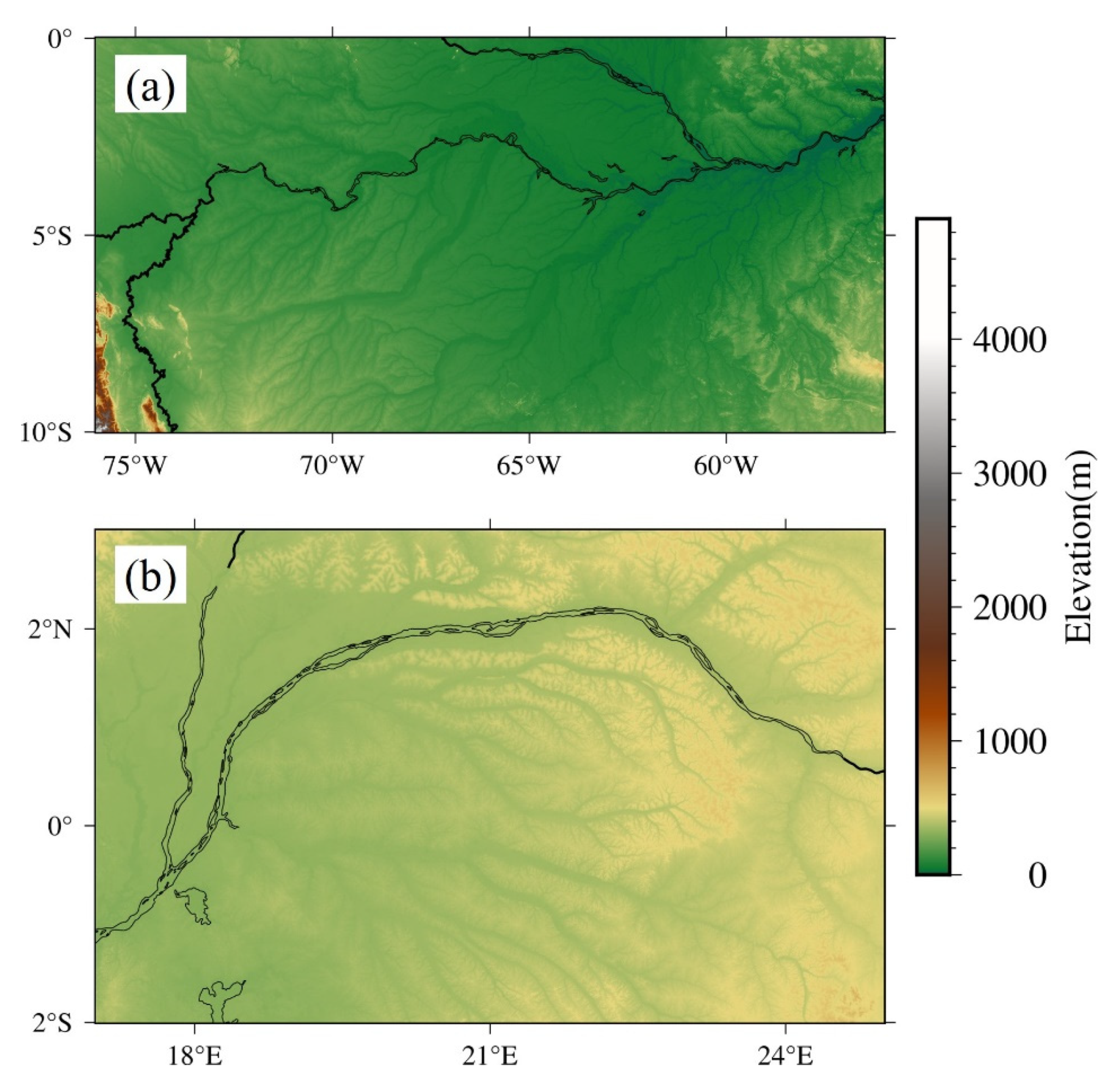
2.1. Study Areas
2.2. Data
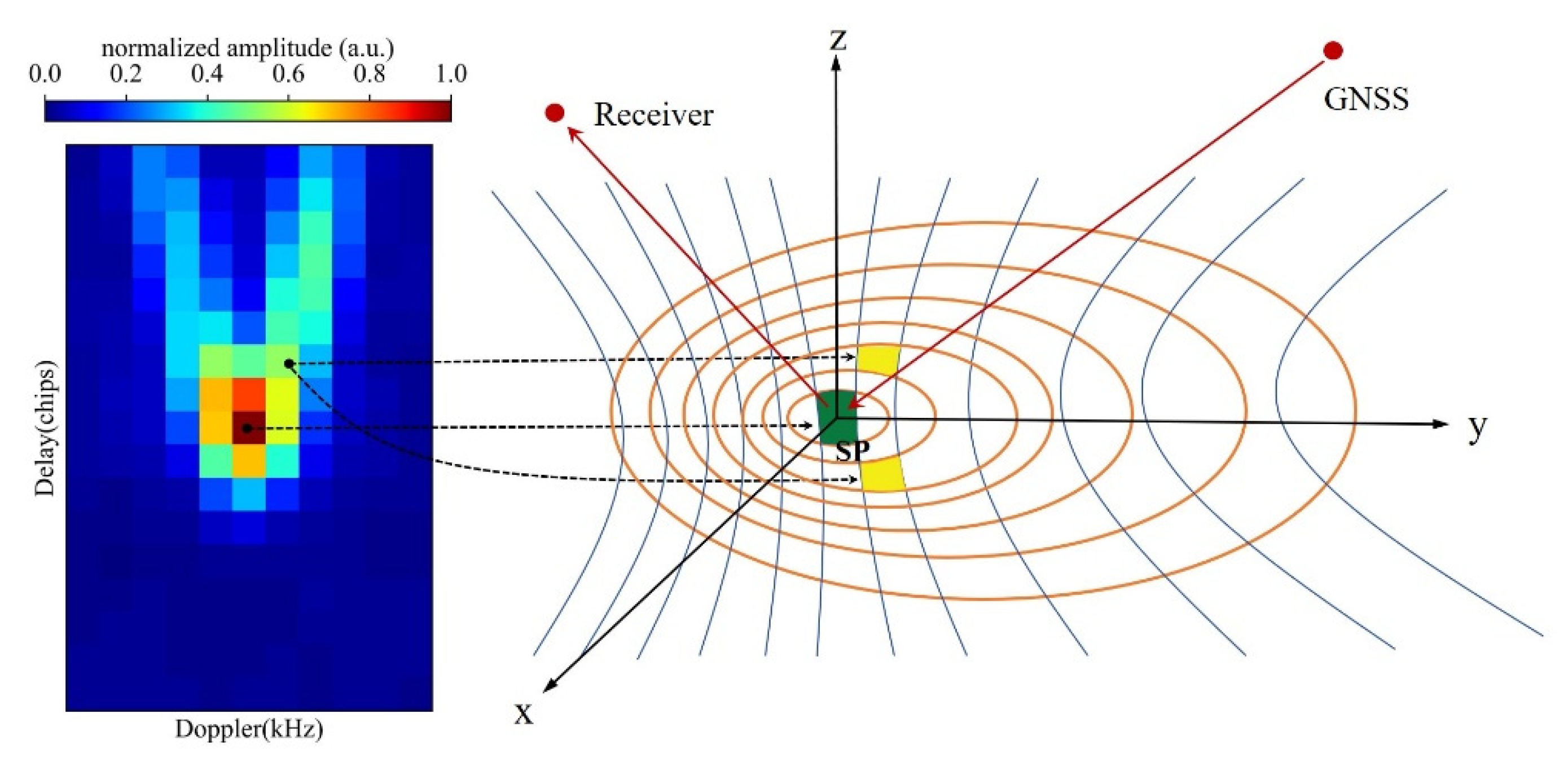
2.2.1. CYGNSS DDM
2.2.2. Global Surface Water Data
2.3. Method
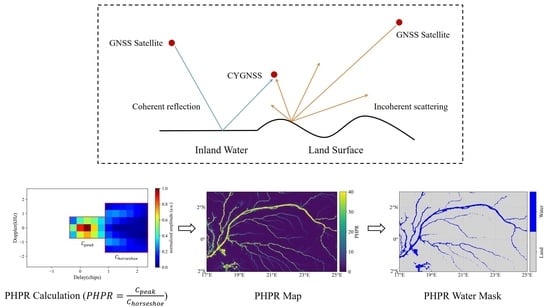
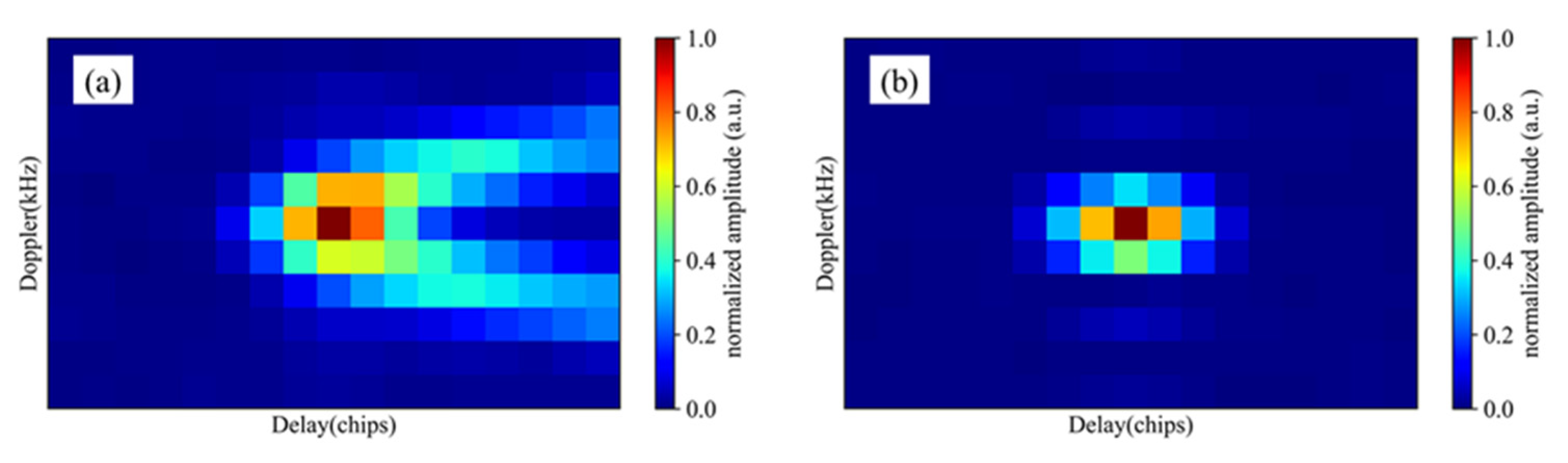
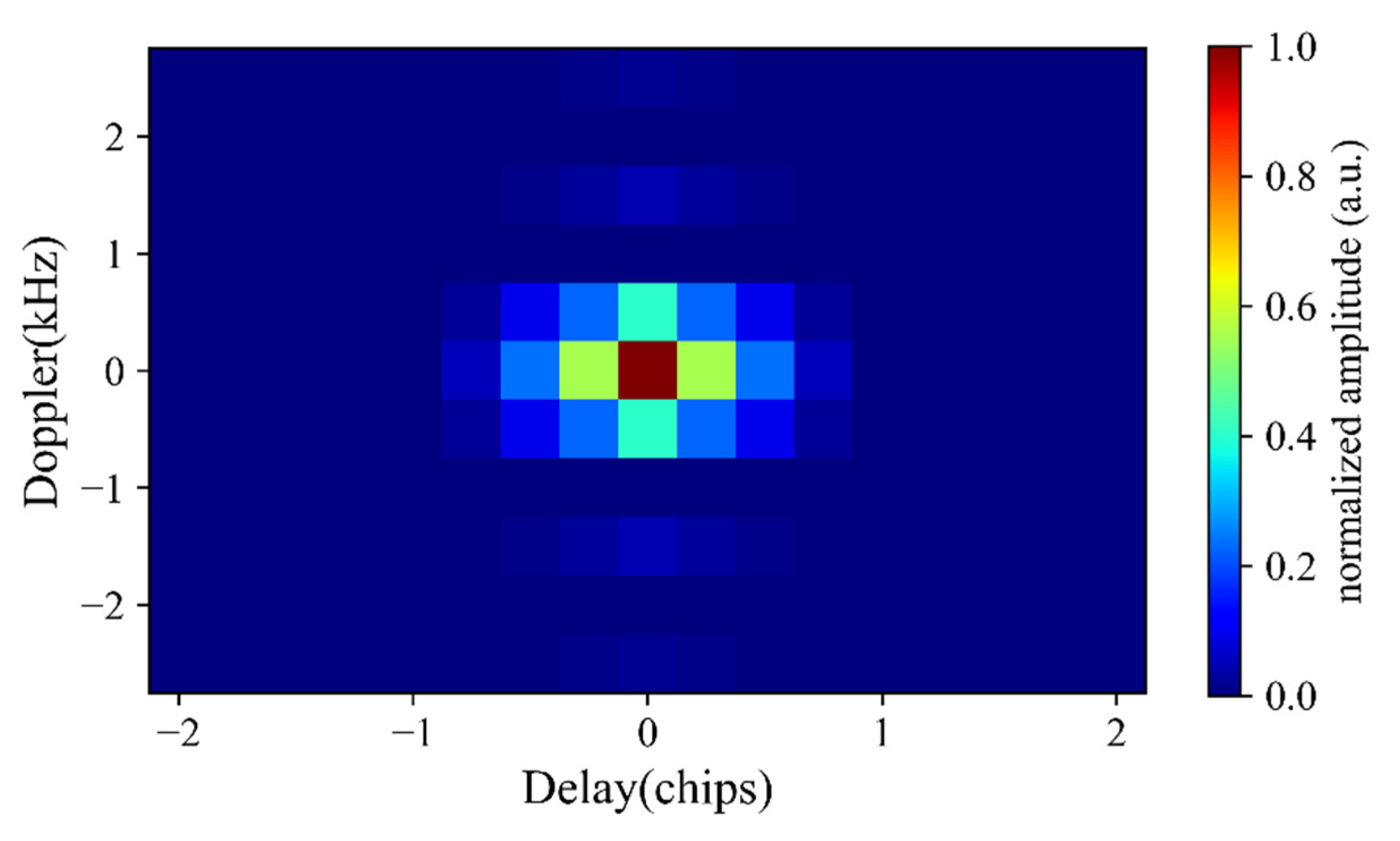
2.3.1. DPSD Method
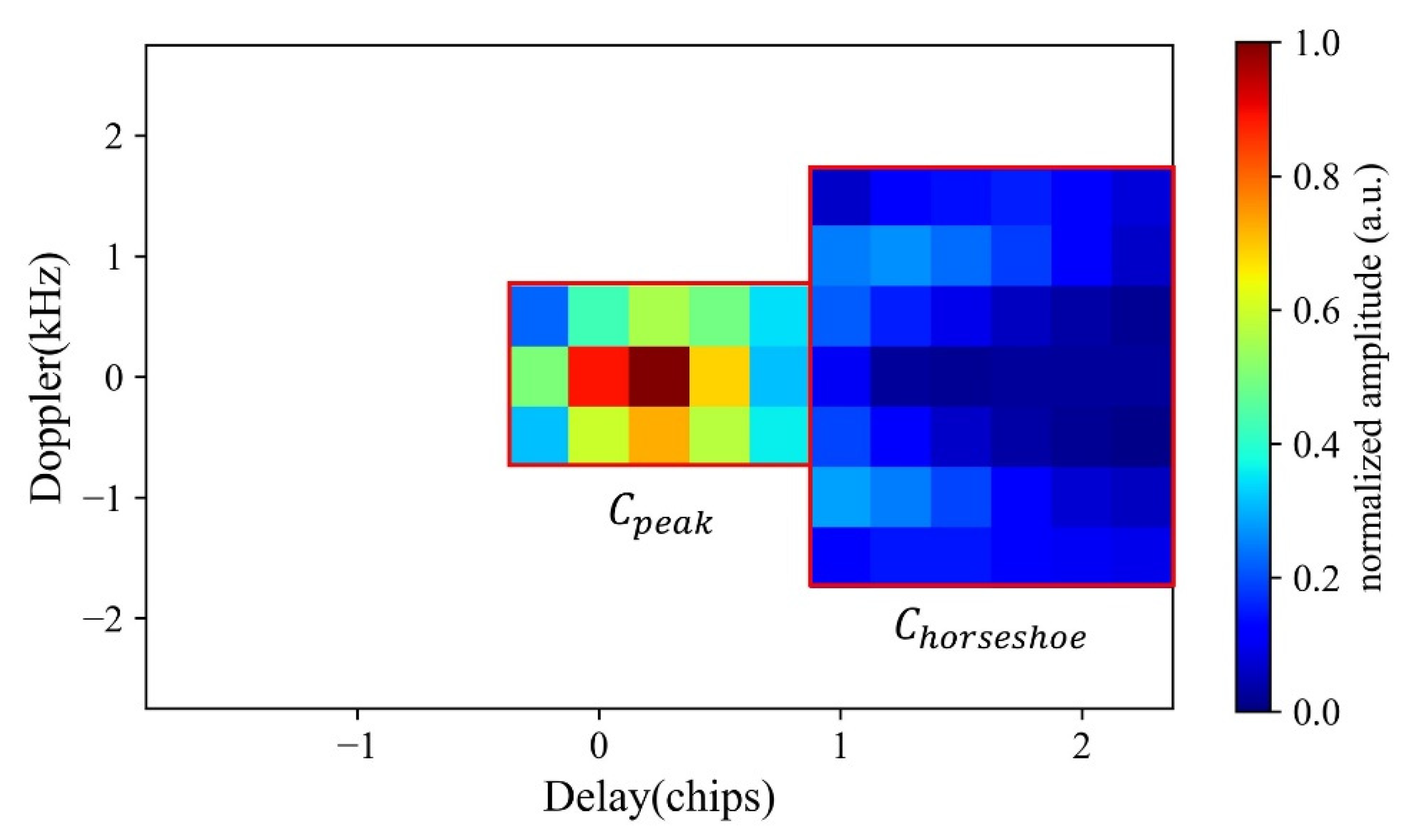
2.3.2. New Coherence Detection Method
2.3.3. Random Walker Segmentation
2.4. Evaluation Indices
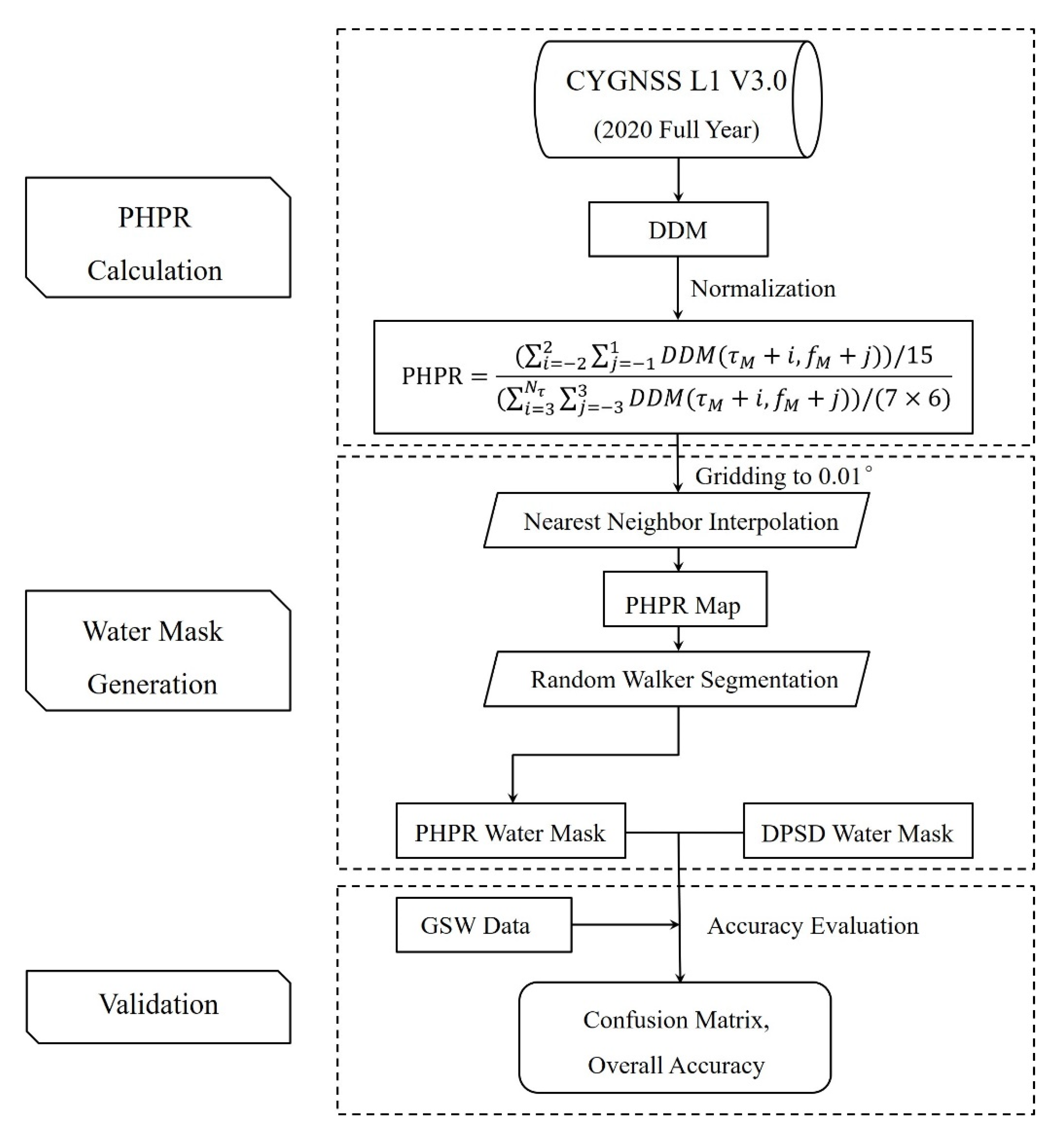
2.5. Steps to Perform New Method
3. Results
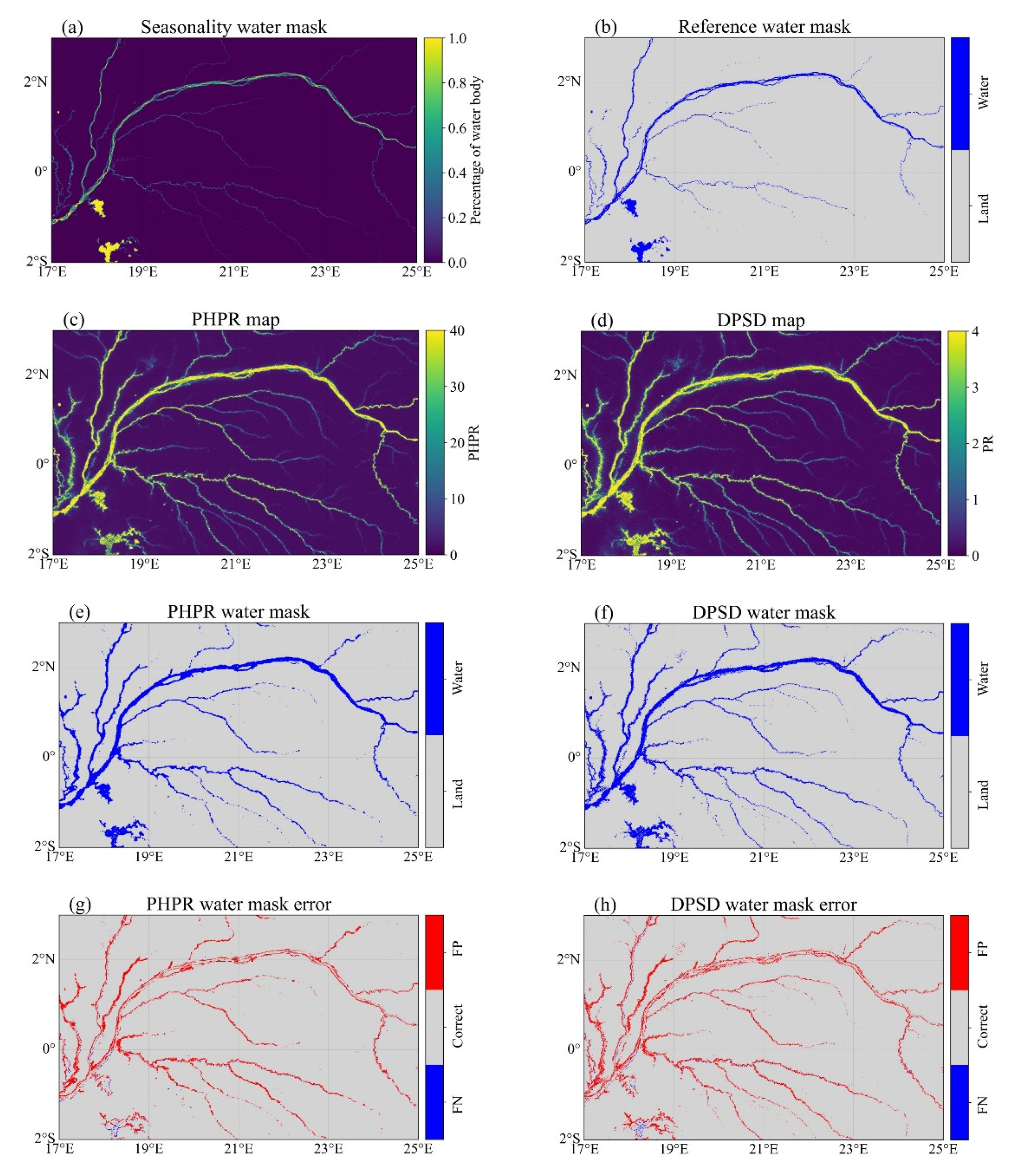
3.1. Water Detection Results in the Amazon Basin
3.2. Water Detection Results in the Congo Basin
4. Discussion
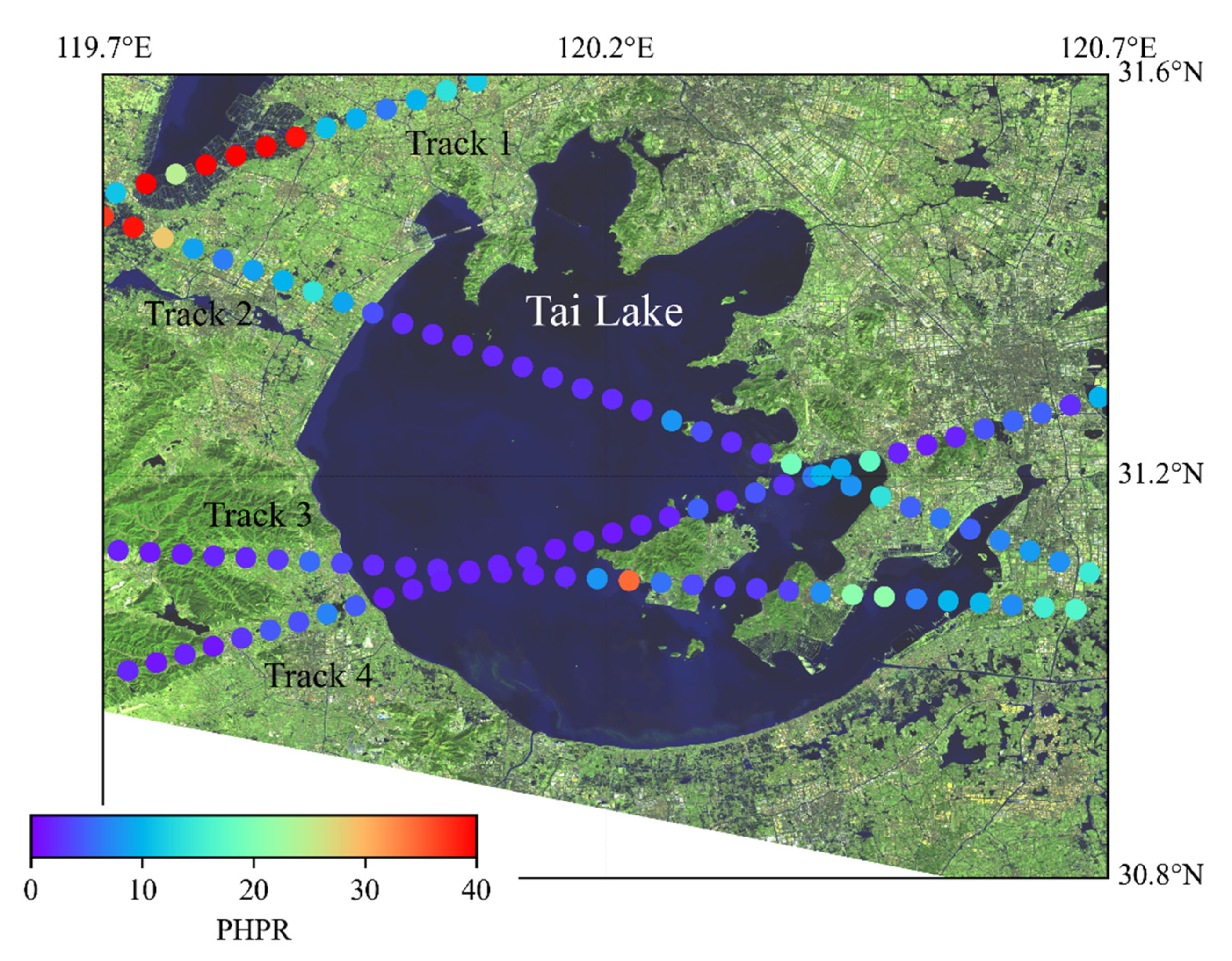
4.1. Limitation on Detecting Big Water Bodies
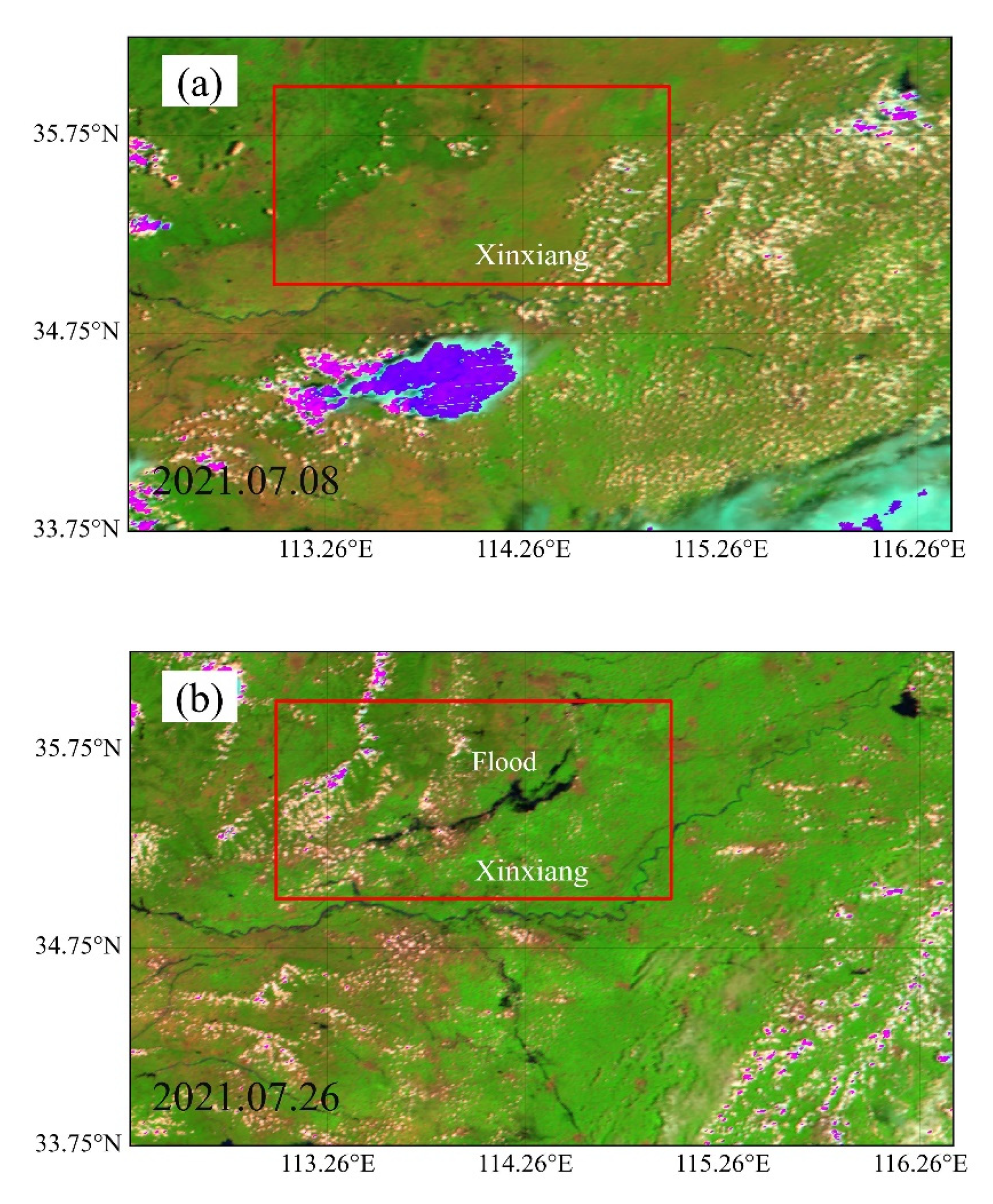
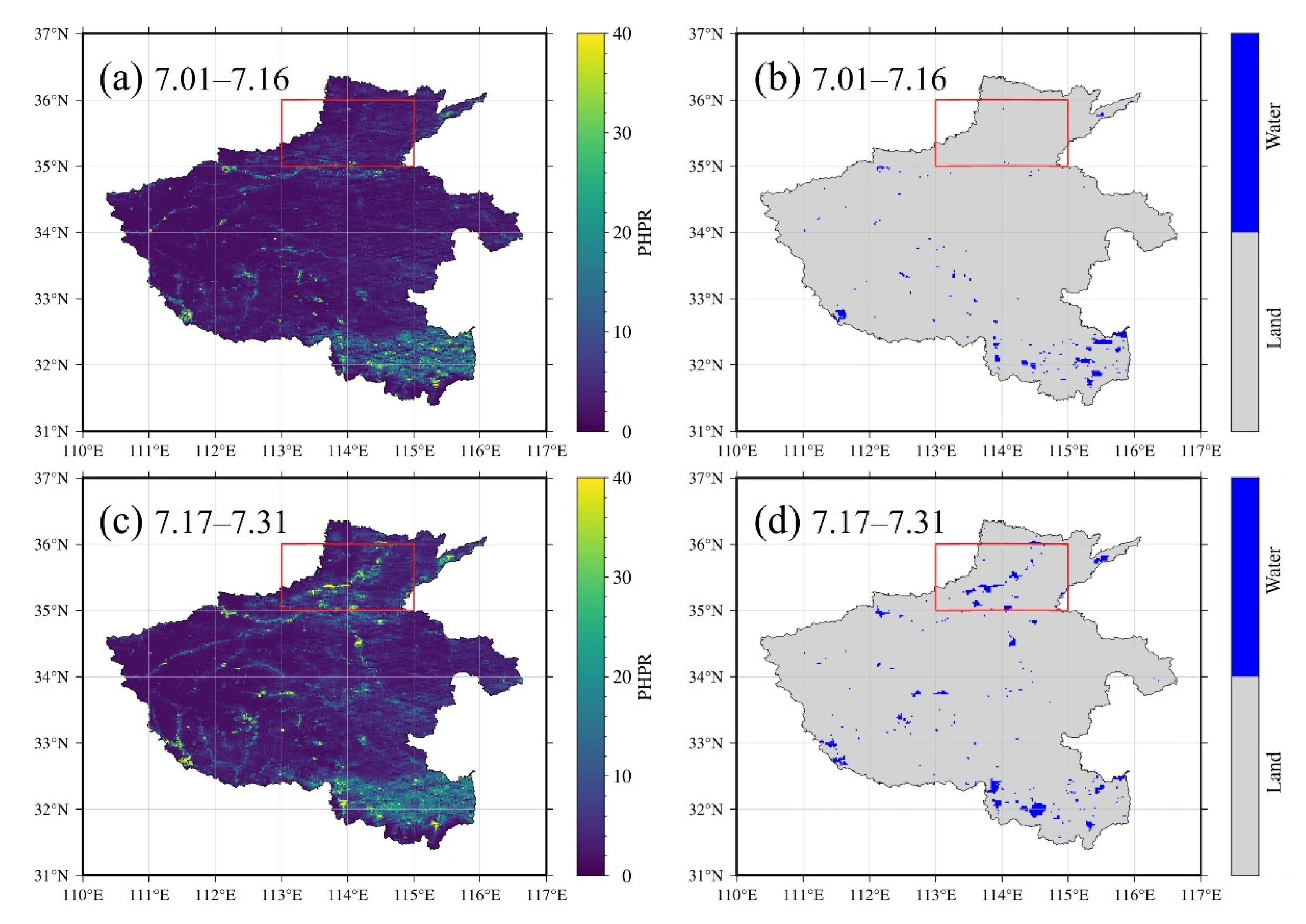
4.2. Ability for Flood Inundation Detection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [Green Version]
- Bastin, L.; Gorelick, N.; Saura, S.; Bertzky, B.; Dubois, G.; Fortin, M.J.; Pekel, J.F. Inland surface waters in protected areas globally: Current coverage and 30-year trends. PLoS ONE 2019, 14, e0210496. [Google Scholar] [CrossRef]
- Holgerson, M.A.; Raymond, P.A. Large contribution to inland water CO2 and CH4 emissions from very small ponds. Nat. Geosci. 2016, 9, 222–226. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Martins, V.S.; Novo, E.M.L.M.; Lyapustin, A.; Aragão, L.E.O.C.; Freitas, S.R.; Barbosa, C.C.F. Seasonal and interannual assessment of cloud cover and atmospheric constituents across the Amazon (2000–2015): Insights for remote sensing and climate analysis. ISPRS J. Photogramm. Remote Sens. 2018, 145, 309–327. [Google Scholar] [CrossRef] [Green Version]
- Geudtner, D.; Torres, R. Sentinel-1 system overview and performance. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1719–1721. [Google Scholar]
- Mason, D.C.; Speck, R.; Devereux, B.; Schumann, G.J.P.; Neal, J.C.; Bates, P.D. Flood Detection in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 882–894. [Google Scholar] [CrossRef] [Green Version]
- Gleason, S.; Hodgart, S.; Yiping, S.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and Processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef] [Green Version]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-Reflectometry on TechDemoSat-1: Early Mission Operations and Exploitation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J.; et al. New Ocean Winds Satellite Mission to Probe Hurricanes and Tropical Convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Li, C.; Huang, W. An Algorithm for Sea-Surface Wind Field Retrieval From GNSS-R Delay-Doppler Map. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2110–2114. [Google Scholar] [CrossRef]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Chew, C.C.; Small, E.E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef] [Green Version]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.-W.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Lake Level and Surface Topography Measured With Spaceborne GNSS-Reflectometry From CYGNSS Mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 13332–13341. [Google Scholar] [CrossRef]
- Morris, M.; Chew, C.; Reager, J.T.; Shah, R.; Zuffada, C. A novel approach to monitoring wetland dynamics using CYGNSS: Everglades case study. Remote Sens. Environ. 2019, 233, 111417. [Google Scholar] [CrossRef]
- Wu, X.; Dong, Z.; Jin, S.; He, Y.; Song, Y.; Ma, W.; Yang, L. First Measurement of Soil Freeze/Thaw Cycles in the Tibetan Plateau Using CYGNSS GNSS-R Data. Remote Sens. 2020, 12, 2361. [Google Scholar] [CrossRef]
- Chew, C.; Reager, J.T.; Small, E. CYGNSS data map flood inundation during the 2017 Atlantic hurricane season. Sci. Rep. 2018, 8, 9336. [Google Scholar] [CrossRef]
- Wan, W.; Liu, B.; Zeng, Z.; Chen, X.; Wu, G.; Xu, L.; Chen, X.; Hong, Y. Using CYGNSS Data to Monitor China’s Flood Inundation during Typhoon and Extreme Precipitation Events in 2017. Remote Sens. 2019, 11, 854. [Google Scholar] [CrossRef] [Green Version]
- Chew, C.; Small, E. Estimating inundation extent using CYGNSS data: A conceptual modeling study. Remote Sens. Environ. 2020, 246, 111869. [Google Scholar] [CrossRef]
- Zavorotny, V.; Loria, E.; O’Brien, A.; Downs, B.; Zuffada, C. Investigation of Coherent and Incoherent Scattering from Lakes Using Cygnss Observations. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5917–5920. [Google Scholar]
- Loria, E.; O’Brien, A.; Zavorotny, V.; Downs, B.; Zuffada, C. Analysis of scattering characteristics from inland bodies of water observed by CYGNSS. Remote Sens. Environ. 2020, 245, 111825. [Google Scholar] [CrossRef]
- Ghasemigoudarzi, P.; Huang, W.; De Silva, O.; Yan, Q.; Power, D. A Machine Learning Method for Inland Water Detection Using CYGNSS Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3020223. [Google Scholar] [CrossRef]
- Gerlein-Safdi, C.; Ruf, C.S. A CYGNSS-Based Algorithm for the Detection of Inland Waterbodies. Geophys. Res. Lett. 2019, 46, 12065–12072. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; Gleason, S.; Loria, E.; O’Brien, A.J.; Yi, Y. An Algorithm for Detecting Coherence in Cyclone Global Navigation Satellite System Mission Level-1 Delay-Doppler Maps. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4454–4463. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-Series Retrieval of Soil Moisture Using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; Gleason, S.; Chew, C.C.; Gerlein-Safdi, C.; Shah, R.; Zuffada, C. Inland Water Body Mapping Using CYGNSS Coherence Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7385–7394. [Google Scholar] [CrossRef]
- Sorribas, M.V.; Paiva, R.C.D.; Melack, J.M.; Bravo, J.M.; Jones, C.; Carvalho, L.; Beighley, E.; Forsberg, B.; Costa, M.H. Projections of climate change effects on discharge and inundation in the Amazon basin. Clim. Chang. 2016, 136, 555–570. [Google Scholar] [CrossRef]
- Villar, J.C.E.; Guyot, J.L.; Ronchail, J.; Cochonneau, G.; Filizola, N.; Fraizy, P.; Labat, D.; de Oliveira, E.; Ordoñez, J.J.; Vauchel, P. Contrasting regional discharge evolutions in the Amazon basin (1974–2004). J. Hydrol. 2009, 375, 297–311. [Google Scholar] [CrossRef]
- Richey, J.E.; Meade, R.H.; Salati, E.; Devol, A.H.; Nordin, C.F., Jr.; Santos, U.D. Water discharge and suspended sediment concentrations in the Amazon River: 1982–1984. Water Resour. Res. 1986, 22, 756–764. [Google Scholar] [CrossRef]
- Laurance, W.F.; Lovejoy, T.E.; Vasconcelos, H.L.; Bruna, E.M.; Didham, R.K.; Stouffer, P.C.; Gascon, C.; Bierregaard, R.O.; Laurance, S.G.; Sampaio, E. Ecosystem decay of Amazonian forest fragments: A 22-year investigation. Conserv. Biol. 2002, 16, 605–618. [Google Scholar] [CrossRef] [Green Version]
- Davidson, E.A.; de Araujo, A.C.; Artaxo, P.; Balch, J.K.; Brown, I.F.; MM, C.B.; Coe, M.T.; DeFries, R.S.; Keller, M.; Longo, M.; et al. The Amazon basin in transition. Nature 2012, 481, 321–328. [Google Scholar] [CrossRef]
- Nicholson, S.E. A revised picture of the structure of the “monsoon” and land ITCZ over West Africa. Clim. Dyn. 2009, 32, 1155–1171. [Google Scholar] [CrossRef]
- Laraque, A.; Castellanos, B.; Steiger, J.; Lòpez, J.L.; Pandi, A.; Rodriguez, M.; Rosales, J.; Adèle, G.; Perez, J.; Lagane, C. A comparison of the suspended and dissolved matter dynamics of two large inter-tropical rivers draining into the Atlantic Ocean: The Congo and the Orinoco. Hydrol. Process. 2013, 27, 2153–2170. [Google Scholar] [CrossRef]
- Hansen, M.C.; Roy, D.P.; Lindquist, E.; Adusei, B.; Justice, C.O.; Altstatt, A. A method for integrating MODIS and Landsat data for systematic monitoring of forest cover and change in the Congo Basin. Remote Sens. Environ. 2008, 112, 2495–2513. [Google Scholar] [CrossRef]
- Laporte, N.T.; Goetz, S.J.; Justice, C.O.; Heinicke, M. A new land cover map of central Africa derived from multi-resolution, multi-temporal AVHRR data. Int. J. Remote Sens. 2010, 19, 3537–3550. [Google Scholar] [CrossRef]
- Laraque, A.; Bricquet, J.P.; Pandi, A.; Olivry, J.C. A review of material transport by the Congo river and its tributaries. Hydrol. Process. 2009, 23, 3216–3224. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS nanosatellite constellation hurricane mission. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef] [Green Version]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results From the U.K. TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, K.; Zou, J.; Wickert, J. Sea Ice Detection Based on Differential Delay-Doppler Maps from UK TechDemoSat-1. Sensors 2017, 17, 1614. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea Ice Detection Using U.K. TDS-1 GNSS-R Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Jin, S. Evaluation of the Land GNSS-Reflected DDM Coherence on Soil Moisture Estimation from CYGNSS Data. Remote Sens. 2021, 13, 570. [Google Scholar] [CrossRef]
- Grady, L. Random walks for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef] [Green Version]
- Loria, E.; O’Brien, A.; Zavorotny, V.; Zuffada, C. Wind Vector and Wave Height Retrieval in Inland Waters Using CYGNSS. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 7029–7032. [Google Scholar]
- Zhang, S.; Ma, Z.; Li, Z.; Zhang, P.; Liu, Q.; Nan, Y.; Zhang, J.; Hu, S.; Feng, Y.; Zhao, H. Using CYGNSS Data to Map Flood Inundation during the 2021 Extreme Precipitation in Henan Province, China. Remote Sens. 2021, 13, 5181. [Google Scholar] [CrossRef]
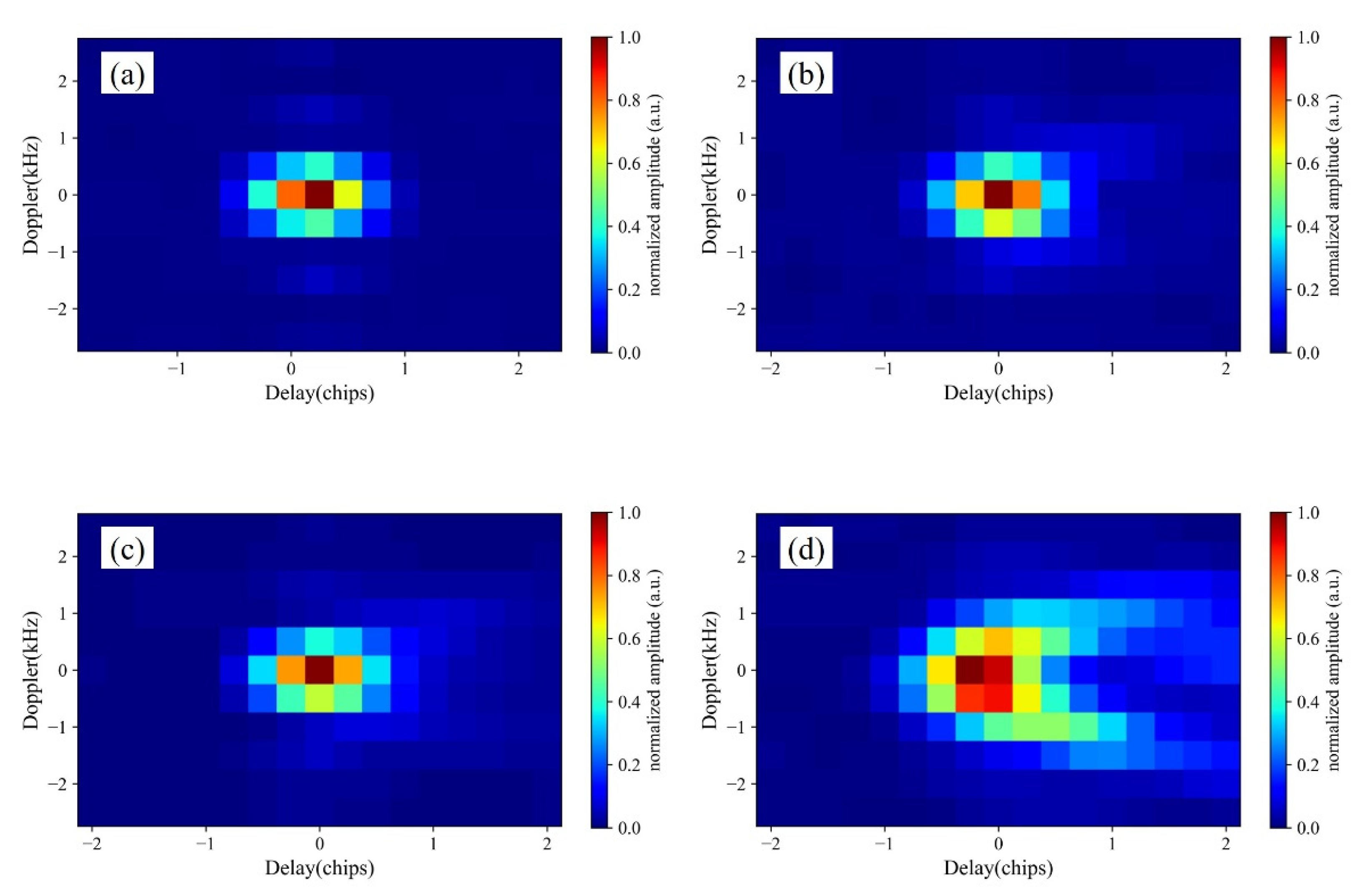



| No. | Lon | Lat | SNR (dB) | Type | PR | PHPR |
|---|---|---|---|---|---|---|
| (a) | 65.375°W | 0.327°S | 12.47 | Water | 3.61 | 37.78 |
| (b) | 66.924°W | 2.327°S | 11.20 | Land | 2.91 | 11.08 |
| (c) | 67.098°W | 2.456°S | 12.96 | Land | 3.32 | 10.32 |
| (d) | 61.527°W | 8.414°S | 10.42 | Land | 1.26 | 3.22 |
| Reference | Detected Results | |
|---|---|---|
| Land | Water | |
| Land | TN | FP |
| Water | FN | TP |
| Study Area | Method | Reference | Detection * | Overall Accuracy | |
|---|---|---|---|---|---|
| Land | Water | ||||
| Amazon Basin | PHPR | Land | 94.56% (1,821,102) | 5.44% (104,689) | 94.48% |
| Water | 7.77% (5767) | 92.23% (68,442) | |||
| DPSD | Land | 93.43% (1,799,396) | 6.56% (126,395) | 93.36% | |
| Water | 8.55% (6348) | 91.45% (67,861) | |||
| Congo Basin | PHPR | Land | 96.21% (374,256) | 3.79% (14,760) | 96.12% |
| Water | 6.84% (751) | 93.16% (10,233) | |||
| DPSD | Land | 95.78% (372,616) | 4.22% (16,400) | 95.66% | |
| Water | 8.77% (963) | 91.23% (10,021) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Hu, Y.; Li, Z. A New Coherence Detection Method for Mapping Inland Water Bodies Using CYGNSS Data. Remote Sens. 2022, 14, 3195. https://doi.org/10.3390/rs14133195
Wang J, Hu Y, Li Z. A New Coherence Detection Method for Mapping Inland Water Bodies Using CYGNSS Data. Remote Sensing. 2022; 14(13):3195. https://doi.org/10.3390/rs14133195
Chicago/Turabian StyleWang, Ji, Yufeng Hu, and Zhenhong Li. 2022. "A New Coherence Detection Method for Mapping Inland Water Bodies Using CYGNSS Data" Remote Sensing 14, no. 13: 3195. https://doi.org/10.3390/rs14133195
APA StyleWang, J., Hu, Y., & Li, Z. (2022). A New Coherence Detection Method for Mapping Inland Water Bodies Using CYGNSS Data. Remote Sensing, 14(13), 3195. https://doi.org/10.3390/rs14133195