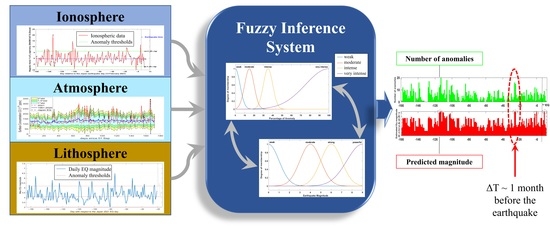
Developing a Fuzzy Inference System Based on Multi-Sensor Data to Predict Powerful Earthquake Parameters

Abstract

Predicting the parameters of upcoming earthquakes has always been one of the most challenging topics in studies related to earthquake precursors. Increasing the number of sensors and satellites and consequently incrementing the number of observable possible earthquake precursors in different layers of the lithosphere, atmosphere, and ionosphere of the Earth has opened the possibility of using data fusion methods to estimate and predict earthquake parameters with low uncertainty. In this study, a Mamdani fuzzy inference system (FIS) was proposed and implemented in five case studies. In particular, the magnitude of Ecuador (16 April 2016), Iran (12 November 2017), Papua New Guinea (14 May 2019), Japan (13 February 2021), and Haiti (14 August 2021) earthquakes were estimated by FIS. The results showed that in most cases, the highest number of anomalies was usually observed in the period of about one month before the earthquake and the predicted magnitude of the earthquake in these periods was slightly different from the actual magnitude value. Therefore, based on the results of this study, it could be concluded that if a significant number of anomalies are observed in the time series of different precursors, it is likely that an earthquake of the magnitude predicted by the proposed FIS system within the Dobrovolsky area of the studied location will happen during the next month.

1. Introduction

Due to the loss of life and heavy material damage of powerful earthquakes, many efforts have been made to predict the principal parameters of earthquakes, i.e., at least the date, magnitude, and location. However, this goal seems still far, and nowadays, it is still not possible to make a prediction of an earthquake. To be able to better understand the preparation phase of an earthquake, several studies have been conducted for decades. For example, in interpreting several possible precursors, a possible general model called “Dilatancy” was proposed by Scholz et al. [1]. For this purpose, any abnormal change in the physical and chemical observables in different layers of the Earth (lithosphere, atmosphere, and ionosphere) in the absence of other causes can probably be considered as one of the possible signs of an impending earthquake, and hence, it can be classified as an earthquake precursor candidate [2,3,4,5]. Therefore, for several decades, different parameters have been proposed to be altered before the occurrence of an earthquake: for example, Wyss [6] identified seismic, ground deformation, and magnetic alteration by investigating a very long time series before the M7.1 Sitka 1972 earthquake; Fraser-Smith et al. [7] claimed that extremely low frequency (ELF)/very low frequency (VLF) anomalies were detected from ground observatories some weeks before the M7.1 Loma Prieta earthquake occurred in 1989; Molchanov et al. [8] reported disturbances in VLF signal transmissions before the M7.2 Kobe 1995 earthquake. Wu and Tikhonov [9] searched for a systematic occurrence of atmospheric jet streams in China and the northwestern part of the Pacific seismic belt before the M6+ earthquakes from 2006 to 2021. Shou and Fang [10] formulated a model proposing that earthquakes can release thermal vapor (geoeruption), inducing the formation of clouds. Such “earthquake clouds” can be distinguished from other geological or weather phenomena as they are supposed to suddenly appear, being vapor-based, having a fixed source, and displaying a high-temperature and high-pressure state. The location of geoeruption would predict the epicentre, the amount of vapor, the magnitude, and the time after a complete geoeruption empirically could predict the time of the earthquake within days of precision [10]. With the launch of various satellites with different sensors such as optical and radar as well as accelerometers, magnetometers, electric field detectors, particle tracers, calorimeters, etc., the number of readable precursors for earthquakes has increased. The large availability of big data archives has permitted researchers to identify a chain of processes in the lithosphere, the atmosphere, and the ionosphere before the occurrence of several earthquakes in the world, such as M7.8 Nepal 2015 [11], the M6.0 and 6.5 Italy 2016 seismic sequence [12], the M7.5 Indonesia 2018 earthquake [13], and the M7.1 Ridgecrest, California 2019 earthquake [14]. Statistical proof of the existence of ionospheric precursors analysing DEMETER and Swarm satellites has also prompted some worldwide investigations of M5.5+ (or M4.8+ in the case of DEMETER) shallow earthquakes [15,16,17,18,19]. Creating cloud computing systems such as Google Earth Engine (GEE) has greatly helped to analyse various precursors without the necessity of downloading their corresponding raw data [20]. It can be reasonable that as the number of anomalies observed in different precursors increases, the degree of uncertainty in predicting the parameters of upcoming earthquakes decreases. An investigation of 12 earthquakes from magnitude 6.1 to 8.3 that occurred between 2014 and 2016 identified a linear relationship between ionospheric anomalies identified by Swarm and the magnitude of the incoming earthquake [21]. Fortunately, the number of classical and intelligent anomaly detection methods in the time series of various precursors has improved considerably [22,23]. Therefore, it is necessary to use methods to fuse the results of these predictors to estimate earthquake parameters. In this study, a fuzzy inference system (FIS) was proposed to estimate the magnitude of the impending powerful earthquakes.

Case Studies

In particular, we investigated here five strong earthquakes to evaluate the proposed fuzzy system for earthquake magnitude estimation.

Table 1. The characteristics of the investigated earthquakes (reported by United States Geological Survey, http://earthquake.usgs.gov/ (accessed on 5 June 2022)).

Region	Date	Time (UTC)	Geographic Latitude, Longitude	Magnitude (MW)	Focal Depth (km)
Ecuador	16 April 2016	23:58:36	0.382°N, 79.922°W	7.8	20.6
Iran	12 November 2017	18:18:17	34.911°N, 45.959°E	7.3	19
Papua New Guinea	14 May 2019	12:58:25	4.051°S, 152.597°E	7.6	10
Japan	13 February 2021	14:07:50	37.73°N, 141.77°E	7.1	44
Haiti	14 August 2021	12:29:08	18.434°N, 73.482°W	7.2	10

summarises the real characteristics of the five analysed earthquakes and Figure 1 shows their location and their focal mechanism. A powerful earthquake of magnitude Mw = 7.8 occurred on 16 April 2016 at 23:58:36 UTC (LT = UTC + λ_epicenter/15 = 18:38:55) on the coast of Ecuador, approximately 27 km south-southeast of Muisne in the province of Esmeraldas at a depth of 20.6 km [24]. We also analysed as another case study an M_w = 7.3 strong earthquake that took place at 18:18:17 UTC (LT = 21:22:07) on 12 November 2017 along the border region between Iran and Iraq close to the town of Sarpol-e Zahab (34.911°N, 45.959°E, 19.00 km depth) [25]. The third analysed earthquake had a magnitude M_w = 7.6 and happened at 12:58:25 UTC (LT = 23:08:48) on 14 May 2019, 46 km South-Southeast of Namatanai in Papua New Guinea (4.051°S, 152.597°E) at a shallow estimated depth of about 10 km [26]. The fourth strong earthquake of M_w = 7.1 occurred at 14:07:50 UTC (LT = 23:34:55) on 13 February 2021 near the east coast of Honshu, Japan (37.727°N, 141.775°E, 44 km depth) as the result of thrust faulting near the subduction zone interface plate boundary between the Pacific and North America plates [23]. We analysed another strong earthquake of M_w = 7.2 that happened at 12:29:08 UTC (LT = 7:35:12) on 14 August 2021 (18.434°N, 73.482°W, 10 km depth).

2. Methodology

Fuzzy logic is a set of mathematical principles for knowledge representation based on degrees of membership. Unlike two-valued Boolean logic, fuzzy logic is multi-valued. It deals with degrees of membership and degrees of truth [27]. Fuzzy logic uses a continuum of logical values between 0 (completely false) and 1 (completely true). In 1965, Lotfi Zadeh published his famous paper “Fuzzy sets” [28]. Zadeh extended the work on possibility theory into a formal system of mathematical logic and introduced a new concept for applying natural language terms. This new logic for representing and manipulating fuzzy terms was called fuzzy logic [27].

A fuzzy inference system (FIS) is a way of mapping an input space to an output space using fuzzy logic. An FIS tries to formalise the reasoning process of the human language by means of fuzzy logic (that is, by building fuzzy IF-THEN rules). FIS methods are used to solve decision problems, i.e., to make a decision and act accordingly. The FIS is based on converting a set of numerical variables (i.e., crisp) to a set of fuzzy variables. This is obtained using a series of logical rules and linguistic variables. These rules are organised in the “IF-THEN” format and constitute the FIS’s core. Before applying these rules, the input and output variables must be fuzzified, and the conversion is conducted using membership functions. Membership functions are mathematical functions that illustrate an element’s membership in a fuzzy set [29].

The structure of an FIS is as follows (see also Figure 2):

• Fuzzification module: transforms the system inputs, which are crisp numbers, into fuzzy sets. This is done by applying a fuzzification function.
• Knowledge base: stores IF-THEN rules provided by experts.
• Inference engine: simulates the human reasoning process by making fuzzy inferences on the inputs and IF-THEN rules.
• Defuzzification module: transforms the fuzzy set obtained by the inference engine into a crisp value.

Fuzzy inference methods are classified into direct methods and indirect methods. Direct methods, such as Mamdani’s approach, are the most commonly used. In 1974, British E.H. Mamdani applied fuzzy logic and fuzzy reasoning to real life for the first time [30].

The realisation process of the Mamdani FIS flow chart in this study is shown in Figure 3. The choice of the membership function for input variables depends on user knowledge about the system behaviour. The Gaussian membership function “gaussmf” is applied to map the daily value of every precursor into [0…1] numerical range.

It should be noted that for each precursor time series, the median and the inter-quartile range of data are calculated to construct their upper and lower bound in order to separate potentially seismic anomalies from the background of natural variations. The upper and lower bounds of the mentioned range can be calculated using the following equations:

$$x_{high}=m+k\times iqr$$

(1)

$$x_{low}=m-k\times iqr$$

(2)

$$Dx=(\left(\frac{x-m}{iqr}\right)-1)\ast 100$$

(3)

where $x_{}$, $x_{high}$, $x_{low}$, m, iqr, and $Dx$ are the parameter value, upper bound, lower bound, median value, inter-quartile range, and differential of x, respectively. It should be noted that the Dx value is considered the input value in FIS. Therefore, the input (precursor) ranges from 0 to 100. It is clear that the number of input variables is equal to the number of analysed precursors for each case study. The range of input variables for each precursor is divided into four parts corresponding to semantic subsets: weak, moderate, intense, and very intense (Figure 4). The Gaussian membership function is also applied for the earthquake magnitude output value. The predicted earthquake magnitude ranges from 0 to 9. This range is divided into four orders of magnitude, which are semantic sets composed of the following four subsets: weak, moderate, strong, and powerful (Figure 5). This study used the Mamdani reasoning method, established rules, and then applied the “min” implication method. All rules were applied to input and output values, and then the results of implications (conclusions) were aggregated using the “max” method. The defuzzification method used in this study was largest of maximum (LOM). After defuzzification, the final output was proposed as the predicted earthquake magnitude.

3. Observations

Table 2. The analysed precursors (D: day, N: night, Ne: electron density, Te: electron temperature, STEC: slant TEC, VTEC: vertical TEC, LST: Land Surface Temperature, AOD: Aerosol Optical Depth, AOT: Aerosol Optical Thickness).

Precursor			Ecuador [24]	Iran [25]	Papua New Guinea [26]	Japan [23]	Haiti
Layer	Satellite	Parameter
Ionosphere (plasma)	Swarm A	Ne (D&N)	√	√	√	√	√
		Te (D&N)	√	√	√	√	√
		STEC (D&N)	-	-	√	√	-
		VTEC (D&N)	-	-	√	√	-
	Swarm B	Ne (D&N)	√	√	√	√	√
		Te (D&N)	√	√	√	√	√
		STEC (D&N)	-	-	√	√	-
		VTEC (D&N)	-	-	√	√	-
	Swarm C	Ne (D&N)	√	√	√	√	√
		Te (D&N)	√	√	√	√	√
		STEC (D&N)	-	-	√	√	-
		VTEC (D&N)	-	-	√	√	-
	Swarm A–C	Ne (D&N)	√	√	√	√	√
	Swarm A–C	Te (D&N)	√	√	√	√	√
	CSES	Ne (D&N)	-	-	√	-	√
		Te (D&N)	-	-	-	-	√
	GPS	TEC	√	√	√	-	√
Ionosphere (magnetic)	Swarm A	MS (D&N)	√	√	√	√	√
		MVx (D&N)	√	√	√	√	√
		Mvy (D&N)	√	√	√	√	√
		MVz (D&N)	√	√	√	√	√
	Swarm B	MS (D&N)	√	√	√	√	√
		MVx (D&N)	√	√	√	√	√
		Mvy (D&N)	√	√	√	√	√
		MVz (D&N)	√	√	√	√	√
	Swarm C	MS (D&N)	√	√	√	√	√
		MVx (D&N)	√	√	√	√	√
		Mvy (D&N)	√	√	√	√	√
		MVz (D&N)	√	√	√	√	√
Atmosphere	MODIS	AOD	√	-	-	-	-
	Climatological data	AOT	√	√	√	√	√
		CO	√	√	√	√	√
		SO2	√	√	√	√	√
		DMS	√	-	√	√	√
		CH4	-	√	-	-	-
Atmosphere (surface)	MODIS	LST (D&N)	√	-	-	-
Lithosphere	Seismic data	Eqs magnitude	√	√	√	√	√
		Eqs number	√	√	√	√	√
Number of Precursors (D&N)			50	47	61	58	51

shows the analysed precursors concerning each case study. It is seen that 50, 47, 61, 58, and 51 precursors were investigated for Ecuador, Iran, Papua New Guinea, Japan and Haiti earthquakes, respectively. The details of the investigated data and implemented methods are found in [23,24,25,26]. As mentioned before in the methodology section, the Dx values for all detected anomalies during the quiet solar and geomagnetic activities were obtained and applied as input data for the proposed fuzzy inference system.

In order to investigate the three geo-layers, we included data from earthquake catalogues or lithosphere and from Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2 [31]) and methane data for the Iran earthquake retrieved from the AIRS instrument onboar the NASA Earth observation system satellite Aqua [32] and from low Earth orbit (LEO) satellites such as Swarm [33] or CSES [34] missions to investigate the ionosphere. A sketch of the techniques of the investigation in this paper of earthquake catalogues and atmospheric data is given in the following.

3.1. Earthquake Catalogues

In order to obtain higher quality results, regional catalogues are preferred over global ones as they are able to provide a more complete catalogue, i.e., to have a lower magnitude of completeness. Despite this, for Papua New Guinea and Haiti case studies, we did not find local catalogues, so we used the United States Geological Survey (USGS) global earthquake catalogue. We note that Haiti is in a region well-covered by the seismic network of USGS, and Papua New Guinea provides a sufficient number of events due to its intrinsically high seismicity rate. For Ecuador, we retrieved the earthquake catalogue from “Instituto Geofísico de la Escuela Politécnica Nacional” (download from https://www.igepn.edu.ec/ (accessed on 30 April 2022). For the Iran earthquake catalogue, we used the one provided by Mousavi-Bafrouei and Mahani [35], which includes the period investigated in this paper. Finally, we retrieved the Japan Meteorological Agency (JMA) Unified Hypocenter Catalog for the Japan earthquake. For all the catalogues, we extracted the events within 1000 km distance from the investigated case study, and we checked the completeness of magnitude (Mc) by the software Z-Map [36]. We found that the best completeness was achieved by the Japanese catalogue (Mc = 1.1), and the worst was in the case of Papua New Guinea (Mc = 4.3) as reported in Supplementary Materials Figure S1 with the Gutenberg–Richter [37] distribution for each case study. After selecting only the earthquakes with magnitude M ≥ Mc, we computed two time series for each case study: one with the daily number of seismic events and a second one with the maximum recorded daily magnitude. Such time series were then truncated on the day before the mainshock and passed to the FIS algorithm. For the figures, we reported the observed magnitudes also during and after the mainshock.

3.2. Atmospheric Data Preparation

To investigate eventual atmospheric anomalies, we selected four parameters from the MERRA-2 climatological archive: aerosol optical thickness (AOT), SO₂, CO, and dimethyl sulfide (DMS). The last parameter had negligible concentration above land areas, so for the Iran earthquake, we substituted it with CH4 measurements. All the parameters were analysed by the algorithm MERRA-2 analysis to search for seismic precursors (MEANS) fully described in [38]. Essentially, we retrieved the time series of the specific parameter in the year affected by the earthquake and a historical time series from the mean values estimated in the other available years (generally from 1980 to 2021). The obtained time series are included in the Supplementary Materials in Figures S2–S21, but the specific discussion is considered out of the scope of this paper. In fact, with such a time series, we provided four additional inputs from the atmosphere for the FIS algorithm as the daily deviation of the specific parameter, i.e., the time series in the year of the earthquake minus the historical one.

3.3. Results Applying FIS to the Five Investigated Earthquakes

3.3.1. Ecuador 2016

Figure 6a illustrates the variation in the number of anomalies (green curve), (b) the variation in the predicted earthquake magnitude (red curve), and (c) the variation in the maximum daily observed earthquake magnitude (blue curve) for the Ecuador earthquake (16 April 2016) from 1 November 2015 to 30 April 2016. In all panels, the x-axis represents the day relative to the earthquake day which is indicated as a vertical dotted line. Figure 6b indicates that the FIS predicted a magnitude M_w = 7.02 earthquake 38 days before the event (the black dotted ellipsoid in Figure 6b). It should be noted that the maximum number of anomalies (N = 10) was observed on this date (Figure 6a). The reported earthquake magnitude was M_w = 7.8 (Figure 6c).

3.3.2. Iran 2017

Figure 7a shows the daily variation in the number of detected anomalies (green curve) among 47 precursors and (b) the variation in the predicted earthquake magnitude (red curve) for the Iran earthquake (12 November 2017) from 1 August to 30 November 2017. The maximum number of detected anomalies (N = 13) was observed 19 days before the earthquake (Figure 7a). FIS estimated an earthquake with magnitude Mw = 7.02 (the black dotted ellipsoid in Figure 7b). The registered magnitude of the actual earthquake was Mw = 7.3.

3.3.3. Papua New Guinea 2019

Figure 8a indicates the daily variation in the number of anomalies (green curve) and (b) the variation in the predicted earthquake magnitude (red curve) for the Papua New Guinea earthquake (14 May 2019) from 1 January to 30 June 2019. Figure 8a shows that the maximum number of anomalies (N = 21) was observed 32 days prior to the earthquake. FIS predicted an impending earthquake with a magnitude of 9 32, 33, and 35 days before the mainshock.

3.3.4. Japan 2021

Figure 9a shows the variations in the number of anomalies (green curve) and (b) the variation in the predicted earthquake magnitude (red curve) for the Japan earthquake (13 February 2021) from 1 September 2020 to 18 February 2021. FIS predicted the magnitude of the impending earthquake with the values of Mw = 7.30, 6.85, 7.51, 7.47, and 7.51 on 6, 8, 19, 31, and 32 days preceding the earthquake, respectively (marked by the black dotted ellipsoid in Figure 9b). A noticeable number of anomalies (N = 16) was observed 31 and 32 days before the earthquake. The maximum number of detected anomalies (N = 20) was observed 119 days before the earthquake when FIS predicted an earthquake with magnitude Mw = 7.508. The reported magnitude of the mentioned earthquake was Mw = 7.1. It should be noted that FIS predicted an impending earthquake with a magnitude of Mw = 7.75 3 days after the earthquake and 32 days before the next powerful earthquake (Mw = 7.0) that happened close to the first epicentre at 38.452°N, 141.648°E, 43.0 km depth, 09:09:43 UTC on 20 March 2021 (indicated by the black arrow (4) in Figure 9b).

3.3.5. Haiti 2021

Figure 10a illustrates the variation in the number of anomalies (green curve), (b) the variation in the predicted earthquake magnitude (red curve), and (b) the variation in the observed earthquake magnitude (blue curve) for the Haiti earthquake (14 August 2021) from 1 June to 31 August 2021. Figure 10b shows that the FIS predicted magnitude Mw = 7.24, 6.44, and 7.60 earthquakes 38, 40, and 45 days before the event, respectively (marked by a black dotted ellipsoid in Figure 9b). It should be noted that the maximum number of anomalies (N = 19) was observed 40 and 45 days before the main shock (Figure 10a). Actually, the reported earthquake magnitude was Mw = 7.2 (Figure 10c).

3.4. Validation of FIS

In order to evaluate the efficiency of the FIS system, a confutation analysis was performed. Among the analysed case studies, the Iran earthquake was selected, and the time series of 41 different precursors in the same time period set one year before the earthquake was analysed. Figure 11a shows the variations in the number of anomalies (green curve) and Figure 11b the variations in the predicted earthquake magnitude (red curve) from 1 August to 30 November 2016. It is worth noting that the maximum predicted earthquake magnitude by FIS was M_w = 3.42. Figure 11a shows no noticeable anomalies close to the selected day (12 November 2016), i.e., one year before the Iran 2017 mainshock.

In order to finally validate and refine the obtained result, a plot of the estimated earthquake magnitude versus the observed one is reported in Figure 12. Here, all five case studies are shown with a black dot, and in addition, the validation case was taken into account. For this last case, we considered the maximum observed magnitude as the one of the event that occurred on 26 October 2016 at 39.485°N, 54.509°E, 26 km depth and with a magnitude of 5.4. We performed a robust linear fit of the six experimental points shown as the red line. The M7.8 Ecuador 2016 case study was considered an outlier by the linear fit and thus excluded by the computation. The goodness of the fit was evaluated by the adjusted coefficient of determination that even with the low number of degrees of freedom (dof = 4) confirmed the reliability of the fit as R² was slightly greater than 0.9.

Finally, we tried to use the fit to apply a correction to the estimated magnitude obtained from the FIS algorithm, and we report in

Table 3. Estimated magnitudes and comparison with the real one after correction.

Case Study	Estimated Magnitude by FIS	Corrected Magnitude	Real Magnitude	Error in the Estimation of the Magnitude after Correction
Ecuador 2016	7.02	6.92	7.8	0.88
Iran 2017	7.92	7.30	7.3	0.0046
Papua New Guinea 2019	9.00	7.75	7.6	0.15
Japan 2021	7.53	7.13	7.1	0.032
Haiti 2021	7.60	7.16	7.2	0.038

the calculated values. The correction was applied by inverting the linear fit equation, i.e.:

$$\mathrm{corrected} \mathrm{magnitude}=\frac{\mathrm{estimated} \mathrm{magnitude}+9.37}{2.37}$$

(4)

It is outstanding to note that after the correction, all the predicted magnitudes were equal to the real one within one decimal digit, except for the case of Ecuador, where the estimated magnitude remained too low with a magnitude that was estimated to be 0.9 less than the real one.

4. Conclusions

Creating an earthquake prediction system requires estimating the event location, future time, and magnitude with low uncertainty. Fortunately, with the increase in the number of geosphere observables and various anomaly detection methods, significant progress has been made in studies related to the possible earthquake precursors. Using data fusion algorithms leads to a more accurate estimation of earthquake parameters. In the first step, the deviation values (Dx) of different possible precursors’ time series from the allowable limits were calculated for each studied area for several parameters of the lithosphere, atmosphere, and ionosphere. In most case studies, the highest number of anomalies in different precursors occurred about one month before the investigated M > 7 earthquakes. Therefore, it can be mentioned that by observing a significant number of anomalies (N > 5) in a study area, an earthquake could have a higher probability of occurrence in the next 1 to 40 days. To estimate the magnitude of the earthquake, a data fusion system based on the Mamdani fuzzy inference system was proposed. The Dx values were considered as input data to the FIS. The results showed that the predicted magnitude values differed slightly from the recorded ones. It is worth noting that the two most recent earthquakes that occurred in 2021 in Japan and Haiti had a good estimation of the magnitude, probably due to the improved satellite coverage by joint analysis of Swarm and CSES missions. The Dobrovolsky equation (R = 10 ^0.43∙M, where R is the radius in kilometres of the earthquake preparation zone and M is the earthquake magnitude [39]) based on the estimated magnitude of the FIS could also be used to predict the affected area of the impending earthquake.

It is important to note that in this work, we tried to estimate only the magnitude of the impending earthquake, but due to differences in physical and tectonic settings of each event, the pattern of eventual precursors can be different. For example, the focal mechanism is expected to play a role in the preparation phase of each earthquake as several works have proposed and searched for preliminary pieces of evidence [18,40]. The present work investigated a limited number of earthquakes with different focal mechanisms. Future research needs to clarify and better explore such aspects, including the geological, topographic, and overall tectonic settings to study the pre-earthquake anomaly patterns. We expected that the estimated values of the incoming earthquake magnitude could be improved. To conclude, the FIS method with the applied correction seems a very promising tool, and future studies can confirm or improve the methodology, expand the prediction to other parameters of the earthquakes, and extend it to smaller magnitude events following the approach successfully applied to worldwide M5.5+ by De Santis et al. [16] and Marchetti et al. [18].