Soil Moisture Retrieval Using SAR Backscattering Ratio Method during the Crop Growing Season
Abstract
:1. Introduction
2. Materials
2.1. Ground Measurements
2.2. RADARSAT-2 Data
3. Methods
3.1. Vegetation Correction
3.1.1. Ratio Method
3.1.2. WCM
3.2. Surface Backscatter Modeling
3.2.1. CIEM Model
3.2.2. Optimal Roughness Parameters
3.3. Accuracy Assessment
4. Results and Discussion
4.1. Optimal Roughness Parameter Selection
4.2. Soil Moisture Estimation Results
4.3. Reference Incidence Angle
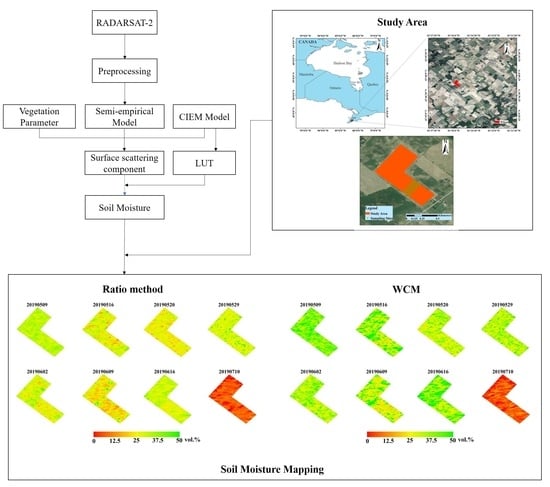
4.4. Regional Soil Moisture Mapping
4.5. Limitations and Potential Improvements
5. Conclusions
- (1)
- As an empirical coefficient in the scattering model, the optimal roughness parameter could effectively improve the estimation accuracy of SMC.
- (2)
- A reference incident angle could be used as an effective adjustment parameter to improve the estimation accuracy of SMC.
- (3)
- Comparing with LAI and RVI, NDVI is more suitable as the vegetation description parameter of the model.
- (4)
- In general, the estimation performance of the ratio method is better than that of WCM.
Author Contributions
Funding
Conflicts of Interest
References
- Lievens, H.; Vernieuwe, H.; Alvarez-Mozos, J.; De Baets, B.; Verhoest, N.E. Error in radar-derived soil moisture due to roughness parameterization: An analysis based on synthetical surface profiles. Sensors 2009, 9, 1067–1093. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Li, X.; Han, X.; Jin, R. Estimation of surface soil moisture and roughness from multi-angular ASAR imagery in the Watershed Allied Telemetry Experimental Research (WATER). Hydrol. Earth Syst. Sci. 2011, 15, 1415–1426. [Google Scholar] [CrossRef] [Green Version]
- Prakash, R.; Singh, D.; Pathak, N.P. A fusion approach to retrieve soil moisture with SAR and optical data. IEEE J.-Stars 2011, 5, 196–206. [Google Scholar] [CrossRef]
- De Keyser, E.; Vernieuwe, H.; Lievens, H.; Álvarez-Mozos, J.; De Baets, B.; Verhoest, N.E. Assessment of SAR-retrieved soil moisture uncertainty induced by uncertainty on modeled soil surface roughness. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 176–182. [Google Scholar] [CrossRef]
- Bao, Y.; Zhang, Y.; Wang, J.; Min, J. Surface soil moisture estimation over dense crop using Envisat ASAR and Landsat TM imagery: An approach. Int. J. Remote Sens. 2014, 35, 6190–6212. [Google Scholar] [CrossRef]
- Li, Z.-L.; Leng, P.; Zhou, C.; Chen, K.-S.; Zhou, F.-C.; Shang, G.-F. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, X.; Wang, J.; Yang, H.; Huang, W.; Feng, H. A method of estimating soil moisture based on the linear decomposition of mixture pixels. Math. Comput. Model. 2013, 58, 606–613. [Google Scholar] [CrossRef]
- Haubrock, S.N.; Chabrillat, S.; Lemmnitz, C.; Kaufmann, H. Surface soil moisture quantification models from reflectance data under field conditions. Int. J. Remote Sens. 2008, 29, 3–29. [Google Scholar] [CrossRef]
- Liu, W.; Baret, F.; Gu, X.; Zhang, B.; Tong, Q.; Zheng, L. Evaluation of methods for soil surface moisture estimation from reflectance data. Int. J. Remote Sens. 2003, 24, 2069–2083. [Google Scholar] [CrossRef]
- Engstrom, R.; Hope, A.; Kwon, H.; Stow, D. The relationship between soil moisture and NDVI near Barrow, Alaska. Phys. Geogr. 2008, 29, 38–53. [Google Scholar] [CrossRef]
- Schnur, M.T.; Xie, H.; Wang, X. Estimating root zone soil moisture at distant sites using MODIS NDVI and EVI in a semi-arid region of southwestern USA. Ecol. Inform. 2010, 5, 400–409. [Google Scholar] [CrossRef]
- Zribi, M.; Paris Anguela, T.; Duchemin, B.; Lili, Z.; Wagner, W.; Hasenauer, S.; Chehbouni, A. Relationship between soil moisture and vegetation in the Kairouan plain region of Tunisia using low spatial resolution satellite data. Water Resour. Res. 2010, 46, W06508. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.-Y.; Wang, Y.-C.; Feng, C.-C.; Ziegler, A.D.; Giambelluca, T.W.; Liou, Y.-A. Estimation of root zone soil moisture using apparent thermal inertia with MODIS imagery over a tropical catchment in Northern Thailand. IEEE J.-Stars 2012, 5, 752–761. [Google Scholar] [CrossRef]
- Matsushima, D.; Kimura, R.; Shinoda, M. Soil moisture estimation using thermal inertia: Potential and sensitivity to data conditions. J. Hydrometeorol. 2012, 13, 638–648. [Google Scholar] [CrossRef]
- Minacapilli, M.; Cammalleri, C.; Ciraolo, G.; D’Asaro, F.; Iovino, M.; Maltese, A. Thermal inertia modeling for soil surface water content estimation: A laboratory experiment. Soil Sci. Soc. Am. J. 2012, 76, 92–100. [Google Scholar] [CrossRef]
- Bindlish, R.; Jackson, T.; Gasiewski, A.; Stankov, B.; Klein, M.; Cosh, M.; Mladenova, I.; Watts, C.; Vivoni, E.; Lakshmi, V. Aircraft based soil moisture retrievals under mixed vegetation and topographic conditions. Remote Sens. Environ. 2008, 112, 375–390. [Google Scholar] [CrossRef]
- Yan, F.; Qin, Z.; Li, M.; Li, W. Progress in soil moisture estimation from remote sensing data for agricultural drought monitoring. Remote Sens. Environ. Monit. GIS Appl. Geol. VI 2006, 6366, 636601. [Google Scholar]
- Zhang, D.; Zhou, G. Estimation of soil moisture from optical and thermal remote sensing: A review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef] [Green Version]
- Bhogapurapu, N.; Dey, S.; Mandal, D.; Bhattacharya, A.; Karthikeyan, L.; McNairn, H.; Rao, Y. Soil moisture retrieval over croplands using dual-pol L-band GRD SAR data. Remote Sens. Environ. 2022, 271, 112900. [Google Scholar] [CrossRef]
- Chen, L.; Xing, M.; He, B.; Wang, J.; Shang, J.; Huang, X.; Xu, M. Estimating soil moisture over winter wheat fields during growing season using machine-learning methods. IEEE J.-Stars 2021, 14, 3706–3718. [Google Scholar] [CrossRef]
- Xing, M.; He, B.; Ni, X.; Wang, J.; An, G.; Shang, J.; Huang, X. Retrieving surface soil moisture over wheat and soybean fields during growing season using modified water cloud model from Radarsat-2 SAR data. Remote Sens. 2019, 11, 1956. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.S.; Patel, P.; Sharma, Y.; Navalgund, R.R. Large-area soil moisture estimation using multi-incidence-angle RADARSAT-1 SAR data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2528–2535. [Google Scholar] [CrossRef]
- Lakhankar, T.; Ghedira, H.; Temimi, M.; Azar, A.E.; Khanbilvardi, R. Effect of land cover heterogeneity on soil moisture retrieval using active microwave remote sensing data. Remote Sens. 2009, 1, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Sang, H.; Zhang, J.; Lin, H.; Zhai, L. Multi-polarization ASAR backscattering from herbaceous wetlands in Poyang Lake region, China. Remote Sens. 2014, 6, 4621–4646. [Google Scholar] [CrossRef] [Green Version]
- Xiao, T.; Xing, M.; He, B.; Wang, J.; Shang, J.; Huang, X.; Ni, X. Retrieving Soil Moisture Over Soybean Fields During Growing Season Through Polarimetric Decomposition. IEEE J.-Stars 2020, 14, 1132–1145. [Google Scholar] [CrossRef]
- Gherboudj, I.; Magagi, R.; Berg, A.A.; Toth, B. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular RADARSAT-2 SAR data. Remote Sens. Environ. 2011, 115, 33–43. [Google Scholar] [CrossRef]
- Notarnicola, C.; Angiulli, M.; Posa, F. Use of radar and optical remotely sensed data for soil moisture retrieval over vegetated areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 925–935. [Google Scholar] [CrossRef]
- Bolten, J.D.; Lakshmi, V.; Njoku, E.G. Soil moisture retrieval using the passive/active L-and S-band radar/radiometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2792–2801. [Google Scholar] [CrossRef]
- Chen, L.; Xing, M.F.; He, B.B.; Wang, J.F.; Xu, M.; Song, Y.; Huang, X.D. Estimating Soil Moisture over Winter Wheat Fields during Growing Season Using RADARSAT-2 Data. Remote Sens. 2022, 14, 2232. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, T.; Qiu, J.; Zhao, X.; Wang, S. Microwave-based vegetation descriptors in the parameterization of water cloud model at L-band for soil moisture retrieval over croplands. Gisci. Remote Sens. 2020, 58, 48–67. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of Estimating Soil Moisture Under Vegetation Cover by Means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef] [Green Version]
- Jagdhuber, T.; Hajnsek, I.; Bronstert, A.; Papathanassiou, K.P. Soil Moisture Estimation Under Low Vegetation Cover Using a Multi-Angular Polarimetric Decomposition. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2201–2215. [Google Scholar] [CrossRef]
- Martino, G.D.; Iodice, A.; Natale, A.; Riccio, D. Polarimetric Two-Scale Two-Component Model for the Retrieval of Soil Moisture Under Moderate Vegetation via L-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2470–2491. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Sarabandi, K.; Mcdonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Lang, R.H.; Sighu, J.S. Electromagnetic Backscattering From a Layer of Vegetation: A Discrete Approach. IEEE Trans. Geosci. Remote Sens. 1983, GE-21, 62–71. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L. Emissivity of vegetation: Theory and computational aspects. J. Electromagn. Waves Appl. 1996, 10, 609–628. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Ian, P.; Liu, J.; Shang, J. A Spatio-Temporal Data Fusion Model for Generating NDVI Time Series in Heterogeneous Regions. Remote Sens. 2017, 9, 1125. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Verhoest, N.E. On the retrieval of soil moisture in wheat fields from L-band SAR based on water cloud modeling, the IEM, and effective roughness parameters. IEEE Geosci. Remote Sens. Lett. 2011, 8, 740–744. [Google Scholar] [CrossRef]
- Baghdadi, N.; Holah, N.; Zribi, M. Calibration of the Integral Equation Model for SAR data in C-band and HH and VV polarizations. Int. J. Remote Sens. 2006, 27, 805–816. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, V.2: Radar Remote Sensing and Surface Scattering and Emission Theory; Addison-Wesley Pub. Co. Advanced Book Program/World Science Division: Reading, MA, USA, 1982. [Google Scholar]
- Long, W.; Quan, X.; He, B.; Yebra, M.; Liu, X.J.R.S. Assessment of the Dual Polarimetric Sentinel-1A Data for Forest Fuel Moisture Content Estimation. Remote Sens. 2019, 11, 1568. [Google Scholar]
- Joseph, A.T.; van der Velde, R.; O’Neill, P.E.; Lang, R.H.; Gish, T. Soil Moisture Retrieval During a Corn Growth Cycle Using L-Band (1.6 GHz) Radar Observations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2365–2374. [Google Scholar] [CrossRef] [Green Version]
- Joseph, A.T.; van der Velde, R.; O’Neill, P.E.; Lang, R.; Gish, T. Effects of corn on C- and L-band radar backscatter: A correction method for soil moisture retrieval. Remote Sens. Environ. 2010, 114, 2417–2430. [Google Scholar] [CrossRef]
- Bai, X.J.; He, B.B.; Xing, M.F.; Li, X.W. Method for soil moisture retrieval in arid prairie using TerraSAR-X data. J. Appl. Remote Sens. 2015, 9, 096062. [Google Scholar] [CrossRef]
- Mironov, V.L.; Dobson, M.C.; Kaupp, V.H.; Komarov, S.A.; Kleshchenko, V.N. Generalized refractive mixing dielectric model for moist soils. IEEE Trans. Geosci. Remote Sens. 2004, 42, 773–785. [Google Scholar] [CrossRef]
- Kseneman, M.; Gleich, D. Soil-Moisture Estimation From X-Band Data Using Tikhonov Regularization and Neural Net. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3885–3898. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.Q.; Chen, K.S. Backscattering From a Randomly Rough Dielectric Surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Bryant, R.; Moran, M.S.; Thoma, D.P.; Collins, C.H.; Skirvin, S.; Rahman, M.; Slocum, K.; Starks, P.; Bosch, D.; Dugo, M.G. Measuring Surface Roughness Height to Parameterize Radar Backscatter Models for Retrieval of Surface Soil Moisture. IEEE Geosci. Remote Sens. Lett. 2007, 4, 137–141. [Google Scholar] [CrossRef]
- Bai, X.J.; He, B.B.; Li, X.W. Optimum Surface Roughness to Parameterize Advanced Integral Equation Model for Soil Moisture Retrieval in Prairie Area Using Radarsat-2 Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2437–2449. [Google Scholar] [CrossRef]















| SAR Acquisition Date | Optical Image Acquisition Date |
|---|---|
| 9 May 2019 | / |
| 16 May 2019 | 15 May 2019 |
| 20 May 2019 | / |
| 29 May 2019 | 27 May 2019 |
| 2 June 2019 | 4 June 2019 |
| 9 June 2019 | 11 June 2019 |
| 16 June 2019 | 14 June 2019 |
| 10 July 2019 | 9 July 2019 |
| Vegetation Parameters | Semi-Empirical Models | Sampling Date | HH | VV | ||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | |||
| RVI | Ratio method/WCM | 9 May | 0.28/−0.85 | 0.21/179.04 | −1.09/ | −0.40/−0.44 | 0.85/24.95 | 0.25/ |
| 16 May | 0.62/−1.18 | 0.06/8.94 | −1.72/ | 0.53/−0.15 | 0.13/−0.08 | −1.02/ | ||
| 20 May | 0.36/−0.76 | 0.30/13.50 | −1.11/ | 0.28/−0.09 | 0.24/0.49 | −0.85/ | ||
| 29 May | −11.92/−0.51 | 12.25/18.26 | 0.92/ | −6.85/−0.25 | 7.17/3.43 | 0.87/ | ||
| 2 June | 0.38/−0.38 | 0.26/97.41 | −0.72/ | 0.36/−0.27 | 0.12/15.82 | −1.18/ | ||
| 9 June | 0.32/−0.53 | 0.52/52.86 | −0.58/ | −0.2/−0.09 | 0.78/4.07 | 0.16/ | ||
| 16 June | 0.13/−0.39 | 0.33/5.95 | −0.45/ | 0.09/0.03 | 0.36/−0.70 | −0.2/ | ||
| 10 July | 0.46/−0.22 | 0.28/1.16 | −1.30/ | 0.08/−2.16 | 0.72/15.24 | −0.32/ | ||
| LAI | Ratio method/WCM | 9 May | 0.83/−0.77 | 0.05/81.16 | −1.39/ | 0.78/−0.44 | 0.04/14.48 | −1.63/ |
| 16 May | 0.44/−0.28 | 0.13/108.07 | −1.70/ | −16.46/−0.16 | 17.02/16.78 | 0.97/ | ||
| 20 May | −3.92/−0.16 | 4.48/83.29 | 0.91/ | −4.77/−0.06 | 5.26/8.82 | 0.93/ | ||
| 29 May | −0.05/−0.07 | 0.57/22.56 | 0.15/ | −0.53/−0.04 | 0.96/4.29 | 0.67/ | ||
| 2 June | 0.20/−0.10 | 0.39/14.93 | −1.83/ | 0.21/−0.08 | 0.40/3.90 | −3.60/ | ||
| 9 June | −2.97/−0.11 | 3.58/5.74 | 0.87/ | −3.05/−0.05 | 3.56/1.05 | 0.89/ | ||
| 10 July | 0.45/−0.03 | 70.21/1.57 | −12.55/ | 0.42/−1.23 | 4.24/31.73 | −6.23/ | ||
| NDVI | Ratio method/WCM | 16 May | 0.35/−1.95 | 0.15/77.68 | −1.26/ | 0.99/−0.86 | 0.00/14.68 | −10.33/ |
| 29 May | −14.13/−1.10 | 14.53/25.03 | 0.93/ | −2.66/−3.84 | 3.19/40.17 | 0.92/ | ||
| 2 June | −1.53/−0.52 | 1.75/0.27 | 0.10/ | −0.42/−0.54 | 0.70/0.47 | −0.35/ | ||
| 9 June | −17.08/−0.46 | 17.67/1.15 | 0.94/ | −14.20/−0.21 | 14.67/−0.02 | 0.94/ | ||
| 16 June | −1.26/−7.09 | 1.79/1532 | 0.85/ | −4.85/−0.19 | 5.29/14.94 | 0.90/ | ||
| 10 July | −8.45/−1197 | 8.13/124,336 | 0.67/ | −15.51/−5718 | 14.79/184,373 | 0.75/ | ||
| Date | Optimal Roughness Parameter (cm) | ||
|---|---|---|---|
| RVI | NDVI | LAI | |
| 9 May | 2.78. | / | 2.71 |
| 16 May | 2.73 | 2.99 | 2.64 |
| 20 May | 1.35 | / | 2.45 |
| 29 May | 2.86 | 2.49 | 2.05 |
| 2 June | 1.26 | 2.34 | 1.87 |
| 9 June | 0.71 | 1.53 | 1.69 |
| 16 June | 2.78 | 2.80 | / |
| 10 July | 2.28 | 2.77 | 1.58 |
| Date | Optimal Roughness Parameter (cm) | ||
|---|---|---|---|
| RVI | NDVI | LAI | |
| 9 May | 0.10 | / | 0.12 |
| 16 May | 0.46 | 0.15 | 0.10 |
| 20 May | 0.28 | / | 0.10 |
| 29 May | 0.18 | 0.22 | 0.12 |
| 2 June | 0.10 | 3.00 | 0.14 |
| 9 June | 0.13 | 1.57 | 0.26 |
| 16 June | 0.32 | 0.10 | / |
| 10 July | 1.32 | 0.16 | 0.58 |
| Vegetation Correction Model | Vegetation Parameters | R2 | RMSE (vol.%) |
|---|---|---|---|
| Ratio method | RVI (all dates) | 0.48 | 5.90 |
| LAI/RVI (exclude 16 June) | 0.56/0.48 | 5.58/6.15 | |
| NDVI/RVI (exclude 9 May, 20 May) | 0.65/0.44 | 4.35/6.28 | |
| LAI/NDVI (exclude 9 May, 20 May, 16 June) | 0.57/0.65 | 5.27/4.43 | |
| WCM | RVI (all dates) | 0.34 | 7.17 |
| LAI/RVI (exclude 16 June) | 0.47/0.36 | 6.07/7.15 | |
| NDVI/RVI (exclude 9 May, 20 May) | 0.64/0.28 | 4.33/7.52 | |
| LAI/NDVI (exclude 9 May, 20 May, 16 June) | 0.52/0.62 | 5.45/4.63 |
| Vegetation Correction Model | Vegetation Parameters | Reference Incidence Angle (°) | R2 | RMSE (vol.%) |
|---|---|---|---|---|
| RVI | 21 | 0.56 | 5.10 | |
| Ratio method | LAI | 22 | 0.59 | 5.22 |
| NDVI | 21 | 0.68 | 4.15 | |
| RVI | 40 | 0.41 | 6.34 | |
| WCM | LAI | 36 | 0.49 | 5.95 |
| NDVI | 36 | 0.66 | 4.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, M.; Chen, L.; Wang, J.; Shang, J.; Huang, X. Soil Moisture Retrieval Using SAR Backscattering Ratio Method during the Crop Growing Season. Remote Sens. 2022, 14, 3210. https://doi.org/10.3390/rs14133210
Xing M, Chen L, Wang J, Shang J, Huang X. Soil Moisture Retrieval Using SAR Backscattering Ratio Method during the Crop Growing Season. Remote Sensing. 2022; 14(13):3210. https://doi.org/10.3390/rs14133210
Chicago/Turabian StyleXing, Minfeng, Lin Chen, Jinfei Wang, Jiali Shang, and Xiaodong Huang. 2022. "Soil Moisture Retrieval Using SAR Backscattering Ratio Method during the Crop Growing Season" Remote Sensing 14, no. 13: 3210. https://doi.org/10.3390/rs14133210
APA StyleXing, M., Chen, L., Wang, J., Shang, J., & Huang, X. (2022). Soil Moisture Retrieval Using SAR Backscattering Ratio Method during the Crop Growing Season. Remote Sensing, 14(13), 3210. https://doi.org/10.3390/rs14133210