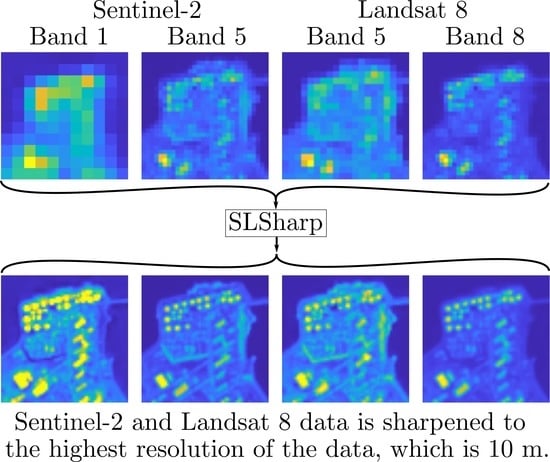
Fusing Sentinel-2 and Landsat 8 Satellite Images Using a Model-Based Method
Abstract
:1. Introduction
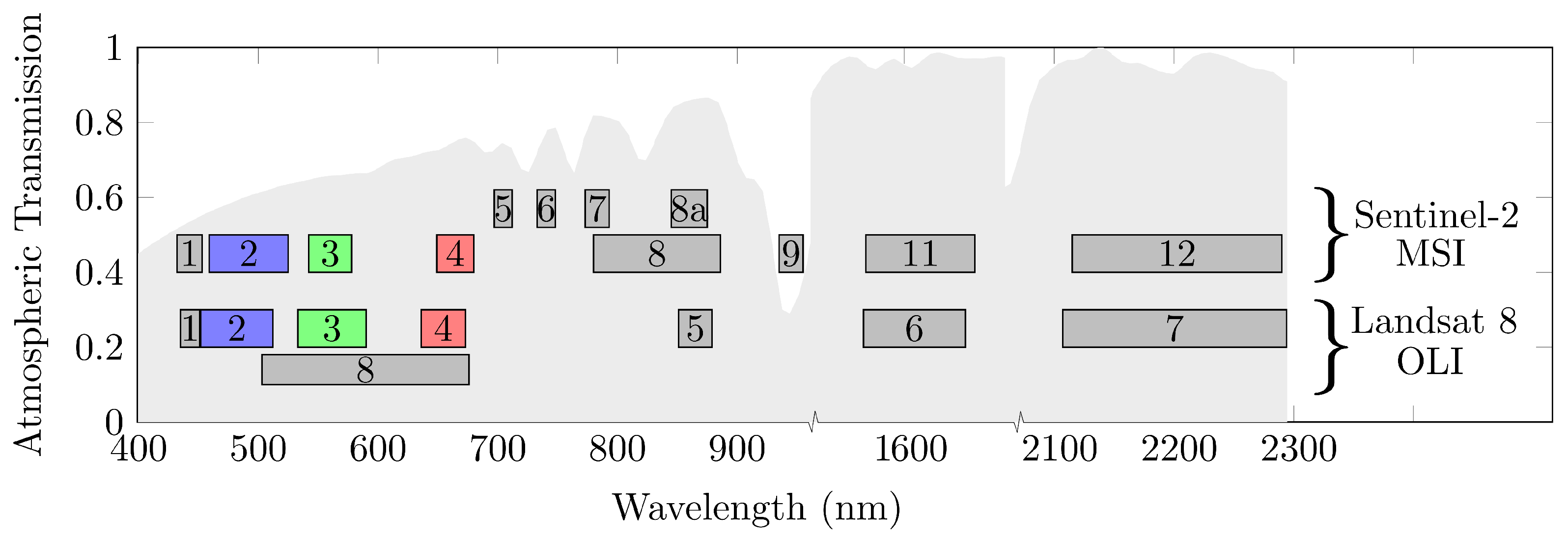
2. The Method
- (1)
- The cost function used by S2Sharp (1) needed to be modified to include the L8 bands;
- (2)
- The point spread function (PSF) of the L8 data needed to be estimated;
- (3)
- The 15 m panchromatic band of the L8 data needed to be resampled.
3. Evaluation
- The ATPRK method obtained better SRE, SSIM, and UIQI scores in the simulated NIR bands B11, B12, L6, and L7;
- The baseline method obtained better SRE, SSIM, and UIQI scores in the simulated 60 m bands B1 and B9;
- Although SLSharp performed the best in most of the simulated bands, the baseline method obtained the best ERGAS, SRE, and SSIM scores and the ATPRK method obtained a better UIQI score when averaged across all bands.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| ATPRK | Area-to-Point Regression Kriging |
| AZ | Arizona |
| ERGAS | Relative Dimensionless Global Error |
| IS | Iceland |
| L8 | Landsat 8 |
| MSI | Multispectral Imager |
| MTF | Modulation Transfer Function |
| OLI | Operational Land Imager |
| PSF | Point Spread Function |
| RMSE | Root Mean Square Error |
| ROI | Region of Interest |
| S1 | Sentinel-1 |
| S2 | Sentinel-2 |
| S2Sharp | Sentinel-2 Sharpening |
| SAM | Spectral Angle Mapper |
| SLSharp | Sentinel-2 Landsat 8 Sharpening |
| SRE | Signal-to-Reconstruction Error |
| SSIM | Structural Similarity Index Measure |
| UAV | Unpiloted Aerial Vehicle |
| UIQI | Universal Image Quality Index |
References
- USGS EROS Archive—Sentinel-2—Comparison of Sentinel-2 and Landsat. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-sentinel-2-comparison-sentinel-2-and-landsat. (accessed on 25 January 2022).
- Wang, Q.; Shi, W.; Li, Z.; Atkinson, P.M. Fusion of Sentinel-2 Images. Remote Sens. Environ. 2016, 187, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Brodu, N. Super-Resolving Multiresolution Images With Band-Independent Geometry of Multispectral Pixels. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4610–4617. [Google Scholar] [CrossRef] [Green Version]
- Lanaras, C.; Bioucas-Dias, J.; Baltsavias, E.; Schindler, K. Super-Resolution of Multispectral Multiresolution Images from a Single Sensor. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1505–1513. [Google Scholar]
- Lanaras, C.; Bioucas-Dias, J.M.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-Resolution of Sentinel-2 Images: Learning a Globally Applicable Deep Neural Network. ISPRS J. Photogramm. Remote Sens. 2018, 146, 305–319. [Google Scholar] [CrossRef] [Green Version]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Sentinel-2 Image Fusion Using a Deep Residual Network. Remote Sens. 2018, 10, 1290. [Google Scholar] [CrossRef] [Green Version]
- Ulfarsson, M.O.; Palsson, F.; Dalla Mura, M.; Sveinsson, J.R. Sentinel-2 Sharpening Using a Reduced-Rank Method. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6408–6420. [Google Scholar] [CrossRef]
- Paris, C.; Bioucas-Dias, J.; Bruzzone, L. A Novel Sharpening Approach for Superresolving Multiresolution Optical Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1545–1560. [Google Scholar] [CrossRef]
- Lin, C.H.; Bioucas-Dias, J.M. An Explicit and Scene-Adapted Definition of Convex Self-Similarity Prior With Application to Unsupervised Sentinel-2 Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3352–3365. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Sigurdsson, J. Zero-Shot Sentinel-2 Sharpening Using a Symmetric Skipped Connection Convolutional Neural Network. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R.; Mura, M.D. Sentinel-2 Sharpening Using a Single Unsupervised Convolutional Neural Network With MTF-Based Degradation Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6882–6896. [Google Scholar] [CrossRef]
- Sentinel-2s Observation Scenario. Available online: https://sentinels.copernicus.eu/web/success-stories/-/sentinel-2-s-observation-scenario (accessed on 21 June 2022).
- Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1204–1211. [Google Scholar] [CrossRef] [Green Version]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of Hyperspectral and LIDAR Remote Sensing Data for Classification of Complex Forest Areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef] [Green Version]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of Multispectral Images to High Spatial Resolution: A Critical Review of Fusion Methods Based on Remote Sensing Physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef] [Green Version]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote. Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Sigurdsson, J.; Ulfarsson, M.O.; Sveinsson, J.R. Fusing Sentinel-2 Satellite Images and Aerial RGB Images. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4444–4447. [Google Scholar]
- Useya, J.; Chen, S. Comparative Performance Evaluation of Pixel-Level and Decision-Level Data Fusion of Landsat 8 OLI, Landsat 7 ETM+ and Sentinel-2 MSI for Crop Ensemble Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4441–4451. [Google Scholar] [CrossRef]
- Fernandez-Beltran, R.; Pla, F.; Plaza, A. Sentinel-2 and Sentinel-3 Intersensor Vegetation Estimation via Constrained Topic Modeling. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1531–1535. [Google Scholar] [CrossRef]
- Albright, A.; Glennie, C. Nearshore Bathymetry From Fusion of Sentinel-2 and ICESat-2 Observations. IEEE Geosci. Remote Sens. Lett. 2021, 18, 900–904. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Drakonakis, G.I.; Tsagkatakis, G.; Fotiadou, K.; Tsakalides, P. OmbriaNet—Supervised Flood Mapping via Convolutional Neural Networks Using Multitemporal Sentinel-1 and Sentinel-2 Data Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2341–2356. [Google Scholar] [CrossRef]
- Hafner, S.; Nascetti, A.; Azizpour, H.; Ban, Y. Sentinel-1 and Sentinel-2 Data Fusion for Urban Change Detection Using a Dual Stream U-Net. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, Y.; Bruzzone, L. Self-Supervised SAR-Optical Data Fusion of Sentinel-1/-2 Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.K.; Roy, D.P.; Yan, L.; Huang, H. Sharpening the Sentinel-2 10 and 20 m Bands to Planetscope-0 3 m Resolution. Remote Sens. 2020, 12, 2406. [Google Scholar] [CrossRef]
- Clerici, N.; Calderon, C.A.V.; Posada, J.M. Fusion of Sentinel-1A and Sentinel-2A data for land cover mapping: A case study in the lower Magdalena region, Colombia. J. Maps 2017, 13, 718–726. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Chen, H.; Zhao, G.; Wang, Z.; Wang, D. Spectral Index Fusion for Salinized Soil Salinity Inversion Using Sentinel-2A and UAV Images in a Coastal Area. IEEE Access 2020, 8, 159595–159608. [Google Scholar] [CrossRef]
- Ao, Z.; Sun, Y.; Xin, Q. Constructing 10 m NDVI Time Series From Landsat 8 and Sentinel 2 Images Using Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1461–1465. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J.; Fu, P.; Hu, L.; Lui, T. Deep learning-based fusion of Landsat-8 and Sentinel-2 images for a harmonized surface reflectance product. Remote Sens. Environ. 2019, 235, 111425. [Google Scholar] [CrossRef]
- Sentinel-2 MSI Technical Guide. Available online: https://sentinels.copernicus.eu/web/sentinel/technical-guides/sentinel-2-msi (accessed on 15 November 2021).
- Spatial Performance of Landsat 8 Instruments. Available online: https://www.usgs.gov/core-science-systems/nli/landsat/spatial-performance-landsat-8-instruments (accessed on 15 November 2021).
- Armannsson, S.E.; Sigurdsson, J.; Sveinsson, J.R.; Ulfarsson, M.O. Tuning Parameter Selection for Sentinel-2 Sharpening Using Wald’s Protocol. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2871–2874. [Google Scholar] [CrossRef]
- Armannsson, S.E.; Ulfarsson, M.O.; Sigurdsson, J.; Nguyen, H.V.; Sveinsson, J.R. A Comparison of Optimized Sentinel-2 Super-Resolution Methods Using Wald’s Protocol and Bayesian Optimization. Remote Sens. 2021, 13, 2192. [Google Scholar] [CrossRef]
- Wang, Q.; Blackburn, G.A.; Onojeghuo, A.O.; Dash, J.; Zhou, L.; Zhang, Y.; Atkinson, P.M. Fusion of Landsat 8 OLI and Sentinel-2 MSI Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3885–3899. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q. GitHub Page. Available online: https://github.com/qunmingwang (accessed on 1 January 2022).
- Wald, L. Assessing the Quality of Synthesized Images. In Data Fusion. Definitions and Architectures—Fusion of Images of Different Spatial Resolutions; Les Presses de l’École des Mines: Paris, France, 2002. [Google Scholar]
- Wang, Z.; Bovik, A. A Universal Image Quality Index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Jagalingam, P.; Hegde, A.V. A Review of Quality Metrics for Fused Image. Aquat. Procedia 2015, 4, 133–142. [Google Scholar] [CrossRef]
- Blau, Y.; Michaeli, T. The Perception-Distortion Tradeoff. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6228–6237. [Google Scholar] [CrossRef] [Green Version]




| Escondido | AZ | IS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | S | A | B | S | A | B | S | ||
| ERGAS | 20 m | 7.57 | 7.31 | 7.75 | 7.64 | 6.17 | 5.99 | 19.36 | 12.42 | 12.10 |
| 30 m | 4.40 | 1.86 | 2.67 | 7.47 | 4.93 | 4.78 | 14.87 | 9.19 | 8.64 | |
| 60 m | 1.28 | 0.69 | 1.48 | 4.03 | 3.30 | 2.73 | 7.07 | 3.97 | 3.18 | |
| RMSE | 20 m | 0.01 | 0.01 | 0.01 | 0.03 | 0.03 | 0.02 | 0.04 | 0.03 | 0.03 |
| 30 m | 0.01 | 0.00 | 0.00 | 0.06 | 0.04 | 0.04 | 0.05 | 0.03 | 0.03 | |
| 60 m | 0.00 | 0.00 | 0.00 | 0.05 | 0.05 | 0.04 | 0.07 | 0.04 | 0.03 | |
| All | 0.01 | 0.01 | 0.01 | 0.05 | 0.04 | 0.03 | 0.05 | 0.03 | 0.03 | |
| SAM | 20 m | 8.24 | 8.00 | 7.91 | 4.93 | 4.73 | 4.81 | 8.53 | 7.48 | 8.00 |
| 30 m | 4.08 | 1.96 | 1.73 | 11.35 | 3.47 | 4.38 | 12.97 | 6.01 | 6.23 | |
| SRE | SSIM | UIQI | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Escondido | AZ | IS | Escondido | AZ | IS | Escondido | AZ | IS | |||||||||||||||||||
| A | B | S | A | B | S | A | B | S | A | B | S | A | B | S | A | B | S | A | B | S | A | B | S | A | B | S | |
| B5 | 20.32 | 23.64 | 25.86 | 16.28 | 19.52 | 19.14 | 12.70 | 14.18 | 14.25 | 0.97 | 0.98 | 0.99 | 0.87 | 0.92 | 0.92 | 0.90 | 0.91 | 0.91 | 0.88 | 0.90 | 0.97 | 0.79 | 0.85 | 0.85 | 0.66 | 0.57 | 0.57 |
| B6 | 20.09 | 20.52 | 25.75 | 16.90 | 19.42 | 19.39 | 14.65 | 15.74 | 16.20 | 0.96 | 0.95 | 0.99 | 0.88 | 0.91 | 0.92 | 0.90 | 0.90 | 0.92 | 0.88 | 0.83 | 0.96 | 0.80 | 0.84 | 0.85 | 0.65 | 0.58 | 0.57 |
| B7 | 20.46 | 21.04 | 29.02 | 17.02 | 19.43 | 19.55 | 14.88 | 16.25 | 16.78 | 0.96 | 0.96 | 0.99 | 0.89 | 0.91 | 0.93 | 0.90 | 0.91 | 0.93 | 0.90 | 0.87 | 0.99 | 0.80 | 0.84 | 0.85 | 0.66 | 0.59 | 0.60 |
| B8A | 22.15 | 22.95 | 27.18 | 17.19 | 19.27 | 19.49 | 14.98 | 16.26 | 16.74 | 0.98 | 0.98 | 0.99 | 0.89 | 0.91 | 0.93 | 0.90 | 0.91 | 0.93 | 0.92 | 0.90 | 0.97 | 0.80 | 0.84 | 0.85 | 0.66 | 0.61 | 0.60 |
| B11 | 31.19 | 25.66 | 16.72 | 19.25 | 20.21 | 20.26 | 16.47 | 16.45 | 16.48 | 1.00 | 1.00 | 0.98 | 0.91 | 0.92 | 0.91 | 0.89 | 0.89 | 0.90 | 0.79 | 0.57 | 0.35 | 0.84 | 0.86 | 0.85 | 0.69 | 0.59 | 0.55 |
| B12 | 48.57 | 25.03 | 16.71 | 18.72 | 19.50 | 19.77 | 14.80 | 14.33 | 14.09 | 1.00 | 1.00 | 0.99 | 0.90 | 0.91 | 0.91 | 0.89 | 0.86 | 0.86 | 0.86 | 0.11 | 0.05 | 0.83 | 0.84 | 0.84 | 0.69 | 0.56 | 0.53 |
| L8d | 9.46 | 9.72 | 9.69 | 16.90 | 17.59 | 18.82 | 5.16 | 14.36 | 14.86 | 0.89 | 0.90 | 0.89 | 0.85 | 0.84 | 0.91 | 0.70 | 0.94 | 0.95 | 0.84 | 0.86 | 0.85 | 0.79 | 0.75 | 0.85 | 0.34 | 0.69 | 0.73 |
| 20 m | 24.60 | 21.22 | 21.56 | 17.46 | 19.28 | 19.49 | 13.38 | 15.37 | 15.63 | 0.96 | 0.97 | 0.98 | 0.88 | 0.90 | 0.92 | 0.87 | 0.90 | 0.91 | 0.87 | 0.72 | 0.73 | 0.81 | 0.83 | 0.85 | 0.62 | 0.60 | 0.59 |
| L1 | 19.65 | 29.04 | 28.15 | 12.77 | 15.02 | 14.91 | 8.54 | 12.35 | 13.36 | 0.96 | 0.99 | 0.99 | 0.81 | 0.84 | 0.88 | 0.85 | 0.89 | 0.92 | 0.77 | 0.91 | 0.91 | 0.75 | 0.75 | 0.81 | 0.65 | 0.61 | 0.65 |
| L2 | 17.39 | 27.52 | 31.73 | 13.10 | 15.71 | 15.70 | 8.77 | 12.92 | 13.73 | 0.94 | 0.99 | 1.00 | 0.80 | 0.84 | 0.88 | 0.85 | 0.90 | 0.93 | 0.79 | 0.95 | 0.98 | 0.76 | 0.77 | 0.83 | 0.68 | 0.67 | 0.71 |
| L3 | 15.82 | 25.56 | 30.06 | 14.15 | 17.88 | 18.26 | 9.14 | 14.35 | 15.03 | 0.94 | 0.99 | 1.00 | 0.80 | 0.85 | 0.90 | 0.85 | 0.92 | 0.94 | 0.82 | 0.95 | 0.99 | 0.78 | 0.80 | 0.87 | 0.68 | 0.69 | 0.76 |
| L4 | 14.77 | 23.91 | 33.70 | 14.43 | 19.49 | 20.28 | 9.05 | 14.76 | 15.26 | 0.94 | 0.99 | 1.00 | 0.78 | 0.86 | 0.91 | 0.84 | 0.92 | 0.93 | 0.84 | 0.95 | 1.00 | 0.78 | 0.83 | 0.89 | 0.65 | 0.65 | 0.72 |
| L5 | 16.22 | 22.98 | 27.12 | 14.52 | 18.96 | 19.31 | 11.96 | 17.15 | 17.34 | 0.89 | 0.98 | 0.99 | 0.75 | 0.82 | 0.88 | 0.77 | 0.90 | 0.92 | 0.57 | 0.90 | 0.97 | 0.75 | 0.79 | 0.86 | 0.53 | 0.66 | 0.70 |
| L6 | 30.77 | 25.68 | 17.15 | 14.68 | 19.08 | 19.87 | 12.93 | 16.17 | 16.31 | 1.00 | 1.00 | 0.98 | 0.75 | 0.81 | 0.89 | 0.82 | 0.87 | 0.88 | 0.79 | 0.58 | 0.36 | 0.75 | 0.79 | 0.86 | 0.57 | 0.63 | 0.66 |
| L7 | 49.64 | 25.03 | 17.05 | 14.35 | 19.17 | 19.79 | 13.23 | 14.19 | 14.01 | 1.00 | 1.00 | 0.99 | 0.73 | 0.82 | 0.88 | 0.86 | 0.86 | 0.87 | 0.90 | 0.11 | 0.04 | 0.74 | 0.79 | 0.86 | 0.65 | 0.59 | 0.62 |
| 30 m | 23.47 | 25.68 | 26.42 | 14.00 | 17.90 | 18.30 | 10.52 | 14.56 | 15.01 | 0.95 | 0.99 | 0.99 | 0.77 | 0.83 | 0.89 | 0.83 | 0.89 | 0.91 | 0.78 | 0.76 | 0.75 | 0.76 | 0.79 | 0.85 | 0.63 | 0.64 | 0.69 |
| B1 | 23.34 | 27.78 | 26.27 | 12.66 | 14.73 | 16.31 | 11.40 | 15.07 | 17.75 | 0.98 | 0.99 | 0.99 | 0.84 | 0.86 | 0.92 | 0.80 | 0.89 | 0.94 | 0.77 | 0.89 | 0.87 | 0.84 | 0.85 | 0.92 | 0.66 | 0.84 | 0.81 |
| B9 | 21.54 | 27.64 | 18.73 | 14.41 | 15.63 | 17.40 | 9.68 | 15.70 | 17.01 | 0.99 | 1.00 | 0.99 | 0.82 | 0.80 | 0.89 | 0.54 | 0.82 | 0.83 | 0.47 | 0.72 | 0.47 | 0.80 | 0.77 | 0.87 | 0.45 | 0.62 | 0.66 |
| 60 m | 22.44 | 27.71 | 22.50 | 13.54 | 15.18 | 16.85 | 10.54 | 15.38 | 17.38 | 0.99 | 1.00 | 0.99 | 0.83 | 0.83 | 0.90 | 0.67 | 0.86 | 0.89 | 0.62 | 0.81 | 0.67 | 0.82 | 0.81 | 0.90 | 0.55 | 0.73 | 0.73 |
| All | 23.84 | 23.98 | 23.81 | 15.46 | 18.16 | 18.64 | 11.77 | 15.02 | 15.58 | 0.96 | 0.98 | 0.98 | 0.83 | 0.86 | 0.90 | 0.83 | 0.89 | 0.91 | 0.80 | 0.75 | 0.73 | 0.79 | 0.81 | 0.86 | 0.62 | 0.63 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigurdsson, J.; Armannsson, S.E.; Ulfarsson, M.O.; Sveinsson, J.R. Fusing Sentinel-2 and Landsat 8 Satellite Images Using a Model-Based Method. Remote Sens. 2022, 14, 3224. https://doi.org/10.3390/rs14133224
Sigurdsson J, Armannsson SE, Ulfarsson MO, Sveinsson JR. Fusing Sentinel-2 and Landsat 8 Satellite Images Using a Model-Based Method. Remote Sensing. 2022; 14(13):3224. https://doi.org/10.3390/rs14133224
Chicago/Turabian StyleSigurdsson, Jakob, Sveinn E. Armannsson, Magnus O. Ulfarsson, and Johannes R. Sveinsson. 2022. "Fusing Sentinel-2 and Landsat 8 Satellite Images Using a Model-Based Method" Remote Sensing 14, no. 13: 3224. https://doi.org/10.3390/rs14133224
APA StyleSigurdsson, J., Armannsson, S. E., Ulfarsson, M. O., & Sveinsson, J. R. (2022). Fusing Sentinel-2 and Landsat 8 Satellite Images Using a Model-Based Method. Remote Sensing, 14(13), 3224. https://doi.org/10.3390/rs14133224