Machine-Learning Functional Zonation Approach for Characterizing Terrestrial–Aquatic Interfaces: Application to Lake Erie
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Site
2.2. Spatial Data Layers
2.2.1. Land Cover Map
2.2.2. Topographic Metrics
2.2.3. Time-Series Landsat Satellite Images
2.2.4. Soil Texture
2.3. Zonation Analysis
2.3.1. Grid
2.3.2. Unsupervised Clustering for Functional Zonation
3. Results
3.1. Lake Erie’s TAI Land Cover and Soil Texture
3.2. Wetland Characterization
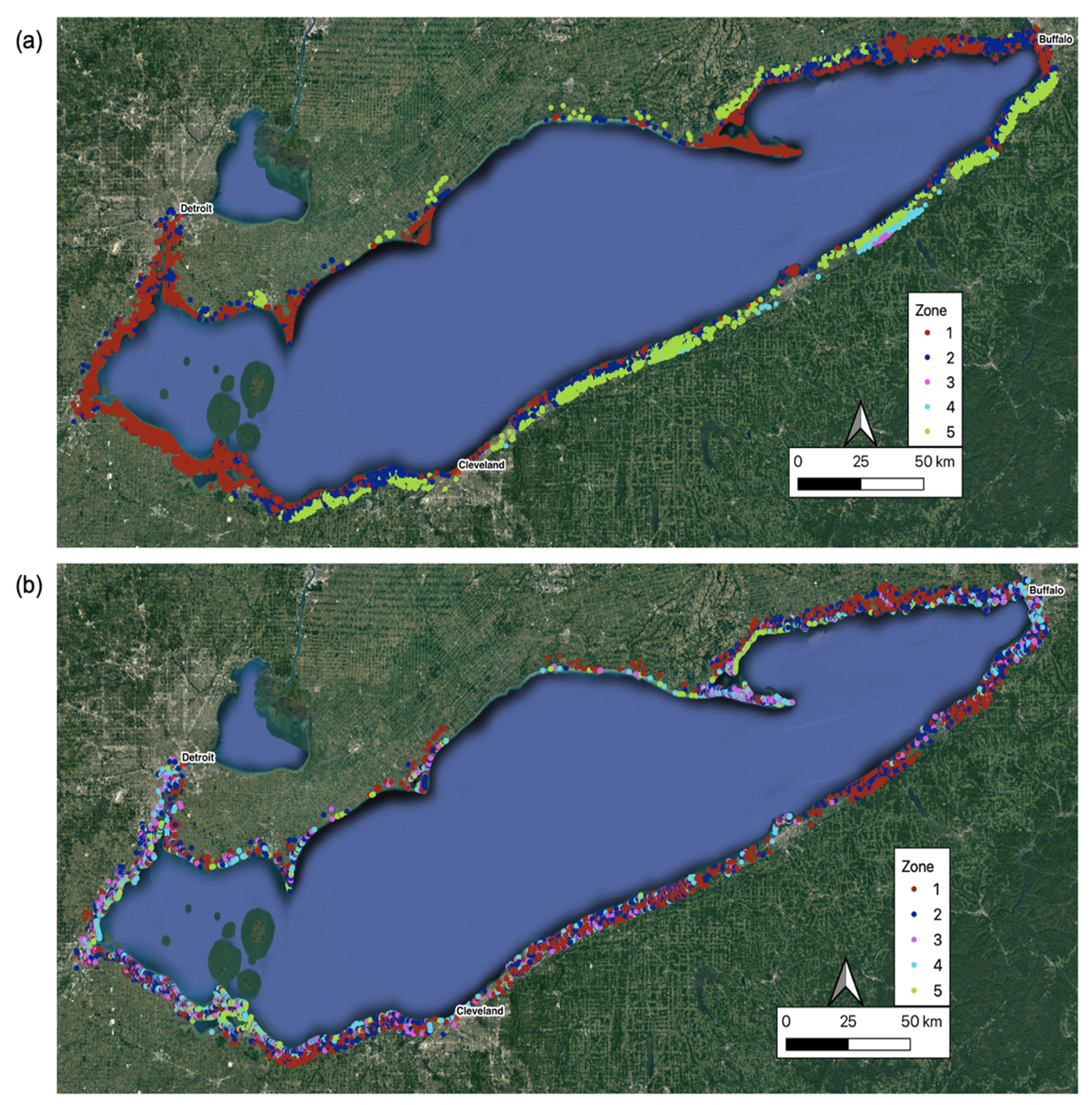
3.3. Functional Zonations
3.3.1. All-Metrics Based Zonation
3.3.2. EVI-Based Zonation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spivak, A.C.; Sanderman, J.; Bowen, J.L.; Canuel, E.A.; Hopkinson, C.S. Global-change controls on soil-carbon accumulation and loss in coastal vegetated ecosystems. Nat. Geosci. 2019, 12, 685–692. [Google Scholar] [CrossRef]
- Bauer, J.E.; Cai, W.-J.; Raymond, P.A.; Bianchi, T.; Hopkinson, C.; Regnier, P.A.G. The changing carbon cycle of the coastal ocean. Nature 2013, 504, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Grizzetti, B.; Liquete, C.; Pistocchi, A.; Vigiak, O.; Zulian, G.; Bouraoui, F.; De Roo, A.; Cardoso, A.C. Relationship between ecological condition and ecosystem services in European rivers, lakes and coastal waters. Sci. Total Environ. 2019, 671, 452–465. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Wong, P.P.; Burkett, V.; Codignotto, J.; Hay, J.; McLean, R.; Ragoonaden, S.; Woodroffe, C.D. Coastal systems and low-lying areas. In Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 315–356. [Google Scholar]
- Gronewold, A.D.; Fortin, V.; Lofgren, B.; Clites, A.; Stow, C.A.; Quinn, F. Coasts, water levels, and climate change: A Great Lakes perspective. Clim. Chang. 2013, 120, 697–711. [Google Scholar] [CrossRef]
- Tremblay, N.W.; Gilman, A.P. Human health, the Great Lakes, and environmental pollution: A 1994 perspective. Environ. Health Perspect. 1995, 103, 3–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bourgeau-Chavez, L.; Endres, S.; Battaglia, M.; Miller, M.E.; Banda, E.; Laubach, Z.; Higman, P.; Chow-Fraser, P.; Marcaccio, J. Development of a Bi-National Great Lakes Coastal Wetland and Land Use Map Using Three-Season PALSAR and Landsat Imagery. Remote Sens. 2015, 7, 8655–8682. [Google Scholar] [CrossRef] [Green Version]
- Dahl, T.E. Wetlands Losses in the United States 1780s to 1980s, 1st ed.; US Fish and Wildlife Service: St Petersburg, FL, USA, 1990.
- Smith, I.M.; Fiorino, G.E.; Grabas, G.P.; Wilcox, D.A. Wetland vegetation response to record-high Lake Ontario water levels. J. Great Lakes Res. 2020, 47, 160–167. [Google Scholar] [CrossRef]
- Ward, N.D.; Megonigal, J.P.; Bond-Lamberty, B.; Bailey, V.L.; Butman, D.; Canuel, E.A.; Diefenderfer, H.; Ganju, N.K.; Goñi, M.A.; Graham, E.B.; et al. Representing the function and sensitivity of coastal interfaces in Earth system models. Nat. Commun. 2020, 11, 2458. [Google Scholar] [CrossRef]
- Correll, M.D.; Hantson, W.; Hodgman, T.P.; Cline, B.B.; Elphick, C.S.; Shriver, W.G.; Tymkiw, E.L.; Olsen, B.J. Fine-Scale Mapping of Coastal Plant Communities in the Northeastern USA. Wetlands 2018, 39, 17–28. [Google Scholar] [CrossRef]
- Zhang, C.; Denka, S.; Mishra, D.R. Mapping freshwater marsh species in the wetlands of Lake Okeechobee using very high-resolution aerial photography and lidar data. Int. J. Remote Sens. 2018, 39, 5600–5618. [Google Scholar] [CrossRef]
- Duncan, J.M.; Groffman, P.M.; Band, L.E. Towards closing the watershed nitrogen budget: Spatial and temporal scaling of deni-trification: Scaling denitrification. J. Geophys. Res. Biogeosci. 2013, 118, 1105–1119. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef] [PubMed]
- Devadoss, J.; Falco, N.; Dafflon, B.; Wu, Y.; Franklin, M.; Hermes, A.; Hinckley, E.-L.; Wainwright, H. Remote Sensing-Informed Zonation for Understanding Snow, Plant and Soil Moisture Dynamics within a Mountain Ecosystem. Remote Sens. 2020, 12, 2733. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Dafflon, B.; Smith, L.J.; Hahn, M.S.; Curtis, J.B.; Wu, Y.; Ulrich, C.; Peterson, J.E.; Torn, M.S.; Hubbard, S.S. Identifying multiscale zonation and assessing the relative importance of polygon geomorphology on carbon fluxes in an Arctic tundra ecosystem: Zonation approach in an arctic ecosystem. J. Geophys. Res. Biogeosci. 2015, 120, 788–808. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Uhlemann, S.; Franklin, M.; Falco, N.; Bouskill, N.J.; Newcomer, M.E.; Dafflon, B.; Siirila-Woodburn, E.R.; Minsley, B.J.; Williams, K.H.; et al. Watershed zonation through hillslope clustering for tractably quantifying above- and be-low-ground watershed heterogeneity and functions. Hydrol. Earth Syst. Sci. 2022, 26, 429–444. [Google Scholar] [CrossRef]
- Tu, W.; Hu, Z.; Li, L.; Cao, J.; Jiang, J.; Li, Q.; Li, Q. Portraying Urban Functional Zones by Coupling Remote Sensing Imagery and Human Sensing Data. Remote Sens. 2018, 10, 141. [Google Scholar] [CrossRef] [Green Version]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef] [Green Version]
- Wainwright, H.M.; Steefel, C.; Trutner, S.D.; Henderson, A.N.; Nikolopoulos, E.I.; Wilmer, C.F.; Chadwick, K.D.; Falco, N.; Schaettle, K.B.; Brown, J.B.; et al. Satellite-derived foresummer drought sensitivity of plant productivity in Rocky Mountain headwater catchments: Spatial heterogeneity and geological-geomorphological control. Environ. Res. Lett. 2020, 15, 084018. [Google Scholar] [CrossRef]
- Herdendorf, C.E. Lake Erie Coastal Wetlands: An Overview. J. Great Lakes Res. 1992, 18, 533–551. [Google Scholar] [CrossRef]
- Theuerkauf, E.J.; Braun, K.N. Rapid water level rise drives unprecedented coastal habitat loss along the Great Lakes of North America. J. Great Lakes Res. 2021, 47, 945–954. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Leeuwen, W.V.; Jacobson, A.; Solanos, R.; Laing, T. MODIS vegetation index (MOD13). Algorithm Theor. Basis Doc. 1999, 3, 295–309. [Google Scholar]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kassambra, A. Practical Guide to Cluster Analysis in R: Unsupervised Machine Leaning; STHDA: Paris, France, 2017; Volume 1.
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Newcomer, M.E.; Kuss, A.J.M.; Ketron, T.; Remar, A.; Choksi, V.; Skiles, J.W. Estuarine sediment deposition during wetland restoration: A GIS and remote sensing modeling approach. Geocarto Int. 2013, 29, 451–467. [Google Scholar] [CrossRef] [Green Version]
- Enguehard , L.; Falco, N.; Schmutz, M.E.; Newcomer, M.; Ladau, J.; Brown, J.B.; Bourgeau-Chavez, L.; Wainwright, H.M. Data used in “Enguehard et al. 2022, Machine-Learning Functional Zonation Approach for Characterizing Terrestrial–Aquatic Interfaces: Application to Lake Erie”. COMPASS-FME, ESS-DIVE Repository. Dataset. doi:10.15485/1876578. Available online: https://data.ess-dive.lbl.gov/datasets/doi:10.15485/1876578 (accessed on 28 April 2022).







| Phragmite | Emergent Wetland | Shrub Wetland | Forested Wetland | |
|---|---|---|---|---|
| Distance from the shore | 750 m | 1000 m | 1300 m | 1800 m |
| Elevation | 176 m | 183 m | 185 m | 200 m |
| Slope | 0° | 0.6° | 1.0° | 1.5° |
| Enhanced Vegetation Index | 0.5 | 0.54 | 0.60 | 0.65 |
| Zone 1 | Zone 2 | Zone 3 | Zone 4 | Zone 5 | |
|---|---|---|---|---|---|
| Location | Low-lying lands, peninsulas | Transition between inland and the water | Inland, high hilly region | Inland, hilly region | Inland |
| Predominant soil type | Silty, sandy, clayey | Silty, sandy, clayey | Silty | Silty | Silty, clayey |
| Elevation | 173 m | 186 m | 408 m | 284 m | 208 m |
| Slope | 1.1° | 4.6° | 3.1° | 5.4° | 2.3° |
| Peak EVI | 0.49 | 0.53 | 0.65 | 0.63 | 0.56 |
| Zone 1 | Zone 2 | Zone 3 | Zone 4 | Zone 5 | |
|---|---|---|---|---|---|
| Description | Highest plant productivity regions | High plant productivity regions | Medium plant productivity regions | Low plant productivity regions | Water/misclassification |
| Predominant soil type | Silty, clayey | Silty, clayey, sandy | Silty, clayey, sandy | Silty, clayey, sandy | Silty, sandy |
| Elevation | 179 m | 176 m | 174 m | 173 m | 172 m |
| Slope | 2.0° | 1.9° | 1.5° | 1.8° | 3.2° |
| Peak EVI | 0.62 | 0.53 | 0.46 | 0.36 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enguehard, L.; Falco, N.; Schmutz, M.; Newcomer, M.E.; Ladau, J.; Brown, J.B.; Bourgeau-Chavez, L.; Wainwright, H.M. Machine-Learning Functional Zonation Approach for Characterizing Terrestrial–Aquatic Interfaces: Application to Lake Erie. Remote Sens. 2022, 14, 3285. https://doi.org/10.3390/rs14143285
Enguehard L, Falco N, Schmutz M, Newcomer ME, Ladau J, Brown JB, Bourgeau-Chavez L, Wainwright HM. Machine-Learning Functional Zonation Approach for Characterizing Terrestrial–Aquatic Interfaces: Application to Lake Erie. Remote Sensing. 2022; 14(14):3285. https://doi.org/10.3390/rs14143285
Chicago/Turabian StyleEnguehard, Léa, Nicola Falco, Myriam Schmutz, Michelle E. Newcomer, Joshua Ladau, James B. Brown, Laura Bourgeau-Chavez, and Haruko M. Wainwright. 2022. "Machine-Learning Functional Zonation Approach for Characterizing Terrestrial–Aquatic Interfaces: Application to Lake Erie" Remote Sensing 14, no. 14: 3285. https://doi.org/10.3390/rs14143285
APA StyleEnguehard, L., Falco, N., Schmutz, M., Newcomer, M. E., Ladau, J., Brown, J. B., Bourgeau-Chavez, L., & Wainwright, H. M. (2022). Machine-Learning Functional Zonation Approach for Characterizing Terrestrial–Aquatic Interfaces: Application to Lake Erie. Remote Sensing, 14(14), 3285. https://doi.org/10.3390/rs14143285








