Aeronautics Application of Direct-Detection Doppler Wind Lidar: An Adapted Design Based on a Fringe-Imaging Michelson Interferometer as Spectral Analyzer †
Abstract
:1. Introduction
- Updated rate of the LOS wind measurements from 10 Hz to 20 Hz over the full field (i.e., over several viewing directions, e.g., within a cone);
- Wind speed precision of around or less 1 m/s in cone-like or screen-like scanning or multiple direction setups;
- Spatial resolution from 10 m to 30 m, depending on the aircraft mass, wingspan and flight speed (and thus its frequency response to turbulence);
- Distance ranges of 50 m to 350 m ahead of the aircraft;
- Consideration of eye safety issues; and
- Full and provable availability of sufficient functionality in cruise flight conditions.
2. Methods for Validating the Applicability of Direct-Detection Doppler Wind Lidar as Aeronautics Gust Load Alleviation Sensor System
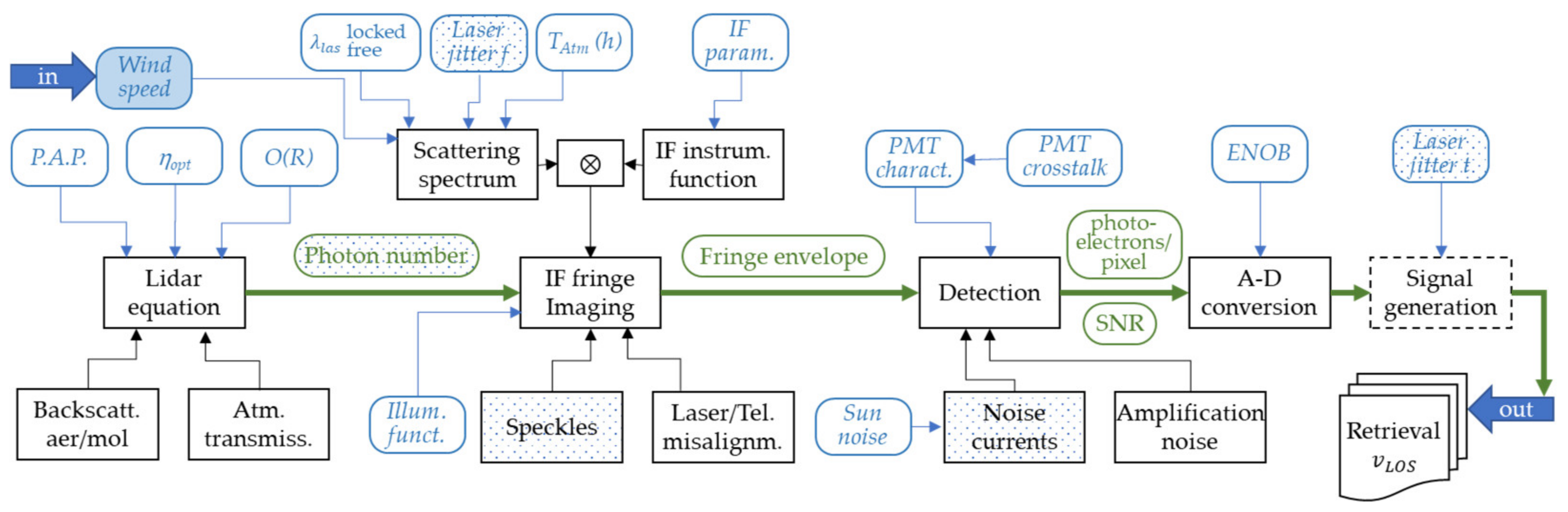
2.1. Analytical Model of a Direct-Detection Doppler Wind Lidar
- The first term represents the Doppler wind lidar technical optics architecture and implementation and remains constant for given (typical) lidar performance values.
- The second term, the atmospheric contribution, is constant for a given flight altitude h (thus mission profile). Since for realistic (and worst case) estimations, a pure molecular atmosphere should be considered, the backscatter coefficient collapses into a mere function of the atmospheric temperature that in turn may be determined by a certain model atmosphere.
- The third term contains the lidar system design variables; these should be adopted to meet the requirements of the wind reconstruction algorithm to retrieve the LOS wind speed with a certain precision.
- For a decent overall optical efficiency of about 25%, together with a good detector quantum efficiency (giving a responsivity of 0.12 A/W for the photomultiplier tube (PMT) as used in our demonstrator), the first factor is around .
- The atmospheric term amounts to a value around for an altitude of 10,000 m and considering a UV wavelength of 355 nm.
- Together, these factors amount to around that must be accommodated by the third factor to achieve a wind speed distribution on the level.
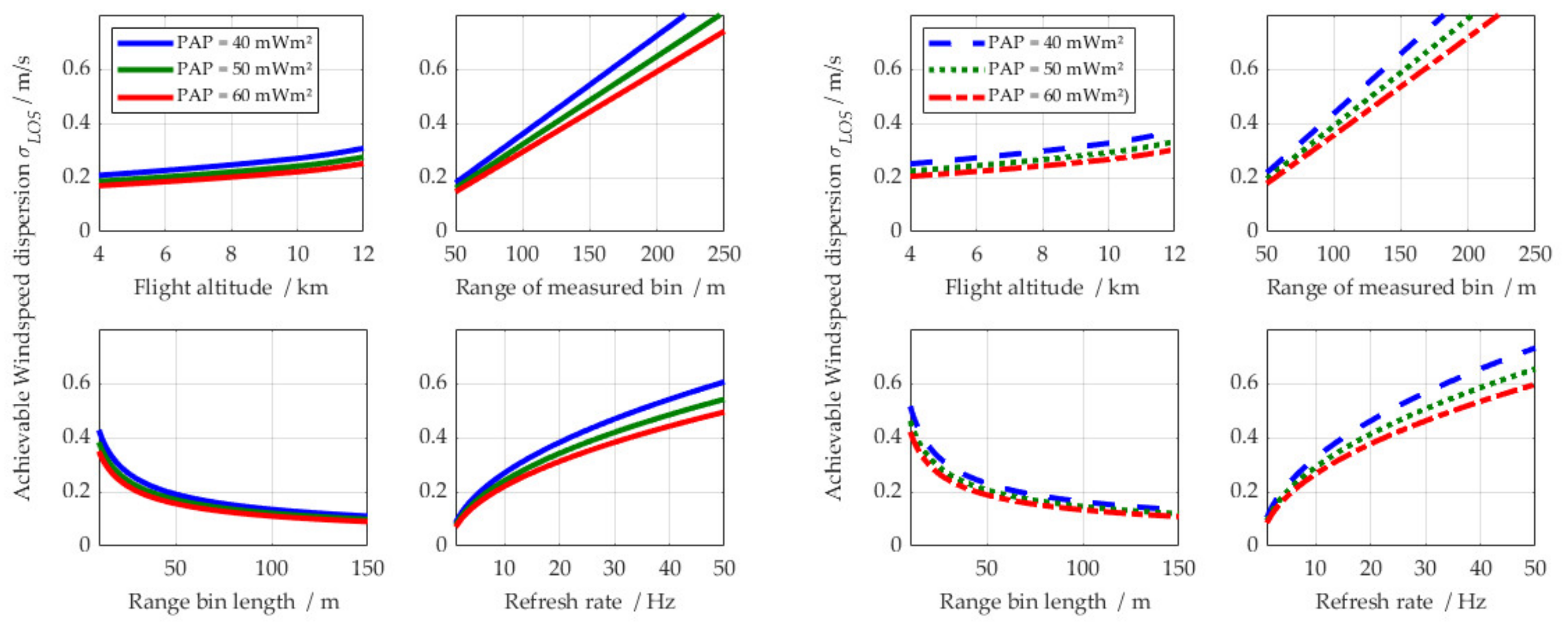
- Taking as an example, and for ease of calculation, 10 Hz for , 10 m for the resolution and 100 m for the considered detection distance , it may be deduced that a of around 50 mWm² would deliver good wind estimation results of around 0.5 m/s dispersion. Such a may be achieved with a 5 W laser and an effective receiver aperture diameter of 11 cm. Note that the actual laser pulse repetition frequency (PRF) is not a subject here. However, when going into more technical detail, it should be analyzed in detail since too high as well as too low pulse energies may be detrimental for the outcome, either due to overexposing the detector on very short distances, or due to too high noise per pulse, inhibiting a good averaging even with high pulse numbers .
2.2. Physics-Based End-to-End Simulator
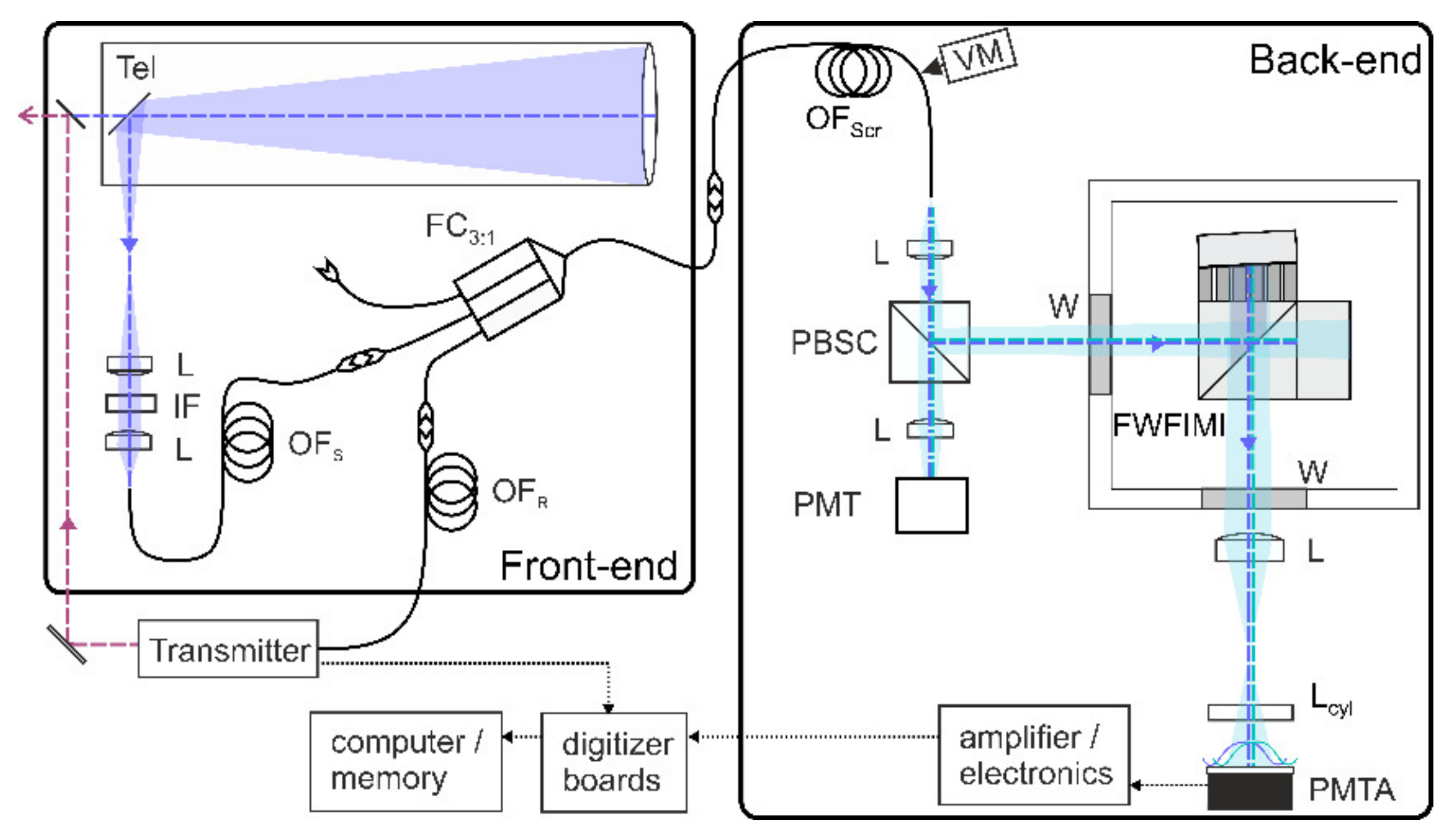
2.3. Demonstrator of the DD-DWL for Gust Load Alleviation (GLA) Application
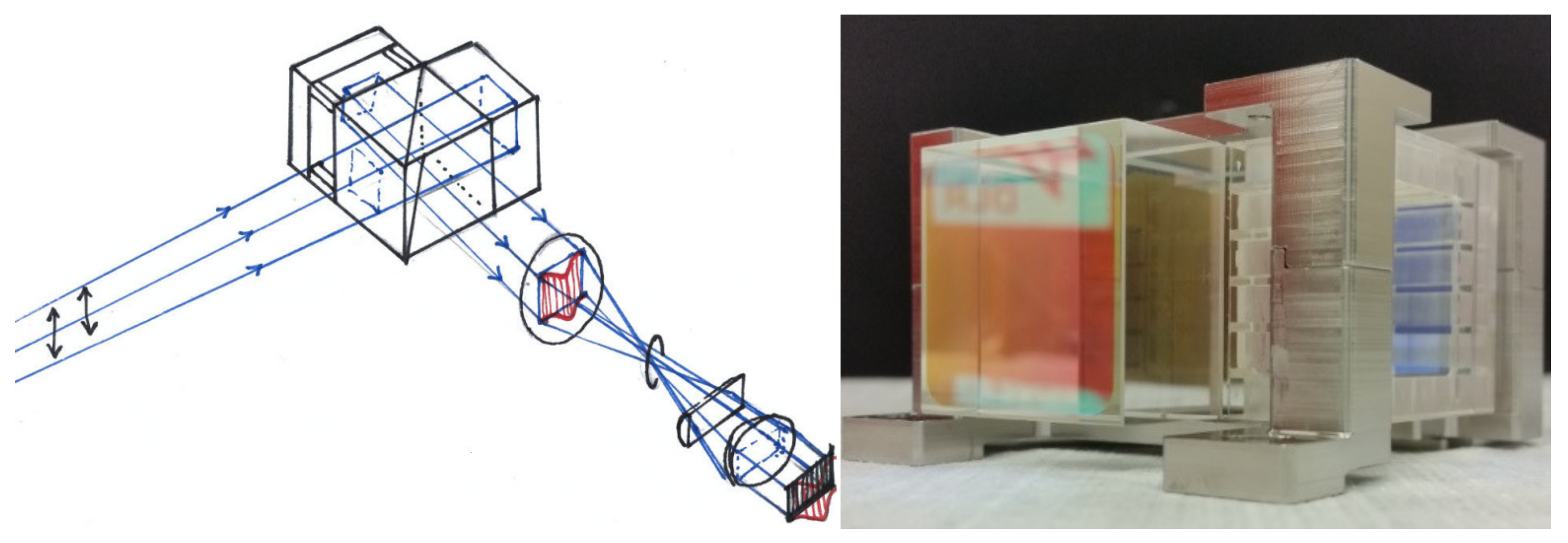
2.3.1. The Spectral Analyzing Part: FW-FIMI
2.3.2. Receiver Front-End: Light Collection and Fiber Architecture
2.3.3. Laser Transmitter
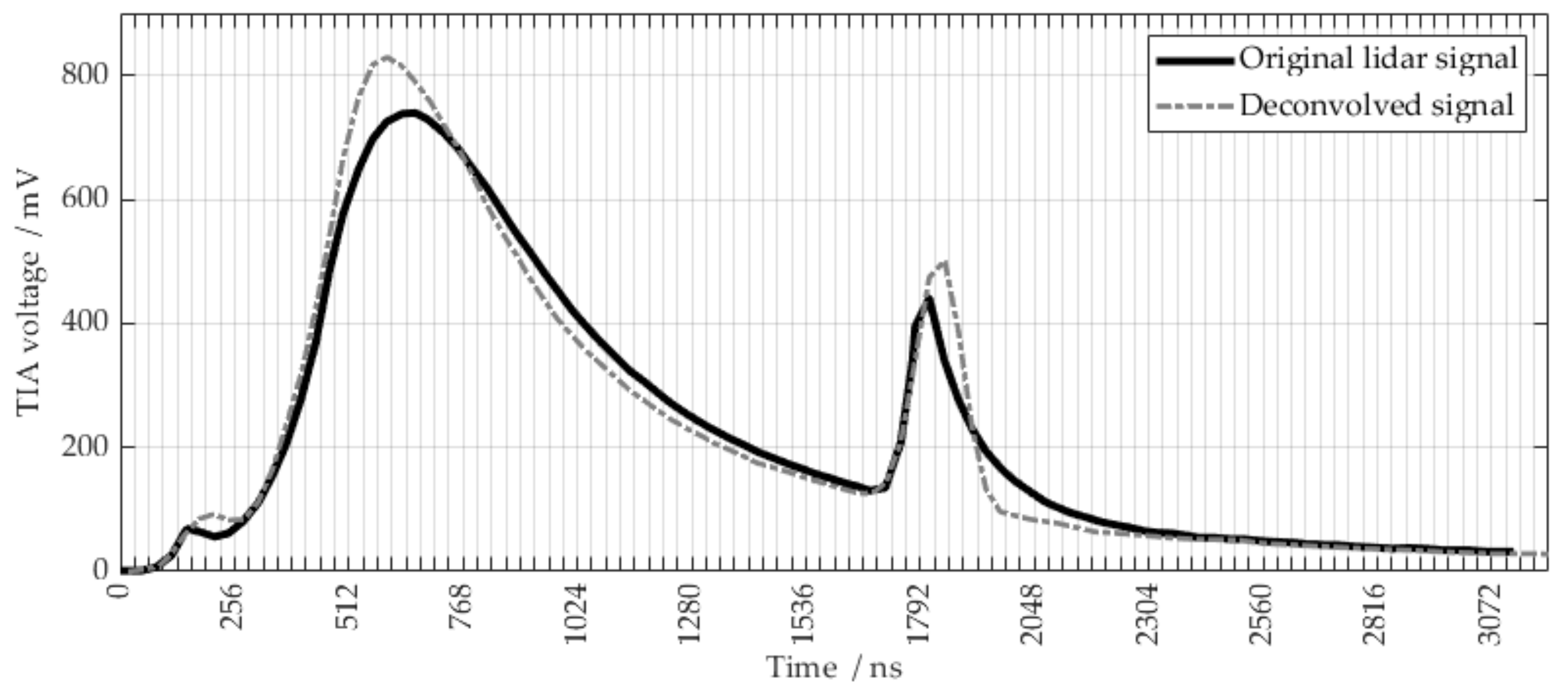
2.3.4. Data Acquisition and Wind Retrieval
2.3.5. DWL Demonstrator Summary and Note
- Use of only one polarization instead of unpolarized (rather arbitrarily polarized) light due to the imperfect beam splitter coating within the FIMI;
- Implementation of only the transmitted channel of the FIMI;
- Photon loss and crosstalk on the PMT detector array;
- Non-optimized overlap integral on very short ranges between transmit beam and telescope receiver field of view due to mono-static co-axial setup, small laser beam divergence and fiber étendue neglection;
- Simplistic imaging optic setups resulting in image aberrations;
- Diverse non-optimized optical surfaces (mirrors, fiber facets) resulting in losses;
- Deficient thermal stabilization, particularly of the FIMI compartment as well as the whole receiver back-end setup;
- Limited fiber scrambling/inchoate use of the potential of fiber scrambling possibilities; and
- Unexploited potentials in terms of routines (e.g., illumination function determination procedure) and retrieval methods (fringe function approximation).
3. Comparative Analysis of Wind Measurement Performance
3.1. Measurement Campaign Setup
- Deployment of demonstrator lidar in a controlled environment (for ease of implementation);
- Laser beam operation in non-eye-safe conditions;
- Intervention on laser/lidar beam for hard target measurement and laser beam angular fluctuation analysis (due to inherent instability and local turbulence);
- Control of Windcube® wind measurements by sonic anemometers; and
- Possibility of performing also vertical wind measurements.
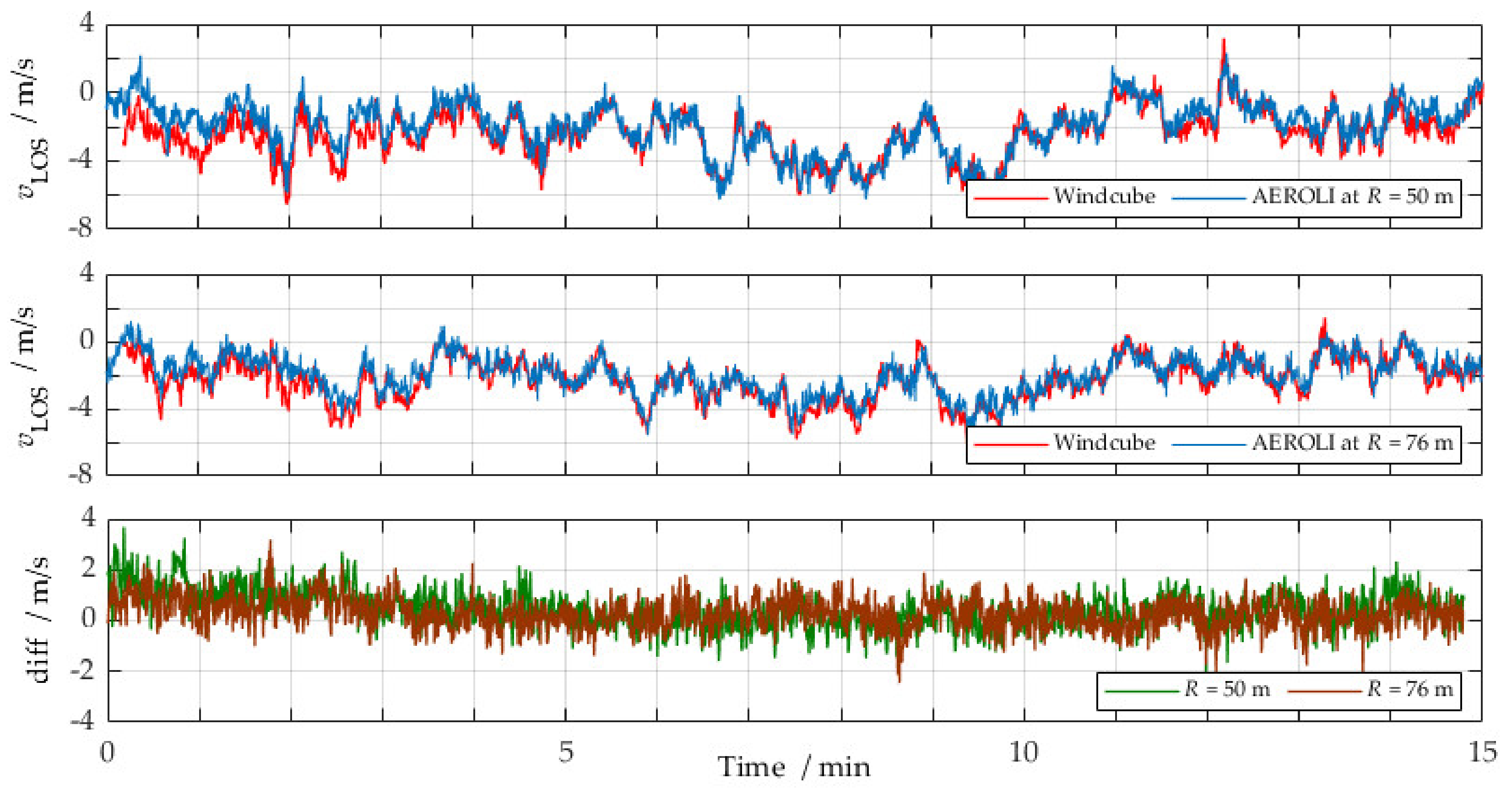
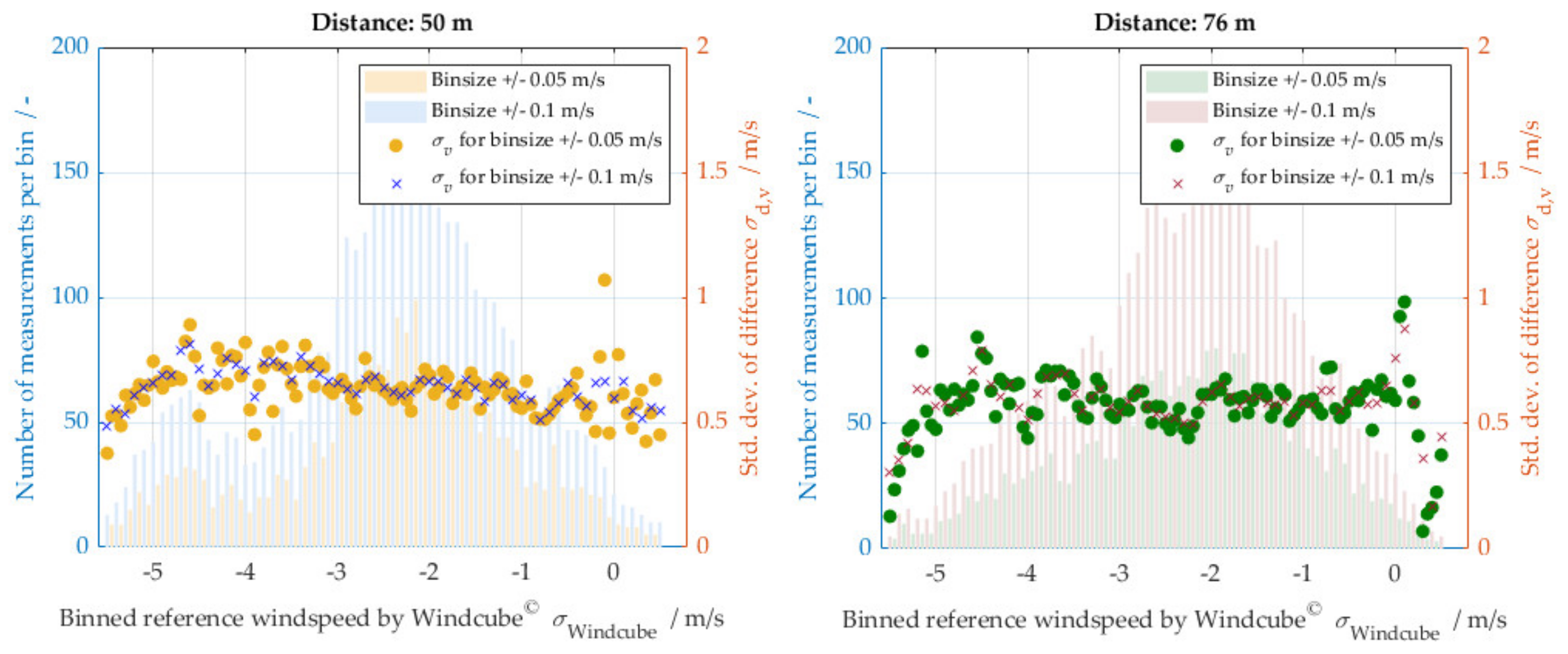
3.2. Wind Measurement Comparisons and Analysis
4. Discussion
4.1. Reciprocal Validation and Confirmation of Approach
4.2. Ongoing and Future Orientations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Willis, D.J.; Niezrecki, C.; Kuchma, D.; Hines, E.; Arwade, S.R.; Barthelmie, R.J.; DiPaola, M.; Drane, P.J.; Hansen, C.J.; Inalpolat, M.; et al. Wind Energy Research: State-of-the-Art and Future Research Directions. Renew. Energy 2018, 125, 133–154. [Google Scholar] [CrossRef]
- Thobois, L.; Cariou, J.P.; Gultepe, I. Review of Lidar-Based Applications for Aviation Weather. Pure Appl. Geophys. 2018, 176, 1959–1976. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, D.; Chen, T.; Dou, X.F.; Zhao, R.; Li, Z.; Zhou, A.; Zhang, N.; Gao, J.; Wang, G. Wind Profiling from High Troposphere to Low Stratosphere Using a Scanning Rayleigh Doppler Lidar. Opt. Rev. 2018, 25, 720–728. [Google Scholar] [CrossRef]
- Marksteiner, U.; Lemmerz, C.; Lux, O.; Rahm, S.; Schäfler, A.; Witschas, B.; Reitebuch, O. Calibrations and Wind Observations of an Airborne Direct-Detection Wind LiDAR Supporting ESA’s Aeolus Mission. Remote Sens. 2018, 10, 2056. [Google Scholar] [CrossRef] [Green Version]
- Franken, P.; Jenney, J.; Rank, D. Airborne Investigations of Clear-Air Turbulence with Laser Radars. IEEE J. Quantum Electron. 1966, 2, 147. [Google Scholar] [CrossRef]
- Vrancken, P. Airborne Remote Detection of Turbulence with Forward-Pointing LIDAR. In Aviation Turbulence; Sharman, R., Lane, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-23629-2. [Google Scholar]
- European Aviation Safety Agency (EASA). Annual Safety Review 2013; EASA: Cologne, Germany, 2013; ISBN 978-92-9230-187-9. [Google Scholar]
- Federal Aviation Administratuion (FAA). Advisory Circular 120-88A—Preventing Injuries Caused by Turbulence; FAA: Washington, DC, USA, 2006. [Google Scholar]
- Flightpath 2050: Europe’s Vision for Aviation; European Commission (Ed.) Policy/European Commission; Publications Office of the European Union: Luxembourg, 2011; ISBN 978-92-79-19724-6. [Google Scholar]
- Advisory Council for Aviation Research and Innovation in Europe (ACARE). Strategic Research & Innovation Agenda—Update 2017; ACARE: Brussels, Belgium, 2017. [Google Scholar]
- European Commission EGP—European Green Deal—Transport. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal/transport-and-green-deal_en (accessed on 28 September 2021).
- European Aviation Safety Agency (EASA). Certification Specification for Large Aeroplanes (CS-25); Amendment 3; EASA: Cologne, Germany, 2007. [Google Scholar]
- International Air Transport Association (IATA). 20 Year Passenger Forecast. Available online: https://www.iata.org/en/publications/store/20-year-passenger-forecast/ (accessed on 28 September 2021).
- Williams, P.D. Increased Light, Moderate, and Severe Clear-Air Turbulence in Response to Climate Change. Adv. Atmos. Sci. 2017, 34, 576–586. [Google Scholar] [CrossRef] [Green Version]
- Grewe, V.; Matthes, S.; Frömming, C.; Brinkop, S.; Jöckel, P.; Gierens, K.; Champougny, T.; Fuglestvedt, J.; Haslerud, A.; Irvine, E.; et al. Feasibility of Climate-Optimized Air Traffic Routing for Trans-Atlantic Flights. Environ. Res. Lett. 2017, 12, 034003. [Google Scholar] [CrossRef]
- Vrancken, P.; Wirth, M.; Ehret, G.; Barny, H.; Rondeau, P.; Veerman, H. Airborne Forward-Pointing UV Rayleigh Lidar for Remote Clear Air Turbulence Detection: System Design and Performance. Appl. Opt. 2016, 55, 9314–9328. [Google Scholar] [CrossRef] [Green Version]
- Bellamy, W. Boeing to Use LIDAR for Industry First on EcoDemonstrator. Aviation Today 2018. [Google Scholar]
- Sishtla, V.; Kameyama, S.; Finley, J.; Gidner, D.; Nguyen, L.; Hofmann, K.; Berthier, J.B.; Lefez, T.; Xiao, Z.F.; Koch, G.; et al. Feasibility Study: Airborne LIDAR for Clear Air Turbulence Detection; RTCA Inc.: Washington, DC, USA, 2020; p. 108. [Google Scholar]
- Fezans, N.; Schwithal, J.; Fischenberg, D. In-Flight Remote Sensing and Identification of Gusts, Turbulence, and Wake Vortices Using a Doppler LIDAR. CEAS Aeronaut J. 2017, 8, 313–333. [Google Scholar] [CrossRef] [Green Version]
- Fezans, N.; Joos, H.-D.; Deiler, C. Gust Load Alleviation for a Long-Range Aircraft with and without Anticipation. CEAS Aeronaut J. 2019, 10, 1033–1057. [Google Scholar] [CrossRef] [Green Version]
- Fezans, N.; Joos, H.-D. Combined Feedback and LIDAR-Based Feedforward Active Load Alleviation. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics: Denver, CO, USA, 2017. [Google Scholar]
- Ehlers, J.; Fischenberg, D.; Niedermeier, D. Wake Identification Based Wake Impact Alleviation Control. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014; American Institute of Aeronautics and Astronautics: Atlanta, GA, USA, 2014. [Google Scholar]
- Kauffmann, P.-P. Market Assessment of Forward-Looking Turbulence Sensing Systems; DIANE Publishing: Collingdale, PA, USA, 2001. [Google Scholar]
- Vrancken, P.; Fezans, N.; Kiehn, D.; Kliebisch, O.; Linsmayer, P.; Thurn, J. Aeronautics Application of Direct-Detection Doppler Wind Lidar: Alleviation of Airframe Structural Loads Caused by Turbulence and Gusts. In Proceedings of the 3rd European Lidar Conference, Granada, Spain, 18 November 2021. [Google Scholar]
- Cavaliere, D.; Fezans, N.; Kiehn, D.; Quero, D.; Vrancken, P. Gust Load Control Design Challenge Including Lidar Wind Measurements and Based on the Common Research Model. In Proceedings of the 2022 AIAA Scitech Forum, San Diego, CA, USA, 3 January 2022. [Google Scholar]
- Kiehn, D.; Fezans, N.; Vrancken, P. Frequency-domain performance characterization of lidar-based gust detection systems for load alleviation. In Proceedings of the DLRK 2021, Online, 1 September 2021. [Google Scholar]
- Kiehn, D.; Fezans, N.; Vrancken, P.; Deiler, C. Parameter Analysis of a Doppler Lidar Sensor for Gust detection and Load Alleviation. In Proceedings of the IFASD 2022, Madrid, Spain, 17 June 2022. [Google Scholar]
- Khalil, A.; Fezans, N. A Multi-Channel H∞ Preview Control Approach to Load Alleviation Design for Flexible Aircraft. CEAS Aeronaut J. 2021, 12, 401–412. [Google Scholar] [CrossRef]
- Fezans, N.; Vrancken, P.; Linsmayer, P.; Wallace, C.; Deiler, C. Designing and Maturating Doppler Lidar Sensors for Gust Load Alleviation: Progress Made Since AWIATOR. In Proceedings of the AEC 2020, Bordeaux, France, 25 February 2020. [Google Scholar]
- Witschas, B.; Rahm, S.; Wagner, J.; Dörnbrack, A. Airborne Coherent Doppler Wind Lidar Measurements of Vertical and Horizontal Wind Speeds for the Investigation of Gravity Waves. In Proceedings of the 18th Coherent Laser Radar Conference, Boulder, CO, USA, 27 June–1 July 2016. [Google Scholar]
- Inokuchi, H.; Akiyama, T. Performance Evaluation of an Airborne Coherent Doppler Lidar and Investigation of Its Practical Application. Trans. Jpn. Soc. Aeronaut. Space Sci. 2022, 65, 47–55. [Google Scholar] [CrossRef]
- Schmitt, N.P.; Rehm, W.; Pistner, T.; Zeller, P.; Diehl, H.; Navé, P. The AWIATOR Airborne LIDAR Turbulence Sensor. Aerosp. Sci. Technol. 2007, 11, 546–552. [Google Scholar] [CrossRef]
- Rabadan, G.J.; Schmitt, N.P.; Pistner, T.; Rehm, W. Airborne Lidar for Automatic Feedforward Control of Turbulent In-Flight Phenomena. J. Aircr. 2010, 47, 392–403. [Google Scholar] [CrossRef]
- Rye, B.J.; Hardesty, R.M. Discrete Spectral Peak Estimation in Incoherent Backscatter Heterodyne Lidar. I. Spectral Accumulation and the Cramer-Rao Lower Bound. IEEE Trans. Geosci. Remote Sens. 1993, 31, 16–27. [Google Scholar] [CrossRef]
- Bruneau, D. Mach–Zehnder Interferometer as a Spectral Analyzer for Molecular Doppler Wind Lidar. Appl. Opt. 2001, 40, 391–399. [Google Scholar] [CrossRef]
- McKay, J.A. Modeling of Direct Detection Doppler Wind Lidar I The Edge Technique. Appl. Opt. 1998, 37, 6480–6486. [Google Scholar] [CrossRef]
- Cezard, N.; Dolfi-Bouteyre, A.; Huignard, J.-P.; Flamant, P. Development of a Short-Range 355-Nm Rayleigh-Mie Lidar Using a Michelson Interferometer for Wind Speed Measurements. In Proceedings of the Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing III, Florence, Italy, 17–20 September 2007; International Society for Optics and Photonics: Bellingham, WA, USA, 2007; Volume 6750, p. 675008. [Google Scholar]
- Herbst, J. Development and Test of a UV Lidar Receiver for the Measurement of Wind Velocities Aiming at the Near-Range Characterization of Wake Vortices and Gusts in Clear Air. Ph.D. Thesis, Ludwig-Maximilians-Universität, Munich, Germany, 2019. [Google Scholar]
- McGill, M.J.; Spinhirne, J.D. Comparison of Two Direct-Detection Doppler Lidar Techniques. Opt. Eng. 1998, 37, 2675–2687. [Google Scholar] [CrossRef]
- McKay, J.A. Assessment of a Multibeam Fizeau Wedge Interferometer for Doppler Wind Lidar. Appl. Opt. 2002, 41, 1760–1767. [Google Scholar] [CrossRef]
- Bruneau, D. Fringe-Imaging Mach-Zehnder Interferometer as a Spectral Analyzer for Molecular Doppler Wind Lidar. Appl. Opt. 2002, 41, 503–510. [Google Scholar] [CrossRef]
- Cezard, N. Etude de Faisabilité d’un Lidar Rayleigh-Mie Pour Des Mesures à Courte Portée de La Vitesse de l’air, de Sa Température et de Sa Densité. Ph.D. Thesis, Ecole Polytechnique, Palaiseau, France, 2008. [Google Scholar]
- Herbst, J.; Vrancken, P. Design of a Monolithic Michelson Interferometer for Fringe Imaging in a Near-Field, UV, Direct-Detection Doppler Wind Lidar. Appl. Opt. 2016, 55, 6910–6929. [Google Scholar] [CrossRef]
- Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C. (Ed.) Springer Series in Optical Sciences; Springer: New York, NY, USA, 2005; ISBN 978-0-387-40075-4. [Google Scholar]
- Endemann, M. ADM-Aeolus: The First Spaceborne Wind Lidar; Singh, U.N., Itabe, T., Rao, D.N., Eds.; SPIE Asia-Pacific Remote Sensing Symposium: Goa, India, 2006; p. 64090G. [Google Scholar]
- Vrancken, P.; Herbst, J. Development and Test of a Fringe-Imaging Direct-Detection Doppler Wind Lidar for Aeronautics. In Proceedings of the EPJ Web of Conferences, Hefei, China, 24–28 June 2019. [Google Scholar]
- Bruneau, D.; Pelon, J.; Blouzon, F.; Spatazza, J.; Genau, P.; Buchholtz, G.; Amarouche, N.; Abchiche, A.; Aouji, O. 355-Nm High Spectral Resolution Airborne Lidar LNG: System Description and First Results. Appl. Opt. 2015, 54, 8776–8785. [Google Scholar] [CrossRef]
- Tucker, S.C.; Weimer, C.; Adkins, M.; Delker, T.; Gleeson, D.; Kaptchen, P.; Good, B.; Kaplan, M.; Applegate, J.; Taudien, G. Optical Autocovariance Wind Lidar (OAWL): Aircraft Test-Flight History and Current Plans. In Lidar Remote Sensing for Environmental Monitoring XV; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9612, p. 96120E. [Google Scholar]
- Tucker, S.C.; Weimer, C. Benefits of a Quadrature Mach Zehnder Interferometer as Demonstrated in the Optical Autocovariance Wind and Lidar (OAWL) Wind and Aerosol Measurements. In Proceedings of the Remote Sensing of the Atmosphere, Clouds, and Precipitation VII, Honolulu, HI, USA, 24–26 September 2018; Im, E., Yang, S., Eds.; SPIE: Honolulu, HI, USA, 2018; p. 13. [Google Scholar]
- Grund, C.J.; Eloranta, E.W. Fiber-Optic Scrambler Reduces the Bandpass Range Dependence of Fabry–Perot Étalons Used for Spectral Analysis of Lidar Backscatter. Appl. Opt. 1991, 30, 2668–2670. [Google Scholar] [CrossRef]
- Avila, G.; Singh, P.; Chazelas, B. Results on Fibre Scrambling for High Accuracy Radial Velocity Measurements; SPIE: San Diego, CA, USA, 2010; p. 773588. [Google Scholar]
- Wirth, M.; Fix, A.; Mahnke, P.; Schwarzer, H.; Schrandt, F.; Ehret, G. The Airborne Multi-Wavelength Water Vapor Differential Absorption Lidar WALES: System Design and Performance. Appl. Phys. B 2009, 96, 201–213. [Google Scholar] [CrossRef] [Green Version]
- Wirth, M. MERLIN Algorithm Theoretical Basis Document: Top Level Algorithms for Primary L1/2 Products; DLR/CNES Methane Remote Sensing Lidar Mission (MERLIN) Documentation Base: Cologne, Germany, 2017. [Google Scholar]
- Gagné, J.-M.; Saint-Dizier, J.-P.; Picard, M. Méthode d’echantillonnage Des Fonctions Déterministes En Spectroscopie: Application à Un Spectromètre Multicanal Par Comptage Photonique. Appl. Opt. 1974, 13, 581–588. [Google Scholar] [CrossRef]
- Paffrath, U. Performance Assessment of the Aeolus Doppler Wind Lidar Prototype. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2006. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Leosphere WINDCUBE© 100S, 200S, 400S Hardware System v1.3.5 User Guide—Version 6; Vaisala/Leosphere: Paris, France, 2016.
- Cariou, J.P.; Thobois, L.; Parmentier, R.; Boquet, M.; Loaec, S. Assessing the Metrological Capabilities of Wind Doppler Lidars. In Proceedings of the CLRC, Barcelona, Spain, 17–20 June 2013. [Google Scholar]
- Fezans, N.; Wallace, C.; Kiehn, D.; Cavaliere, D.; Vrancken, P. Lidar-Based Gust Load Alleviation—Results Obtained on the Clean Sky 2 Load Alleviation Benchmark. In Proceedings of the IFASD 2022, Madrid, Spain, 17 June 2022. [Google Scholar]




| Technique (Interferometer) | Abbreviation | Literature | |
|---|---|---|---|
| Dual-channel Fabry–Pérot | DFP | 2.4 | [36] |
| Fringe-imaging Fabry–Pérot | FIFPI | 3.1 | [39] |
| Fringe-imaging Fizeau | FIFI | 2–4 | [40] |
| Dual-channel Mach–Zehnder | DMZ | 1.65 | [35] |
| Four-channel Mach–Zehnder | QMZ | 2.3 | [35] |
| Fringe-imaging Mach–Zehnder | FIMZ | 2.3 | [41] |
| Dual fringe-imaging Michelson | FIMI | 4.4 | [42] |
| Oblique-incidence (dual-channel) Fringe-imaging Michelson | FW-FIMI | 2.3 | [43] |
| Perpendicular-incidence (single-channel) Fringe-imaging Michelson | 4.4 |
| Variable | AEROLI Demonstrator | Optimized Hypothesis |
|---|---|---|
| 4.4 | 2.3 | |
| 1.7 | 1.3 | |
| 0.9% | 22% | |
| 100 mWm2 | 50 mWm2 |
| Parameter | Variable |
|---|---|
| 0.5 s to 10 s | |
| , physical and processed | 25 m, 50 m, 75 m, 100 m |
| <0.5 m/s | |
| ≥50 | |
| ≤5 mW | |
| 1543 nm | |
| 400 ns, 200 ns or 100 ns | |
| , | 10 kHz, 20 kHz, 40 kHz * |
| Series (Start Time UTC) | at 50 m | at 76 m | Laser Setting | Windcube® CNR Observation |
|---|---|---|---|---|
| 13:16 | 0.83 m/s | 0.93 m/s | locked | medium |
| 16:29 | 1.14 m/s | 1.13 m/s | locked | low |
| 16:48 | 1.29 m/s | 1.35 m/s | locked | low (>−34 dB) |
| 18:25 | 0.77 m/s | 0.73 m/s | free running | good (>−28 dB) |
| 19:19 | 0.68 m/s | 0.64 m/s | locked | good |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrancken, P.; Herbst, J. Aeronautics Application of Direct-Detection Doppler Wind Lidar: An Adapted Design Based on a Fringe-Imaging Michelson Interferometer as Spectral Analyzer. Remote Sens. 2022, 14, 3356. https://doi.org/10.3390/rs14143356
Vrancken P, Herbst J. Aeronautics Application of Direct-Detection Doppler Wind Lidar: An Adapted Design Based on a Fringe-Imaging Michelson Interferometer as Spectral Analyzer. Remote Sensing. 2022; 14(14):3356. https://doi.org/10.3390/rs14143356
Chicago/Turabian StyleVrancken, Patrick, and Jonas Herbst. 2022. "Aeronautics Application of Direct-Detection Doppler Wind Lidar: An Adapted Design Based on a Fringe-Imaging Michelson Interferometer as Spectral Analyzer" Remote Sensing 14, no. 14: 3356. https://doi.org/10.3390/rs14143356
APA StyleVrancken, P., & Herbst, J. (2022). Aeronautics Application of Direct-Detection Doppler Wind Lidar: An Adapted Design Based on a Fringe-Imaging Michelson Interferometer as Spectral Analyzer. Remote Sensing, 14(14), 3356. https://doi.org/10.3390/rs14143356






