Comprehensive Analysis and Validation of the Atmospheric Weighted Mean Temperature Models in China
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Description
2.2. Data Pre-Processing
2.3. Tm Derived from RS Data
2.4. Tm Derived from Empirical Models
- Linear model
- 2.
- GPT3 model
- 3.
- CTm model
- 4.
- GTm-H model
- 5.
- GTrop model
2.5. Statistical Metrics for Tm Model Evaluation
3. Accuracy Analysis of Tm Models
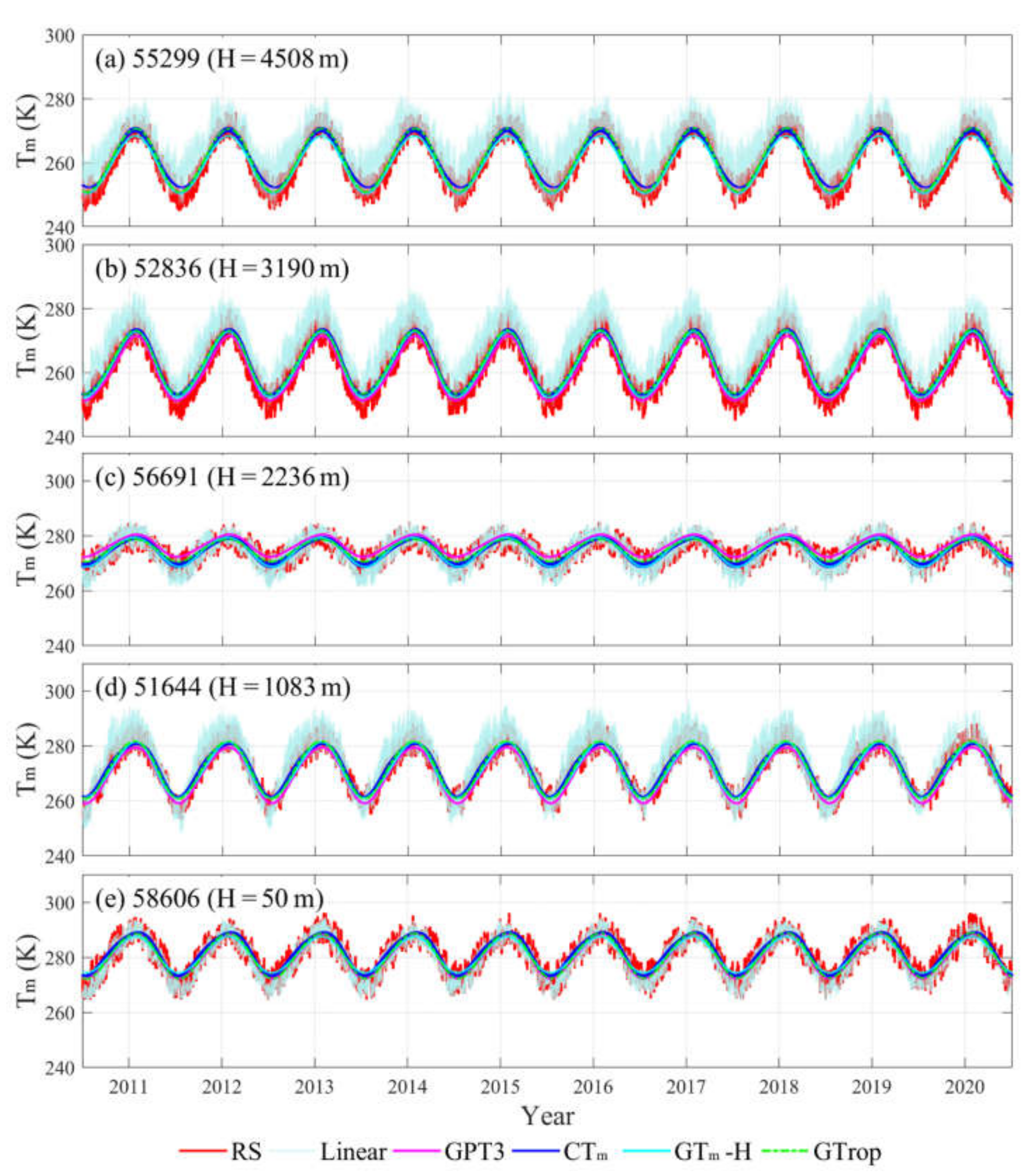
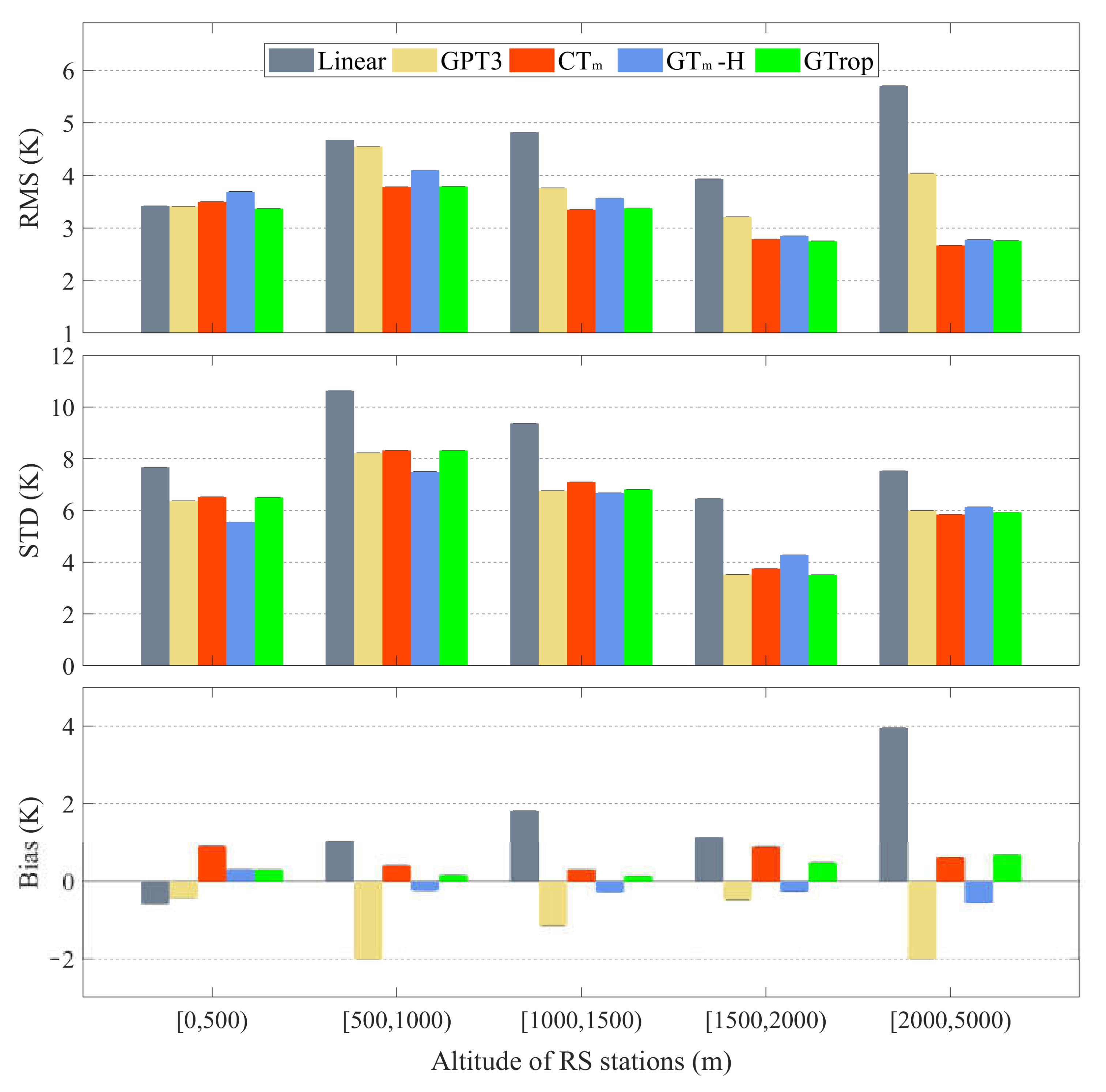
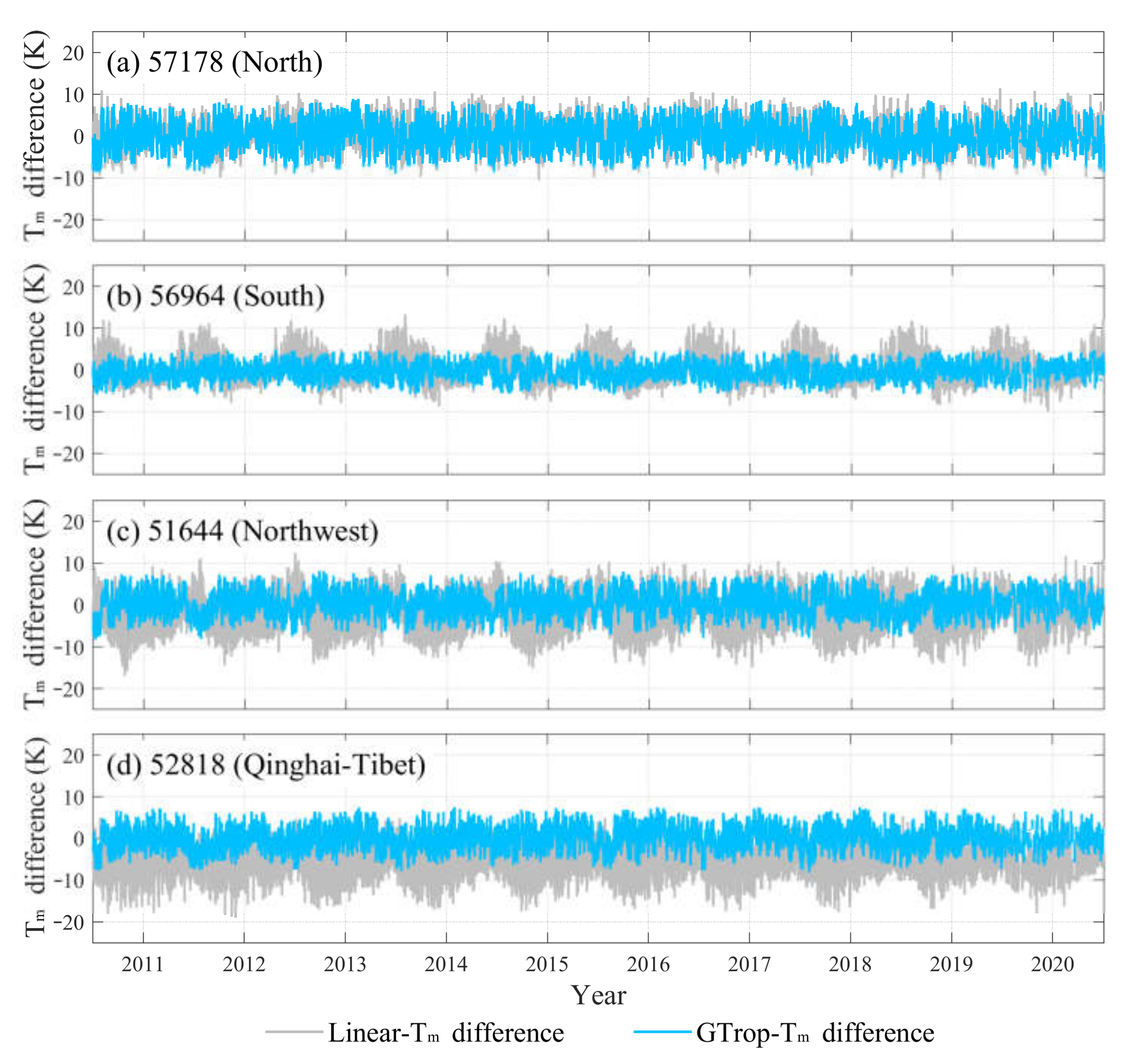
3.1. Accuracy Analysis at Different Altitudes
3.2. Accuracy Analysis at Different Latitudes
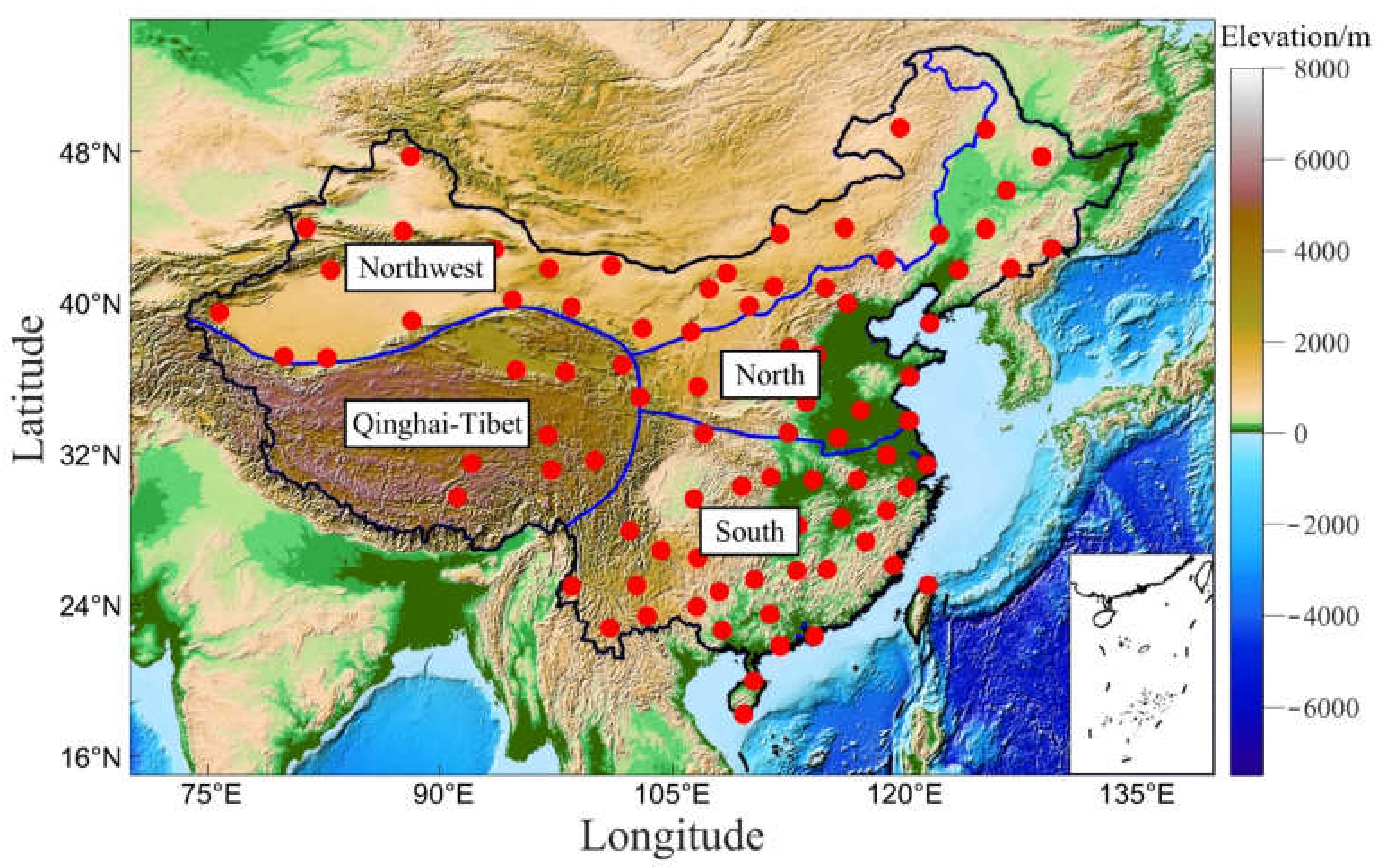
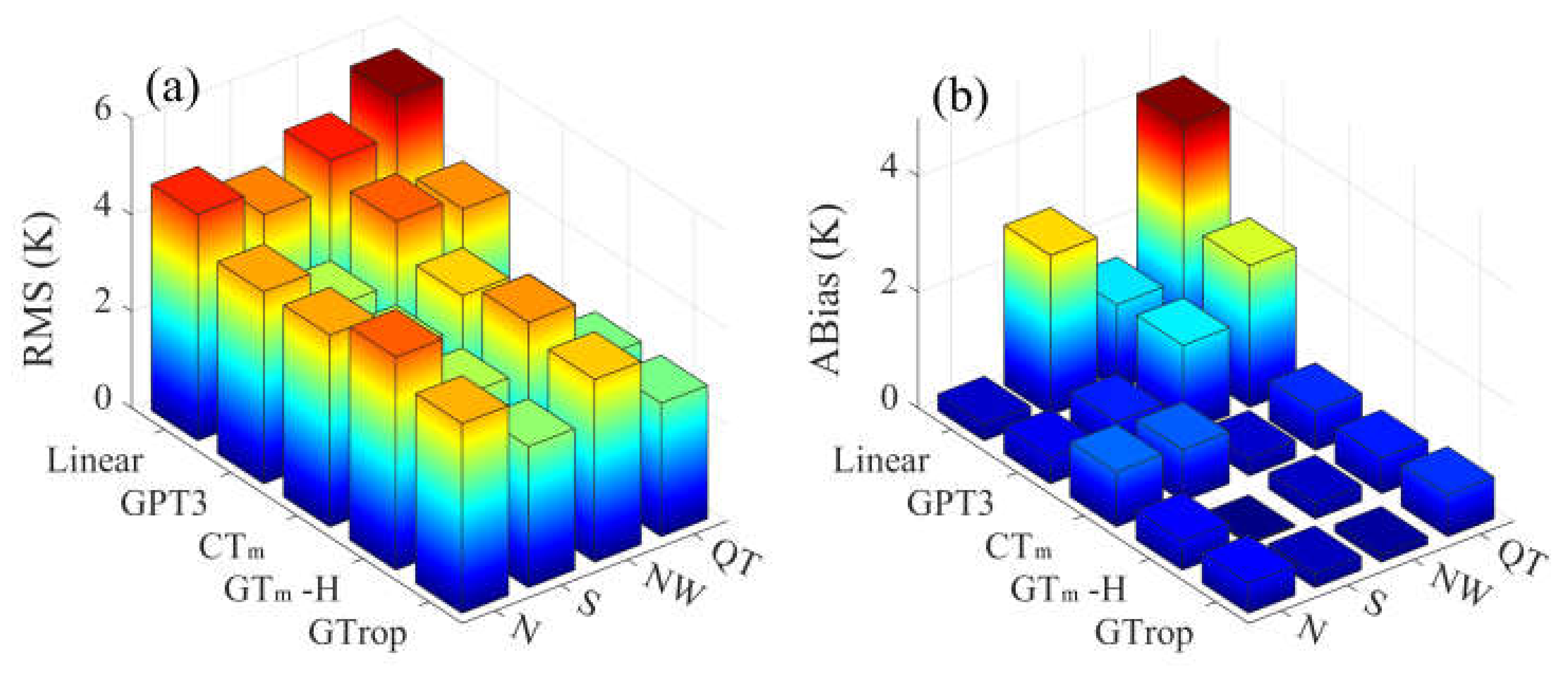
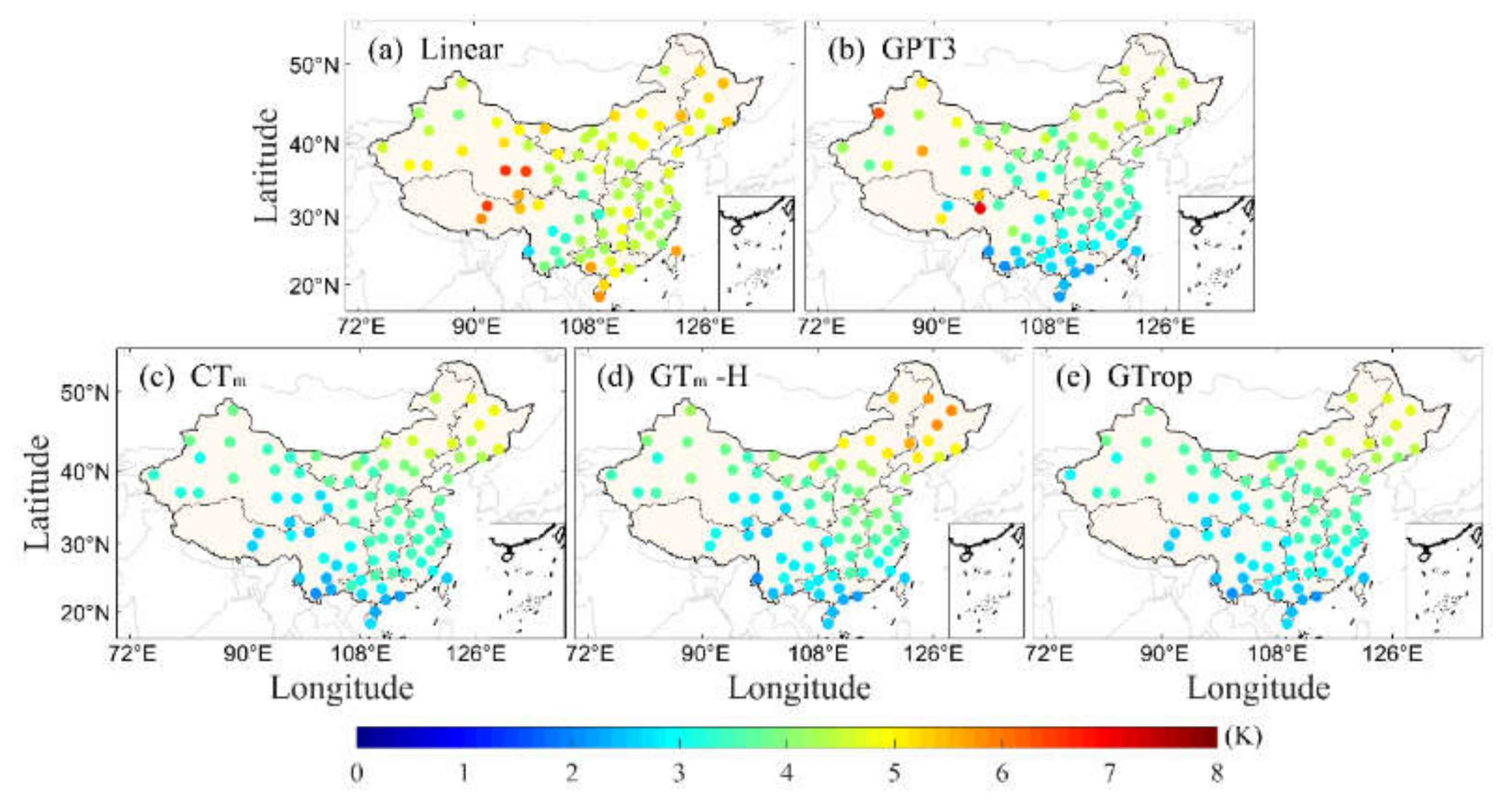
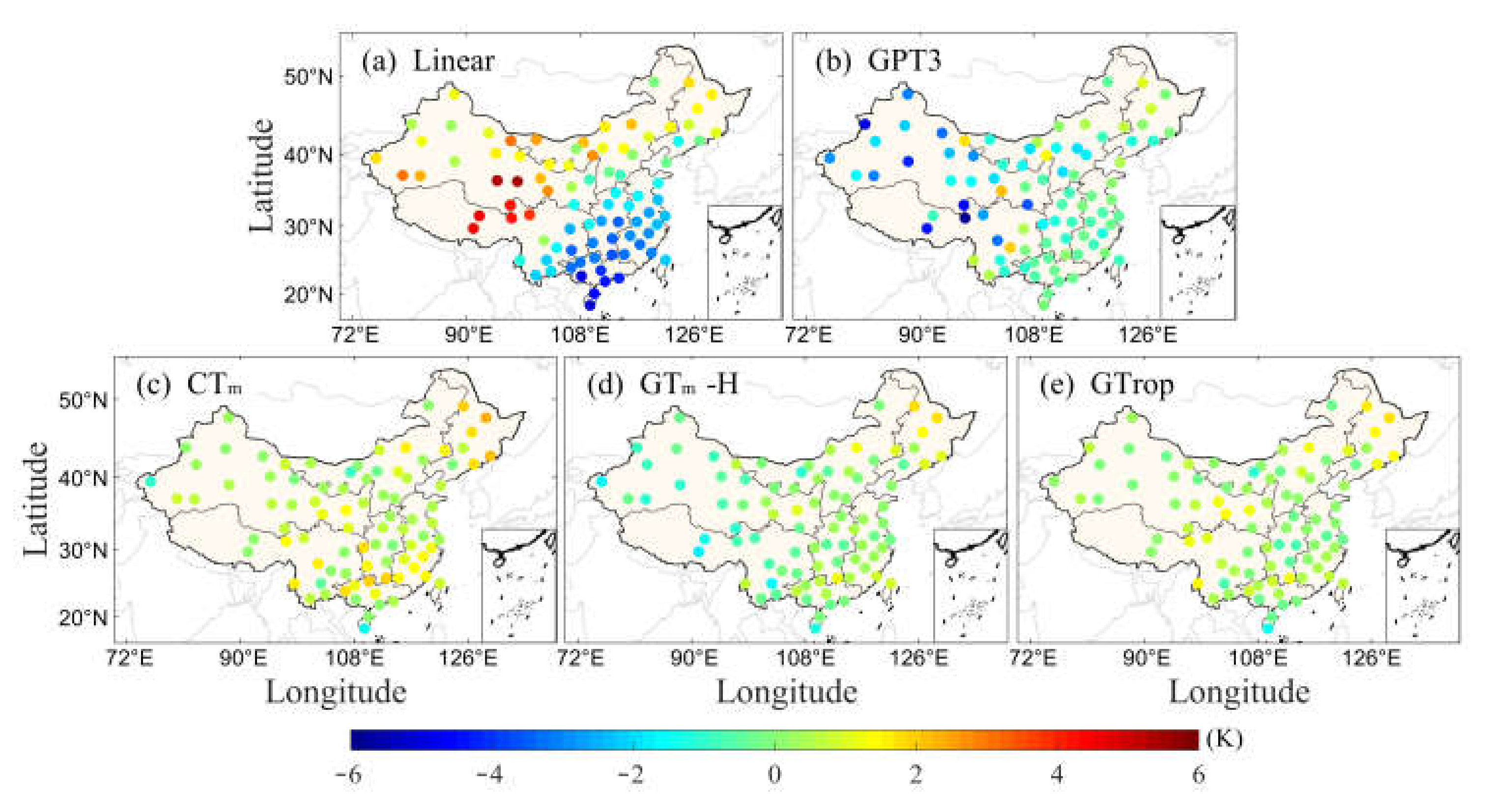
3.3. Accuracy Analysis at Different Geographical Regions in China
3.4. Overall Evaluation of Tm Models in China
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Q.; Liu, Y.; Yao, W.; Yao, Y. Hourly rainfall forecast model using supervised learning algorithm. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4100509. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Ma, X.; Yao, W.; Yao, Y.; Li, L. An improved rainfall forecasting model based on GNSS observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4891–4900. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Chen, H.; Jiang, W. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China. GPS Solut. 2019, 23, 51. [Google Scholar] [CrossRef]
- Yao, Y.; Sun, Z.; Xu, C. Applicability of Bevis Formula at Different Height Levels and Global Weighted Mean Temperature Model Based on Near-earth Atmospheric Temperature. J. Geod. Geoinf. Sci. 2020, 3, 1–11. [Google Scholar]
- Lee, S.-W.; Choi, B.I.; Woo, S.-B.; Kim, J.C.; Kim, Y.-G. Calibration of a radiosonde humidity sensor at low temperature and low pressure. Metrologia 2019, 56, 055008. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Zhao, Q.; Du, Z.; Li, Z.; Yao, W.; Yao, Y. Two-Step Precipitable Water Vapor Fusion Method. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5801510. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, C.; Zhang, B.; Cao, N. GTm-III: A new global empirical model for mapping zenith wet delays onto precipitable water vapour. Geophys. J. Int. 2014, 197, 202–212. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Jiang, W.; Liu, L.; Chen, H.; Ye, S. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor. J. Geod. 2019, 93, 159–176. [Google Scholar] [CrossRef]
- Ding, M.; Hu, W. A further contribution to the seasonal variation of weighted mean temperature. Adv. Space Res. 2017, 60, 2414–2422. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Ding, M. A neural network model for predicting weighted mean temperature. J. Geod. 2018, 92, 1187–1198. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Meng, X.; Shi, J.; Zhang, D.; Zhao, Y. An improved weighted mean temperature (Tm) model based on GPT2w with Tm lapse rate. GPS Solut. 2020, 24, 46. [Google Scholar] [CrossRef]
- Gao, W.; Gao, J.; Yang, L.; Wang, M.; Yao, W. A novel modeling strategy of weighted mean temperature in China using RNN and LSTM. Remote Sens. 2021, 13, 3004. [Google Scholar] [CrossRef]
- Böhm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [Green Version]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.B.; Zhang, B.; Yue, S.Q.; Xu, C.Q.; Peng, E.F. Global empirical model for mapping zenith wet delays onto precipitable water. J. Geod. 2013, 87, 439–448. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B.; Xu, C.; Yan, F. Improved one/multi-parameter models that consider seasonal and geographic variations for estimating weighted mean temperature in ground-based GPS meteorology. J. Geod. 2014, 88, 273–282. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. A global model for estimating tropospheric delay and weighted mean temperature developed with atmospheric reanalysis data from 1979 to 2017. Remote Sens. 2019, 11, 1893. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Peng, H.; Liu, L.; Li, C.; Kang, C.; Xie, S. An empirical atmospheric weighted mean temperature model considering the lapse rate function for China. Acta Geod. Cartogr. Sin. 2020, 49, 432–442. [Google Scholar]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Nistor, S.; Suba, N.S.; Buda, A.S. The impact of tropospheric mapping function on PPP determination for one-month period. Acta Geodyn. Geomater. 2020, 17, 237–252. [Google Scholar] [CrossRef]
- Mao, J.; Han, J.; Cui, T. Development and Assessment of Improved Global Pressure and Temperature Series Models. IEEE Access 2021, 9, 104429–104447. [Google Scholar] [CrossRef]
- Li, T.; Wang, L.; Chen, R.; Fu, E.; Xu, W.; Jiang, P.; Liu, J.; Zhou, H.; Han, Y. Refining the empirical global pressure and temperature model with the ERA5 reanalysis and radiosonde data. J. Geod. 2021, 95, 31. [Google Scholar] [CrossRef]
- Yao, Y.; Sun, Z.; Xu, C.; Xu, X. Global Weighted Mean Temperature Model Considering Nonlinear Vertical Reduction. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 106–111. [Google Scholar]
- Zhu, M.; Hu, W.; Sun, W. Advanced grid model of weighted mean temperature based on feedforward neural network over China. Earth Space Sci. 2021, 8, e2020EA001458. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, G.; Liu, L.; Chen, H.; Jiang, W. A global grid model for the correction of the vertical zenith total delay based on a sliding window algorithm. GPS Solut. 2021, 25, 98. [Google Scholar] [CrossRef]
- Mo, Z.X.; Huang, L.K.; Peng, H.; Liu, L.L.; Kang, C.L. Atmospheric Weighted Mean Temperature Model in Guilin. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 42, 1155–1160. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Mo, Z.; Liu, L.; Xie, S. An empirical model for the vertical correction of precipitable water vapor considering the time-varying lapse rate for Mainland China. Acta Geod. Cartogr. Sin. 2021, 50, 1320–1330. [Google Scholar]
- Gao, Z.; He, X.; Chang, L. Accuracy Analysis of GPT3 Model in China. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 538–545. [Google Scholar]
- Zhu, H.; Chen, K.; Huang, G. A Weighted Mean Temperature Model with Nonlinear Elevation Correction Using China as an Example. Remote Sens. 2021, 13, 3887. [Google Scholar] [CrossRef]
- Long, F.; Gao, C.; Yan, Y.; Wang, J. Enhanced neural network model for worldwide estimation of weighted mean temperature. Remote Sens. 2021, 13, 2405. [Google Scholar] [CrossRef]
- Durre, I.; Yin, X.; Vose, R.S.; Applequist, S.; Arnfield, J. Enhancing the data coverage in the integrated global radiosonde archive. J. Atmos. Ocean. Technol. 2018, 35, 1753–1770. [Google Scholar] [CrossRef]
- Makama, E.K.; Lim, H.S. Variability and Trend in Integrated Water Vapour from ERA-Interim and IGRA2 Observations over Peninsular Malaysia. Atmosphere 2020, 11, 1012. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, P.; Yao, W.; Yao, W. Adaptive AOD Forecast Model Based on GNSS-Derived PWV and Meteorological Parameters. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5800610. [Google Scholar] [CrossRef]
- Martin, A.; Weissmann, M.; Reitebuch, O.; Rennie, R.; Geiß, A.; Cress, A. Validation of Aeolus winds using radiosonde observations and numerical weather prediction model equivalents. Atmos. Meas. Tech. 2021, 14, 2167–2183. [Google Scholar] [CrossRef]
- Zhao, Q.; Su, J.; Li, Z.; Yang, P.; Yao, Y. Adaptive aerosol optical depth forecasting model using GNSS observation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4105009. [Google Scholar] [CrossRef]
- Van Zoest, V.M.; Stein, A.; Hoek, G. Outlier detection in urban air quality sensor networks. Water Air Soil Pollut. 2018, 229, 111. [Google Scholar] [CrossRef] [Green Version]
- Bărbulescu, A.; Dumitriu, C.S.; Ilie, I.; Barbeş, S.-B. Influence of Anomalies on the Models for Nitrogen Oxides and Ozone Series. Atmosphere 2022, 13, 558. [Google Scholar]
- Li, L.; Li, Y.; He, Q.; Wang, X. Weighted Mean Temperature Modelling Using Regional Radiosonde Observations for the Yangtze River Delta Region in China. Remote Sens. 2022, 14, 1909. [Google Scholar] [CrossRef]
- Czernecki, B.; Głogowski, A.; Nowosad, J. Climate: An R package to access free in-situ meteorological and hydrological datasets for environmental assessment. Sustainability 2020, 12, 394. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Zhang, B.; Yao, Y. An ERA5-based model for estimating tropospheric delay and weighted mean temperature over China with improved spatiotemporal resolutions. Earth Space Sci. 2019, 6, 1926–1941. [Google Scholar] [CrossRef]
- Choi, B.I.; Lee, S.W.; Woo, S.B.; Kim, J.C.; Kim, Y.-G.; Yang, S.G. Evaluation of radiosonde humidity sensors at low temperature using ultralow-temperature humidity chamber. Adv. Sci. Res. 2018, 15, 207–212. [Google Scholar] [CrossRef]
- Ding, J.; Chen, J. Assessment of empirical troposphere model GPT3 based on NGL’s global troposphere products. Sensors 2020, 20, 3631. [Google Scholar] [CrossRef]
- Li, J.; Zhang, B.; Yao, Y.; Liu, L.; Sun, Z.; Yan, X. A refined regional model for estimating pressure, temperature and water vapor pressure for geodetic applications in China. Remote Sens. 2020, 12, 1713. [Google Scholar] [CrossRef]
- Ding, M. A second generation of the neural network model for predicting weighted mean temperature. GPS Solut. 2020, 24, 61. [Google Scholar] [CrossRef]
- Yu, H.; Miao, S.; Xie, G.; Guo, X.; Chen, Z.; Favre, A. Contrasting floristic diversity of the Hengduan Mountains, the Himalayas and the Qinghai-Tibet Plateau sensu stricto in China. Front. Ecol. Evol. 2020, 8, 136. [Google Scholar] [CrossRef]




| Models | Input Parameters | Applicable Area | Data | Period |
|---|---|---|---|---|
| Linear | Ts | China | RS | 2011–2020 |
| GPT3 | lat., lon., altitude, time | Global | ECMWF, VLBI | 1999–2014 |
| CTm | lat., lon., altitude, time | China | GGOS | 2007–2014 |
| GTm-H | lat., lon., altitude, time | Global | ECMWF | 2013–2015 |
| GTrop | lat., lon., altitude, time | Global | ECMWF | 1979–2017 |
| Model | RMS (K) | Bias (K) | ||||
|---|---|---|---|---|---|---|
| Max. | Min. | Aver. | Max. | Min. | Aver. | |
| Linear | 7.1 | 2.1 | 4.2 | 5.9 | −2.8 | 0.7 |
| GPT3 | 7.1 | 2.1 | 3.7 | 2.1 | −6.7 | −1.0 |
| CTm | 4.9 | 2.1 | 3.4 | 2.3 | −1.4 | 0.7 |
| GTm-H | 5.8 | 2.0 | 3.6 | 1.9 | −1.8 | −0.1 |
| GTrop | 4.7 | 2.1 | 3.3 | 1.7 | −1.4 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Zhao, Q.; Wu, K.; Yao, W.; Liu, Y.; Li, Z.; Shi, Y. Comprehensive Analysis and Validation of the Atmospheric Weighted Mean Temperature Models in China. Remote Sens. 2022, 14, 3435. https://doi.org/10.3390/rs14143435
Ma Y, Zhao Q, Wu K, Yao W, Liu Y, Li Z, Shi Y. Comprehensive Analysis and Validation of the Atmospheric Weighted Mean Temperature Models in China. Remote Sensing. 2022; 14(14):3435. https://doi.org/10.3390/rs14143435
Chicago/Turabian StyleMa, Yongjie, Qingzhi Zhao, Kan Wu, Wanqiang Yao, Yang Liu, Zufeng Li, and Yun Shi. 2022. "Comprehensive Analysis and Validation of the Atmospheric Weighted Mean Temperature Models in China" Remote Sensing 14, no. 14: 3435. https://doi.org/10.3390/rs14143435