Assessment of Suitable Gridded Climate Datasets for Large-Scale Hydrological Modelling over South Korea
Abstract
:1. Introduction
2. Materials and Methods
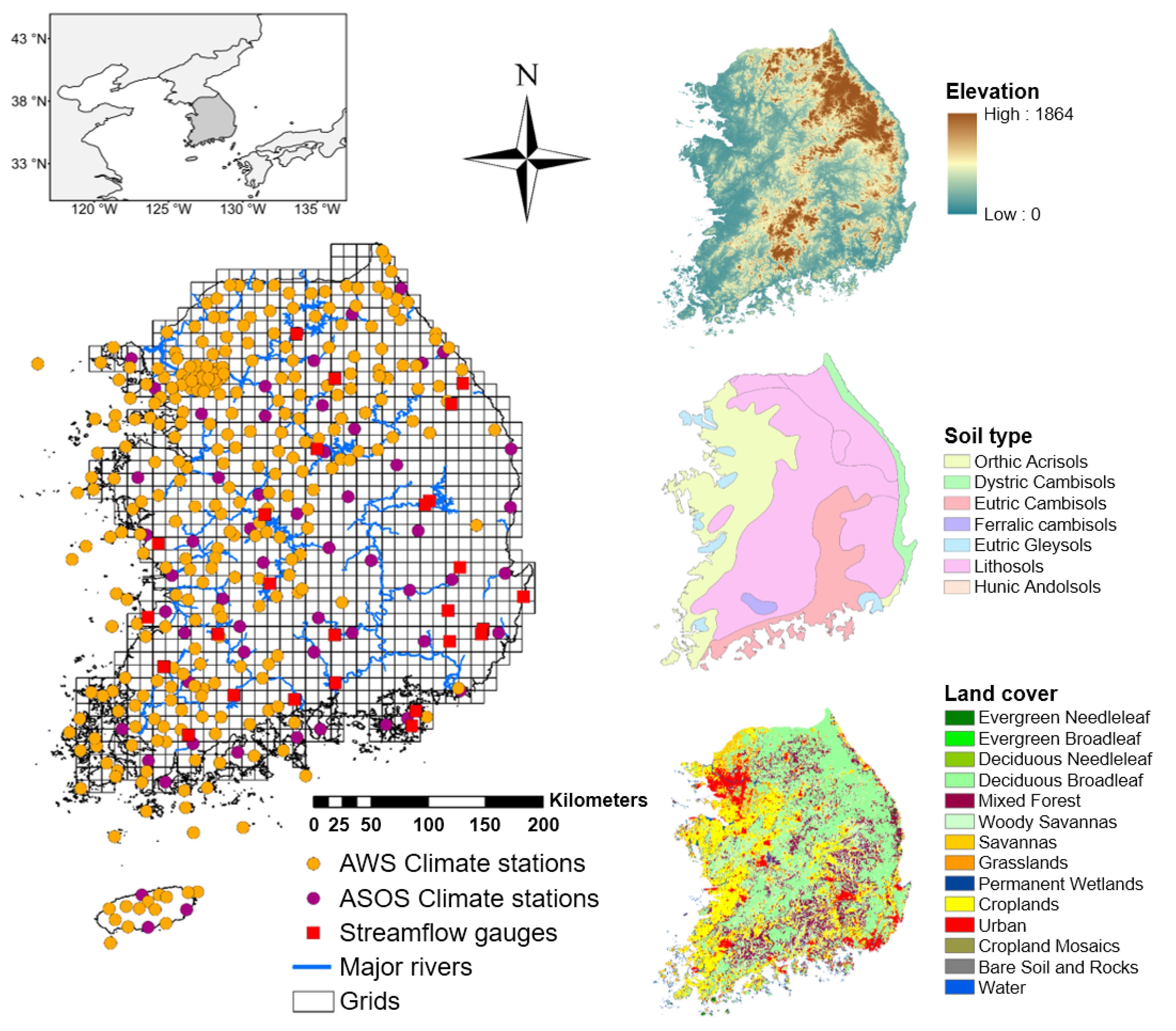
2.1. Meteorological Grid-Based Datasets
2.2. Observed Hydrometeorological Datasets
3. Methodology
3.1. Evaluation of Gridded Climate Datasets
3.2. Evaluation Using Hydrological Modeling
3.2.1. Hydrological Model Setup
3.2.2. Evaluation in Hydrological Modeling
4. Results
4.1. Evaluation of Gridded Climate Datasets
4.2. Evaluation of Hydrological Modeling
4.3. Evaluation of Hydrological Performance by Combining Multiple Datasets
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dembélé, M.; Schaefli, B.; Van De Giesen, N.; Mariéthoz, G. Suitability of 17 Gridded Rainfall and Temperature Datasets for Large-Scale Hydrological Modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Zandler, H.; Haag, I.; Samimi, C. Evaluation Needs and Temporal Performance Differences of Gridded Precipitation Products in Peripheral Mountain Regions. Sci. Rep. 2019, 9, 15118. [Google Scholar] [CrossRef] [Green Version]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Urita, S.; Saito, H.; Matsuyama, H. Temporal and Spatial Discontinuity of Radar/Raingauge-Analyzed Precipitation That Appeared in Relation to the Modification of Its Spatial Resolution. Hydrol. Res. Lett. 2011, 5, 37–41. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Xiong, A. Validation and Comparison of a New Gauge-Based Precipitation Analysis over Mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Sarachi, S.; Hsu, K.; Sorooshian, S. A Statistical Model for the Uncertainty Analysis of Satellite Precipitation Products. J. Hydrometeorol. 2015, 16, 2101–2117. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Bosilovich, M.G.; Chen, J.; Robertson, F.R.; Adler, R.F. Evaluation of Global Precipitation in Reanalyses. J. Appl. Meteorol. Climatol. 2008, 47, 2279–2299. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.; Lai, R.; Zhu, Z. Performance of Satellite-Based and Reanalysis Precipitation Products under Multi-Temporal Scales and Extreme Weather in Mainland China. J. Hydrol. 2021, 605, 127389. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global Precipitation Measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D. A Preliminary Assessment of GPM-Based Multi-Satellite Precipitation Estimates over a Monsoon Dominated Region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite-Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef] [Green Version]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Turk, F.J.; Mostovoy, G.V.; Anantharaj, V.G. Soil Moisture Sensitivity to NRL-Blend High-Resolution Precipitation Products: Analysis of Simulations with Two Land Surface Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 3, 32–48. [Google Scholar] [CrossRef]
- Alazzy, A.A.; Lü, H.; Chen, R.; Ali, A.B.; Zhu, Y.; Su, J. Evaluation of Satellite Precipitation Products and Their Potential Influence on Hydrological Modeling over the Ganzi River Basin of the Tibetan Plateau. Adv. Meteorol. 2017, 2017, 3695285. [Google Scholar] [CrossRef] [Green Version]
- Berg, P.; Donnelly, C.; Gustafsson, D. Near-Real-Time Adjusted Reanalysis Forcing Data for Hydrology. Hydrol. Earth Syst. Sci. 2018, 22, 989–1000. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.-G.; Ahn, K.-H. A Stacking Ensemble Model for Hydrological Post-Processing to Improve Streamflow Forecasts at Medium-Range Timescales over South Korea. J. Hydrol. 2021, 600, 126681. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.; Huffman, G.J.; Li, H.; Wang, J. Real-Time Global Flood Estimation Using Satellite-Based Precipitation and a Coupled Land Surface and Routing Model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef] [Green Version]
- Buarque, D.C.; de Paiva, R.C.D.; Clarke, R.T.; Mendes, C.A.B. A Comparison of Amazon Rainfall Characteristics Derived from TRMM, CMORPH and the Brazilian National Rain Gauge Network. J. Geophys. Res. Atmos. 2011, 116, D19105. [Google Scholar] [CrossRef]
- He, Z.; Yang, L.; Tian, F.; Ni, G.; Hou, A.; Lu, H. Intercomparisons of Rainfall Estimates from TRMM and GPM Multisatellite Products over the Upper Mekong River Basin. J. Hydrometeorol. 2017, 18, 413–430. [Google Scholar] [CrossRef]
- Le Coz, C.; van de Giesen, N. Comparison of Rainfall Products over Sub-Saharan Africa. J. Hydrometeorol. 2020, 21, 553–596. [Google Scholar] [CrossRef]
- Caroletti, G.N.; Coscarelli, R.; Caloiero, T. Validation of Satellite, Reanalysis and Rcm Data of Monthly Rainfall in Calabria (Southern Italy). Remote Sens. 2019, 11, 1625. [Google Scholar] [CrossRef] [Green Version]
- Gupta, V.; Jain, M.K.; Singh, P.K.; Singh, V. An Assessment of Global Satellite-Based Precipitation Datasets in Capturing Precipitation Extremes: A Comparison with Observed Precipitation Dataset in India. Int. J. Climatol. 2020, 40, 3667–3688. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground Validation of GPM IMERG and TRMM 3B42V7 Rainfall Products over Southern Tibetan Plateau Based on a High-Density Rain Gauge Network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H. Evaluation and Comparison of Newest GPM and TRMM Products over Mekong River Basin at Daily Scale. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 613–616. [Google Scholar]
- Nanding, N.; Wu, H.; Tao, J.; Maggioni, V.; Beck, H.E.; Zhou, N.; Huang, M.; Huang, Z. Assessment of Precipitation Error Propagation in Discharge Simulations over the Contiguous United States. J. Hydrometeorol. 2021, 22, 1987–2008. [Google Scholar] [CrossRef]
- Nkiaka, E.; Nawaz, N.; Lovett, J.C. Evaluating Global Reanalysis Datasets as Input for Hydrological Modelling in the Sudano-Sahel Region. Hydrology 2017, 4, 13. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Hu, H.; Tian, F.; Ni, G.; Hu, Q. Correcting the TRMM Rainfall Product for Hydrological Modelling in Sparsely-Gauged Mountainous Basins. Hydrol. Sci. J. 2017, 62, 306–318. [Google Scholar] [CrossRef]
- Camici, S.; Ciabatta, L.; Massari, C.; Brocca, L. How Reliable Are Satellite Precipitation Estimates for Driving Hydrological Models: A Verification Study over the Mediterranean Area. J. Hydrol. 2018, 563, 950–961. [Google Scholar] [CrossRef]
- Poméon, T.; Jackisch, D.; Diekkrüger, B. Evaluating the Performance of Remotely Sensed and Reanalysed Precipitation Data over West Africa Using HBV Light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- Wang, N.; Liu, W.; Sun, F.; Yao, Z.; Wang, H.; Liu, W. Evaluating Satellite-Based and Reanalysis Precipitation Datasets with Gauge-Observed Data and Hydrological Modeling in the Xihe River Basin, China. Atmos. Res. 2020, 234, 104746. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Clark, M.P. HESS Opinions: The Complementary Merits of Competing Modelling Philosophies in Hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3953–3973. [Google Scholar] [CrossRef] [Green Version]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and Spatial Evaluation of Satellite-Based Rainfall Estimates across the Complex Topographical and Climatic Gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef] [Green Version]
- Maggioni, V.; Massari, C. On the Performance of Satellite Precipitation Products in Riverine Flood Modeling: A Review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Laiti, L.; Mallucci, S.; Piccolroaz, S.; Bellin, A.; Zardi, D.; Fiori, A.; Nikulin, G.; Majone, B. Testing the Hydrological Coherence of High-Resolution Gridded Precipitation and Temperature Data Sets. Water Resour. Res. 2018, 54, 1999–2016. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, T.; Khare, D.; Arora, M. A Case Study for the Assessment of the Suitability of Gridded Reanalysis Weather Data for Hydrological Simulation in Beas River Basin of North Western Himalaya. Appl. Water Sci. 2019, 9, 110. [Google Scholar] [CrossRef] [Green Version]
- Blacutt, L.A.; Herdies, D.L.; de Gonçalves, L.G.G.; Vila, D.A.; Andrade, M. Precipitation Comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme Datasets in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 Reanalysis Precipitation Dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 Reanalysis as a Potential Reference Dataset for Hydrological Modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Kim, J.P.; Jung, I.W.; Park, K.W.; Yoon, S.K.; Lee, D. Hydrological Utility and Uncertainty of Multi-Satellite Precipitation Products in the Mountainous Region of South Korea. Remote Sens. 2016, 8, 608. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Zhang, C.; Fu, G.; Sweetapple, C.; Zhou, H. Evaluation of Global Fine-Resolution Precipitation Products and Their Uncertainty Quantification in Ensemble Discharge Simulations. Hydrol. Earth Syst. Sci. 2016, 20, 903–920. [Google Scholar] [CrossRef] [Green Version]
- Shawul, A.A.; Chakma, S. Suitability of Global Precipitation Estimates for Hydrologic Prediction in the Main Watersheds of Upper Awash Basin. Environ. Earth Sci. 2020, 79, 53. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, J.; Gao, C.; Ruben, G.B.; Wang, G. Assessing the Uncertainties of Four Precipitation Products for Swat Modeling in Mekong River Basin. Remote Sens. 2019, 11, 304. [Google Scholar] [CrossRef] [Green Version]
- Tramblay, Y.; Thiemig, V.; Dezetter, A.; Hanich, L. Evaluation of Satellite-Based Rainfall Products for Hydrological Modelling in Morocco. Hydrol. Sci. J. 2016, 61, 2509–2519. [Google Scholar] [CrossRef] [Green Version]
- Stisen, S.; Højberg, A.; Troldborg, L.; Refsgaard, J.; Christensen, B.; Olsen, M.; Henriksen, H. On the Importance of Appropriate Precipitation Gauge Catch Correction for Hydrological Modelling at Mid to High Latitudes. Hydrol. Earth Syst. Sci. 2012, 16, 4157–4176. [Google Scholar] [CrossRef] [Green Version]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef] [Green Version]
- Schreiner-McGraw, A.P.; Ajami, H. Impact of Uncertainty in Precipitation Forcing Data Sets on the Hydrologic Budget of an Integrated Hydrologic Model in Mountainous Terrain. Water Resour. Res. 2020, 56, e2020WR027639. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, X.; Xu, Y.-P.; Tian, Y. Merging Multi-Source Precipitation Products or Merging Their Simulated Hydrological Flows to Improve Streamflow Simulation. Hydrol. Sci. J. 2019, 64, 910–920. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Kim, Y.-O. Incorporating Climate Model Similarities and Hydrologic Error Models to Quantify Climate Change Impacts on Future Riverine Flood Risk. J. Hydrol. 2019, 570, 118–131. [Google Scholar] [CrossRef]
- Alcantara, A.L.; Ahn, K.-H. Probability Distribution and Characterization of Daily Precipitation Related to Tropical Cyclones over the Korean Peninsula. Water 2020, 12, 1214. [Google Scholar] [CrossRef]
- Tsai, C.-L.; Kim, K.; Liou, Y.-C.; Lee, G.; Yu, C.-K. Impacts of Topography on Airflow and Precipitation in the Pyeongchang Area Seen from Multiple-Doppler Radar Observations. Mon. Weather Rev. 2018, 146, 3401–3424. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; Roo, A. de MSWEP: 3-Hourly 0.25 Global Gridded Precipitation (1979–2015) by Merging Gauge, Satellite, and Reanalysis Data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Noh, G.-H.; Ahn, K.-H. New Gridded Rainfall Dataset over the Korean Peninsula: Gap Infilling, Reconstruction, and Validation. J. Int. Climatol. 2021, 42, 435–452. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing Objective Techniques for Gauge-Based Analyses of Global Daily Precipitation. J. Geophys. Res. Atmos. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.; Fiorino, M.; Potter, G. Ncep–Doe Amip-Ii Reanalysis (r-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- WMO. Guide to the Global Observing System, 2010th ed.; Updated in 2017; WMO: Geneva, Switzerland, 2010; ISBN 978-92-63-10488-5. [Google Scholar]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive Automated Quality Assurance of Daily Surface Observations. J. Appl. Meteorol. Climatol. 2010, 49, 1615–1633. [Google Scholar] [CrossRef] [Green Version]
- Pellarin, T.; Román-Cascón, C.; Baron, C.; Bindlish, R.; Brocca, L.; Camberlin, P.; Fernández-Prieto, D.; Kerr, Y.H.; Massari, C.; Panthou, G.; et al. The Precipitation Inferred from Soil Moisture (PrISM) near Real-Time Rainfall Product: Evaluation and Comparison. Remote Sens. 2020, 12, 481. [Google Scholar] [CrossRef] [Green Version]
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product. USGS Rest. VA USA 2018, 1, 18. [Google Scholar]
- Wieder, W.; Boehnert, J.; Bonan, G.; Langseth, M. Regridded Harmonized World Soil Database v1.2. ORNL DAAC 2014. [Google Scholar] [CrossRef]
- Chen, C.; Li, Z.; Song, Y.; Duan, Z.; Mo, K.; Wang, Z.; Chen, Q. Performance of Multiple Satellite Precipitation Estimates over a Typical Arid Mountainous Area of China: Spatiotemporal Patterns and Extremes. J. Hydrometeorol. 2020, 21, 533–550. [Google Scholar] [CrossRef]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L. Propagation of Satellite Precipitation Uncertainties through a Distributed Hydrologic Model: A Case Study in the Tocantins–Araguaia Basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Kurtzman, D.; Navon, S.; Morin, E. Improving Interpolation of Daily Precipitation for Hydrologic Modelling: Spatial Patterns of Preferred Interpolators. Hydrol. Process. Int. J. 2009, 23, 3281–3291. [Google Scholar] [CrossRef]
- Gilewski, P. Impact of the Grid Resolution and Deterministic Interpolation of Precipitation on Rainfall-Runoff Modeling in a Sparsely Gauged Mountainous Catchment. Water 2021, 13, 230. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Evaporation Models in Hydrology. In Land Surface Evaporation; Springer: Berlin/Heidelberg, Germany, 1991; pp. 93–120. [Google Scholar]
- Zhenghui, X.; Fengge, S.; Xu, L.; Qingcun, Z.; Zhenchun, H.; Yufu, G. Applications of a Surface Runoff Model with Horton and Dunne Runoff for VIC. Adv. Atmos. Sci. 2003, 20, 165–172. [Google Scholar] [CrossRef]
- Lohmann, D.; Raschke, E.; Nijssen, B.; Lettenmaier, D. Regional Scale Hydrology: I. Formulation of the VIC-2L Model Coupled to a Routing Model. Hydrol. Sci. J. 1998, 43, 131–141. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Shi, X.; Zhu, C.; Bohn, T.; Su, F.; Pan, M.; Sheffield, J.; Lettenmaier, D.; Wood, E. Water Budget Record from Variable Infiltration Capacity (VIC) Model. In Algorithm Theoretical Basis Document, version 1.2; Department of Civil and Environmental Engineering, University of Washington: Seattle, WA, USA, 2009. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Tolson, B.A.; Shoemaker, C.A. Dynamically Dimensioned Search Algorithm for Computationally Efficient Watershed Model Calibration. Water Resour. Res. 2007, 43, 1–16. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Palmer, R.; Steinschneider, S. A Hierarchical Bayesian Model for Regionalized Seasonal Forecasts: Application to Low Flows in the Northeastern United States. Water Resour. Res. 2017, 53, 503–521. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting Satellite-Based Surface Soil Moisture for Flood Forecasting in the Mediterranean Area: State Update versus Rainfall Correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef] [Green Version]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Large-Scale Analysis of Global Gridded Precipitation and Temperature Datasets for Climate Change Impact Studies. J. Hydrometeorol. 2020, 21, 2623–2640. [Google Scholar] [CrossRef]
- Noh, G.-H.; Ahn, K.-H. Long-Lead Predictions of Early Winter Precipitation over South Korea Using a SST Anomaly Pattern in the North Atlantic Ocean. Clim. Dyn. 2022, 58, 3455–3469. [Google Scholar] [CrossRef]
- Qiu, L.; Im, E.-S. Added Value of High-Resolution Climate Projections over South Korea on the Scaling of Precipitation with Temperature. Environ. Res. Lett. 2021, 16, 124034. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Merwade, V. The Effect of Land Cover Change on Duration and Severity of High and Low Flows. Hydrol. Process. 2017, 31, 133–149. [Google Scholar] [CrossRef]
- Bevelhimer, M.S.; McManamay, R.A.; O’connor, B. Characterizing Sub-Daily Flow Regimes: Implications of Hydrologic Resolution on Ecohydrology Studies. River Res. Appl. 2015, 31, 867–879. [Google Scholar] [CrossRef]
- Haile, A.T.; Rientjes, T.; Gieske, A.; Gebremichael, M. Multispectral Remote Sensing for Rainfall Detection and Estimation at the Source of the Blue Nile River. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S76–S82. [Google Scholar] [CrossRef]
- Silvestro, F.; Gabellani, S.; Rudari, R.; Delogu, F.; Laiolo, P.; Boni, G. Uncertainty Reduction and Parameter Estimation of a Distributed Hydrological Model with Ground and Remote-Sensing Data. Hydrol. Earth Syst. Sci. 2015, 19, 1727–1751. [Google Scholar] [CrossRef] [Green Version]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale Parameter Regionalization of a Grid-Based Hydrologic Model at the Mesoscale. Water Resour. Res. 2010, 46, W05523. [Google Scholar] [CrossRef] [Green Version]







| Symbol | Full Name | Data Source | Adopted Variable | Spatial Resolution | Temporal Resolution | References |
|---|---|---|---|---|---|---|
| CMORPH | Climate Predition Center (CPC) MORPHing technique (CMORPH) bias corrected V1.0 | S, A | P | Daily | [53] | |
| MSWEP | Multi-Source Weighted Ensemble Precipitation (MSWEP) V2.2 | S, A, R | P | 3-h | [54] | |
| MERRA | Modern-Era Retrospective Analysis for Research and Application 2 (rainfall: M2T1NXFLX_V5.12.4; temperature: M2SDNXSLV_ V5.12.4) | S, A, R | P, Tmax, Tmin | Hourly | [55] | |
| ERA5 | European Centre for Medium-range Weather Forecasts Reanalysis 5 (ERA5) hourly data | R | P, Tmax, Tmin | Hourly | [56] | |
| TRMM | TRMM Multi-satellite Precipitation Analysis (TMPA) 3B42 V7 | S, A | P | 3-h | [10] | |
| TRMM-RT | TRMM Multi-satellite Precipitation Analysis (TMPA) 3B42 Real Time V7 | S | P | 3-h | [10] | |
| PERSIANN | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN) Climate Data Record (CDR) V1.0 | S, A | P | Daily | [57] | |
| K-Hidra | Korean High-resolution Daily Rainfall (K-Hidra) V2020 | A, R | P | Daily | [58] | |
| JRA-55 | Japanese 55-year Reanalysis (rainfall: fcst_phy2m125) | R | P | 3-h | [59] | |
| CPC-U | Climate Predition Center (CPC) global unified daily data | A, R | P, Tmax, Tmin | Daily | [60] | |
| NCEP-DOE | National Centers for Environmental Prediction (NCEP)–Department of Energy (DOE) reanalysis 2 project | A, R | P, Tmax, Tmin | 6-h | [61] |
| No. | Parameter | Description | Feasible Range |
|---|---|---|---|
| 1 | b | Variable infiltration curve parameter | 0.0~0.5 |
| 2 | Ds | Fraction of Dsmax where non-linear baseflow begins | 0.0~1.0 |
| 3 | Dm | Maximum velocity of baseflow | 0.0~30 |
| 4 | Ws | Fraction of maximum soil moisture where non-linear baseflow occurs | 0.0~1.0 |
| 5 | S1 | Depth of the second layer of soil (m) | 0.0~1.5 |
| 6 | S2 | Depth of the third layer of soil (m) | 0.0~2.0 |
| 7 | Velo | Wave velocity in the linearized Saint-Venant equation (m/s) | 0.0~5.0 |
| 8 | Diff | Diffusivity in the linearized Saint-Venant equation (m2/s) | 100~900 |
| 9 | Num | Grid Unit Hydrograph parameter (number of linear reservoirs) | 0.0~20 |
| 10 | Sto | Grid Unit Hydrograph parameter (reservoir storage constant) | 0.0~20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-G.; Ahn, K.-H. Assessment of Suitable Gridded Climate Datasets for Large-Scale Hydrological Modelling over South Korea. Remote Sens. 2022, 14, 3535. https://doi.org/10.3390/rs14153535
Lee D-G, Ahn K-H. Assessment of Suitable Gridded Climate Datasets for Large-Scale Hydrological Modelling over South Korea. Remote Sensing. 2022; 14(15):3535. https://doi.org/10.3390/rs14153535
Chicago/Turabian StyleLee, Dong-Gi, and Kuk-Hyun Ahn. 2022. "Assessment of Suitable Gridded Climate Datasets for Large-Scale Hydrological Modelling over South Korea" Remote Sensing 14, no. 15: 3535. https://doi.org/10.3390/rs14153535
APA StyleLee, D.-G., & Ahn, K.-H. (2022). Assessment of Suitable Gridded Climate Datasets for Large-Scale Hydrological Modelling over South Korea. Remote Sensing, 14(15), 3535. https://doi.org/10.3390/rs14153535






