Improvement and Assessment of Ocean Color Algorithms in the Northwest Pacific Fishing Ground Using Himawari-8, MODIS-Aqua, and VIIRS-SNPP
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
2.1.1. Satellite Chl-a Data
2.1.2. In Situ Chl-a Data
2.1.3. Chl-a Data from Argo
2.1.4. Marine Environmental Data
2.1.5. ENSO Index
2.2. Chl-a Data Preprocessing
2.3. Assessment Metrics
2.4. Remote Sensing Chl-a Algorithm Development
2.4.1. Current Chl-a Algorithms
2.4.2. Coefficient Optimization
2.4.3. Blending Windows
2.5. Data Merging
3. Results
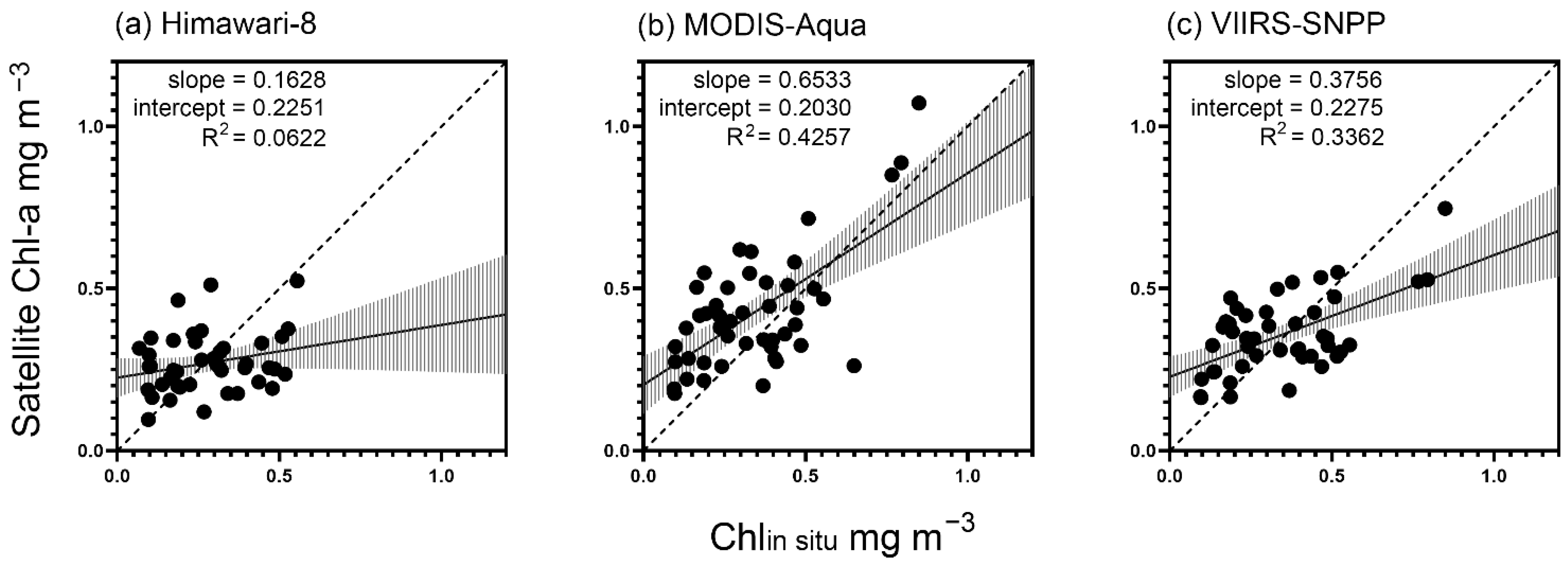
3.1. Matchups of Chl-a Data
3.2. Adjustment of Chl-a Algorithm Coefficients
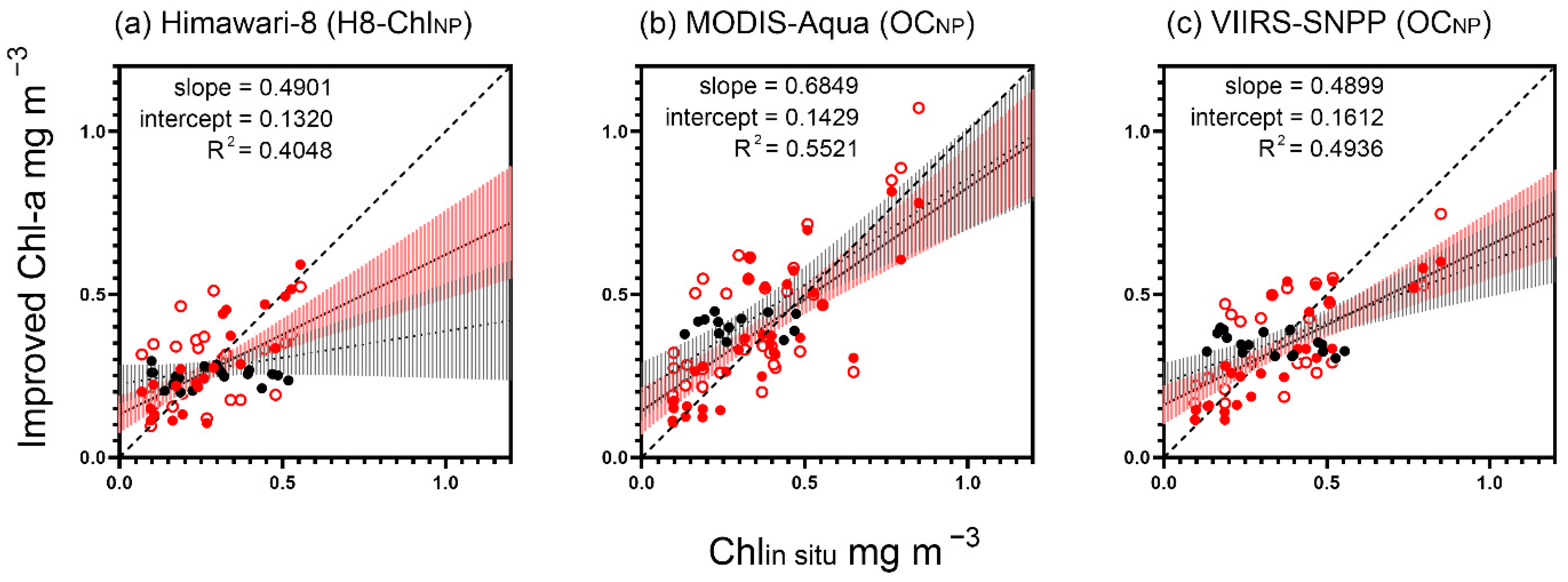
3.3. Performance of Improved Chl-a Algorithms
3.4. Establishment of Chl-a Blending Algorithm
3.5. Merged Data of Himawari-8, MODIS-Aqua, and VIIRS-SNPP
4. Discussion
4.1. Comparison of the Chl-a Products of Himawari-8, MODIS-Aqua, and VIIRS-SNPP
4.2. Evaluation of Chl-a Algorithm Coefficient Optimization
4.3. Influence of Chl-a Algorithm Blending Method
4.4. Variation of NPFG and Kuroshio Extension Represented by the Merged Chl-a Data
4.5. Reflection of Mesoscale Eddies in Merged Chl-a Data
4.6. Responses of Merged Chl-a Data to ENSO
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. FAO Yearbook. Fishery and Aquaculture Statistics 2017; FAO: Rome, Italy, 2019. [Google Scholar]
- Yasuda, I.; Watanabe, T. Chlorophyll a variation in the Kuroshio Extension revealed with a mixed-layer tracking float: Implication on the long-term change of Pacific saury (Cololabis saira). Fish. Oceanogr. 2007, 16, 482–488. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, R.; Yu, Y.; Ji, F. Variability in the Sea Surface Temperature Gradient and Its Impacts on Chlorophyll-a Concentration in the Kuroshio Extension. Remote Sens. 2021, 13, 888. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, G.; Liu, H.; Li, Z.; Cheng, X. Mesoscale Eddy-Induced Ocean Dynamic and Thermodynamic Anomalies in the North Pacific. Front. Mar. Sci. 2021, 8, 756918. [Google Scholar] [CrossRef]
- Messié, M.; Radenac, M.H.; Lefèvre, J.; Marchesiello, P. Chlorophyll bloom in the western Pacific at the end of the 1997–1998 El Niño: The role of the Kiribati Islands. Geophys. Res. Lett. 2006, 33, L14601. [Google Scholar] [CrossRef] [Green Version]
- Yatsu, A.; Chiba, S.; Yamanaka, Y.; Ito, S.-I.; Shimizu, Y.; Kaeriyama, M.; Watanabe, Y. Climate forcing and the Kuroshio/Oyashio ecosystem. ICES J. Mar. Sci. 2013, 70, 922–933. [Google Scholar] [CrossRef] [Green Version]
- Behrenfeld, M.J.; O’Malley, R.T.; Siegel, D.A.; McClain, C.R.; Sarmiento, J.L.; Feldman, G.C.; Milligan, A.J.; Falkowski, P.G.; Letelier, R.M.; Boss, E.S. Climate-driven trends in contemporary ocean productivity. Nature 2006, 444, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Boyce, D.G.; Lewis, M.R.; Worm, B. Global phytoplankton decline over the past century. Nature 2010, 466, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Chavez, F.P.; Strutton, P.G.; Friederich, G.E.; Feely, R.A.; Feldman, G.C.; Foley, D.G.; McPhaden, M.J. Biological and Chemical Response of the Equatorial Pacific Ocean to the 1997–98 El Nino. Science 1999, 286, 2126–2131. [Google Scholar] [CrossRef] [PubMed]
- Chavez, F.P.; Ryan, J.; Lluch-Cota, S.E.; Niquen, C.M. From anchovies to sardines and back: Multidecadal change in the Pacific Ocean. Science 2003, 299, 217–221. [Google Scholar] [CrossRef] [Green Version]
- Dutkiewicz, S.; Hickman, A.E.; Jahn, O.; Henson, S.; Beaulieu, C.; Monier, E. Ocean colour signature of climate change. Nat. Commun. 2019, 10, 578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McClain, C.R. A decade of satellite ocean color observations. Annu. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef] [Green Version]
- Groom, S.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, R.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.-K.; Chuprin, A.; et al. Satellite Ocean Colour: Current Status and Future Perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef] [Green Version]
- Werdell, P.J.; McClain, C.R. Satellite Remote Sensing: Ocean Color. In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 443–455. [Google Scholar]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Ocean. 1998, 103, 24937–24953. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, J.E.; Maritorena, S.; O’Brien, M.C.; Siegel, D.A.; Toole, D.; Menzies, D.; Smith, R.C.; Mueller, J.L.; Mitchell, B.G.; Kahru, M.; et al. SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3; NASA Tech. Memo. Seawifs Postlaunch; NASA: Washington, DC, USA, 2000; Volume 11.
- Dierssen, H.M. Perspectives on empirical approaches for ocean color remote sensing of chlorophyll in a changing climate. Proc. Natl. Acad. Sci. USA 2010, 107, 17073–17078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll Algorithms for Ocean Color Sensors-Oc4, Oc5 & Oc6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Feng, L.; Lee, Z.; Franz, B.A.; Bailey, S.W.; Werdell, P.J.; Proctor, C.W. Improving Satellite Global Chlorophyll a Data Products Through Algorithm Refinement and Data Recovery. J. Geophys. Res. Ocean. 2019, 124, 1524–1543. [Google Scholar] [CrossRef]
- Szeto, M.; Werdell, P.J.; Moore, T.S.; Campbell, J.W. Are the world’s oceans optically different? J. Geophys. Res. Ocean. 2011, 116, C7. [Google Scholar] [CrossRef] [Green Version]
- Cota, G.F.; Wang, J.; Comiso, J.C. Transformation of global satellite chlorophyll retrievals with a regionally tuned algorithm. Remote Sens. Environ. 2004, 90, 373–377. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Pardo, S.; Dall’Olmo, G.; Brewin, R.J.W.; Nencioli, F.; Dessailly, D.; Kwiatkowska, E.; Casal, T.; Donlon, C. Performance of Ocean Colour Chlorophyll a algorithms for Sentinel-3 OLCI, MODIS-Aqua and Suomi-VIIRS in open-ocean waters of the Atlantic. Remote Sens. Environ. 2021, 260, 112444. [Google Scholar] [CrossRef]
- Gómez Jakobsen, F.J.; Mercado, J.M.; Tovar-Salvador, M.L.; Cortés, D.; Yebra, L.; Salles, S.; Sánchez, A.; Valcárcel-Pérez, N.; Alonso, A. New algorithms for estimating chlorophyll-a in the Spanish waters of the Western Mediterranean Sea from multiplatform imagery. Int. J. Remote Sens. 2018, 39, 8837–8858. [Google Scholar] [CrossRef]
- Johnson, R.; Strutton, P.G.; Wright, S.W.; McMinn, A.; Meiners, K.M. Three improved satellite chlorophyll algorithms for the Southern Ocean. J. Geophys. Res. Ocean. 2013, 118, 3694–3703. [Google Scholar] [CrossRef]
- Wojtasiewicz, B.; Hardman-Mountford, N.J.; Antoine, D.; Dufois, F.; Slawinski, D.; Trull, T.W. Use of bio-optical profiling float data in validation of ocean colour satellite products in a remote ocean region. Remote Sens. Environ. 2018, 209, 275–290. [Google Scholar] [CrossRef]
- Pittman, N.A.; Strutton, P.G.; Johnson, R.; Matear, R.J. An Assessment and Improvement of Satellite Ocean Color Algorithms for the Tropical Pacific Ocean. J. Geophys. Res. Ocean. 2019, 124, 9020–9039. [Google Scholar] [CrossRef]
- Gregg, W.W.; Casey, N.W. Global and regional evaluation of the SeaWiFS chlorophyll data set. Remote Sens. Environ. 2004, 93, 463–479. [Google Scholar] [CrossRef]
- Wang, M.; Son, S. VIIRS-derived chlorophyll-a using the ocean color index method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Hammond, M.L.; Beaulieu, C.; Henson, S.A.; Sahu, S.K. Assessing the Presence of Discontinuities in the Ocean Color Satellite Record and Their Effects on Chlorophyll Trends and Their Uncertainties. Geophys. Res. Lett. 2018, 45, 7654–7662. [Google Scholar] [CrossRef] [Green Version]
- IOCCG. Ocean-Colour Data Merging. In Reports of the International Ocean-Colour Coordinating Group, No. 6; Gregg, W., Ed.; IOCCG: Dartmouth, NS, Canada, 2007. [Google Scholar]
- Chen, S.; Hu, C.; Barnes, B.B.; Xie, Y.; Lin, G.; Qiu, Z. Improving ocean color data coverage through machine learning. Remote Sens. Environ. 2019, 222, 286–302. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Manzano-Sarabia, M.; Greg Mitchell, B. Trends in the surface chlorophyll of the California Current: Merging data from multiple ocean color satellites. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2012, 77–80, 89–98. [Google Scholar] [CrossRef]
- Ito, S.-i.; Sugisaki, H.; Tsuda, A.; Yamamura, O.; Okuda, K. Contributions of the VENFISH program: Meso-zooplankton, Pacific saury (Cololabis saira) and walleye pollock (Theragra chalcogramma) in the northwestern Pacific. Fish. Oceanogr. 2004, 13, 1–9. [Google Scholar] [CrossRef]
- Sugisaki, H.; Kurita, Y. Daily rhythm and seasonal variation of feeding habit of Pacific saury (Cololabis saira) in relation to their migration and oceanographic conditions off Japan. Fish. Oceanogr. 2004, 13, 63–73. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M. Global daily gap-free ocean color products from multi-satellite measurements. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102714. [Google Scholar] [CrossRef]
- Huang, W.-B. Comparisons of monthly and geographical variations in abundance and size composition of Pacific saury between the high-seas and coastal fishing grounds in the northwestern Pacific. Fish. Sci. 2009, 76, 21–31. [Google Scholar] [CrossRef]
- Kouketsu, S.; Kaneko, H.; Okunishi, T.; Sasaoka, K.; Itoh, S.; Inoue, R.; Ueno, H. Mesoscale eddy effects on temporal variability of surface chlorophyll a in the Kuroshio Extension. J. Oceanogr. 2016, 72, 439–451. [Google Scholar] [CrossRef]
- Cheung, H.-F.; Pan, J.; Gu, Y.; Wang, Z. Remote-sensing observation of ocean responses to Typhoon Lupit in the northwest Pacific. Int. J. Remote Sens. 2012, 34, 1478–1491. [Google Scholar] [CrossRef]
- Chiba, S.; Di Lorenzo, E.; Davis, A.; Keister, J.E.; Taguchi, B.; Sasai, Y.; Sugisaki, H. Large-scale climate control of zooplankton transport and biogeography in the Kuroshio-Oyashio Extension region. Geophys. Res. Lett. 2013, 40, 5182–5187. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
- Chavez, F.P.; Buck, K.R.; Bidigare, R.R.; Karl, D.M.; Hebel, D.; Latasa, M.; Campbell, L.; Newton, J. On the Chlorophyll a Retention Properties of Glass-Fiber GF/F Filters. Limnol. Oceanogr. 1995, 40, 428–433. [Google Scholar] [CrossRef]
- Zhang, T.; Hoell, A.; Perlwitz, J.; Eischeid, J.; Murray, D.; Hoerling, M.; Hamill, T.M. Towards Probabilistic Multivariate ENSO Monitoring. Geophys. Res. Lett. 2019, 46, 10532–10540. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of satellite data products: An ocean color case study. Opt. Express 2018, 26, 7404–7422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frouin, R.J.; Shenoi, S.C.; Rao, K.H.; Murakami, H. Ocean color estimation by Himawari-8/AHI. In Remote Sensing of the Oceans and Inland Waters: Techniques, Applications, and Challenges; SPIE: Bellingham, WA, USA, 2016. [Google Scholar]
- IOCCG. Mission Requirements for Future Ocean-Colour Sensors. In Reports of the International Ocean-Colour Coordinating Group, No. 13; McClain, C.R., Meister, G., Eds.; IOCCG: Dartmouth, NS, Canada, 2012. [Google Scholar]
- El-Habashi, A.; Ahmed, S. Analyses of satellite ocean color retrievals show advantage of neural network approaches and algorithms that avoid deep blue bands. J. Appl. Remote Sens. 2019, 13, 024509. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.W. An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Chuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the fitness-for-purpose of satellite multi-mission ocean color climate data records: A protocol applied to OC-CCI chlorophyll-a data. Remote Sens. Environ. 2017, 203, 139–151. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.-T.; Sun, C.-L.; Belkin, I.M.; Yeh, S.-Z.; Kuo, C.-L.; Liu, D.-C. Sea surface temperature fronts affect distribution of Pacific saury (Cololabis saira) in the Northwestern Pacific Ocean. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2014, 107, 15–21. [Google Scholar] [CrossRef]
- Tian, Y.; Akamine, T.; Suda, M. Modeling the influence of oceanic-climatic changes on the dynamics of Pacific saury in the northwestern Pacific using a life cycle model. Fish. Oceanogr. 2004, 13, 125–137. [Google Scholar] [CrossRef]
- Tian, H.; Liu, Y.; Tian, Y.; Alabia, I.D.; Qin, Y.; Sun, H.; Li, J.; Ma, S.; Saitoh, S.-I. A Comprehensive Monitoring and Assessment System for Multiple Fisheries Resources in the Northwest Pacific Based on Satellite Remote Sensing Technology. Front. Mar. Sci. 2022, 9, 808282. [Google Scholar] [CrossRef]
- Yasuda, I.; Watanabe, Y. On the relationship between the Oyashio front and saury fishing grounds in the north-western Pacific: A forecasting method for fishing ground locations. Fish. Oceanogr. 1994, 3, 172–181. [Google Scholar] [CrossRef]
- Saitoh, S.-I.; Kosaka, S.; Iisaka, J. Satellite infrared observations of Kuroshio warm-core rings and their application to study of Pacific saury migration. Deep. Sea Res. Part A Oceanogr. 1986, 33, 1601–1615. [Google Scholar] [CrossRef]
- Siegel, D.A.; Peterson, P.; McGillicuddy, D.J.; Maritorena, S.; Nelson, N.B. Bio-optical footprints created by mesoscale eddies in the Sargasso Sea. Geophys. Res. Lett. 2011, 38, L13608. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Xu, Y.; Zhang, X.; Huang, C. Global chlorophyll distribution induced by mesoscale eddies. Remote Sens. Environ. 2021, 254, 112245. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, G.; Hu, K.; Wu, R.; Gong, H.; Chen, X.; Tao, W. Diverse Relationship between ENSO and the Northwest Pacific Summer Climate among CMIP5 Models: Dependence on the ENSO Decay Pace. J. Clim. 2017, 30, 109–127. [Google Scholar] [CrossRef]
- Henson, S.A.; Sarmiento, J.L.; Dunne, J.P.; Lima, L.; Doney, S.C.; John, J.; Beaulieu, C. Detection of anthropogenic climate change in satellite records of ocean chlorophyll and productivity. Biogeosciences 2010, 7, 621–640. [Google Scholar] [CrossRef] [Green Version]













| Country & Agency | Sensor | Satellite | Launch Date | Resolution (m) | # of Bands | Spectral Coverage (nm) |
|---|---|---|---|---|---|---|
| USA NASA | CZCS | Nimbus-7 | 1978 | 825 | 6 | 433–12,500 |
| SeaWIFS | OrbView-2 | 1997 | 1100 | 8 | 402–885 | |
| MISR | Terra | 1999 | 250 | 4 | 446–867 | |
| MODIS | Terra, Aqua | 1999, 2002 | 1000 | 36 | 405–14,385 | |
| VIIRS | SNPP, JPSS | 2011, 2017 | 370/740 | 22 | 402–11,800 | |
| NASA, ONR and DOD | HICO | JEM-EF International Space Station | 2009 | 100 | 124 | 380–1000 |
| France CNES | POLDER, -2, -3 | ADEOS (Japan), -II (Japan), Parasol | 1996, 2002, 2004 | 600 | 9 | 443–910, 443–910, 443–1020 |
| Germany DLR | MOS | IRS-P3 (India) | 1996 | 500 | 18 | 408–1600 |
| Japan NASDA | OCTS | ADEOS | 1996 | 700 | 12 | 402–12,500 |
| GLI | ADEOS-II | 2002 | 250/1000 | 36 | 375–12,500 | |
| Japan NEC | OCI | ROCSAT-1 (Taiwan) | 1999 | 825 | 6 | 433–12,500 |
| Japan JAXA | SGLI | GCOM-C | 2017 | 250/1000 | 19 | 375–12,500 |
| India ISRO | OCM, -2 | IRS-P4, Oceansat-2 | 1999, 2009 | 350, 100–400 | 8 | 402–885, 400–900 |
| Korea KARI | KOMPSAT | OSMI | 1999 | 850 | 6 | 400–900 |
| GOCI, -II | COMS, GEOKompsat-2B | 2010, 2020 | 500, 250 | 8, 13 | 400–865, 380–900 | |
| Europe ESA | MERIS | Envisat-1 | 2002 | 300/1200 | 15 | 412–1050 |
| MSI | Sentinel-2A, -2B | 2015, 2017 | 10/20/60 | 13 | 442–2202 | |
| OLCI | Sentinel-3A, -3B | 2016, 2018 | 300/1200 | 21 | 400–1020 | |
| China CNSA | CMODIS | Shen Zhou-3 | 2002 | 400 | 34 | 403–12,500 |
| China CMA | MERSI-1, -2, -3 | FY-3A, -3B, -3C | 2008, 2010, 2013 | 250/1000 | 20 | 402–2155 |
| China SOA | COCTS | HY-1B, -1C, -1D | 2007, 2018, 2020 | 1100 | 10 | 402–12,500 |
| CZI | HY-1B, -1C, -1D | 2007, 2018, 2020 | 250, 50, 50 | 4 | 433–885 |
| Satellite | Rrs (nm) | Rrs (nm) | a0 | a1 | a2 | a3 | a4 |
|---|---|---|---|---|---|---|---|
| Himawari-8 | 470 | 510 | 0.0388 | −4.2500 | # | # | # |
| MODIS-Aqua | 443 > 488 | 547 | 0.2424 | −2.7423 | 1.8017 | 0.0015 | −1.2280 |
| VIIRS-SNPP | 443 > 486 | 551 | 0.2228 | −2.4683 | 1.5867 | −0.4275 | −0.7768 |
| Temporal Average | Pixel Average | Matches | Match Percent % | R2 |
|---|---|---|---|---|
| Himawari-8 | ||||
| 1 day | 1 × 1 | 60 | 70.59% | 0.7814 |
| 1 day | 3 × 3 | 66 | 77.65% | 0.6228 |
| 1 day | 5 × 5 | 68 | 80.00% | 0.7174 |
| 3 (1 ± 1) days | 1 × 1 | 77 | 90.59% | 0.6542 |
| 3 (1 ± 1) days | 3 × 3 | 79 | 92.94% | 0.4934 |
| 3 (1 ± 1) days | 5 × 5 | 82 | 96.47% | 0.3082 |
| 5 (1 ± 2) days | 1 × 1 | 78 | 91.76% | 0.5652 |
| 5 (1 ± 2) days | 3 × 3 | 81 | 95.29% | 0.4882 |
| 5 (1 ± 2) days | 5 × 5 | 82 | 96.47% | 0.4205 |
| MODIS-Aqua | ||||
| 1 day | 1 × 1 | 13 | 15.29% | 0.9523 |
| 1 day | 3 × 3 | 18 | 21.18% | 0.9762 |
| 1 day | 5 × 5 | 22 | 25.88% | 0.9683 |
| 3 (1 ± 1) days | 1 × 1 | 26 | 30.59% | 0.9822 |
| 3 (1 ± 1) days | 3 × 3 | 38 | 44.71% | 0.9421 |
| 3 (1 ± 1) days | 5 × 5 | 42 | 49.41% | 0.9836 |
| 5 (1 ± 2) days | 1 × 1 | 35 | 41.18% | 0.9706 |
| 5 (1 ± 2) days | 3 × 3 | 51 | 60.00% | 0.9534 |
| 5 (1 ± 2) days | 5 × 5 | 58 | 68.24% | 0.9673 |
| VIIRS-SNPP | ||||
| 1 day | 1 × 1 | 15 | 17.65% | 0.9601 |
| 1 day | 3 × 3 | 18 | 21.18% | 0.9635 |
| 1 day | 5 × 5 | 21 | 24.71% | 0.9721 |
| 3 (1 ± 1) days | 1 × 1 | 30 | 35.29% | 0.9716 |
| 3 (1 ± 1) days | 3 × 3 | 37 | 43.53% | 0.9864 |
| 3 (1 ± 1) days | 5 × 5 | 40 | 47.06% | 0.9589 |
| 5 (1 ± 2) days | 1 × 1 | 43 | 50.59% | 0.9733 |
| 5 (1 ± 2) days | 3 × 3 | 55 | 64.71% | 0.9806 |
| 5 (1 ± 2) days | 5 × 5 | 57 | 67.06% | 0.983 |
| Coefficients | a0 | a1 | a2 | a3 | a4 |
|---|---|---|---|---|---|
| Himawari-8 (<0.3) | −0.1955 | −4.1326 | # | # | # |
| Himawari-8 (>0.3) | 0.0309 | −3.1143 | # | # | # |
| MODIS-Aqua (<0.3) | −0.0449 | −2.7701 | 1.9857 | 0.2703 | −1.2280 |
| MODIS-Aqua (>0.3) | 0.1949 | −2.5475 | 2.0539 | 0.0015 | −1.2280 |
| VIIRS-SNPP (<0.3) | 0.0064 | −2.4903 | 1.7050 | −0.2460 | −0.6793 |
| VIIRS-SNPP (>0.3) | 0.1773 | −2.3933 | 2.0942 | −0.4275 | −0.7768 |
| Satellite | Mean | Bias | MAE | ||||
|---|---|---|---|---|---|---|---|
| Before Improvement | After Improvement | In Situ | Before Improvement | After Improvement | Before Improvement | After Improvement | |
| Himawari-8 (<0.3) | 0.2642 | 0.1755 | 0.1767 | 1.5092 | 1.0382 | 1.6281 | 1.4236 |
| Himawari-8 (>0.3) | 0.278 | 0.4147 | 0.4173 | 0.6547 | 1 | 1.5274 | 1.2007 |
| Himawari-8 (all) | 0.2699 | 0.2733 | 0.2751 | 1.0724 | 1.0224 | 1.5862 | 1.3278 |
| MODIS-Aqua (<0.3) | 0.3622 | 0.1934 | 0.186 | 1.9546 | 1.0558 | 1.9546 | 1.2839 |
| MODIS-Aqua (>0.3) | 0.4803 | 0.4744 | 0.4728 | 0.9729 | 0.9999 | 1.3175 | 1.2635 |
| MODIS-Aqua (all) | 0.4264 | 0.3462 | 0.3419 | 1.3378 | 1.025 | 1.5774 | 1.2728 |
| VIIRS-SNPP (<0.3) | 0.3141 | 0.1959 | 0.1876 | 1.675 | 1.0589 | 1.6943 | 1.2928 |
| VIIRS-SNPP (>0.3) | 0.3952 | 0.4157 | 0.4839 | 0.8066 | 0.8668 | 1.3658 | 1.2871 |
| VIIRS-SNPP (all) | 0.3574 | 0.3132 | 0.3456 | 1.1344 | 0.9516 | 1.5103 | 1.2897 |
| Satellite | Slope | Intercept | R2 | |||
|---|---|---|---|---|---|---|
| Before Improvement | After Improvement | Before Improvement | After Improvement | Before Improvement | After Improvement | |
| Himawari-8 | 0.1628 | 0.7869 | 0.2251 | 0.0569 | 0.0622 | 0.7020 |
| MODIS-Aqua | 0.6533 | 0.8159 | 0.2030 | 0.0672 | 0.4257 | 0.6909 |
| VIIRS-SNPP | 0.3756 | 0.6192 | 0.2275 | 0.0992 | 0.3362 | 0.7089 |
| Satellite | Chlin-situ < 0.3 mg m−3 Algorithm | Default Algorithm | Chlin-situ > 0.3 mg m−3 Algorithm |
|---|---|---|---|
| Himawari-8 | <0.2 mg m−3 | 0.2–0.3 mg m−3 | >0.3 mg m−3 |
| MODIS-Aqua | <0.35 mg m−3 | 0.35–0.45 mg m−3 | >0.45 mg m−3 |
| VIIRS-SNPP | <0.3 mg m−3 | 0.3–0.4 mg m−3 | >0.4 mg m−3 |
| Blending Algorithm | Mean | Bias | MAE | ||||
|---|---|---|---|---|---|---|---|
| Before Improvement | After Improvement | In Situ | Before Improvement | After Improvement | Before Improvement | After Improvement | |
| H8-ChlNP | 0.2699 | 0.2668 | 0.2751 | 1.0724 | 1.0413 | 1.5862 | 1.3278 |
| OCNP (M) | 0.4264 | 0.3771 | 0.3419 | 1.3378 | 1.1402 | 1.5774 | 1.3776 |
| OCNP (V) | 0.3574 | 0.3305 | 0.3456 | 1.1344 | 1.0158 | 1.5103 | 1.3956 |
| Data Group | Himawari-8 to MODIS-Aqua | Himawari-8 to VIIRS-SNPP | VIIRS-SNPP to MODIS-Aqua |
|---|---|---|---|
| Bias before improvement | 0.697 | 0.803 | 0.8324 |
| Bias after improvement | 0.9279 | 0.967 | 0.9281 |
| Satellite | Himawari-8 | MODIS-Aqua | VIIRS-SNPP | |||
|---|---|---|---|---|---|---|
| Default Algorithm | Blending Algorithm | Default Algorithm | Blending Algorithm | Default Algorithm | Blending Algorithm | |
| Weights of three satellites | 0.3120 | 0.3540 | 0.3187 | 0.3277 | 0.3693 | 0.3183 |
| Weights of two satellites | 0.4947 | 0.5192 | 0.5053 | 0.4808 | # | # |
| 0.4580 | 0.5266 | # | # | 0.5420 | 0.4743 | |
| # | # | 0.4632 | 0.5073 | 0.5368 | 0.4927 | |
| Data Group | Mean | Bias | MAE | ||||
|---|---|---|---|---|---|---|---|
| Before Improvement | After Improvement | Sample | Before Improvement | After Improvement | Before Improvement | After Improvement | |
| Argo data (<0.3) | 0.3012 | 0.2023 | 0.1682 | 1.7754 | 1.2173 | 1.9497 | 1.5386 |
| Argo data (>0.3) | 0.3935 | 0.4263 | 0.6197 | 0.5168 | 0.6491 | 2.1304 | 1.6375 |
| Argo data (All) | 0.3512 | 0.3238 | 0.4131 | 0.9091 | 0.8656 | 2.0460 | 1.5915 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Liu, Y.; Luo, Y.; Wang, Y.; Liu, X.; Zhang, Y.; Zhuang, Y.; Tian, Y. Improvement and Assessment of Ocean Color Algorithms in the Northwest Pacific Fishing Ground Using Himawari-8, MODIS-Aqua, and VIIRS-SNPP. Remote Sens. 2022, 14, 3610. https://doi.org/10.3390/rs14153610
Huang C, Liu Y, Luo Y, Wang Y, Liu X, Zhang Y, Zhuang Y, Tian Y. Improvement and Assessment of Ocean Color Algorithms in the Northwest Pacific Fishing Ground Using Himawari-8, MODIS-Aqua, and VIIRS-SNPP. Remote Sensing. 2022; 14(15):3610. https://doi.org/10.3390/rs14153610
Chicago/Turabian StyleHuang, Chuanyang, Yang Liu, Yanping Luo, Yuntao Wang, Xudong Liu, Yong Zhang, Yunyun Zhuang, and Yongjun Tian. 2022. "Improvement and Assessment of Ocean Color Algorithms in the Northwest Pacific Fishing Ground Using Himawari-8, MODIS-Aqua, and VIIRS-SNPP" Remote Sensing 14, no. 15: 3610. https://doi.org/10.3390/rs14153610
APA StyleHuang, C., Liu, Y., Luo, Y., Wang, Y., Liu, X., Zhang, Y., Zhuang, Y., & Tian, Y. (2022). Improvement and Assessment of Ocean Color Algorithms in the Northwest Pacific Fishing Ground Using Himawari-8, MODIS-Aqua, and VIIRS-SNPP. Remote Sensing, 14(15), 3610. https://doi.org/10.3390/rs14153610









