Dual-Branch-AttentionNet: A Novel Deep-Learning-Based Spatial-Spectral Attention Methodology for Hyperspectral Data Analysis

Abstract

Recently, deep learning-based classification approaches have made great progress and now dominate a wide range of applications, thanks to their Herculean discriminative feature learning ability. Despite their success, for hyperspectral data analysis, these deep learning based techniques tend to suffer computationally as the magnitude of the data soars. This is mainly because the hyperspectral imagery (HSI) data are multidimensional, as well as giving equal importance to the large amount of temporal and spatial information in the HSI data, despite the redundancy of information in the temporal and spatial domains. Consequently, in literature, this equal information emphasis has proven to affect the classification efficacy negatively in addition to increasing the computational time. As a result, this paper proposes a novel dual branch spatial-spectral attention based classification methodology that is computationally cheap and capable of selectively accentuating cardinal spatial and spectral features while suppressing less useful ones. The theory of feature extraction with 3D-convolutions alongside a gated mechanism for feature weighting using bi-directional long short-term memory is used as a spectral attention mechanism in this architecture. In addition, a union of 3D convolutional neural network (3D-CNN) and a residual network oriented spatial window-based attention mechanism is proposed in this work. To validate the efficacy of our proposed technique, the features collected from these spatial and spectral attention pipelines are transferred to a feed-forward neural network (FNN) for supervised pixel-wise classification of HSI data. The suggested spatial-spectral attention based hyperspectral data analysis and image classification methodology outperform other spatial-only, spectral-only, and spatial-spectral feature extraction based hyperspectral image classification methodologies when compared, according to experimental results.

1. Introduction

Hyperspectral imaging, widely referred to as image spectroscopy, aims at capturing electromagnetic energy emitted off the land cover under observation, over hundreds of contiguous, narrow spectral bands between infrared and visible wavelength ranges. Hyperspectral remote sensing data thus collected with the aid of multiple unmanned aerial devices such as drones, satellites, etc. have strongly favored the emergence of numerous hyperspectral remote sensing applications built around land cover classification for farming [1] for earth observation and monitoring, planning the cities [2], aerial devices based supervision [3], weather forecasting and climate monitoring [4], observations on changes in climatic conditions [5], etc. Over the last decade, breakthroughs in artificial intelligence (especially in machine learning and deep learning) have prompted the hyperspectral remote sensing community to focus on developing efficient hyperspectral image classification approaches for feature extraction [6,7], HSI data classification [6,8] and object detection for HSI based applications [9].

With most of the aforementioned remote sensing application frameworks, classification of HSI data acts as the center piece. While traditional machine learning-based HSI data classification and object detection frameworks rely primarily on spectral information as features [10,11], spectral feature-based classification approaches are unable to capture and use the spatial variability present in high-dimensional HSI data [6,8]. Distance measure [12], KNN (K-Nearest Neighbors) [13], maximum likelihood criteria [14], AdaBoost [15] , random forest classification [16], and logistic regression [17] are some of the frameworks that operate on spectral-only features that have been described in the literature and have proven to be useful in categorizing HSI data. Furthermore, literature has shown that combining a large number of spectral and spatial data in a complementary form can considerably improve the efficacy of HSI classification frameworks [18,19,20].

Over the past few years, deep learning based HSI classification frameworks with stratified feature learning ability have dominated the domain of computer vision, and have produced superlative results in various remote sensing applications [21,22,23]. Not only do these deep learning-based models have the capability to learn more convoluted and abstract features in the data [24,25], they also hold the intrinsic capability of learning higher level features present in the shallow part of the network. Such models are typically not affected by the changes to the input, and have produced unprecedented results in spectral-spatial feature extraction-based HSI classification frameworks [6,8].

Unsupervised and supervised feature extraction and data analysis methodologies applying convolution operation based neural networks, recurrent neural networks, residual networks, and additional models are used in deep learning-based frameworks for HSI classification, which fosters process automation through progressive data-learning. These approaches generally operate on HSI data that are represented in a lower dimensional space in comparison with the raw HSI data which is high dimensional in nature through incorporation of an effective dimensionality reduction technique producing promising results. A few such dimensionality reduction techniques that we come across in literature are principal component analysis (PCA) [26], linear discriminant analysis (LDA) [27], local fisher discriminant analysis (LFDA) [28], random projections (RPs) [6,8,29,30], etc. However, it is evidently noticeable in the hyperspectral remote sensing community that the following questions have not been addressed effectively in literature to date [31]:

• Do all the spatial and spectral information extracted contribute equally towards effectively classifying HSI data with a deep learning framework?
• If no, is there a technique to discriminate between less informative and more informative spectral bands that contribute towards effective HSI classification?
• Is there a strategy that can improve HSI data classification in a comprehensive classification methodology by emphasizing the contribution of data points which happen to be more informative in a local spatial windowed area around the data point of interest?
• Is it possible to improve the efficacy of an HSI classification methodology based on deep learning by highlighting more informative features and suppressing less valuable ones?

These questions fuel our motivation to devise a novel functional methodology to efficiently emphasize more informative pixels in a spatial neighborhood and spectral bands in the temporal domain which aid in boosting the efficacy of a HSI data classification framework. This phenomenon has widely been recognised as “ATTENTION” in the machine learning and deep learning community [7,32,33]. Attention methodologies have recently been used extensively in language modeling and computer vision applications. Its accomplishment is based mostly on the fair presumption that human vision only pivots on specific sections of the entire visual expanse when and where required. Researchers over the past few years have extensively worked on such attention-based methodologies in the remote sensing community and produced exceptional results. For instance, Zhang et al. in [34] proposed a saliency detection technique to extract salient areas in the input data which can be used for data representation and sampling. In a similar work, Diao et al. [35] proposed an alternative technique where norm gradient maps could be effectively used as saliency maps for data representation. However, Wang et al. in [36] claim that salient areas are not necessarily cardinal in achieving exceptional results in applications related to remote sensing data classification. Following this claim, they proposed to use LSTM networks to recurrently extract attention maps from deep convolutional features of a CNN based architecture. However, combining LSTM and CNN to extract attention features made the proposed methodology too complex and introduces scaling issues [36]. Later, Haut et al. in [37] proposed a two-branch attention module, where one branch is utilized to generate an attention mask and the other branch is utilized to extract convolutional features. Then, attention features are obtained by multiplying the attention mask with the convolutional features which proved to be an effective technique for hyperspectral data analysis and classification. With this phenomenon as an inspiration, we propose dual branch spectral–spatial attention based methodology for hyperspectral image classification. We aim to use attention mechanisms to improve the classification framework’s representation capacity, allowing us to focus on more selective spectral bands and spatial positions while repressing those that are not.

Hence, in this work, we propose a dual branch attention and classification framework for HSI data in order to address the aforementioned problems. To begin, principal component analysis was used as a computationally efficient dimensionality reduction component in this study to effectively extract spectral information, to reduce noise, and to bring down the redundancy in spectral information. Then, using a 3D-convolution based automated feature engineering technique and a bi-directional long short term memory (LSTM) based gated attention mechanism, a spectral attention and feature encoding mechanism that delivers enhanced hyperspectral data learning that emphasizes spectral information that is important for hyperspectral data review. Another significant contribution of this work is the proposal of a 3D-convolutional neural network and softmax activation based spatial attention technique to adaptively diversify spatial information around the pixel of interest into features of higher importance and into features that contribute less towards making classification decisions on input data. This is followed by a ResNet based feature encoding mechanism to encode this spatial information into a feature vector for classification. In addition, to evaluate the efficacy of this automated hyperspectral image classification methodology, a FNN-based supervised classification on the feature vectors derived from the spatial and spectral attention blocks is included.

Therefore, the novel contributions of the proposed dual-branched spatial-spectral attention and classification framework are summarized as follows:

• A novel framework of spectral attention mechanism and feature encoding scheme using 3D-convolutions for volumetric feature analysis and feature extraction jointly with bi-directional LSTMs for spectral features based attention is proposed for hyperspectral image classification. Bi-directional LSTMs, in our work, offer an effective means to discriminate between features that are of less importance and emphasize more principle spectral information through a gating mechanism with softmax activation function. This technique also presents an effective way to encode spectral information, thus aiding in restoration and enhancement of spectral relationship between spectral bands in hyperspectral imagery data.
• A unique combination of 3D-CNN based spatial attention mechanism and a ResNet based information encoding scheme is proposed, which not only constructively preserves the spatial relationship between pixels in a windowed region around the input data point, but also accents the weightage for features which have a dominant contribution in the ground truth based decision-making process of a HSI classification framework.
• This work also proposes a capable technique for combining encoded characteristics from the spectral and spatial attention frameworks before being produced as an input to a feed-forward neural network (FNN) based supervised classification network to demonstrate the efficacy of our approach. In this work, the proposed dual-branched spatial-spectral attention and classification architecture is aimed at improving automated hyperspectral data analysis.
• This paper also introduces a number of unique spatial-only and spectral-only attention based approaches and frameworks to conduct a brief evaluation on the effects of incorporation of attention methodology in hyperspectral image classification.

The following is a summary of the remainder of this paper: The theoretical description of each component in the proposed design is presented in Section 2. This is continued by a detailed discussion on the proposed architecture in Section 3, followed by a brief discussion about all the other methodologies used in our work as a means to compare the efficacy of our proposed methodology in Section 4, which are then evaluated in Section 5. Finally, in the conclusion Section 6, the analysis on the efficacy of our proposed work is summarized.

2. Approach Overview

This section examines the different components of the proposed dual-branched spatial-spectral attention and classification framework from a theoretical standpoint.

2.1. Principal Component Analysis

Principal Component Analysis (PCA) is a dimensionality technique which is linear in nature used to transfer input data to a new coordinate system such that the first coordinate (which is generally referred to as the first principal component) achieved through scalar projection has the highest variance, the second projected coordinate has the second highest variance, and so on. With this data transformation methodology, the goal is to project every data point to a new coordinate system and retain the first few principal components and preserve the maximum amount of variance possible and discard the rest, which indirectly transforms the input to a lower dimension when compared to that of the high dimensional input. In addition, it is to be noted that the ith principal component (PC) retains the maximum variance of the data projected data in a direction that is orthogonal to the first ${\displaystyle i-1}$ principal components [26,38,39].

Let $\mathbf{P}\in {\mathcal{R}}^{n\times d}$ be the data with a column-wise empirical mean of 0, n rows representing the number of data vectors, and d columns representing the data’s features or dimensions. The PCA transformation is defined mathematically as a linear combination of d-dimensional basis vectors ${\mathbf{u}}_{\left(k\right)}=(u_1,\dots ,u_d){}_{\left(k\right)}$ which maps every row vector ${\mathbf{p}}_{\left(i\right)}$ of $\mathbf{P}$ to a new vector of principal component scores ${\mathbf{t}}_{\left(i\right)}=(t_1,\dots ,t_l){}_{\left(i\right)}$ computed as:

$${\mathbf{t}}_{k\left(i\right)}={\mathbf{p}}_{\left(i\right)}.{\mathbf{u}}_{\left(k\right)}$$

(1)

where $i=\{1,\dots ,n\}$, $k=\{1,\dots ,l\}$ and $l\le d$. For the variance to be maximized, the initial weight vector ${\mathbf{u}}_{\left(1\right)}$ which is in direct correlation to the first principal component has to satisfy:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{\left(1\right)}& =argma{x}_{\Vert \mathbf{u}\Vert =1}\left\{\Sigma \left({\mathbf{t}}_1\right){}_{\left(i\right)}^2\right\}\hfill \\ \hfill & =argma{x}_{\Vert \mathbf{u}\Vert =1}\left\{\Sigma ({\mathbf{p}}_{\left(i\right)}.\mathbf{u}){}^2\right\}\hfill \end{array}$$

(2)

As a result, Equation (2) can be enunciated in the form of a matrix as:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{\left(1\right)}& =argma{x}_{\Vert \mathbf{u}\Vert =1}{\{\Vert \mathbf{P}\mathbf{u}\Vert }^2\}\hfill \\ \hfill & =argma{x}_{\Vert \mathbf{u}\Vert =1}\left\{{\mathbf{u}}^T{\mathbf{P}}^T\mathbf{P}\mathbf{u}\right\}\hfill \end{array}$$

(3)

As ${\mathbf{u}}_{\left(1\right)}$ has been specified as a unit vector, it likewise satisfies (4), as shown below:

$${\mathbf{u}}_{\left(1\right)}=argmax\left\{\frac{{\mathbf{u}}^T{\mathbf{C}}_m\mathbf{u}}{{\mathbf{u}}^T\mathbf{u}}\right\}$$

(4)

where the highest eigen values (decreasing order) corresponding to the largest eigen vectors $\mathbf{u}$ of the data are represented by ${\mathbf{C}}_m={\mathbf{P}}^T\mathbf{P}$, which is the covariance matrix of the data. Finally, the initial $d_r$ principal components of all the computed D principal components are retained where $d_r\ll d$ [6].

2.2. 3D-Convolutional Neural Network

Convolutional neural network (CNN) is a kind of an artificial neural network with a convolution layer as its building block. The integral part of this convolution layer is a mathematical convolution operator, which comprises of a sequence of kernels/filters which has a receptive field that is usually narrow in nature but traverses across the depth of the volume of the input data. CNN-based techniques, like traditional deep learning-based classification frameworks, are hierarchical designs with several convolution layers stacked one on top of the other. In traditional CNN-based frameworks, 2D convolutional kernels are used for any operations that take place on 2D image inputs. 2D convolution operations, on the other hand, are incapable of capturing differentiating features along the spectral/temporal dimension and can only extract spatial information. To overcome this issue, Ji et al. demonstrated the application of a 3D convolution operation on video-based classification which acted along both space (which is two-dimensional in nature) and also along the third dimension, which is time in this case [40]. Since HSI data are usually extracted and processed as a data cube which is three-dimensional in nature, extraction of low level features for HSI data cube can be effectively constructed using 3D-convolutions. As a result, 3D convolutions are considered for learning and capturing 3D local patterns, as well as preserving local spatial dependency around a neighborhood and spectral dependencies across the entire hyperspectral data cube for comprehensive volumetric data analysis, hence enhancing the effectiveness of the underlying framework. The value at position ($p,q,r$) on the jth feature map in the ith layer is produced using 3D convolution, as demonstrated in Equation (5):

$$h_{p,q,r}^{i,j}=f((W_{i,j}\ast V^{i-1}){}_{p,q,r}+b_{i,j})$$

(5)

where the weights and biases for the corresponding jth feature map are denoted by $W_{i,j}$ and $b_{i,j}$, respectively; $V^{i-1}$ represents the input feature maps from the $(i-1)$th layer connected to the current layer; the nonlinear function is denoted using f; and ∗ is the obvious convolution operation. It is also noteworthy that there is a direct relationship between how complex the learned patterns/features are of a data and the total number of 3D convolutional kernels used for the purpose of feature extraction. However, the network usually tends to be adversely affected by over-fitting with a drastic increase in the number of kernels used to extract meaningful patterns from the input data. However, a general notion is that the underlying network should consist of a big enough number of convolutional layers to extract finer and deeper data patterns and lesser number of feature maps in every layer so that it does not adversely take a toll on the overall computational cost (training and testing) [8].

2.3. Bi-Directional Long Short Term Memory

Bi-Directional Long Short Term Memory (LSTM) is an extension of traditional LSTMs and was introduced by Paliwal et al. in 1997 [41]. They are constructed by just putting two independent LSTMs together. This structure inherently facilitates the network to encode and extract information in both the directions, i.e., in the forward direction from time step $t_0,\dots ,t_n$ and also in the backward direction from time step $t_n,\dots ,t_0$, where n is the total number of time steps in input data. This encoded information along both the directions is put together and produced as an input to the subsequent layer in the underlying neural network framework. As a result, bi-directional LSTMs have the potential in enhancing the efficacy of information extraction and encoding (spectral information) while applied on high dimensional hyperspectral data, which results in the underlying network to perform robustly and produce better classification results.

Mathematically, let t be the time step, given a minibatch input ${\mathbf{X}}_t\in {\mathcal{R}}^{n\times d}$ (where n is the number of samples and d is the number of inputs per example), and let $\varphi$ be the hidden layer activation function, and assuming that $\overrightarrow{{\mathbf{H}}_t}\in {\mathcal{R}}^{n\times h}$ is the forward hidden state and $\overleftarrow{{\mathbf{H}}_t}\in {\mathcal{R}}^{n\times h}$ is the backward hidden unit for this particular time step, where h is the number of neurons in the hidden layer in the network, the forward and backward hidden state updates are as follows:

$$\begin{array}{c}\hfill \overrightarrow{{\mathbf{H}}_t}=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}^{\left(f\right)}+{\overrightarrow{\mathbf{H}}}_{t-1}{\mathbf{W}}_{hh}^{\left(f\right)}+{\mathbf{b}}_h^{\left(f\right)})\end{array}$$

(6)

$$\begin{array}{c}\hfill \overleftarrow{{\mathbf{H}}_t}=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}^{\left(b\right)}+{\overleftarrow{\mathbf{H}}}_{t+1}{\mathbf{W}}_{hh}^{\left(b\right)}+{\mathbf{b}}_h^{\left(b\right)})\end{array}$$

(7)

where the weights ${\mathbf{W}}_{xh}^{\left(f\right)}\in {\mathcal{R}}^{d\times h}$, ${\mathbf{W}}_{hh}^{\left(f\right)}\in {\mathcal{R}}^{h\times h}$, ${\mathbf{W}}_{xh}^{\left(b\right)}\in {\mathcal{R}}^{d\times h}$, ${\mathbf{W}}_{hh}^{\left(b\right)}\in {\mathcal{R}}^{h\times h}$, and biases ${\mathbf{b}}_h^{\left(f\right)}\in {\mathcal{R}}^{1\times h}$ and ${\mathbf{b}}_h^{\left(b\right)}\in {\mathcal{R}}^{1\times h}$ are all the model parameters.

Consequently, the forward and backward hidden states, $\overrightarrow{{\mathbf{H}}_t}$ and $\overleftarrow{{\mathbf{H}}_t}$ are concatenated to obtain the resultant hidden state output, ${\mathbf{H}}_t\in {\mathcal{R}}^{n\times 2h}$. In the case of deep bi-directional LSTMs with multiple hidden layers, ${\mathbf{H}}_t$ is produced on as an input to the sequential bi-directional LSTM layer. Lastly, the output layer computes the output ${\mathbf{O}}_t\in {\mathcal{R}}^{n\times q}$ (q: number of outputs). It is denoted mathematically in Equation (8) where the output ${\mathbf{O}}_t$ is obtained as a result of matrix multiplication between ${\mathbf{H}}_t\in {\mathcal{R}}^{n\times 2h}$ and ${\mathbf{W}}_{hq}\in {\mathcal{R}}^{2h\times q}$, which is finally added to a bias term ${\mathbf{b}}_q\in {\mathcal{R}}^{1\times q}$:

$$\begin{array}{c}\hfill {\mathbf{O}}_t={\mathbf{H}}_t{\mathbf{W}}_{hq}+{\mathbf{b}}_q\end{array}$$

(8)

In fact, the two directional units (forward and backward) can contain a varied number of hidden units within them in the underlying classification network.

2.4. Residual Neural Networks

A residual neural network (ResNet) is building blocks in a type where skip connections, or shortcuts, are used in ResNets to leap over some layers in the underlying network, simulating this capability of pyramidal cells in the cerebral cortex of a human brain. Most ResNet-based neural network topologies use double- or triple-layer skip connections with a nonlinear activation layer, such as the ReLU and batch normalization between these skip connections [42].

The two principal reasons to introduce skip connections in ResNets are as follows:

• To effectively avoid and overcome the issue of vanishing/diminishing gradients;
• To avoid the deterioration (accuracy saturation) problem, which occurs when a deep neural network has too many hidden layers, resulting in increased training errors.

As there are just a few layers to transport gradients through in the backward direction, introducing skip connections effectively simplifies the neural network’s training process, lessening the influence of vanishing gradients.

Mathematically, for a single skip connection, the layers of a neural network can either be indexed as $l-2$ to l or as l to $l+2$. These indexing paradigms work conveniently while defining skip connections in the backward or forward direction. It is convenient to describe the skip as $l+k$ from the current layer of the neural network as information is propagated forward through the network, but as a learning rule during back propagation, it is more convenient to describe the activation layer that is being reused as $l-k$, where $k-1$ turns out to be the skip number. Given a weight matrix ${\mathbf{W}}^{l-1,l}$, for weights between layer $l-1$ and l, and a weight matrix ${\mathbf{W}}^{l-2,l}$, for weights between layer $l-2$ and l, the resultant output of the residual connection is defined as shown in Equation (9):

$$\begin{array}{cc}\hfill {\mathbf{a}}^l& =\mathbf{g}({\mathbf{W}}^{l-1,l}·{\mathbf{a}}^{l-1}+{\mathbf{b}}^l+{\mathbf{W}}^{l-2,l}·{\mathbf{a}}^{l-2})\hfill \\ \hfill & =\mathbf{g}({\mathbf{Z}}^l+{\mathbf{W}}^{l-2,l}·{\mathbf{a}}^{l-2})\hfill \end{array}$$

(9)

where

• ${\mathbf{a}}^l$ is the activation output of neurons in layer l,
• $\mathbf{g}$ is the activation function of layer l,
• ${\mathbf{W}}^{l-1,l}$ is the weight matrix between layer $l-1$ and layer l in the neural network, and
• ${\mathbf{Z}}^l={\mathbf{W}}^{l-1,l}·{\mathbf{a}}^{l-1}+{\mathbf{b}}^l$

2.5. Feed-Forward Neural Network

A feed-forward neural network (FNN) is the simplest form of neural networks. It consists of a number of simple neuron-like processing units, usually organised in layers, and there is a connection between any two neurons in adjacent layers. While the preceding statement is true, each of those connections may have different strengths, which are vastly recognised as weights. The weights on these connections encode the knowledge of the defined neural network. In a classification framework, which is the area of focus here, all the FNN weights are modified in a way that, when an input pattern is presented to the network, the output units rightly categorize the input into one of the ground-truth classes present in the data set [43].

The FNN uses a supervised learning approach to know what category the input pattern belongs to. FNNs majorly rely on backpropagation to propagate the gradients from the classification decisions through a mathematically formulated loss function at the end of the forward pass. These propagation of gradients results in alteration of weights in the hidden layers pushing the gross value of the loss function to a global minimum. This technique is repeated a number of times, generally denoted as iterations or epochs, until either the loss function hits a global minimum or the changes in weights are no more significant [43].

3. Proposed Classification Methodology (SPAT-SPEC-HYP-ATTN)

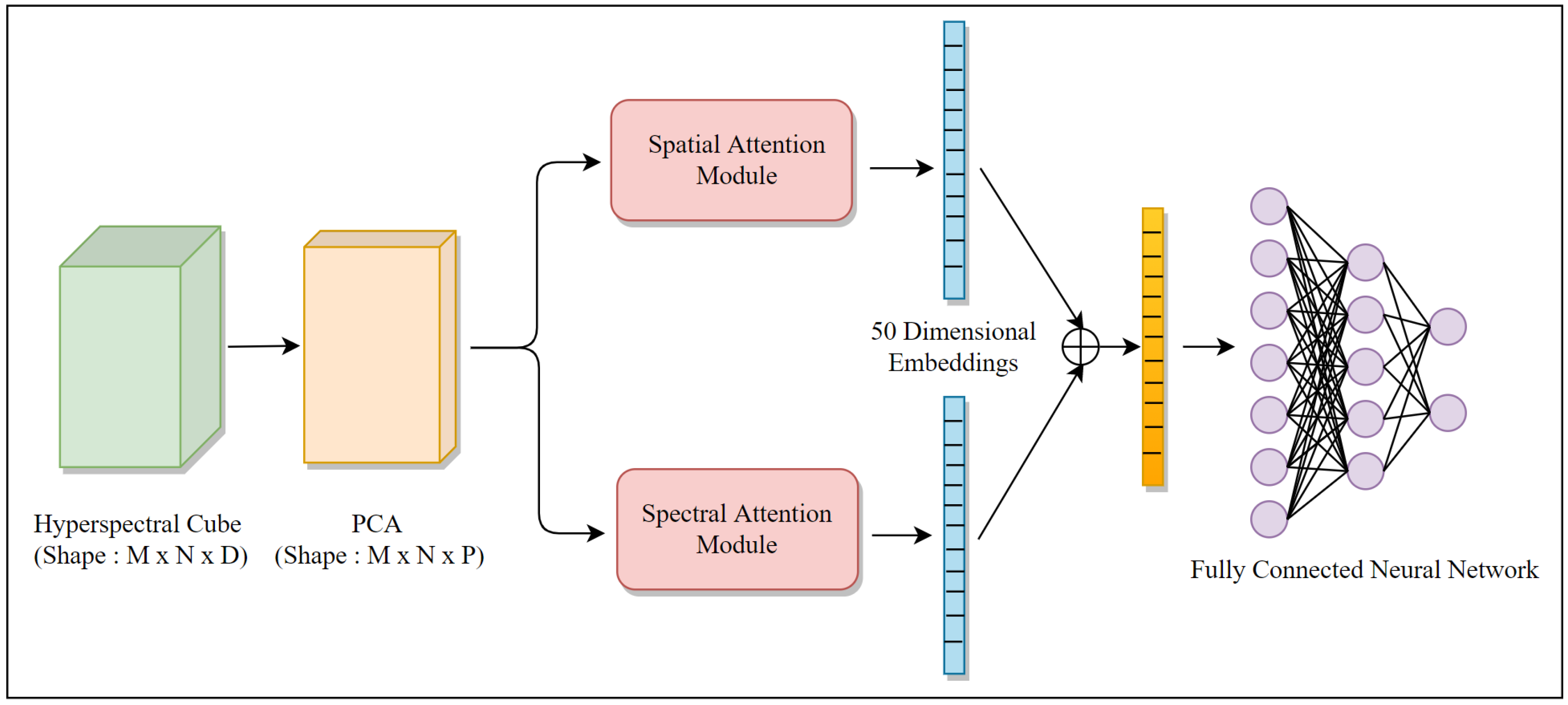
In our proposed methodology, the input high-dimensional hyperspectral cube is dimensionally reduced utilizing principal component analysis (PCA). PCA on raw input data minimizes noise, redundancy in data along the spectral dimension, and makes the process of mapping decision boundaries for classification easier. As a result, the input hyperspectral data cube, with a spatial resolution of $(M\times N)$ and a temporal resolution/dimension of D, has been reduced in dimension to $(M\times N\times P)$, where P is the new reduced spectral dimension. Furthermore, the result from PCA is now sent into two parallel attention modules as denoted in Figure 1, one for spatial attention mechanism and the other for spectral attention mechanism where more informative spatial and spectral features are selectively emphasized and the less useful ones are suppressed respectively for a superior classification efficacy. The architectural details of the spatial and spectral attention modules are as follows.

3.1. Spectral Attention Module

In this module, we propose a 3D-convolution based feature extraction and a bi-directional LSTM based spectral attention methodology to emphasize data along spectral bands that are of greater importance in achieving higher classification accuracy and suppressing information from spectral bands that are of lesser importance. The input to the spectral attention module is of dimension $(M\times N\times P)$ from which 3D windows of data around the image pixel of interest ($11\times 11$ in our work) are extracted to preserve closely related dependency between pixels in the windowed spatial area in tandem with the spectrally/temporally constructed features for the purpose of feature engineering with 3D convolutions. As a result, the shape of the modified input for the spectral attention model turns out to be $(11\times 11\times P)$.

This windowed information is now passed on to a 3D convolution layer as an input with 16 kernels of shape $(3\times 3\times 32)$, which is followed immediately by a 3D average pooling layer of size $(2\times 2\times 2)$. The resultant features from this pooling layer are forwarded into a second 3D convolution based feature extraction layer with 32 filters of the shape $(3\times 3\times 8)$, which efficiently extracts local spatial neighborhood information from the input data whilst conserving spectral band correlation. The output from this phase of the feature extraction and attention module is flattened to produce an output of shape $(L\times 1)$ as denoted in Figure 2.

As explained in Equations (6)–(11), this vector of size $(L\times 1)$ was successively passed as an input to a bi-directional LSTM-based spectral attention gating mechanism. This attention gating technique highlights relevant informative pixels while suppressing data from less informative spectral regions. Using forward and backward hidden state implementation of a bi-directional LSTM, where $\overrightarrow{{\mathbf{H}}_t}\in {\mathcal{R}}^{n\times h}$ represents the forward hidden state implementation and $\overleftarrow{{\mathbf{H}}_t}\in {\mathcal{R}}^{n\times h}$ represents the backward hidden state implementation, and their outputs are defined in Equations (6) and (7), where the number of hidden units is represented by h and the number of inputs is denoted by n; the attention gating mechanism is mathematically represented as follows:

The output of the final hidden state output, defined as ${\mathbf{H}}_t$, is obtained as a result of element-wise multiplication between $\overrightarrow{{\mathbf{H}}_t}$ and $\overleftarrow{{\mathbf{H}}_t}$, which is depicted in Equation (10). The mathematical calculations outlined in Equations (6), (7), and (10) are performed twice before the attention gating mechanism’s final output ${\mathbf{O}}_{t3}$ is achieved, as illustrated in Equations (11) and (12). The notation ⊗ in Equations (10) and (12) denotes element-wise multiplication, and ⊕ in Equation (12) denotes element-wise addition.

For a 50-dimensional feature embedding vector, these produced input data representations are now utilized as an input for a two dense layer based feed forward neural network (FNN) with 100 and 50 nodes in the first and second layer, respectively, with an inclusion of a dropout layer between these two dense layers and has a value of 0.2. The complete proposed spectral feature extraction and bi-directional LSTM-based attention module is denoted in Figure 2:

$$\begin{array}{c}\hfill {\mathbf{H}}_t=\overrightarrow{{\mathbf{H}}_t}\otimes \overleftarrow{{\mathbf{H}}_t}\end{array}$$

(10)

$$\begin{array}{c}\hfill {\mathbf{O}}_{t1}=softmax\left({\mathbf{H}}_t\right)\end{array}$$

(11)

$$\begin{array}{c}\hfill {\mathbf{O}}_{t2}={\mathbf{O}}_{t1}\otimes {\mathbf{X}}_t\mathrm{and}{\mathbf{O}}_{t3}={\mathbf{O}}_{t2}\oplus {\mathbf{X}}_t\end{array}$$

(12)

3.2. Spatial Attention Module

In this module, we propose a 3D-convolution based spatial attention paradigm which selectively amplifies weightage to specific areas of feature maps through a softmax activation-based gating mechanism which effectively captures the spatial relationship between data pixels in a window, boosting the feature representation capability. In addition, a ResNet-based feature extraction and encoding methodology has been discussed in this work, which effectively extracts spatial information and encodes it into a 50-dimensional vector to achieve superior classification performance.

Firstly, a spatial window of $(11\times 11)$ around every data point is extracted which transforms the input shape of the spatial attention module to $(11\times 11\times P)$, from $(M\times N\times P)$, which was the output shape from the PCA implementation block. Furthermore, this input is forwarded to a 3D-convolution-based feature extraction layer with 1 filter of shape $(1\times 1\times 25)$, which is serially followed by a second 3d-convolution layer with 1 filter of shape $(1\times 1\times 26)$. The choice of the number of convolutional kernels and their shape are astutely made to ensure that the output spectral dimension of the convolution operations precisely matches the spectral dimension of the input data block. These convolution operations are followed by a softmax activation layer which produces an attention map which produces the probabilistic weightage of pixels in the feature map ranging between 0 and 1. Consequently, the spatial attention gating mechanism proposed in our work is clearly described in Figure 3.

If $\mathbf{X}\in \in {\mathcal{R}}^{11\times 11\times P}$ is the input to the spatial attention module, then the output of the first and the second 3D-convolution operations are obtained as shown in Equations (13) and (14):

$$\begin{array}{c}\hfill {\mathbf{O}}_1=f(({\mathbf{W}}_1\ast \mathbf{X})+{\mathbf{b}}_1)\end{array}$$

(13)

$$\begin{array}{c}\hfill {\mathbf{O}}_2=f(({\mathbf{W}}_2\ast {\mathbf{O}}_1)+{\mathbf{b}}_2)\end{array}$$

(14)

where ${\mathbf{O}}_1$ and ${\mathbf{O}}_2$ are the outputs of the first and the second 3D-convolution operations, respectively, ${\mathbf{W}}_1$ and ${\mathbf{W}}_2$ are the weights of the first and second convolution layer in the defined network, the nonlinear activation function is denoted by f, while the convolution operator is denoted by ∗. Furthermore, Equations (15) and (16) denote the gated weighting spatial attention mechanism implemented in our work where ${\mathbf{O}}_{final}$ is the final output. The notation ⊗ denotes element-wise multiplication and ⊕ denotes element-wise addition as seen in Equation (16):

$$\begin{array}{c}\hfill {\mathbf{O}}_3=softmax\left({\mathbf{O}}_2\right)\end{array}$$

(15)

$$\begin{array}{c}\hfill {\mathbf{O}}_4={\mathbf{O}}_3\otimes \mathbf{X}\mathrm{and}{\mathbf{O}}_{final}={\mathbf{O}}_4\oplus \mathbf{X}\end{array}$$

(16)

The resultant output from the 3D-CNN based attention mechanism is produced as an input to a set of three identical and sequential residual blocks for spatial feature extraction. An advantage that residual blocks brings to the table is their ability to solve the vanishing gradient problem when the depth of neural network increases by allowing an alternate path through skip connections for the gradient to flow through. In addition, these skip connections aid in facilitating the underlying neural network framework to learn the identity functions which ensure that the deeper layers in the network perform equally as well as the shallow layers in the network. This proposed 3D-CNN-based attention methodology and ResNet-based feature extraction mechanism is shown in Figure 3. The three 2D-convolution layers in every residual block are equipped with 32 feature extraction filters of shape $(3\times 3)$, 64 kernels of shape $(3\times 3)$ and 64 filters with a dimension of $(1\times 1)$. The features extracted from the residual blocks are now input to FNN for 50-dimensional feature encoding. The number of layers in the FNN used is two, which consists of 100 neurons in the first hidden layer of the FNN and 50 neurons in the second layer of the FNN network.

Finally, the encoded features from both the spatial attention module and spectral attention module and added together element-wise and input to another FNN for classification are depicted in Figure 1. This FNN based network has two fully connected layers where the first layer has 25 neurons and the second fully connected layer, which is the final layer of the network, consists of C neurons with an added dropout functionality between the two layers with a dropout value of $0.2$. C here denotes the total number of classes present in the datasets used for assessing the efficacy of our proposed methodology.

4. Methodologies for Comparison

4.1. SPEC-HYP-ATTN

There is no explicit spatial attention mechanism in this technique. The goal of this research work is to see how well a hyperspectral image (HSI) classification framework based solely on a light-weighted, computationally efficient spectral attention mechanism performs. As a result, this model uses principal component analysis directly on input data for spectral feature extraction, noise reduction, and spectral information redundancy minimization. Section 5 briefly discusses the experimentally measured size of the lower dimensional space P. Now, data, which are in a lower dimensional feature space, are spatially windowed to extract patches for bi-directional LSTM-based spectral attention and FNN-based classification, where window size is fixed to $(11\times 11\times P)$. The generalized framework for this methodology SPEC-HYP-ATTN is exactly as depicted in Figure 2 with a minute alteration to the FNN architecture at the tail-end of the architecture. The FNN network in this approach has three dense layers with 100, 50 and C neurons in the first, second, and third layer of FNN, respectively. There also is an inclusion of a dropout of 0.2 in the first two fully connected layers. C here denotes the total number of classes present in the datasets used for assessing the efficacy which is discussed in Section 5 of this work.

4.2. SPAT-HYP-ATTN

In this methodology, we study the contributions of a spatial attention-based classification framework on hyperspectral data analysis using this methodology. In SPAT-HYP-ATTN, a PCA based dimensionality reduction module is integrated to linearly project input HSI data in its original dimensional space to an orthogonally projected lower dimensional space to extract temporal information off the input data and also as a noise reduction technique. Therefore, this PCA based hyperspectral data analysis technique used for noise reduction characterizes the robustness of the proposed methodology especially in conditions where the input data are noisy. The output from PCA is windowed to a shape of $(11\times 11\times P)$ and passed to a 3D-CNN based spatial attention module exactly as depicted in Figure 3 which is forwarded to a ResNet based spatial feature extraction and feature embedding framework. Finally, these encoded features are classified with a FNN-based classification framework. The framework for this methodology is a carbon copy of the architecture presented in Figure 3 with a tiny modification to the FNN at the end of the network. Here, the FNN has three dense layers for classification, with 100 neurons in the first layer, 50 neurons in the second layer, and C number of neurons in the final layer of the FNN-based architecture, with a 0.2 dropout between the first two dense layers. In addition, as in Section 4.1, C here denotes the total number of classes present in the datasets used for assessing the efficacy in this comprehensive HSI data analysis.

4.3. GAB-RP-S-3DCNN

We compare the proposed attention models introduced in this work with a prior work in [8], which developed a unique spatial-spectral feature extraction and HSI classification based analysis model. The methodology in [8] consisted of a spatial feature extraction technique using Gabor filtering on raw hyperspectral data cube in their research. This technique achieved spatial feature extraction by convolving individual temporal bands of HSI data with distinct Gabor filters which differed from one another in terms of frequency responses and orientation information embedded within the individual Gabor filters [44].

In prior work [8], the Gabor filtering greatly varies based on the values chosen for frequency f and the orientation of the Gabor filters denoted by $\theta$, and that the choice of these values majorly impact the results achieved in this HSI data classification and analysis methodology. As a result, the empirical values of $f=0.8$ and $\theta =0$ were picked since they generated the best outcomes in their research. In conjunction, sparse random projections (sparse RPs) are also used for the purpose of dimensionality reduction, and to offer a computationally light-weighted spectral information extraction. In this study, the size of the subspace to which high dimensional HSI data are projected to using sparse RPs is set to 30. Finally, the data are windowed to $(21\times 21\times 30)$ and fed into a 3D-CNN based classification network.

The initial layer of this 3D-CNN based classification method is a convolutional layer with 8 convolution filters of size $(3\times 3\times 7)$ which is immediately followed by a max pooling layer with $(2\times 2\times 2)$ as a dimension. This is followed by two 3D convolution operations with 16 and 32 filters with filter dimensions of $(3\times 3\times 5)$ and $(3\times 3\times 3)$ respectively. This part of the classification methodology is now followed by a 2D convolution operation for spatial feature construction and engineering with 64 filters of size $(3\times 3)$. The final part of the network consists of three dense layers with 256 nodes in the first layer, 128 nodes in the second layer and C number of nodes in the final layer with a dropout layer with a value of $0.4$ between every two of three layers. C here denotes the total number of classes present in the datasets used for assessing the efficacy in this comprehensive HSI data analysis [8].

4.4. SSAN (Spectral-Spatial Attention Network)

Sun et al. in [45] introduce a comprehensive spatial-spectral attention-based methodology for pixel-wise HSI data classification. Their proposed framework has a separate spatial and spectral modules for feature extraction in which 3D-convolutions play a prominent role. The spectral-attention module introduced in this work is comprised of two back-to-back convolution operations with 32 filters each which are of $(1\times 1\times 7)$ in dimension, with a combination of two layers of batch normalisation and rectified linear units (ReLU) based activation layers. However, the spatial module is composed of two convolutional layers with 64 kernels of shape $(3\times 3\times q)$ where q is the spectral dimension of the input, two batch normalization layers, two ReLU activation layers, and two attention modules after each 3D-convolution layer. Additionally, a 3D-convolution, matrix reshaping and multiplication, matrix addition-based attention module is introduced in this work for a comprehensive analysis on improvements in classification efficacy through the attention mechanism. The window size of HSI data around the pixel of interest is set to $(7\times 7)$ in this work. The detailed discussion on this generalized classification framework and its results is clearly documented in [45].

4.5. SVM-CK

In this work, we include the state-of-the-art composite kernel oriented support vector machine (SVM) proposed in [20] to test our proposed dual branch spatial-spectral attention-based HSI pixel-wise data classification algorithm. For spatial-spectral information retrieval and classification, this technique combined a spatial mean kernel which is of size $(3\times 3)$ for spatial feature learning in combination with an RBF spectral kernel for spectral feature analysis and learning. The input for the RBF based spectral kernel is the raw input hyperspectral pixel vector along the temporal domain in SVM-CK, whereas the spatial mean kernel is applied on the input data which is windowed in the shape of $(3\times 3)$ to effectively include spatial information present around the pixel of interest. LIBSVM is the platform that was used to analyze and conduct all the experimentation related to SVM-CK, and no dimensionality reduction technique was applied on the input data here and instead data in its original format and dimensions were used for experimentation.

5. Experimental Results

The efficacy of our proposed methodology, dual-branch spatial-spectral attention-based HSI classification framework SPAT-SPEC-HYP-ATTN, as defined in Section 3, is validated and compared against five other classification methodologies, namely SPAT-HYP-ATTN, SPEC-HYP-ATTN, GAB-RP-S-3DCNN, SSAN, and SVM-CK in this part of the paper.

5.1. Datasets

All our studies were conducted on three datasets, two of which were collected using an Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor and are named Salinas Valley and Indian Pines. The third dataset was collected using a Reflective Optics System Imaging Spectrometer (ROSIS) sensor by flying the sensor over the University of Pavia in Northern Italy [46]. The Salinas dataset consists of 224 spectral bands; however, after deletion of 20 water absorption bands present in the data, the number of spectral dimensions are brought down to 204. Similarly, Indian Pines has 220 spectral bands and, with the removal of 20 water absorption bands, the final spectral dimension turns out to be 200. The Salinas datasets have the spatial resolution of $(512\times 217)$ with 16 ground-truth classes which includes fruits, vegetables, different phases in growing lettuce, vineyard fields, etc. The Indian Pines dataset has a spatial resolution of $(145\times 145)$ with 16 classes consisting of alfalfa, different variations of corn vegetation, grass pastures, etc. The ROSIS sensor captures data with a spectral dimension of 103, and each of those spectral bands are made up of a spatial dimension of $(610\times 340)$ with a spatial resolution of 1.3 m, spanning across nine land-cover categories. As a result, in our proposed work, the value of C is set to 16, 16, and 9 for the Salinas dataset, Indian Pines dataset, and the University of Pavia dataset respectively. The training set for each dataset was picked at random, ranging from 1% to 10% of the total.

5.2. Parameter Tuning and Experimental Setup

In our work, all the parameters that were used in the experimentation phase were carefully chosen and optimized empirically. All the experiments were run thrice and averaged over these three trials to effectively avoid introduction of bias that may be caused by sampling the training and testing data points randomly. Alongside this, the average accuracies produced by experimentation in our work with a detailed documentation of the execution times are made in this study. Categorical cross-entropy is used as the objective function in all of our experiments, with a learning rate of 0.0001 and a decay of ${10}^{-6}$. All the experiments related to SPAT-SPEC-HYP-ATTN, SPAT-HYP-ATTN, SPEC-HYP-ATTN and GAB-RP-S-3DCNN use the Adams optimizer. The suggested SPAT-SPEC-HYP-ATTN architecture has, in total, 223,820 number of trainable parameters, and a batch size of 32 was determined empirically. On Salinas and Pavia University datasets, the proposed classification frameworks were trained for 60 epochs, whereas the networks were trained for 100 epochs in the case of the Indian Pines dataset. Apart from experiments related to SSAN, no GPUs were made us of while conducting experiments on any of the aforementioned techniques in our research work. All our experiments were conducted on a workstation with an Intel(R) Core(TM) i7-7700HQ processor and 16 GB RAM, whereas SSAN was executed on a workstation with an Intel Core i7-5930K processor with 64 GB RAM and a GeForce GTX Titan X graphics card [45].

Additionally, it is to be noted that the value of P, which is representation of the data in the reduced feature space and the output of the PCA module on the input raw HSI data cube, as denoted in Figure 1, Figure 2 and Figure 3, is empirically set to 50 in all the experiments related to SPAT-SPEC-HYP-ATTN, SPAT-HYP-ATTN and SPEC-HYP-ATTN for all the three datasets as it generated optimal results. In addition, the value of L in Figure 2 is set to be 256 in number for all the three datasets, namely, Salinas, Pavia University and Indian Pines dataset.

5.3. Discussion

The classification maps for $5\%$ of randomly chosen training samples spanning the proposed dual-branch spatial-spectral attention and classification framework and other data analysis approaches for the Salinas dataset are presented in Figure 4 in this paper. The classification maps for all of the approaches covered in our study for the Pavia University scene are shown in Figure 5. Similarly, the classification maps for the Indian Pines dataset along with their respective classification accuracies are clearly documented in Figure 6.

Table 1. Total number of class-specific training and testing samples used for a Salinas dataset for 5% training data.

#	Class Name	# of Training Samples	# of Testing Samples
1	Brocoli-green-weeds-1	100	1909
2	Brocoli-green-weeds-2	186	3540
3	Fallow	99	1877
4	Fallow-rough-plow	70	1324
5	Fallow-smooth	134	2544
6	Stubble	198	3761
7	Celery	179	3400
8	Grapes-untrained	564	10,707
9	Soil-vinyard-develop	310	5893
10	Corn-senesced-green-weeds	164	3114
11	Lettuce-romaine-4wk	53	1015
12	Lettuce-romaine-5wk	96	1831
13	Lettuce-romaine-6wk	46	870
14	Lettuce-romaine-7wk	54	1016
15	Vinyard-untrained	363	6905
16	Vinyard-vertical-trellis	90	1717
	Total	2706	51,423

,

Table 2. Total number of class-specific training and testing samples used for Pavia University dataset for 5% training data.

#	Class Name	# of Training Samples	# of Testing Samples
1	Asphalt	332	6299
2	Meadows	932	17,717
3	Gravel	105	1994
4	Trees	153	2911
5	Painted Metal Sheets	67	1278
6	Bare Soil	251	4778
7	Bitumen	67	1263
8	Self-Blocking Bricks	184	3498
9	Shadows	47	900
	Total	2138	40,638

and

Table 3. Total number of class-specific training and testing samples used for Indian Pines dataset for 5% training data.

#	Class Name	# of Training Samples	# of Testing Samples
1	Alfalfa	2	44
2	Corn-notill	71	1357
3	Corn-mintill	41	789
4	Corn	12	225
5	Grass-pasture	24	459
6	Grass-trees	37	693
7	Grass-pasture-mowed	1	27
8	Hay-Windrowed	24	454
9	Oats	1	19
10	Soybean-notill	49	923
11	Soybean-mintill	123	2332
12	Soybean-clean	30	563
13	Wheat	10	195
14	Woods	63	1202
15	Buildings-Grass-Trees-Drives	19	367
16	Stone-Steel-Towers	5	88
	Total	512	9737

, respectively, show the result of randomly sampling data points for training and testing purposes from every class for a train–test split of $5\%$ and and $95\%$, respectively, used in all the experimentation detailed in Section 3 and Section 4.

When compared to other methodologies, our proposed bi-directional LSTM-based and 3D-CNN based spectral and spatial attention techniques respectively coupled with FNN-based HSI classification framework produce more coherent classification regions in the classification maps and very few misclassifications, as shown in Figure 4, Figure 5 and Figure 6. Additionally,

Table 4. Class-specific accuracies of the Salinas dataset for 5% of training data for the proposed classification methodologies and models used for comparison.

#	Class Name	SPAT-SPEC-HYP-ATTN	SPAT-HYP-ATTN	SPEC-HYP-ATTN	GAB-RP-S-3DCNN	SSAN	SVM-CK
1	Brocoli-green-weeds-1	100	99.9	100	99.9	100	99.6
2	Brocoli-green-weeds-2	100	100	100	100	100	99.8
3	Fallow	100	100	99.9	100	100	99.9
4	Fallow-rough-plow	98.9	99.1	99.5	99.5	99.6	98.3
5	Fallow-smooth	99.7	99.4	99.3	99.5	99.7	97.6
6	Stubble	100	100	100	100	100	99.8
7	Celery	99.9	100	100	100	100	99.1
8	Grapes-untrained	99.4	95.5	92.3	94.0	96.2	90.3
9	Soil-vinyard-develop	100	100	99.8	99.8	100	98.6
10	Corn-senesced-green-weeds	99.6	99.5	99.0	99.0	99.9	98.7
11	Lettuce-romaine-4wk	99.9	100	99.1	99.0	99.8	99.5
12	Lettuce-romaine-5wk	99.9	100	99.8	99.9	99.9	99.5
13	Lettuce-romaine-6wk	99.9	99.7	92.8	99.6	99.4	98.3
14	Lettuce-romaine-7wk	98.1	99.5	92.2	99.3	99.1	96.5
15	Vinyard-untrained	100	93.8	87.2	90.2	94.0	83.2
16	Vinyard-vertical-trellis	100	99.8	99.4	89.7	99.8	99.3
	OA (%)	99.01	98.00	96.10	97.24	98.24	93.36
	$\kappa$ (%)	98.94	97.90	95.82	96.93	98.16	92.37

,

Table 5. Class-specific accuracies of Pavia University dataset for 5% of training data for the proposed classification methodologies and models used for comparison.

#	Class Name	SPAT-SPEC-HYP-ATTN	SPAT-HYP-ATTN	SPEC-HYP-ATTN	GAB-RP-S-3DCNN	SSAN	SVM-CK
1	Asphalt	99.0	99.0	97.7	96.8	97.8	91.1
2	Meadows	100	99.8	98.9	98.9	100	94.7
3	Gravel	98.8	95.3	86.3	91.6	94.6	86.5
4	Trees	99.1	98.9	98.5	97.2	97.9	85.7
5	Painted Metal Sheets	100	99.4	100	99.1	99.4	99.4
6	Bare Soil	99.9	100	96.0	96.5	99.9	90.9
7	Bitumen	99.8	99.8	95.6	99.8	98.9	93.8
8	Self-Blocking Bricks	98.7	95.9	87.9	92.1	95.8	82.7
9	Shadows	97.7	99.4	98.8	97.1	98.0	97.5
	OA (%)	99.52	98.33	96.77	97.13	99.25	91.62
	$\kappa$ (%)	99.38	98.12	96.02	96.53	98.87	91.03

and

Table 6. Class-specific accuracies of Indian Pines dataset for 5% of training data for the proposed classification methodologies and models used for comparison.

#	Class Name	SPAT-SPEC-HYP-ATTN	SPAT-HYP-ATTN	SPEC-HYP-ATTN	GAB-RP-S-3DCNN	SSAN	SVM-CK
1	Alfalfa	61.1	86.2	92.8	82.8	94.3	89.6
2	Corn-notill	96.0	94.4	86.9	82.7	92.1	89.4
3	Corn-mintill	94.7	83.5	84.1	78.2	83.4	89.5
4	Corn	95.4	92.2	77.9	79.4	82.6	92.3
5	Grass-pasture	95.6	94.1	99.3	94.8	94.7	90.3
6	Grass-trees	97.7	97.8	65.0	98.7	93.6	80.1
7	Grass-pasture-mowed	89.4	57.8	80.6	87.9	92.1	92.4
8	Hay-Windrowed	96.8	99.4	70.7	98.5	75.2	87.0
9	Oats	75.2	68.3	87.5	52.6	88.8	86.1
10	Soybean-notill	93.2	95.7	89.4	83.4	91.4	89.4
11	Soybean-mintill	87.3	92.0	94.0	83.8	91.5	91.7
12	Soybean-clean	99.4	95.4	95.6	96.7	90.7	84.5
13	Wheat	98.9	98.3	98.5	94.6	92.5	93.0
14	Woods	96.5	97.6	86.6	87.1	93.8	89.2
15	Buildings-Grass-Trees-Drives	94.3	98.1	83.7	81.4	90.0	90.7
16	Stone-Steel-Towers	95.8	93.3	97.8	96.6	86.4	91.9
	OA (%)	96.21	94.06	83.86	91.57	88.71	87.93
	$\kappa$ (%)	95.72	93.66	83.01	90.45	88.13	86.34

present the effectiveness of the proposed methodology SPAT-SPEC-HYP-ATTN through their class-wise classification performance evaluation for all the hyperspectral data analysis models in this study for the Salinas, Pavia University, and Indian Pines datasets, respectively. From Table 4, Table 5 and Table 6, it is evident that SPAT-SPEC-HYP-ATTN indeed outperformed other comparison hyperspectral data analysis frameworks in terms of its classification performance.

The overall classification accuracy performance depicted in Figure 7, Figure 8 and Figure 9 for the Salinas dataset and Pavia University dataset, respectively, further affirms the superior classification performance of our proposed methodology, SPAT-SPEC-HYP-ATTN. In particular, SPAT-SPEC-HYP-ATTN outperformed all other HSI data analysis methodologies of comparison used in this work, particularly when compared with the traditional 3D-CNN based feature construction and hyperspectral image classification model, GAB-RP-S-3DCNN, a bi-directional LSTM-based spectral attention-only classification framework, SPEC-HYP-ATTN, and a conventionally used SVM-based spatial-spectral information inclusion model, SVM-CK as demonstrated in the aforementioned figures.

The major reason for the proposed approach SPAT-SPEC-HYP-ATTN exhibits superior classification performance when compared to all the other methodologies used for comparison is that the SPAT-SPEC-HYP-ATTN framework has two separate intrinsic modules for spatial attention and spectral attention which bring forward the enhanced ability of the model to selectively emphasize information, spatially through a 3DCNN-based spatial attention and a ResNet-based feature encoding scheme and spectrally through a bi-directional LSTM-based spectral attention mechanism. These softmax activation function based gating attention-mechanism schemes aid in engineering and weighting features that effectively boost the overall performance of the framework. Even when only $5\%$ of the samples were used to train the model, our technique SPAT-SPEC-HYP-ATTN achieved the best classification results.

The overall execution time of the approaches presented in our study for the Salinas, Pavia University, and Indian Pines datasets is tabulated in

Table 7. Overall execution time (in minutes) of all the methodologies in comparison for 5% training data.

Dataset	SPAT-SPEC-	SPAT-	SPEC-	GAB-RP-	SSAN	SVM-
(5% Training)	HYP-ATTN	HYP-ATTN	HYP-ATTN	S-3DCNN		CK
# of Trainable Parameters	224,214	150,846	15,957	313,472	180,930	-
Salinas	103.31	35.77	28.18	40.36	86.28	14.42
Pavia University	103.79	33.97	22.95	66.20	53.25	14.29
Indian Pines	60.51	18.67	13.71	21.75	16.95	13.46

. Furthermore,

Table 8. Classification results of the proposed SPAT-SPEC-HYP-ATTN methodology on varying spatial window sizes for 5% training data.

	Salinas Dataset		Pavia University Dataset		Indian Pines Dataset
Window Size	Accuracy (%)	Time (min)	Accuracy (%)	Time (min)	Accuracy (%)	Time (min)
$(3\times 3)$	96.38	20.53	96.62	14.77	81.29	4.01
$(5\times 7)$	96.87	24.22	97.54	18.96	82.39	4.53
$(7\times 7)$	97.93	47.38	98.60	30.60	91.14	14.33
$(9\times 9)$	98.71	45.00	99.33	59.05	93.80	20.28
$(11\times 11)$	99.01	103.31	99.52	103.79	96.21	60.51
$(13\times 13)$	99.83	246.19	99.67	290.60	97.32	99.08

presents the overall classification results of the proposed approach SPAT-SPEC-HYP-ATTN on varying spatial window sizes along with their execution times for $5\%$ training data samples for all the datasets used in our study. In addition, to empirically justify that our proposed methodology does not suffer over-fitting due to training with limited number of samples (i.e., 5% in our case), a graphical plot of loss value versus number of epochs during training and validation phases of our experimentation is documented in Figure 10 for all the three datasets. Thus, Figure 10 shows that both the training and validation losses gracefully converge to their optimal values without any over-fitting issues for all the three datasets during training and validation in a limited samples scenario.

Furthermore, Table 8 shows the impact of different window sizes on the proposed technique SPAT-SPEC-HYP-ATTN’s performance and supports our argument for using a window size of (11 × 11), since it produces the best trade-off between computational efficiency and the classification performance that is desired when contrasted with the other state-of-the-art methodologies discussed in our work. Table 7 shows that, when compared to alternative HSI data analysis models discussed in this work, SPAT-SPEC-HYP-ATTN gave improved classification performance to the desired extent.

6. Conclusions

In this work, several novel deep-learning-based spatial-spectral, spatial-only, and spectral-only attention and hyperspectral classification frameworks, namely, SPAT-SPEC-HYP-ATTN, SPAT-HYP-ATTN, and SPEC-HYP-ATTN, respectively, are introduced. Compared to the traditional HSI data analysis and classification methodologies in literature, a gating mechanism-based spatial and spectral attention technique proposed in our work aids in selectively emphasizing important features present in hyperspectral data; at the same time, it suppresses information that is of lesser importance, thus helping the classification framework to produce superior results. When compared to other spatial attention- and spectral-attention-only based classification approaches, the proposed deep-learning-based spatial-spectral attention and classification methodology SPAT-SPEC-HYP-ATTN yields outstanding classification performance while being robust under limited training sample scenarios, paving the way for new research avenues in hyperspectral remote sensing.