Mapping Seasonal Leaf Nutrients of Mangrove with Sentinel-2 Images and XGBoost Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Sampling
2.2. Chemical Analysis of Leaf Nutrients
2.3. Sentinel-2 Images Pre-Processing and Vegetation Indices Extraction
2.4. Estimation of Mangrove Seasonal Leaf Nutrients with Machine Learning Method
2.4.1. Three Machine Learning Models
2.4.2. Two Modeling Strategies
2.4.3. Model Evaluation
2.5. Mapping of Seasonal Mangrove Leaf Nutrients
3. Results
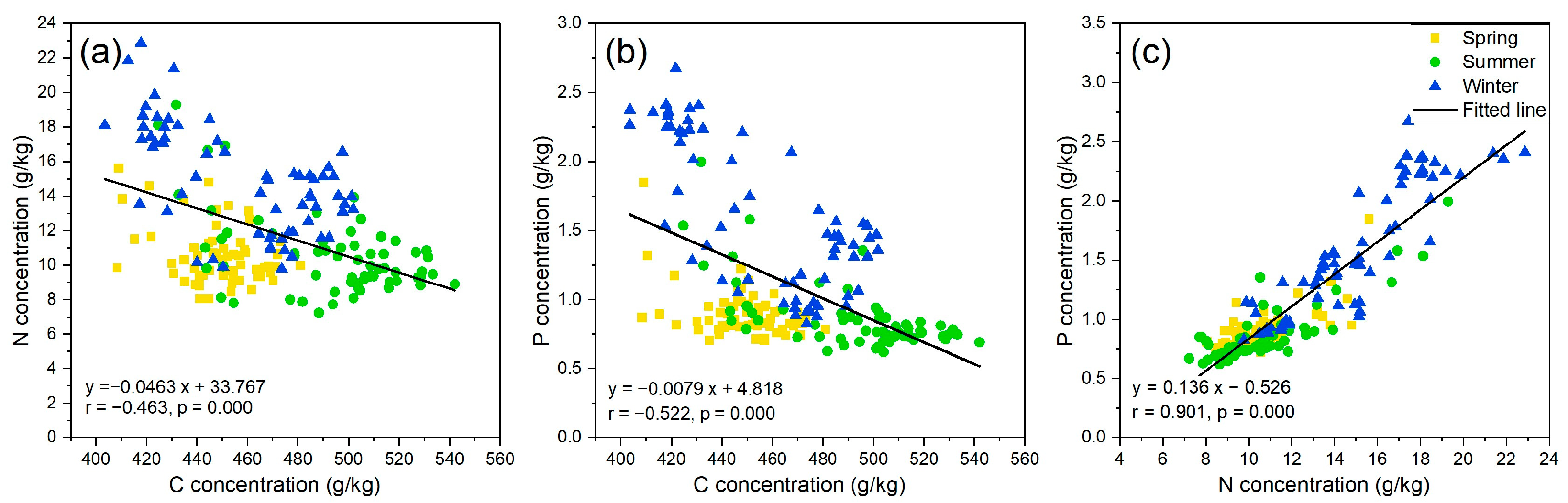
3.1. Seasonal Variation of Mangrove Leaf Nutrients
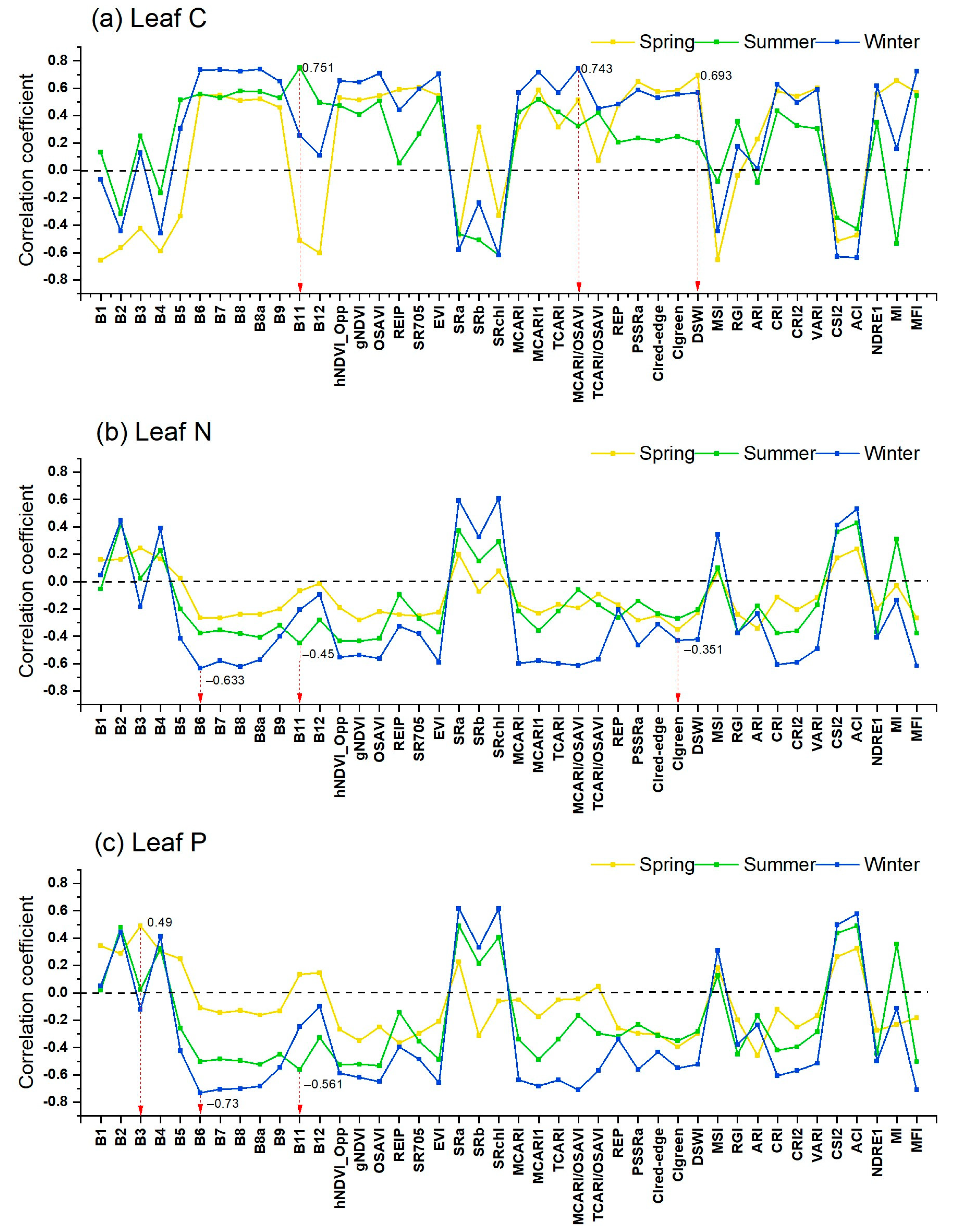
3.2. Correlation of Leaf Nutrients against Spectral Features of Seasonal Sentinel-2 Images
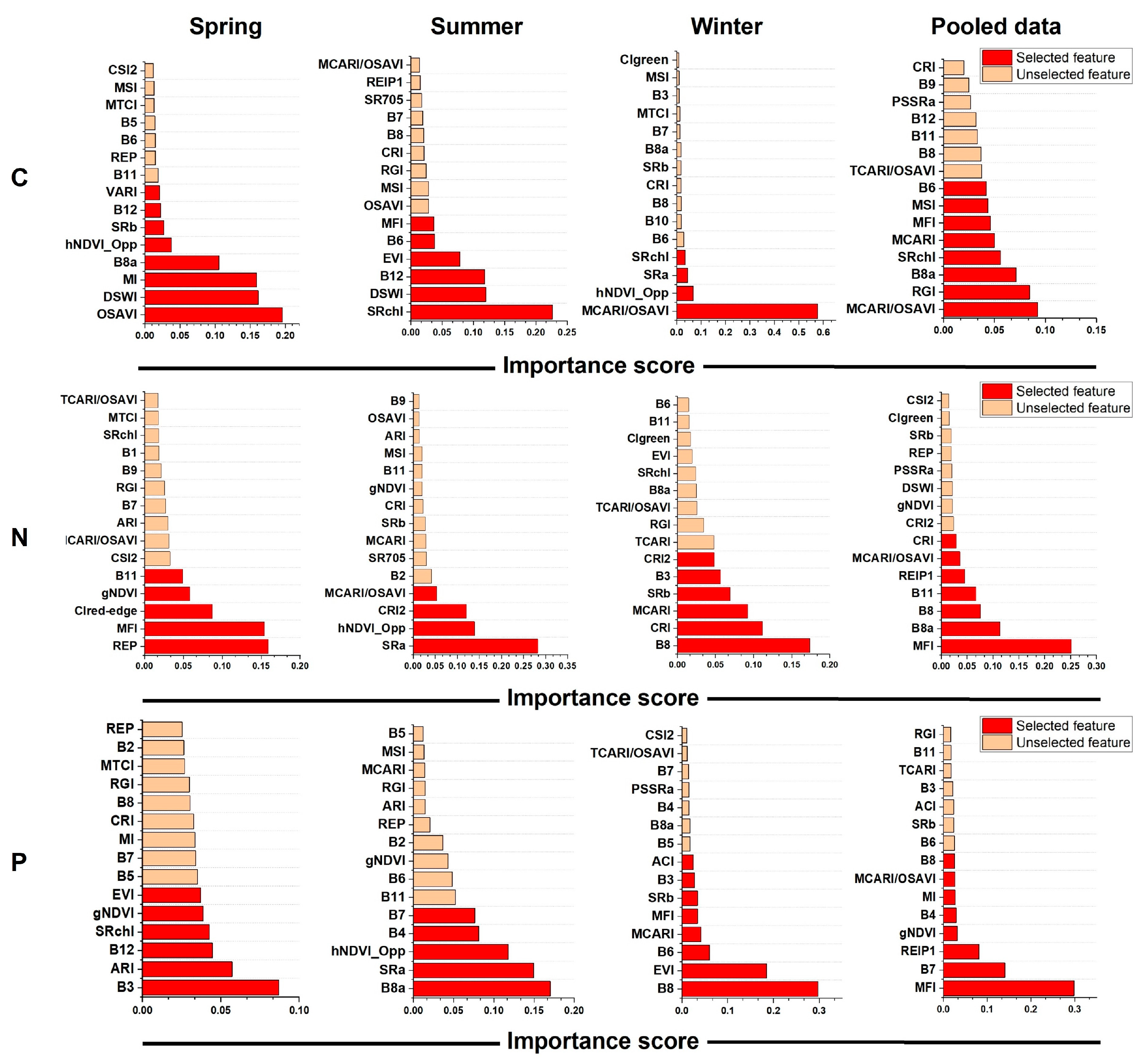
3.3. Comparison of Three Machine Learning Models in Estimating Leaf Nutrients
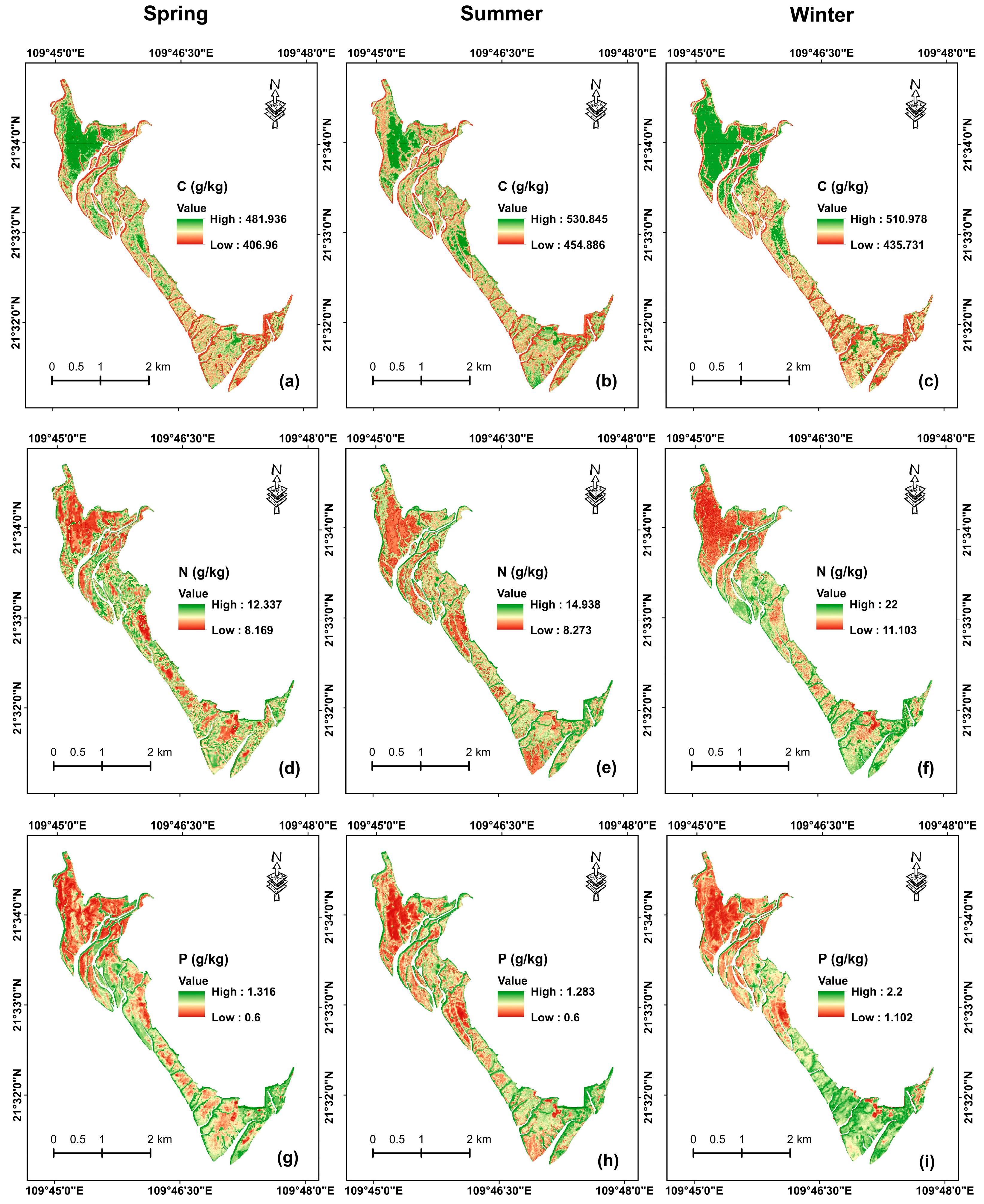
3.4. Mapping Seasonal Leaf Nutrients with XGBoost Model
3.4.1. Mapping Leaf C, N, and P Concentrations in Three Seasons
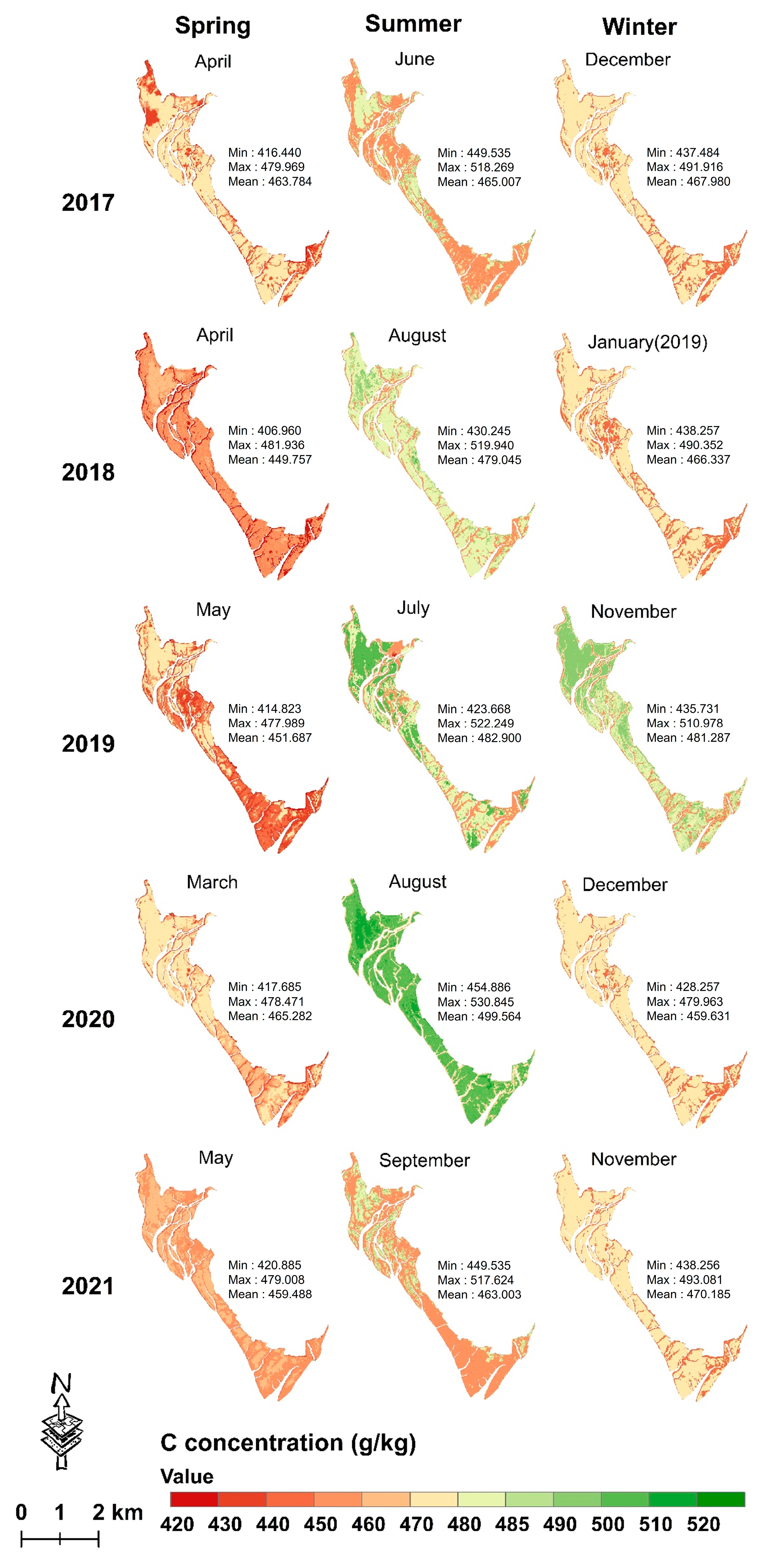
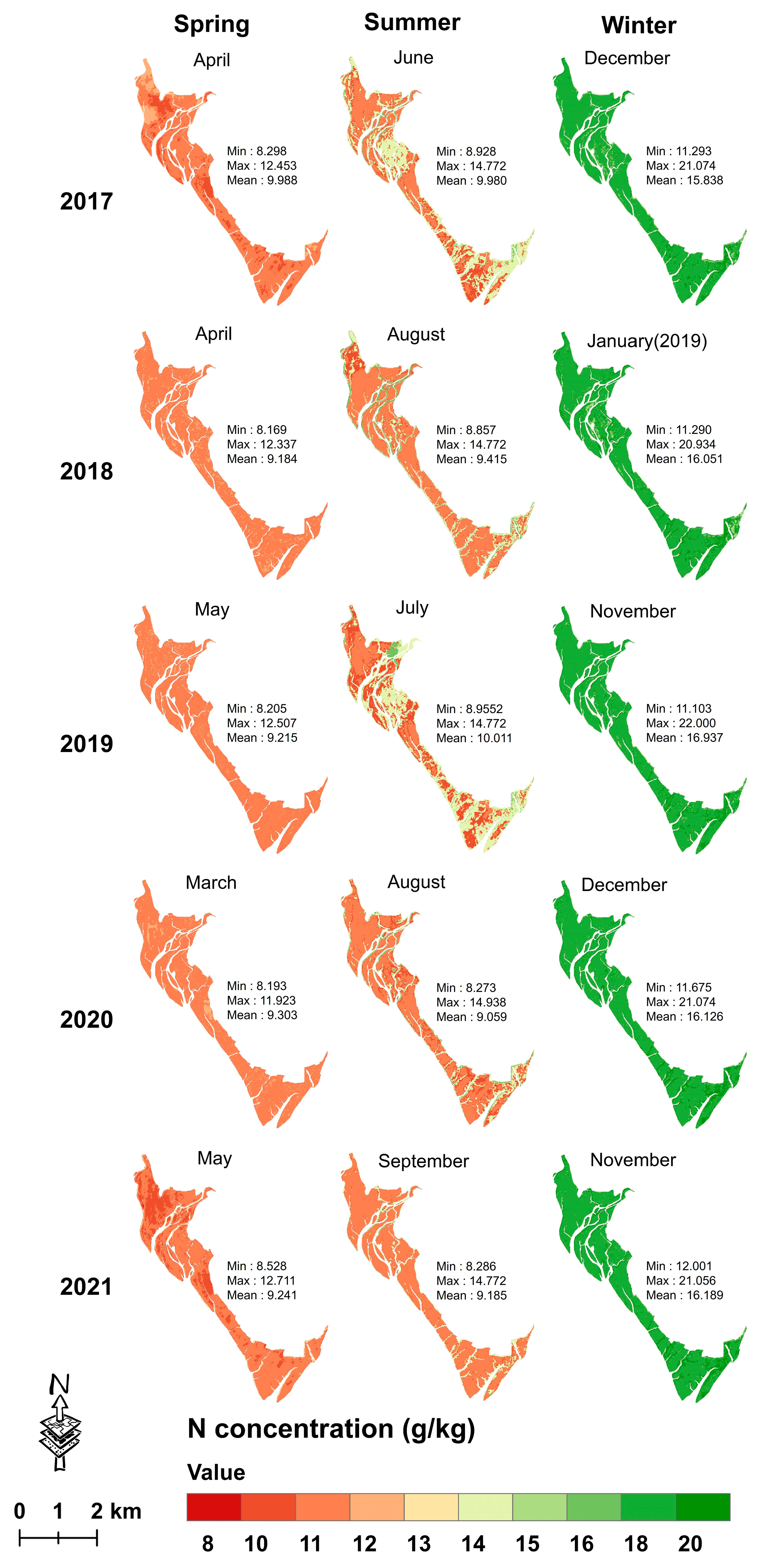
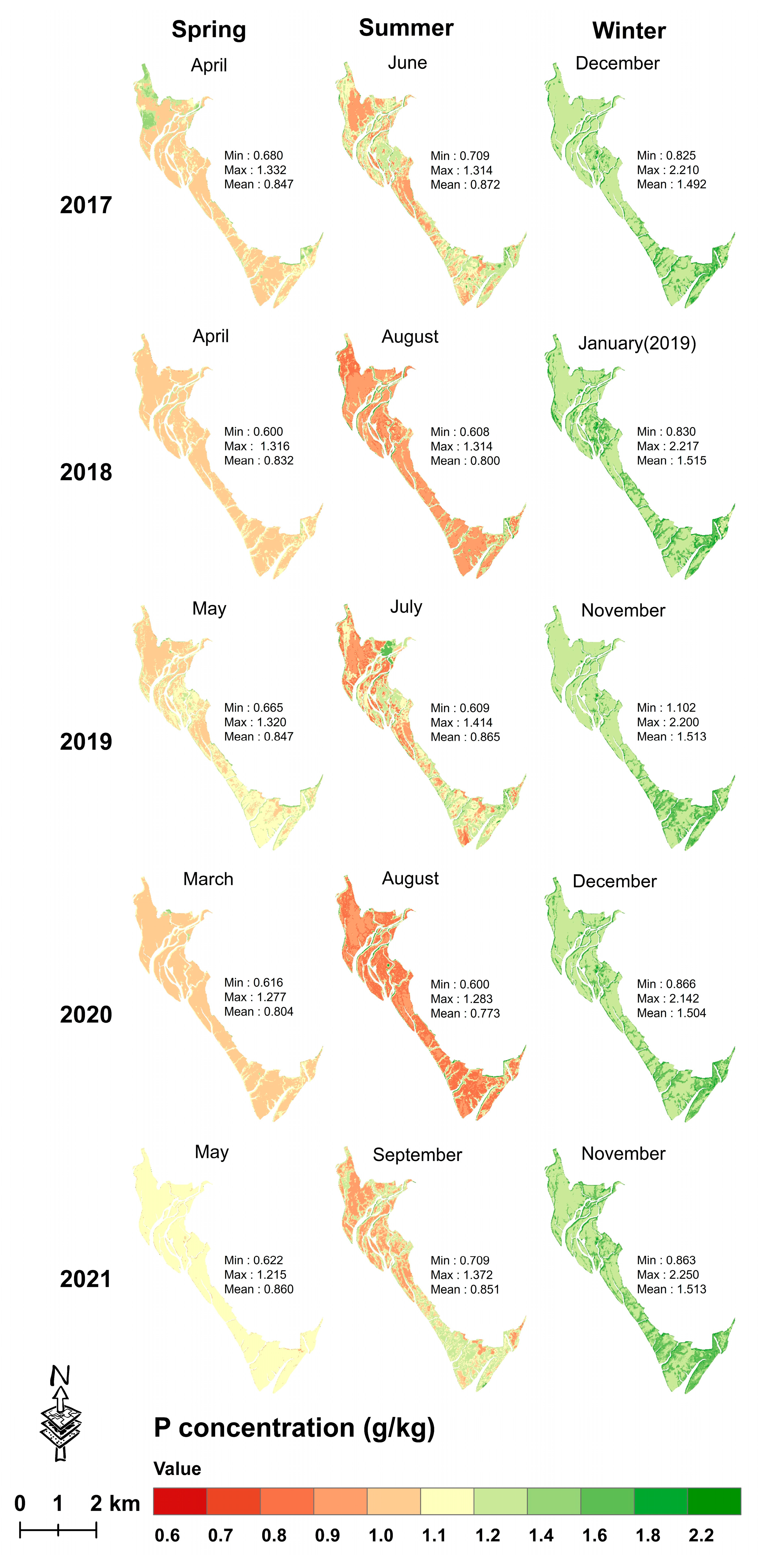
3.4.2. Mapping Seasonal Leaf C, N and P Concentrations from 2017 to 2021
4. Discussion
4.1. The Stoichiometry of Mangrove Leaf Nutrients across Different Seasons
4.2. Sensitive Features Related to Mangrove Leaf Nutrients
4.3. The Advantage of XGBoost in Estimating Mangrove Leaf Nutrients
4.4. Limitation of Leaf Nutrients Estimation with Seasonal Sentinel-2 Images
5. Conclusions
- (1)
- The XGBoost method had great potential for accurate estimation of mangrove leaf nutrients with seasonal Sentinel-2 images.
- (2)
- Among the three nutrients, leaf C concentrations were the most accurately estimated, followed by leaf N and P.
- (3)
- Red-edge (especially B6) and near-infrared bands (B8 and B8a) of Sentinel-2 images were efficient estimators of mangrove leaf nutrients.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xing, K.X.; Zhao, M.F.; Niinemets, U.; Niu, S.L.; Tian, J.; Jiang, Y.; Chen, H.Y.H.; White, P.J.; Guo, D.L.; Ma, Z.Q. Relationships between Leaf Carbon and Macronutrients across Woody Species and Forest Ecosystems Highlight How Carbon Is Allocated to Leaf Structural Function. Front. Plant Sci. 2021, 12, 674932. [Google Scholar] [CrossRef] [PubMed]
- Leghari, S.J.; Wahocho, N.A.; Laghari, G.M.; HafeezLaghari, A.; MustafaBhabhan, G.; HussainTalpur, K.; Bhutto, T.A.; Wahocho, S.A.; Lashari, A.A. Role of nitrogen for plant growth and development: A review. Adv. Environ. Biol. 2016, 10, 209–219. [Google Scholar]
- Friess, D.A.; Rogers, K.; Lovelock, C.E.; Krauss, K.W.; Hamilton, S.E.; Lee, S.Y.; Lucas, R.; Primavera, J.; Rajkaran, A.; Shi, S.H. The State of the World’s Mangrove Forests: Past, Present, and Future. Annu. Rev. Environ. Resour. 2019, 44, 89–115. [Google Scholar] [CrossRef]
- McLeod, E.; Chmura, G.L.; Bouillon, S.; Salm, R.; Bjork, M.; Duarte, C.M.; Lovelock, C.E.; Schlesinger, W.H.; Silliman, B.R. A blueprint for blue carbon: Toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 2011, 9, 552–560. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.B.; Wei, S.D.; Zhang, L.H.; Zhou, H.C.; Lin, Y.M. Nutrient Resorption and Phenolics Concentration Associated with Leaf Senescence of the Subtropical Mangrove Aegiceras corniculatum: Implications for Nutrient Conservation. Forests 2016, 7, 290. [Google Scholar] [CrossRef]
- Howarth, R.W.; Marino, R. Nitrogen as the limiting nutrient for eutrophication in coastal marine ecosystems: Evolving views over three decades. Limnol. Oceanogr. 2006, 51 Pt 2, 364–376. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote Sensing of Mangrove Ecosystems: A Review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Guo, X.X.; Wang, M.; Jia, M.M.; Wang, W.Q. Estimating mangrove leaf area index based on red-edge vegetation indices: A comparison among UAV, WorldView-2 and Sentinel-2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102493. [Google Scholar] [CrossRef]
- Jiang, X.; Zhen, J.; Miao, J.; Zhao, D.; Shen, Z.; Jiang, J.; Gao, C.; Wu, G.; Wang, J. Newly-developed three-band hyperspectral vegetation index for estimating leaf relative chlorophyll content of mangrove under different severities of pest and disease. Ecol. Indic. 2022, 140, 108978. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Clevers, J.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and-3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Diaz, B.M.; Blackburn, G.A. Remote sensing of mangrove biophysical properties: Evidence from a laboratory simulation of the possible effects of background variation on spectral vegetation indices. Int. J. Remote Sens. 2003, 24, 53–73. [Google Scholar] [CrossRef]
- Xiao, H.; Su, F.Z.; Fu, D.J.; Lyne, V.; Liu, G.H.; Pan, T.T.; Teng, J.K. Optimal and robust vegetation mapping in complex environments using multiple satellite imagery: Application to mangroves in Southeast Asia. Int. J. Appl. Earth Obs. Geoinf. 2021, 99, 102320. [Google Scholar] [CrossRef]
- Pastor-Guzman, J.; Atkinson, P.M.; Dash, J.; Rioja-Nieto, R. Spatiotemporal Variation in Mangrove Chlorophyll Concentration Using Landsat 8. Remote Sens. 2015, 7, 14530–14558. [Google Scholar] [CrossRef]
- Younes, N.; Joyce, K.E.; Northfield, T.D.; Maier, S.W. The effects of water depth on estimating Fractional Vegetation Cover in mangrove forests. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101924. [Google Scholar] [CrossRef]
- Annala, L.; Ayramo, S.; Polonen, I. Comparison of Machine Learning Methods in Stochastic Skin Optical Model Inversion. Appl. Sci. 2020, 10, 7097. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Tian, Y.C.; Huang, H.; Zhou, G.Q.; Zhang, Q.; Tao, J.; Zhang, Y.L.; Lin, J.L. Aboveground mangrove biomass estimation in Beibu Gulf using machine learning and UAV remote sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Yang, X.; Yang, R.; Ye, Y.; Yuan, Z.R.; Wang, D.Z.; Hua, K.K. Winter wheat SPAD estimation from UAV hyperspectral data using cluster-regression methods. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102618. [Google Scholar] [CrossRef]
- Blair, G.J.; Lefroy, R.D.B.; Lise, L. Soil carbon fractions based on their degree of oxidation, and the development of a carbon management index for agricultural systems. Aust. J. Agric. Res. 1995, 46, 1459–1466. [Google Scholar] [CrossRef]
- Hiller, A.; Plazin, J.; Vanslyke, D.D. A study of conditions for Kjeldahl determination of nitrogen in proteins; description of methods with mercury as catalyst, and titrimetric and gasometric measurements of the ammonia formed. J. Biol. Chem. 1948, 176, 1401–1420. [Google Scholar] [CrossRef]
- Harborne, J.B. (Ed.) Methods of Plant Analysis. In Phytochemical Methods: A Guide to Modern Techniques of Plant Analysis; Springer: Dordrecht, The Netherlands, 1984; pp. 1–36. [Google Scholar]
- Brodu, N. Super-Resolving Multiresolution Images With Band-Independent Geometry of Multispectral Pixels. IEEE Trans. Geosci. Electron. 2017, 55, 4610–4617. [Google Scholar] [CrossRef]
- El-Mejjaouy, Y.; Lahrir, M.; Naciri, R.; Zeroual, Y.; Mercatoris, B.; Dumont, B.; Oukarroum, A. How far can chlorophyll a fluorescence detect phosphorus status in wheat leaves (Triticum durum L.). Environ. Exp. Bot. 2022, 194, 104762. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Chlorophyll a, Chlorophyll b, Chlorophyll a+b, and Total Carotenoid Content in Eucalyptus Leaves. Remote Sens. Environ. 1998, 66, 111–121. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 2007, 4, 273–288. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W. A comparison of vegetation indices global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Haboudane, D. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G.; Begue, A.; Maurel, P.; Podaire, A. Complementarity of middle-infrared with visible and near-infrared reflectance for monitoring wheat canopies. Remote Sens. Environ. 1988, 26, 213–225. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 2010, 19, 657–675. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Vina, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Galvão, L.S.; Formaggio, A.R.; Tisot, D.A. Discrimination of sugarcane varieties in Southeastern Brazil with EO-1 Hyperion data. Remote Sens. Environ. 2005, 94, 523–534. [Google Scholar] [CrossRef]
- Hunt, E.R.; Rock, B.N. Detection of changes in leaf water content using near-and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar]
- Zarcotejada, P.; Berjon, A.; Lopezlozano, R.; Miller, J.; Martin, P.; Cachorro, V.; Gonzalez, M.; Defrutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens. 2007, 15, 697–703. [Google Scholar] [CrossRef]
- Fang, H.L.; Liu, W.W.; Li, W.J.; Wei, S.S. Estimation of the directional and whole apparent clumping index (ACI) from indirect optical measurements. ISPRS J. Photogramm. Remote Sens. 2018, 144, 1–13. [Google Scholar] [CrossRef]
- Imran, A.B.; Khan, K.; Ali, N.; Ahmad, N.; Ali, A.; Shah, K. Narrow band based and broadband derived vegetation indices using Sentinel-2 Imagery to estimate vegetation biomass. Glob. J. Environ. Sci. Manag. 2020, 6, 97–108. [Google Scholar]
- Darmawan, S.; Takeuchi, W.; Vetrita, Y.; Winarso, G.; Wikantika, K.; Sari, D.K. Iop Characterization. In Proceedings of the 7th IGRSM International Remote Sensing and GIS Conference and Exhibition, Kuala Lumpur, Malaysia, 22–23 April 2014. [Google Scholar]
- Jia, M.; Wang, Z.; Wang, C.; Mao, D.; Zhang, Y. A New Vegetation Index to Detect Periodically Submerged Mangrove Forest Using Single-Tide Sentinel-2 Imagery. Remote Sens. 2019, 11, 2043. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.S.; Gifford, E.M. Extreme Gradient Boosting as a Method for Quantitative Structure-Activity Relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Meng, F.; Fu, P.J.; Yang, X.Y.; Zhang, Y.X.; Liu, P.D. Application of hyperspectral analysis of chlorophyll a concentration inversion in Nansi Lake. Ecol. Inform. 2021, 64, 101360. [Google Scholar] [CrossRef]
- Yuan, Z.R.; Ye, Y.; Wei, L.F.; Yang, X.; Huang, C. Study on the Optimization of Hyperspectral Characteristic Bands Combined with Monitoring and Visualization of Pepper Leaf SPAD Value. Sensors 2022, 22, 183. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.L.; Meng, Q.; Finley, T.; Wang, T.F.; Chen, W.; Ma, W.D.; Ye, Q.W.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Elser, J.J.; Fagan, W.F.; Denno, R.F.; Dobberfuhl, D.R.; Folarin, A.; Huberty, A.; Interlandi, S.; Kilham, S.S.; McCauley, E.; Schulz, K.L.; et al. Nutritional constraints in terrestrial and freshwater food webs. Nature 2000, 408, 578–580. [Google Scholar] [CrossRef]
- Hu, Y.K.; Liu, X.Y.; He, N.P.; Pan, X.; Long, S.Y.; Li, W.; Zhang, M.Y.; Cui, L.J. Global patterns in leaf stoichiometry across coastal wetlands. Glob. Ecol. Biogeogr. 2021, 30, 852–869. [Google Scholar] [CrossRef]
- Abbas, M.; Ebeling, A.; Oelmann, Y.; Ptacnik, R.; Roscher, C.; Weigelt, A.; Weisser, W.W.; Wilcke, W.; Hillebrand, H. Biodiversity Effects on Plant Stoichiometry. PLoS ONE 2013, 8, e58179. [Google Scholar] [CrossRef]
- Duarte, C.M.; Cebrian, J. The fate of marine autotrophic production. Limnol. Oceanogr. 1996, 41, 1758–1766. [Google Scholar] [CrossRef]
- Koerselman, W.; Meuleman, A.F.M. The vegetation N:P ratio: A new tool to detect the nature of nutrient limitation. J. Appl. Ecol. 1996, 33, 1441–1450. [Google Scholar] [CrossRef]
- Qin, J.; Shangguan, Z.; Xi, W. Seasonal variations of leaf traits and drought adaptation strategies of four common woody species in South Texas, USA. J. For. Res. 2019, 30, 1715–1725. [Google Scholar] [CrossRef]
- Milla, R.; Maestro-Martinez, M.; Montserrat-Marti, G. Seasonal branch nutrient dynamics in two Mediterranean woody shrubs with contrasted phenology. Ann. Bot. 2004, 93, 671–680. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, F.D.; Liu, Y.H.; Wang, G.M.; Song, Y.; Liu, Q.; Li, D.S.; Mao, P.L.; Zhang, H. Seasonal Variations of C: N: P Stoichiometry and Their Trade-offs in Different Organs of Suaeda salsa in Coastal Wetland of Yellow River Delta, China. PLoS ONE 2015, 10, e0138169. [Google Scholar] [CrossRef] [PubMed]
- Almahasheer, H.; Duarte, C.M.; Irigoien, X. Nutrient Limitation in Central Red Sea Mangroves. Front. Mar. Sci. 2016, 3, 271. [Google Scholar] [CrossRef]
- Ma, S.H.; He, F.; Tian, D.; Zou, D.T.; Yan, Z.B.; Yang, Y.L.; Zhou, T.C.; Huang, K.Y.; Shen, H.H.; Fang, J.Y. Variations and determinants of carbon content in plants: A global synthesis. Biogeosciences 2018, 15, 693–702. [Google Scholar] [CrossRef]
- Michaels, A.F. Ecological stoichiometry—The biology of elements from molecules to the biosphere. Science 2003, 300, 906–907. [Google Scholar] [CrossRef]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The worldwide leaf economics spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
- Zhang, C.H.; Kovacs, J.M.; Wachowiak, M.P.; Flores-Verdugo, F. Relationship between Hyperspectral Measurements and Mangrove Leaf Nitrogen Concentrations. Remote Sens. 2013, 5, 891–908. [Google Scholar] [CrossRef]
- Zhen, J.; Jiang, X.; Xu, Y.; Miao, J.; Zhao, D.; Wang, J.; Wang, J.; Wu, G. Mapping leaf chlorophyll content of mangrove forests with Sentinel-2 images of four periods. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102387. [Google Scholar] [CrossRef]
- Saeys, W.; Mouazen, A.M.; Ramon, H. Potential for Onsite and Online Analysis of Pig Manure using Visible and Near Infrared Reflectance Spectroscopy. Biosyst. Eng. 2005, 91, 393–402. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Hadavimoghaddam, F.; Pourmahdi, M.; Atashrouz, S.; Munir, M.T.; Hemmati-Sarapardeh, A.; Mosavi, A.H.; Mohaddespour, A. Modeling hydrogen solubility in hydrocarbons using extreme gradient boosting and equations of state. Sci. Rep. 2021, 11, 17911. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Jin, S.G.; Savi, P.; Gao, Y.; Tang, J.; Chen, Y.X.; Li, W.M. GNSS-R Soil Moisture Retrieval Based on a XGboost Machine Learning Aided Method: Performance and Validation. Remote Sens. 2019, 11, 1655. [Google Scholar] [CrossRef]


| Season | Spring in 2018 | Summer in 2020 | Winter in 2019 | |
|---|---|---|---|---|
| Species | ||||
| Aegiceras corniculatum | 35 | 16 | 23 | |
| Bruguiear gymnorrhiza | 10 | 13 | 22 | |
| Avicennia marina | 0 | 16 | 6 | |
| Rhizophora stylosa | 3 | 6 | 8 | |
| Sonneratia apetala | 1 | 3 | 0 | |
| Kandelia candel | 4 | 3 | 3 | |
| Season (Number of Samples) | Nutrient | Min | Max | Mean | CV (%) |
|---|---|---|---|---|---|
| Spring (53) | C | 408.38 | 481.02 | 449.07 | 3.54 |
| N | 8.05 | 15.61 | 10.58 | 15.49 | |
| P | 0.70 | 1.85 | 0.90 | 19.21 | |
| Summer (62) | C | 424.73 | 542.08 | 492.75 | 5.93 |
| N | 7.23 | 19.28 | 10.59 | 22.64 | |
| P | 0.62 | 2.00 | 0.86 | 28.24 | |
| Winter (57) | C | 403.48 | 501.87 | 456.66 | 6.49 |
| N | 9.77 | 22.86 | 14.94 | 20.98 | |
| P | 0.83 | 2.68 | 1.57 | 33.99 |
| Band | Center Wavelength/nm | Bandwidth/nm | Spatial Resolution/m |
|---|---|---|---|
| B1 (Coastal aerosol) | 443 | 20 | 60 |
| B2 (Blue) | 490 | 65 | 10 |
| B3 (Green) | 560 | 35 | 10 |
| B4 (Red) | 665 | 30 | 10 |
| B5 (Red-edge1) | 705 | 15 | 20 |
| B6 (Red-edge2) | 740 | 15 | 20 |
| B7 (Red-edge3) | 783 | 20 | 20 |
| B8 (NIR) | 842 | 115 | 10 |
| B8a (Narrow NIR) | 865 | 20 | 20 |
| B9 (Water Vapor) | 945 | 20 | 60 |
| B10 (Cirrus) | 1380 | 30 | 60 |
| B11 (SWIR1) | 1610 | 90 | 20 |
| B12 (SWIR2) | 2190 | 180 | 20 |
| Vegetation Index | Formula | Sentinel-2 Bands | Reference |
|---|---|---|---|
| Normalized Difference Vegetation Index (NDVI) | B5, B8 | [27] | |
| Green NDVI (gNDVI) | B3, B6 | ||
| Optimized Soil-Adjusted Vegetation Index (OSAVI) | B4, B8 | [28] | |
| Red-Edge Inflection Point (REIP) | B4, B5, B6, B7 | [29] | |
| Simple Ratio Index (SR705) | B5, B6 | [30] | |
| Enhanced Vegetation Index (EVI) | B2, B4, B8 | [31] | |
| SRChl a | B3, B4, B5 | [27] | |
| SRChl b | B3, B4 | ||
| SRchl | B3, B5, B8 | ||
| Modified Cab Absorption in Reflectance Index (MCARI) | B3, B4, B5 | [32] | |
| Modified Chlorophyll Absorption in Reflectance Index (MCARI1) | B3, B4, B8 | ||
| Transformed CARI (TCARI) | B3, B4, B5 | [33] | |
| MCARI/OSAVI | B3, B4, B5, B8 | [34] | |
| TCARI/OSAVI | B3, B4, B5, B8 | ||
| Red-Edge Position (REP) | B4, B5, B6, B7 | [35] | |
| Pigment Specific Simple Ratio for Chla (PSSRa) | B4, B8 | [36] | |
| Green chlorophyll index (CIgreen) | B3, B7 | [37] | |
| Green chlorophyll index (CIred-edge) | B5, B7 | ||
| Disease Water Stress Index (DSWI) | B3, B4, B8, B11 | [38] | |
| Moisture Stress Index (MSI) | B8, B11 | [39] | |
| Red and Green Pigment Indices (RGI) | B3, B5 | [40] | |
| Anthocyanin Reflectance Index (ARI) | B3, B8a | [30] | |
| Carotenoid Reflectance (CRI) | B2, B3 | ||
| Carotenoid Reflectance (CRI2) | B2, B5 | ||
| Visible Atmospherically Resistant Index (VARIgreen) | B2, B3, B4 | ||
| Cater Stress Index (CSI2) | B5, B7 | [41] | |
| Apparent Clumping Index (ACI) | B3, B8 | [42] | |
| Red-Edge Normalized Difference Vegetation Index (NDRE1) | B5, B6 | [43] | |
| Mangrove Index (MI) | B8, B12 | [44] | |
| Mangrove Forest Index (MFI) | B4, B5, B6, B7, B8a, B12 | [45] |
| Algorithm | Algorithm Library | Main Parameter Settings |
|---|---|---|
| XGBoost | https://github.com/dmlc/xgboost/ (accessed on 20 September 2021), version 1.5.0 | max_depth = 5, learning_rate = 0.1, n_estimators = 200, min_child_weight = 1 |
| RF | https://github.com/kjw0612/awesome-random-forest (accessed on 20 September 2021), version 1.2.2 | n_estimators = 200, criterion = ‘mse’, max_depth = None, min_samples_split = 2, min_samples_leaf = 1 |
| LightGBM | https://github.com/microsoft/LightGBM (accessed on 20 September 2021), version 3.3.1 | learning_rate = 0.1, num_leaves = 31, min_data_in_leaf = 20, n_estimators = 200 |
| Year | Season | Acquisition Date |
|---|---|---|
| 2017 | Spring | 8 April 2017 |
| Summer | 27 June 2017 | |
| Winter | 19 December 2017 | |
| 2018 | Summer | 31 August 2018 |
| Winter | 23 January 2019 | |
| 2019 | Spring | 23 May 2019 |
| Summer | 2 July 2019 | |
| 2020 | Spring | 8 March 2020 |
| Winter | 8 December 2020 | |
| 2021 | Spring | 17 May 2021 |
| Summer | 4 September 2021 | |
| Winter | 28 November 2021 |
| Nutrient | Season | Spring | Summer | Winter |
|---|---|---|---|---|
| C | Spring | |||
| Summer | 0.000 * | |||
| Winter | 0.078 | 0.000 * | ||
| N | Spring | |||
| Summer | 0.978 | |||
| Winter | 0.000 * | 0.000 * | ||
| P | Spring | |||
| Summer | 0.586 | |||
| Winter | 0.000 * | 0.000 * |
| Model | Nutrient | Spring | Summer | Winter | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RRMSE(%) | RPD | R2 | RRMSE(%) | RPD | R2 | RRMSE(%) | RPD | ||
| XGBoost | C | 0.655 | 1.687 | 1.703 | 0.799 | 2.408 | 2.230 | 0.829 | 2.401 | 2.418 |
| N | 0.668 | 6.090 | 1.736 | 0.743 | 9.668 | 1.973 | 0.704 | 8.998 | 1.838 | |
| P | 0.539 | 4.659 | 1.473 | 0.622 | 16.251 | 1.627 | 0.596 | 19.560 | 1.573 | |
| RF | C | 0.549 | 1.717 | 1.489 | 0.811 | 2.314 | 2.300 | 0.824 | 2.420 | 2.383 |
| N | 0.629 | 13.699 | 1.642 | 0.684 | 10.063 | 1.779 | 0.637 | 9.944 | 1.660 | |
| P | 0.415 | 6.168 | 1.309 | 0.652 | 14.662 | 1.700 | 0.613 | 18.156 | 1.607 | |
| LightGBM | C | 0.415 | 1.952 | 1.308 | 0.401 | 3.014 | 1.292 | 0.803 | 2.538 | 2.253 |
| N | 0.654 | 5.512 | 1.700 | 0.133 | 9.813 | 1.074 | 0.015 | 3.835 | 1.008 | |
| P | 0.273 | 6.755 | 1.173 | 0.207 | 14.292 | 1.122 | 0.627 | 17.596 | 1.637 | |
| Model | Nutrient | Spring | Summer | Winter | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RRMSE(%) | RPD | R2 | RRMSE(%) | RPD | R2 | RRMSE(%) | RPD | ||
| XGBoost | C | 0.218 | 1.842 | 1.131 | 0.788 | 1.604 | 2.171 | 0.534 | 2.599 | 1.464 |
| N | 0.021 | 9.757 | 1.011 | 0.504 | 9.321 | 1.419 | 0.516 | 10.481 | 1.438 | |
| P | 0.057 | 15.218 | 1.030 | 0.434 | 13.635 | 1.329 | 0.677 | 14.180 | 1.759 | |
| RF | C | 0.133 | 1.987 | 1.074 | 0.730 | 1.818 | 1.924 | 0.569 | 2.543 | 1.523 |
| N | 0.038 | 11.251 | 1.020 | 0.294 | 11.894 | 1.190 | 0.453 | 9.933 | 1.352 | |
| P | 0.079 | 16.392 | 1.042 | 0.439 | 12.993 | 1.335 | 0.611 | 15.016 | 1.603 | |
| LightGBM | C | 0.169 | 2.094 | 1.097 | 0.758 | 1.714 | 2.035 | 0.432 | 2.882 | 1.327 |
| N | 0.000 | 12.883 | 1.000 | 0.405 | 10.167 | 1.297 | 0.290 | 12.965 | 1.186 | |
| P | 0.000 | 19.315 | 1.000 | 0.417 | 15.544 | 1.309 | 0.573 | 16.101 | 1.530 | |
| Leaf Nutrient | Data Group | Spring | Summer | Winter | |||
|---|---|---|---|---|---|---|---|
| n | MAE(%) | n | MAE(%) | n | MAE(%) | ||
| C | 414.16–443.63 | 14 | 1.98 | 4 | 3.06 | 24 | 2.37 |
| 443.63–473.10 | 39 | 1.28 | 7 | 1.59 | 10 | 2.07 | |
| 473.10–502.57 | 0 | -- | 22 | 2.52 | 28 | 1.98 | |
| 502.57–532.04 | 0 | -- | 24 | 1.84 | 0 | -- | |
| N | 8.52–11.72 | 46 | 6.68 | 50 | 8.55 | 7 | 6.87 |
| 11.72–14.92 | 7 | 5.53 | 3 | 9.53 | 22 | 6.30 | |
| 14.92–18.12 | 0 | -- | 4 | 12.22 | 27 | 9.14 | |
| 18.12–21.33 | 0 | -- | 0 | -- | 6 | 7.81 | |
| P | 0.71–1.12 | 53 | 7.62 | 49 | 9.50 | 14 | 9.02 |
| 1.12–1.54 | 0 | -- | 6 | 21.41 | 19 | 22.09 | |
| 1.54–1.95 | 0 | -- | 2 | 25.52 | 7 | 22.59 | |
| 1.95–2.37 | 0 | -- | 0 | -- | 22 | 15.36 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, J.; Zhen, J.; Wang, J.; Zhao, D.; Jiang, X.; Shen, Z.; Gao, C.; Wu, G. Mapping Seasonal Leaf Nutrients of Mangrove with Sentinel-2 Images and XGBoost Method. Remote Sens. 2022, 14, 3679. https://doi.org/10.3390/rs14153679
Miao J, Zhen J, Wang J, Zhao D, Jiang X, Shen Z, Gao C, Wu G. Mapping Seasonal Leaf Nutrients of Mangrove with Sentinel-2 Images and XGBoost Method. Remote Sensing. 2022; 14(15):3679. https://doi.org/10.3390/rs14153679
Chicago/Turabian StyleMiao, Jing, Jianing Zhen, Junjie Wang, Demei Zhao, Xiapeng Jiang, Zhen Shen, Changjun Gao, and Guofeng Wu. 2022. "Mapping Seasonal Leaf Nutrients of Mangrove with Sentinel-2 Images and XGBoost Method" Remote Sensing 14, no. 15: 3679. https://doi.org/10.3390/rs14153679
APA StyleMiao, J., Zhen, J., Wang, J., Zhao, D., Jiang, X., Shen, Z., Gao, C., & Wu, G. (2022). Mapping Seasonal Leaf Nutrients of Mangrove with Sentinel-2 Images and XGBoost Method. Remote Sensing, 14(15), 3679. https://doi.org/10.3390/rs14153679








