A Simple Statistical Model of the Uncertainty Distribution for Daily Gridded Precipitation Multi-Platform Satellite Products
Abstract
:1. Introduction
2. Data and Method
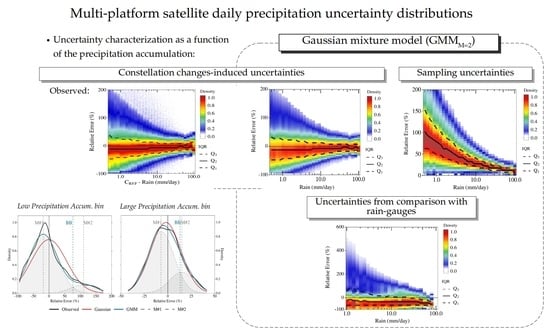
2.1. Uncertainty Distribution as a Function of the Precipitation Accumulation
2.2. Sources of Uncertainty and Datasets
2.2.1. Constellation Changes-Induced Uncertainties
2.2.2. Sampling Uncertainties
2.2.3. Uncertainties Obtained by Comparisons with Rain-Gauge Network
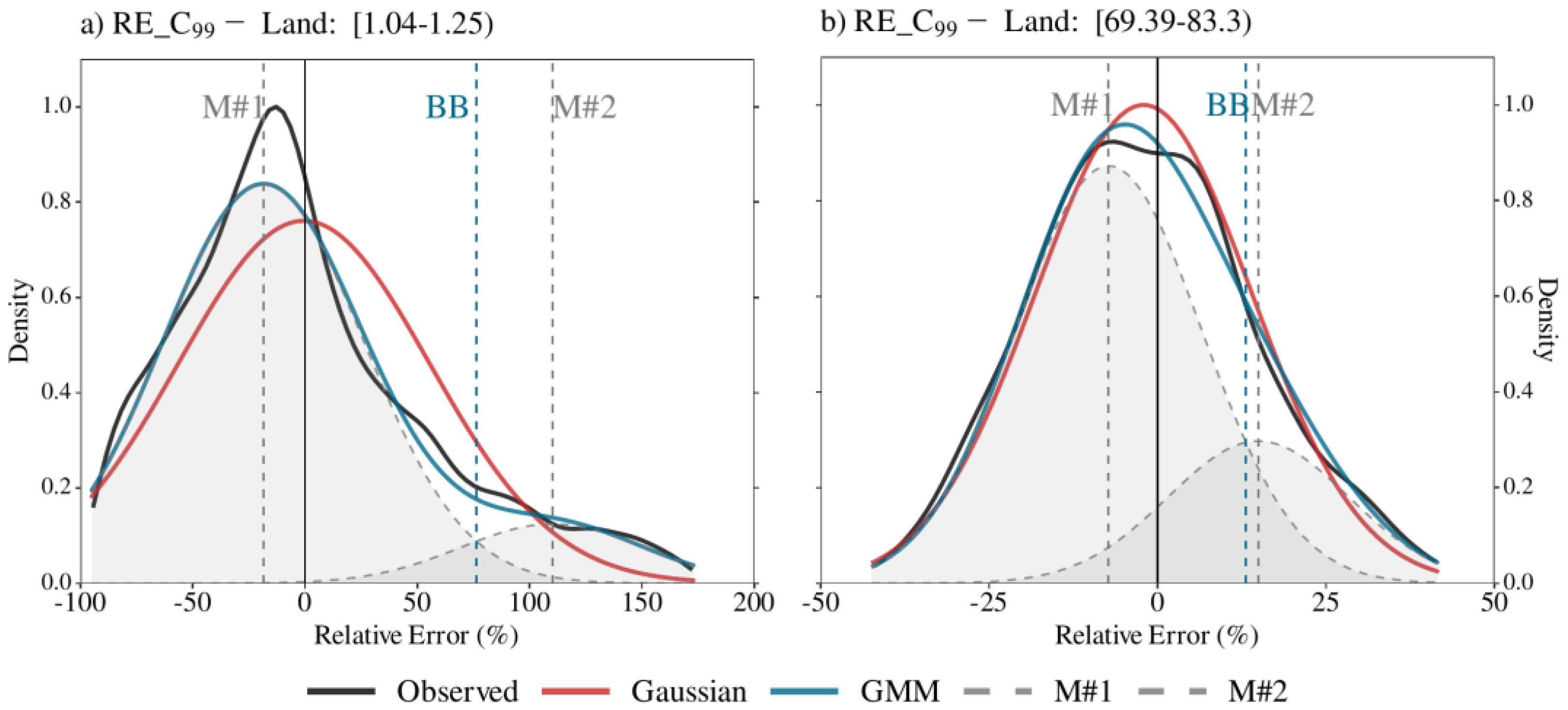
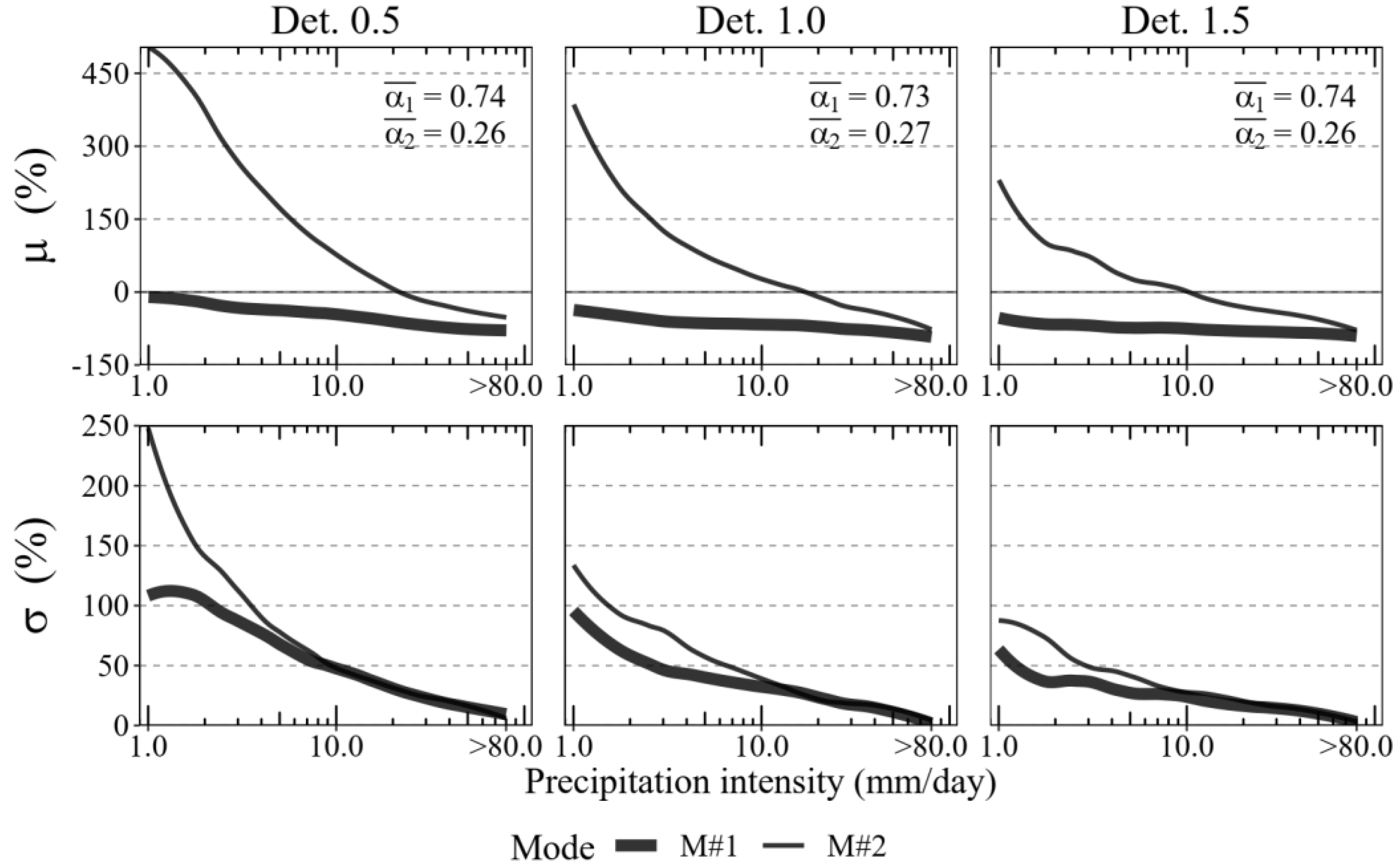
2.3. The Gaussian Mixture Model
3. Satellite Precipitation Uncertainty Distribution Approximation
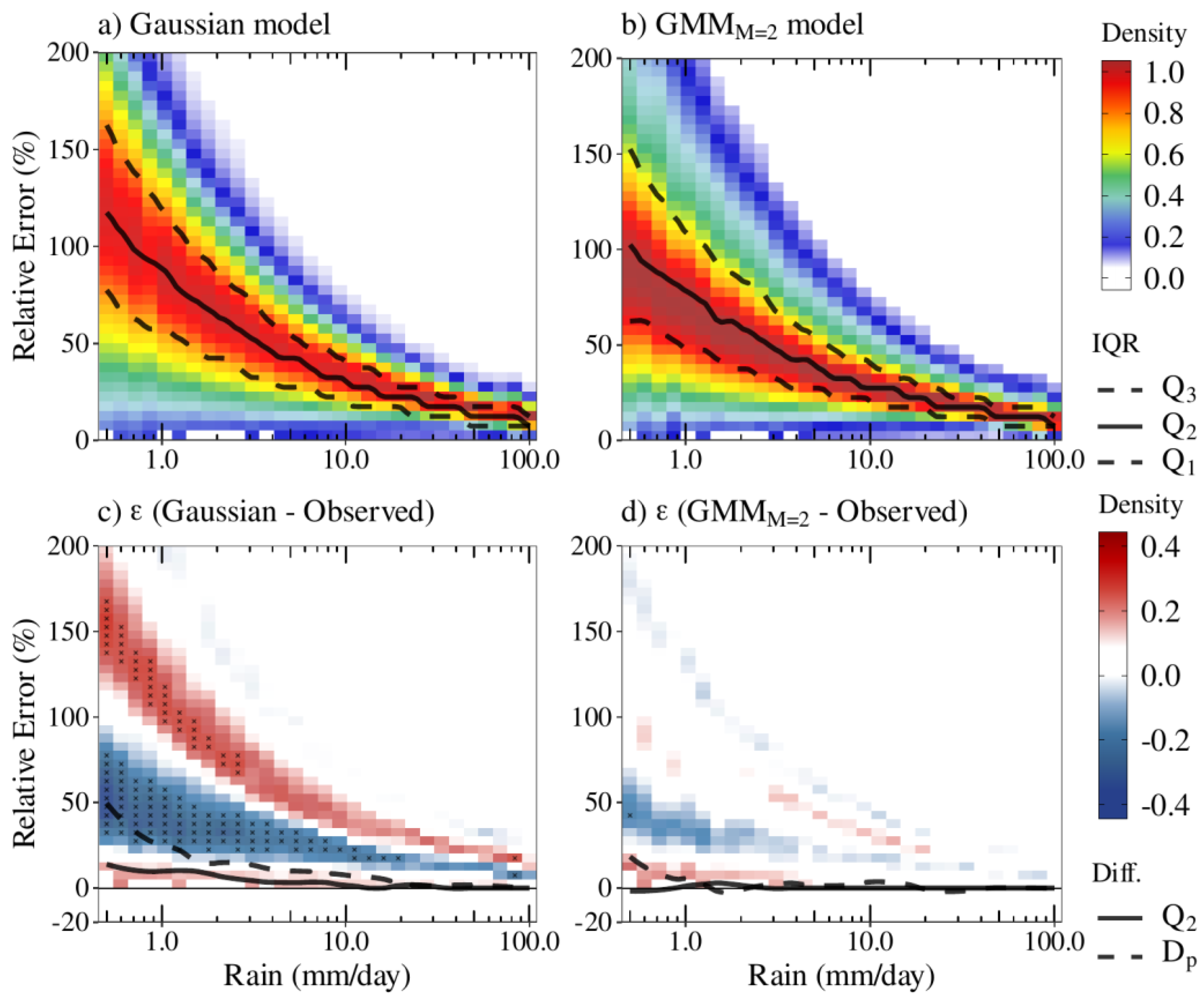
3.1. The GMM Model Distributions and Performances
3.2. Constellation Changes-Induced Uncertainties
3.3. Sampling Uncertainties
3.4. Comparison with Rain-Gauges Network
4. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stephens, G.L.; Slingo, J.M.; Rignot, E.; Reager, J.T.; Hakuba, M.Z.; Durack, P.J.; Worden, J.; Rocca, R. Earth’s water reservoirs in a changing climate. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levizzani, V.; Kidd, C.; Aonashi, K.; Bennartz, R.; Ferraro, R.R.; Huffman, G.; Roca, R.; Turk, F.J.; Wang, N. The activities of the international precipitation working group. Q. J. R. Meteorol. Soc. 2018, 144, 3–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roca, R.; Alexander, L.V.; Potter, G.; Bador, M.; Jucá, R.; Contractor, S.; Bosilovich, M.G.; Cloché, S. FROGS: A daily 1 × 1 gridded precipitation database of rain gauge, satellite and reanalysis products. Earth Syst. Sci. Data 2019, 11, 1017–1035. [Google Scholar] [CrossRef] [Green Version]
- Madakumbura, G.D.; Thackeray, C.W.; Norris, J.; Goldenson, N.; Hall, A. Anthropogenic influence on extreme precipitation over global land areas seen in multiple observational datasets. Nat. Commun. 2021, 12, 3944. [Google Scholar] [CrossRef] [PubMed]
- Tapiador, F.; Navarro, A.; Levizzani, V.; García-Ortega, E.; Huffman, G.; Kidd, C.; Kucera, P.; Kummerow, C.; Masunaga, H.; Petersen, W.; et al. Global precipitation measurements for validating climate models. Atmos. Res. 2017, 197, 1–20. [Google Scholar] [CrossRef]
- Martinez-Villalobos, C.; Neelin, J.D. Climate models capture key features of extreme precipitation probabilities across regions. Environ. Res. Lett. 2021, 16, 024017. [Google Scholar] [CrossRef]
- Roca, R. Estimation of extreme daily precipitation thermodynamic scaling using gridded satellite precipitation products over tropical land. Environ. Res. Lett. 2019, 14, 095009. [Google Scholar] [CrossRef]
- Alexander, L.V.; Bador, M.; Roca, R.; Contractor, S.; Donat, M.G.; Nguyen, P.L. Intercomparison of annual precipitation indices and extremes over global land areas from in situ, space-based and reanalysis products. Environ. Res. Lett. 2020, 15, 055002. [Google Scholar] [CrossRef]
- Roca, R.; Haddad, Z.S.; Akimoto, F.F.; Alexander, L.; Behrangi, A.; Huffman, G.; Kato, S.; Kidd, C.; Kirstetter, P.-E.; Kubota, T.; et al. The Joint IPWG/GEWEX Precipitation Assessment; Roca, R., Haddad, Z.S., Eds.; World Climate Research Programme: Geneva, Switzerland, 2021; p. 125. [Google Scholar]
- Elsaesser, G.S.; Kummerow, C.D. The Sensitivity of Rainfall Estimation to Error Assumptions in a Bayesian Passive Microwave Retrieval Algorithm. J. Appl. Meteorol. Clim. 2015, 54, 408–422. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Haddad, Z.S.; Turk, F.J.; Utsumi, N.; Kirstetter, P. Assessment of the Sub-Daily Global Satellite Precipitation Products; Roca, R., Haddad, Z.S., Eds.; World Climate Research Programme (WCRP): Geneva, Switzerland, 2021; pp. 1–22. [Google Scholar]
- Maggioni, V.; Sapiano, M.R.P.; Adler, R.F.; Tian, Y.; Huffman, G.J. An Error Model for Uncertainty Quantification in High-Time-Resolution Precipitation Products. J. Hydrometeorol. 2014, 15, 1274–1292. [Google Scholar] [CrossRef]
- Oliveira, R.; Maggioni, V.; Vila, D.; Porcacchia, L. Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall Estimates over the Central Amazon Region. Remote Sens. 2018, 10, 336. [Google Scholar] [CrossRef] [Green Version]
- Gosset, M.; Alcoba, M.; Roca, R.; Cloché, S.; Urbani, G. Evaluation of TAPEER daily estimates and other GPM-era products against dense gauge networks in West Africa, analysing ground reference uncertainty. Q. J. R. Meteorol. Soc. 2018, 144, 255–269. [Google Scholar] [CrossRef] [Green Version]
- Chambon, P.; Jobard, I.; Roca, R.; Viltard, N. An investigation of the error budget of tropical rainfall accumulation derived from merged passive microwave and infrared satellite measurements. Q. J. R. Meteorol. Soc. 2012, 139, 879–893. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef] [Green Version]
- Chambon, P.; Roca, R.; Jobard, I.; Capderou, M. The Sensitivity of Tropical Rainfall Estimation from Satellite to the Configuration of the Microwave Imager Constellation. IEEE Geosci. Remote Sens. Lett. 2013, 10, 996–1000. [Google Scholar] [CrossRef]
- Roca, R.; Taburet, N.; Lorant, E.; Chambon, P.; Alcoba, M.; Brogniez, H.; Cloché, S.; Dufour, C.; Gosset, M.; Guilloteau, C. Quantifying the contribution of the Megha-Tropiques mission to the estimation of daily accumulated rainfall in the Tropics. Q. J. R. Meteorol. Soc. 2018, 144, 49–63. [Google Scholar] [CrossRef] [Green Version]
- Roca, R.; Chambon, P.; Jobard, I.; Kirstetter, P.-E.; Gosset, M.; Bergès, J.C. Comparing Satellite and Surface Rainfall Products over West Africa at Meteorologically Relevant Scales during the AMMA Campaign Using Error Estimates. J. Appl. Meteorol. Clim. 2010, 49, 715–731. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Roca, R.; Guérou, A.; Oliveira, R.A.J.; Chambon, P.; Gosset, M.; Cloché, S.; Schröder, M. Merging the Infrared Fleet and the Microwave Constellation for Tropical Hydrometeorology (TAPEER) and Global Climate Monitoring (GIRAFE) Applications. In Satellite Precipitation Measurement. In Advances in Global Change Research; Levizzani, V., Kidd, C., Kirschbaum, D., Kummerow, C., Nakamura, K., Turk, F., Eds.; Springer: Cham, Switzerland, 2020; Volume 67, pp. 429–450. [Google Scholar] [CrossRef]
- Chambon, P.; Roca, R.; Jobard, I.; Aublanc, J. The TAPEER-BRAIN product: Algorithm theoretical basis document, level 4. Megha-Tropiques Technol. Memo 2012, 4, 13. [Google Scholar]
- Xu, L.; Gao, X.; Sorooshian, S.; Arkin, P.; Imam, B. A Microwave Infrared Threshold Technique to Improve the GOES Precipitation Index. J. Appl. Meteorol. 1999, 38, 569–579. [Google Scholar] [CrossRef]
- Kidd, C.; Kniveton, D.R.; Todd, M.C.; Bellerby, T.J. Satellite Rainfall Estimation Using Combined Passive Microwave and Infrared Algorithms. J. Hydrometeorol. 2003, 4, 1088–1104. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Randel, D.L.; Kulie, M.; Wang, N.-Y.; Ferraro, R.; Munchak, S.J.; Petkovic, V. The Evolution of the Goddard Profiling Algorithm to a Fully Parametric Scheme. J. Atmospheric Ocean. Technol. 2015, 32, 2265–2280. [Google Scholar] [CrossRef]
- Kidd, C.; Matsui, T.; Ringerud, S. Precipitation Retrievals from Passive Microwave Cross-Track Sensors: The Precipitation Retrieval and Profiling Scheme. Remote Sens. 2021, 13, 947. [Google Scholar] [CrossRef]
- Oliveira, R.A.J.; Roca, R.; Finkensieper, S.; Cloché, S.; Schröder, M. A time-dependent error model for satellite constellation-based daily precipitation estimates. Atmos. Res. 2022; accepted. [Google Scholar]
- Oliveira, R.A.J.; Gosset, M.; Roca, R.; Kidd, C. Impact of Level-2 satellite rainfall retrievals’ characteristics on daily accumulated rainfall estimates: A sensitivity analysis based on the TAPEER framework. 2022; in preparation. [Google Scholar]
- Guilloteau, C.; Foufoula-Georgiou, E.; Kummerow, C.D. Global Multiscale Evaluation of Satellite Passive Microwave Retrieval of Precipitation during the TRMM and GPM Eras: Effective Resolution and Regional Diagnostics for Future Algorithm Development. J. Hydrometeorol. 2017, 18, 3051–3070. [Google Scholar] [CrossRef]
- Guilloteau, C.; Foufoula-Georgiou, E.; Kirstetter, P.; Tan, J.; Huffman, G.J. How Well Do Multisatellite Products Capture the Space–Time Dynamics of Precipitation? Part I: Five Products Assessed via a Wavenumber–Frequency Decompo-sition. J. Hydrometeorol. 2021, 22, 2805–2823. [Google Scholar]
- Kidd, C.; Tan, J.; Kirstetter, P.-E.; Petersen, W.A. Validation of the Version 05 Level 2 precipitation products from the GPM Core Observatory and constellation satellite sensors. Q. J. R. Meteorol. Soc. 2018, 144, 313–328. [Google Scholar] [CrossRef] [Green Version]
- Kidd, C.; Huffman, G.; Maggioni, V.; Chambon, P.; Oki, R. The Global Satellite Precipitation Constellation: Current Status and Future Requirements. Bull. Am. Meteorol. Soc. 2021, 102, E1844–E1861. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirchengast, G.; Goodrich, D.C.; Wolff, D.B. Evaluation of Global Precipitation Measurement Rainfall Estimates against Three Dense Gauge Networks. J. Hydrometeorol. 2018, 19, 517–532. [Google Scholar] [CrossRef]
- You, Y.; Petkovic, V.; Tan, J.; Kroodsma, R.; Berg, W.; Kidd, C.; Peters-Lidard, C. Evaluation of V05 Precipitation Estimates from GPM Constellation Radiometers Using KuPR as the Reference. J. Hydrometeorol. 2020, 21, 705–728. [Google Scholar] [CrossRef]
- Roca, R.; Brogniez, H.; Chambon, P.; Chomette, O.; Clochãé, S.; Gosset, M.E.; Mahfouf, J.-F.; Raberanto, P.; Viltard, N. The Megha-Tropiques mission: A review after three years in orbit. Front. Earth Sci. 2015, 3, 17. [Google Scholar] [CrossRef]
- Kubota, T.; Aonashi, K.; Ushio, T.; Shige, S.; Takayabu, Y.N.; Kachi, M.; Arai, Y.; Tashima, T.; Kawamoto, N.; Mega, T.; et al. Global Satellite Mapping of Precipitation (GSMaP) Products in the GPM Era. In Satellite Pre-Cipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D., Kummerow, C., Nakamura, K., Turk, F.J., Eds.; Springer: Cham, Switzerland, 2020; pp. 355–373. [Google Scholar]
- Reboita, M.S.; Gan, M.A.; Da Rocha, R.P.; Ambrizzi, T. Regimes de precipitação na América do Sul: Uma revisão bibliográfica. Rev. Bras. Meteorol. 2010, 25, 185–204. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef] [Green Version]
- Maggioni, V.; Massari, C.; Kidd, C. Errors and uncertainties associated with quasiglobal satellite precipitation products. In Precipitation Science; Michaelides, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Volume 1, pp. 377–390. [Google Scholar] [CrossRef]
- Oliveira, R.; Maggioni, V.; Vila, D.; Morales, C. Characteristics and Diurnal Cycle of GPM Rainfall Estimates over the Central Amazon Region. Remote Sens. 2016, 8, 544. [Google Scholar] [CrossRef] [Green Version]
- Rozante, J.R.; Vila, D.A.; Chiquetto, J.B.; Fernandes, A.D.A.; Alvim, D.S. Evaluation of TRMM/GPM Blended Daily Products over Brazil. Remote Sens. 2018, 10, 882. [Google Scholar] [CrossRef] [Green Version]
- Gadelha, A.N.; Coelho, V.H.R.; Xavier, A.C.; Barbosa, L.R.; Melo, D.C.; Xuan, Y.; Huffman, G.J.; Petersen, W.A.; Almeida, C.D.N. Grid box-level evaluation of IMERG over Brazil at various space and time scales. Atmos. Res. 2018, 218, 231–244. [Google Scholar] [CrossRef] [Green Version]
- Satgé, F.; Pillot, B.; Roig, H.; Bonnet, M.-P. Are gridded precipitation datasets a good option for streamflow simulation across the Juruá river basin, Amazon? J. Hydrol. 2021, 602, 126773. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Kain, J.S. A Gaussian Mixture Model Approach to Forecast Verification. Weather Forecast. 2010, 25, 908–920. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhang, Y.; Giangrande, S.E. Rainfall-Rate Estimation Using Gaussian Mixture Parameter Estimator: Training and Validation. J. Atmos. Ocean. Technol. 2012, 29, 731–744. [Google Scholar] [CrossRef] [Green Version]
- Ling, H.; Zhu, K. Predicting Precipitation Events Using Gaussian Mixture Model. J. Data Anal. Inf. Process. 2017, 5, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Crawford, A. The Use of Gaussian Mixture Models with Atmospheric Lagrangian Particle Dispersion Models for Density Estimation and Feature Identification. Atmosphere 2020, 11, 1369. [Google Scholar] [CrossRef]
- Scrucca, L. GA: A Package for Genetic Algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Ultsch, A.; Thrun, M.C.; Hansen-Goos, O.; Lötsch, J. Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss). Int. J. Mol. Sci. 2015, 16, 25897–25911. [Google Scholar] [CrossRef] [PubMed]
- Lerch, F.; Ultsch, A.; Lötsch, J. Distribution Optimization: An evolutionary algorithm to separate Gaussian mixtures. Sci. Rep. 2020, 10, 648. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Joyce, R.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG). In NASA Algorithm Theoretical Basis Document, Version 06; NASA: Washington, DC, USA, 2019; p. 38. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V06.pdf (accessed on 1 February 2021).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Hsu, K.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using arti-ficial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evolution of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Amer. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef] [Green Version]
- de Paiva, R.C.D.; Buarque, D.C.; Collischonn, W.; Bonnet, M.-P.; Frappart, F.; Calmant, S.; Bulhões Mendes, C.A. Large-scale hydrologic and hydrodynamic modeling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef] [Green Version]







| Experiment | Available Period | Plat. N° | Platforms |
|---|---|---|---|
| CREF | 4 March 2014–8 April 2015 | 12 | SSMI/S(3), GCOMW1, TMI, GMI, SAPHIR *, MHS(4), ATMS |
| C99 | 1 January 1988–31 December 1990 | 1 | SSMI/S(1) |
| C04 | 1 December 2006–29 February 2008 | 10 | SSMI/S(3), GCOMW1, TMI, MHS(4), ATMS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, R.A.J.; Roca, R. A Simple Statistical Model of the Uncertainty Distribution for Daily Gridded Precipitation Multi-Platform Satellite Products. Remote Sens. 2022, 14, 3726. https://doi.org/10.3390/rs14153726
Oliveira RAJ, Roca R. A Simple Statistical Model of the Uncertainty Distribution for Daily Gridded Precipitation Multi-Platform Satellite Products. Remote Sensing. 2022; 14(15):3726. https://doi.org/10.3390/rs14153726
Chicago/Turabian StyleOliveira, Rômulo A. J., and Rémy Roca. 2022. "A Simple Statistical Model of the Uncertainty Distribution for Daily Gridded Precipitation Multi-Platform Satellite Products" Remote Sensing 14, no. 15: 3726. https://doi.org/10.3390/rs14153726
APA StyleOliveira, R. A. J., & Roca, R. (2022). A Simple Statistical Model of the Uncertainty Distribution for Daily Gridded Precipitation Multi-Platform Satellite Products. Remote Sensing, 14(15), 3726. https://doi.org/10.3390/rs14153726