Many-Objective RadarCom Signal Design via NSGA-II Genetic Algorithm Implementation and Simulation Analysis

Abstract

In this communication, we investigate the performance of the Non-dominated Sorting Genetic Algorithm II (NSGA-II) in many-objective optimization scenarios pertaining to joint radar and communication functionality. We introduce five objectives relevant to sensing and secure communications and develop a cost function where these objectives can be individually prioritized by a user. We consider three scenarios: Radar Priority, Communication Priority, and All (Objectives) Equal; we then demonstrate the optimization results using an orthogonal frequency-division multiplexing (OFDM) radarcom signal. The objectives with selected weights are shown to improve system performance and thereby validate the viability of our approach. The Radar Priority scenario showed the best improvement in probability of detection, PSLR, and PAPR. Compared to the baseline performance values, the improvements were: from 94.05% to 96%, from 11.7 to 13.6 dB, and from 9.46 to 7.09 dB, respectively. The communication scenario saw the best improvement in BER and clutter similarity (measured by NRMSE) from 3.52% to 0.39% and 0.87 to 0.59, respectively.

1. Introduction

The fusion of radar and communications, often known as radarcom, has become an area of interest for research in the last decade. This fusion has the advantage of reduced spectrum usage at a time when the spectrum is being increasingly divided among a variety of applications. Furthermore, it also has the potential to reduce the SWaP (Size Weight and Power) and hardware complexity of analog front ends (AFE) [1,2,3]. However, it can be difficult to design a radarcom signal with optimized performance in both functionalities [4]. When other factors besides radar and communication performance become of interest, the problem becomes even more complicated, leading to the consideration of multi-/many-objective optimization (MOO) techniques.

In this letter, we consider the orthogonal frequency-division multiplexing (OFDM) modulation scheme, which has been proposed for use in radarcom before [5]. Recently, several works have been dedicated to OFDM signal optimization for use in radarcom, where a certain parameter was of interest, e.g., peak sidelobe level or power minimization for a low probability of intercept (LPI) functionality [5,6,7,8]. However, when the number of optimized parameters exceeds four, other specialized approaches need to be considered.

Evolutionary algorithms (EA) have been investigated for the case of multiple-input and multiple-output (MIMO) radar systems to find the optimal transmitter parameters, reduce the peak-to-sidelobe ratio (PSLR), and improve the detection of weak targets [9,10,11,12]. In this letter, we propose to use an EA that is a genetic algorithm (GA), specifically the Non-dominated Sorting Genetic Algorithm II (NSGA-II). This GA has been applied to various problems since it was introduced in 2002 [13], e.g., in [14] it was used to improve radar detection performance in sparse regions; the authors also show that NSGA-II can perform well for MOO problems. In [15], the authors demonstrate that this algorithm can be used in many-objective problems (where there are four or more objectives in a problem).

In [16]—which is the closest work to our topic—the authors employ NSGA-II to perform two-objective optimization of OFDM radar signals and investigate the feasibility of using EA for such purposes. Our work differs from [16] in that we expand the optimization problem to MOO and develop a method suitable for the optimal design of joint radar-communication waveforms, wherein both radar and communication aspects can be affected. To put it another way, we expand the MOO problem from a single domain (i.e., radar, as in [16]) to three domains: radar, communications, and data security. Thus, not only is the number of objectives greater in our work, but also the number of domains from which these objectives are selected is increased three-fold.

In this letter, we will use the NSGA-II to create an OFDM radarcom signal with weighted and optimized PSLR, peak-to-average power ratio (PAPR), LPI, radar detection/identification, and communication bit error rate (BER) parameters. We also propose to achieve the characteristic of LPI via masking our transmissions as local radar clutter [17], which is implemented via a random sequence encoding (RSE) [18].

We discuss OFDM radarcom signal design setup with MOO in Section 2; Section 3 discusses the application of NSGA-II to our MOO problem; Section 4 then presents the simulation results, while Section 5 offers concluding remarks.

2. Materials and Methods

2.1. RadarCom Signal Construction

The analog time-domain representation of an OFDM transmit signal is shown in (1), while (2) shows its samples ${\mathrm{s}}_{\mathrm{n}}$ formed from frequency-domain sub-carrier coefficients $S$ [5]:

$${\mathrm{S}}_{\mathrm{TX}}\left(\mathrm{t}\right)={\displaystyle \sum }_{\mathrm{n}=1}^{2\mathrm{N}+1}{\mathrm{s}}_{\mathrm{n}}·{\displaystyle \prod }_{\mathsf{\tau }=1/{\mathrm{f}}_{\mathrm{s}}}\left(\mathrm{t}-\frac{\mathrm{n}-1}{{\mathrm{f}}_{\mathrm{s}}}\right)$$

(1)

$${\mathrm{s}}_{\mathrm{n}}=\frac{1}{2\mathrm{N}+1}{\displaystyle \sum }_{\mathrm{k}=1}^{2\mathrm{N}+1}\mathrm{S}\left(\mathrm{k}\right)·{\mathrm{e}}^{\mathrm{j}2\mathsf{\pi }\frac{\left(\mathrm{k}-1\right)\left(\mathrm{n}-1\right)}{2\mathrm{N}+1}}$$

(2)

where ${\displaystyle \prod }_{\mathsf{\tau }=1/{\mathrm{f}}_{\mathrm{s}}}\left(\mathrm{t}-{\mathrm{t}}_0\right)$ represents a square pulse of duration ($1/{\mathrm{f}}_{\mathrm{s}}$) centered at time ${\mathrm{t}}_0$, ${\mathrm{f}}_{\mathrm{s}}$ is the sampling frequency of the digital-to-analog converter (DAC) in the OFDM transmitter [5], $\mathrm{N}$ is the total number of sub-carriers, and $\mathrm{S}\left(\mathrm{k}\right)$ is the coefficient of the kth sub-carrier containing amplitude and phase. In this study, we choose 1024-element vectors of these coefficients S and optimize them using the GA. We also propose to use quadrature phase shift keying (QPSK) to follow the OFDM modulation.

As mentioned above, the RSE can be used to generate samples of local clutter and then use them as sub-carrier coefficients $S$, where a parameter of the clutter’s probability density function (pdf) can be modified to encode communications. To make communications more efficient, however, we can use several sub-carrier coefficients to directly encode the data on.

2.2. Multiple-Objective Setup

In this sub-section, we will introduce the following five objectives that affect the performance of the proposed radarcom signals:

Radar-related Objectives: PAPR, PSLR, and Probability of Correct detection/identification (${\mathrm{P}}_{\mathrm{DI}}$);

Communication-related Objective: BER;

LPI Objective: Clutter-Masking Efficiency (measured via the normalized root-mean-square error (NRMSE)).

2.2.1. Peak-to-Average Power Ratio (PAPR)

We define the PAPR as per (3) below:

$$\mathrm{PAPR}=10{\log }_{10}\left(\frac{\max \left({\mathrm{S}}_{\mathrm{TX}}\left(\mathrm{t}\right)\right)}{{\overline{\mathrm{S}}}_{\mathrm{TX}}\left(\mathrm{t}\right)}\right)$$

(3)

where ${\overline{\mathrm{S}}}_{\mathrm{TX}}\left(\mathrm{t}\right)$ denotes the mean value of (1). It is well known that OFDM signals often suffer from high values of PAPR, which adversely affect the signal integrity by causing signal clipping in the transmitter. OFDM signals used in radar have been analyzed from this perspective before, and several methods of PAPR reduction have been introduced, e.g., in [19,20]. We will be seeking to minimize this parameter.

2.2.2. Peak-to-Sidelobe Ratio (PSLR)

We define the PSLR as per (4) and (5) below:

$$\mathrm{u}\left(\mathrm{t}\right)={\mathrm{S}}_{\mathrm{RX}}\left(\mathrm{t}\right)⨂{\mathrm{S}}_{\mathrm{TX}}\left(\mathrm{t}\right)$$

(4)

$$\mathrm{PSLR}=10{\log }_{10}\left(\frac{\max \left(\mathrm{u}\left(\mathrm{t}\right)\right)}{\underset{2}{\max }\left(\mathrm{u}\left(\mathrm{t}\right)\right)}\right),$$

(5)

where $\mathrm{u}\left(\mathrm{t}\right)$ is the matched filtered return signal, ${\mathrm{S}}_{\mathrm{RX}}\left(\mathrm{t}\right)$ represents the received signal, $⨂$ denotes convolution, and $\underset{2}{\max }\left(·\right)$ denotes the second-largest peak of the function within parentheses. We will be seeking to maximize this parameter.

2.2.3. Bit Error Rate (BER)

It is the BER defined as the number of bits in communication data that were reconstructed incorrectly upon reception, divided by the total number of bits encoded onto the transmit signal. We will be seeking to minimize this parameter.

2.2.4. Probability of Correct Detection/Identification (${\mathrm{P}}_{\mathrm{DI}}$)

To test the performance in a radar target detection/identification scenario, we used our previous work setup described in [21]. In it, we performed a Monte Carlo analysis of an ultra-wideband (UWB) OFDM radar identification of two possible targets (trihedral metal corner reflector and metal cylinder) with known radar cross sections (RCS). The radar signals were randomly encoded, and target reflections were simulated over multiple angles of incidence and at the frequency locations corresponding to the OFDM signal sub-carriers. Additive white Gaussian noise with varying signal-to-noise ratio (SNR) was introduced. In this work, we use the same setup, but instead of randomly encoding the OFDM signals we used RSE–QPSK–OFDM waveforms with MOO.

2.2.5. Low Probability of Intercept (LPI)

We first use the general expression for normalized root-mean-square error (NRMSE) to quantify the deviation between measured clutter returns and the proposed model:

$$\mathrm{NRMSE}\mathrm{Power}=({\displaystyle \sum }_{\mathrm{j}}{\displaystyle \sum }_{\mathrm{i}}\frac{{\mathrm{x}}_{\mathrm{r},\mathrm{i}}-{\mathrm{x}}_{\mathrm{j},\mathrm{i}}}{{\mathrm{x}}_{\mathrm{r},\mathrm{i}}-\overline{{\mathrm{x}}_{\mathrm{r}}}})/3,$$

(6)

where ${\mathrm{x}}_{\mathrm{r}}$ is the reference pdf vector and ${\mathrm{x}}_{\mathrm{j}}$ is the pdf of the sample vector being evaluated. There are three such pdfs that we evaluate the NRMSE function for, corresponding to the samples in the time domain, the samples of frequency-domain magnitudes, and the samples of phase. We average the resultant NRMSEs into what we define as NRMSE Power (6). Our goal here is to measure how similar the resultant signal is to a clutter return, which is performed in the time and frequency domains using (6). As per [5], we assume that the power of clutter returns in the time domain has a Weibull distribution with a shape parameter $\mathrm{k}=3$ and scale parameter $\mathsf{\lambda }=0.5$. The corresponding distributions for the frequency magnitude and phase were a Rayleigh distribution with scale parameter $\mathsf{\sigma }=345$ and a uniform distribution within [0, 2π], respectively. We then generated 200 NRMSE Power values by using a reference vector of simulated clutter of length 100,000 with 200 random simulated clutter vectors of length 1024. The resultant NRMSE Power values ranged within a [0.22, 0.95] interval, with a mean of 0.48 and a standard deviation of 0.14. It is assumed that unauthorized platforms will classify signals within one standard deviation from the mean as clutter, so an NRMSE Power below 0.62 (= 0.48 + 0.14) is the goal.

While not an objective to be optimized, communication throughput can be varied in this scheme by changing the number of sub-carrier coefficients used directly for communications, as explained at the end of Section 2.1. In subsequent analysis, we used 25% of the sub-carrier frequencies, equally spaced, for this purpose. It is assumed that the friendly receiver knows this scheme and thus demodulates only every fourth sub-carrier to extract the communication data.

It is intuitively clear that adjusting the RSE–QPSK–OFDM signal via manipulating its sub-carrier coefficients may cause certain objectives to be met, while others are not met. However, there may be circumstances where some of the objectives are considered more important than others. This leads us to the formulation of the cost function containing objective weights, which is discussed in Section 2.3.

2.3. Multi-Objective Cost Function Setup

We use the cost function described in [22] to allow for proper prioritization. We normalize the value of each objective across the population before sorting is performed in each generation. We also add user-defined weights ${\mathrm{a}}_{\mathrm{i}},\mathrm{i}=1\dots 5$, so that certain objectives can be prioritized. Subsequently, they are combined into a single function that is used for sorting. The cost function we will use in the NSGA-II is shown in (7), while (8) shows the mean of the weighted objectives and (9) shows how we performed the normalization:

$$\mathrm{C}=\underset{{\mathrm{S}}_{\mathrm{TX}}}{\min }{\displaystyle \sum }_{\mathrm{i}=1}^5\left(1-\mathsf{\gamma }\right){\mathrm{a}}_{\mathrm{i}}{{\mathrm{f}}^{\prime }}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{TX}}\right)+\mathsf{\gamma }\mathrm{M},$$

(7)

$$\mathrm{M}=\frac{1}{5}{\displaystyle \sum }_{\mathrm{i}=1}^5{\mathrm{a}}_{\mathrm{i}}{{\mathrm{f}}^{\prime }}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{TX}}\right),$$

(8)

$${{\mathrm{f}}^{\prime }}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{TX}}\right)=\frac{{\mathrm{f}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{TX}}\right)-{\mathrm{f}}_{\min }\left({\mathrm{S}}_{\mathrm{TX}}\right)}{{\mathrm{f}}_{\max }\left({\mathrm{S}}_{\mathrm{TX}}\right)-{\mathrm{f}}_{\min }\left({\mathrm{S}}_{\mathrm{TX}}\right)},$$

(9)

where ${{\mathrm{f}}^{\prime }}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{TX}}\right)$ is the normalized objective, ${\mathrm{f}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{TX}}\right)$ are the objectives, and γ is the parameter that sets the importance of the mean objective score M.

As mentioned in the introduction, when the number of objectives exceeds four, the NSGA-II algorithm has been shown to perform well. In the next section, we outline our method of implementing this GA to optimize the weighted cost function (7).

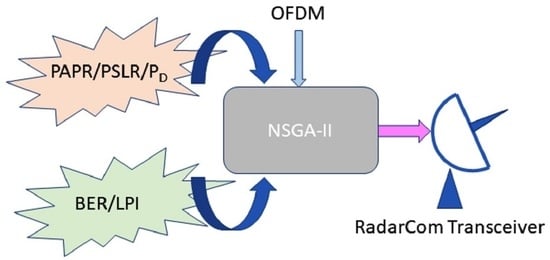
3. Many-Objective Optimization Using a Genetic Algorithm

When using the NSGA-II, a string of 1024 sub-carrier amplitude values is used as the DNA to represent each sample. Then, they are evaluated according to (7), where the five objectives include (3), (5), and (6), along with the probability of detection at 0 dB found as per [21], and the average simulated BER is evaluated at an SNR of 5 dB. We used a population size of 200 and ran the algorithm for up to 1000 generations. The population size and generation number could be increased; however, this will slow down the computing speed. Figure 1 illustrates our algorithm. This algorithm has a complexity of O(M(N²)), where M is the number of objectives and N is the population size [23].

We also investigated NSGA-III [22] and Simulated Annealing (SA) [24] for implementing our MOO. However, in a test scenario of 500 generations with NSGA-III, or 60 iterations in SA, NSGA-II performed the best. This is in agreement with [25], which shows that NSGA-III does not always outperform NSGA-II, especially in cases of maximizing objectives.

4. Simulation Results and Analysis

As mentioned above, all of our simulations were performed with the number of OFDM sub-carriers N = 1024. Each sub-carrier was encoded with an OFDM symbol, resulting in a sub-carrier-to-symbol ratio of 1. To compare the basic performance of our algorithm in one domain only, we first set the weights of all objectives to zeros, except the two radar-relevant objectives, PAPR and PSLR, which were weighted equally. We then ran the analysis with 1000 generations and obtained the following optimal values: PAPR = 7.14 dB and PSLR = 13.77 dB. Contrasting this to [16], we note that while there is no exact match in terms of the OFDM signal setup and MOO analysis parameters, the results shown in Figure 7d on p. 1960 of [16] do allow for basic comparison: for N = 500 and 1000 generations, their equivalent PSLR value with PAPR fixed at 7.5 dB was approximately 14 dB, which matches our obtained results well.

Next, we moved on to MOO analysis across all three domains. Figure 2 shows the results of the NSGA-II in three scenarios described in

Table 1. Scenario Priority Weights.

Scenario	${\mathbf{P}}_{\mathbf{D}\mathbf{I}}$	PSLR	PAPR	BER	NRMSE
All Equal	20%	20%	20%	20%	20%
Radar	50%	40%	0	0	10%
Comm.	0	0	10%	80%	10%

. The scenarios were designed according to their priority weights, all of which add up to 50. The parameter $\mathsf{\gamma }$ was set to 0.25, and the mutation and crossover parameters were both 25%. A higher mutation rate can search a larger space of possibilities but also converges slower. Median values of each of the five objectives (PAPR, NRMSE Power, ${\mathrm{P}}_{\mathrm{DI}}$, BER, and PSLR) were plotted against the number of generations, which were varied from 0 (no optimization, i.e., baseline) to the maximum of 1000 in steps of 250. It is desirable to minimize PAPR, NRMSE Power and BER; the maximization of ${\mathrm{P}}_{\mathrm{D}\mathrm{I}}$ and PSLR is also desirable. The priority weights allocated to each scenario are shown in Table 1. Median values were chosen as we can guarantee that 50% of the signals will have a better performance than the median, which is not the case with the mean. Standard deviation (std) is shown in

Table 2. Standard Deviation Results by Scenario.

Scenario	${\mathbf{P}}_{\mathbf{D}\mathbf{I}},\%$	PSLR, dB	PAPR, dB	BER, %	NRMSE
All Equal	0.8	0.606	0.646	3.94	0.082
Radar	0.9	0.283	0.963	4.10	0.025
Comm.	0.8	0.495	1.33	4.19	0.045

as well. As can be seen from it, most of the std values are well below the corresponding numbers for the parameters shown in Figure 2, which indicates the low spread and, thus, the high reliability of the simulated data. One exception is BER, which exhibits high std.

4.1. Radar Priority (Red Traces)

Here, ${\mathrm{P}}_{\mathrm{DI}}$ has the highest priority, followed by PSLR—we, indeed, observe that ${\mathrm{P}}_{\mathrm{DI}}$ grew from the baseline case of 94.05% to approximately 96% after about 750 generations, which was 32.77% of the 5.95 possible percentage points available. PSLR grew from 11.7 dB to approximately 13.6 dB. The other objectives were improved as well, albeit mildly. In Figure 3 and Figure 4, we show an example of a radar signal after 1000 generations: time domain and frequency domain, as well as its ambiguity function (AF), are illustrated. Similar plots were generated for the other two scenarios (below), and it was established that the time-domain, spectral, and AF plots vary only insignificantly. This is expected, as our MOO does not concern these characteristics. It is also beneficial from the perspective of a radarcom transceiver design, as MOO will not require it to adjust to a specific scenario.

4.2. Communication Priority (Black Traces)

The highest priority goes to BER, with a weight of 80%. BER, indeed, drops from 3.52% to 0.39%—the lowest value in all three scenarios. NRMSE Power also drops from approximately 0.9 to the desired value of 0.6. PAPR proves the most difficult to control, as it rises from 10 dB to 15 dB, indicating that the assigned weight of 10% was insufficient. This result suggests that there is a specific tradeoff between PAPR and BER that needs to be investigated further.

4.3. All-Equal (Blue Traces)

The ${\mathrm{P}}_{\mathrm{D}\mathrm{I}}$, PAPR, and PSLR values are between those for the previous two scenarios, as expected. NRMSE Power drops from the baseline value to approximately 0.7 but then rises with the increased number of generations. BER improvements are the mildest of the three scenarios.

5. Conclusions

In this letter, we introduce an approach to joint radar-communication signal MOO via NSGA-II algorithm, where a user can prioritize certain objectives over others in a novel way. We took advantage of the recent modification to the NSGA-II to improve the optimization. Additionally, we tried optimizing more objectives across more domains than has been attempted before. Using simulated data, we have demonstrated that the NSGA-II can take an OFDM signal with QPSK data encoding and improve it in multiple areas relevant to radar, communications, and LPI needs, with the latter formulated as data communications masked via RSE to resemble clutter returns. This is opposed to some of the other works that use OFDM in a radar-only capacity or do not investigate LPI properties at all. In our future work, we plan to further investigate the limits of this approach, both with respect to the number of objectives and the algorithm parameters, such as the number of generations, as well as consider other metaheuristics.