Backscatter Characteristics Analysis for Flood Mapping Using Multi-Temporal Sentinel-1 Images
Abstract
:1. Introduction
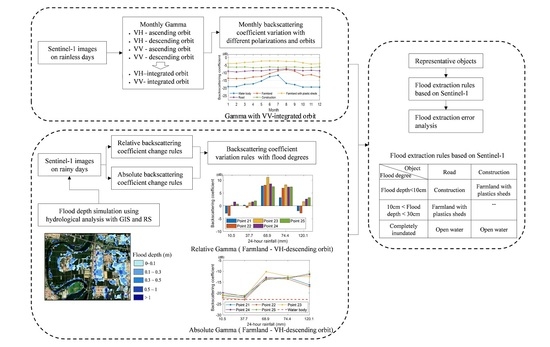
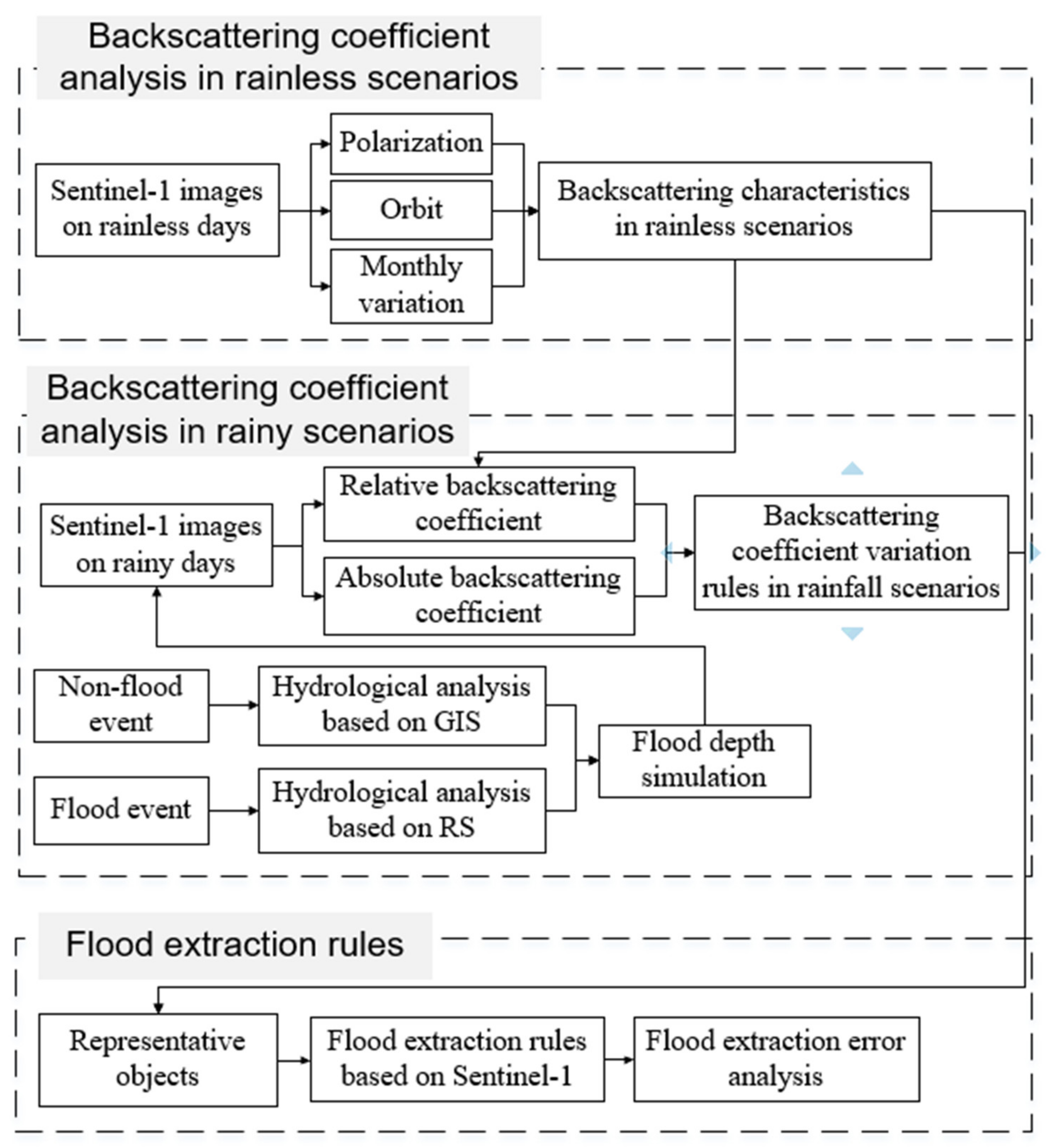
2. Data and Methodology
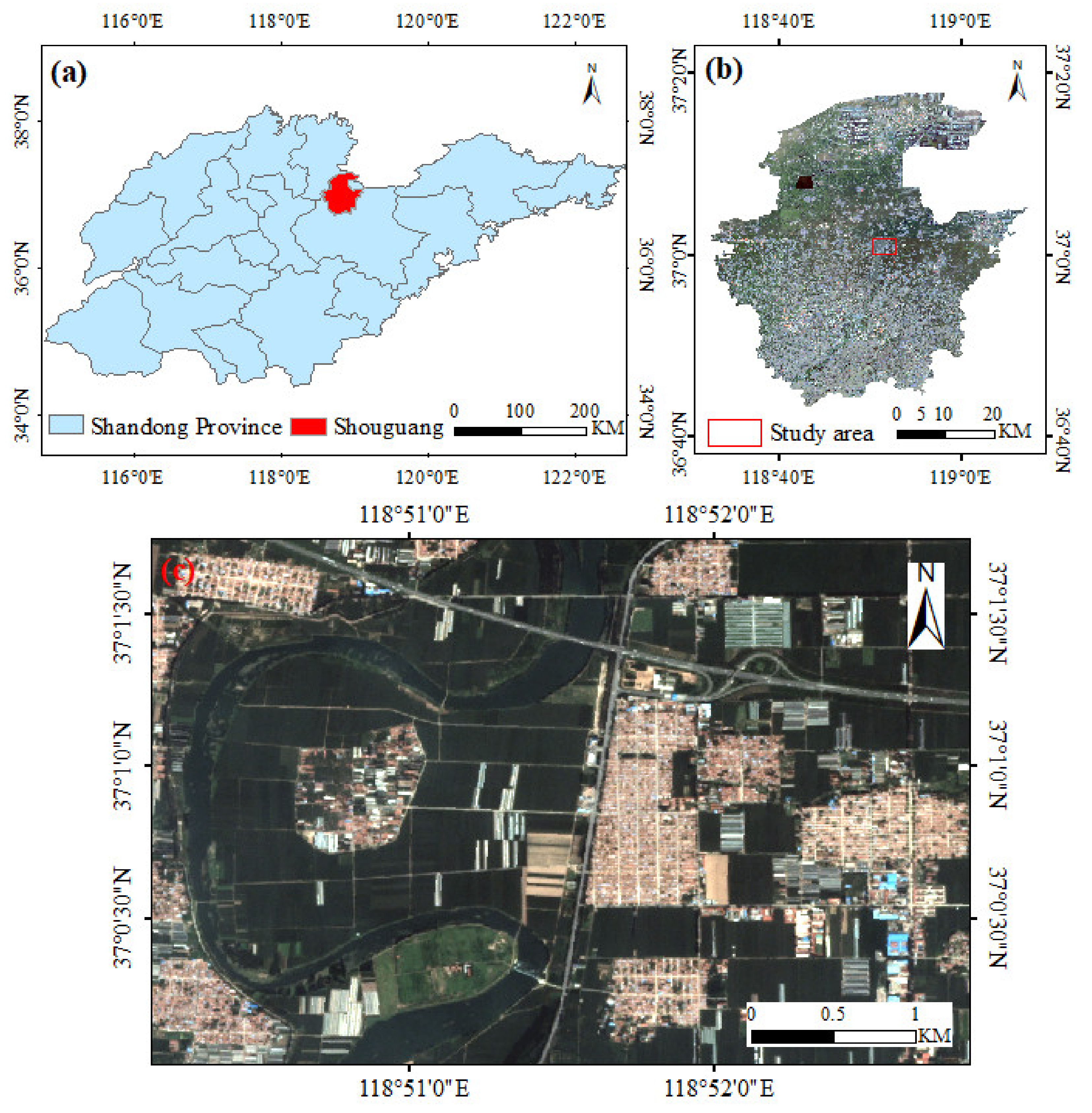
2.1. Study Area
2.2. Data and Pre-Processing
2.2.1. Sentinel-1 Data and Pre-Processing
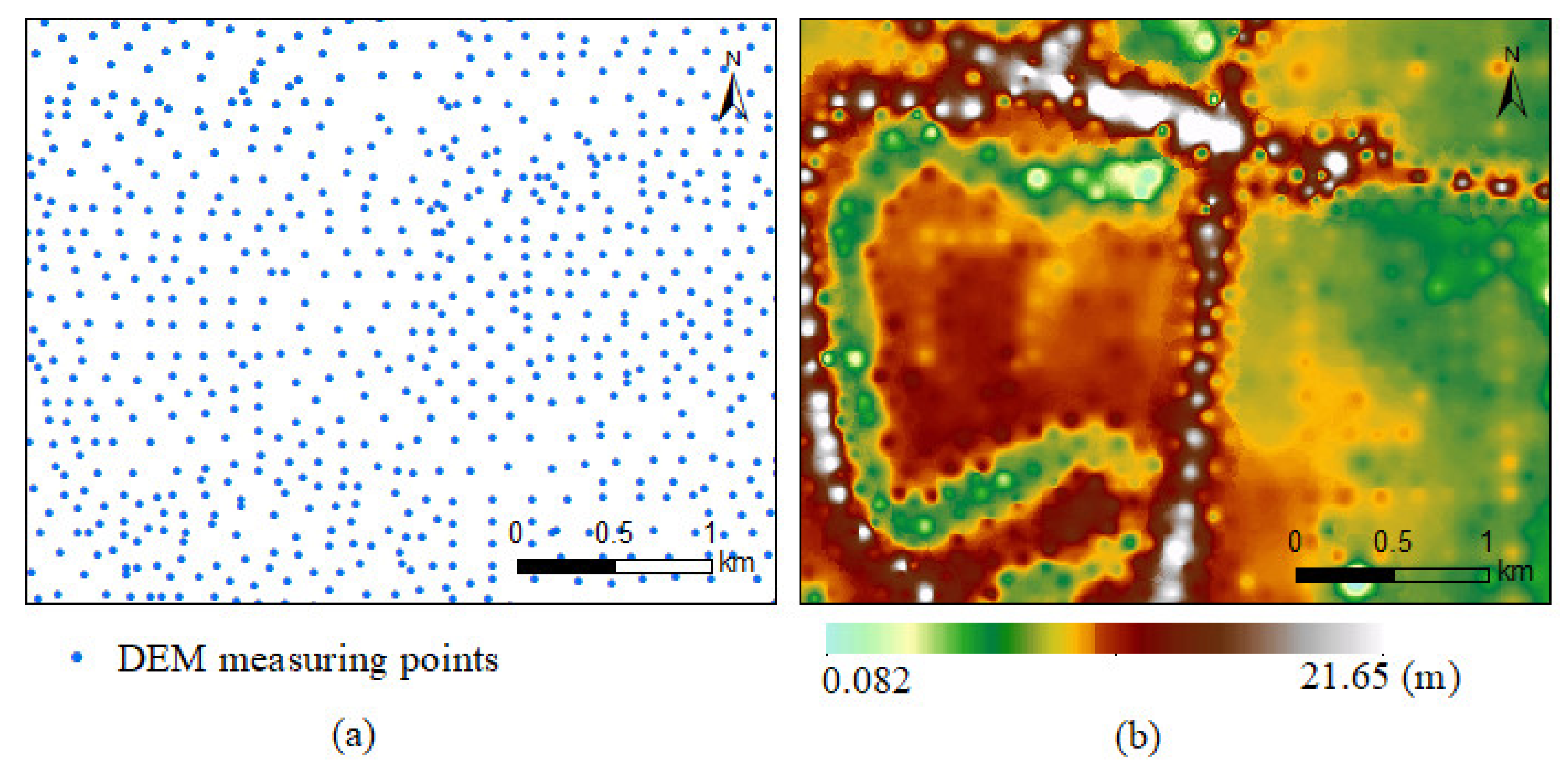
2.2.2. Rainfall and Terrain Data
2.3. Methodology
2.3.1. Flood Inundation Analysis Based on GIS
2.3.2. SCS-CN Model
2.3.3. Three-Level Catchment Division Method
2.3.4. Surface Flood Diffusion Algorithm with Non-Source
2.3.5. Flood Inundation Analysis Based on RS and DEM
3. Results and Discussion
3.1. Backscattering Coefficient of Ground Objects in Rainless Scenarios
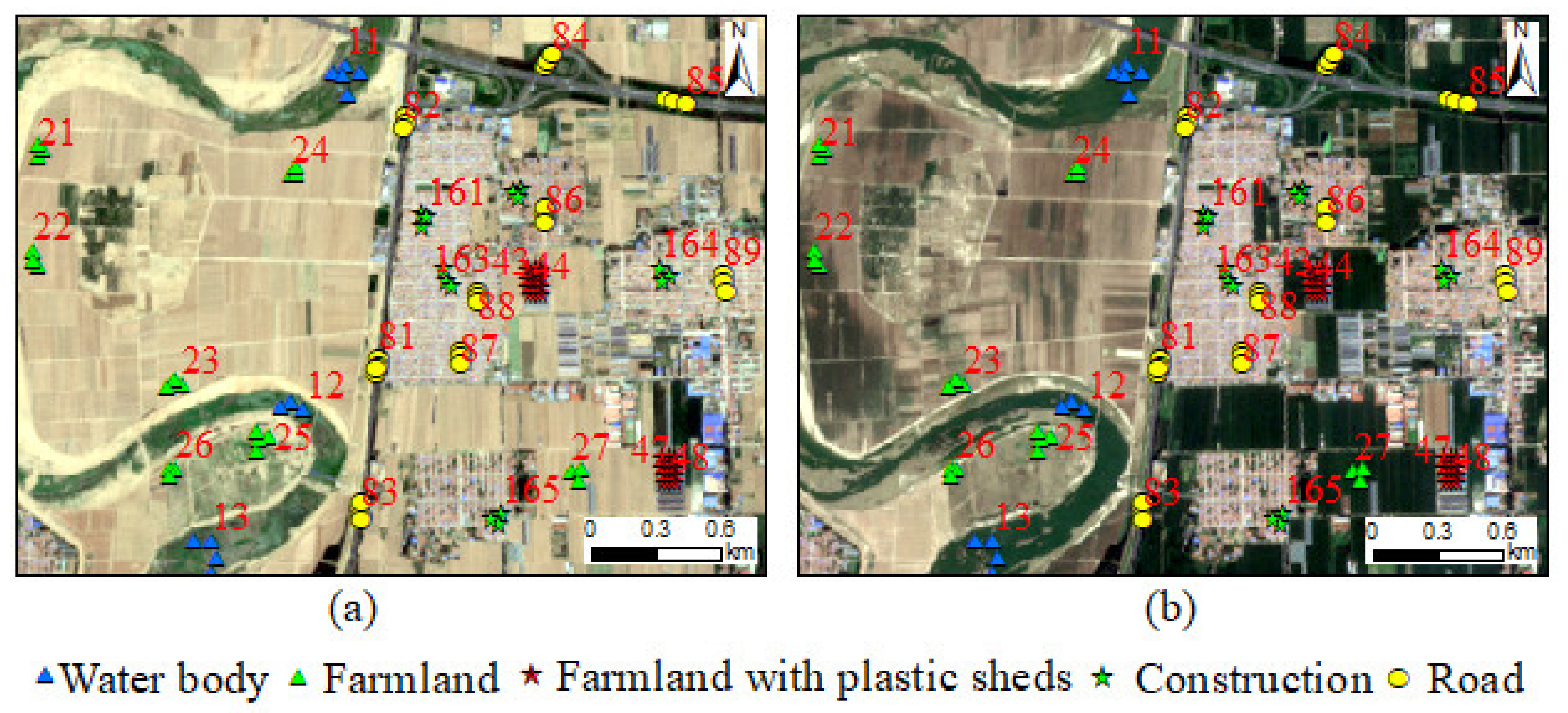
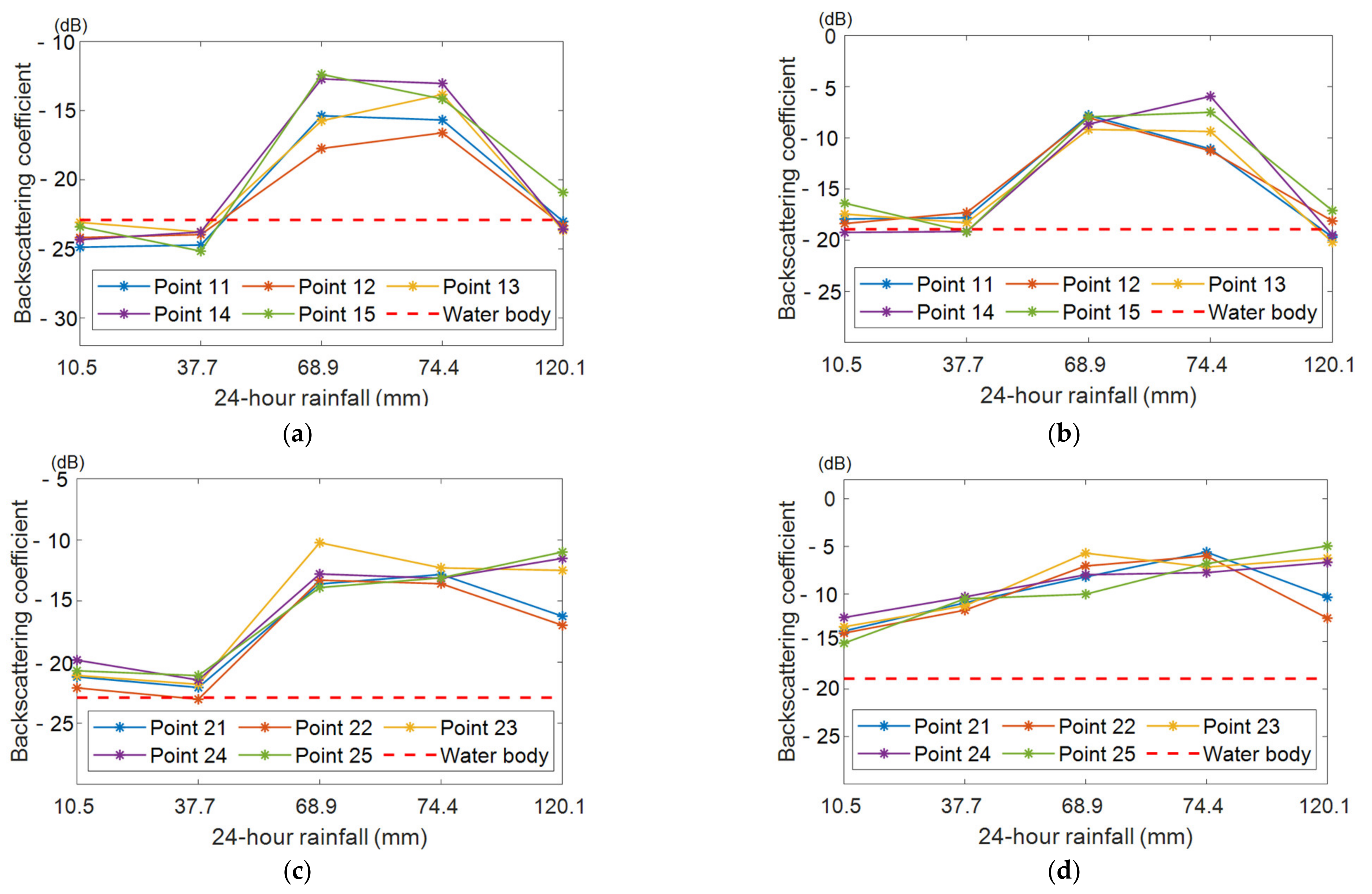
3.1.1. Selection and Statistical Analysis of Sample Points
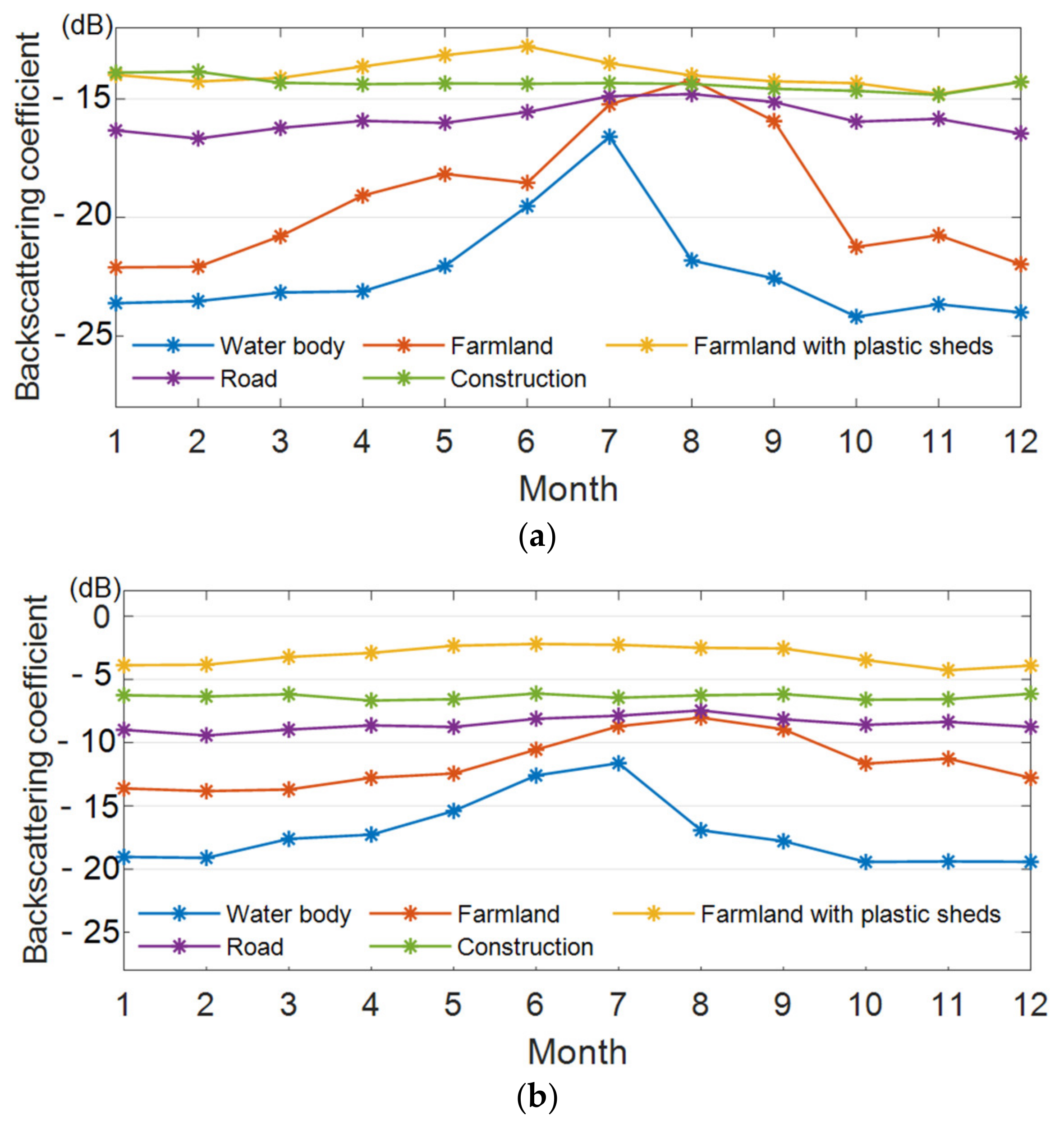
3.1.2. Monthly Variations of Backscattering Coefficients
3.1.3. Influence of Polarization on Backscattering Coefficient
3.1.4. Influence of Orbit on Backscattering Coefficient
3.2. Backscattering Coefficients Change Rules of Ground Objects in Rainy Scenarios
3.2.1. Flood Depth Simulation Based on the GIS and RS Techniques
Rainfall Samples
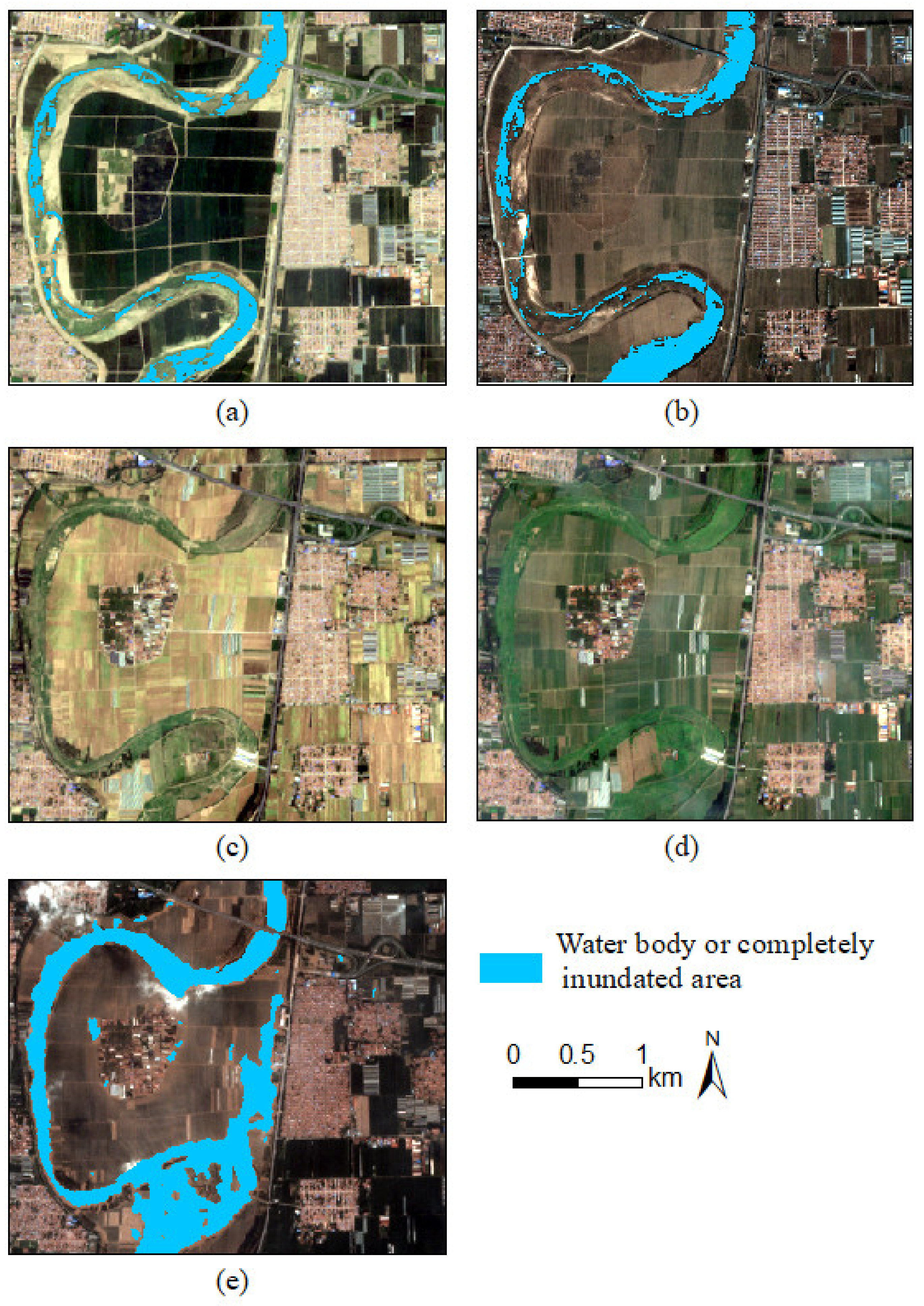
Waterbody Extraction Based on RS Images and Threshold Method
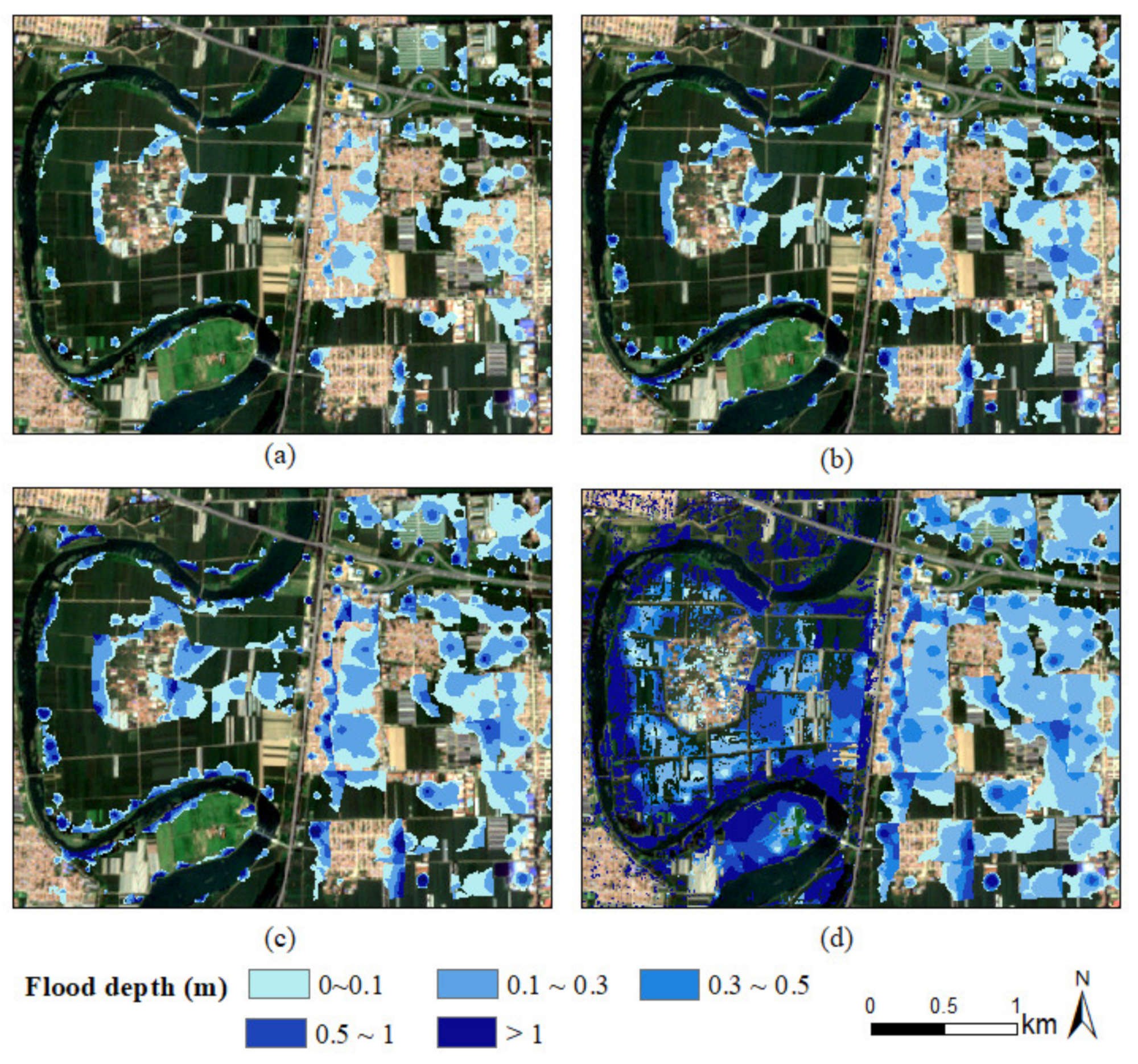
Flood Depth Simulation
3.2.2. Selection and Statistical Analysis of Sample Points in the Context of Flood Mapping
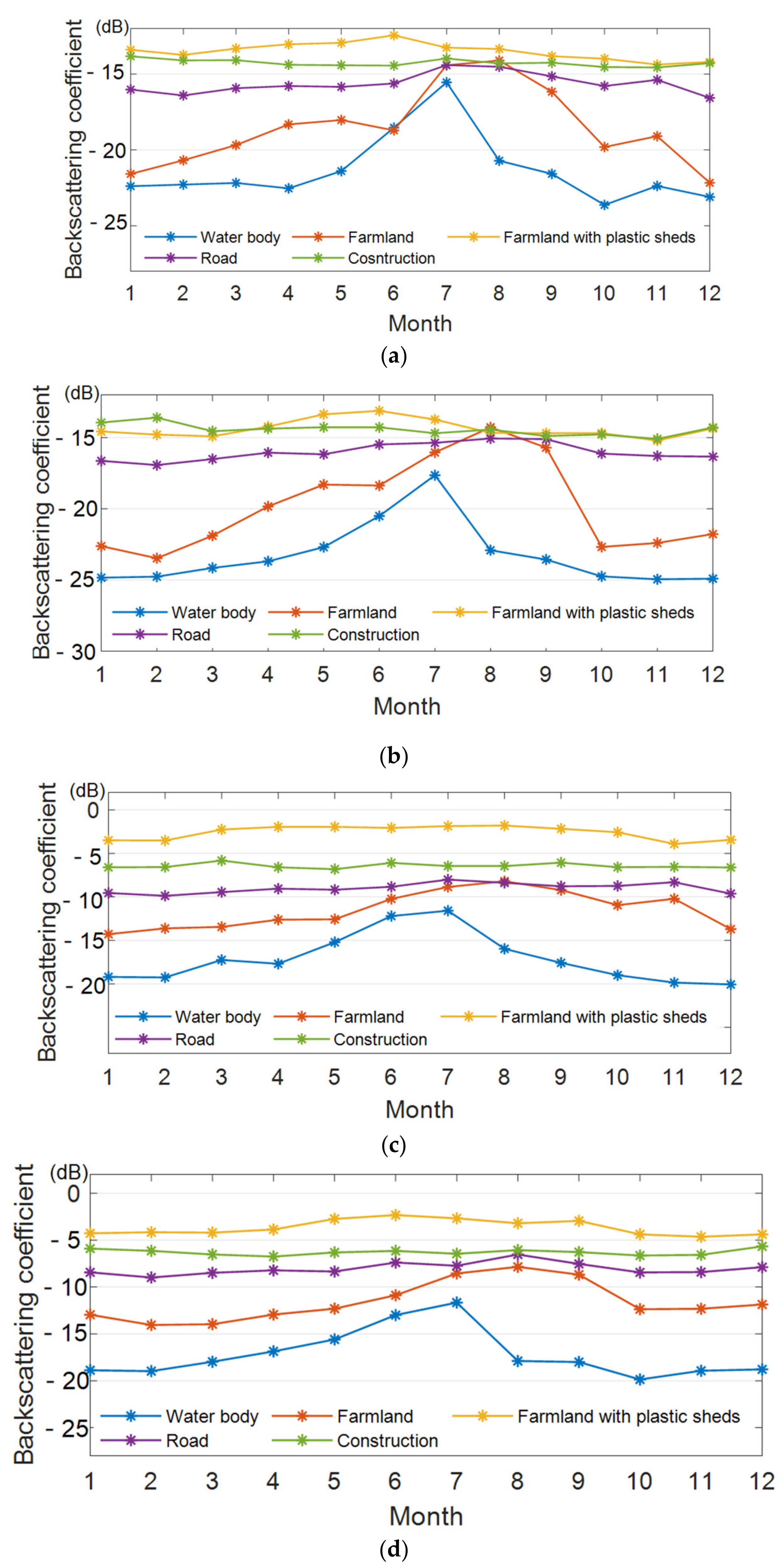
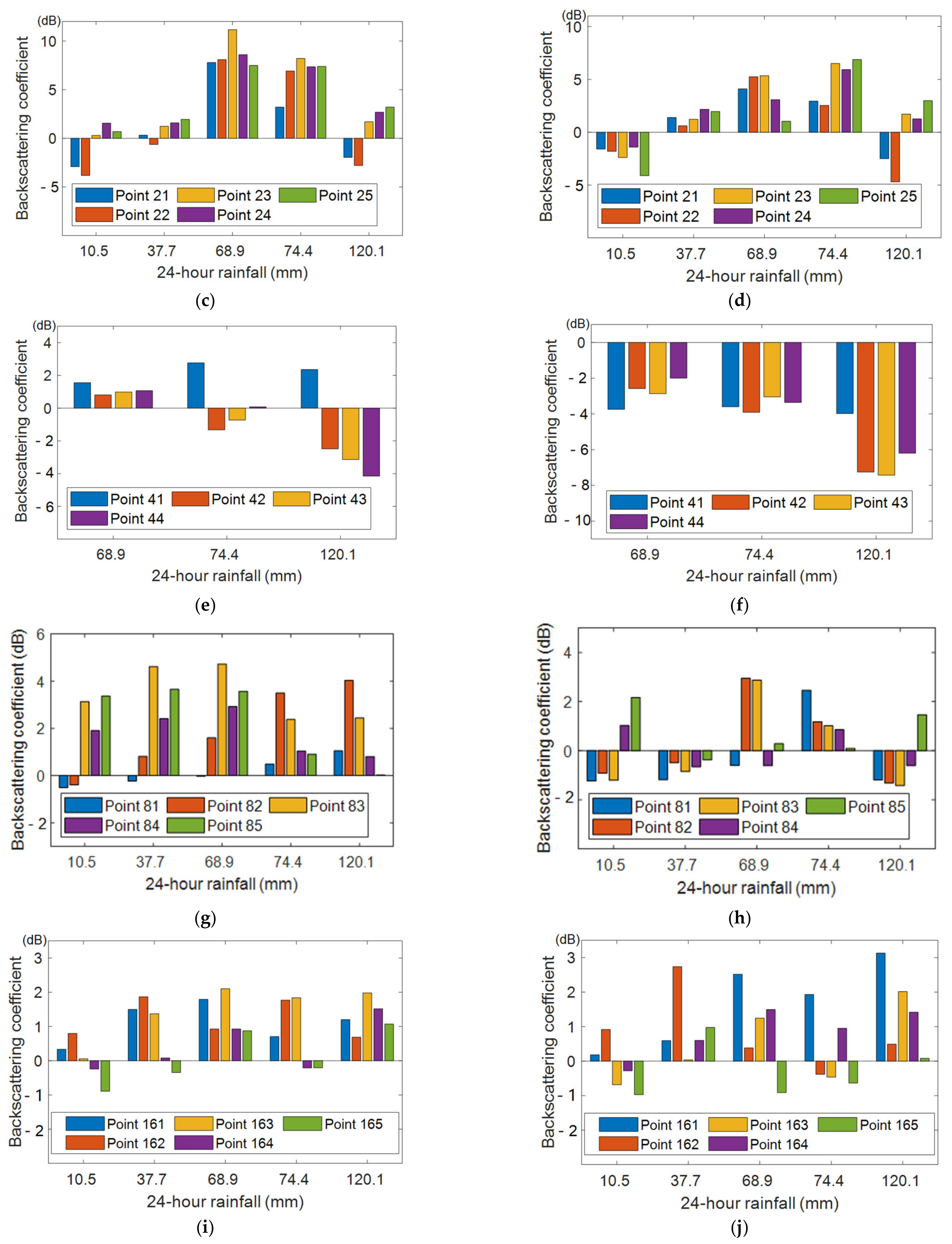
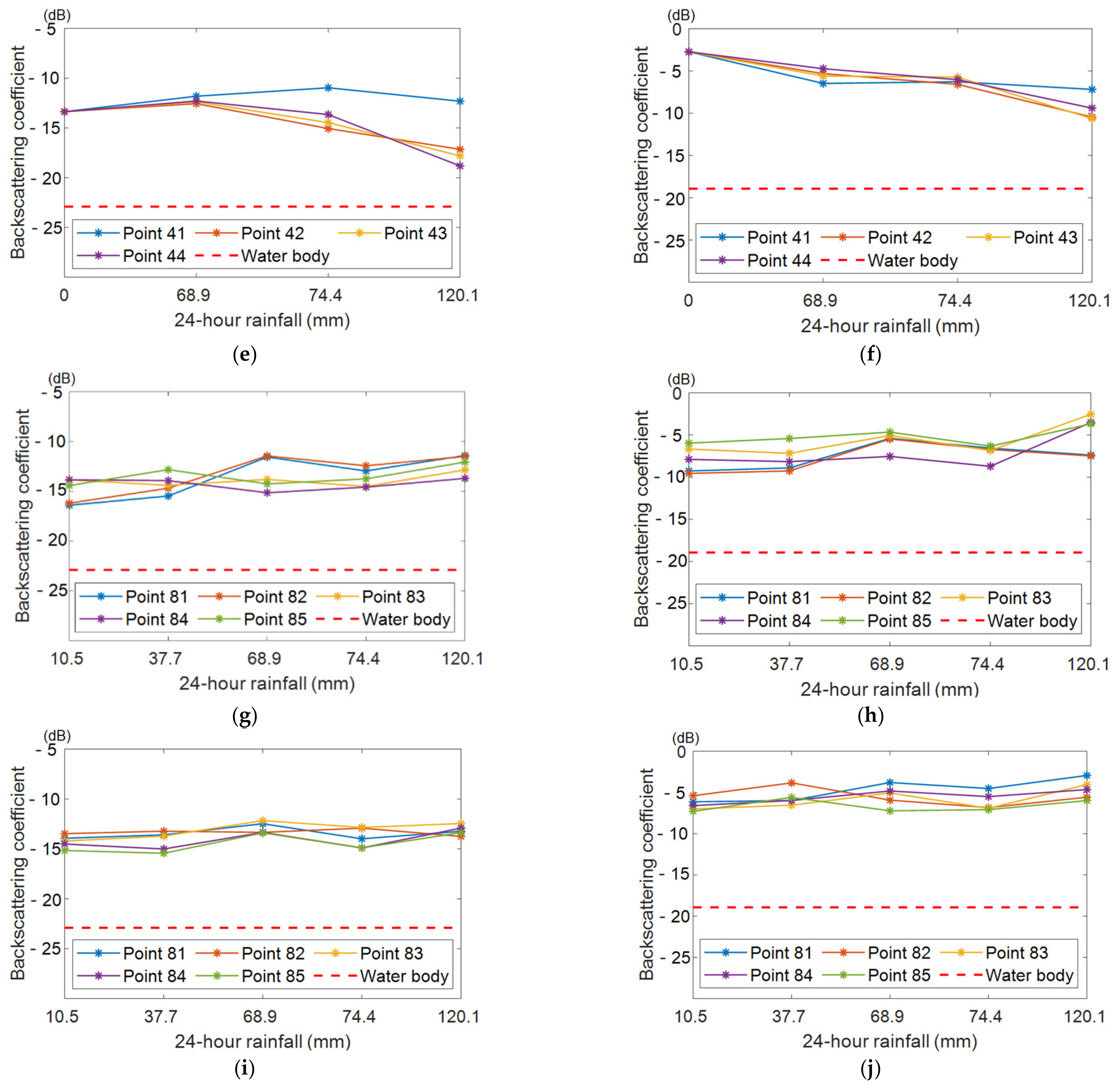
3.2.3. Backscattering Coefficient Change Rules for the Sample Points
3.3. Flood Extraction Rules Based on Sentinel-1
3.3.1. Selection of Representative Objects of Flood State
3.3.2. Flood Degree Estimation Rules of Ground Objects Based on Sentinel-1 Images
3.3.3. Flood Extraction Error Caused by Monthly Object Variation and Orbit Differences
3.3.4. Pre-Flood Reference Image Selection Rules
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Borah, S.B.; Sivasankar, T.; Ramya, M.N.S.; Raju, P.L.N. Flood inundation mapping and monitoring in Kaziranga National Park, Assam using Sentinel-1 SAR data. Environ. Monit. Assess. 2018, 190, 520. [Google Scholar] [CrossRef] [PubMed]
- Grimaldi, S.; Xu, J.; Li, Y.; Pauwels, V.; Walker, J. Flood mapping under vegetation using single SAR acquisitions. Remote Sens. Environ. 2020, 237, 111582. [Google Scholar] [CrossRef]
- Zhang, Y.-P.; Jiang, L.-M.; Qiu, Y.-B.; Wu, S.-L.; Shi, J.-C.; Zhang, L.-X. Study of the microwave emissivity characteristics over different land cover types. Spectrosc. Spectr. Anal. 2010, 30, 1446–1451. [Google Scholar]
- Guccione, P.; Lombardi, A.; Giordano, R. Assessment of seasonal variations of radar backscattering coefficient using sentinel-1 data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3402–3405. [Google Scholar] [CrossRef]
- Schlaffer, S.; Chini, M.; Giustarini, L.; Matgen, P. Probabilistic mapping of flood-induced backscatter changes in SAR time series. Int. J. Appl. Earth Obs. Geoinf. 2017, 56, 77–87. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Z.; Tian, B.; Zhou, J.; Tang, P. The backscattering characteristics of wetland vegetation and water-level changes detection using multi-mode SAR: A case study. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 1–13. [Google Scholar] [CrossRef]
- Zhou, L. Extraction of Planting Structure and Analysis of Spatial-Temporal Distribution Characteristics in Irrigated Areas Based on Sentinel Data. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 10 June 2019. [Google Scholar]
- Pierdicca, N.; Pulvirenti, L.; Boni, G.; Squicciarino, G.; Chini, M. Mapping Flooded Vegetation Using COSMO-SkyMed: Comparison With Polarimetric and Optical Data Over Rice Fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2650–2662. [Google Scholar] [CrossRef]
- Schlaffer, S.; Matgen, P.; Hollaus, M.; Wagner, W. Flood detection from multi-temporal SAR data using harmonic analysis and change detection. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 15–24. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M. Urban flood mapping with an active self-learning convolutional neural network based on TerraSAR-X intensity and interferometric coherence. ISPRS J. Photogramm. Remote Sens. 2019, 152, 178–191. [Google Scholar] [CrossRef]
- Martinis, S.; Rieke, C. Backscatter Analysis Using Multi-Temporal and Multi-Frequency SAR Data in the Context of Flood Mapping at River Saale, Germany. Remote Sens. 2015, 7, 7732–7752. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Huang, S.; Li, J.; Ling, X.; Ma, J.; Qu, W. The Downstream flood monitoring application of Myanmar Irrawaddy River based on Sentinel-1A SAR. Remote Sens. Technol. Appl. 2017, 32, 282–288. [Google Scholar] [CrossRef]
- Hess, L.L.; Melack, J.M. Remote sensing of vegetation and flooding on Magela Creek Floodplain (Northern Territory, Australia) with the SIR-C synthetic aperture radar. Hydrobiologia 2003, 500, 65–82. [Google Scholar] [CrossRef]
- Voormansik, K.; Praks, J.; Antropov, O.; Jagomagi, J.; Zalite, K. Flood Mapping With TerraSAR-X in Forested Regions in Estonia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 562–577. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Pierdicca, N.; Chini, M.; Guerriero, L. Monitoring Flood Evolution in Vegetated Areas Using COSMO-SkyMed Data: The Tuscany 2009 Case Study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1807–1816. [Google Scholar] [CrossRef]
- Kundu, S.; Aggarwal, S.P.; Kingma, N.C.; Mondal, A.; Khare, D. Flood monitoring using microwave remote sensing in a part of Nuna river basin, Odisha, India. Nat. Hazards 2015, 76, 123–138. [Google Scholar] [CrossRef]
- Richards, J.A.; Woodgate, P.W.; Skidmore, A.K. An explanation of enhanced radar backscattering from flooded forests. Int. J. Remote Sens. 1987, 8, 1093–1100. [Google Scholar] [CrossRef]
- Bhogapurapu, N.; Dey, S.; Bhattacharya, A.; Mandal, D.; Lopez-Sanchez, J.M.; McNairn, H.; López-Martínez, C.; Rao, Y. Dual-polarimetric descriptors from Sentinel-1 GRD SAR data for crop growth assessment. ISPRS J. Photogramm. Remote Sens. 2021, 178, 20–35. [Google Scholar] [CrossRef]
- Ezzine, A.; Darragi, F.; Rajhi, H.; Ghatassi, A. Evaluation of Sentinel-1 data for flood mapping in the upstream of Sidi Salem dam (Northern Tunisia). Arab. J. Geosci. 2018, 11, 170. [Google Scholar] [CrossRef]
- Zhang, B.; Wdowinski, S.; Gann, D.; Hong, S.-H.; Sah, J. Spatiotemporal variations of wetland backscatter: The role of water depth and vegetation characteristics in Sentinel-1 dual-polarization SAR observations. Remote Sens. Environ. 2022, 270, 112864. [Google Scholar] [CrossRef]
- Jo, M.-J.; Osmanoglu, B.; Zhang, B.; Wdowinski, S. Flood extent mapping using dual-polarimetric sentinel-1 synthetic aperture radar imagery. In Proceedings of the ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 7–10 May 2018; Volume XLII-3. [Google Scholar] [CrossRef] [Green Version]
- Grimaldi, S.; Li, Y.; Pauwels, V.R.N.; Walker, J.P. Remote Sensing-Derived Water Extent and Level to Constrain Hydraulic Flood Forecasting Models: Opportunities and Challenges. Surv. Geophys. 2016, 37, 977–1034. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Conde, F.C.; Muñoz, M.D.M. Flood Monitoring Based on the Study of Sentinel-1 SAR Images: The Ebro River Case Study. Water 2019, 11, 2454. [Google Scholar] [CrossRef] [Green Version]
- The China Meteorological Data Service Center. Available online: http://data.cma.cn (accessed on 30 December 2020).
- Chen, C.; Zhao, N.; Yue, T.; Guo, J. A generalization of inverse distance weighting method via kernel regression and its application to surface modeling. Arab. J. Geosci. 2014, 8, 6623–6633. [Google Scholar] [CrossRef] [Green Version]
- Maleika, W. Inverse distance weighting method optimization in the process of digital terrain model creation based on data collected from a multibeam echosounder. Appl. Geomat. 2020, 12, 397–407. [Google Scholar] [CrossRef]
- Zhang, D.-H.; Li, X.-R.; Zhang, F.; Zhang, Z.-S.; Chen, Y.-L. Effects of rainfall intensity and intermittency on woody vegetation cover and deep soil moisture in dryland ecosystems. J. Hydrol. 2016, 543, 270–282. [Google Scholar] [CrossRef]
- Haiyan, D.; Haimei, W. Influence of rainfall events on soil moisture in a typical steppe of Xilingol. Phys. Chem. Earth Parts A/B/C 2021, 121, 102964. [Google Scholar] [CrossRef]
- Babaei, S.; Ghazavi, R.; Erfanian, M. Urban flood simulation and prioritization of critical urban sub-catchments using SWMM model and PROMETHEE II approach. Phys. Chem. Earth Parts A/B/C 2018, 105, 3–11. [Google Scholar] [CrossRef]
- Ma, B.; Wu, Z.; Hu, C.; Wang, H.; Xu, H.; Yan, D.; Soomro, S.-E. Process-oriented SWMM real-time correction and urban flood dynamic simulation. J. Hydrol. 2022, 605, 127269. [Google Scholar] [CrossRef]
- Yazdi, M.N.; Ketabchy, M.; Sample, D.J.; Scott, D.; Liao, H. An evaluation of HSPF and SWMM for simulating streamflow regimes in an urban watershed. Environ. Model. Softw. 2019, 118, 211–225. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. A local thresholding approach to flood water delineation using Sentinel-1 SAR imagery. ISPRS J. Photogramm. Remote Sens. 2020, 159, 53–62. [Google Scholar] [CrossRef]
- Shi, W.; Huang, M.; Gongadze, E.; Wu, L. A Modified SCS-CN Method Incorporating Storm Duration and Antecedent Soil Moisture Estimation for Runoff Prediction. Water Resour. Manag. 2017, 31, 1713–1727. [Google Scholar] [CrossRef]
- Khzr, B.O.; Ibrahim, G.R.F.; Hamid, A.A.; Ail, S.A. Runoff estimation using SCS-CN and GIS techniques in the Sulaymaniyah sub-basin of the Kurdistan region of Iraq. Environ. Dev. Sustain. 2022, 24, 2640–2655. [Google Scholar] [CrossRef]
- Shi, Z.-H.; Chen, L.-D.; Fang, N.-F.; Qin, D.-F.; Cai, C.-F. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- Walega, A.; Amatya, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 100645. [Google Scholar] [CrossRef]
- Walega, A.; Salata, T. Influence of land cover data sources on estimation of direct runoff according to SCS-CN and modified SME methods. Catena 2019, 172, 232–242. [Google Scholar] [CrossRef]
- Liu, W.; Feng, Q.; Wang, R.; Chen, W. Effects of initial abstraction ratios in SCS-CN method on runoff prediction of green roofs in a semi-arid region. Urban For. Urban Green. 2021, 65, 127331. [Google Scholar] [CrossRef]
- Kumar, A.; Kanga, S.; Taloor, A.K.; Singh, S.K.; Đurin, B. Surface runoff estimation of Sind river basin using integrated SCS-CN and GIS techniques. HydroResearch 2021, 4, 61–74. [Google Scholar] [CrossRef]
- Costa-Cabral, M.C.; Burges, S.J. Digital Elevation Model Networks (DEMON): A model of flow over hillslopes for computation of contributing and dispersal areas. Water Resour. Res. 1994, 30, 1681–1692. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Jimenez-Hornero, F.J.; de Ravé, E.G. Influence of DEM resolution on drainage network extraction: A multifractal analysis. Geomorphology 2015, 241, 243–254. [Google Scholar] [CrossRef]
- Li, J.; Li, T.; Zhang, L.; Sivakumar, B.; Fu, X.; Huang, Y.; Bai, R. A D8-compatible high-efficient channel head recognition method. Environ. Model. Softw. 2020, 125, 104624. [Google Scholar] [CrossRef]
- Guth, N.; Klingel, P. Demand Allocation in Water Distribution Network Modelling—A GIS-Based Approach Using Voronoi Diagrams with Constraints. In Application of Geographic Information Systems; Alam, B.M., Ed.; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Jin, S. A methodology for simple 2-D inundation analysis in urban area using SWMM and GIS. Nat. Hazards 2019, 97, 15–43. [Google Scholar] [CrossRef]
- Bi, J.; Huang, H.; Liu, Y. Flood Trace Extraction and Flood Inundation Estimation Using Remote Sensing and GIS. Remote Sens. Inf. 2016, 31, 147–152. [Google Scholar] [CrossRef]
- Long, S.; Fatoyinbo, T.; Policelli, F. Flood extent mapping for Namibia using change detection and thresholding with SAR. Environ. Res. Lett. 2014, 9, 035002. [Google Scholar] [CrossRef]


| Category | Water | Grassland | Cultivated Land | Construction | Road |
|---|---|---|---|---|---|
| CN | 100 | 69 | 71 | 98 | 98 |
| Polarization | Category | Mean | STD | Maximum | Minimum | D-Value |
|---|---|---|---|---|---|---|
| VH | Water body | −22.2 | 2.2 | −16.6 | −24.2 | 7.6 |
| Farmland | −19.2 | 2.6 | −15.0 | −22.1 | 7.1 | |
| Farmland with plastic sheds | −13.9 | 0.5 | −12.8 | −14.8 | 2.0 | |
| Road | −15.0 | 0.3 | −14.3 | −15.5 | 1.1 | |
| Construction | −14.4 | 0.3 | −13.9 | −14.8 | 1.0 | |
| VV | Water body | −17.0 | 2.6 | −11.6 | −19.4 | 7.8 |
| Farmland | −11.6 | 1.9 | −8.4 | −13.8 | 5.4 | |
| Farmland with plastic sheds | −3.1 | 0.7 | −2.2 | −4.3 | 2.1 | |
| Road | −8.5 | 0.5 | −7.5 | −9.4 | 2.0 | |
| Construction | −6.4 | 0.2 | −6.1 | −6.7 | 0.6 |
| Polarization | Mean | STD | |||
|---|---|---|---|---|---|
| Category | VH | VV | Absolute Value of D-Value | VH | VV |
| Water body | −22.2 | −17.0 | 5.2 | −17.0 | 2.6 |
| Farmland | −19.2 | −11.6 | 7.7 | −11.6 | 1.9 |
| Farmland with plastic sheds | −13.9 | −3.1 | 10.8 | −3.1 | 0.7 |
| Road | −15.0 | −8.5 | 6.5 | −8.5 | 0.5 |
| Construction | −14.4 | −6.4 | 8.0 | −6.4 | 0.2 |
| Max D-value | 8.3 | 13.9 | |||
| Polarization | Category | Mean | Std | |||
|---|---|---|---|---|---|---|
| Ascending Orbit | Descending Orbit | D-Value | Ascending Orbit | Descending Orbit | ||
| VH | Water body | −21.4 | −23.1 | −1.7 | 2.2 | 2.2 |
| Farmland | −18.6 | −19.9 | −1.4 | 2.5 | 2.8 | |
| Farmland with plastic sheds | −13.5 | −14.3 | −0.8 | 0.5 | 0.6 | |
| Road | −15.6 | −14.4 | 1.2 | 0.8 | 0.4 | |
| Construction | −14.3 | −14.5 | −0.2 | 0.2 | 0.4 | |
| VV | Water body | −17.1 | −16.9 | 0.1 | 2.7 | 2.5 |
| Farmland | −11.5 | −11.6 | −0.1 | 2.0 | 1.9 | |
| Farmland with plastic sheds | −2.6 | −3.6 | −1.0 | 0.8 | 0.8 | |
| Road | −9.0 | −8.0 | 1.0 | 0.6 | 0.7 | |
| Construction | −6.4 | −6.3 | 0.1 | 0.3 | 0.3 | |
| Date | Satellite | Orbit | 0–24 h | 24–48 h | 48–72 h | 72–168 h | Sum of the First 72 h | Sum of the First 168 h |
|---|---|---|---|---|---|---|---|---|
| 2020.05.05 | S1-B | Descending | 10.5 | 5.2 | 0 | 0 | 15.7 | 15.7 |
| 2020.11.18 | S1-B | Descending | 37.7 | 8 | 0 | 0 | 45.7 | 45.7 |
| 2018.05.16 | S1-B | Descending | 68.9 | 3.5 | 0 | 0.1 | 72.4 | 72.5 |
| 2018.07.15 | S1-B | Descending | 74.4 | 16.1 | 0 | 5.7 | 90.5 | 96.2 |
| 2018.08.20 | S1-B | Descending | 120.1 | 41.3 | 21.2 | 45.4 | 182.6 | 228 |
| Rainfall Date | Satellite/Products (Date) | Mi River Runoff Status | Surface Inundation | |
|---|---|---|---|---|
| Before Rain | After Rain | |||
| 5 May 2020 | Planet/NDWI (6 May 2020) | Runoff is limited, and the water body is discontinuous | The same as before the rain | No completely inundated area |
| 18 November 2020 | Planet/NDWI (16 November 2020) | Runoff and water boys are limited | The same as before the rain | No completely inundated area |
| 16 May 2018 | Planet/NDWI (13 May 2020) | No runoff | No runoff | No completely inundated area |
| 15 July 2018 | Planet/NDWI (16 July 2018) | No runoff | No runoff | No completely inundated area |
| 20 August 2018 | Sentinel-1/VH (20 August 2018) | The river is full of water. | The water body is larger than before the flood | A large area is completely submerged |
| Category | ID | 18 November 2020 | 16 May 2018 | 15 July 2018 | 20 August 2018 |
|---|---|---|---|---|---|
| Farmland | 21 | 0.11 | 0.21 | 0.26 | 0.37 |
| 22 | 0.08 | 0.16 | 0.21 | 0.33 | |
| 23 | 0.09 | 0.16 | 0.19 | 0.29 | |
| 24 | 0.04 | 0.12 | 0.16 | 0.26 | |
| 25 | 0.10 | 0.18 | 0.22 | 0.32 | |
| Farmland with plastic sheds | 41 | -- | 0.02 | 0.06 | 0.17 |
| 42 | -- | 0.10 | 0.13 | 0.43 | |
| 43 | -- | 0.09 | 0.12 | 0.41 | |
| 44 | -- | 0.06 | 0.09 | 0.37 | |
| Road | 81 | 0.11 | 0.22 | 0.28 | 0.44 |
| 82 | 0.09 | 0.17 | 0.27 | 0.42 | |
| 83 | 0.12 | 0.24 | 0.31 | 0.50 | |
| 84 | 0.07 | 0.12 | 0.15 | 0.23 | |
| 85 | 0.01 | 0.07 | 0.10 | 0.18 | |
| Construction | 161 | 0.04 | 0.17 | 0.24 | 0.43 |
| 162 | 0.20 | 0.27 | 0.30 | 0.40 | |
| 163 | 0.05 | 0.12 | 0.16 | 0.25 | |
| 164 | 0.08 | 0.21 | 0.28 | 0.47 | |
| 165 | 0.05 | 0.16 | 0.22 | 0.38 |
| Polarization | Category | Min Gamma D-Value Due to Flood | Max Gamma D-Value Due to Monthly Variation | Gamma D-Value Due to Orbit |
|---|---|---|---|---|
| VH | Farmland | 1.2 | 7.1 | 1.4 |
| Farmland with plastic sheds | 2.5 | 2.0 | 0.8 | |
| Road | 0.2 | 1.1 | 1.2 | |
| Construction | 0.3 | 1.0 | 0.2 | |
| VV | Farmland | 2.8 | 5.4 | 0.1 |
| Farmland with plastic sheds | 7.3 | 2.1 | 1.0 | |
| Road | 1.8 | 2.0 | 1.0 | |
| Construction | 0.2 | 0.6 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Jin, S. Backscatter Characteristics Analysis for Flood Mapping Using Multi-Temporal Sentinel-1 Images. Remote Sens. 2022, 14, 3838. https://doi.org/10.3390/rs14153838
Huang M, Jin S. Backscatter Characteristics Analysis for Flood Mapping Using Multi-Temporal Sentinel-1 Images. Remote Sensing. 2022; 14(15):3838. https://doi.org/10.3390/rs14153838
Chicago/Turabian StyleHuang, Minmin, and Shuanggen Jin. 2022. "Backscatter Characteristics Analysis for Flood Mapping Using Multi-Temporal Sentinel-1 Images" Remote Sensing 14, no. 15: 3838. https://doi.org/10.3390/rs14153838
APA StyleHuang, M., & Jin, S. (2022). Backscatter Characteristics Analysis for Flood Mapping Using Multi-Temporal Sentinel-1 Images. Remote Sensing, 14(15), 3838. https://doi.org/10.3390/rs14153838