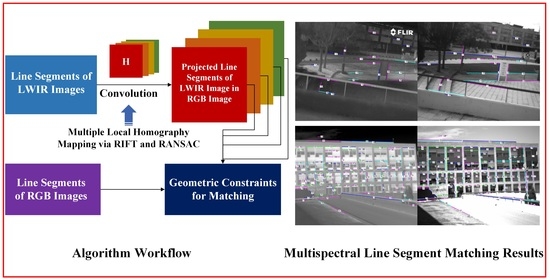
A Novel Multispectral Line Segment Matching Method Based on Phase Congruency and Multiple Local Homographies
Abstract
:1. Introduction
2. Related Works
2.1. Single-Spectral Feature Matching
2.2. Multispectral Feature Matching
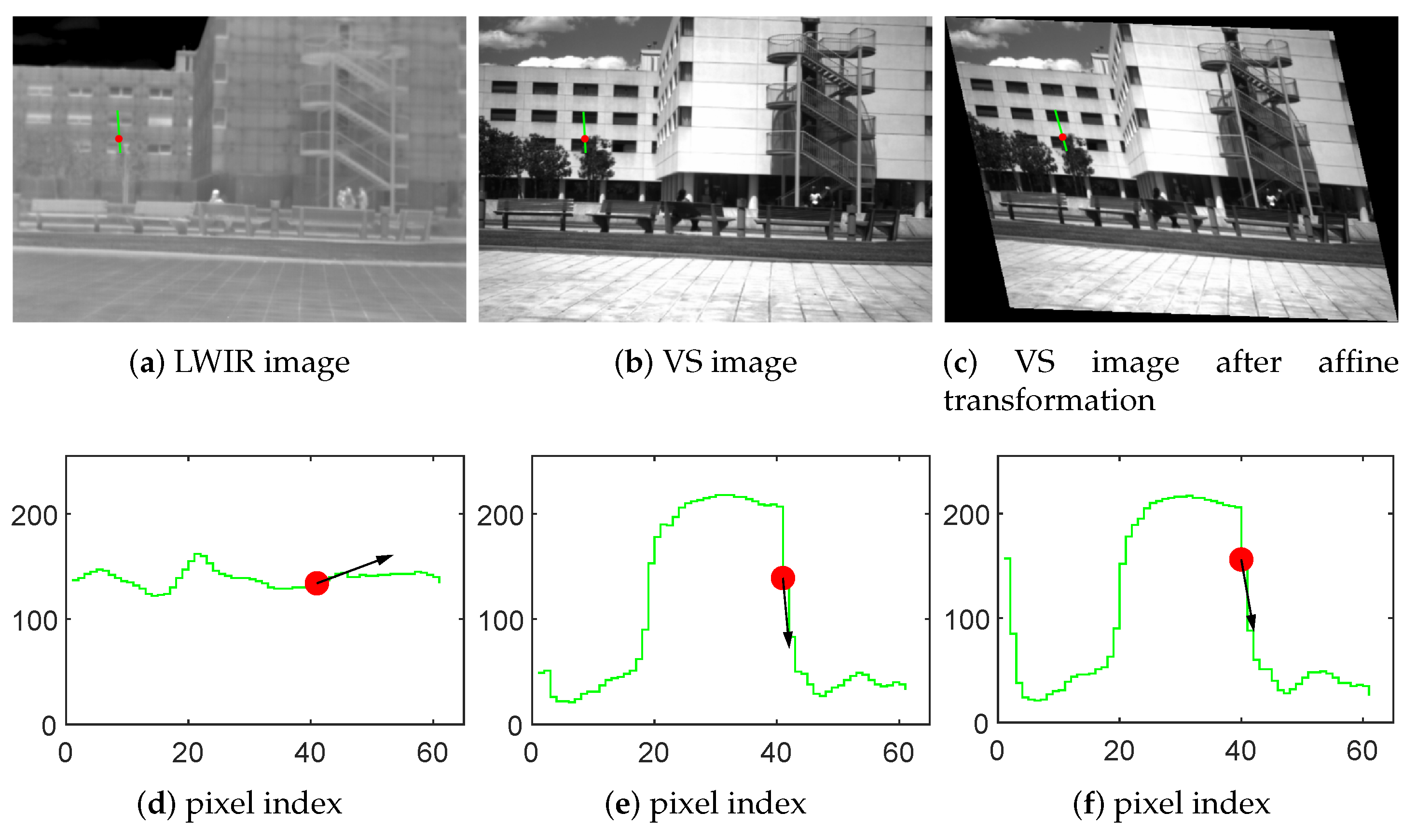
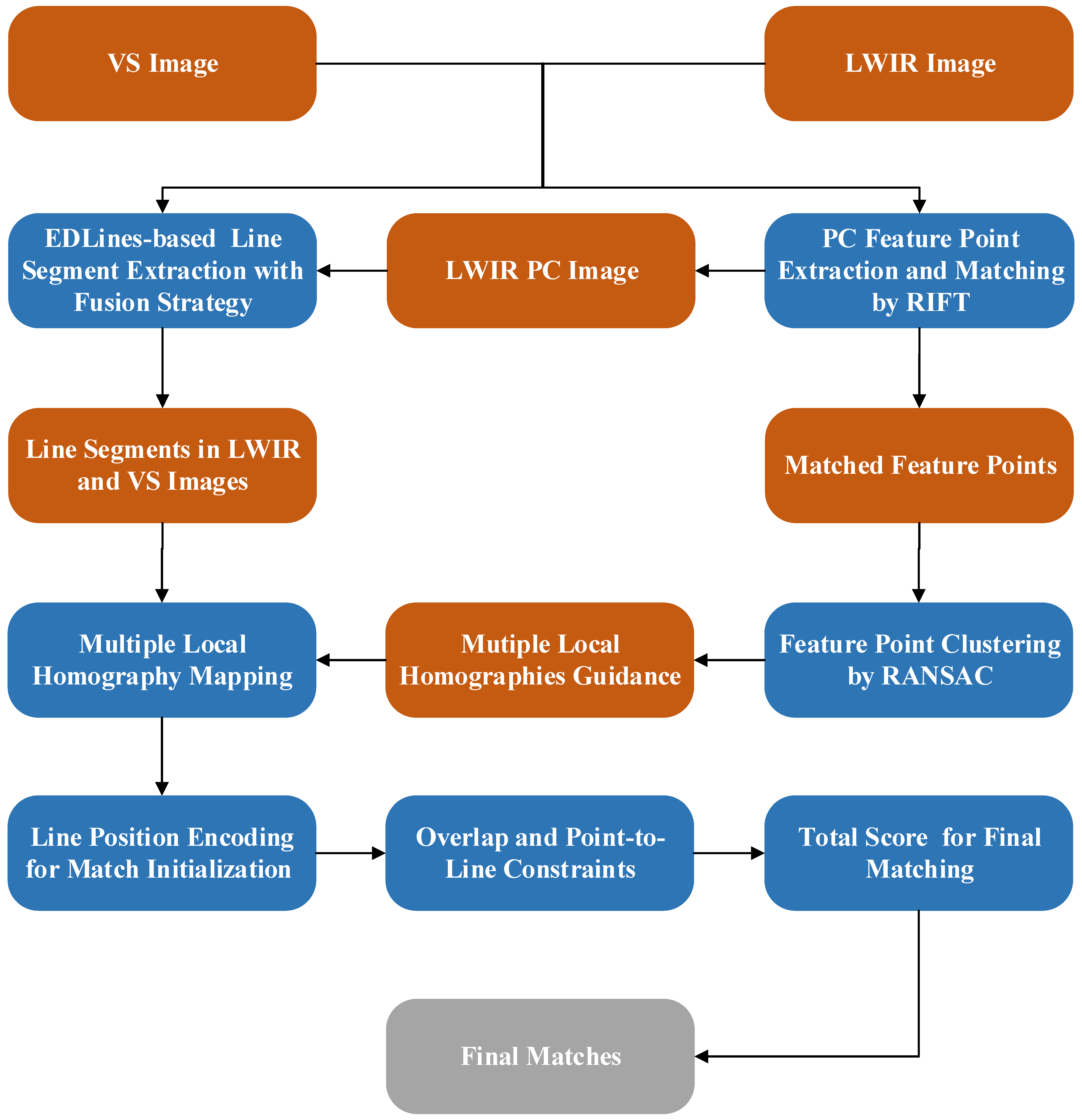
3. Methodology
3.1. Feature Point Matching and Clustering
3.1.1. PC and Feature Point Matching
3.1.2. Clustering of the Matched Multispectral Feature Points
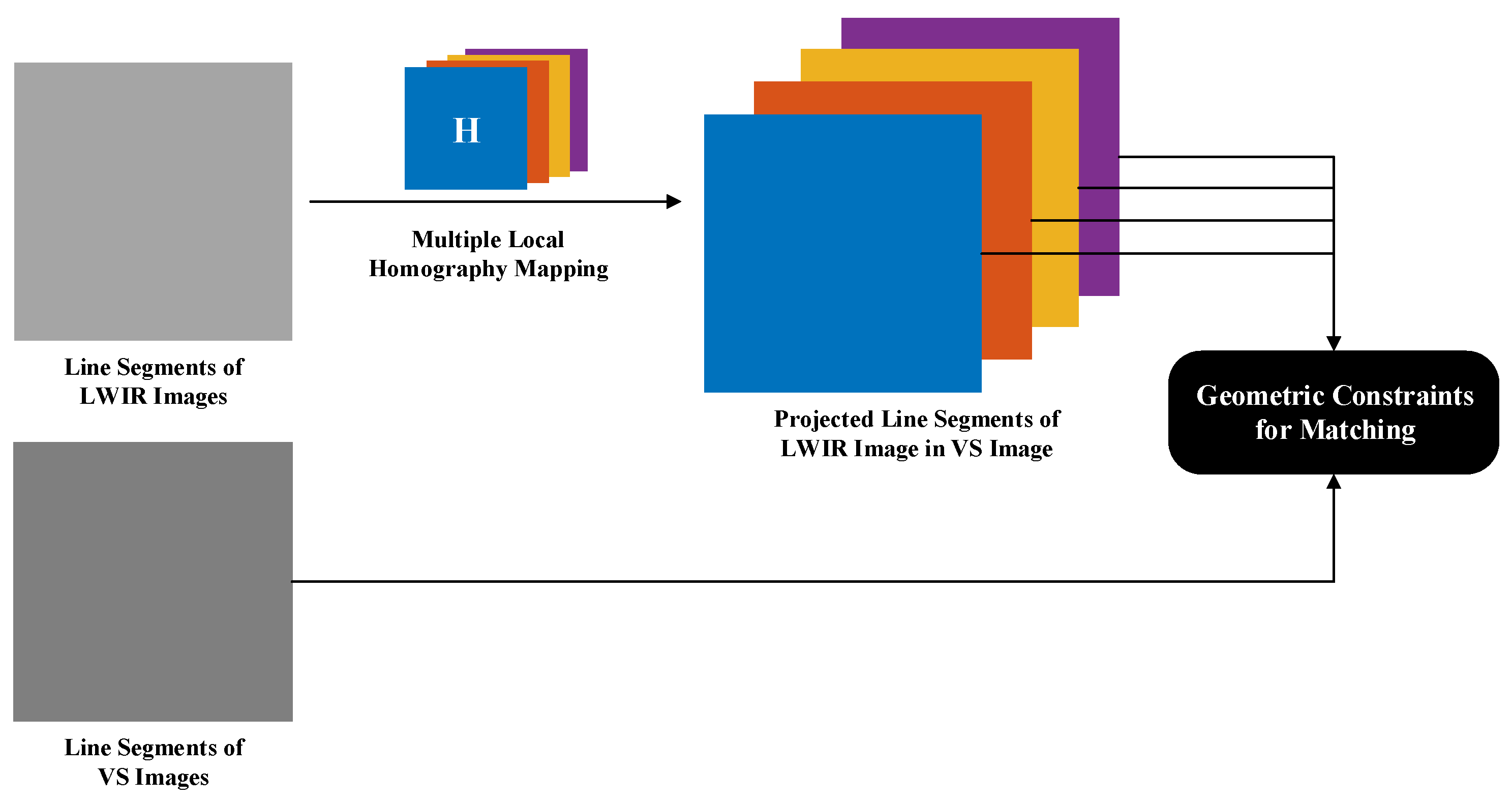
3.2. Line Segment Fusion and Multi-Layer Local Homography Mapping
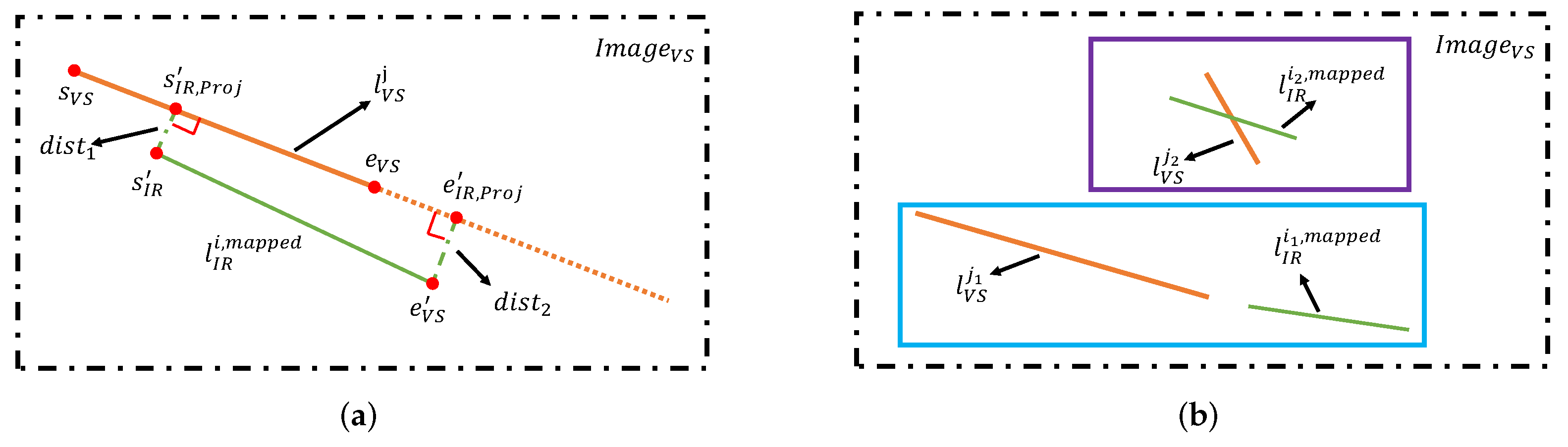
3.3. Geometric Constraints for Matching Candidates Selection
| Algorithm 1 PC-MLH for Multispectral Line Segment Matching |
|
4. Experiment Results
4.1. Datasets and Evaluation Criterion
4.2. Parameters Analysis
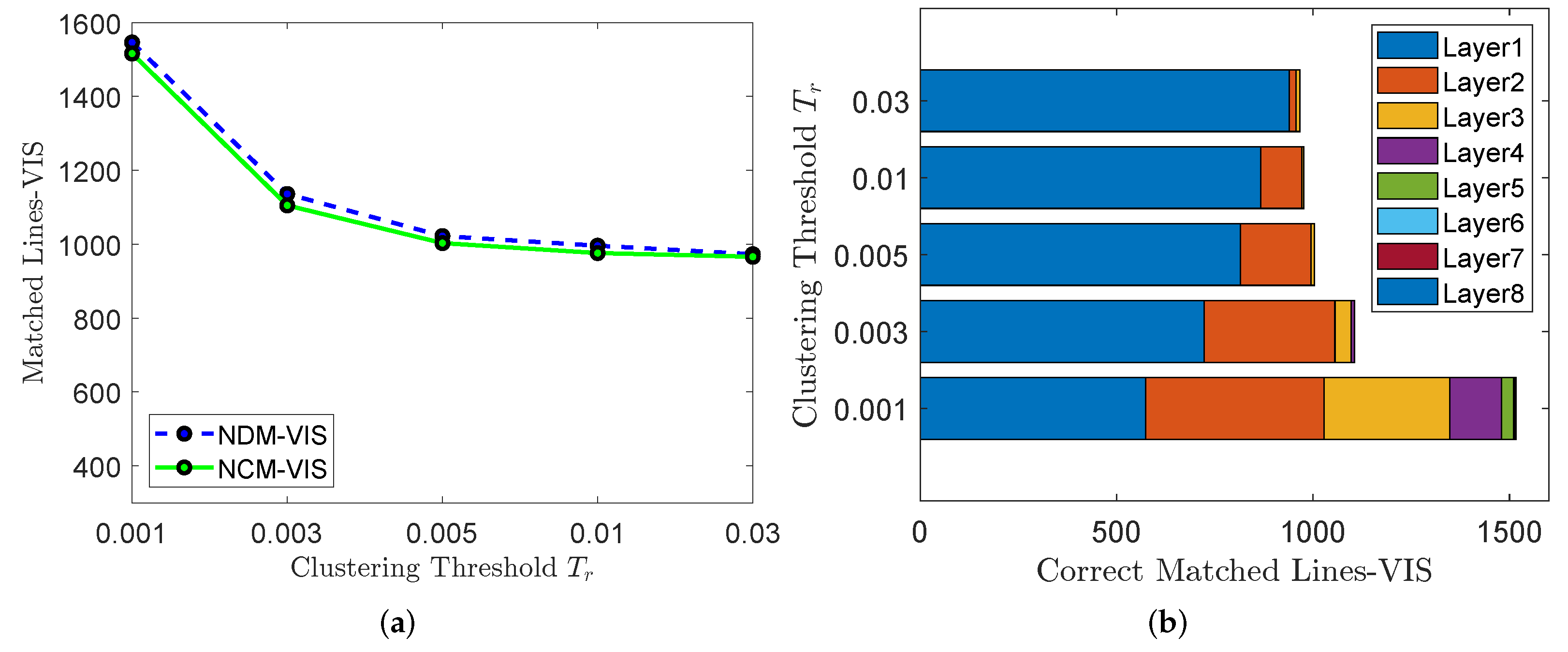
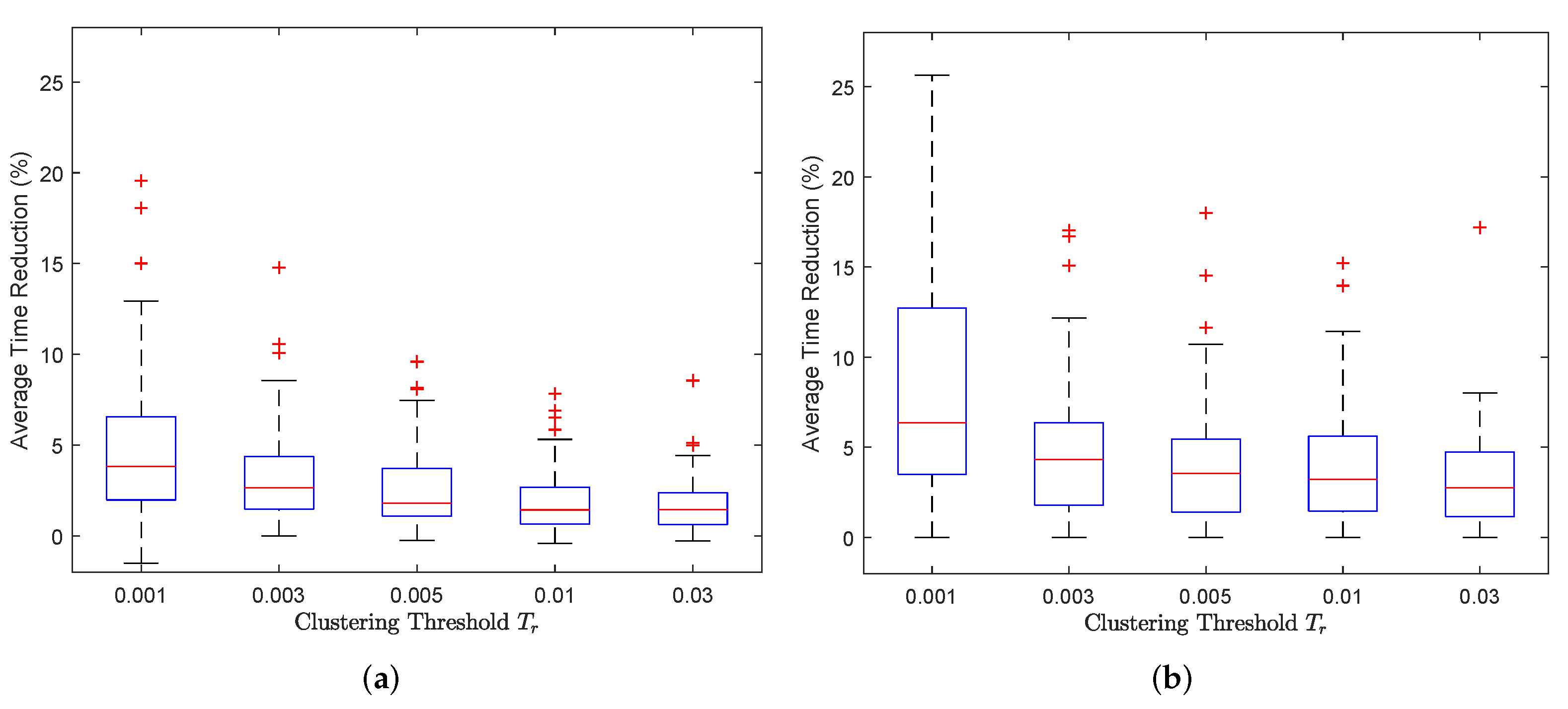
4.2.1. Clustering Threshold
4.2.2. Line Detection Threshold and Parameters of Line Position Encoding
4.2.3. Matching Thresholds , , ,
4.3. Matching Performance Comparison
4.4. Limitation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PC | Phase Congruency |
| MLH | Multiple Local Homographies |
| RANSAC | RANdom SAmple Consensus |
| NRD | Nonlinear Radiation Distortion |
| PCM | Percentage of Correct Matching |
| IR | Infrared |
| VS | Visible Spectrum |
| NIR | Near-Infrared |
| MWIR | Middle-Wavelength Infrared |
| LWIR | Long-Wavelength Infrared |
| LJL | Line-Junction-Line |
| LS | Line Signature |
| LBD | Line Band Descriptor |
| EOH | Edge-Oriented Histogram |
| LG filter | Log-Gabor filter |
| NCM | Number of Correct Matches |
| NDM | Number of Detected Matches |
References
- Wang, L.; Neumann, U.; You, S. Wide-baseline image matching using line signatures. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 1311–1318. [Google Scholar]
- Li, K.; Yao, J.; Lu, X.; Li, L.; Zhang, Z. Hierarchical line matching based on line–junction–line structure descriptor and local homography estimation. Neurocomputing 2016, 184, 207–220. [Google Scholar] [CrossRef]
- Zhang, L.; Koch, R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency. J. Vis. Commun. Image Represent. 2013, 24, 794–805. [Google Scholar] [CrossRef]
- Zhang, G.; Lee, J.H.; Lim, J.; Suh, I.H. Building a 3-D line-based map using stereo SLAM. IEEE Trans. Robot. 2015, 31, 1364–1377. [Google Scholar] [CrossRef]
- Gomez-Ojeda, R.; Moreno, F.A.; Zuniga-Noël, D.; Scaramuzza, D.; Gonzalez-Jimenez, J. PL-SLAM: A stereo SLAM system through the combination of points and line segments. IEEE Trans. Robot. 2019, 35, 734–746. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.H.; Wu, P.T.; Fu, L.C. Robust 2D indoor localization through laser SLAM and visual SLAM fusion. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 1263–1268. [Google Scholar]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM integrated navigation system based on graph optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Duan, J.; Ai, P.; Chen, Z.; Yang, Z.; Zou, X. Rachis detection and three-dimensional localization of cut off point for vision-based banana robot. Comput. Electron. Agric. 2022, 198, 107079. [Google Scholar] [CrossRef]
- Wang, H.; Lin, Y.; Xu, X.; Chen, Z.; Wu, Z.; Tang, Y. A Study on Long-Close Distance Coordination Control Strategy for Litchi Picking. Agronomy 2022, 12, 1520. [Google Scholar] [CrossRef]
- Khattak, S.; Papachristos, C.; Alexis, K. Visual-thermal landmarks and inertial fusion for navigation in degraded visual environments. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–9. [Google Scholar]
- Chen, L.; Sun, L.; Yang, T.; Fan, L.; Huang, K.; Xuanyuan, Z. Rgb-t slam: A flexible slam framework by combining appearance and thermal information. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5682–5687. [Google Scholar]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform. IEEE Trans. Image Process. 2019, 29, 3296–3310. [Google Scholar] [CrossRef]
- Nunes, C.F.; Pádua, F.L. A local feature descriptor based on log-Gabor filters for keypoint matching in multispectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1850–1854. [Google Scholar] [CrossRef]
- Li, S.; Lv, X.; Ren, J.; Li, J. A Robust 3D Density Descriptor Based on Histogram of Oriented Primary Edge Structure for SAR and Optical Image Co-Registration. Remote Sens. 2022, 14, 630. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Hu, Z. MSLD: A robust descriptor for line matching. Pattern Recognit. 2009, 42, 941–953. [Google Scholar] [CrossRef]
- Verhagen, B.; Timofte, R.; Van Gool, L. Scale-invariant line descriptors for wide baseline matching. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Steamboat Springs, CO, USA, 24–26 March 2014; pp. 493–500. [Google Scholar]
- Li, K.; Yao, J. Line segment matching and reconstruction via exploiting coplanar cues. ISPRS J. Photogramm. Remote Sens. 2017, 125, 33–49. [Google Scholar] [CrossRef]
- Li, Y.; Wang, F.; Stevenson, R.; Fan, R.; Tan, H. Reliable line segment matching for multispectral images guided by intersection matches. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2899–2912. [Google Scholar] [CrossRef]
- Chen, M.; Yan, S.; Qin, R.; Zhao, X.; Fang, T.; Zhu, Q.; Ge, X. Hierarchical line segment matching for wide-baseline images via exploiting viewpoint robust local structure and geometric constraints. ISPRS J. Photogramm. Remote Sens. 2021, 181, 48–66. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. Surf: Speeded up robust features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 224–236. [Google Scholar]
- Fan, B.; Wu, F.; Hu, Z. Robust line matching through line–point invariants. Pattern Recognit. 2012, 45, 794–805. [Google Scholar] [CrossRef]
- Al-Shahri, M.; Yilmaz, A. Line matching in wide-baseline stereo: A top-down approach. IEEE Trans. Image Process. 2014, 23, 4199–4210. [Google Scholar]
- Jia, Q.; Gao, X.; Fan, X.; Luo, Z.; Li, H.; Chen, Z. Novel coplanar line-points invariants for robust line matching across views. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 599–611. [Google Scholar]
- Wang, J.; Zhu, Q.; Liu, S.; Wang, W. Robust line feature matching based on pair-wise geometric constraints and matching redundancy. ISPRS J. Photogramm. Remote Sens. 2021, 172, 41–58. [Google Scholar] [CrossRef]
- Lange, M.; Schweinfurth, F.; Schilling, A. Dld: A deep learning based line descriptor for line feature matching. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 5910–5915. [Google Scholar]
- Zhang, H.; Luo, Y.; Qin, F.; He, Y.; Liu, X. ELSD: Efficient Line Segment Detector and Descriptor. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 2969–2978. [Google Scholar]
- Shen, X.; Xu, L.; Zhang, Q.; Jia, J. Multi-modal and multi-spectral registration for natural images. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 309–324. [Google Scholar]
- Brown, M.; Süsstrunk, S. Multi-spectral SIFT for scene category recognition. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 177–184. [Google Scholar]
- Aguilera, C.; Barrera, F.; Lumbreras, F.; Sappa, A.D.; Toledo, R. Multispectral image feature points. Sensors 2012, 12, 12661–12672. [Google Scholar] [CrossRef] [Green Version]
- Aguilera, C.A.; Sappa, A.D.; Toledo, R. LGHD: A feature descriptor for matching across non-linear intensity variations. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 178–181. [Google Scholar]
- Ma, T.; Ma, J.; Yu, K. A local feature descriptor based on oriented structure maps with guided filtering for multispectral remote sensing image matching. Remote Sens. 2019, 11, 951. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Zhao, H.; Lv, J.; Sun, S.; Li, B. Multimodal image matching based on multimodality robust line segment descriptor. Neurocomputing 2016, 177, 290–303. [Google Scholar] [CrossRef]
- Kovesi, P. Image features from phase congruency. Videre J. Comput. Vis. Res. 1999, 1, 1–26. [Google Scholar]
- Ye, Y.; Shan, J.; Bruzzone, L.; Shen, L. Robust registration of multimodal remote sensing images based on structural similarity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2941–2958. [Google Scholar] [CrossRef]
- Liu, X.; Ai, Y.; Zhang, J.; Wang, Z. A novel affine and contrast invariant descriptor for infrared and visible image registration. Remote Sens. 2018, 10, 658. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Xue, N.; Zhang, Y.; Lu, Q.; Xia, G.S. Robust visible-infrared image matching by exploiting dominant edge orientations. Pattern Recognit. Lett. 2019, 127, 3–10. [Google Scholar] [CrossRef]
- Aguilera, C.A.; Aguilera, F.J.; Sappa, A.D.; Aguilera, C.; Toledo, R. Learning cross-spectral similarity measures with deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1–9. [Google Scholar]
- Aguilera, C.A.; Sappa, A.D.; Aguilera, C.; Toledo, R. Cross-spectral local descriptors via quadruplet network. Sensors 2017, 17, 873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Stevenson, R.L. Multimodal image registration with line segments by selective search. IEEE Trans. Cybern. 2016, 47, 1285–1298. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Jin, H.; Wang, F.; Zhang, G.; Li, Y. Combining and matching keypoints and lines on multispectral images. Infrared Phys. Technol. 2019, 96, 316–324. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Zhang, P. A New Line Matching Approach for High-Resolution Line Array Remote Sensing Images. Remote Sens. 2022, 14, 3287. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Akinlar, C.; Topal, C. EDLines: A real-time line segment detector with a false detection control. Pattern Recognit. Lett. 2011, 32, 1633–1642. [Google Scholar] [CrossRef]
- Barrera, F.; Lumbreras, F.; Sappa, A.D. Multispectral piecewise planar stereo using Manhattan-world assumption. Pattern Recognit. Lett. 2013, 34, 52–61. [Google Scholar] [CrossRef]





| ANHL-CVC | 3.59 | 2.15 | 1.68 | 1.42 | 1.06 |
| ANHL-VIS | 3.25 | 1.84 | 1.40 | 1.25 | 1.09 |
| ANHL-ALL | 3.49 | 2.06 | 1.60 | 1.37 | 1.07 |
| NDM | NCM | PCM-CVC (%) | PCM-ALL (%) | |
|---|---|---|---|---|
| LBD | 838 | 116 | 13.55 | 13.84 |
| LS | 2004 | 727 | 33.48 | 36.28 |
| LSM-IM | - | - | 67.69 | - |
| PC-MLH | 2613 | 2456 | 88.10 | 93.99 |
| Clustering Threshold | Avg. Total (s) | Avg RIFT Consuming (%) | Max. (s) | Lower Quarter (s) | Upper Quarter (s) |
|---|---|---|---|---|---|
| CVC-0.001 | 10.30 | 91.81 | 17.59 | 6.88 | 12.66 |
| VIS-0.001 | 13.03 | 85.61 | 19.55 | 10.05 | 15.09 |
| CVC-0.003 | 9.54 | 96.73 | 14.39 | 6.72 | 11.74 |
| VIS-0.003 | 12.97 | 97.21 | 19.20 | 10.15 | 15.16 |
| CVC-0.005 | 9.54 | 97.13 | 13.63 | 6.80 | 11.89 |
| VIS-0.005 | 12.80 | 97.15 | 19.91 | 9.96 | 14.66 |
| CVC-0.01 | 9.51 | 97.31 | 14.09 | 6.67 | 11.88 |
| VIS-0.01 | 12.85 | 97.36 | 19.69 | 10.16 | 14.83 |
| CVC-0.03 | 9.45 | 97.33 | 13.97 | 6.70 | 11.70 |
| VIS-0.03 | 12.81 | 97.38 | 19.97 | 9.92 | 14.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Li, B.; Yang, W.; Wen, C.-Y. A Novel Multispectral Line Segment Matching Method Based on Phase Congruency and Multiple Local Homographies. Remote Sens. 2022, 14, 3857. https://doi.org/10.3390/rs14163857
Hu H, Li B, Yang W, Wen C-Y. A Novel Multispectral Line Segment Matching Method Based on Phase Congruency and Multiple Local Homographies. Remote Sensing. 2022; 14(16):3857. https://doi.org/10.3390/rs14163857
Chicago/Turabian StyleHu, Haochen, Boyang Li, Wenyu Yang, and Chih-Yung Wen. 2022. "A Novel Multispectral Line Segment Matching Method Based on Phase Congruency and Multiple Local Homographies" Remote Sensing 14, no. 16: 3857. https://doi.org/10.3390/rs14163857
APA StyleHu, H., Li, B., Yang, W., & Wen, C.-Y. (2022). A Novel Multispectral Line Segment Matching Method Based on Phase Congruency and Multiple Local Homographies. Remote Sensing, 14(16), 3857. https://doi.org/10.3390/rs14163857